Abstract
The spatiotemporal forecasting of temperature is a critical issue in meteorological prediction, with significant implications for fields such as agriculture and energy. With the rapid advancement of data-driven deep learning methods, deep learning-based spatiotemporal sequence forecasting models have seen widespread application in temperature spatiotemporal forecasting. However, statistical analysis reveals that temperature evolution varies across temporal and spatial scales due to factors like terrain, leading to a lack of existing temperature prediction models that can simultaneously learn both large-scale global features and small to medium-scale local features over time. To uniformly model temperature variations across different temporal and spatial scales, we propose the Multi-Scale Large Kernel Spatiotemporal Attention Neural Network (MSLKSTNet). This model consists of three main modules: a feature encoder, a multi-scale spatiotemporal translator, and a feature decoder. The core module of this network, Multi-scale Spatiotemporal Attention (MSSTA), decomposes large kernel convolutions from multi-scale perspectives, capturing spatial feature information at different scales, and focuses on the evolution of multi-scale spatial features over time, encompassing both global smooth changes and local abrupt changes. The results demonstrate that MSLKSTNet achieves superior performance, with a 35% improvement in the MSE metric compared to SimVP. Ablation studies confirmed the significance of the MSSTA unit for spatiotemporal forecasting tasks. We apply the model to the regional ERA5-Land reanalysis temperature dataset, and the experimental results indicate that the proposed method delivers the best forecasting performance, achieving a 42% improvement in the MSE metric over the widely used ConvLSTM model for temperature prediction. This validates the effectiveness and superiority of MSLKSTNet in temperature forecasting tasks.
1. Introduction
Accurate temperature forecasting holds significant importance in modern society. Precise temperature predictions help individuals and organizations mitigate the impacts of severe weather conditions [1,2]. By forecasting temperatures, people can better adapt to weather fluctuations [3], reduce risks, and enhance efficiency and productivity across various sectors. Temperature forecasting plays a crucial role [4] in agriculture [5,6], energy management [7], ecological environments [8], healthcare [9], and scientific research [10], significantly impacting societal development and sustainability. Therefore, in-depth analysis and prediction of temperature variations facilitate a better understanding of the dynamic patterns of climate systems, providing a scientific basis and decision support for effective climate change mitigation strategies.
Current mainstream weather forecasting methods are based on traditional Numerical Weather Prediction [11] (NWP). This approach utilizes mathematical equations to describe atmospheric motion and physical processes, solving them through numerical simulations. However, due to the complexity of atmospheric systems and the high precision required for forecasts, NWP methods necessitate the use of high-resolution grids to capture detailed information. This high-resolution grid not only increases computational demands but also requires substantial computational resources and storage capacity. Additionally, the inherent complexity of actual physical processes in the atmosphere means that parameterization models inevitably introduce simplifications and assumptions. Inaccuracies in initial conditions and limitations in parameter selection [12,13] can lead to model errors, thereby affecting the reliability of the final forecasts.
In recent years, the rapid advancement of data-driven deep learning methods has positioned deep learning-based weather forecasting as a powerful complement to traditional approaches [11]. Models for spatiotemporal sequence prediction [14] based on deep learning have been applied to temperature forecasting [15,16], effectively capturing spatiotemporal correlations and nonlinear features in temperature data. By learning from historical meteorological data, these models uncover hidden patterns and trends within the climate system, enabling predictions of future temperature changes. ConvLSTM [17] represents a pioneering development in spatiotemporal sequence prediction, extending fully connected LSTM (FC-LSTM) into Convolutional LSTM (ConvLSTM) to better capture spatiotemporal dependencies. Subsequent research based on ConvLSTM includes PredRNN [18], which introduces the Spatiotemporal LSTM unit (ST-LSTM) to simultaneously address spatial and temporal representations. Memory In Memory [19] (MIM) enhances ST-LSTM by effectively extracting non-stationary information. PredRNN++ [20] further advances this by incorporating a cascading MIN mechanism to create a new LSTM unit (Causal LSTM) and introduces the Gradient Highway Unit (GHU) to address gradient vanishing issues. Despite the impressive performance of these recurrent-based models, their complexity has increased with advancements. The CNN-based model SimVP [21], inspired by the Unet architecture, proposes a simplified model based on an Encoder–Translator–Decoder pure CNN network, achieving commendable results.
However, the challenges faced by spatiotemporal forecasting of temperatures using deep learning are more complex. This complexity arises because temperatures are influenced by terrain [22], resulting in large-scale plain land temperatures and small to medium-scale localized temperatures influenced by features such as valleys [23] and lakes. Generally, large-scale plain land temperatures tend to be more uniform, while valleys, canyons, and lakes create local climate effects. Understanding the patterns of temperature variations caused by terrain-influenced local climate effects and the overall changes in temperature across large plain land areas will be beneficial for improving temperature predictions. Figure 1 visualizes the temperature characteristics at different scales every 3 h, with the blue boxes outlining the temperature features at different scales. The dashed lines in the figure depict the temporal trends of the overall global features at different scales over time. Currently, deep learning-based spatiotemporal sequence forecasting lacks attention to the changes in multi-scale feature information and also lacks learning about the evolution of temporal dimension features.
Based on the aforementioned research, we propose an end-to-end neural network termed the Multi-Scale Large Kernel Spatiotemporal Attention Network (MSLKSTNet). This model comprises three primary components: a feature encoder, a multi-scale spatiotemporal translator, and a feature decoder. The feature encoder is designed to extract spatial features, while the core of the multi-scale spatiotemporal translator is the Multi-scale Spatiotemporal Attention (MSSTA) unit. The MSSTA unit decomposes large kernel convolutions from a multi-scale perspective to capture spatial features across various scales. It also incorporates a time-evolving attention module to discern spatial features with both global smooth changes and local prominent variations over time. The feature decoder integrates spatial information and temporal evolution patterns to achieve comprehensive spatiotemporal predictions. We assess the predictive performance of MSLKSTNet using the publicly available MovingMNIST and temperature datasets. The results demonstrate that MSLKSTNet outperforms existing models across multiple evaluation metrics on both datasets. Our work can be summarized as follows:
- We propose a novel multiscale large-kernel spatiotemporal prediction neural network, with the core being multiscale large-kernel spatiotemporal attention units. These units divide spatiotemporal attention into focusing on local and global features in spatial dimensions, as well as focusing on globally smooth and locally prominent evolution in temporal dimensions. This is crucial for capturing complex spatiotemporal dynamics;
- We conducted experiments on the MovingMNIST dataset to validate the model’s ability to capture spatiotemporal features. Dissolution experiments verified the effectiveness and feasibility of the network. To validate the effectiveness of the model in actual temperature prediction tasks, spatiotemporal predictions were performed on the Temperature dataset. We compared our method with mainstream spatiotemporal sequence prediction methods, and the experimental results showed that our method achieved the best predictive performance on both datasets.
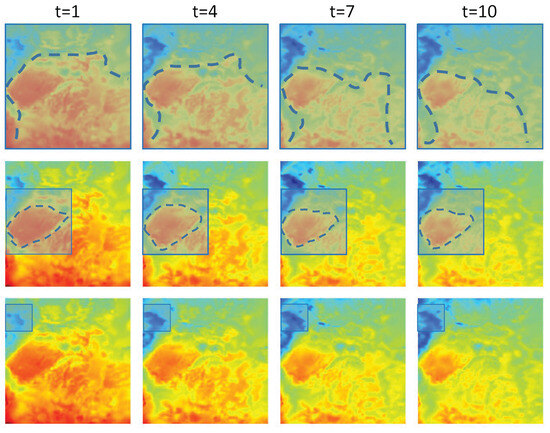
Figure 1.
Temporal evolution of temperature image features at different scales.
2. Related Works
2.1. Model
The development of spatiotemporal sequence prediction models has provided strong support and methodological foundations for spatiotemporal temperature forecasting. Currently, spatiotemporal sequence prediction model architectures are divided into stacked recurrent architectures and Encoder–Translator–Decoder architectures. As shown in Figure 2b, Convlstm [17] opens a new chapter in spatiotemporal sequence prediction based on stacked recurrent architecture, replacing fully connected (FC-LSTM) layers with convolutional layers to extract both temporal and spatial information, followed by a series of excellent models that further advance spatiotemporal sequence prediction. PredRNN [18] introduces a spatiotemporal LSTM unit (ST-LSTM) with a spatiotemporal memory state M for extracting and recalling spatiotemporal information. Based on Memory in Memory [19] analysis (MIM), which identifies stationary and non-stationary information in data, ST-LSTM adds MIM units to effectively extract non-stationary information. Predrnn++ [20] constructs a new LSTM unit (Causal LSTM) in a cascaded manner using the MIN mechanism and combines it with the Gradient Highway Unit (GHU) and causal LSTM to address gradient vanishing problems. E3D-LSTM [24] integrates 3D convolutions into RNNs to better preserve short-term features in memory units and builds a gated self-attention module enabling the current memory state to recall stored memories from multiple past time steps. PredRNNv2 [25] proposes a memory decoupling loss function to prevent memory units in PredRNN from learning redundant features, forming a serrated memory flow, enabling different levels of RNNs to exchange spatiotemporal dynamic information, and proposes a reverse sampling strategy to force the model to extract long-term spatiotemporal dynamic information from the contextual framework. SwinLSTM [26] argues that the property of convolutional neural networks learning local spatial features reduces the efficiency of learning spatiotemporal dependencies. SwinLSTM integrates Swin Transformer [27] modules into LSTM, replacing the convolutional structure in Convlstm with self-attention mechanisms, thereby improving the accuracy of spatiotemporal forecasting. Another architecture for spatiotemporal sequence prediction models is the Encoder–Translator–Decoder architecture, as shown in Figure 2a, further divided into two types: RNN as a translator and CNN as a translator, as shown in Figure 2c. The overall architecture uses convolutional neural networks as spatial encoders and decoders. CrevNet [28] proposes using PredRNN as a prediction unit for spatiotemporal prediction and utilizes reversible neural networks based on 3D convolutions for encoding and decoding inputs. PhyDNet [29] employs a similar architecture but constructs a new type of recurrent physical cell (phycell), forming two recurrent neural network branches, phycell, and Convlstm, executing partial differential equation constraints in latent space. SimVP [21] proposes a network architecture based on a pure CNN Encoder–Translator–Decoder structure, as shown in Figure 2d, where the encoder captures only the spatial features of single frames. The spatiotemporal translator learns the temporal evolution between frames, and the decoder integrates spatiotemporal information to complete the prediction.
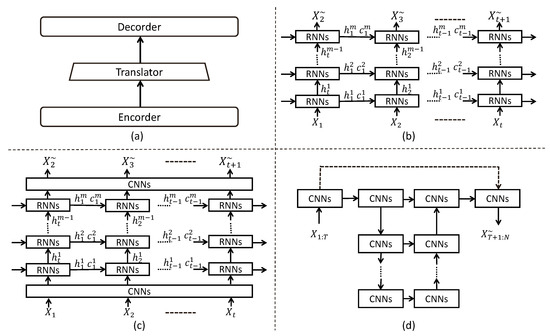
Figure 2.
Common architectures for spatiotemporal sequence prediction models, where RNNs represent Recurrent Neural Networks, and CNNs represent Convolutional Neural Networks. (a) encoder-translator-decoder architecture. (b) RNN. (c) CNN-RNN-CNN. (d) CNN-CNN-CNN.
Recent advancements in deep learning have significantly accelerated the development of spatiotemporal sequence forecasting [30]. Temperature spatiotemporal prediction represents a crucial application within this domain. In recent years, researchers have increasingly employed spatiotemporal sequence prediction models to tackle temperature forecasting challenges. SAVP [31] utilizes a stacked recurrent architecture ConvLSTM [32] to predict the 2 m temperature for the next 12 h and combines ConvLSTM, GAN [33], and VAE [34] architecture components to construct a novel prediction model, achieving superior performance compared to ConvLSTM in temperature spatiotemporal forecasting. Similarly based on ConvLSTM architecture, MFNet [16] introduces a novel LSTM unit MF-LSTM tailored for meteorological forecast (MF) tasks. It incorporates ESP loss to address the non-stationarity and data distribution imbalance in prediction tasks. Additionally, it employs Neural Architecture Search [35] (NAS) techniques for automated design of prediction structures, successfully forecasting U-component of wind, V-component of wind, Temperature, and Relative humidity. Primed Unet-LSTM [36] combines Unet [37] and LSTM [38] for temperature prediction tasks over the 850 hpa temperature dataset in WeatherBench [39], conducting 3-day and 5-day temperature prediction experiments. Efficient spatio-temporal weather forecasting using U-Net [15] applies Unet and its variants such as SmaAt-Unet [40] to temperature prediction, forecasting future 8-h spatiotemporal temperature features based on hourly temperature spatiotemporal data. HU-Net [17], composed of Unet modules with reparameterization techniques and feature extraction modules, focuses on both global and local features. It achieves higher forecast accuracy with faster inference speeds on the temperature dataset of the large-scale weather benchmark dataset WeatherBench [39] at a resolution of 1.40625°.
2.2. Visual Attention Mechanism
The attention mechanism can adaptively adjust the model’s attention weights based on the importance of different input features, allowing the model to focus on the most relevant parts of the input features. This mechanism was introduced into the computer vision field by RAM [41]. The attention mechanism has been widely used in computer vision, including tasks such as image classification [42,43], object detection [44,45], semantic segmentation [46], and pose estimation [26,47]. Due to the outstanding performance of self-attention in the NLP [15,16] field, ViT [48] introduced self-attention into the computer vision field to build the Vision Transformer, followed by a large number of scholars proposing variants. Since ViT is specifically designed for image classification, PVT [47] introduces the Pyramid Vision Transformer to overcome the challenges of porting the Transformer to various dense prediction tasks. DSTT [49] proposes a novel decoupled spatiotemporal transformer, which decouples Transformer blocks from temporal and spatial perspectives to build spatiotemporal attention, enabling the model to accurately handle background textures and moving objects. Swin Transformer [26] introduces a hierarchical construction method based on ViT and proposes Windows Multi-Head Self-Attention (W-MSA) to partition the feature map into multiple disjoint windows, reducing the computational complexity. However, this operation isolates the information transmission between different windows. Therefore, Shifted Windows Multi-Head Self-Attention (SW-MSA) is proposed to transmit feature information between adjacent windows, improving the model’s performance. Some scholars have also achieved good results by introducing self-attention into computer vision. However, the self-attention was originally designed for the NLP field. Van [50] believes that it treats images as one-dimensional sequences, which destroys the two-dimensional nature of images. Moreover, for high-resolution images, the quadratic complexity is too high. Van proposes a visual attention method that decomposes large kernel convolutions, called LKA, which has the advantages of both convolution and self-attention. It focuses on local contextual information and has long-range dependencies. However, it lacks the ability to capture local multiscale feature information and does not pay enough attention to the temporal evolution of features.
Existing spatiotemporal sequence prediction models for temperature forecasting often struggle with capturing either large-scale global features or multiscale local information. Additionally, these models frequently fall short of addressing short-term spatial variations within local data. To address these limitations, this paper introduces an end-to-end spatiotemporal prediction network, termed the Multi-Scale Large Kernel Spatiotemporal Attention Network (MSLKSTNet). The MSLKSTNet leverages a multiscale spatiotemporal attention module that decomposes large kernel convolutions into a combination of multiscale local depth convolutions, depth-wise dilated convolutions, and 1 × 1 convolutions. This decomposition allows the model to effectively capture both multiscale local and global information. Furthermore, the network incorporates temporal evolution attention to account for both gradual and abrupt temporal changes in spatial information.
3. Methods
3.1. Overall Architecture
The overall model structure is illustrated in Figure 3, following the Encoder–Translator–Decoder architecture. The Encoder consists of Ns layers of Conv2D, GroupNorm, and SiLU, while the Decoder is similarly composed of Ns layers of Conv2D, PixelShuffle, GroupNorm, and SiLU. The Translator is positioned between the Encoder and Decoder, consisting of a stack of Nt MSLKA units. Given a batch of input data with dimensions (B, T, C, H, W), where B represents the batch size, T denotes the temporal length of the input, C is the number of channels, and H and W are the width and height of each frame’s temperature grid data, respectively, the Encoder reshapes the data to (B*T, C, H, W). The Encoder focuses on capturing the feature information of individual frames without considering temporal evolution between frames. Upon entering the spatiotemporal translator, we reshape the spatially extracted features from the Encoder to (B, T*C, H, W). The spatiotemporal translator then learns the changes between frames and the patterns of spatiotemporal evolution. Before proceeding to the Decoder, the data dimensions are reshaped back to (B*T, C, H, W), similarly to the Encoder, ignoring temporal changes. From the spatial perspective, the Decoder integrates the spatiotemporal evolution features learned from the translator to predict future frames, with output dimensions matching the input dimensions (B, T, C, H, W). The challenge of spatiotemporal sequence prediction lies in addressing spatial information at various scales—local, mid-level, and global—and learning how this spatial information evolves over time. The MSSTA unit, as the core module of the translator for learning multi-scale spatiotemporal evolution, jointly models temporal and spatial information across different time and space scales. The MSSTA unit is detailed in Section 3.2.
3.2. Multi-Scale Spatiotemporal Attention Unit
Attention mechanisms allow models to selectively highlight or prioritize specific parts of the input data. In the context of spatiotemporal temperature prediction, these mechanisms must not only capture spatial temperature features across various locations and scales at each time point but also learn the temporal evolution of critical temperature information across different time steps. This necessitates simultaneous attention to both spatial and temporal changes in feature information. While self-attention mechanisms [48,51,52,53] have received widespread attention in the field of computer vision, they were initially used in natural language processing. In computer vision, they treat images as one-dimensional sequences, which compromises the two-dimensional nature of images, and they lack channel adaptivity and attention to local information. LKA decomposes large kernel convolutions, possessing the ability to capture local feature information, long-range dependencies, and channel and spatial adaptivity. However, it lacks the capture of local multiscale feature information and the ability to capture the temporal evolution of important feature information between frames, which is crucial for the task of spatiotemporal temperature prediction.
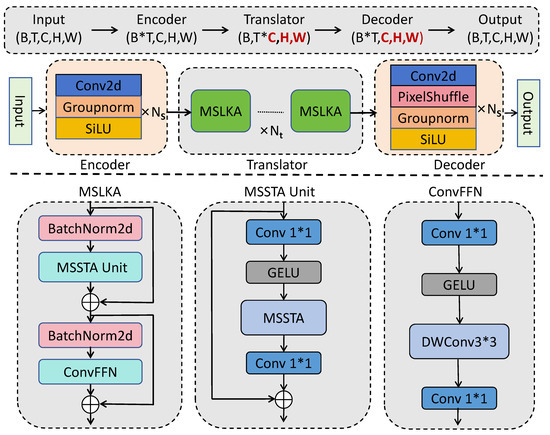
Figure 3.
The overall structure of MSLKSTNet is divided into three parts: Encoder, Translator, and Decoder. At the top are the changes in input data dimensions in each part, where red indicates changes in C, H, and W after passing through the convolutional network.
To address the aforementioned issue, we decompose large kernel convolutions and construct Multi-scale Spatial Attention and Temporal Evolution Attention (MSSA, TEA). MSSA focuses on feature information changes from a multi-scale perspective. As shown in Figure 4, large kernel convolutions are decomposed into three parts: Multi-scale Spatial Local Convolution (Depthwise Convolution), Spatial Dilated Convolution (Depthwise Dilated Convolution), and Channel Convolution (1 × 1 Convolution). Specifically, the multi-scale spatial local convolutions segment the input data into four parts along the channel dimension, applying depth-wise convolutions with kernel sizes of 3 × 3, 5 × 5, 7 × 7, and 9 × 9. The results of these convolutions are concatenated along the channel dimension to form the input for the subsequent processing step. Spatial dilated convolutions use a kernel size of 11 × 11 with a dilation rate of 2 for depth-wise dilated convolutions. Channel convolutions employ a kernel size of 1 × 1 for standard convolutions. Multi-scale spatial local depth-wise convolutions focus on multi-scale local contextual information, spatial dilated convolutions capture long-range dependencies and global feature information, and point convolutions capture inter-channel relationships, enabling information exchange across the channel dimension. Subsequently, temporal evolution attention (TEA) is employed to capture temporal evolution among frames, dividing temporal evolution attention into Gradual Temporal Evolution Attention (GTEA) and Abrupt Temporal Evolution Attention (ATEA). GTEA focuses on minor changes in overall regional features over time, aiding in learning the temporal evolution patterns of global features, while ATEA focuses on significant changes in local regional features over time, aiding in learning prominent changes in local features. The Multi-scale Spatiotemporal Attention Unit (MSSTA) is depicted in Figure 5, and the calculation formula for the MSSTA module is shown in the following Equation (1):
where is the hidden features input to the MSSTA module, , . represents the spatial feature attention, and represent temporal evolution attention. Conv refers to 2D convolution. Avgpool and Maxpool represent average pooling and max pooling. ⊗ denotes the Kronecker product, ⊙ denotes the Hadamard product.
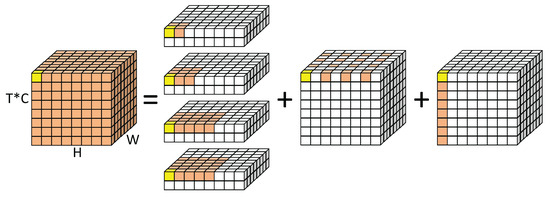
Figure 4.
Decomposition diagram of large kernel convolutions, where large kernel convolutions are divided into three parts: Depthwise Convolution (DW-Conv), Depthwise Dilated Convolution (DW-D-Conv), and Pointwise Convolution (Conv1 × 1). The colored grids represent the location of convolution kernel and the yellow grid means the center point. Zero padding is ignored in the diagram. Colored grids represent the positions of convolution kernels, with yellow grids indicating the central position of the kernels. In the channel dimension, the data are divided into four parts, each undergoing DW-Conv with kernels of size (3, 5, 7, 9), followed by concatenation along the channel dimension and then DW-D-Conv with a kernel size of 7 and a dilation rate of 2, before finally applying Pointwise Convolution.
Overall, the model adheres to an Encoder–Translator–Decoder architecture, with MSSTA serving as the core of the Translator. Its role is to focus on multi-scale spatiotemporal evolution and learn the patterns of feature changes across different temporal and spatial scales. We compare it with currently prominent attention mechanisms, including Self-Attention and LKA. Self-Attention, originally developed for the NLP domain, has been recently adapted for computer vision with promising results. However, Self-Attention treats images as one-dimensional sequences, which disrupts their inherent two-dimensional characteristics and incurs excessive quadratic complexity for high-resolution images. The LKA method proposed by Van combines the advantages of convolution and Self-Attention, addressing both local information and long-range dependencies. However, it falls short of capturing local multi-scale features and the temporal evolution of features. As shown in Table 1, we introduce multi-scale large-kernel convolutions and temporal evolution attention into MSSTA, enabling it to maintain local receptive fields and long-range dependencies. It also has the capability to focus on the feature information of individual frames from a multi-scale perspective while simultaneously capturing the temporal evolution between frames.

Table 1.
Desirable properties belonging to Self-attention, LKA and MSSTA.
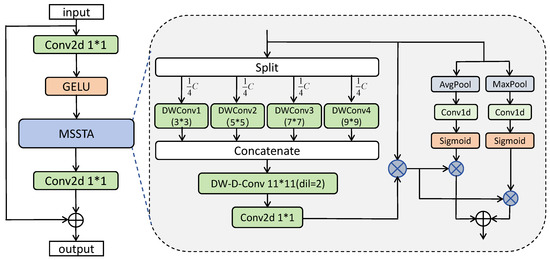
Figure 5.
The structure of the MSSTA (Multi-scale Spatiotemporal Attention) module.
4. Experiments
To assess the model’s proficiency in capturing spatiotemporal information evolution, we evaluated it using the MovingMNIST [54] dataset, a widely recognized benchmark for spatiotemporal prediction tasks, and conducted ablation experiments. Furthermore, we applied the model to the ERA5-Land regional reanalysis temperature dataset [55], which allowed us to further confirm its superior effectiveness in real-world spatiotemporal temperature prediction scenarios. We summarize the statistics of the aforementioned data in Table 2, including the number of training samples and testing samples , as well as the input data shape (C, T, H, W) and output data shape (C, , H, W), C represents the number of channels in the input data, represent the length and width of the input sequence, T and denote the length of the input sequence and the predicted output sequence, respectively. Furthermore, we compared our model with the current state-of-the-art methods on the aforementioned datasets in terms of metrics and provided visual examples to demonstrate the generalization ability and effectiveness of our model across different datasets.

Table 2.
The statistics of datasets.
All experiments were conducted on a server running the Windows 11 operating system. We utilized PyTorch 1.12.0 as the deep learning framework, with programming carried out in Python 3.8.16. The relevant supporting libraries included numpy 1.23.5, timm 0.6.13, matplotlib 3.7.3, and torch 1.12.0. The experiments were performed on a single NVIDIA A100 GPU with 80 GB of memory, and the training was conducted using Mean Squared Error (MSE) loss. For experiments on the MovingMNIST dataset, we referenced the model parameters set in SimVP [21]. We used 16 video sequences as a batch input to the model and trained it with the Adam optimizer [56], setting the learning rate to 0.001. During testing, we selected four video sequences as a batch. We employed the OneCycleLR [57] learning rate adjustment strategy and halted training after 2000 epochs. When applied to the Temperature dataset, the model consisted of four encoder and decoder layers, with 16 channels in the hidden layers of both the encoder and decoder. We included 10 MSST unit layers, and the translator had 256 channels in the hidden layers. Similarly, we used 16 video sequences as a batch input to the model and trained it with the Adam optimizer. However, the learning rate adjustment strategy was switched to the CosineLRScheduler [58], with a learning rate of 0.001. During testing, we selected eight video sequences as a batch and stopped training after 30 epochs.
4.1. Evaluation Index
On the MovingMNIST dataset, we evaluated the results using widely accepted [19,20,21,24,25,26] and recognized evaluation metrics MSE, MAE, and SSIM. On the Temperature dataset, we assessed the prediction results using MSE, MAE, and RMSE, which are commonly used for evaluating meteorological element predictions [16,17,36,39,59].
MAE calculates the average of the absolute differences between predicted and actual values. The calculation formula for MAE is shown in the following Equation (2):
where n represents the number of pixels in the image, denotes the true value, represents the predicted value. A smaller MAE indicates a smaller difference between the model’s prediction and the actual observed values.
SSIM measures the similarity of structural information within the spatial neighborhood and is used in video prediction to measure the structural similarity between the frames generated by the model and the reference frames. The calculation formula for SSIM is shown in the following Equation (3):
In SSIM, x represents the true value, y denotes the predicted value, is the mean of the true values, is the mean of the predicted values, is the variance of the true values, is the variance of the predicted values, is the covariance between the true and predicted values. The constants and are used to maintain stability,, , , , L is the dynamic range of pixel values. The SSIM ranges from −1 to 1, with SSIM equal to 1 only when .
MSE calculates the average of the squared differences between predicted and actual values. The calculation formula for MSE is shown in the following Equation (4):
where n represents the number of pixels in the image, denotes the true value, represents the predicted value. The variable in RMSE is the same as in MSE, with the square root of MSE being taken, the calculation formula for RMSE is shown in the following Equation (5):
4.2. Experiments on MovingMNIST
The MovingMNIST dataset, one of the benchmark datasets for spatiotemporal prediction learning, has been widely utilized. Each video sequence consists of 20 frames, where the first ten frames serve as inputs and the subsequent ten frames serve as targets. Each frame comprises two handwritten digits within a 64 × 64 grid. These digits move within the grid, bouncing off the boundaries, thus altering their positions within the grid and generating the video sequence.
4.2.1. Experimental Results and Analysis
First, we evaluated our proposed method against recent strong baselines, as shown in Table 3. This includes competitive recurrent architectures as well as networks based on the Encoder–Translator–Decoder architecture. Our proposed model outperforms the state-of-the-art spatiotemporal prediction, SwinLSTM [26], based on a self-attention mechanism, by approximately 13% in terms of MSE (reducing MSE from 17.7 to 15.4). It also outperforms SimVP [21], a network based on a pure convolutional Encoder–Translator–Decoder architecture, by around 35% (reducing MSE from 23.8 to 15.4). Our method surpasses the above baselines on three different evaluation metrics. Additionally, we visualize the predicted results of the model, as shown in Figure 6, where the digits 2 and 4 transition from overlapping to separated and then overlapping again. The visualization results demonstrate that our method can capture the spatiotemporal distribution of sequential images as well as the trends in long-term and short-term motion changes. This approach enables more accurate prediction of future sequential images in the MovingMNIST dataset.

Table 3.
Quantitative results of different methods on the Moving MNIST dataset. ↓ (or ↑) means lower (or higher) is better. The best results are highlighted in bold.
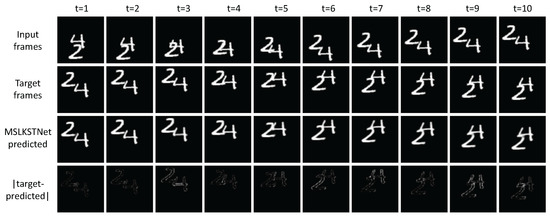
Figure 6.
Qualitative visualization of predicted results on MovingMNIST dataset.
4.2.2. Ablation Experiments
Ablation experiments refer to selectively removing components or functionalities of a neural network to evaluate their impact on the model’s performance. In this section, to validate the rationality of the network structure, we conducted ablation experiments on the MSSTA module of MSLKSTNet. Each comparison method was uniformly trained for 100 epochs, and the performance of each method was evaluated using the MSE, MAE, and SSIM metrics, as shown in Table 4.

Table 4.
Ablation study on different convolution combinations and decomposition of spatiotemporal attention in the MSSTA module of MSLKSTNet on Moving MNIST.
Method 1 employs LKA as a spatiotemporal translator. Comparing Method 1 with Method 2 demonstrates the importance of multi-scale spatial modeling. Comparing Method 2 with Method 3 shows that decomposing the large kernel convolution into a large-scale global depth-wise dilated convolution with a kernel size of 11 and dilation rate of 2 is superior to a kernel size of 7 and dilation rate of 3. Comparing Method 3 with Method 4 indicates that introducing a gentle spatiotemporal evolution attention can better learn the temporal evolution patterns of spatial features. Method 5 shows that separating the spatiotemporal evolution attention into multi-scale spatial attention and temporal evolution attention, and adding abrupt temporal evolution achieves the best results. The ablation experiments demonstrate that introducing multi-scale large kernel spatiotemporal attention improves the prediction performance.
4.3. Experiments on Temperature
Temperature spatiotemporal prediction is one of the crucial tasks in spatiotemporal prediction learning. Currently, traditional physics-based computational methods are constrained by computational capabilities when solving control equations on discrete numerical grids. Moreover, traditional methods are susceptible to uncertainties arising from initial conditions and parameterization choices, leading to increased errors. Hence, there is an urgent need for robust data-driven spatiotemporal prediction learning models to enhance the accuracy and efficiency of temperature forecasting. We applied the model to the temperature spatiotemporal prediction task using the ERA5-Land dataset (European Centre for Medium-Range Weather Forecasts Fifth Generation Reanalysis Land dataset). The ERA5 dataset has a spatial resolution of 0.1° × 0.1° for ground data and a temporal resolution of 1 h. To conduct a comprehensive analysis and reflect the current temperature change trends, data spanning from 2015 to 2023 were utilized. As shown in Figure 7, the selected geographical region covers longitudes from 115.7° E to 103.0° E and latitudes from 36.7° N to 24.0° N. Data from 2015 to 2021 were designated as the training set, 2022 data served as the validation set, and data from 2023 were used as the test set. All data underwent standardization to conform to a standard normal distribution. Consequently, the final input data shape is (12, 1, 128, 128), where the model is trained to predict the temperature for the next 12 h based on the past 12 h of temperature data.
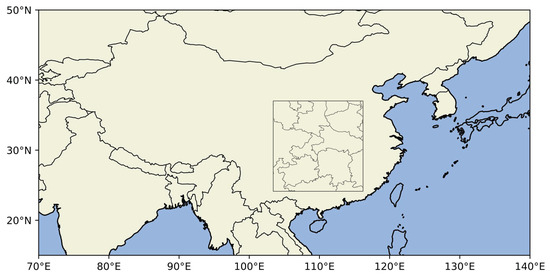
Figure 7.
Visualization of the study area in the Temperature dataset.
Experimental Results and Analysis
In this section, we compare the model proposed in this paper with the current state-of-the-art models applied to temperature spatiotemporal prediction, including the recurrent neural network ConvLSTM [32] and its variant PredRNNv2 [25]. We also contrast it with the convolutional neural networks UNet [15] and SmaAt-UNet [40], both applied to temperature spatiotemporal prediction. Given SimVP’s superiority [21] in other spatiotemporal prediction tasks, we also apply it to temperature spatiotemporal prediction. To ensure a fair comparison of model performance, we followed the experimental settings and training methods described in the literature. The quantitative results are shown in Table 5. We incorporated the large-kernel attention LKA from Van into SimVP to construct the En–Van–De model, which serves as a spatiotemporal translator. This approach improved the MSE metric by approximately 13% (from 1.989 to 1.719) compared to SimVP. Our model, MSLKSTNet, further enhances the large-kernel attention LKA from Van by integrating multi-scale convolutions and decomposing spatiotemporal attention into temporal and spatial attention components. This results in a 6% improvement in prediction performance over SimVP (MSE reduced from 1.719 to 1.619). The results demonstrate that our proposed method outperforms the baseline models in terms of MSE, MAE, and RMSE, indicating superior overall prediction performance.

Table 5.
Quantitative results of different methods on the Temperature dataset. The best results are highlighted in bold.
Figure 8 evaluates the performance of each model in terms of frame-wise predictions on the test set of the temperature dataset. As depicted in the figure, MSLKSTNet consistently outperforms other models in terms of both MSE and MAE metrics, with the exception of PredRNNv2. The predictive performance of MSLKSTNet for the first two hours is comparable to that of PredRNNv2; however, beyond this period, MSLKSTNet demonstrates significantly superior performance compared to PredRNNv2. Moreover, as the prediction horizon extends, the relative increase in prediction error for MSLKSTNet is smaller compared to that of PredRNNv2. This indicates that MSLKSTNet possesses a superior capability for long-term forecasting tasks. This advantage can be attributed to the inherent limitations of stack-based recurrent neural networks in learning long-term spatiotemporal dynamics, which often leads to the neglect of historical spatiotemporal information.
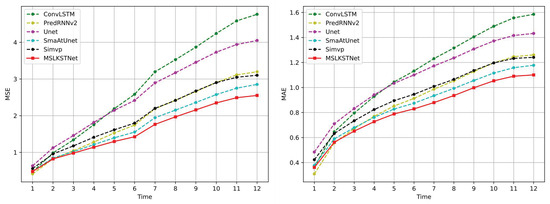
Figure 8.
The model trained on the fixed Temperature training set provides frame-wise predictions on the temperature test set.
As shown in Figure 9, we visualize the temperature predictions made by various models using data from the first 1–12 h to forecast temperatures for the subsequent 13–24 h. Additionally, we visualize the prediction errors for all models. While all models exhibit relatively small prediction errors at the 14th h, these errors increase as time progresses. However, MSLKSTNet demonstrates relatively lower growth in prediction errors compared to other models, indicating its superior ability to capture long-term spatial feature evolution. Furthermore, comparative analysis of prediction error visualizations reveals that MSLKSTNet outperforms other models in forecasting temperature features at both small and large scales. This further underscores MSLKSTNet’s superiority in capturing both overall global and multiscale local spatial information over time. The visualization of prediction results and errors suggests that our approach can more accurately capture the overall temperature trends and perform better in forecasting temperature features at small scales compared to other methods. Additionally, our model exhibits higher prediction accuracy as the forecast horizon increases, relative to other models.
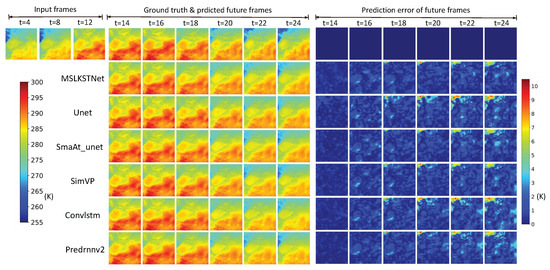
Figure 9.
Qualitative visualization of predicted results on temperature dataset.
5. Discussion
In this paper, we propose a novel spatiotemporal sequence prediction model that originates from the influence of geographical factors on temperature. Through statistical analysis of spatiotemporal temperature datasets, our model reveals the formation of large-scale plain landform temperature and small to medium-scale local temperature influenced by geographical factors. However, existing models either fail to capture large-scale global features or do not adequately address multiscale local information, and they often lack the capability to model short-term abrupt changes in local spatial data. In response to these limitations, we propose a spatiotemporal sequence prediction model featuring an Encoder–Translator–Decoder architecture. The encoder is used to extract spatial features. The core of the translator is the Multi-Scale Spatiotemporal Attention unit (MSSTA). Inspired by Van’s work [50], we introduce multiscale convolution into Large Kernel Attention (LKA) to construct a novel Large Kernel Multi-Scale Spatiotemporal Attention mechanism (MSSTA) from a multiscale perspective. MSSTA divides spatiotemporal evolution attention into spatial attention and temporal attention. Multiscale spatial attention focuses on spatial feature information from a multiscale perspective, while temporal evolution attention learns the spatial feature changes over time from the perspectives of smooth temporal evolution and abrupt temporal evolution. The decoder integrates the spatiotemporal sequence information learned by the translator to predict future frames. Our model better captures the complex evolution patterns in spatiotemporal data, thus improving the accuracy and stability of spatiotemporal sequence prediction.
In the experiments on the MovingMNIST dataset, MSLKSTNet achieved the best forecasting performance, thereby validating its exceptional capability in spatiotemporal sequence prediction tasks. The ablation experiments on the MovingMNIST dataset also validated the effectiveness of multiscale spatiotemporal motion modeling, with noticeable performance differences among various comparative methods, further emphasizing the importance of decomposing multiscale spatiotemporal attention into multiscale spatial attention and temporal attention. In the experiments on the Temperature dataset, MSLKSTNet achieved superior results in terms of MSE, MAE, and RMSE evaluation metrics. This indicates that the model exhibits stronger performance and generalization ability in handling temperature spatiotemporal prediction tasks. Additionally, MSLKSTNet utilizes multiscale large kernel convolution as the spatiotemporal translator, which enhances its capability to capture multiscale features influenced by factors such as terrain in temperature data. The experimental results validate the importance of capturing multiscale spatiotemporal evolution information. Through comparative analysis of experimental results on two distinct datasets, we clearly observe the robustness and efficiency of MSLKSTNet across various spatiotemporal sequence prediction tasks. The MovingMNIST dataset illustrates the model’s excellent predictive capability in handling motion sequences, while the Temperature dataset validates the model’s strong performance in temperature forecasting tasks. These results not only demonstrate the broad applicability of MSLKSTNet but also provide new breakthroughs and insights for research and practical applications in spatiotemporal sequence prediction. The successful application of MSLKSTNet highlights the potential of advanced multi-scale spatiotemporal modeling techniques in complex predictive tasks, with anticipated impact in future research. These findings open new research directions in the field of spatiotemporal sequence prediction and offer more precise and reliable solutions for related applications.
In the field of spatiotemporal sequence prediction, despite significant advancements made by deep learning models, there are still some challenges. Firstly, as the forecast horizon increases, the prediction accuracy of deep learning models tends to be affected, with errors gradually accumulating over time. This issue is particularly prominent for long-term spatiotemporal sequences, as models need to maintain accuracy over longer time spans, which is often a challenging task. To address this issue, researchers are exploring various methods such as introducing more complex model structures, optimizing training algorithms, and improving data preprocessing techniques to reduce error accumulation and enhance the accuracy of long-term predictions. Secondly, in the field of meteorological detection, the application of multi-meteorological element data extraction techniques is of significant importance. These techniques can not only extract feature information directly related to individual meteorological elements from historical data but also learn the coupling relationships between different meteorological elements. By combining feature information from different elements, more comprehensive and enriched feature representation can be obtained, thereby improving the accuracy and robustness of prediction models. For example, in meteorological forecasting tasks, besides using single meteorological element data to predict individual meteorological elements, consideration can also be given to the interactions between multiple meteorological elements, thus enabling more accurate prediction of future meteorological conditions.
6. Conclusions
Through statistical analysis of the spatiotemporal distribution and variation in temperature features, we found that temperature exhibits multiscale characteristics in spatial dimensions, and the temporal evolution patterns of temperature features vary across different scales. Learning the temporal evolution of multiscale spatial features is crucial for predicting results accurately. To address this, we designed the Multi-scale Large Kernel Spatiotemporal Attention Neural Network (MSLKSTNet), which compensates for the network’s lack of ability to capture multiscale features and learns the spatial feature evolution over time from the perspectives of gradual and abrupt changes. The backbone of the model consists of three parts: the feature encoder, the multiscale spatiotemporal translator, and the feature decoder. Specifically, the feature encoder extracts spatial features, transforming the input spatiotemporal data into high-dimensional feature representations. The core of the multiscale spatiotemporal change translator is the Multi-scale Spatiotemporal Attention (MSSTA) unit, which uses large kernel convolutions to decompose spatial features from multiple scales, capturing information at different scales, and constructs a time-evolving attention module to extract both global smooth changes and local abrupt changes in spatial features over time. The feature decoder combines spatial information and temporal evolution patterns to complete the prediction of spatiotemporal data. Experiments on the MovingMNIST dataset demonstrate that MSLKSTNet outperforms previous methods in terms of MSE, MAE, and SSIM indices. In comparative experiments with SimVP, it shows significant advantages, with a 35% improvement in the MSE metric and a 13% enhancement over the current best-performing recurrent neural network, SWinLSTM. Ablation studies further validate the effectiveness of the MSSTA unit design. Results on the temperature dataset indicate that our method surpasses existing approaches in MSE, MAE, and RMSE. Compared to ConvLSTM, which is widely used for temperature forecasting, the MSE metric improves by 42%, and compared to SimVP, it improves by 18%. These results further substantiate the efficacy of our novel spatiotemporal translation unit and its potential for application in spatiotemporal forecasting. The design and experimental outcomes of MSLKSTNet highlight the importance of focusing on multi-scale spatiotemporal feature evolution and provide an effective solution for spatiotemporal prediction tasks.
Author Contributions
Conceptualization, J.F., Y.Y. and F.G.; Data curation, J.F.; Funding acquisition, F.G. and C.L.; Investigation, J.F., F.G., Y.Y. and C.L.; Methodology, J.F.; Resources, F.G. and C.L.; Software, Y.Y.; Supervision, F.G., Y.Y. and C.L.; Validation, F.G., C.L. and Y.Y.; Visualization, J.F.; Writing—original draft, J.F.; Writing—review and editing, F.G., Y.Y. and C.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the National Key R&D Program of Heilongjiang Province (No. 2022ZX01A15), the Cultivation Project of Qingdao Science and Technology Plan Park (No. 23-1-55-yqpy-11-qy).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
Author Chang Liu was employed by the company Qingdao Hatran Ocean Intelligence Technology Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- O’Neill, M.S.; Ebi, K.L. Temperature extremes and health: Impacts of climate variability and change in the United States. J. Occup. Environ. Med. 2009, 51, 13–25. [Google Scholar] [CrossRef] [PubMed]
- Sun, C.; Jiang, Z.; Li, W.; Hou, Q.; Li, L. Changes in extreme temperature over China when global warming stabilized at 1.5 °C and 2.0 °C. Sci. Rep. 2019, 9, 14982. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, G. World view. Nature 2024, 627, 467. [Google Scholar] [CrossRef] [PubMed]
- Bidarmaghz, A.; Narsilio, G.A.; Johnston, I.W.; Colls, S. The importance of surface air temperature fluctuations on long-term performance of vertical ground heat exchangers. Geomech. Energy Environ. 2016, 6, 35–44. [Google Scholar] [CrossRef]
- Asseng, S.; Foster, I.; Turner, N.C. The impact of temperature variability on wheat yields. Glob. Chang. Biol. 2011, 17, 997–1012. [Google Scholar] [CrossRef]
- Mcclung, C.R.; Lou, P.; Hermand, V.; Kim, J.A. The importance of ambient temperature to growth and the induction of flowering. Front. Plant Sci. 2016, 7, 204980. [Google Scholar] [CrossRef]
- Khatib, T.; Mohamed, A.; Sopian, K. A review of solar energy modeling techniques. Renew. Sustain. Energy Rev. 2012, 16, 2864–2869. [Google Scholar] [CrossRef]
- Clarke, A. Principles of Thermal Ecology: Temperature, Energy and Life; Oxford University Press: Oxford, UK, 2017. [Google Scholar]
- Bertrand, I.; Schijven, J.; Sánchez, G.; Wyn-Jones, P.; Ottoson, J.; Morin, T.; Muscillo, M.; Verani, M.; Nasser, A.; de Roda Husman, A.; et al. The impact of temperature on the inactivation of enteric viruses in food and water: A review. J. Appl. Microbiol. 2012, 112, 1059–1074. [Google Scholar] [CrossRef]
- Richard, C.; Gratton, D. The importance of the air temperature variable for the snowmelt runoff modelling using the SRM. Hydrol. Process. 2001, 15, 3357–3370. [Google Scholar] [CrossRef]
- Bauer, P.; Thorpe, A.; Brunet, G. The quiet revolution of numerical weather prediction. Nature 2015, 525, 47–55. [Google Scholar] [CrossRef]
- Palmer, T.; Shutts, G.; Hagedorn, R.; Doblas-Reyes, F.; Jung, T.; Leutbecher, M. Representing model uncertainty in weather and climate prediction. Annu. Rev. Earth Planet. Sci. 2005, 33, 163–193. [Google Scholar] [CrossRef]
- Allen, M.R.; Kettleborough, J.; Stainforth, D. Model error in weather and climate forecasting. In Proceedings of the ECMWF Predictability of Weather and Climate Seminar; European Centre for Medium Range Weather Forecasts: Reading, UK, 2002; pp. 279–304. [Google Scholar]
- Shi, X.; Yeung, D.Y. Machine learning for spatiotemporal sequence forecasting: A survey. arXiv 2018, arXiv:1808.06865. [Google Scholar]
- Punjabi, A.; Ayala, P.I. Efficient spatio-temporal weather forecasting using U-Net. arXiv 2021, arXiv:2112.06543. [Google Scholar]
- Zhang, X.; Jin, Q.; Xiang, S.; Pan, C. MFNet: The spatio-temporal network for meteorological forecasting with architecture search. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1006605. [Google Scholar] [CrossRef]
- Xu, B.; Wang, X.; Li, J.; Liu, C. Hierarchical U-net with re-parameterization technique for spatio-temporal weather forecasting. Mach. Learn. 2024, 113, 3399–3417. [Google Scholar] [CrossRef]
- Wang, Y.; Long, M.; Wang, J.; Gao, Z.; Yu, P.S. Predrnn: Recurrent neural networks for predictive learning using spatiotemporal lstms. Adv. Neural Inf. Process. Syst. 2017, 30, 1–10. [Google Scholar]
- Wang, Y.; Zhang, J.; Zhu, H.; Long, M.; Wang, J.; Yu, P.S. Memory in memory: A predictive neural network for learning higher-order non-stationarity from spatiotemporal dynamics. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 10–15 June 2019; pp. 9154–9162. [Google Scholar]
- Wang, Y.; Gao, Z.; Long, M.; Wang, J.; Philip, S.Y. Predrnn++: Towards a resolution of the deep-in-time dilemma in spatiotemporal predictive learning. In Proceedings of the International Conference on Machine Learning; PMLR: Birmingham, UK, 2018; pp. 5123–5132. [Google Scholar]
- Gao, Z.; Tan, C.; Wu, L.; Li, S.Z. Simvp: Simpler yet better video prediction. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 3170–3180. [Google Scholar]
- Sun, R.; Zhang, B. Topographic effects on spatial pattern of surface air temperature in complex mountain environment. Environ. Earth Sci. 2016, 75, 621. [Google Scholar] [CrossRef]
- He, J.; Zhao, W.; Li, A.; Wen, F.; Yu, D. The impact of the terrain effect on land surface temperature variation based on Landsat-8 observations in mountainous areas. Int. J. Remote Sens. 2019, 40, 1808–1827. [Google Scholar] [CrossRef]
- Wang, Y.; Jiang, L.; Yang, M.H.; Li, L.J.; Long, M.; Fei-Fei, L. Eidetic 3D LSTM: A model for video prediction and beyond. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Wang, Y.; Wu, H.; Zhang, J.; Gao, Z.; Wang, J.; Philip, S.Y.; Long, M. Predrnn: A recurrent neural network for spatiotemporal predictive learning. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 45, 2208–2225. [Google Scholar] [CrossRef]
- Tang, S.; Li, C.; Zhang, P.; Tang, R. Swinlstm: Improving spatiotemporal prediction accuracy using swin transformer and lstm. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 1–6 October 2023; pp. 13470–13479. [Google Scholar]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin transformer: Hierarchical vision transformer using shifted windows. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 10–17 October 2021; pp. 10012–10022. [Google Scholar]
- Yu, W.; Lu, Y.; Easterbrook, S.; Fidler, S. Crevnet: Conditionally reversible video prediction. arXiv 2019, arXiv:1910.11577. [Google Scholar]
- Guen, V.L.; Thome, N. Disentangling physical dynamics from unknown factors for unsupervised video prediction. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 11474–11484. [Google Scholar]
- Fang, W.; Chen, Y.; Xue, Q. Survey on research of RNN-based spatio-temporal sequence prediction algorithms. J. Big Data 2021, 3, 97. [Google Scholar] [CrossRef]
- Gong, B.; Langguth, M.; Ji, Y.; Mozaffari, A.; Stadtler, S.; Mache, K.; Schultz, M.G. Temperature forecasting by deep learning methods. Geosci. Model Dev. 2022, 15, 8931–8956. [Google Scholar] [CrossRef]
- Shi, X.; Chen, Z.; Wang, H.; Yeung, D.Y.; Wong, W.K.; Woo, W.c. Convolutional LSTM network: A machine learning approach for precipitation nowcasting. Adv. Neural Inf. Process. Syst. 2015, 28. [Google Scholar]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial networks. Commun. ACM 2020, 63, 139–144. [Google Scholar] [CrossRef]
- Kingma, D.P.; Welling, M. Auto-encoding variational bayes. arXiv 2013, arXiv:1312.6114. [Google Scholar]
- Elsken, T.; Metzen, J.H.; Hutter, F. Neural architecture search: A survey. J. Mach. Learn. Res. 2019, 20, 1–21. [Google Scholar]
- Volkovs, K.; Urtans, E.; Caune, V. Primed UNet-LSTM for Weather Forecasting. In Proceedings of the 2023 7th International Conference on Advances in Artificial Intelligence, Istanbul, Turkiye, 13–15 October 2023; pp. 13–17. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention–MICCAI 2015: 18th International Conference, Munich, Germany, 5–9 October 2015; pp. 234–241. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Rasp, S.; Dueben, P.D.; Scher, S.; Weyn, J.A.; Mouatadid, S.; Thuerey, N. WeatherBench: A benchmark data set for data-driven weather forecasting. J. Adv. Model. Earth Syst. 2020, 12, e2020MS002203. [Google Scholar] [CrossRef]
- Trebing, K.; Stanczyk, T.; Mehrkanoon, S. SmaAt-UNet: Precipitation nowcasting using a small attention-UNet architecture. Pattern Recognit. Lett. 2021, 145, 178–186. [Google Scholar] [CrossRef]
- Mnih, V.; Heess, N.; Graves, A. Recurrent models of visual attention. Adv. Neural Inf. Process. Syst. 2014, 27. [Google Scholar]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-excitation networks. In Proceedings of the IEEE conference on computer vision and pattern recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 7132–7141. [Google Scholar]
- Woo, S.; Park, J.; Lee, J.Y.; Kweon, I.S. Cbam: Convolutional block attention module. In Proceedings of the European Conference on Computer Vision (ECCV); Springer: Cham, Switzerland, 2018; pp. 3–19. [Google Scholar]
- Dai, J.; Qi, H.; Xiong, Y.; Li, Y.; Zhang, G.; Hu, H.; Wei, Y. Deformable convolutional networks. In Proceedings of the IEEE international Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 764–773. [Google Scholar]
- Hu, H.; Gu, J.; Zhang, Z.; Dai, J.; Wei, Y. Relation networks for object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 3588–3597. [Google Scholar]
- Yuan, Y.; Chen, X.; Wang, J. Object-contextual representations for semantic segmentation. In Proceedings of the Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020; pp. 173–190. [Google Scholar]
- Wang, W.; Xie, E.; Li, X.; Fan, D.P.; Song, K.; Liang, D.; Lu, T.; Luo, P.; Shao, L. Pyramid vision transformer: A versatile backbone for dense prediction without convolutions. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 10–17 October 2021; pp. 568–578. [Google Scholar]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An image is worth 16x16 words: Transformers for image recognition at scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Liu, R.; Deng, H.; Huang, Y.; Shi, X.; Lu, L.; Sun, W.; Wang, X.; Dai, J.; Li, H. Decoupled spatial-temporal transformer for video inpainting. arXiv 2021, arXiv:2104.06637. [Google Scholar]
- Guo, M.H.; Lu, C.Z.; Liu, Z.N.; Cheng, M.M.; Hu, S.M. Visual attention network. Comput. Vis. Media 2023, 9, 733–752. [Google Scholar] [CrossRef]
- Wang, X.; Girshick, R.; Gupta, A.; He, K. Non-local neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 7794–7803. [Google Scholar]
- Yuan, Y.; Huang, L.; Guo, J.; Zhang, C.; Chen, X.; Wang, J. Ocnet: Object context network for scene parsing. arXiv 2018, arXiv:1809.00916. [Google Scholar]
- Zhang, H.; Goodfellow, I.; Metaxas, D.; Odena, A. Self-attention generative adversarial networks. In Proceedings of the International Conference on Machine Learning; PMLR: Birmingham, UK, 2019; pp. 7354–7363. [Google Scholar]
- Srivastava, N.; Mansimov, E.; Salakhudinov, R. Unsupervised learning of video representations using lstms. In Proceedings of the International Conference on Machine Learning; PMLR: Birmingham, UK, 2015; pp. 843–852. [Google Scholar]
- Muñoz-Sabater, J.; Dutra, E.; Agustí-Panareda, A.; Albergel, C.; Arduini, G.; Balsamo, G.; Boussetta, S.; Choulga, M.; Harrigan, S.; Hersbach, H.; et al. ERA5-Land: A state-of-the-art global reanalysis dataset for land applications. Earth Syst. Sci. Data 2021, 13, 4349–4383. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Smith, L.N.; Topin, N. Super-convergence: Very fast training of neural networks using large learning rates. In Proceedings of the Artificial Intelligence and Machine Learning for Multi-Domain Operations Applications; SPIE: Bellingham, WA, USA, 2019; Volume 11006, pp. 369–386. [Google Scholar]
- Loshchilov, I.; Hutter, F. Sgdr: Stochastic gradient descent with warm restarts. arXiv 2016, arXiv:1608.03983. [Google Scholar]
- Wang, Z. Image quality assessment: Form error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 604–606. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).