Investigating the Turbulent Vertical Dispersion in a Strong Shear Dominated Neutral Atmospheric Boundary Layer

Abstract

The primary focus of this article is to derive a solution to obtain the asymptotic turbulent dispersion parameter provided by the spectral Taylor statistical diffusion model. Unlike previous articles, which employed the Dirac delta function to solve the eddy diffusivity formula, in this study, we used the Dirac delta function properties to obtain directly the asymptotic turbulent dispersion parameter from the particles’ spatial dispersion variance described in terms of the Eulerian turbulence spectrum and of the scale factor defined formally as the ratio between Lagrangian and Eulerian timescales. From the Kolmogorov 1941 theory, a detailed derivation for this scale factor is presented. Furthermore, using high mean wind speed data generated by local topographic features, a magnitude for the Kolmogorov constant for the neutral atmospheric boundary layer is evaluated. Thus, this magnitude when added to other values obtained from the selected studies found in the literature provides an average value for the Kolmogorov constant that agrees with large eddy simulation data results. Therefore, this average value allows to obtain a more reliable description of this scale factor. Finally, employing analytical formulations for the observed neutral turbulent spectra and for the velocity variances as well as turbulent statistical quantities measured in a surface neutral atmospheric boundary layer, a vertical dispersion parameter is derived. This vertical dispersion parameter when utilized in a simple Gaussian diffusion model is able to reproduce well contaminant observed concentrations.The Gaussian simulated concentrations also compare well with those simulated by a Lagrangian stochastic particle dispersion model that uses observed vertical spectral peak frequency values at distinct levels of the neutral surface boundary layer. Therefore, the present study shows that the observational determination of a single vertical spectral peak frequency is sufficient to obtain a realistic vertical dispersion parameter characterizing the dispersive effect in the turbulent environment of the surface neutral atmospheric boundary layer.

1. Introduction

The study and application of operational mathematical models at different scales to evaluate environmental impact conditions are methodologies of fundamental relevance in the investigation of anthropomorphic pollutant effects acting on ecosystems far from equilibrium. Following this conception, contaminant dispersion models in the lower atmosphere are mathematical tools that allow determining the harmful effect of the concentration of atmospheric pollutants acting on human health and in agricultural and urban environments. These atmospheric air quality models are used to evaluate atmospheric pollution quantitative indices in an Atmospheric Boundary Layer (ABL) controlled by turbulent forcings.

Atmospheric turbulence, a highly nonlinear type of motion, presents a myriad of scales interacting with each other. Therefore, it is necessary to develop a parameterization that allows modeling these states characterized by distinct degrees of freedom. In atmospheric dispersion models, the choice of a turbulent parameterization is decisive, as it represents an idealized solution that allows the turbulent transport phenomenon to be represented. In this case, approximate mathematical relationships are introduced into the air pollution models to replace the unknown terms present in the natural phenomenon of turbulent exchange.

For a fully developed atmospheric turbulence, the presence of the Eulerian observed turbulence spectrum opens up the possibility of obtaining a large number of turbulent parameterizations. From a phenomenological point of view, the Eulerian observed turbulent spectra obtained from the sonic anemometers generally show well-behaved experimental curves described by well-evident spectral peaks associated with frequencies describing the timescales of the energy-containing eddies. Moreover, the observed spectral curves can be described by simple mathematical relationships due to their simplicity [1]. Therefore, using the scale factor between Lagrangian and Eulerian frameworks for the turbulent velocity components, the mathematical relationships describing the observed curves and the phenomenological spectral peak frequencies can be used to parameterize the turbulent transport associated with different types of turbulence in the atmospheric boundary layer. Following the above consideration, the aim of this study is to reinforce the importance of applying physical properties derived from the turbulent energy spectra in Taylor’s Statistical Diffusion Theory to calculate contaminant mean concentrations. The main focus is to demonstrate that from a practical point of view, in turbulent transport studies, the choice of velocity autocorrelation functions must be replaced by Eulerian observed energy spectra. To accomplish this objective, we present a mathematical derivation that uses the scale factor between Lagrangian and Eulerian timescales to obtain a Lagrangian spatial variance. Using the turbulent properties generated by an intense airflow topographically induced in south Brazil known as Vento Norte (Portuguese for “North Wind”), magnitudes for the Kolmogorov constant ($C_0$) in a constant stress region in the neutral ABL has been evaluated. Incorporating this new value with those presented in the literature, it is possible to obtain an average value for the Kolmogorov constant. Finally, with this mean value for $C_0$ and from Kolmogorov 1941 theory, it is possible to establish a relation for the scale factor between Lagrangian and Eulerian frameworks in the neutral ABL, purely shear-dominated turbulence. An additional aim is to use Taylor’s Statistical Diffusion Theory, together with a model describing the turbulent velocity spectra, to derive Lagrangian vertical diffusion coefficients. This vertical diffusivity has been introduced into an asymptotic formulation of the vertical dispersion parameter (vertical particle dispersion variance) to obtain a turbulent parameterization that provides continuous values for the neutral ABL at all elevations. Additionally, using simulations performed by a simple Gaussian model, the new turbulent parameterization is evaluated using concentration data measured at ground level in classical Prairie–Grass dispersion experiments.

2. Spectral Representation of the Taylor Statistical Diffusion Theory

The turbulent dispersion parameter derived from the Taylor statistical diffusion theory can be written in the form of the following theorem:

$${\sigma }_{\alpha }^2=2{\sigma }_i^2{\int }_0^t(t-\tau ){\rho }_{L_i}\left(\tau \right)d\tau$$

(1)

where $\alpha =x,y,z$ are the spatial coordinates, $\tau$ is the time lag, ${\sigma }_i^2$ is the variance of the turbulent velocities ($i=u,v,w$ are the velocity components), and ${\rho }_{L_i}\left(\tau \right)$ is the Lagrangian velocity autocorrelation function of a fluid particle [2]. The correlation effects and, therefore the memory between the particles velocities, caused by the eddies in the turbulent flow, are described by this autocorrelation function and are quantified by the following Lagrangian integral timescale [3]

$$T_{L_i}={\int }_0^{\infty }{\rho }_{L_i}\left(\tau \right)d\tau$$

(2)

For turbulent dispersion travel times t much longer than the integral timescale $T_{L_i}$ ($t>>T_{L_i}$), Equation (1) can be approximated by

$${\sigma }_{\alpha }^2=2{\sigma }_i^2{T}_{L_i}t=2K_{\alpha }t$$

(3)

with $K_{\alpha }$ being a type of Lagrangian eddy diffusivity. The asymptotic approximation of the dispersion parameter (Equation (3)) is employed in air quality operational models that simulate the measured contaminant concentration [4,5,6]. Despite the fact that expression (3) is well established and utilized in air pollution models, determining the Lagrangian integral timescales and the variance of the turbulent velocities in the Atmospheric Boundary Layer (ABL) is always a difficult problem to solve. The reason for this complexity lies in the kinematic representation given by Equation (1). In this representation, the autocorrelation function, the most important term in the integral (1), plays a crucial role to calculate the particles’ dispersion variances. Theoretical and experimental studies on atmospheric turbulence have shown uncertainties regarding the universality of the autocorrelation function [7]. However, different from the autocorrelation function, the observed Eulerian turbulent energy spectrum for a fully developed atmospheric turbulence exhibits a universal form, which explains and demonstrates the functionality of the different frequency windows associated with the turbulence freedom degrees. Therefore, written in the spectral representation, Equation (1) utilizes the functional organization provided by the shape of the Eulerian observed spectrum to consider the dispersive effects provoked by the energy-containing eddies controlling the turbulent dispersion of particles.

The Wiener–Khinchin theorem establishes a fundamental result that relates the Fourier transform of the autocorrelation function to the energy spectrum. In this way, replacing ${\rho }_{L_i}\left(\tau \right)$ by its Fourier transform

$${\rho }_{L_i}\left(\tau \right)={\int }_0^{\infty }{F}_{L_i}\left(n\right)cos\left(2\pi n\tau \right)dn,$$

(4)

in Equation (1), resulting

$${\sigma }_{\alpha }^2={\sigma }_i^2{t}^2{\int }_0^{\infty }{F}_{L_i}\left(n\right){\displaystyle \frac{{sin}^2\left(n\pi t\right)}{{\left(n\pi t\right)}^2}}dn,$$

(5)

where $F_{L_i}$ is the Lagrangian turbulent energy spectrum normalized by the velocity variance, n is the frequency in Hertz and ${sin}^2\left(n\pi t\right){\left(n\pi t\right)}^{-2}$ is a low-pass filter function. As time proceeds, the low-pass filter function begins to remove the energy associated with high frequencies in the Lagrangian turbulent spectrum. The asymptotic behavior of Equation (5) for $t\gg T_{L_i}$ has been obtained for using a solution that employs the Dirac delta function [8], yielding

$${\sigma }_{\alpha }^2={\displaystyle \frac{1}{2}}{\sigma }_i^{2}t{F}_{L_i}(n\to 0)=2{\sigma }_i^2{T}_{L_i}t.$$

(6)

Dirac’s delta function, an extremely restrictive operator, selects only the very low-frequency components ($n\to 0$) of the turbulent spectrum.

The Lagrangian description of turbulence adopts a system of reference that follows atmospheric fluid particles’ motions. In the atmosphere, it is almost impossible to obtain ideal Lagrangian series because most tracers follow the air quite imperfectly. Therefore, observational measures of Lagrangian turbulent statistics in the ABL are very difficult to obtain [9,10,11]. As a consequence of this difficulty, the presence of the Lagrangian spectrum in Equation (6) becomes the practical use of this relation in air pollution models very uncertain.

Differently from the Lagrangian approach, an Eulerian turbulent measurement is one made by an instrument whose position is fixed in one way or another, for example, an anemometer on a tower or a Pitot tube on an airplane. In practice, only Eulerian turbulent statistics parameters are calculated in a fixed reference frame. Therefore, in turbulent dispersion problems, we must describe Lagrangian diffusion using Eulerian measurements, so that one of the fundamental questions in turbulence and diffusion studies is the relation between the Lagrangian and Eulerian frames of reference for measuring turbulence [12]. Since both Lagrangian and Eulerian autocorrelation functions are determined by the same turbulence field, it is reasonable to expect a more or less close relationship between the two [3]. Refs. [9,13] made the very useful assumption that the Lagrangian and Eulerian autocorrelation functions were similar in shape but were displaced by a scale factor ${\beta }_i$. The same assumption is valid for the energy spectra. Mathematically, this assumption can be stated as

$${\rho }_{L_i}\left({\beta }_i\tau \right)={\rho }_i\left(\tau \right),$$

(7)

where ${\rho }_i\left(\tau \right)$ is the Eulerian autocorrelation coefficient and ${\beta }_i$ is the scale factor for the i-component of the turbulent velocity. Therefore, at a first approximation, Eulerian and Lagrangian correlation functions are identical after an appropriate rescaling of the time axis is completed. ${\beta }_i$ is defined formally as the ratio of the Lagrangian and Eulerian timescales, that is

$${\beta }_i={\displaystyle \frac{T_{L_i}}{T_{E_i}}},$$

(8)

with $T_{E_i}$ representing the Eulerian integral timescale. The relation between Lagrangian and Eulerian spectra can be found by considering the Wiener–Khinchin theorem, relating the Fourier transform of the Eulerian autocorrelation function to the spectrum

$$F_i\left(n\right)=4{\int }_0^{\infty }{\rho }_i\left(\tau \right)cos\left(2\pi \tau \right)d\tau ,$$

(9)

where $F_i\left(n\right)$ is the Eulerian observed spectrum normalized by ${\sigma }_i^2$. The substitution of Equation (7) in Equation (9) yields

$$F_{L_i}\left(n\right)=4{\beta }_i{\int }_0^{\infty }{\rho }_{L_i}\left({\beta }_i\tau \right)cos\left(2\pi n{\beta }_i\tau \right)d\tau .$$

(10)

Comparing Equations (9) and (10), we obtain

$$n{F}_{L_i}\left(n\right)={\beta }_{i}n{F}_i\left({\beta }_{i}n\right).$$

(11)

By using Equation (11), the generalized spectral dispersion parameter (Equation (5)) can be related to the scale factor ${\beta }_i$ by the following relationship

$${\sigma }_{\alpha }^2={\displaystyle \frac{{\sigma }_i^2{\beta }_i^2}{{\pi }^2}}{\int }_0^{\infty }{F}_i\left(n\right){\displaystyle \frac{{sin}^2\left(\frac{n\pi t}{{\beta }_i}\right)}{n^2}}dn.$$

(12)

Equation (12), from the practical point of view, is the fundamental relation of the Taylor statistical diffusion model in the energy representation. It quantifies the Lagrangian spatial diffusion of the particles from knowledge of the observed Eulerian turbulent energy spectrum. Since the turbulent kinetic energy is the same in both Lagrangian and Eulerian reference schemes, the Eulerian and Lagrangian velocity variances are assumed to be equal [14]. The presence of ${\beta }_i$ in the filter function into the integral of Equation (12) describes the generally observed fact that Lagrangian spectra are concentrated at lower frequencies than Eulerian spectra. Because Equation (12) contains ${\beta }_i$, it too describes ${\sigma }_{\alpha }^2$ from a Lagrangian perspective. The spectral asymptotic behavior of the Equation (12) for $t\gg T_{L,i}$ (when $t\to \infty$) can be now obtained. Changing the variables, we write $g=n\pi$, with $dn=dg{\pi }^{-1}$, yielding

$${\sigma }_{\alpha }^2={\displaystyle \frac{{\sigma }_i^2{\beta }_i^2}{2}}{\int }_{-\infty }^{\infty }{F}_i\left({\displaystyle \frac{g}{\pi }}\right){\displaystyle \frac{sin\left(\frac{gt}{{\beta }_i}\right)}{g}}{\displaystyle \frac{sin\left(\frac{gt}{{\beta }_i}\right)}{\pi g}}dg.$$

(13)

Consider in Equation (12) that $F_i\left(n\right)$ is an even function of n. For dispersion travel times that are much larger than the Lagrangian integral scale $T_{L_i}$, i.e., with $t\to \infty$, it follows:

$$\underset{t\to \infty }{lim}{\displaystyle \frac{sin\left(\frac{gt}{{\beta }_i}\right)}{\pi g}}=\delta \left(g\right)$$

(14)

The above Equation (14) is a well-known representation of the Dirac delta function and can be used to simplify the derivation of the asymptotic behavior of the Equation (12)

$${\sigma }_{\alpha }^2={\displaystyle \frac{{\sigma }_i^2{\beta }_i^2}{2}}{\int }_{-\infty }^{\infty }{F}_i\left({\displaystyle \frac{g}{\pi }}\right){\displaystyle \frac{sin\left(\frac{gt}{{\beta }_i}\right)}{g}}\delta \left(g\right)dg.$$

(15)

Equation (15) can be considered the property defining the Delta function. The action of the Dirac’s delta function, a notably restrictive operator, allows functions in the integration signal (Equation (15)), to be written in the following form

$${\sigma }_{\alpha }^2={\displaystyle \frac{{\sigma }_i^2{\beta }_i^2}{2}}{F}_i(n\to 0)\underset{g\to 0}{lim}{\displaystyle \frac{sin\left(\frac{gt}{{\beta }_i}\right)}{g}}.$$

(16)

Considering that $F_i(n\to 0)=4T_i$, results for Equation (16)

$${\sigma }_{\alpha }^2={\displaystyle \frac{{\sigma }_i^2}{2}}{\beta }_i{F}_i(n\to 0)t=2{\sigma }_i^2{\beta }_i{T}_{E_i}t.$$

(17)

By the definition of ${\beta }_i$ (Equation (8)), from the point of view of physical information, Equation (17) is identical to Equation (6).

Therefore, the derivation of a formulation for ${\beta }_i$ and the discovery of magnitudes for this quantity is extremely relevant in problems involving turbulent dispersion in atmospheric boundary layers.

Considering here that turbulence can be associated with the superdiffusion regime of disturbance propagation, according to the observational Richardson scaling law [15], it is important to notice that Equations (3) and (17) describe the diffusive regime predicted by Taylor’s theory for $t\gg T_L$. This Taylor’s diffusion regime for large times has been demonstrated by [15] from direct numerical simulation.

3. A Formulation for the Scale Factor ${\mathit{\beta }}_{\mathit{i}}$ from the Kolmogorov 1941 Theory: Application to Neutral Boundary Layer and Comparison with Large Eddy Simulation (LES) Data

In the inertial subrange of the turbulent energy spectrum, the dynamic of turbulence is controlled by the inertial terms in the Navier–Stokes equation, comprising all but the viscous and forcing terms [16]. In this particular range, in which eddies are small compared with the energy-containing eddies, energy neither enters the system nor is dissipated. It is merely transmitted at rate from large-scale toward small-scale motion. It is reasonable to consider that such small-scale turbulence, far from solid bodies and free of the mechanisms producing the turbulent flow, is homogeneous and isotropic [17]. This local isotropy is essential (key) for the development of physical quantities describing small-scale turbulence. Kolmogorov, who first conceived the existence of an inertial subrange, derived from dimensional arguments the following equations, which are valid for the inertial subrange [17,18],

$$D_{L_i}\left(\tau \right)=C_0\epsilon \tau ,$$

(18)

$$S_{L_i}\left(n\right)={\displaystyle \frac{B_0}{2\pi }}\epsilon n^{-2}n>n_L,$$

(19)

$$D_{E_i}\left(\tau \right)=C_i{C}_s{\left(\epsilon U\right)}^{2/3}{\tau }^{2/3},$$

(20)

$$S_{E_i}\left(n\right)={\displaystyle \frac{C_i{\alpha }_u}{{\left(2\pi \right)}^{2/3}}}{\left(\epsilon U\right)}^{2/3}{n}^{-5/3}n>n_E,$$

(21)

where $D_{L_i}\left(\tau \right)$ and $D_{E_i}\left(\tau \right)$ are the second-order Lagrangian and Eulerian velocity structure functions, $S_{L_i}\left(n\right)$ and $S_{E_i}\left(n\right)$ are the Lagrangian and Eulerian energy spectra, $\epsilon$ is the ensemble average rate of dissipation of turbulent kinetic energy, U is the mean wind speed, $C_u=1$, $C_v=C_w=4/3$ [19] and $B_0$, $C_0$, $C_s$ and ${\alpha }_u$ are numerical constants. $n_L$ and $n_E$ can be considered cutoff or limiting initial frequencies for the inertial subrange (in the average sense, the lower frequencies for this inertial subrange) and thus are associated with the energy-bearing part of the Lagrangian and Eulerian spectra. Therefore, they may be regarded as the inverse of the characteristic timescale $T_{L_i}$ and $T_{E_i}$.

Following Corrsin [20], let us integrate Equations (19) and (21) from $n_L$ and $n_E$ to infinite, yielding

$${\sigma }_{L_i}^2={\displaystyle \frac{B_0}{2\pi }}{\int }_{n_L}^{\infty }{n}^{-2}dn={\displaystyle \frac{B_0}{2\pi }}{\displaystyle \frac{\epsilon }{n_L}},$$

(22)

and

$${\sigma }_{E_i}^2={\displaystyle \frac{C_i{\alpha }_u}{{\left(2\pi \right)}^{2/3}}}{\left(\epsilon U\right)}^{2/3}{\int }_{n_E}^{\infty }{n}^{-5/3}dn={\displaystyle \frac{3}{2}}{\displaystyle \frac{C_i{\alpha }_u}{{\left(2\pi \right)}^{2/3}}}{\left({\displaystyle \frac{\epsilon U}{n_E}}\right)}^{2/3}.$$

(23)

The equivalence of Lagrangian and Eulerian variances is an exact result for homogeneous turbulence [17]. Employing large eddy simulation-generated turbulent data for distinct stability patterns in the ABL, ref. [14] found that there is an agreement between the correspondent Eulerian and Lagrangian velocity variances. As a consequence from this approximately homogeneous and quasistationary turbulence obtained by the numerical experimental data generated by large eddy simulation, one can assume in the present development that ${\sigma }_{L_i}^2={\sigma }_{E_i}^2\equiv {\sigma }_i^2$. Therefore, the elimination of $\epsilon$ utilizing Equations (22) and (23) provides

$${\displaystyle \frac{n_E}{n_L}}={\displaystyle \frac{T_{L_i}}{T_{E_i}}}={\left({\displaystyle \frac{3}{2}}\right)}^{3/2}{\displaystyle \frac{{\left(C_i{\alpha }_u\right)}^{3/2}}{B_0}}{\displaystyle \frac{U}{{\sigma }_i}}.$$

(24)

Therefore, Equation (24) can be compared with the following largely used relation to evaluate the ratio between the Lagrangian and Eulerian timescales [9,10,12,21,22,23]:

$${\displaystyle \frac{T_{L_i}}{T_{E_i}}}=\gamma {\displaystyle \frac{U}{{\sigma }_i}},$$

(25)

where $\gamma$ is a numerical coefficient. Ref. [24] have shown rigorously that the ratio $T_{L_i}/T_{E_i}$ can be performed by Equation (25) [25]. They found that for the case of a fully developed isotropic homogeneous turbulence, $\gamma ={\displaystyle \frac{\sqrt{\pi }}{4}}$. On the other hand, for inhomogeneous turbulence, the coefficient of ${\displaystyle \frac{U}{{\sigma }_i}}$ lies in the range $0.4$–$0.7$ [22].

A comparison between Equations (24) and (25) allows us to obtain the following formulation for $\gamma$:

$$\gamma ={\left({\displaystyle \frac{3}{2}}\right)}^{3/2}{\displaystyle \frac{{\left(C_i{\alpha }_u\right)}^{3/2}}{B_0}}.$$

(26)

To proceed with the development, some derivations will be performed. The starting point is given by the following general relationship linking, in the Lagrangian framework, the structure function, the autocorrelation function and the energy spectrum. Using Equation (19) and integrating over n, yields

$$D_{L_i}\left(\tau \right)={\displaystyle \frac{\epsilon B_0}{\pi }}{\int }_0^{\infty }[1-cos\left(2\pi \tau n\right)]n^{-2}dn=\epsilon B_0\pi \tau ,$$

(27)

where the following approximation has been used

$${\int }_0^{\infty }{\displaystyle \frac{[1-cos(x\left)\right]}{x^2}}dx\cong {\displaystyle \frac{\pi }{2}}.$$

(28)

Comparing Equations (27) and (18) results, we obtain

$$B_0={\displaystyle \frac{C_0}{\pi }}.$$

(29)

For the Eulerian framework, the following general relationship can be written:

$$D_{E_i}\left(\tau \right)={\displaystyle \frac{2C_i{\alpha }_u}{{\left(2\pi \right)}^{2/3}}}{\left(\epsilon U\right)}^{2/3}{\int }_0^{\infty }[1-cos\left(2\pi \tau n\right)]n^{-5/3}dn=4C_i{\alpha }_u{\left(\epsilon U\tau \right)}^{2/3},$$

(30)

where, in this case, the following approximation is employed

$${\int }_0^{\infty }{\displaystyle \frac{[1-cos(x\left)\right]}{x^{5/3}}}dx\cong 2.$$

(31)

Comparing Equations(30) and (20), we obtain

$${\alpha }_u\cong {\displaystyle \frac{C_s}{4}}.$$

(32)

By inserting Equations (29) and (32) into Equation (26), we are now in position to calculate the coefficient $\gamma$ from the following relation

$$\gamma ={\left({\displaystyle \frac{3}{8}}\right)}^{3/2}{\displaystyle \frac{{\left(C_i{C}_s\right)}^{3/2}\pi }{C_0}},$$

(33)

in which the magnitude of $C_0$ is a function of the turbulent forcing. The estimate of the $C_s$ value, obtained for the three wind components, gave $1.8$, $1.6$ and $1.7$, respectively, which is approximately constant, with an average value of $1.7$ [26]. Ref. [27] calculated a value of $C_0=5.7$ for the constant-stress region in the neutral boundary layer. On the other hand, a magnitude of $C_0=7$ has been obtained by fitting a Lagrangian stochastic model of turbulent dispersion to the direct simulation data [28]. Furthermore, ref. [29], by using the [30] Lagrangian and Eulerian simultaneous measurements in slightly stable conditions, calculated a value of $C_0$ of the order of $C_0=7$.

Recently, while studying the influence of a downslope windstorm on the turbulent properties of the ABL, ref. [31] derived a new set of turbulent parameterizations. In this study, using micrometeorological data from a tower equipped with sonic anemometers at four levels (3, 6, 14, and 30 m), high mean wind speed events generated by topographic features were analyzed to obtain turbulent velocity spectra. The energy-containing eddy scales were used to derive neutral ABL turbulent parameters. Moreover, ref. [31] provided formulations for the vertical profiles of wind turbulent velocity variances and Lagrangian timescales.

Furthermore, the observations show that the surface friction velocity in the surface neutral boundary layer is of the order of $u_{*0}\cong 0.7$ m ${\mathrm{s}}^{-1}$ ([31], Table 1). This elevated magnitude of $u_{*0}$, measured at first three levels (3, 6 and 14 m) in the micrometeorological tower characterizes a region of constant stress in the neutral ABL, and therefore, the calculation of $C_0$, as proposed by [27] can be accomplished using the observed data by [31]. Following the development proposed by [27] for the vertical turbulent velocity component, $C_0$ can be written as

$$C_0={\displaystyle \frac{2}{\epsilon }}{\displaystyle \frac{{\sigma }_w^2}{T_{L_w}}},$$

(34)

or also in the form

$$C_0={\displaystyle \frac{2}{\epsilon }}{\displaystyle \frac{{\sigma }_w^4}{{\sigma }_w^2{T}_{L_w}}},$$

(35)

where ${\sigma }_w^2{T}_{L_w}$ represents a vertical eddy diffusivity $\left(K_z\right)$.

For the constant-stress region, $\epsilon \approx {\displaystyle \frac{u_{*0}^3}{\kappa z}}$ and $K_z=\kappa u_{*0}z$, where $\kappa$ is the Von Karman constant ($\kappa \approx 0.35$ or 0.4). Replacing the above equalities, which are valid in the constant-stress region, into Equation (35)

$$C_0={\displaystyle \frac{2}{{\varphi }_{\epsilon }}}{\left({\displaystyle \frac{{\sigma }_w}{u_{*0}}}\right)}^4,$$

(36)

where ${\varphi }_{\epsilon }={\displaystyle \frac{\epsilon \kappa z}{u_{*0}^3}}=1.1$ and ${\left({\displaystyle \frac{{\sigma }_w}{u_{*0}}}\right)}^4=1.3$ ([31], Table 2), resulting in $C_0$ with magnitude of the order of $5.2$. For a neutral ABL, these four values for $C_0$ ($5.7$; $7.0$; $7.0$; $5.2$) suggest an average value of $C_0=6.2$. Therefore, replacing the constants $C_v=C_w=4/3$, $C_s=1.7$ and $C_0=6.2$ into Equation (33) results in a $\gamma$ value of the order of $0.4$. Employing large eddy simulation-generated turbulent data, [14,32] investigated the ratio $\beta ={\displaystyle \frac{T_{L_i}}{T_{E_i}}}$ between the Lagrangian and Eulerian timescales. For a neutral ABL with high wind speed, large eddy simulation data suggest a value of $\gamma =0.4$ and $C_0=6.1$.

Considering the above detailed discussion, the formulation for the scale factor ${\beta }_i$ which will be used in Equation (17) to parameterize turbulent dispersion in air pollution models for a shear dominated ABL, will be written as

$${\beta }_i=0.4{\displaystyle \frac{U}{{\sigma }_i}}$$

(37)

4. Derivation of the Vertical Eddy Diffusivity for the Constant Stress Region in the Neutral ABL

In southern Brazil, in the winter period, there is a topographically forced airflow pattern which develops over an extensive horizontal area. This meteorological geophysical flow is known as “Vento Norte” (VNOR, Portuguese for North Wind [31]). The VNOR windstorm is provoked by a particular configuration of a large-scale atmospheric pressure system and locally reinforced by an accentuated difference in height (≈400 m), specifying the plateau–plain interface in central Rio Grande do Sul state (Figure 1, [31]). The VNOR generates elevated mean wind speed magnitudes and a well-characterized surface neutral ABL. Recently, employing turbulent velocity data originated from the VNOR [31] obtained observed turbulent velocity spectra at four levels (3, 6, 14, and 30 m). With a mean value of the surface friction velocity $u_{*0}=0.7$ m/s, this vertical region can be considered a constant stress depth in the neutral ABL. Furthermore, the observed VNOR spectra were well fitted by the following shear-driven neutral ABL spectral formula [31,33,34]

$${\displaystyle \frac{n{S}_i\left(n\right)}{u_{*}^2}}={\displaystyle \frac{1.5C_i{\varphi }_{\epsilon }^{2/3}f}{\left(1+\frac{1.5f^{5/3}}{f{m}_i^{5/3}}\right)f{m}_i^{5/3}}},$$

(38)

where $u_{*}^2=u_{*0}^2{\left(1-(z/h)\right)}^{1.7}$ is the local friction velocity for a neutral ABL, $f{m}_i$ is the nondimensional frequency of the neutral spectral peak and $C_i={\alpha }_i{\alpha }_u{\left(2\pi \kappa \right)}^{-2/3}$, ${\alpha }_u=0.5\pm 0.05$ and ${\alpha }_i=1,4/3,4/3$ for u, v and w components, respectively.

Considering the development as well as the derivations presented in Section 2, the Lagrangian integral timescale can be expressed as

$$T_{Li}={\displaystyle \frac{{\beta }_i{F}_i(n\to 0)}{4}}$$

(39)

where ${\beta }_i=0.4U/{\sigma }_i$ and $F_i(n\to 0)=S_i(n\to 0)/{\sigma }_i^2$ represents the spectra in which the high frequencies were filtered. Moreover, an analytical integration of Equation (38) over the whole frequency domain leads to the following turbulent velocity variances

$${\sigma }_i^2={\displaystyle \frac{2.32C_i{\varphi }_{\epsilon }^{2/3}{u}_{*}^2}{f{m}_i^{2/3}}}$$

(40)

From the physical point of view, the analytical solution as given by Equation (40) allows you to identify in a single formula all the quantities that characterize the turbulence and have a decisive influence on the direct calculation of the turbulent velocity variances. Regarding Equation (40), it exhibits that ${\sigma }_i^2$ is directly proportional to the magnitude of $\epsilon$ (dissipation of the energy-containing eddies) and also of the energy-containing timescales. Finally, the quantity providing dimensionality in Equation (40) is the characteristic velocity scale ($u_{*}$) in a neutral ABL. Furthermore, Equation (40) is used to normalize the spectrum. Therefore, the normalized spectrum can be written as follows:

$$F_i(n\to 0)={\displaystyle \frac{S_i(n\to 0)}{{\sigma }_i^2}}={\displaystyle \frac{0.64z}{f{m}_{i}U}}.$$

(41)

In neutral conditions, the Lagrangian integral timescales can be derived from Equations (39) and (41) as

$$T_{Li}={\displaystyle \frac{0.064z}{{\sigma }_{i}f{m}_i}}.$$

(42)

From Equations (40) and (42), we can derive a Lagrangian eddy diffusivity for a shear-dominated ABL. For the spatial components $\alpha =y,z$, this eddy diffusivity describes the magnitude of the turbulent transport and can be written as

$$K_{\alpha }={\displaystyle \frac{0.06u_{*}z}{f{m}_i^{4/3}}}.$$

(43)

The peak frequencies are important for studies of scalars turbulent transport in ABL. These peak frequencies describe the spatial and temporal scales of the energy-containing eddies. For a neutral ABL, $f{m}_i$ can be written as [19,35,36]

$$f{m}_i=f{m}_{0i}\left(1+{\displaystyle \frac{0.03a_i{f}_{c}z}{u_{*0}}}\right)$$

(44)

where $f{m}_{0i}$ is the spectral peak at the surface, and $f_c$ is the Coriolis parameter with $a_w=500$ and $a_v=1094$ [12,33].

In air pollution dispersion models, the parameterization of the contaminant vertical transport is of fundamental importance. Thus, to proceed with the present development, we need in Equation (44) the observed values of $f{m}_{0w}$. A mean value for this quantity can be extracted from the sonic anemometers observations ([31], Figure 4). At the heights of 3, 6 and 14 m has been calculated ([31]) the magnitudes of $f{m}_{0w}=$ 0.516, 0.239 and 0.138, respectively, resulting a mean value of $f{m}_{0w}$ of the order of 0.3. The substitution of this value of 0.3 in Equation (44) and using the expression (43) results in the following formulation for the vertical eddy diffusivity in a neutral ABL

$${\displaystyle \frac{K_z}{u_{*0}h}}={\displaystyle \frac{0.3z/h{(1-z/h)}^{0.85}}{{\left(1+15f_{c}z/u_{*0}\right)}^{4/3}}}$$

(45)

where h is the depth of the neutral ABL, which is given by [37]

$$h={\displaystyle \frac{0.2u_{*0}}{f_c}}.$$

(46)

Thus, the substitution of Equation (46) into Equation (45) yields

$${\displaystyle \frac{K_z}{u_{*0}h}}={\displaystyle \frac{0.3z/h{(1-z/h)}^{0.85}}{{\left(1+3z/h\right)}^{4/3}}}.$$

(47)

The vertical Lagrangian eddy diffusivity provided by Equation (47) shows magnitudes that agree with those proposed by [34].

5. Simulating the Contaminant Dispersion for the Constant-Stress Region in the Neutral ABL

In this section, we test the values of turbulent quantities measured from the VNOR events in application in the air contaminant dispersion. Therefore, Equation (17) written for the vertical dispersion parameter ${\sigma }_z$ is now used in a Gaussian diffusion model to evaluate the ground-level crosswind integrated concentration in the Prairie Grass neutral dispersion experiment. The Prairie Grass experiment was realized in O’Neil, Nebraska, in 1956. The contaminant (CO₂) was released without buoyancy at a height of 0.5 m on flat ground and was collected by samplers at a height of 1.5 m at the following five downwind distances from the source (50, 100, 200, 400, 800 m). In this study, we selected thirteen runs of the Prairie Grass dispersion observations in which the mean wind speed was greater than 6.0 m ${\mathrm{s}}^{-1}$ with values of ($u_{*0}$) ≥ 0.4 m ${\mathrm{s}}^{-1}$. The values of U and $u_{*0}$ exhibited in

Table 1. Micrometeorological parameters and continuous point source strength of the neutral Prairie Grass runs [31].

Experiment	h (m)	${\mathrm{u}}_{*0}$ (m ${\mathrm{s}}^{-1}$)	U (m ${\mathrm{s}}^{-1}$)	Q (g ${\mathrm{s}}^{-1}$)
5	780	0.40	7.0	78
9	550	0.48	8.4	92
19	650	0.41	7.2	102
20	710	0.63	11.3	102
26	900	0.45	7.8	98
27	1280	0.44	7.6	99
30	1560	0.48	8.5	98
43	600	0.40	6.1	99
44	1450	0.42	7.2	101
49	550	0.47	8.0	102
50	750	0.46	8.0	103
51	1880	0.47	8.0	102
61	450	0.53	9.3	102

represent characteristic magnitudes of a neutral PBL.

The dispersion model used to simulate the Prairie Grass ground-level crosswind integrated concentration is given by the following formulation [2].

$$C_y(x,0)={\displaystyle \frac{Q}{\sqrt{2\pi }U{\sigma }_z}}$$

(48)

where Q is the continuous point source strength, and the vertical dispersion parameter (${\sigma }_z$) represents the width of the mean concentration distribution.

The vertical variance of particle position is given by Equation (17)

$${\sigma }_z^2=2{\sigma }_w^2{T}_{Lw}t=2K_{z}t$$

(49)

where $t=x/U$ is the diffusion travel time and $K_z$ is the vertical Lagrangian eddy diffusivity provided by Equation (47). In the first three distances (50, 100 and 200 m) from the source, the following equation for ${\sigma }_z$ was used

$${\sigma }_z={\left(0.6u_{*0}\right)}^{1/2}{\left({\displaystyle \frac{x}{U}}\right)}^{1/2}$$

(50)

where the height z was chosen as one meter ($z=1$ m). Nonetheless, for the distances of 200 and 400 m, the following parameterization for ${\sigma }_z$ has been selected:

$${\sigma }_z={\left(2K_z{\displaystyle \frac{x}{U}}\right)}^{1/2}$$

(51)

in which

$$K_z=0.01u_{*0}h.$$

(52)

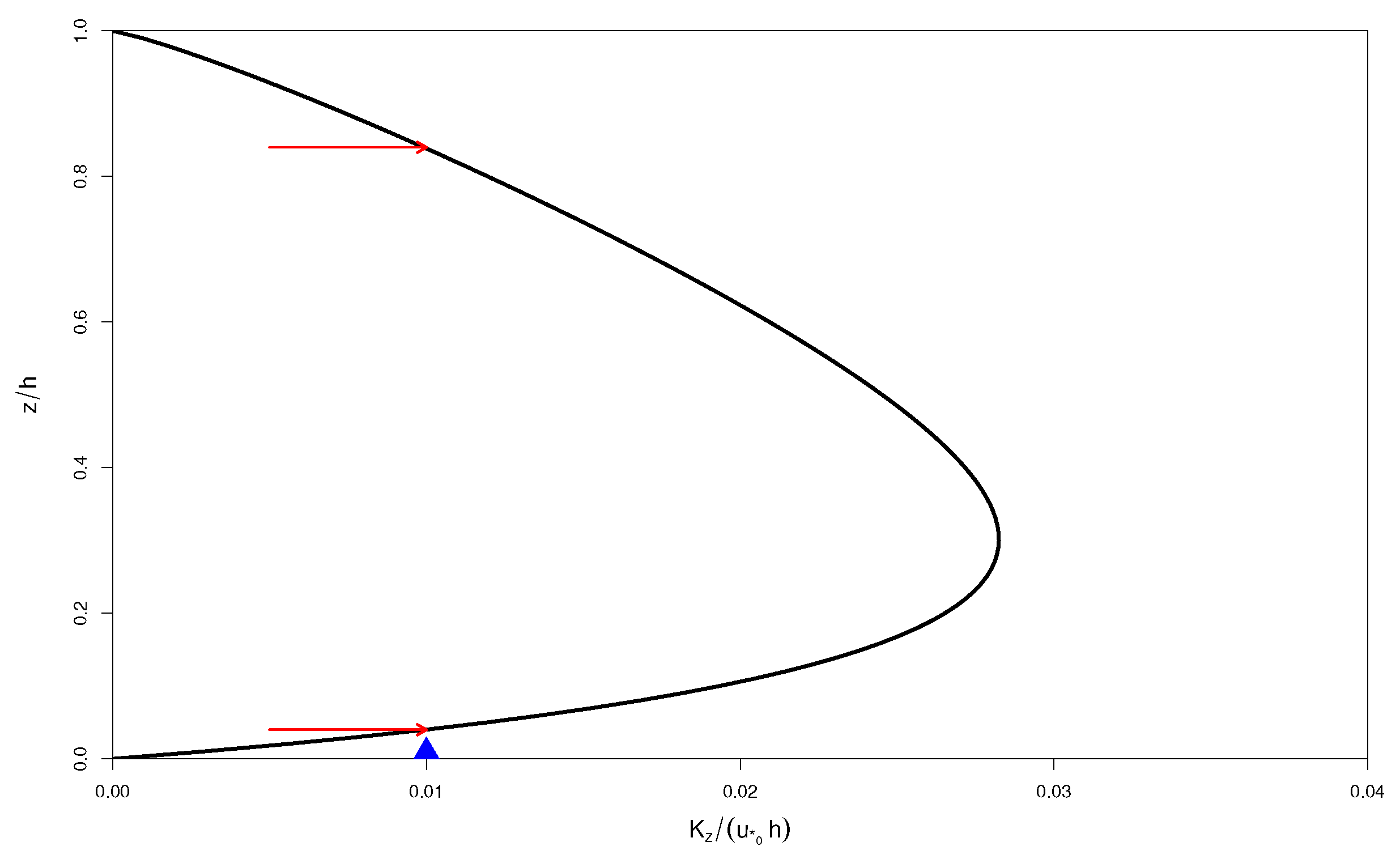
The representation of $K_z$, as given by Equation (52), was extracted from Figure 1. This figure shows that the magnitude of $K_z/u_{*0}h=0.01$ occurs at a height $z/h$ of the order of 0.035. Thus, it is considered here that as contaminants travel and move away from the source, they try a turbulent transport characterized by a single eddy diffusivity (z-less dependence) in the constant-stress region of a neutral ABL.

It is important to note that Equation (52) obtained from the Taylor spectral diffusion model has the same magnitude as the relationship $K=\kappa u_{*0}z$ valid for the constant stress region [27].

The results of the simulated ground-level crosswind concentrations employing a Gaussian diffusion model (Equation (48)) with the vertical turbulent dispersion parameters, provided by Equations (49)–(51), are shown in

Table 2. Statistical evaluation indices considering the Prairie Grass neutral diffusion experiment.

NMSE	R	FB	FS	FA2
0.05	0.95	0.11	−0.05	0.96

. Table 2 displays the well-known Hanna’s statistical indices [38], which are widely used to evaluate air pollution dispersion models, and it shows the result of the statistical analysis made with observed and predicted values of concentrations. The comparison of simulated and measured concentrations exhibits a good agreement between the results of the proposed approach and the experimental one. The magnitudes of the statistical indices are within an acceptable range of values with NMSE (normalized mean squared error), FB (fractional bias), and FS (fractional standard deviation) close to zero and R (correlation coefficient) close to one. Moreover, Figure 2 shows the observed and the predicted scatter diagram of ground-level crosswind integrated concentrations. Concerning to the scattering over the central line allied to the magnitude of the FA2 (factor two) near to unity (Table 2), it is possible to conclude that the vertical turbulent dispersion parameters derived in this study reproduce well the observed Prairie Grass concentration data in the constant-stress region of the neutral ABL. Comparing the results of the present study with those obtained by [31], it can be seen that both approaches reproduce well-observed Prairie Grass concentrations. However, it should be highlighted that [31] in their simulation used a Lagrangian stochastic dispersion model parameterized by timescales obtained at different heights of the surface neutral ABL. These timescales were calculated from the vertical spectral peak frequencies measured by sonic anemometers installed at four levels in a micrometeorological tower. Therefore, the present analysis demonstrates that a single value of the vertical spectral peak frequency at the surface, $f{m}_{0w}=0.3$, is sufficient to derive a Lagrangian timescale whole representative of the constant-stress region in the neutral ABL.

6. Conclusions

In this study, employing the Dirac Delta function properties, we derived a solution to obtain the asymptotic turbulent dispersion parameter originated from the spectral Taylor statistical dispersion model described by the observed Eulerian turbulence spectra and the scale factor ${\beta }_i=T_{Li}/T_{Ei}$ given by the ratio between the Lagrangian and Eulerian timescales. Using Lagrangian and Eulerian velocity structure functions and energy spectra valid for the inertial subrange, a thorough development for this scale factor is accomplished. Utilizing turbulent parameters generated by an intense topographic wind, a magnitude of the Kolmogorov constant of the order of $C_0=5.2$ is determined by the neutral ABL. This magnitude of $C_0$ when added to other values found in the literature provides an average value of $C_0=6.1$ that is in agreement with large eddy simulation data results. Furthermore, the substitution of $C_0=6.1$ into the equation providing $\gamma$ yields a formula for ${\beta }_i$ in the neutral ABL that can be written as ${\beta }_i=0.4U/{\sigma }_i$. Using a single vertical spectral peak frequency $f{m}_{w0}=0.3$ and analytical formulations for the Eulerian neutral turbulent spectra and for the velocity variances, a vertical dispersion parameter for the stress-constant region in neutral ABL has been calculated. This vertical turbulent parameterization used in a simple Gaussian diffusion model simulates well the measured ground-level crosswind integrated concentrations $Cy(x,0)$ for the Prairie Grass neutral dispersion experiments. Moreover, the Gaussian simulated concentrations agree with those simulated by a Lagrangian stochastic dispersion model that employs measured vertical spectral peak frequencies magnitudes at distinct levels of the stress-constant region in the neutral ABL. Thus, the present investigation points out that a single magnitude of a vertical spectral peak frequency is already sufficient to obtain a Lagrangian timescale representative of the constant-stress region. The turbulent parameters as $C_0$, $\gamma$, $K_z$ and ${\sigma }_z$ developed and evaluated in the present study may be suitable for applications in regulatory air pollution modeling.