Quantifying Tornado Outbreak Intensity and Frequency Relationships with Interannual and Monthly Variability
Abstract
1. Introduction
2. Data and Methods
2.1. Datasets

2.2. Methods
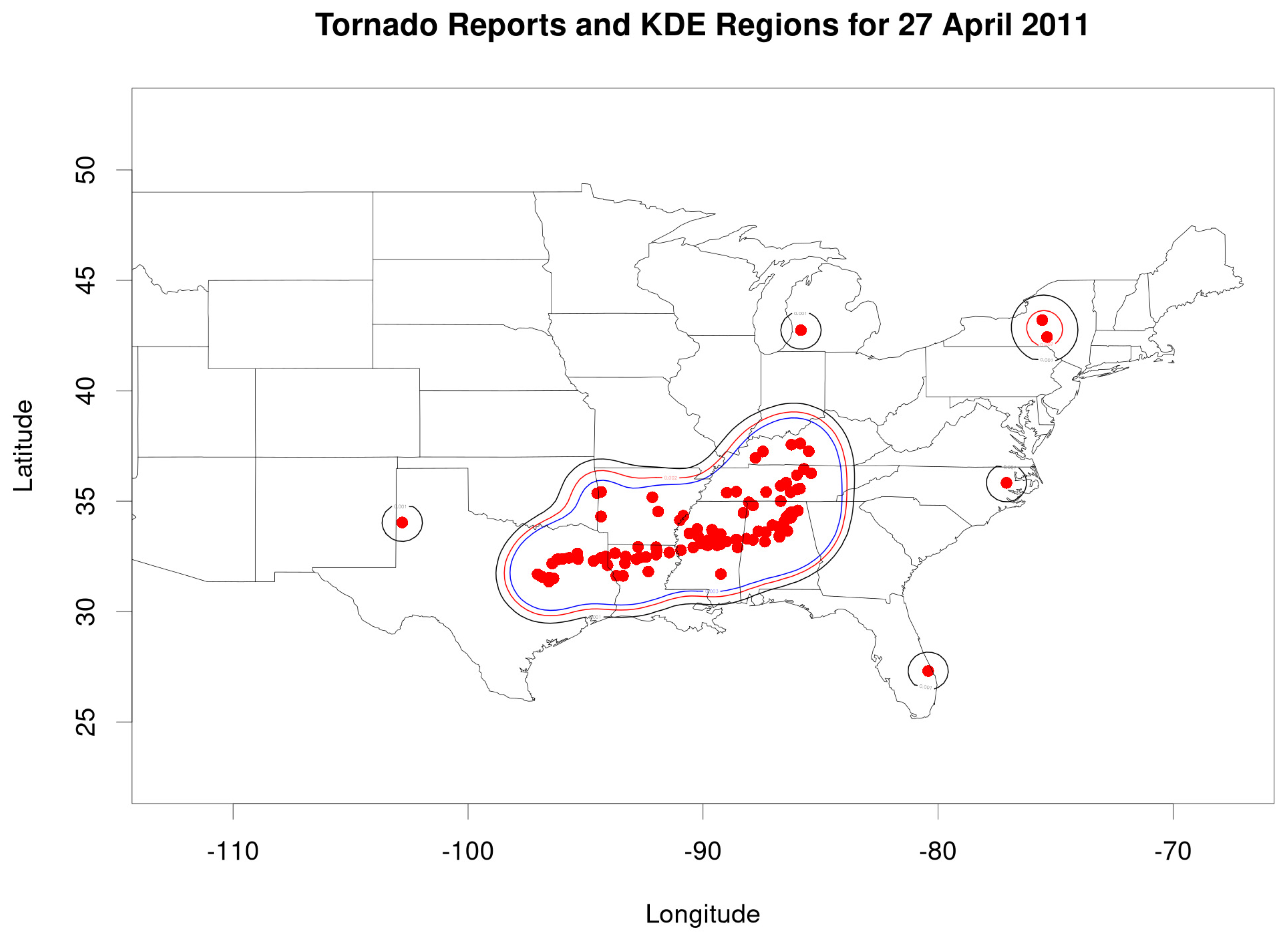
2.2.1. Defining a TO
- Number of tornadoes—the total count of tornadoes in the given outbreak;
- Number of EF0 and EF1 tornadoes (weak tornadoes);
- Number of EF2 and EF3 tornadoes (strong tornadoes);
- Number of EF4 and EF5 tornadoes (violent tornadoes);
- Total adjusted Fujita miles (AFM), computed following [17] for the TO.
2.2.2. Detrending TO Diagnostic Variables
2.2.3. Quantifying TO Intensity from Diagnostic Variables
3. Results
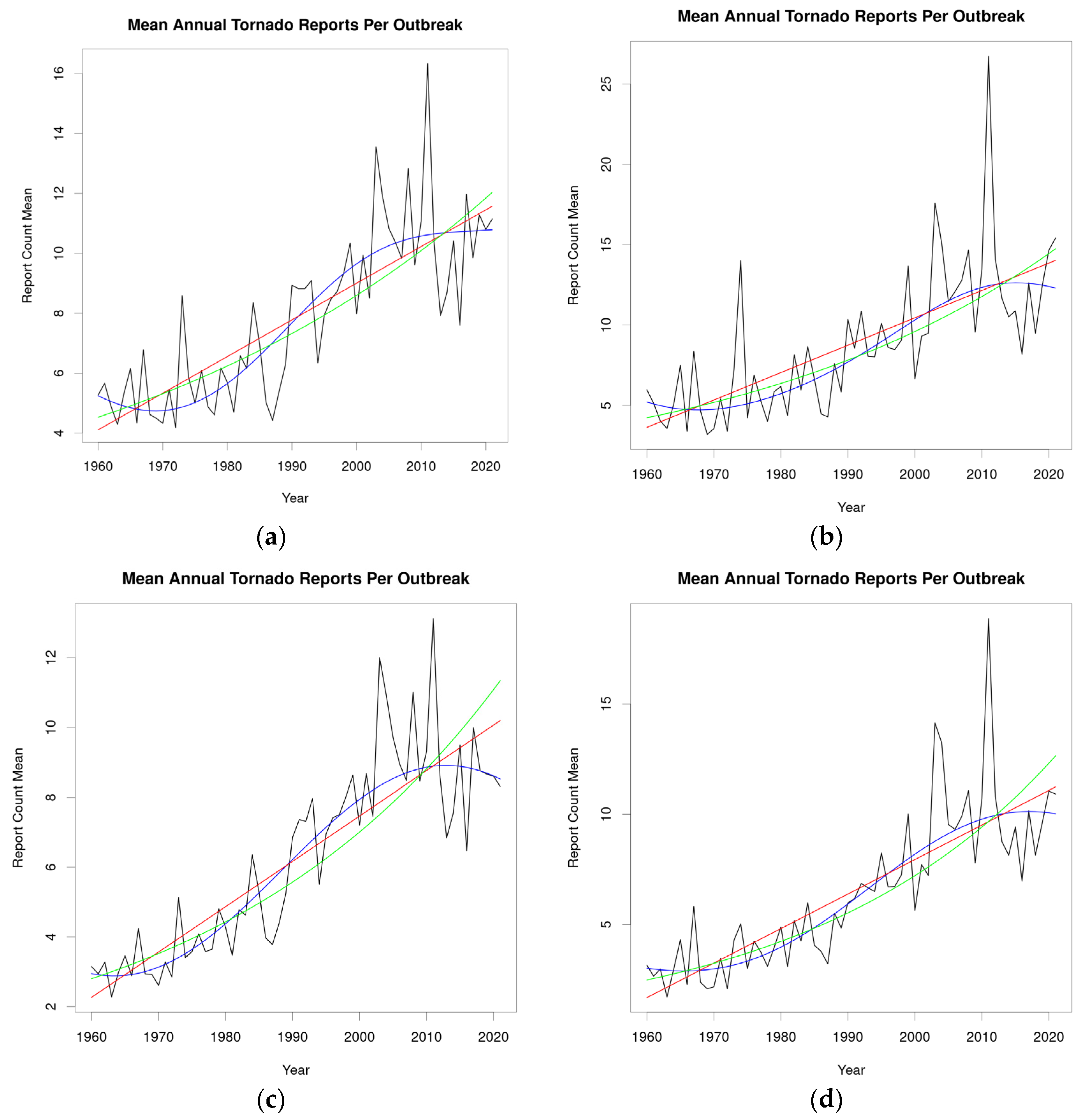
3.1. Intensity Index Results
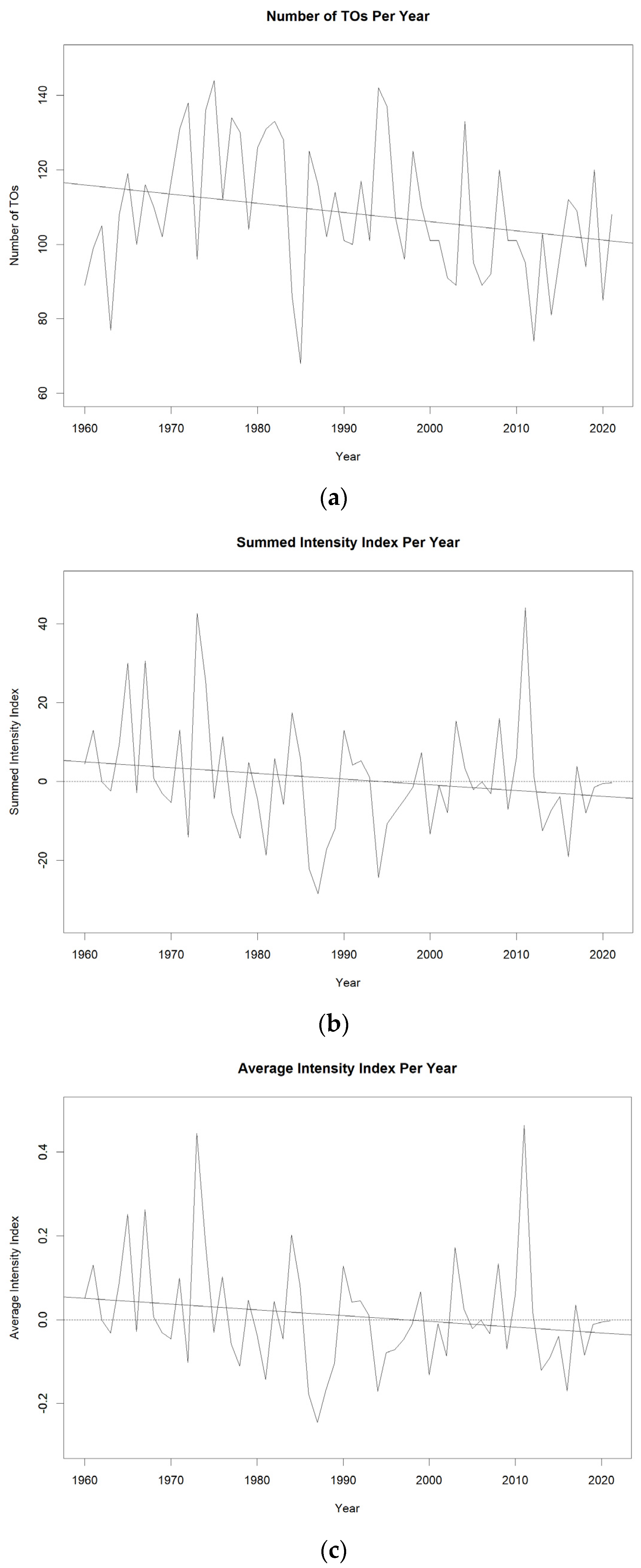
3.2. TO Frequency with Interannual Variability Indices
3.2.1. ENSO and Annual TO Activity
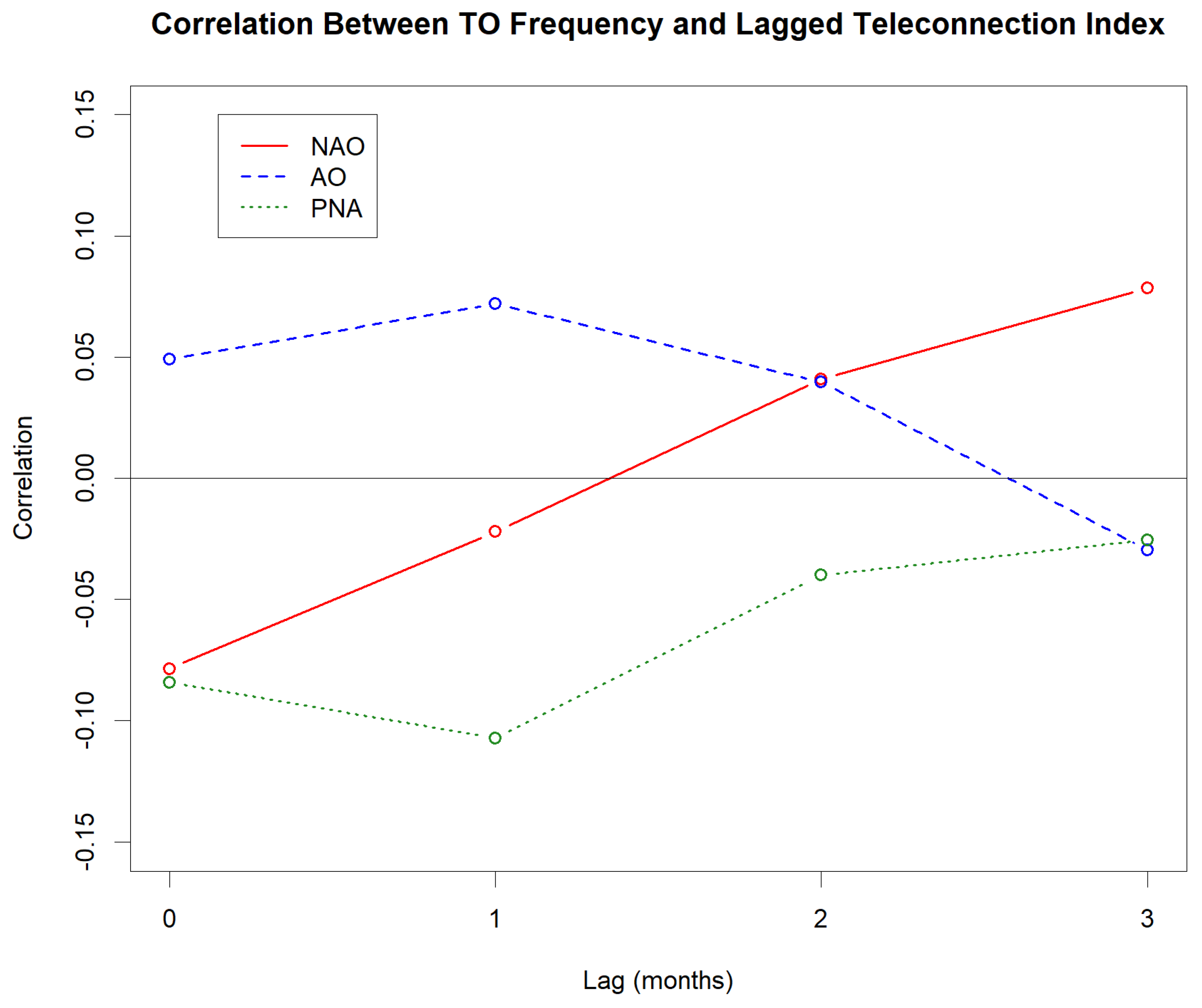
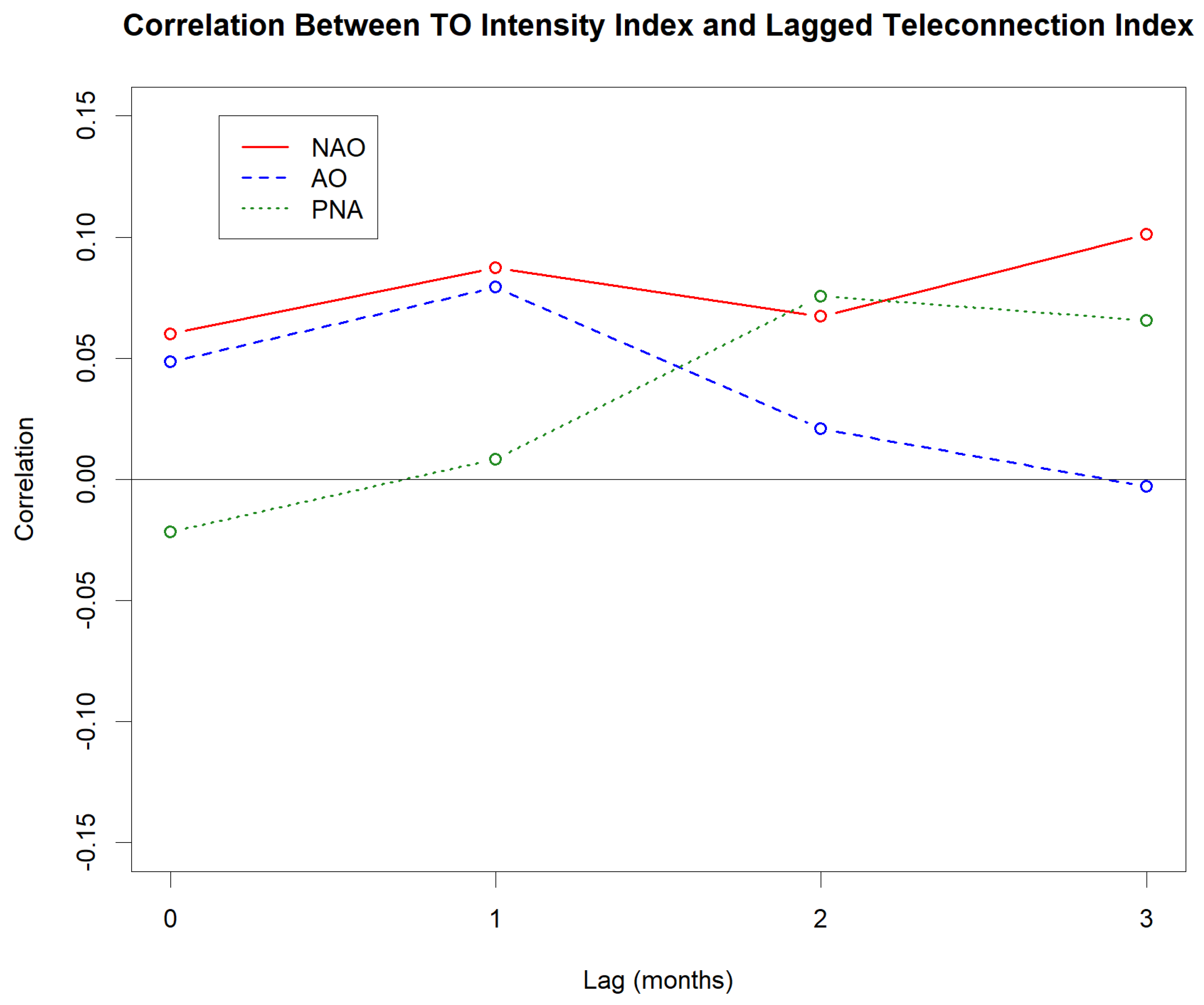
3.2.2. Monthly Indices and Monthly TO Activity
4. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cook, A.R.; Leslie, L.M.; Parsons, D.B.; Schaefer, J.T. The impact of El Niño-Southern Oscillation (ENSO) on winter and early spring U.S. tornado outbreaks. J. Appl. Meteor. Climo. 2017, 56, 2455–2478. [Google Scholar] [CrossRef]
- Cook, A.R.; Schaefer, J.T. The relation of El Niño-Southern Oscillation (ENSO) to winter tornado outbreaks. Mon. Wea. Rev. 2008, 136, 3121–3137. [Google Scholar] [CrossRef]
- Sparrow, K.R.; Mercer, A.E. Predictability of US tornado outbreak seasons using ENSO and northern hemisphere geopotential height variability. Geosmin. Front. 2016, 7, 21–31. [Google Scholar] [CrossRef]
- Carr, J.A. A preliminary report on the tornadoes of 21–22 March 1952. Mon. Wea. Rev. 1952, 80, 50–58. [Google Scholar] [CrossRef]
- Beebe, R.G. Tornado composite charts. Mon. Wea. Rev. 1956, 84, 127–142. [Google Scholar] [CrossRef]
- Wolford, L.V. Tornado Occurrences in the United States; U.S. Government Printing Office: Washington, DC, USA, 1960; pp. 339–343. [Google Scholar]
- Maddox, R.A.; Gray, W.M. A study of tornado proximity data and an observationally derived model of tornado genesis. Colo. State Univ. Atmos. Sci. Pap. 1973, 212, 202. [Google Scholar]
- Galway, J.G. Some climatological aspects of tornado outbreaks. Mon. Wea. Rev. 1977, 105, 477–484. [Google Scholar] [CrossRef]
- Pautz, M.E. Severe Local Storm Occurrences, 1955–1967; Environmental Science Services Administration Rep.: Rockville, MD, USA, 1969; p. 71. [Google Scholar]
- Mercer, A.E.; Shafer, C.M.; Doswell, C.A.; Leslie, L.M.; Richman, M.B. Synoptic composites of tornadic and nontornadic outbreaks. Mon. Wea. Rev. 2012, 140, 2590–2608. [Google Scholar] [CrossRef]
- Doswell, C.M.; Edwards, R.; Thompson, R.L.; Hart, J.A.; Crosbie, K.C. A simple and flexible method for ranking severe weather events. Wea. Forecast. 2006, 21, 939–951. [Google Scholar] [CrossRef]
- Ćwik, P.; McPherson, R.A.; Brooks, H.E. What is a tornado outbreak?: Perspectives through time. Bull. Amer. Meteor. Soc. 2021, 102, E817–E835. [Google Scholar] [CrossRef]
- American Meteorological Society Glossary of Meteorology. Available online: https://glossary.ametsoc.org/wiki/Tornado_outbreak (accessed on 5 June 2024).
- Shafer, C.M.; Doswell, C.A. A multivariate index for ranking and classifying severe weather outbreaks. Elec. J. Sev. Storms Meteor. 2010, 5, 1–39. [Google Scholar] [CrossRef]
- Shafer, C.M.; Doswell, C.A. Using kernel density estimation to identify, rank, and classify severe weather outbreak events. Elec. J. Sev. Storms Meteor. 2011, 6, 1–28. [Google Scholar] [CrossRef]
- Schaefer, J.T.; Edwards, R. 1999: The SPC tornado/severe thunderstorm database. Preprints, 11th Conf. Applied Climo. 1999. Available online: https://www.spc.noaa.gov/publications/schaefer/database.htm (accessed on 1 June 2024).
- Fuhrmann, C.M.; Konrad, C.E.; Kovach, M.M.; McLeod, J.T.; Schmitz, W.G.; Dixon, P.G. Ranking of tornado outbreaks across the United States and their climatological impacts. Wea. Forecast. 2014, 29, 684–701. [Google Scholar] [CrossRef]
- Edwards, R.; Brooks, H.E.; Cohn, H. Changes in tornado climatology accompanying the enhanced Fujita scale. J. Appl. Meteor. Climo. 2021, 60, 1465–1482. [Google Scholar] [CrossRef]
- Barnston, A.G.; Chelliah, M.; Goldenberg, S.B. Documentation of a highly ENSO-related SST region in the equatorial Pacific, research note. Atmos-Ocean 1997, 35, 367–383. [Google Scholar] [CrossRef]
- Huang, B.; Thorne, P.W.; Banzon, V.F.; Boyer, T.; Chepurin, G.; Lawrimore, J.H.; Menne, M.J.; Smith, T.M.; Vose, R.S.; Zhang, H.-M. Extended reconstructed sea surface temperature version 5 (ERSSTv5): Upgrades, validations, and intercomparisons. J. Clim. 2017, 30, 8179–8205. [Google Scholar] [CrossRef]
- Barnston, A.B.; Livezey, R. Classification, seasonality, and persistence of low-frequency atmospheric circulation patterns. Mon. Wea. Rev. 1987, 115, 1083–1126. [Google Scholar] [CrossRef]
- Thompson, D.; Wallace, J. The arctic oscillation signature in wintertime geopotential heights and temperature fields. Geophys. Res. Lett. 1998, 25, 1297–1300. [Google Scholar] [CrossRef]
- Climate Prediction Center. Teleconnection Indices. Available online: https://www.cpc.ncep.noaa.gov (accessed on 4 June 2024).
- SPC National Severe Weather Database Browser Severe Plot. Available online: https://www.spc.noaa.gov/climo/online/sp3/ (accessed on 5 June 2024).
- Doswell, C.A.; Brooks, H.E.; Kay, M.P. Climatological estimates of daily nontornadic severe thunderstorm probability for the United States. Wea. Forecast. 2005, 20, 577–595. [Google Scholar] [CrossRef]
- Cristianini, N.; Shawe-Taylor, J. An Introduction to Support Vector Machines and Other Kernel-Based Methods; Cambridge University Press: Cambridge, UK, 2000; pp. 149–161. [Google Scholar]
- Fujita, T. Jumbo tornado outbreak of 3 April 1974. Weatherwise 1974, 27, 116–126. [Google Scholar] [CrossRef]
- Corfidi, S.; Weiss, S.; Kain, J.; Corfidi, S.; Rabin, R.; Levit, J. Revisiting the 3-4 April 1974 super outbreak of tornadoes. Wea. Forecast. 2010, 25, 465–510. [Google Scholar] [CrossRef][Green Version]
- Knupp, K.; Murphy, T.; Coleman, T.; Wade, R.; Mullins, S.; Schultz, C.; Schultz, E.; Carey, L.; Sherrer, A.; McCaul, E.; et al. Meteorological overview of the devastating 27 April 2011 tornado outbreak. Bull. Am. Meteor. Soc. 2014, 95, 1041–1062. [Google Scholar] [CrossRef]
- Chasteen, M.; Koch, S. Multiscale aspects of the 26-27 April 2011 tornado outbreak. Part I: Outbreak chronology and environmental evolution. Mon. Wea. Rev. 2022, 150, 309–335. [Google Scholar] [CrossRef]
- Fujita, T.; Bradbury, D.; Thullenar, C. Palm Sunday tornadoes of 11 April 1965. Mon. Wea. Rev. 1970, 98, 29–69. [Google Scholar] [CrossRef]
- Efron, B.; Tibshirani, R. An Introduction to the Bootstrap; CRC Press: Boca Raton, FL, USA, 1994; p. 456. [Google Scholar]
- Wang, L.; Ting, M.; Kushner, P. A robust empirical seasonal prediction of winter NAO and surface climate. Sci. Rep. 2017, 7, 279. [Google Scholar] [CrossRef] [PubMed]
- Bove, M. Impacts of ENSO on United States tornado activity. Prepr. 19th Conf. Sev. Local Storms 1998, 313, 316. [Google Scholar]
- Allen, J.; Molina, M.; Gensini, V. Modulation of annual cycle of tornadoes by El Niño-Southern Oscillation. Geophys. Res. Lett. 2018, 45, 5708–5717. [Google Scholar] [CrossRef]
- Brooks, H.; Doswell, C.; Kay, M. Climatological estimates of local daily tornado probability for the United States. Wea. Forecast. 2003, 18, 626–640. [Google Scholar] [CrossRef]
- McCormick, A.; Mercer, A. Diagnosing the relationship between the Madden–Julian Oscillation and United States severe convective weather outbreaks. Int. J. Climatol. 2023, 43, 6963–6978. [Google Scholar] [CrossRef]


| Diagnostic | γ | Cost | R2 (Linear) | R2 (Exponential) | R2 (SVR) |
|---|---|---|---|---|---|
| Total tornadoes (mean) | 0.4 | 10 | 0.645 | 0.635 | 0.697 |
| Total tornadoes (std. dev.) | 0.4 | 10 | 0.506 | 0.496 | 0.533 |
| Weak tornadoes (mean) | 0.1 | 10 | 0.748 | 0.682 | 0.813 |
| Weak tornadoes (std. dev.) | 0.2 | 10 | 0.671 | 0.638 | 0.716 |
| Percentile | El Niño (N = 21) | Neutral (N = 21) | La Niña (N = 20) | El Niño (N = 21) | Neutral (N = 21) | La Niña (N = 20) |
|---|---|---|---|---|---|---|
| 2.5% | 105.4 | 98.9 | 98.7 | −0.051 | −0.033 | −0.047 |
| 50% | 111.6 | 106.2 | 107.5 | −0.009 | 0.023 | 0.010 |
| 97.5% | 117.9 | 114.0 | 116.2 | 0.033 | 0.090 | 0.080 |
| Percentile | Degrees of Freedom | Sum of Squares | Mean Sum Sq. | F | p |
|---|---|---|---|---|---|
| Regression | 3 | 373 | 124.33 | 2.01 | 0.112 |
| Residuals | 740 | 45,823 | 61.92 |
| Percentile | Degrees of Freedom | Sum of Squares | Mean Sum Sq. | F | p |
|---|---|---|---|---|---|
| Regression | 3 | 849 | 283 | 4.62 | 0.003 |
| Residuals | 740 | 45,347 | 61.28 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mercer, A.; Swan, K.; Knight, A. Quantifying Tornado Outbreak Intensity and Frequency Relationships with Interannual and Monthly Variability. Atmosphere 2024, 15, 909. https://doi.org/10.3390/atmos15080909
Mercer A, Swan K, Knight A. Quantifying Tornado Outbreak Intensity and Frequency Relationships with Interannual and Monthly Variability. Atmosphere. 2024; 15(8):909. https://doi.org/10.3390/atmos15080909
Chicago/Turabian StyleMercer, Andrew, Kenneth Swan, and Adonte Knight. 2024. "Quantifying Tornado Outbreak Intensity and Frequency Relationships with Interannual and Monthly Variability" Atmosphere 15, no. 8: 909. https://doi.org/10.3390/atmos15080909
APA StyleMercer, A., Swan, K., & Knight, A. (2024). Quantifying Tornado Outbreak Intensity and Frequency Relationships with Interannual and Monthly Variability. Atmosphere, 15(8), 909. https://doi.org/10.3390/atmos15080909







