Abstract
This study delves into the application of Shannon entropy to analyze the long-term variability in climate data, specifically focusing on precipitation and temperature. By employing data from 1901 to 2010 across 377 catchments worldwide, we investigated the dynamics of climate variables using the generalized extreme value (GEV) distribution and Shannon entropy measures. The methodology hinged on the robust bootstrap technique to accommodate the inherent uncertainties in climatic data, enhancing the reliability of our entropy estimates. Our analysis revealed significant trends in entropy values, suggesting variations in the unpredictability and complexity of climate behavior over the past century. These trends were critically assessed using non-parametric tests to discern the underlying patterns and potential shifts in climate extremes. The results underscore the profound implications of entropy trends in understanding climate variability and aiding the prediction of future climatic conditions. This research not only confirms the utility of Shannon entropy in climatological studies but also highlights its potential in enhancing our understanding of complex and chaotic climate systems. The study’s findings are vital for developing adaptive strategies in response to the evolving nature of climate extremes, thus contributing to more informed decision-making in environmental management and policy formulation.
1. Introduction
Climate extremes such as droughts, floods, high and low temperature extremes, and storms have the potential to significantly impact economic sectors closely linked to climate, such as water management, agriculture, food security, energy security, forestry, health, and tourism. Changes in these sectors can have far-reaching consequences for countries whose economies rely heavily on them [1,2,3]. Most research work performed to date on climate change unfortunately overlooks or downplays the importance of the variability in climate extremes [3]. This is evident in studies focused on reducing the vulnerability of agriculture to short-term hydrometeorological events, which compound the challenge [4,5,6]. Given the existing needs, climate change adaptation policies are insufficient [7].
The variability of climate characteristics such as temperature and precipitation is an important aspect of climate change risk assessment, as it affects the intensity and frequency of extreme events. The IPCC report [8,9,10] points out that expected changes in the variability of precipitation and temperature in the future will be characterized by a high degree of uncertainty. Additionally, there is a need to develop methods and algorithms that can improve the efficiency of predicting and estimating the intensity of climate hazards, as suggested by other studies [3,11]. The Earth’s atmospheric system is too complex to be described deterministically, meaning that predicting its future state is difficult or impossible [12]. It is an open system, driven mainly by the continuous influx of solar radiation and the Earth’s rotation. The system is too large to solve deterministically due to the following factors: the amount of data needed to describe its state, incomplete instrumentation to monitor its state, the lack of a correct way to spatially partition the system for long-term analysis, and the absence of accurate historical data prior to 1900. Therefore, stochastic analyses can be useful in assessing the variability of climatic conditions [12]. Analyses of entropy directions show that if global warming were to continue, a decrease in thermodynamic entropy would mean more free energy driving the weather; an increase in informational entropy would mean difficulty in predicting the direction of the process [12]. One potential tool to assist with this is the Shannon entropy trend assessment. Entropy analysis can provide information on the degree of irregularity, unpredictability, and variability in climate systems, which can be valuable for developing more accurate forecasts and risk management strategies for extreme climate events [13].
Climate change is a phenomenon that leads to significant spatial and temporal heterogeneity in its impacts on biological systems, health, and economic sectors [14]. Studies have shown that global increases in average temperature obscure important differences in temperature changes between land and sea, as well as across small and large regions [15,16,17]. Furthermore, climate change inevitably results in alterations to the frequency, intensity, spatial extent, duration, and timing of extreme weather and climate events [3,18]. Extreme values can be analyzed in terms of changes in the types and parameters of probability distributions and trends in statistical characteristics (e.g., minimum and maximum values) [19]. Additionally, the variability of extreme values can be examined through the characteristics of the tails of extreme distributions [20]. An effective tool in this analysis is time–frequency analysis, which facilitates the study of changes over time and frequency, proving especially valuable for examining correlations between various characteristics that describe climate variability [21,22,23]. It is also feasible to monitor changes in Shannon entropy and its trends as a measure of climate variability and the extreme phenomena resulting from this variability [13,24,25]. Shannon entropy measures the degree of disorder or unpredictability within a system, and an increase in entropy can signify greater climate variability. The analysis of Shannon entropy and other statistical measures can be instrumental in assessing climate variability and extremes.
Projections indicate that climate and weather variability will increase as the planet warms. Changes in the frequency and intensity of climate extremes, along with the instability of weather patterns, will have significant consequences for both human and natural systems. By the end of this century, the frequency of extreme conditions, such as heat stress, droughts, and floods, is projected to increase, leading to numerous negative impacts beyond those resulting from changes in mean values alone [1,2]. Given the uncertainty associated with forecasts of changes in extremes and the limited confidence in these forecasts, it is crucial to perform trend analyses and analyses of extreme values based on the longest possible series of measurements. The low certainty of forecasts and high confidence in these forecasts do not eliminate the possibility of extreme changes. Considering the limitations in understanding climate processes in different regions, there exists the possibility of extreme changes with low probability but significant impact. The observed changes in extremes provide evidence that some of these changes are due to anthropogenic influences [1]. The analysis of historical observations of climate variables indicates anthropogenic climate change [26,27,28]. Studying changes in precipitation and temperature variability [29,30,31], depending on the observed period, reveals changes in trends and allows us to assess the direction of these changes [32,33]. However, attributing individual extreme events to these influences remains a challenge. An example includes analyses performed on climate variability at different periods and scales within a region (e.g., in the rhythm of multi-decadal oscillations) [34,35,36]. The observed changes in the magnitude, frequency, and timing of extreme events represent one of the first analyses of this under-researched phenomenon, in which patterns have been shown to be complex and not always consistent with previous studies [10,26,36,37,38].
The increase in entropy significantly impacts the unpredictability of weather, which complicates the planning of adaptation measures. This can lead to sudden transitions between extreme states in a short period. A rise in the entropy of the climate system heightens the degree of chaos and unpredictability, resulting in increased weather variability, more frequent extreme climatic events, and challenges in predicting long-term trends. Elevated entropy can adversely affect sectors like agriculture, which depend on stable weather conditions for efficient production. Conversely, an increase in entropy might also enhance biodiversity, as organisms are forced to adapt to more variable environmental conditions.
There is a complex interaction between polarization feedback and the increased entropy within the climate system [39,40]. Polarization feedback refers to rapid changes in the direction and intensity of climatic phenomena over a brief period. Abrupt shifts between weather extremes, such as sudden transitions from drought to torrential rain or from extreme cold to heat, are examples of polarization feedback. The interplay between polarization and increased entropy suggests that these phenomena mutually reinforce each other. Rapid weather changes, a characteristic of polarization, contribute to greater weather variability and a rise in entropy. Consequently, an increase in entropy can lead to larger jumps between extreme weather states, further amplifying polarization. Thus, understanding the positive feedback mechanisms in the climate system, including polarization and entropy, is crucial for comprehending climate change and devising effective management and adaptation strategies.
The interactions among climate variables can affect the occurrence of hurricanes, tornadoes, and droughts. Moreover, these interactions can impact a measure of risk encompassing threats to life, livelihoods, health, well-being, ecosystems, species, and economic, social, and cultural resources, including services and infrastructure. Risk emerges from the interplay between system vulnerability, exposure, and external forcing [15,41,42]. Consequently, one phenomenon can either amplify or mitigate another, complicating the understanding of climate change’s scope. Anthropogenic factors, such as industrial activities, deforestation, land use changes, pollutant emissions, and greenhouse gas emissions [43,44,45], can influence the variability of extreme values and the polarization of climate factors [15,39,46].
The overarching goal of this study is to address this gap by applying Shannon entropy—an informational measure that quantifies uncertainty and randomness within a system—to long-term climate data sequences. By doing so, this research aims to offer a new perspective in the assessment of climate variability and change.
The specific objectives of this study include the following:
- employing Shannon entropy to quantify the unpredictability and complexity of precipitation and temperature distributions over a century-long period across 377 global catchments.
- utilizing the bootstrap method to enhance the reliability of entropy calculations given the constraints of data sequence lengths and volumes.
- analyzing trends in entropy values to discern significant changes and patterns in climatic data, which can offer insights into the future direction of climate variability and extremes.
By explicitly framing these objectives and the scientific questions they address, this study underlines the importance of understanding entropy trends in climatic data for predicting future climate conditions. Such insights are critical not only for advancing scientific understanding but also for informing policy and decision-making processes related to climate risk management and adaptation strategies. Through rigorous statistical analysis and the innovative application of Shannon entropy, this research endeavors to contribute a unique methodological approach to the study of climate dynamics and its implications on a global scale.
2. Data Preparation for Analysis
This paper utilizes grided data for the monthly precipitation totals from the Global Precipitation Climatology Center (GPCC) and grided data for monthly mean temperatures from the National Oceanic and Atmospheric Administration (NOAA). The data have a spatial resolution of 0.5° by 0.5° and maintain consistency in spatial and temporal dimensions. Products from both GPCC and NOAA are accessible online [47,48,49,50], though they are not available in real time.
This study investigates global Shannon entropy trends in monthly precipitation totals and monthly mean temperatures across 377 river basins spanning all continents. These 377 river basins were selected based on data provided by the Global Runoff Data Centre (GRDC) and identified as areas at risk of extreme events [44,51,52].
With an assumed total land area of 509.9 million square kilometers, the analysis encompasses 12.76% of the world’s land area. Table 1 details the geographic coverage of the analysis.

Table 1.
Areas covered in the World Meteorological Organization (WMO) region analysis [38].
Data from GPCC and NOAA were converted to represent catchment areas. This process produced a sequence of monthly precipitation and temperatures, forming the basis of the analyses presented in this article, which span the years from 1901 to 2010.
3. Methodology
There is now a growing body of scientific evidence confirming that human activities are influencing climate change, leading to shorter periods of high-intensity precipitation and longer phases of high temperatures alongside low precipitation. The variability of extreme events, such as floods and droughts, has become increasingly apparent and can be attributed to the erratic nature and intensity of human activities. Therefore, investigating the factors associated with climate variability, particularly monthly precipitation and mean monthly temperatures, is crucial for understanding climate change at the regional level. Such understanding is key to developing strategies for managing water resources and reducing the risk of floods and droughts.
For the analysis, minimum and maximum values of monthly precipitation, along with minimum and maximum mean monthly temperatures over the year, were selected. Given the goal of assessing long-term climate variability, it is advantageous to perform analyses on averages rather than on extreme values for several reasons. Analyses based on averages offer greater statistical stability. Averages exhibit less variability than extreme values, which means that for the same dataset, the standard error of the average estimator will be smaller than that of the extreme value estimator. Statistical stability is particularly crucial for long-term analyses, as variability in values can significantly impact the interpretation of results and subsequent decision-making. Another advantage is the larger number of observations available; analyses on averages can be conducted on a more extensive set of observations than analyses on extreme values, yielding more representative results. It should be noted that analyses based on averages better reflect reality, providing insights into typical values that are more indicative of long-term changes than extreme values. Furthermore, extreme values may result from random factors or unpredictable events that do not represent typical conditions. In summary, for identifying long-term changes, analysis based on averages offers more statistical stability and allows for a greater number of observations, presenting a more accurate reflection of typical values. This approach is essential for informed decision-making and effective planning.
Calculations of Shannon’s entropy variability were conducted for the left constraint based on the minimum values of monthly precipitation and the monthly mean temperature. For the right-hand constraint, Shannon entropy variability calculations were carried out using the maximum values of monthly precipitation and the mean monthly temperature. Given the dataset’s limited size, a bootstrap technique [53,54] was employed to evaluate the extreme distributions of the minimum and maximum values of Shannon entropy variability.
4. Bootstrap Resampling Technique
In this study, the bootstrap resampling technique was employed to estimate the parameters of the distribution for extreme precipitation and temperature values. The fundamental principle of the bootstrap method involves generating large samples through resampling from the original data with replacement, under the assumption that these samples are independent and identically distributed. This method is favored not only for its computational efficiency but also for its simplicity, which allows for the creation of bootstrap replications without relying on the assumption of a known underlying distribution [55]. It operates solely based on the information derived from the sample data.
The steps of the bootstrap method used in this study are described as follows:
- Population sequences of annual minimum and maximum values from monthly precipitation and annual minimum and maximum values from monthly average temperatures were created:
- For the estimation of GEV parameters describing the minimum values:
- For the estimation of the GEV parameters describing the maximum values:
The number of elements in both the precipitation and temperature sequence does not reliably allow an assessment of Shannon entropy values at the 5% significance level. A 1000-fold number of draws from the seventy-element sequence was assumed. For the assessment of Shannon entropy trends, the seventy-element strings were assumed to be created in the following recursive manner:
- For the estimation of Shannon entropy values based on the GEV distribution describing minimum values:
- For the estimation of Shannon entropy values based on the GEV distribution describing the maximum values:
Forty seventy-element strings were arbitrarily obtained in this way. These strings provided a resource for 1000-fold bootstrap draws. In this way, forty 1000-fold bootstrapped strings were created, from which the Shannon entropy was calculated at the 5% significance level for both precipitation and temperature for minimum and maximum values (Figure 1).
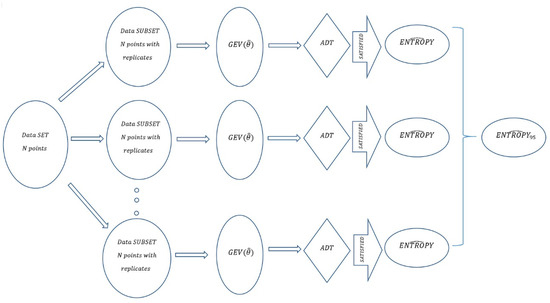
Figure 1.
Schematic of the bootstrap process for estimating Shannon entropy at the 5% significance level for a selected catchment for a seventy-element sequence.
- 2.
- It was assumed that the series of annual minimum and maximum monthly precipitation and average temperature values were original samples, and the total length of multi-year records.
- 3.
- Bootstrap samples of the minimum and maximum series of precipitation and temperature were drawn using the bootstrapping process, which involves randomly selecting values to replace the original sample.
- 4.
- The above analysis was performed on all analyzed catchments.
For each sequence drawn, the Anderson–Darling Test (ADT) was conducted to assess the fit of the GEV distribution at the 5% significance level (Figure 1). If the fit was not confirmed, the results of that experiment were disregarded, and the process proceeded to the next draw. In estimating the GEV parameters for the minimum values, the ADT test confirmed agreement at the 5% significance level in 91% of occasions, and for the maximum values, this level was achieved in 99.6% of cases. The GEV parameters were estimated using the maximum likelihood method [56,57,58]. The ADT test was chosen for its emphasis on the tail values of the distribution, which is crucial for extreme distributions. Subsequently, the Shannon entropy estimator’s value was calculated at the 5% significance level [54]. This methodology was applied to each of the 377 analyzed catchments (Figure 1). The analysis code was developed using Matlab software (R2021).
5. Fitting the GEV Distribution
Modeling the variability in climate extremes necessitates the consideration of extreme values for phenomena including precipitation, temperature, evaporation, and atmospheric pressure [59]. A commonly used approach in modeling extreme values involves extracting a sequence of observations from equal periods, such as the maximum of monthly totals or the minimum of monthly precipitation totals for a given year. Similarly, this approach is applied for the maximum from mean temperatures or the minimum from mean temperatures within a year, assuming that the set of extremes is independent and identically distributed. These data sets are then fitted to a probability distribution model, such as the Generalized Extreme Value distribution (GEV). As climate change impacts have become increasingly significant, numerous efforts have been directed towards accounting for non-stationarity in hydrological applications. A prevalent method involves applying various non-stationary models to non-stationary data and selecting the most appropriate model based on model diagnostics. Due to its flexibility in accommodating changes in data structures, maximum likelihood estimation for non-stationary model parameters is commonly employed for this purpose [57,58,60,61]. To date, this methodology has been extensively researched and is regarded as a ‘user-friendly’ approach. This study utilized such an approach.
The GEV distribution was used in the calculations [62,63,64].
The parameters refer to the shape parameter, scale and position [62], determined by the method of maximum likelihood (Maximum Likelihood Estimation).
6. Shannon Entropy
The concept of entropy, originally defined in the context of the second law of thermodynamics, quantifies the degree of disorder or randomness within a system. Claude E. Shannon adapted this concept for information theory, fundamentally transforming the way we measure information content in various scientific fields such as statistics, computer science, and beyond [12,54,65,66]. Since its inception, Shannon’s definition of entropy has expanded into applications across a diverse array of systems, including economic, social, financial, and notably, climate systems [12,40,67,68].
Shannon entropy measures the uncertainty involved in predicting the value of a random variable. It is calculated from the probability distribution of the data, with accuracy contingent on the precision of this distribution. A poorly estimated distribution can lead to incorrect entropy calculations, which can significantly affect the conclusions drawn about the system being studied. The formula for the Shannon entropy of a continuous random variable with a probability density function is defined as follows [69]:
where the integral spans all values for which . This measure reflects the amount of uncertainty or entropy associated with the outcomes of the variable .
To approximate the calculation of Shannon entropy for the GEV distribution, we can use the following formula [70,71,72]. It is important to note that the entropy for a continuous distribution, such as GEV, will require integration over the entire space where the probability density function (PDF) is non-zero. However, for simplification and direct application in the context of GEV, we can use the following approximate formula:
where is the Shannon entropy of the random variable with the GEV distribution, σ is the scale parameter of the GEV distribution, ξ is the shape parameter of the GEV distribution, and γ is the Euler–Mascheroni constant, which is approximately 0.5772156649.
In discussing the units of Shannon entropy for continuous distributions, the outcomes are commonly represented in information units, such as nats (derived from natural logarithms) or bits (utilizing base-2 logarithms). Notably, the entropy of continuous probability distributions, also referred to as differential entropy, may vary based on the measurement units of the random variable. Specifically, for the GEV distribution, calculating entropy analytically involves integrating the distribution’s probability density function alongside the logarithm of this function. Within the GEV context, the entropy units are contingent on the scale parameter units, which influence the dispersion of the random variable’s values. Hence, while entropy is denoted in nats or bits, its quantitative measure can be influenced by the units used for the distribution’s parameters, including the scale parameter [70,71].
Despite the widespread application of this measure, it is crucial to acknowledge the drawbacks and potential pitfalls associated with its use. Several limitations of Shannon entropy warrant attention:
- Measurement Scale Sensitivity: Entropy calculations are sensitive to the scale of measurement. The units used can significantly influence the computed entropy, necessitating precise definitions and appropriate scaling.
- Assumption of Even Distribution: In cases like meteorological data, assuming an even distribution across all outcomes may not hold, especially since variables like precipitation have natural bounds. This can result in underestimated entropy values.
- Neglect of Correlations: Ignoring correlations between variables such as temperature and precipitation can lead to oversimplified models that do not capture the full complexity of the data.
- Data Discretization: The process of categorizing data affects entropy calculations. The chosen method of discretization should align closely with the nature of the data to ensure accurate entropy measurement.
This research was dedicated to the calculation of Shannon’s entropy for extreme monthly precipitation totals and average temperatures, utilizing numerical integration techniques. The sequences generated from these calculations were pivotal in our further explorations of entropy’s variability across different climatic conditions. Anticipating critiques of Shannon’s entropy, our approach was rigorously designed to address its known limitations. This included the standardization of measurement units, the selection of GEV distribution parameters based on ADT tests, and the application of a uniform discretization methodology for all data analyzed. The Anderson–Darling Test (ADT), a statistical test for assessing the fit of an empirical distribution to a theoretical model, was employed to validate our data against the extreme value distribution. Through the application of MATLAB’s adtest function, configured for the extreme value distribution (…, ‘Distribution’, ‘ev’), we ensured our data’s compliance with the stringent criteria essential for the analysis of extreme climatic events.
7. Variability of Entropy
In the paper, entropy calculations were performed separately for minimum and maximum values. A measure was introduced to account for the variability in distributions that describe extreme values. The evaluation of Shannon entropy variability was based on the calculated trend values. For this purpose, the use of the Euclidean norm as a measure was proposed [73,74,75].
The Euclidean norm can be written as follows:
where are the coordinates of the vector.
In this study, variability was assessed based on the Shannon entropy trends for distributions describing minimum values and distributions describing maximum values, separately. This approach also facilitated the calculation of the resultant variability in Shannon’s entropy by treating the entropy trends for precipitation and temperature phenomena as separate vector coordinates. Ultimately, a measure was proposed to account for the variability in both precipitation and temperature extremes.
where:
- , [ln(mm)/year]—Shannon entropy trend for minimum rainfall values,
- , [ln(mm)/year]—Shannon’s entropy trend for maximum rainfall values,
- , [ln(°C)/year]—Shannon’s entropy trend for minimum temperature values,
- , [ln(°C)/year]—Shannon’s entropy trend for maximum temperature values,
- , [ln(mm)/year]—variation in Shannon’s entropy for extreme precipitation values,
- , [ln(°C)/year]—variation in Shannon’s entropy for extreme temperature values,
- , ]—variation in Shannon’s entropy for extreme values of precipitation and temperature.
The Euclidean norm is just one among many methods used to measure the dynamics of climate variability. Its application to Shannon entropy trends for temperature and precipitation extremes aids in understanding climate variability. This method facilitates the comparison of different time periods and geographic regions to determine whether the dynamics of climate variability are intensifying, diminishing, or remaining stable. However, the Euclidean norm itself does not reveal the causes behind these changes but merely quantifies the degree of variability. It is important to note that using the Euclidean norm derived from Shannon’s entropy trends for minimum and maximum temperature and precipitation values is only one of several approaches used to analyze climate entropy variability. Therefore, it should be regarded as a complement to other research methodologies, not as the sole method of analysis.
8. Statistical Tests Used
In evaluating the entropy trends for both precipitation and temperature, bootstrap resampling techniques were utilized to generate sequences for calculating the Shannon entropy and estimating the parameters of the Generalized Extreme Value (GEV) distribution. The characteristics and patterns of these trends were verified using the Mann–Kendall Test (MK) at a 5% significance level. Additionally, points of change in the entropy trend were identified using the Pettitt Change Point Test (PCPT), also at the 5% significance level. If a change point was confirmed at this level of significance, a new trend form for the subsequent sub-series was determined using the MK. The suitability of the GEV distribution for each sequence of extreme values analyzed was evaluated through the Anderson–Darling Test (ADT), conducted at the 5% significance level.
To examine trends within a given time series, the MK test was utilized [76,77]. This test, recommended by the World Meteorological Organization for public use, does not depend on the distribution type, and there is no need to assume any specific data distribution function [78]. It has been extensively used in scientific studies to evaluate water resource data trends [19,27,77,79]. The trend magnitude is estimated using a nonparametric median-based slope estimator proposed by Sen [80] and extended by Hirsch [81]. In this study, the Shannon entropy trend was examined with this test.
Several methods [19,38,77,82,83] can be used to determine time series change points. In this analysis, the nonparametric Pettitt change point test [84] was applied to detect change occurrences. The PCPT, an abrupt change test in time sequences, is utilized to identify the turning point where a sudden change, or “spike”, occurs. It involves comparing the sum of the ranks of two subsets of data, divided by a threshold value, to ascertain if there is a statistically significant change. This test, suitable for any data distribution, does not rely on the normality assumption. The Pettitt test result, based on the test statistic value compared against the critical value at the significance level, determines whether the null hypothesis of no abrupt change can be rejected.
The PCPT has been widely applied to detect changes in climatic and hydrological time series [19,85,86,87]. In the current study, the presence of change points in the Shannon entropy time series for extreme values of monthly precipitation totals and monthly mean temperatures was investigated. For series exhibiting a significant change point, the trend test is applied to the sub-series; otherwise, it is applied to the entire series [19].
9. Analysis of Shannon’s Entropy Trend Variation
This paper examines the variability in the Shannon entropy in long-term precipitation and temperature sequences to assess the polarity of climate phenomena. Shannon entropy serves as a measure of indeterminacy and unpredictability in climate phenomena—specifically precipitation and temperature—facilitating an analysis of their variability over time. An increase in Shannon entropy within precipitation sequences suggests heightened variability, potentially heralding extreme weather events such as intense rainfall or droughts. Similarly, a rise in Shannon entropy within temperature sequences indicates greater temperature variability, which could foretell extreme conditions like heatwaves or severe cold spells. Analyzing the variability in Shannon entropy helps identify regions experiencing increased climate polarization. Elevated entropy values signal greater climate variability and unpredictability, which may precipitate significant environmental shifts. These shifts could include alterations in the distribution of flora and fauna, changes in weather patterns, and sea level changes [88].
The variability in entropy trends can serve as a crucial indicator of climate change, aiding in the prediction of future shifts in precipitation and temperature. A decrease in precipitation entropy trends could signify that the region is undergoing periods of drought or experiencing extreme precipitation events, potentially leading to flooding. Conversely, an increase in precipitation entropy trends might reflect greater variability in the amount and timing of rainfall, complicating water resource management. Changes in temperature entropy trends can impact plant growth, biological processes, and animal migration [89,90]. A decrease in temperature entropy trends could indicate a more stable climate, but it may also hinder the ability of organisms to adapt to changing conditions. On the other hand, an increase in temperature entropy trends could signal more unstable climatic conditions, increasing the risk of extreme weather events such as heatwaves or storms.
Assessing the Shannon entropy trends for extreme precipitation and temperature values is a crucial tool in climate variability studies [91,92]. Analyzing historical observations enables an accurate assessment of the variability in precipitation and temperature over the observed period and allows for the determination of the direction of these changes [93]. Studying Shannon entropy facilitates the identification of trends and shifts within these trends in extreme datasets. Employing statistical techniques, such as Shannon entropy trend analysis, improves the accuracy of predictions and informs appropriate preventive measures. Ultimately, the use of statistical techniques in climate variability research is vital, especially in predicting the variability of extreme events [26,94,95,96,97,98,99,100].
The study of entropy trend change points—shifts in the direction or nature of precipitation and temperature trends—may result from various atmospheric factors and phenomena. This study does not delve into the causes of these trend changes. However, it is possible to generally outline potential causes:
- Climate Cycles: Multi-year and decadal climate cycles, such as El Niño, La Niña, the North Atlantic Oscillation (NAO), or the El Niño-Southern Oscillation (ENSO), influence regional and global precipitation patterns. Shifts in these cycles can lead to changes in precipitation trends [101,102,103];
- Changes in Atmospheric Circulation Driven by Solar Radiation: Solar radiation affects atmospheric circulation by modifying wind patterns, atmospheric currents, and high and low-pressure systems. These changes directly impact local precipitation patterns [104];
- Changes in Earth and Ocean Surface Temperatures: Solar radiation causes the heating of the Earth’s surface and oceans, leading to changes in atmospheric circulation. For example, stronger solar radiation in tropical regions can increase convection, leading to more intense rainfall [104];
- Formation and Movement of Pressure Systems: Changes in solar radiation influence the formation of high and low-pressure systems. Increased surface temperatures can lead to the formation of low-pressure areas that attract moist air from the oceans, resulting in increased rainfall in certain regions [10,104];
- Impact on Global Atmospheric Circulation Patterns: Solar radiation affects large-scale atmospheric circulation patterns, such as Hadley cells, polar circulation, and trade winds. Changes in these patterns can influence the shifts in rainfall zones, such as monsoon airflows that determine seasonal rainfall in many parts of the world [21,104];
- Ocean Surface Temperature Changes: These are crucial in shaping regional precipitation patterns, with anomalies like El Niño and La Niña influencing precipitation changes {Formatting Citation};
- Urbanization: Urban expansion and land-use changes can alter local precipitation patterns through the “heat island effect” and changes in air circulation [104];
- Global Climate Change: Human-induced climate changes, such as greenhouse gas emissions and global warming, can influence precipitation patterns on both global and regional scales [104];
- Topography: Landforms, through the “orographic effect”, can impact local precipitation patterns [31,104];
- Ocean–Atmosphere Interactions: Changes in these interactions, including ocean currents and deep ocean upwelling, can influence regional precipitation patterns [105];
- Industrial Development: Industrial activities and associated greenhouse gas emissions and air pollution can affect climate change and precipitation patterns. Emissions like CO2 and CH4 contribute to global warming, while air pollutants can influence cloud formation and rainfall [106];
- Agricultural Development: Changes in land use, deforestation, and soil use can alter air circulation and moisture, affecting local precipitation patterns along with agricultural practices like fertilization and irrigation [104,106];
- Glacial and Ice Cap Melting: The reduction in glaciers and ice caps affects albedo, leading to more heat absorption by the Earth, contributing to global warming [104,106,107];
- Solar Activity Changes: Fluctuations in solar activity affect the amount of solar radiation reaching the Earth, influencing climate and surface temperatures [104,106,108];
- Volcanism: Volcanic eruptions can introduce dust and gases into the atmosphere, affecting short-term global temperature changes [107,109];
- Other Natural Factors: Sometimes, changes in temperature trends may result from natural climate variations, like solar–magnetic cycles and ocean circulation changes [110].
10. Results of the Analyses and Discussion
In this study, Shannon entropy trends were analyzed based on long-term sequences of monthly precipitation totals and mean temperatures across 377 catchments within six WMO regions. Sequences of minimum and maximum values for precipitation and temperatures were extracted from the analyzed data. To clearly assess the entropy trends for both precipitation and temperature, the bootstrap resampling method was utilized to create Shannon entropy sequences and estimate parameters for the Generalized Extreme Value (GEV) distribution. The validity of these trend forms was confirmed using the Mann–Kendall Test (MK) at a 5% significance level. Additionally, the Pettitt Change Point Test (PCPT) was applied at the same significance level to detect any shifts in the entropy trends. If a change point was substantiated at the 5% level, a new trend form for the subsequent data subset was defined using the MK; if not, the corresponding entry was left blank in the tables. The appropriateness of the GEV distribution for each sequence of extreme values was assessed using the Anderson–Darling Test (ADT), also at the 5% significance level. The results are depicted graphically, providing a clearer and more precise visualization of the evolving trends.
Figure 2 illustrates the Shannon entropy trends for the minimum monthly precipitation totals. The least negative entropy trend values for the minimum monthly precipitation occurred in the river catchments listed in Table 2. Notably, in the Daule River catchment in Ecuador, the decreasing trend significantly worsens, almost doubling from a value of (−0.040) to (−0.074) [ln(mm)/year]. The 1980s mark a period of shifting trends. In these catchments, fewer extreme droughts or intense rainfall events can be anticipated, potentially benefiting agriculture and water resource management. A lower entropy for the minimum precipitation may suggest more predictable precipitation patterns, thereby aiding in the planning and management of water resources.
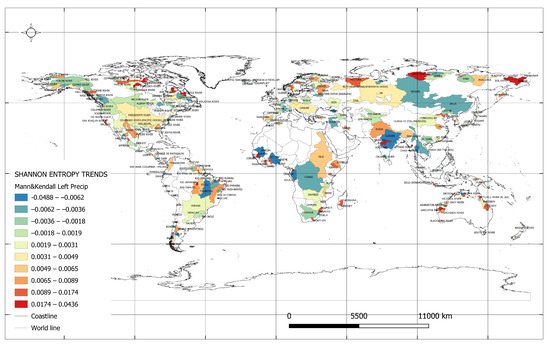
Figure 2.
Shannon entropy trends for values of minimum monthly precipitation totals.

Table 2.
River basins in which the smallest decreasing values of Shannon entropy trends were found for the minimum monthly precipitation values at the 5% level of significance.
The highest entropy trend values for the minimum monthly precipitation were observed in the river catchments listed in Table 3. Notably, in the Anyuy River catchment in the Russian Federation, there was a more than fourfold decrease in Shannon entropy, from a value of 0.036 to 0.008 [ln(mm)/year] in 1990. The early 1990s marked a period of shifting trends. For the Khatanga River catchment, also in the Russian Federation, there was a trend reversal, moving from a value of 0.033 to −0.002 [ln(mm)/year]. This significant change in trend occurred in 1990. In these catchments, an increase in entropy for minimum precipitation signifies greater variability and instability in atmospheric conditions, potentially leading to prolonged drought periods. Such conditions are particularly detrimental to agriculture, leading to reduced crop yields and exacerbating food security concerns.

Table 3.
River catchments in which the largest increasing values of Shannon entropy trends were found for the minimum monthly precipitation values at the 5% level of significance.
Figure 3 illustrates the Shannon entropy trends for the maximum monthly precipitation totals. The lowest entropy trend values for the maximum monthly precipitation were observed in the river catchments listed in Table 4. Specifically, in the St. Johns River catchment in the United States, the trend deepened twofold, shifting from a value of (−0.010) to (−0.020) [ln(mm)/year] in 1994. Similarly, in the Santa Cruz River catchment in Argentina, the trend nearly quadrupled in depth, moving from a value of (−0.008) to (−0.022) [ln(mm)/year] in 1997. In these catchments, a decrease in rainfall intensity variability can be anticipated, potentially impacting the water cycles and natural processes crucial for ecosystem health. However, increased stability in high-intensity precipitation might concurrently lead to flooding, posing significant risks to infrastructure and the safety and well-being of the population.
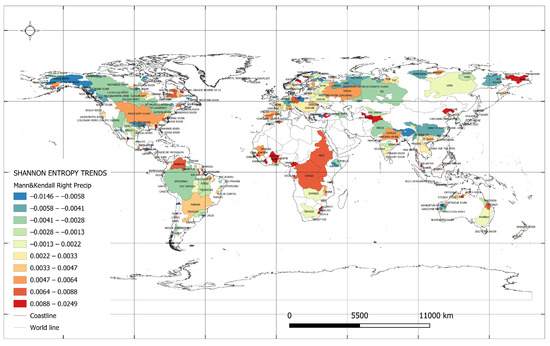
Figure 3.
Shannon entropy trends for values of maximum monthly precipitation totals.

Table 4.
River basins in which the smallest decreasing values of Shannon entropy trends were found for the maximum monthly precipitation values at the 5% level of significance.
The highest entropy trend values for the maximum monthly precipitation were observed in the river catchments listed in Table 5. For the Volta River catchment in Ghana, there was a twofold decrease in trend values from 0.014 to 0.008 [ln(mm)/year] in 1990. A similar trend was observed in the Anyuy River catchment in the Russian Federation, with values decreasing from 0.025 to 0.013 [ln(mm)/year] in the same year. These trends in the catchments suggest an increase in rainfall variability, which can impact water cycles and the natural processes vital for ecosystem health. While an increase in maximum precipitation might benefit the ecosystems of arid regions by providing more water, it can also lead to flooding and soil erosion. Therefore, reducing the variability in maximum precipitation could enhance ecosystem health. In the context of climate change, an increase in maximum precipitation is one of the anticipated consequences of global warming.

Table 5.
River catchments in which the largest increasing values of Shannon entropy trends were found for the monthly precipitation maxima at the 5% significance level.
Figure 4 displays the Shannon entropy trends for the minimum monthly average temperatures. The lowest entropy trend values for the minimum monthly average temperatures were observed in the catchments listed in Table 6. For example, the Churchill River catchment in Canada exhibited a twofold increase in the trend, moving from a value of (−0.007) to (−0.003) [ln(°C)/year] in 1987. In these catchments, the observed change in temperature entropy suggests a decrease in temperature variability compared to the past, indicating a trend towards a more stable climate.
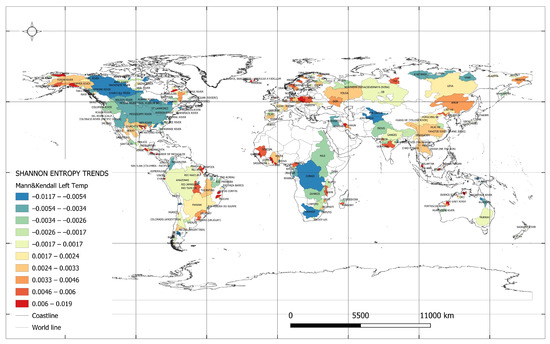
Figure 4.
Shannon entropy trends for minimum values of monthly average temperatures.

Table 6.
River catchments in which the smallest decreasing values of Shannon entropy trends were found for the minimum monthly average temperatures at the 5% level of significance.
The highest entropy trend values for the minimum monthly average temperatures were observed in the catchments listed in Table 7. The Svarta and Skagafjörður catchments in Iceland, along with the Thjorsa and Jökulsá á Fjöllum catchments, exhibited the largest trend values, ranging from 0.016 to 0.019 [ln(°C)/year]. For the first two catchments, there was a threefold decrease in trend values, dropping to magnitudes of 0.006 and 0.005 [ln(°C)/year], respectively. For the third catchment, a change in the trend year (1988) was identified, though a new trend value at the 5% significance level was not established. An increase in temperature entropy can exacerbate extreme weather conditions such as droughts, heatwaves, hurricanes, and storms, negatively impacting human, animal, and environmental health. Conversely, an increase in the entropy of minimum temperatures may benefit agriculture and vegetation growth. Nonetheless, further research is necessary to fully understand the implications of changes in temperature entropy and to devise strategies for adapting to climate change.

Table 7.
River basins in which the largest increasing values of Shannon entropy trends were found for the minimum monthly average temperatures at the 5% level of significance.
Figure 5 illustrates the Shannon entropy trends for the maximum monthly average temperatures. The lowest entropy trend values for the maximum monthly average temperatures were observed in the catchments listed in Table 8. Specifically, in the Nadym River catchment in the Russian Federation, the trend doubled, moving from a value of (−0.011) to (−0.021) [ln(°C)/year] in 1991. In the Loa River catchment in Chile, a reversal of the weather pattern was observed, with a change in trend direction from (−0.011) to 0.003 [ln(°C)/year] in 1983. In these catchments, a decreasing trend in maximum temperature entropy indicates a reduction in the variability of high temperatures, potentially signaling that extreme heat events are becoming less frequent. While this trend could positively impact human health, it might also influence ecosystems, including plants, animals, and microorganisms, that are accustomed to specific temperature ranges.
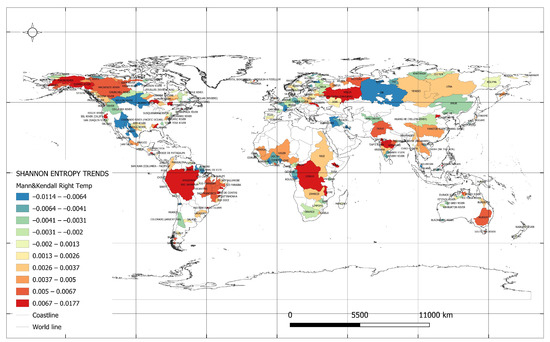
Figure 5.
Shannon entropy trends for maximum values of monthly average temperatures.

Table 8.
River basins in which the smallest decreasing values of Shannon entropy trends were found for the maximum monthly average temperatures at the 5% level of significance.
The highest entropy trend values for the maximum monthly average temperatures were observed in the catchments listed in Table 9. Specifically, the Juba River catchment in Somalia experienced a twofold decrease in trend values, from 0.010 to 0.005 [ln(°C)/year] in 1990. An increase in temperature entropy can lead to more extreme weather conditions, such as droughts, heatwaves, hurricanes, and storms, which may negatively impact human, animal, and environmental health.

Table 9.
River basins in which the largest increasing values of Shannon entropy trends were found for the maximum monthly average temperatures at the 5% level of significance.
Figure 6 displays the spatial locations of catchments where the most dynamic Shannon entropy trends for both minimum and maximum values of precipitation and temperature were identified at the 5% significance level. The maximum norm values reached 0.049 [] in the Daly River catchment, Australia, as shown in Table 10, while the smallest was 4 × 10−16 [] in the Kovda River catchment, Russian Federation. It is noteworthy that the dynamics of Shannon entropy for the minimum and maximum monthly average precipitation, when compared to the dynamics for minimum and maximum monthly average temperatures, exceed 1, ranging from 2.0 to 19.8 [ln(mm)/ln(°C)] (Table 10). The nearly twentyfold greater dynamics observed in the Anyuy River catchment, Russian Federation, in terms of precipitation relative to temperature, suggest that the variability in extreme precipitation values in this catchment far exceeds the variability in extreme temperature values. In simpler terms, extreme precipitation events are more varied and extreme than extreme temperature events. This may suggest that the region is subject to more extreme and varied precipitation-related weather phenomena, such as floods, storms, heavy rains, and droughts, compared to temperature-related phenomena like heatwaves and freezing temperatures.
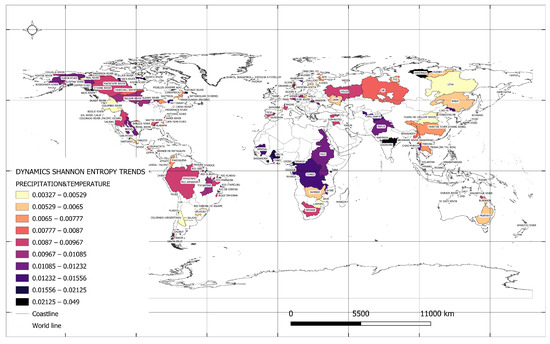
Figure 6.
Catchments in which the most dynamic Shannon entropy trends for extremes of precipitation and temperature were recognized at the 5% significance level.

Table 10.
River basins with the highest dynamics calculated from Shannon entropy trend values for the minimum and maximum monthly average precipitation and minimum and maximum monthly average temperatures at the 5% significance level.
11. Summary
This study underscores the utility of Shannon entropy in quantifying the disorder and complexity within climate distributions, focusing on critical climate variables such as precipitation and temperature. By identifying catchment areas where Shannon entropy trends reached a significant 5% level, this research has illuminated possible weather patterns and their directional changes. The bootstrap method was employed to analyze these entropy trends effectively, providing a robust framework for assessing the variability in climatic conditions across 377 catchment areas.
- Key Conclusions and Implications:
- Increased Variability: The analysis revealed a noticeable increase in the variability of both temperature and precipitation, suggesting that these elements have become less predictable. This increased variability is likely linked to the broader effects of climate change, highlighting a global trend towards more erratic weather patterns.
- Local and Regional Impact: The study pinpointed specific regions where significant changes in entropy were observed. These findings are crucial for local and regional planning as they provide insights into how climate change could affect specific areas differently. For instance, regions with increased entropy in precipitation may need to prepare more robustly for flood management and drought response strategies.
- Local and Regional Impact: The study pinpointed specific regions where significant changes in entropy were observed. These findings are crucial for local and regional planning as they provide insights into how climate change could affect specific areas differently. For instance, regions with increased entropy in precipitation may need to prepare more robustly for flood management and drought response strategies. An increase in precipitation entropy indicates greater variability and unpredictability in rainfall patterns, suggesting that these regions could experience more frequent and intense extreme weather events, such as heavy rainfall leading to floods, or prolonged dry spells resulting in droughts. This heightened variability makes it challenging to predict and manage water resources effectively. Therefore, understanding the relationship between precipitation and entropy helps local authorities to develop better risk management strategies and adaptive measures to mitigate the potential impacts of climate change. For example, regions with rising precipitation entropy should enhance their flood defenses, improve drainage systems, and implement water conservation practices to cope with the increased likelihood of both floods and droughts. These measures are essential to reduce the vulnerability of communities and ensure sustainable water management in the face of a changing climate.
- Global Implications: At a global level, the rise in entropy, particularly in areas critical to biodiversity and agriculture, suggests potential challenges in managing natural resources, food security, and ecosystem stability. This indicates a need for global strategies to mitigate the impact of increased climate unpredictability.
- Strategic Recommendations:
- Adaptive Management Strategies: Given the varied impact of climate change across different regions, adaptive management strategies that are tailored to local conditions are essential. This approach will help communities better prepare for and respond to the specific challenges posed by increased climate variability.
- Enhanced Risk Management: Understanding the trends in Shannon entropy can significantly enhance risk management strategies, particularly in designing infrastructure resilient to more extreme weather events and in developing more accurate forecasting models to predict such events.
- Policy and Practice: Policymakers and practitioners should consider these findings in their strategic planning to improve climate resilience. By integrating insights from entropy analyses, policies can be better shaped to address the unique challenges posed by the changing climate.
- Contribution to Climate Science:
- This study contributes significantly to climate science by providing a novel analytical approach to understanding the complexity and variability in climate systems through Shannon entropy. This method offers a new lens through which climatologists and policymakers can assess and respond to the impacts of climate change.
In conclusion, the application of Shannon entropy provides profound insights into the unpredictability of climate variables over a long-term period. These insights are crucial for developing more dynamic and informed responses to climate variability, urging the integration of entropy considerations into climate-related decision-making processes.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to the size of the data structures.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Rummukainen, M. Changes in climate and weather extremes in the 21st century. Wiley Interdiscip. Rev. Clim. Chang. 2012, 3, 115–129. [Google Scholar] [CrossRef]
- Viner, D.; Ekstrom, M.; Hulbert, M.; Warner, N.K.; Wreford, A.; Zommers, Z. Understanding the dynamic nature of risk in climate change assessments—A new starting point for discussion. Atmos. Sci. Lett. 2020, 21, e958. [Google Scholar] [CrossRef]
- Lal, P.N.; Mitchell, T.; Aldunce, P.; Auld, H.; Mechler, R.; Miyan, A.; Romano, L.E.; Zakaria, S.; Dlugolecki, A.; Masumoto, T.; et al. National Systems for Managing the Risks from Climate Extremes and Disasters; Cambrdige University Press: Cambridge, UK, 2012; Volume 9781107025. [Google Scholar]
- Elahi, E.; Khalid, Z.; Tauni, M.Z.; Zhang, H.; Lirong, X. Extreme weather events risk to crop-production and the adaptation of innovative management strategies to mitigate the risk: A retrospective survey of rural Punjab, Pakistan. Technovation 2022, 117, 102255. [Google Scholar] [CrossRef]
- Waseem, M.; Khurshid, T.; Abbas, A.; Ahmad, I.; Javed, Z. Impact of meteorological drought on agriculture production at different scales in Punjab, Pakistan. J. Water Clim. Chang. 2022, 13, 113–124. [Google Scholar] [CrossRef]
- Ogbuabor, J.E.; Egwuchukwu, E.I. The impact of climate change on the Nigerian economy. Int. J. Energy Econ. Policy 2017, 7, 217–223. [Google Scholar]
- Stephan, G. Intergenerational Fairness and Climate Change Adaptation Policy: An Economic Analysis. Green Low-Carbon Econ. 2023, 1, 105–109. [Google Scholar] [CrossRef]
- Zhang, X.; Alexander, L.; Hegerl, G.C.; Jones, P.; Tank, A.K.; Peterson, T.C.; Trewin, B.; Zwiers, F.W. Indices for monitoring changes in extremes based on daily temperature and precipitation data. Wiley Interdiscip. Rev. Clim. Chang. 2011, 2, 851–870. [Google Scholar] [CrossRef]
- Metz, B.; Meyer, L.; Bosch, P. Climate Change 2007: Mitigation of Climate Change Synthesis Report; Cambridge University Press: Cambridge, UK, 2007; Volume 9780521880114, pp. 1–861. [Google Scholar] [CrossRef]
- Kharin, V.V.; Zwiers, F.W.; Zhang, X.; Hegerl, G.C. Changes in temperature and precipitation extremes in the IPCC ensemble of global coupled model simulations. J. Clim. 2007, 20, 1419–1444. [Google Scholar] [CrossRef]
- Wanson, K.L.; Tsonis, A.A. Has the climate recently shifted? Geophys. Res. Lett. 2009, 36, L06711. [Google Scholar]
- Williams, J.M. Entropy shows that global warming should cause increased variability in the weather. arXiv 2000, arXiv:physics/0008228. [Google Scholar]
- Liu, B.; Chen, X.; Lian, Y.; Wu, L. Entropy-based assessment and zoning of rainfall distribution. J. Hydrol. 2013, 490, 32–40. [Google Scholar] [CrossRef]
- Ramirez-Villegas, J.; Lau, C.; Köhler, A.K.; Signer, J.; Jarvis, A.; Arnell, N.W.; Osborne, T.M.; Hooker, J. Climate analogues: Finding tomorrow’s agriculture today. CCAFS Work. Pap. 2011, 12, 40. [Google Scholar]
- Thornton, P.K.; Ericksen, P.J.; Herrero, M.; Challinor, A.J. Climate variability and vulnerability to climate change: A review. Glob. Chang. Biol. 2014, 20, 3313–3328. [Google Scholar] [CrossRef] [PubMed]
- Pfleiderer, P.; Schleussner, C.F.; Mengel, M.; Rogelj, J. Global mean temperature indicators linked to warming levels avoiding climate risks. Environ. Res. Lett. 2018, 13, 064015. [Google Scholar] [CrossRef]
- Bernstein, L.; Bosch, P.; Canziani, O.; Chen, Z.; Christ, R.; Davidson, O.; Hare, W.; Huq, S.; Karoly, D.; Kattsov, V.; et al. Climate Change 2007: An Assessment of the Intergovernmental Panel on Climate Change. Change 2007, 446, 12–17. [Google Scholar]
- Hussain, A.; Hussain, I.; Ali, S.; Ullah, W.; Khan, F.; Ullah, S.; Abbas, H.; Manzoom, A.; Cao, J.; Zhou, J. Spatiotemporal temperature trends over homogenous climatic regions of Pakistan during 1961–2017. Theor. Appl. Climatol. 2023, 153, 397–415. [Google Scholar] [CrossRef]
- Jaiswal, R.K.; Lohani, A.K.; Tiwari, H.L. Statistical Analysis for Change Detection and Trend Assessment in Climatological Parameters. Environ. Process. 2015, 2, 729–749. [Google Scholar] [CrossRef]
- Katz, R. Statistics of Extremes in Climatology and Hydrology. Adv. Water Resour. 2002, 25, 1287–1304. [Google Scholar] [CrossRef]
- Hussain, A.; Hussain, I.; Ali, S.; Ullah, W.; Khan, F.; Rezaei, A.; Ullah, S.; Abbas, H.; Manzoom, A.; Cao, J.; et al. Assessment of precipitation extremes and their association with NDVI, monsoon and oceanic indices over Pakistan. Atmos. Res. 2023, 292, 106873. [Google Scholar] [CrossRef]
- Hussain, A.; Hussain, I.; Ali, S.; Ullah, W.; Rezaei, A.; Ullah, S.; Abbas, H.; Manzoom, A.; Zhou, J.; Cao, J. Ocean-atmosphere circulation coherences associated with temperature increase in Pakistan. Environ. Res. Lett. 2023, 18, 094028. [Google Scholar] [CrossRef]
- Su, L.; Miao, C.; Duan, Q.; Lei, X.; Li, H. Multiple-Wavelet Coherence of World’s Large Rivers With Meteorological Factors and Ocean Signals. J. Geophys. Res. Atmos. 2019, 124, 4932–4954. [Google Scholar] [CrossRef]
- Saha, S.; Chattopadhyay, S. Exploring of the summer monsoon rainfall around the Himalayas in time domain through maximization of Shannon entropy. Theor. Appl. Climatol. 2020, 141, 133–141. [Google Scholar] [CrossRef]
- da Silva, V.D.P.R.; Belo Filho, A.F.; Almeida, R.S.R.; de Holanda, R.M.; da Cunha Campos, J.H.B. Shannon information entropy for assessing space-time variability of rainfall and streamflow in semiarid region. Sci. Total Environ. 2016, 544, 330–338. [Google Scholar] [CrossRef]
- Romanowicz, R.J.; Bogdanowicz, E.; Debele, S.E.; Doroszkiewicz, J.; Hisdal, H.; Lawrence, D.; Meresa, H.K.; Napiórkowski, J.J.; Osuch, M.; Strupczewski, W.G.; et al. Climate Change Impact on Hydrological Extremes: Preliminary Results from the Polish-Norwegian Project. Acta Geophys. 2016, 64, 477–509. [Google Scholar] [CrossRef]
- Palaniswami, S.; Muthiah, K. Change point detection and trend analysis of rainfall and temperature series over the vellar river basin. Pol. J. Environ. Stud. 2018, 27, 1673–1682. [Google Scholar] [CrossRef] [PubMed]
- Groves, D.G.; Yates, D.; Tebaldi, C. Developing and applying uncertain global climate change projections for regional water management planning. Water Resour. Res. 2008, 44, 1–16. [Google Scholar] [CrossRef]
- Heim, R.R. An overview of weather and climate extremes—Products and trends. Weather Clim. Extrem. 2015, 10, 1–9. [Google Scholar] [CrossRef]
- Ziernicka-Wojtaszek, A.; Kopcińska, J. Variation in atmospheric precipitation in Poland in the years 2001–2018. Atmosphere 2020, 11, 794. [Google Scholar] [CrossRef]
- Singh, P.; Gupta, A.; Singh, M. Hydrological inferences from watershed analysis for water resource management using remote sensing and GIS techniques. Egypt. J. Remote Sens. Space Sci. 2014, 17, 111–121. [Google Scholar] [CrossRef]
- Gómez, J.D.; Etchevers, J.D.; Monterroso, A.I.; Gay, C.; Campo, J.; Martínez, M. Spatial estimation of mean temperature and precipitation in areas of scarce meteorological information. Atmosfera 2008, 21, 35–56. [Google Scholar]
- Zhang, X.; Vincent, L.A.; Hogg, W.D.; Niitsoo, A. Temperature and precipitation trends in Canada during the 20th century. Atmos. Ocean 2000, 38, 395–429. [Google Scholar] [CrossRef]
- Tabari, H.; Madani, K.; Willems, P. The contribution of anthropogenic influence to more anomalous extreme precipitation in Europe. Environ. Res. Lett. 2020, 15, 104077. [Google Scholar] [CrossRef]
- Tabari, H.; Willems, P. Lagged influence of Atlantic and Pacific climate patterns on European extreme precipitation. Sci. Rep. 2018, 8, 5748. [Google Scholar] [CrossRef] [PubMed]
- Da Silva, A.S.A.; Barreto, I.D.D.C.; Cunha-Filho, M.; Menezes, R.S.C.; Stosic, B.; Stosic, T. Multiscale complexity analysis of rainfall in northeast brazil. Water 2021, 13, 3213. [Google Scholar] [CrossRef]
- Venegas-Cordero, N.; Kundzewicz, Z.W.; Jamro, S.; Piniewski, M. Detection of trends in observed river floods in Poland. J. Hydrol. Reg. Stud. 2022, 41, 101098. [Google Scholar] [CrossRef]
- Radziejewski, M.; Bardossy, A.; Kundzewicz, Z.W. Detection of change in river flow using phase randomization. Hydrol. Sci. J. 2000, 45, 547–558. [Google Scholar] [CrossRef]
- Twaróg, B. Assessing the Polarization of Climate Phenomena Based on Long-Term Precipitation and Temperature Sequences. Preprints 2023, 2023040380. [Google Scholar] [CrossRef]
- Silva, A.S.A.; Menezes, R.S.C.; Rosso, O.A.; Stosic, B.; Stosic, T. Complexity entropy-analysis of monthly rainfall time series in northeastern Brazil. Chaos Solitons Fractals 2021, 143, 110623. [Google Scholar] [CrossRef]
- Cardona, O.D.; Van Aalst, M.K.; Birkmann, J.; Fordham, M.; Mc Gregor, G.; Rosa, P.; Pulwarty, R.S.; Schipper, E.L.F.; Sinh, B.T.; Décamps, H.; et al. Determinants of risk: Exposure and vulnerability. In Managing the Risks of Extreme Events and Disasters to Advance Climate Change Adaptation: Special Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2012; Volume 9781107025, pp. 65–108. [Google Scholar] [CrossRef]
- Sillmann, J.; Thorarinsdottir, T.; Keenlyside, N.; Schaller, N.; Alexander, L.V.; Hegerl, G.; Seneviratne, S.I.; Vautard, R.; Zhang, X.; Zwiers, F.W. Understanding, modeling and predicting weather and climate extremes: Challenges and opportunities. Weather Clim. Extrem. 2017, 18, 65–74. [Google Scholar] [CrossRef]
- Chai, Y.; Yue, Y.; Zhang, L.; Miao, C.; Borthwick, A.G.L.; Zhu, B.; Li, Y.; Dolman, A.J. Homogenization and polarization of the seasonal water discharge of global rivers in response to climatic and anthropogenic effects. Sci. Total Environ. 2020, 709, 136062. [Google Scholar] [CrossRef] [PubMed]
- Kundzewicz, Z.W.; Robson, A. Detecting Trend and Other Changes in Hydrological Data. World Clim. Program. Water 2000, 1013, 158. [Google Scholar]
- Christensen, J.H.; Kanikicharla, K.K.; Aldrian, E.; An, S.I.; Albuquerque Cavalcanti, I.F.; de Castro, M.; Dong, W.; Goswami, P.; Hall, A.; Kanyanga, J.K.; et al. Climate phenomena and their relevance for future regional climate change. In Climate Change 2013 the Physical Science Basis: Working Group I Contribution to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2013; Volume 9781107057, pp. 1217–1308. [Google Scholar] [CrossRef]
- Easterling, D.R.; Kunkel, K.E.; Wehner, M.F.; Sun, L. Detection and attribution of climate extremes in the observed record. Weather Clim. Extrem. 2016, 11, 17–27. [Google Scholar] [CrossRef]
- Menne, M.J.; Durre, I.; Vose, R.S.; Gleason, B.E.; Houston, T.G. An overview of the global historical climatology network-daily database. Bull. Am. Meteorol. Soc. 1997, 78, 897–910. [Google Scholar] [CrossRef]
- Donat, M.G.; Alexander, L.V.; Yang, H.; Durre, I.; Vose, R.; Dunn, R.J.H.; Willett, K.M.; Aguilar, E.; Brunet, M.; Caesar, J.; et al. Updated analyses of temperature and precipitation extreme indices since the beginning of the twentieth century: The HadEX2 dataset. J. Geophys. Res. Atmos. 2013, 118, 2098–2118. [Google Scholar] [CrossRef]
- Becker, A.; Finger, P.; Meyer-Christoffer, A.; Rudolf, B.; Schamm, K.; Schneider, U.; Ziese, M. A description of the global land-surface precipitation data products of the Global Precipitation Climatology Centre with sample applications including centennial (trend) analysis from 1901-present. Earth Syst. Sci. Data 2013, 5, 71–99. [Google Scholar] [CrossRef]
- Rudolf, B.; Beck, C.; Grieser, J.; Schneider, U. Global Precipitation Analysis Products of the GPCC. Internet Publ. 2005, 112, 3819–3837. [Google Scholar]
- Arheimer, B.; Pimentel, R.; Isberg, K.; Crochemore, L.; Andersson, J.C.M.; Hasan, A.; Pineda, L. Global catchment modelling using World-Wide HYPE (WWH), open data, and stepwise parameter estimation. Hydrol. Earth Syst. Sci. 2020, 24, 535–559. [Google Scholar] [CrossRef]
- Pechlivanidis, I.G.; Olsson, J.; Bosshard, T.; Sharma, D.; Sharma, K.C. Multi-basin modelling of future hydrological fluxes in the Indian subcontinent. Water 2016, 8, 177. [Google Scholar] [CrossRef]
- Singh, K.; Xie, M. Bootstrap Method. Int. Encycl. Educ. Third Ed. 2010, 46–51. [Google Scholar] [CrossRef]
- DeDeo, S.; Hawkins, R.X.D.; Klingenstein, S.; Hitchcock, T. Bootstrap methods for the empirical study of decision-making and information flows in social systems. Entropy 2013, 15, 2246–2276. [Google Scholar] [CrossRef]
- Ng, J.L.; Abd Aziz, S.; Huang, Y.F.; Mirzaei, M.; Wayayok, A.; Rowshon, M.K. Uncertainty analysis of rainfall depth duration frequency curves using the bootstrap resampling technique. J. Earth Syst. Sci. 2019, 128, 113. [Google Scholar] [CrossRef]
- MATLAB Documentation. Available online: https://www.mathworks.com/help/matlab/ (accessed on 23 April 2023).
- Chowell, G.; Luo, R. Ensemble bootstrap methodology for forecasting dynamic growth processes using differential equations: Application to epidemic outbreaks. BMC Med. Res. Methodol. 2021, 21, 34. [Google Scholar] [CrossRef] [PubMed]
- Huser, R.; Davison, A.C. Space-time modelling of extreme events. J. R. Stat. Soc. Ser. B Stat. Methodol. 2014, 76, 439–461. [Google Scholar] [CrossRef]
- Coles, S. An Introduction to Statistical Modeling of Extreme Values; Springer: Bristol, UK, 2016. [Google Scholar] [CrossRef]
- Ross, S.M. Introduction to Probability and Statistics; Elsevier: Amsterdam, The Netherlands, 2014. [Google Scholar] [CrossRef]
- Kim, H.; Kim, T.; Shin, J.Y.; Heo, J.H. Improvement of Extreme Value Modeling for Extreme Rainfall Using Large-Scale Climate Modes and Considering Model Uncertainty. Water 2022, 14, 478. [Google Scholar] [CrossRef]
- The MathWorks Inc. Statistics and Machine Learning Toolbox Documentation, Natick, Massachusetts: The MathWorks Inc. 2022. Available online: https://www.mathworks.com/help/stats/index.html (accessed on 23 April 2023).
- De Michele, C.; Avanzi, F. Superstatistical distribution of daily precipitation extremes: A worldwide assessment. Sci. Rep. 2018, 8, 14204. [Google Scholar] [CrossRef] [PubMed]
- Kolokytha, E.; Oishi, S.; Teegavarapu, R.S.V. Sustainable Water Resources Planning and Management under Climate Change; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar] [CrossRef]
- Vajapeyam, S. Understanding Shannon’s Entropy metric for Information. arXiv 2014, arXiv:1405.2061. [Google Scholar]
- Guntu, R.K.; Agarwal, A. Investigation of Precipitation Variability and Extremes Using Information Theory. Environ. Sci. Proc. 2021, 4, 14. [Google Scholar] [CrossRef]
- Aubry, N.; Chauve, M.P.; Guyonnet, R. Transition to turbulence on a rotating flat disk. Phys. Fluids 1994, 6, 2800–2814. [Google Scholar] [CrossRef]
- Aubry, N.; Guyonnet, R.; Lima, R. Spatiotemporal analysis of complex signals: Theory and applications. J. Stat. Phys. 1991, 64, 683–739. [Google Scholar] [CrossRef]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; John Wiley and Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
- Młyński, D.; Cebulska, M.; Wałęga, A. Trends, Variability, and Seasonality of Maximum Annual Daily Precipitation in the Upper Vistula Basin, Poland. Atmosphere 2018, 9, 313. [Google Scholar] [CrossRef]
- Chakrabarti, C.G.; Chakrabarty, I. Shannon entropy: Axiomatic characterization and application. Int. J. Math. Math. Sci. 2005, 2005, 2847–2854. [Google Scholar] [CrossRef]
- Lagarias, J.C. Euler’s constant: Euler’s work and modern developments. Bull. Am. Math. Soc. 2013, 50, 527–628. [Google Scholar] [CrossRef]
- Rapp, B.E. Vector Calculus. Microfluid. Model. Mech. Math. 2017, 137–188. [Google Scholar] [CrossRef]
- Rohat, G.; Goyette, S.; Flacke, J. Characterization of European cities’ climate shift—An exploratory study based on climate analogues. Int. J. Clim. Chang. Strateg. Manag. 2018, 10, 428–452. [Google Scholar] [CrossRef]
- Lindfield, G.; Penny, J. Linear Equations and Eigensystems. In Numerical Methods; Academic Press: Cambridge, MA, USA, 2019; pp. 73–156. [Google Scholar] [CrossRef]
- Mann, H.B. Nonparametric Tests Against Trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Salarijazi, M. Trend and change-point detection for the annual stream-flow series of the Karun River at the Ahvaz hydrometric station. Afr. J. Agric. Res. 2012, 7, 4540–4552. [Google Scholar] [CrossRef]
- Yue, S.; Pilon, P.; Phinney, B.; Cavadias, G. The influence of autocorrelation on the ability to detect trend in hydrological series. Hydrol. Process. 2002, 16, 1807–1829. [Google Scholar] [CrossRef]
- da Silva Araújo, L.; da Silva, A.S.A.; Menezes, R.S.C.; Stosic, B.; Stosic, T. Analysis of rainfall seasonality in Pernambuco, Brazil. Theor. Appl. Climatol. 2023, 153, 137–154. [Google Scholar] [CrossRef]
- Sen, P.K. Estimates of the Regression Coefficient Based on Kendall’s Tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Hirsch, R.M.; Slack, J.R.; Smith, R.A. Techniques of trend analysis for monthly water quality data. Water Resour. Res. 1982, 18, 107–121. [Google Scholar] [CrossRef]
- Buishand, T.A. Some methods for testing the homogeneity of rainfall records. J. Hydrol. 1982, 58, 11–27. [Google Scholar] [CrossRef]
- Chen, J.; Gupta, A.K. Parametric Statistical Change Point Analysis; Birkhäuser: Boston, MA, USA, 2011; Volume 951–952, pp. 2013–2015. [Google Scholar] [CrossRef]
- Pettitt, A.N. A Non-Parametric Approach to the Change-Point Problem. J. R. Stat. Soc. Ser. C 1979, 28, 126–135. [Google Scholar] [CrossRef]
- Verstraeten, G.; Poesen, J.; Demarée, G.; Salles, C. Long-term (105 years) variability in rain erosivity as derived from 10-min rainfall depth data for Ukkel (Brussels, Belgium): Implications for assessing soil erosion rates. J. Geophys. Res. Atmos. 2006, 111, 1–11. [Google Scholar] [CrossRef]
- Kundzewicz, Z.W.; Radziejewski, M. Methodologies for trend detection. IAHS-AISH Publ. 2006, 308, 538–549. [Google Scholar]
- Conte, L.C.; Bayer, D.M.; Bayer, F.M. Bootstrap Pettitt test for detecting change points in hydroclimatological data: Case study of Itaipu Hydroelectric Plant, Brazil. Hydrol. Sci. J. 2019, 64, 1312–1326. [Google Scholar] [CrossRef]
- Persson, J.; Blennow, K.; Gonçalves, L.; Borys, A.; Dutca, I.; Hynynen, J.; Janeczko, E.; Lyubenova, M.; Martel, S.; Merganic, J.; et al. No polarization-expected values of climate change impacts among European forest professionals and scientists. Sustainability 2020, 12, 2659. [Google Scholar] [CrossRef]
- Iverson, L.R.; McKenzie, D. Tree-species range shifts in a changing climate: Detecting, modeling, assisting. Landsc. Ecol. 2013, 28, 879–889. [Google Scholar] [CrossRef]
- Franklin, J. Mapping Species Distributions: Spatial Inference and Prediction. Oryx 2010, 44, 615. [Google Scholar] [CrossRef]
- Herschy, R.W. The world’s maximum observed floods. Flow Meas. Instrum. 2002, 13, 231–235. [Google Scholar] [CrossRef]
- Blöschl, G.; Bierkens, M.F.P.; Chambel, A.; Cudennec, C.; Destouni, G.; Fiori, A.; Kirchner, J.W.; McDonnell, J.J.; Savenije, H.H.G.; Sivapalan, M.; et al. Twenty-three unsolved problems in hydrology (UPH)—A community perspective. Hydrol. Sci. J. 2019, 64, 1141–1158. [Google Scholar] [CrossRef]
- Dankers, R.; Hiederer, R. Extreme Temperatures and Precipitation in Europe: Analysis of a High-Resolution Climate Change Scenario. JRC Sci. Tech. Rep. 2008, 82. Available online: https://publications.jrc.ec.europa.eu/repository/handle/JRC44124 (accessed on 23 April 2023).
- Mudelsee, M.; Börngen, M.; Tetzlaff, G.; Grünewald, U. Extreme floods in central Europe over the past 500 years: Role of cyclone pathway “Zugstrasse Vb”. J. Geophys. Res. D Atmos. 2004, 109, 1–21. [Google Scholar] [CrossRef]
- Vavrus, S.J.; Notaro, M.; Lorenz, D.J. Interpreting climate model projections of extreme weather events. Weather Clim. Extrem. 2015, 10, 10–28. [Google Scholar] [CrossRef]
- Angélil, O.; Perkins-Kirkpatrick, S.; Alexander, L.V.; Stone, D.; Donat, M.G.; Wehner, M.; Shiogama, H.; Ciavarella, A.; Christidis, N. Comparing regional precipitation and temperature extremes in climate model and reanalysis products. Weather Clim. Extrem. 2016, 13, 35–43. [Google Scholar] [CrossRef] [PubMed]
- Michaelides, S.; Levizzani, V.; Anagnostou, E.; Bauer, P.; Kasparis, T.; Lane, J.E. Precipitation: Measurement, remote sensing, climatology and modeling. Atmos. Res. 2009, 94, 512–533. [Google Scholar] [CrossRef]
- Das, N.; Bhattacharjee, R.; Choubey, A.; Ohri, A.; Dwivedi, S.B.; Gaur, S. Time series analysis of automated surface water extraction and thermal pattern variation over the Betwa river, India. Adv. Space Res. 2021, 68, 1761–1788. [Google Scholar] [CrossRef]
- Reinking, R.F. An approach to remote sensing and numerical modeling of orographic clouds and precipitation for climatic water resources assessment. Atmos. Res. 1995, 35, 349–367. [Google Scholar] [CrossRef]
- López-Bermeo, C.; Montoya, R.D.; Caro-Lopera, F.J.; Díaz-García, J.A. Validation of the accuracy of the CHIRPS precipitation dataset at representing climate variability in a tropical mountainous region of South America. Phys. Chem. Earth Parts A/B/C 2022, 127, 103184. [Google Scholar] [CrossRef]
- Duan, Q.; Duan, A. The energy and water cycles under climate change. Natl. Sci. Rev. 2020, 7, 553–557. [Google Scholar] [CrossRef] [PubMed]
- Allan, R.P.; Soden, B.J. Atmospheric warming and the amplification of precipitation extremes. Science 2008, 321, 1481–1484. [Google Scholar] [CrossRef]
- Froyland, G.; Giannakis, D.; Lintner, B.R.; Pike, M.; Slawinska, J. Spectral analysis of climate dynamics with operator-theoretic approaches. Nat. Commun. 2021, 12, 6570. [Google Scholar] [CrossRef]
- Meyer, R.K.; Pachauri, L.A. Synthesis Report. Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; IPCC: Geneva, Switzerland, 2014. [Google Scholar]
- Smith, T.M.; Reynolds, R.W.; Peterson, T.C.; Lawrimore, J. Improvements to NOAA’s historical merged land-ocean surface temperature analysis (1880–2006). J. Clim. 2008, 21, 2283–2296. [Google Scholar] [CrossRef]
- Mahmoud, S.H.; Gan, T.Y. Impact of anthropogenic climate change and human activities on environment and ecosystem services in arid regions. Sci. Total Environ. 2018, 633, 1329–1344. [Google Scholar] [CrossRef] [PubMed]
- Stocker, T.F.; Clarke, G.K.C.; Le Treut, H.; Lindzen, R.S.; Meleshko, V.P.; Mugara, R.K.; Palmer, T.N.; Pierrehumbert, R.T.; Sellers, P.J.; Trenberth, K.E.; et al. Physical Climate Processes and Feedbacks. In Climate Change 2001: The Scientific Basis. Contribution of Working Group I to the Third Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2001; p. 881. [Google Scholar]
- Pitt, M.A. Increased Temperature and Entropy Production in the Earth’s Atmosphere: Effect on Wind, Precipitation, Chemical Reactions, Freezing and Melting of Ice and Electrical Activity. J. Mod. Phys. 2019, 10, 966–973. [Google Scholar] [CrossRef]
- Mills, T.C. Applied Time Series Analysis: A Practical Guide to Modeling and Forecasting; Academic Press: Cambridge, MA, USA, 2019. [Google Scholar] [CrossRef]
- Delgado-Bonal, A.; Marshak, A.; Yang, Y.; Holdaway, D. Analyzing changes in the complexity of climate in the last four decades using MERRA-2 radiation data. Sci. Rep. 2020, 10, 922. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).