Physical and Statistical Links between Errors at the Surface, in the Boundary Layer, and in the Free Atmosphere in Medium-Range Numerical Weather Predictions
Abstract
1. Introduction
2. Materials and Methods
2.1. The OP and NEW Configurations
2.2. Surface Fluxes and PBL in GEM
2.3. Vertical Profiles in GEM
2.4. Evaluation Metrics and Diagnostics
2.5. Experimental Setup
3. Results
4. Discussion
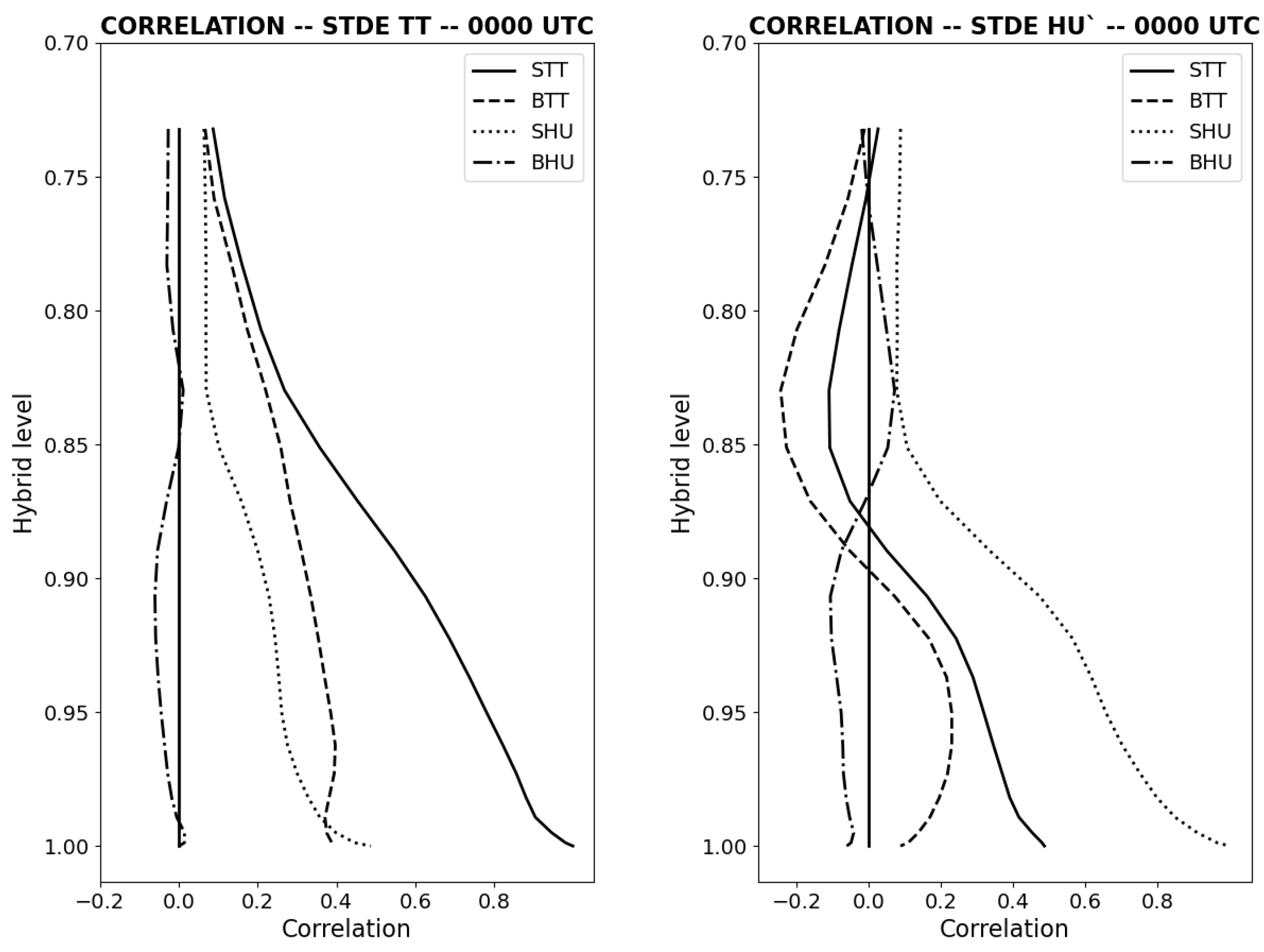
4.1. Statistically Explaining STDE in Upper Boundary Layer
4.2. Physical Links with PBL Diurnal Evolution
4.3. PBL Errors and Upper-Air NWP Evaluation
5. Summary and Conclusions
- The same analysis could be carried out during the winter season and over other areas, when and where the nature of the links between errors at the surface and in the atmosphere could be different.
- It is not clear whether the same kind of statistical and physical links would be found in other atmospheric models.
- Do we see the same kind of behavior for weather prediction based on AI forecasting systems?
- Diagnostics for land–atmosphere coupling could be examined in order to have a more complete understanding of the links between errors at the surface and in the boundary layer.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AIRS | Atmospheric Infrared Sounder |
| CRIS | CRoss-track Infrared Sounder |
| EnKF | Ensemble Kalman Filter data assimilation system |
| EnVar | Ensemble Variational data assimilation system |
| CaLDAS | Canadian Land Data Assimilation System |
| CaPA | Canadian Precipitation Analysis |
| CCMEP | Canadian Centre for Meteorological and Environmental Prediction |
| CTEM | Canadian Terrestrial Ecosystem Model |
| ECCC | Environment and Climate Change Canada |
| GDPS | Global Deterministic Prediction System |
| GEM | Global Environmental Multiscale model |
| GEWEX | Global Energy and Water EXchanges initiative |
| HRRR | High-Resolution Rapid Refresh |
| IASI | Infrared Atmospheric Sounding Interferometer |
| ISBA | Interactions between Soil, Biosphere, and Atmosphere scheme |
| LoCo | Local Land–Atmosphere Coupling |
| NOAA | National Oceanic and Atmospheric Administration |
| NWP | Numerical weather prediction |
| PBL | Planetary boundary layer |
| SMAP | Soil Moisture Active Passive mission |
| SMOS | Soil Moisture and Ocean Salinity mission |
| SVS | Soil, Vegetation, and Snow scheme |
| TKE | Turbulent kinetic energy |
| UTC | Universal Time Coordinated |
References
- Kala, J.; Evans, J.P.; Pitman, A.J. Influence of antecedent soil moisture conditions on the synoptic meteorology of the Black Saturday bushfire event in southeast Australia. Q. J. R. Meteorol. Soc. 2015, 141, 3118–3129. [Google Scholar]
- Zheng, W.; Zhan, X.; Liu, J.; Ek, M. A preliminary assessment of the impact of assimilating satellite soil moisture data products on NCEP Global Forecast System. Adv. Meteorol. 2018, 2018, 7363194. [Google Scholar]
- Crow, W.T.; Gomez, C.A.; Sabater, J.M.; Holmes, T.; Hain, C.R.; Lei, F.; Dong, J.; Alfieri, J.G.; Anderson, M.C. Soil moisture–evapotranspiration overcoupling and L-Band brightness temperature assimilation: Sources and forecast implications. J. Hydrometeorol. 2020, 21, 2359–2374. [Google Scholar]
- Champeaux, J.L.; Arcos, D.; Bazile, E.; Giard, D.; Goutorbe, J.P.; Habets, F.; Noilhan, J.; Roujean, J.L. AVHRR-derived vegetation mapping over Western Europe for use in numerical weather prediction models. Int. J. Remote Sens. 2000, 21, 1183–1199. [Google Scholar]
- Mailhot, J.; Bélair, S.; Charron, M.; Doyle, C.; Joe, P.; Abrahamowicz, M.; Bernier, N.; Denis, B.; Erfani, A.; Frenette, R.; et al. Environment Canada’s experimental numerical weather prediction systems for the Vancouver 2010 Winter Olympic and Paralympic Games. Bull. Am. Meteorol. Soc. 2010, 91, 1073–1086. [Google Scholar]
- Campbell, P.C.; Bash, J.O.; Spero, T.L. Updates to the Noah land surface model in WRF-CMAQ to improve simulated meteorology, air quality, and deposition. J. Adv. Model. Earth Syst. 2019, 11, 231–256. [Google Scholar]
- Husain, S.Z.; Alavi, N.; Bélair, S.; Carrera, M.; Zhang, S.; Fortin, V.; Abrahamowicz, M.; Gauthier, N. The multibudget Soil, Vegetation, and Snow (SVS) scheme for land surface parameterization: Offline warm season evaluation. J. Hydrometeorol. 2016, 17, 2293–2313. [Google Scholar]
- Bakketun, Å.; Blyverket, J.; Müller, M. Using a reanalysis-driven land surface model for initialization of a numerical weather prediction System. Weather Forecast. 2023, 38, 2155–2168. [Google Scholar]
- Benjamin, S.G.; Smirnova, T.G.; James, E.P.; Lin, L.F.; Hu, M.; Turner, D.D.; He, S. Land–snow data assimilation including a moderately coupled initialization method applied to NWP. J. Hydrometeorol. 2022, 23, 825–845. [Google Scholar]
- Sassi, M.Z.; Fourrié, N.; Guidard, V.; Birman, C. Preliminary assimilation of satellite derived land surface temperature from SEVIRI in the surface scheme of the AROME-France model. Tellus A 2023, 75, 88–107. [Google Scholar]
- Bélair, S.; Brown, R.; Mailhot, J.; Bilodeau, B.; Crevier, L.P. Operational implementation of the ISBA land surface scheme in the Canadian regional weather forecast model. Part II: Cold season results. J. Hydrometeorol. 2003, 4, 371–386. [Google Scholar]
- Bélair, S.; Crevier, L.P.; Mailhot, J.; Bilodeau, B.; Delage, Y. Operational implementation of the ISBA land surface scheme in the Canadian regional weather forecast model. Part I: Warm season results. J. Hydrometeorol. 2003, 4, 352–370. [Google Scholar]
- Koster, R.D.; Sud, Y.; Guo, Z.; Dirmeyer, P.A.; Bonan, G.; Oleson, K.W.; Chan, E.; Verseghy, D.; Cox, P.; Davies, H.; et al. GLACE: The Global Land–Atmosphere Coupling Experiment. Part I: Overview. J. Hydrometeorol. 2006, 7, 590–610. [Google Scholar]
- Guo, Z.; Dirmeyer, P.A.; Koster, R.D.; Sud, Y.; Bonan, G.; Oleson, K.W.; Chan, E.; Verseghy, D.; Cox, P.; Gordon, C.; et al. GLACE: The Global Land–Atmosphere Coupling Experiment. Part II: Analysis. J. Hydrometeorol. 2006, 7, 611–625. [Google Scholar]
- Santanello, J.A.; Dirmeyer, P.A.; Ferguson, C.R.; Findell, K.L.; Tawfik, A.B.; Berg, A.; Ek, M.; Gentine, P.; Guillod, B.P.; Van Heerwaarden, C.; et al. Land–atmosphere interactions: The LoCo perspective. Bull. Am. Meteorol. Soc. 2018, 99, 1253–1272. [Google Scholar]
- Santanello, J.A., Jr.; Lawston, P.; Kumar, S.; Dennis, E. Understanding the impacts of soil moisture initial conditions on NWP in the context of land–atmosphere coupling. J. Hydrometeorol. 2019, 20, 793–819. [Google Scholar]
- Lawston-Parker, P.; Santanello, J.A., Jr.; Kumar, S.V. Understanding the impacts of land surface and PBL observations on the terrestrial and atmospheric legs of land–atmosphere coupling. J. Hydrometeorol. 2021, 22, 2241–2258. [Google Scholar]
- Dirmeyer, P.A.; Halder, S. Sensitivity of numerical weather forecasts to initial soil moisture variations in CFSv2. Weather Forecast. 2016, 31, 1973–1983. [Google Scholar]
- Bélair, S.; Alavi, N.; Carrera, M.L.; Abrahamowicz, M.; Bilodeau, B.; Simjanovski, D.; Charpentier, D.; Badawy, B.; Leroyer, S. Evaluating the impact of land surface on medium-range weather forecasts using screen-level analyses. Q. J. R. Meteorol. Soc. 2023, 149, 2146–2175. [Google Scholar]
- Côté, J.; Gravel, S.; Méthot, A.; Patoine, A.; Roch, M.; Staniforth, A. The operational CMC–MRB Global Environmental Multiscale (GEM) model. Part I: Design considerations and formulation. Mon. Weather Rev. 1998, 126, 1373–1395. [Google Scholar]
- Côté, J.; Desmarais, J.G.; Gravel, S.; Méthot, A.; Patoine, A.; Roch, M.; Staniforth, A. The operational CMC–MRB Global Environmental Multiscale (GEM) model. Part II: Results. Mon. Weather Rev. 1998, 126, 1397–1418. [Google Scholar]
- Girard, C.; Plante, A.; Desgagné, M.; McTaggart-Cowan, R.; Côté, J.; Charron, M.; Gravel, S.; Lee, V.; Patoine, A.; Qaddouri, A.; et al. Staggered vertical discretization of the Canadian Environmental Multiscale (GEM) model using a coordinate of the log-hydrostatic-pressure type. Mon. Weather Rev. 2014, 142, 1183–1196. [Google Scholar]
- Husain, S.Z.; Girard, C. Impact of consistent semi-Lagrangian trajectory calculations on numerical weather prediction performance. Mon. Weather Rev. 2017, 145, 4127–4150. [Google Scholar]
- McTaggart-Cowan, R.; Vaillancourt, P.; Zadra, A.; Chamberland, S.; Charron, M.; Corvec, S.; Milbrandt, J.; Paquin-Ricard, D.; Patoine, A.; Roch, M.; et al. Modernization of atmospheric physics parameterization in Canadian NWP. J. Adv. Model. Earth Syst. 2019, 11, 3593–3635. [Google Scholar]
- Buehner, M.; McTaggart-Cowan, R.; Beaulne, A.; Charette, C.; Garand, L.; Heilliette, S.; Lapalme, E.; Laroche, S.; Macpherson, S.R.; Morneau, J.; et al. Implementation of deterministic weather forecasting systems based on ensemble–variational data assimilation at Environment Canada. Part I: The global system. Mon. Weather Rev. 2015, 143, 2532–2559. [Google Scholar]
- Buehner, M. Local ensemble transform Kalman filter with cross validation. Mon. Weather Rev. 2020, 148, 2265–2282. [Google Scholar]
- Caron, J.F.; Buehner, M. Implementation of scale-dependent background-error covariance localization in the Canadian Global Deterministic Prediction System. Weather Forecast. 2022, 37, 1567–1580. [Google Scholar]
- Noilhan, J.; Planton, S. A simple parameterization of land surface processes for meteorological models. Mon. Weather Rev. 1989, 117, 536–549. [Google Scholar]
- Alavi, N.; Bélair, S.; Fortin, V.; Zhang, S.; Husain, S.Z.; Carrera, M.L.; Abrahamowicz, M. Warm season evaluation of soil moisture prediction in the Soil, Vegetation, and Snow (SVS) scheme. J. Hydrometeorol. 2016, 17, 2315–2332. [Google Scholar]
- Arora, V.K. Simulating energy and carbon fluxes over winter wheat using coupled land surface and terrestrial ecosystem models. Agric. For. Meteorol. 2003, 118, 21–47. [Google Scholar]
- Arora, V.K.; Boer, G.J. A parameterization of leaf phenology for the terrestrial ecosystem component of climate models. Glob. Chang. Biol. 2005, 11, 39–59. [Google Scholar]
- Mahfouf, J.F. Analysis of soil moisture from near-surface parameters: A feasibility study. J. Appl. Meteorol. Climatol. 1991, 30, 1534–1547. [Google Scholar]
- Carrera, M.L.; Bélair, S.; Bilodeau, B. The Canadian Land Data Assimilation System (CaLDAS): Description and synthetic evaluation study. J. Hydrometeorol. 2015, 16, 1293–1314. [Google Scholar]
- Carrera, M.L.; Bilodeau, B.; Bélair, S.; Abrahamowicz, M.; Russell, A.; Wang, X. Assimilation of passive L-band microwave brightness temperatures in the Canadian Land Data Assimilation System: Impacts on short-range warm season numerical weather prediction. J. Hydrometeorol. 2019, 20, 1053–1079. [Google Scholar]
- Fortin, V.; Roy, G.; Donaldson, N.; Mahidjiba, A. Assimilation of radar quantitative precipitation estimations in the Canadian Precipitation Analysis (CaPA). J. Hydrol. 2015, 531, 296–307. [Google Scholar]
- Fortin, V.; Roy, G.; Stadnyk, T.; Koenig, K.; Gasset, N.; Mahidjiba, A. Ten years of science based on the Canadian Precipitation Analysis: A CaPA system overview and literature review. Atmosphere-Ocean 2018, 56, 178–196. [Google Scholar]
- Heilliette, S.; Garand, L.; Bilodeau, B.; Carrera, M.; Belair, S. Assimilation of land surface skin temperature observations derived from GOES imagery. In Proceedings of the 21st TOVS Study Conference, Darmstadt, Germany, 29 November–5 December 2017. [Google Scholar]
- Benoit, R.; Côté, J.; Mailhot, J. Inclusion of a TKE boundary layer parameterization in the Canadian regional finite-element model. Mon. Weather Rev. 1989, 117, 1726–1750. [Google Scholar]
- Beljaars, A.; Holtslag, A. Flux parameterization over land surfaces for atmospheric models. J. Appl. Meteorol. Climatol. 1991, 30, 327–341. [Google Scholar]
- Delage, Y.; Girard, C. Stability functions correct at the free convection limit and consistent for for both the surface and Ekman layers. Bound.-Layer Meteorol. 1992, 58, 19–31. [Google Scholar]
- Delage, Y. Parameterising sub-grid scale vertical transport in atmospheric models under statically stable conditions. Bound.-Layer Meteorol. 1997, 82, 23–48. [Google Scholar]
- Bélair, S.; Mailhot, J.; Strapp, J.W.; MacPherson, J.I. An examination of local versus nonlocal aspects of a TKE-based boundary layer scheme in clear convective conditions. J. Appl. Meteorol. Climatol. 1999, 38, 1499–1518. [Google Scholar]
- McTaggart-Cowan, R.; Zadra, A. Representing Richardson number hysteresis in the NWP boundary layer. Mon. Weather Rev. 2015, 143, 1232–1258. [Google Scholar]
- Beljaars, A.C.; Brown, A.R.; Wood, N. A new parametrization of turbulent orographic form drag. Q. J. R. Meteorol. Soc. 2004, 130, 1327–1347. [Google Scholar]
- Carminati, F.; Migliorini, S.; Ingleby, B.; Bell, W.; Lawrence, H.; Newman, S.; Hocking, J.; Smith, A. Using reference radiosondes to characterise NWP model uncertainty for improved satellite calibration and validation. Atmos. Meas. Tech. 2019, 12, 83–106. [Google Scholar]
- Ling, F.; Ouyang, L.; Larbi, B.R.; Luo, J.J.; Han, T.; Zhong, X.; Bai, L. Is artificial intelligence providing the second revolution for weather forecasting? arXiv 2024, arXiv:2401.16669. [Google Scholar]
- Yokota, S.; Banno, T.; Oigawa, M.; Akimoto, G.; Kawano, K.; Ikuta, Y. JMA operational hourly hybrid 3DVar with singular vector-based mesoscale ensemble prediction system. J. Meteorol. Soc. Jpn. Ser. II 2024, 102, 129–150. [Google Scholar]







Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bélair, S.; Alavi, N.; Leroyer, S.; Carrera, M.L.; Abrahamowicz, M.; Bilodeau, B.; Simjanovski, D.; Charpentier, D.; Badawy, B. Physical and Statistical Links between Errors at the Surface, in the Boundary Layer, and in the Free Atmosphere in Medium-Range Numerical Weather Predictions. Atmosphere 2024, 15, 1012. https://doi.org/10.3390/atmos15081012
Bélair S, Alavi N, Leroyer S, Carrera ML, Abrahamowicz M, Bilodeau B, Simjanovski D, Charpentier D, Badawy B. Physical and Statistical Links between Errors at the Surface, in the Boundary Layer, and in the Free Atmosphere in Medium-Range Numerical Weather Predictions. Atmosphere. 2024; 15(8):1012. https://doi.org/10.3390/atmos15081012
Chicago/Turabian StyleBélair, Stéphane, Nasim Alavi, Sylvie Leroyer, Marco L. Carrera, Maria Abrahamowicz, Bernard Bilodeau, Dragan Simjanovski, Dorothée Charpentier, and Bakr Badawy. 2024. "Physical and Statistical Links between Errors at the Surface, in the Boundary Layer, and in the Free Atmosphere in Medium-Range Numerical Weather Predictions" Atmosphere 15, no. 8: 1012. https://doi.org/10.3390/atmos15081012
APA StyleBélair, S., Alavi, N., Leroyer, S., Carrera, M. L., Abrahamowicz, M., Bilodeau, B., Simjanovski, D., Charpentier, D., & Badawy, B. (2024). Physical and Statistical Links between Errors at the Surface, in the Boundary Layer, and in the Free Atmosphere in Medium-Range Numerical Weather Predictions. Atmosphere, 15(8), 1012. https://doi.org/10.3390/atmos15081012




