WRF-Chem Modeling of Tropospheric Ozone in the Coastal Cities of the Gulf of Finland
Abstract
1. Introduction
2. Materials and Methods
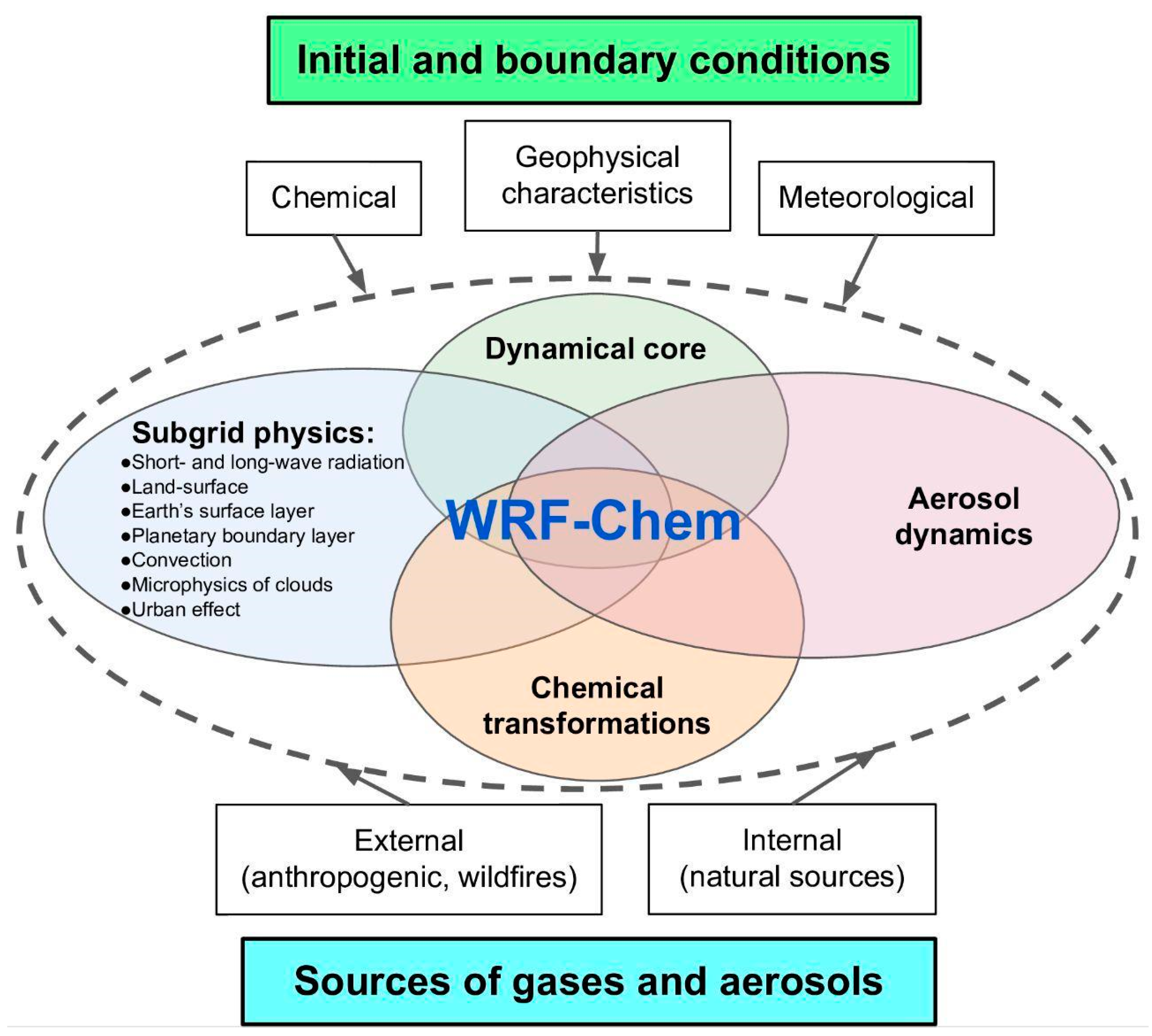
2.1. WRF-Chem Model
2.1.1. Initial and Boundary Conditions
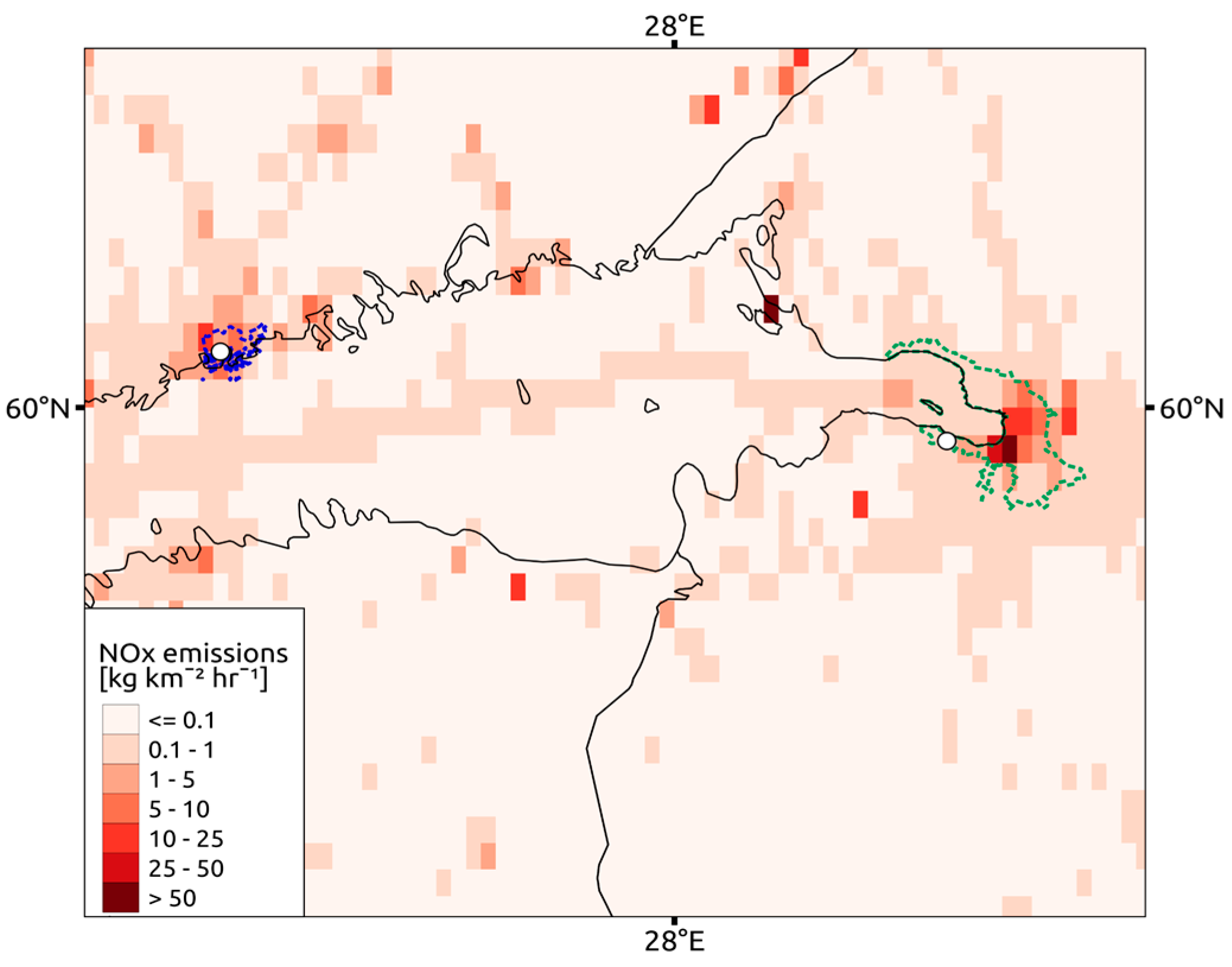
2.1.2. Sources of Gases and Aerosols
| Process | Scheme |
|---|---|
| Transfer of shortwave EM radiation in the atmosphere | Dudhia Shortwave Scheme [36] |
| Transfer of longwave EM radiation in the atmosphere | RRTM Longwave Scheme [37] |
| Model of land surface layers’ interaction | Unified Noah Land Surface Model [38] |
| Earth’s surface layer model | Revised MM5 Scheme [39] |
| Earth’s boundary layer model | Yonsei University Scheme (YSU) [40] |
| Vertical transport and convective clouds | Grell–Freitas Ensemble Scheme [41] |
| Microphysics of clouds | Morrison 2–Moment Scheme [42] |
| Urban effect | Urban Canopy Model [43] (Default Setup) |
2.1.3. Chemical Transformation and Aerosol Dynamics
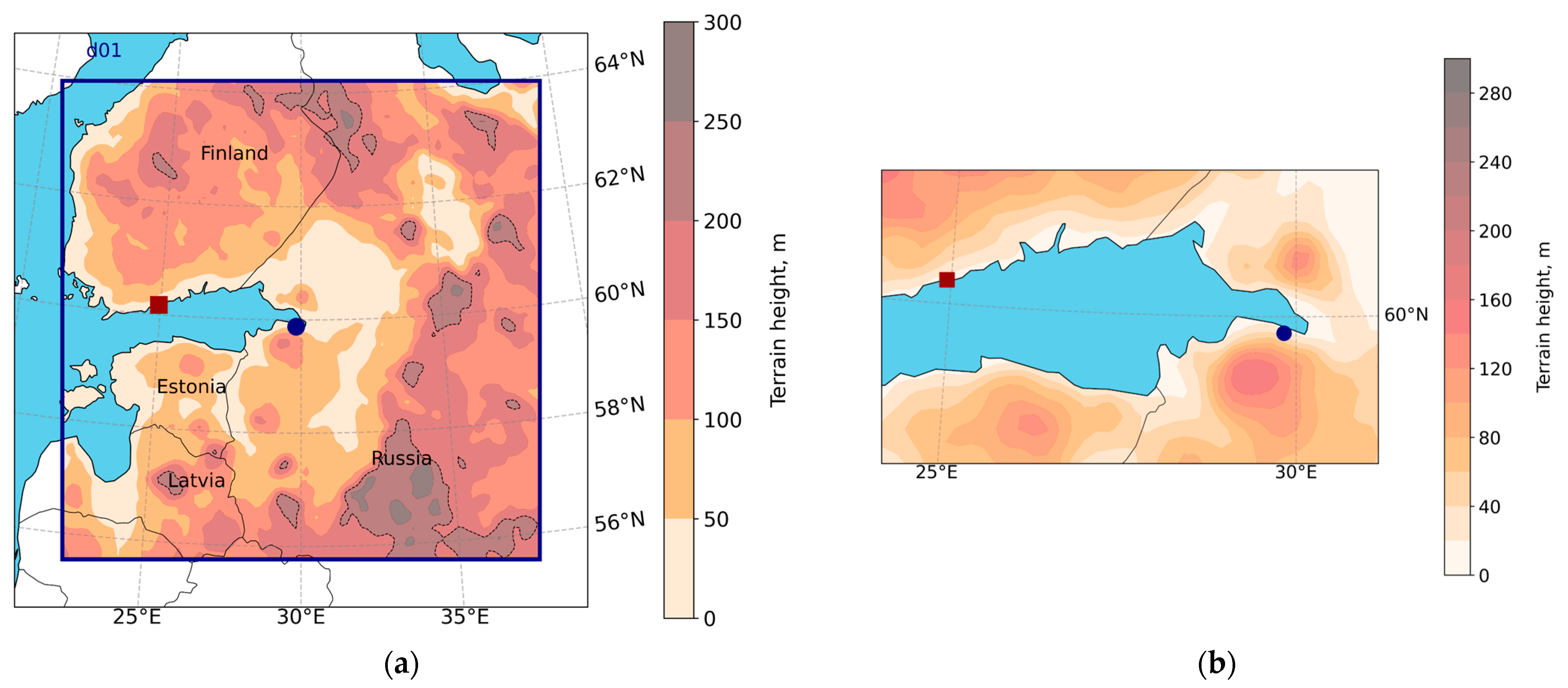
2.2. Data for the Model Validation and Analysis
2.2.1. Local Measurements of Ozone and Its Precursors
St. Petersburg, Russia
Helsinki, Finland
2.2.2. Tropospheric Ozone Measurements at St. Petersburg
2.2.3. Meteorological Measurements in St. Petersburg and Helsinki
2.2.4. ERA5 Meteorological Reanalysis Data
3. Results and Discussion
3.1. Analysis of the WRF-Chem Modeling in St. Petersburg and Helsinki
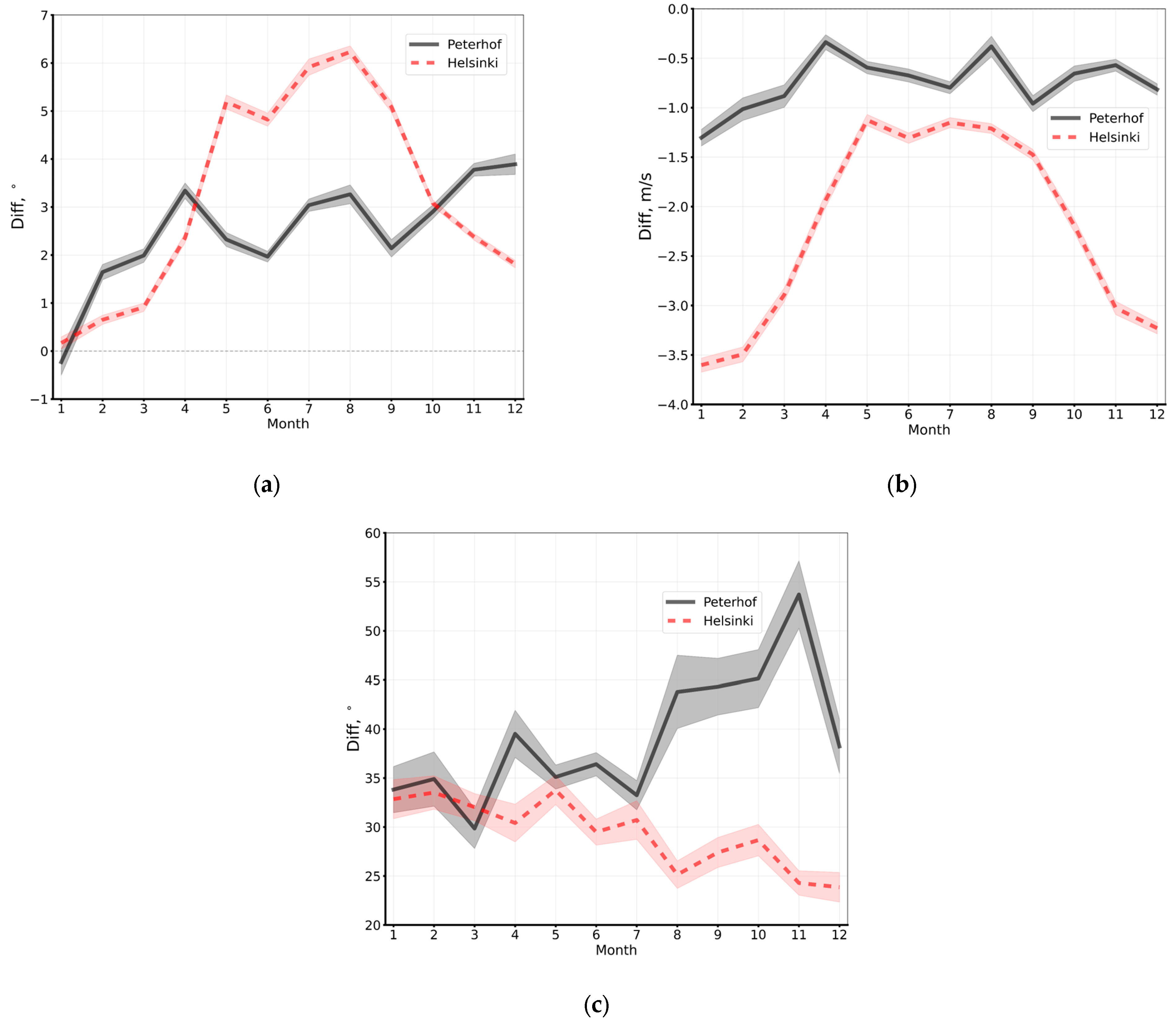
3.1.1. Near-Surface Meteorological Parameters
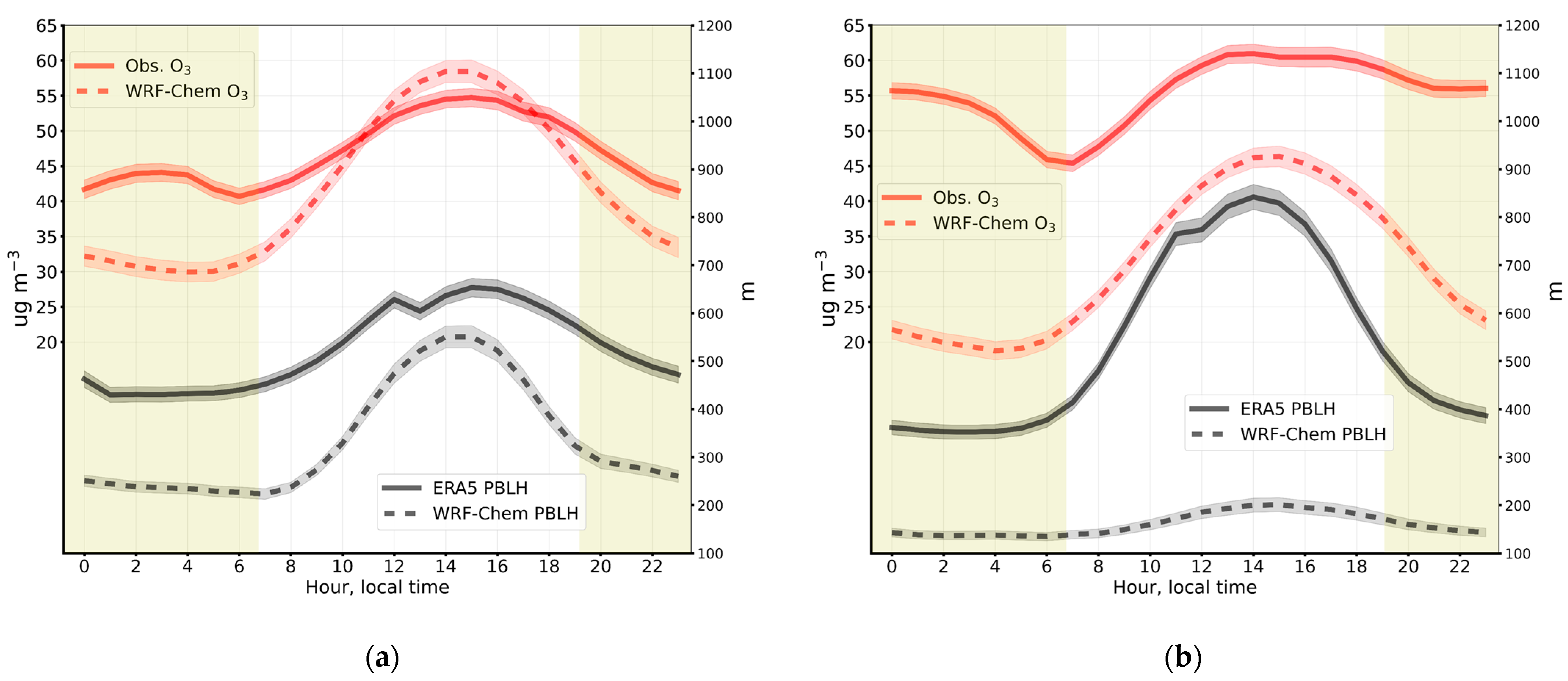
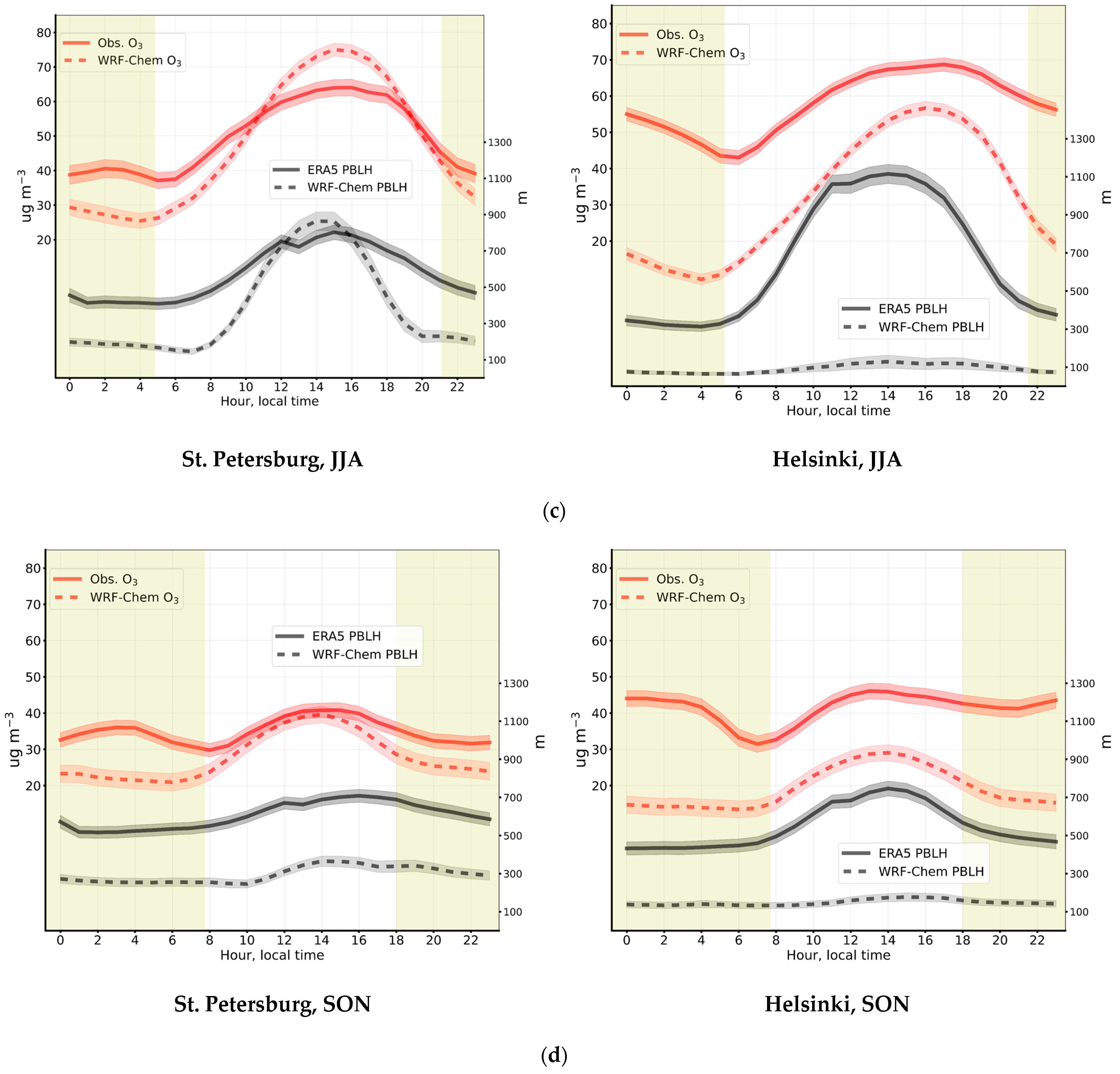
3.1.2. Near-Surface Ozone Concentrations
Diurnal Variations in NSOCs
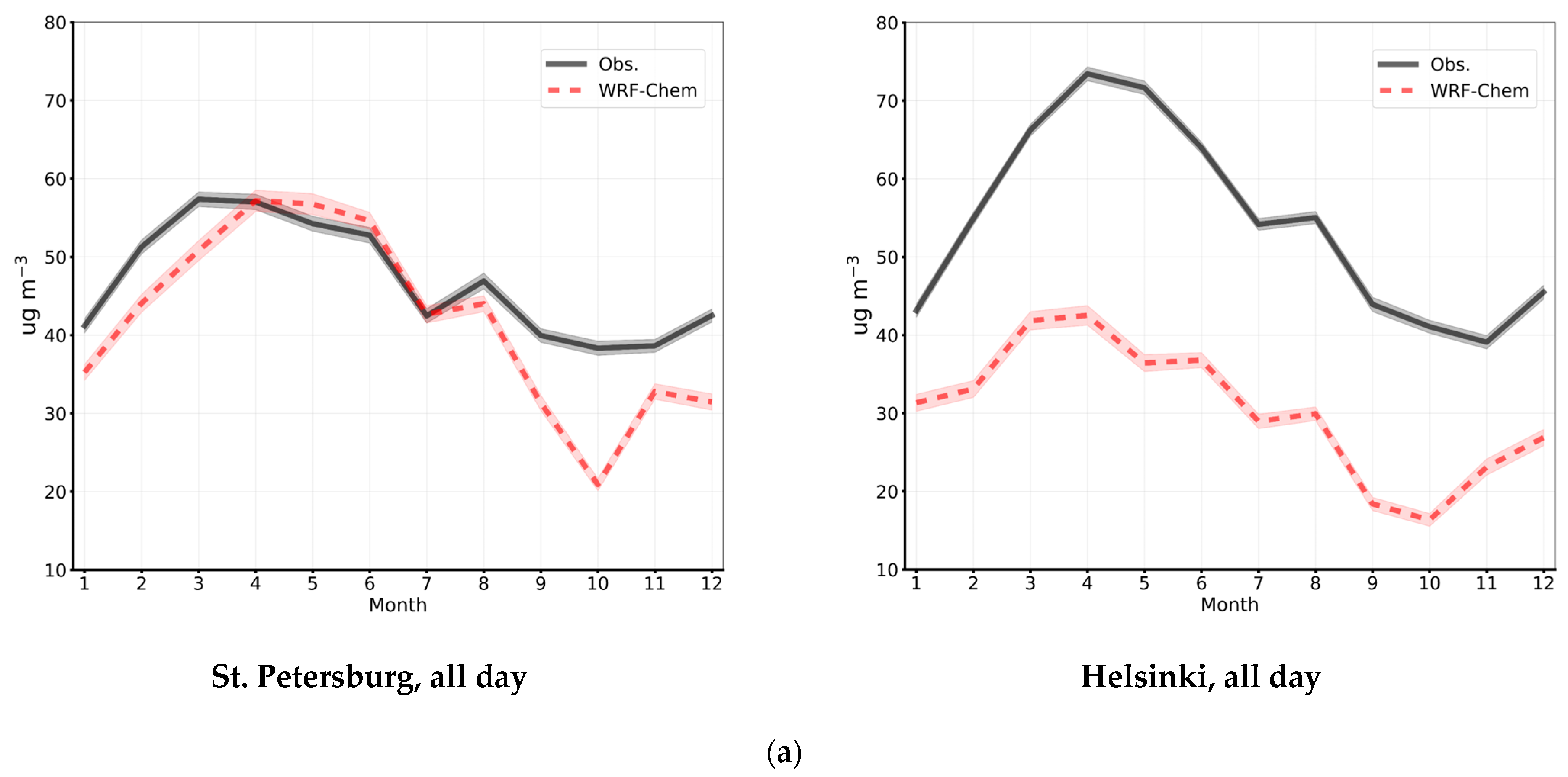
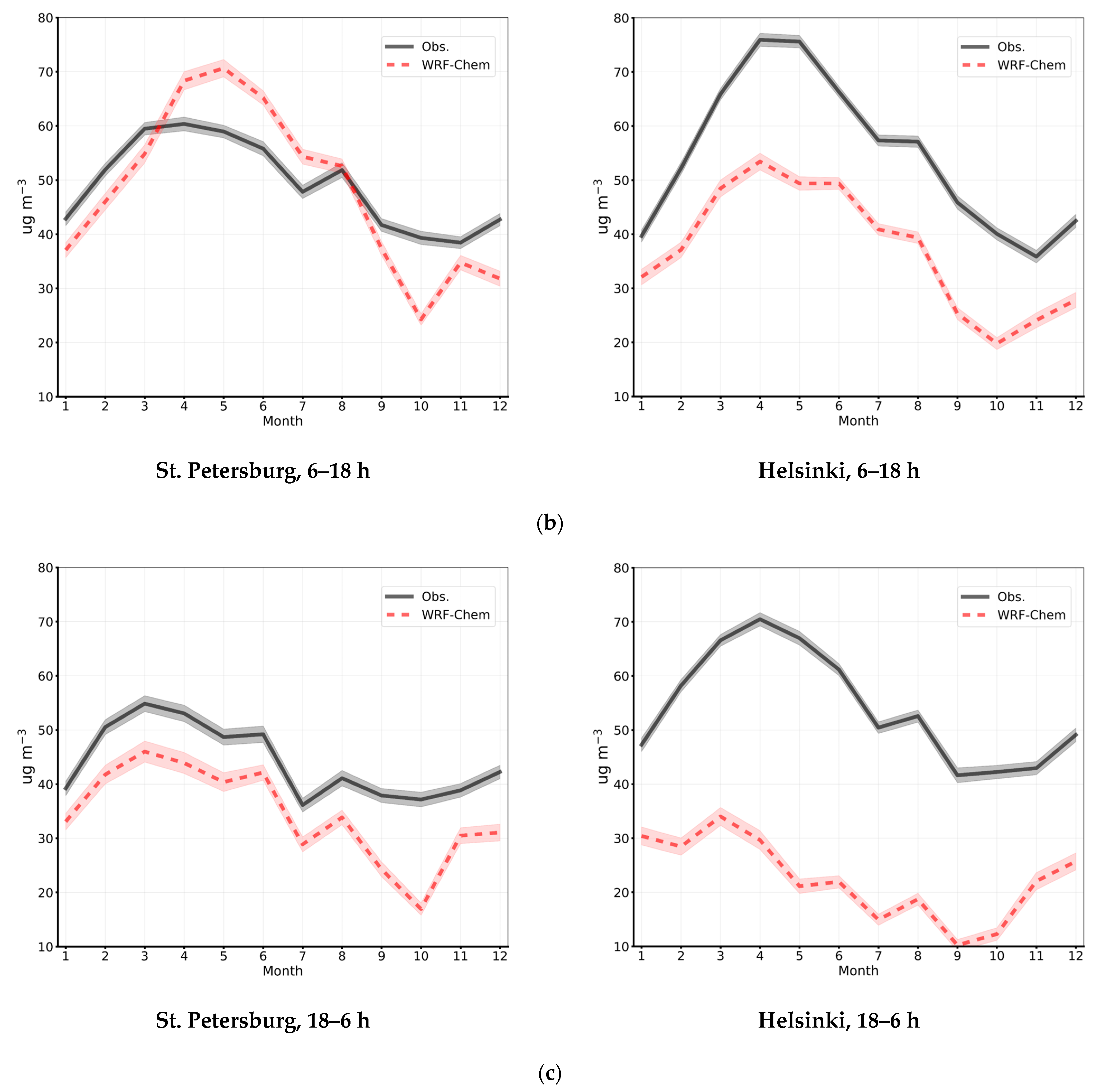
Seasonal Variations in NSOCs
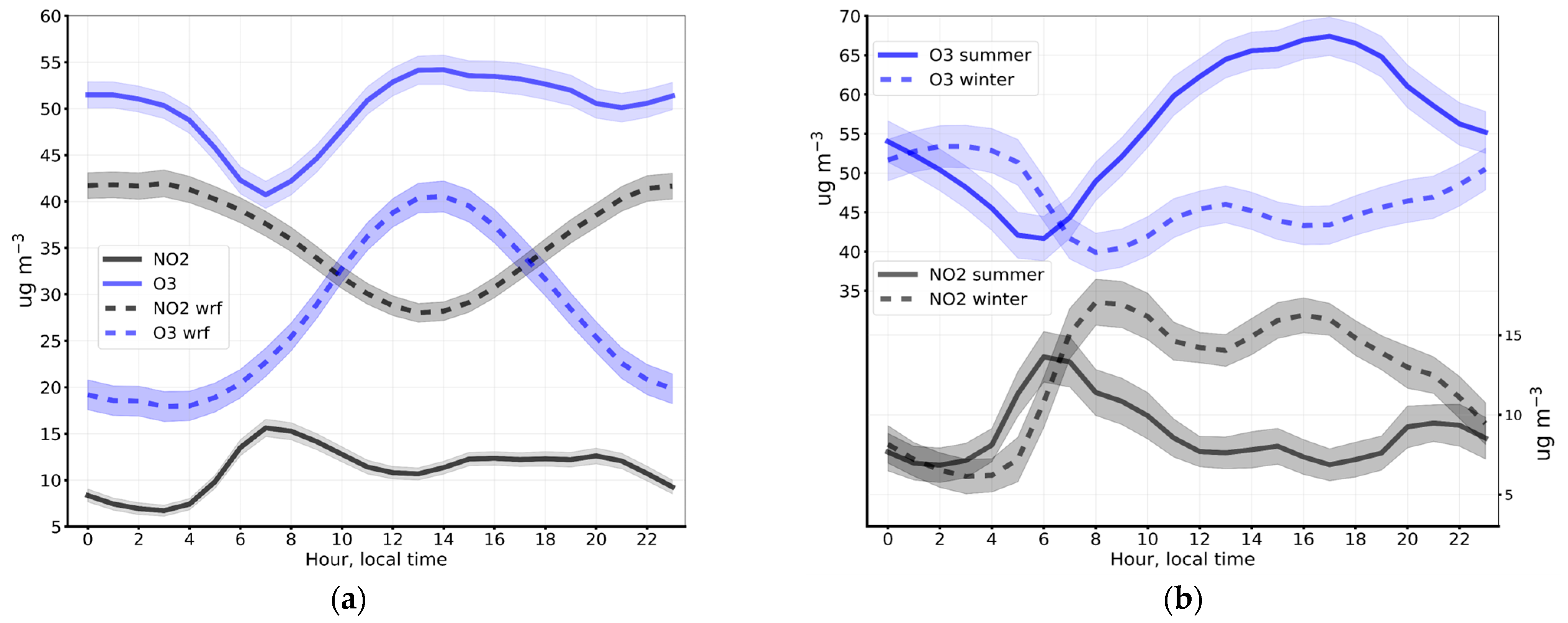
3.1.3. Near-Surface NO2 Concentrations in Helsinki
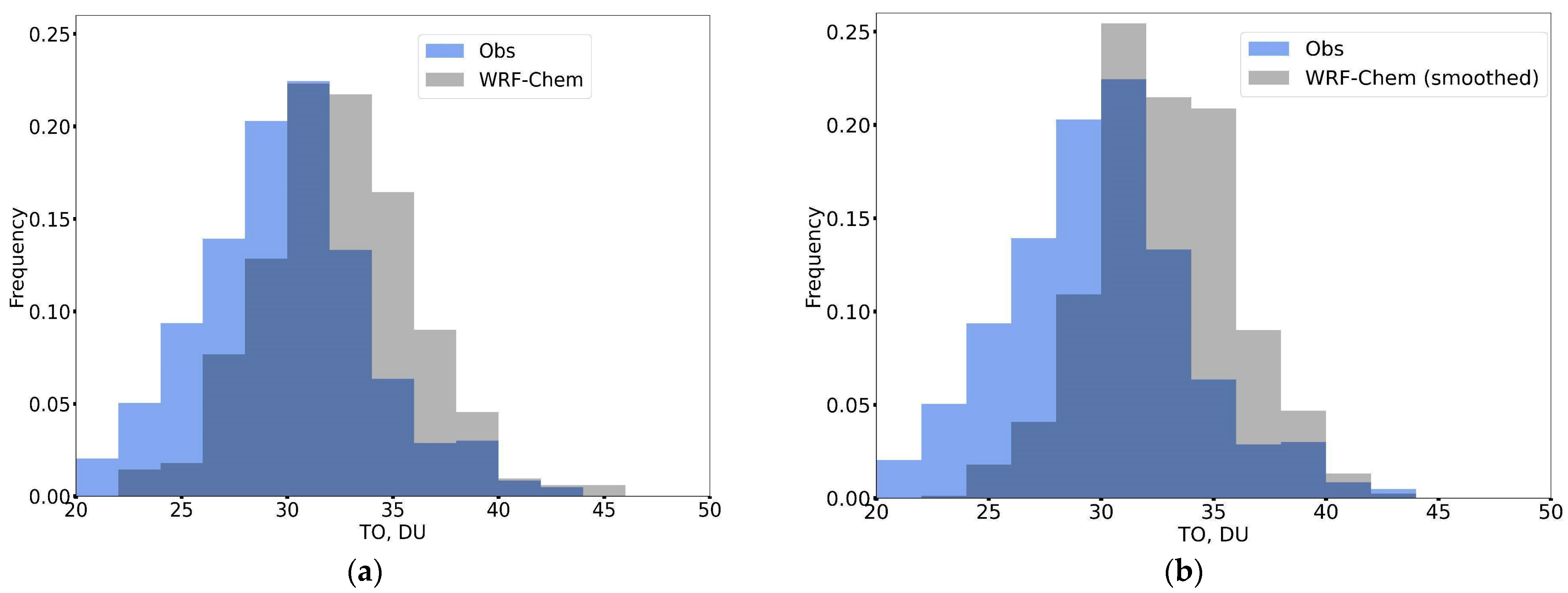
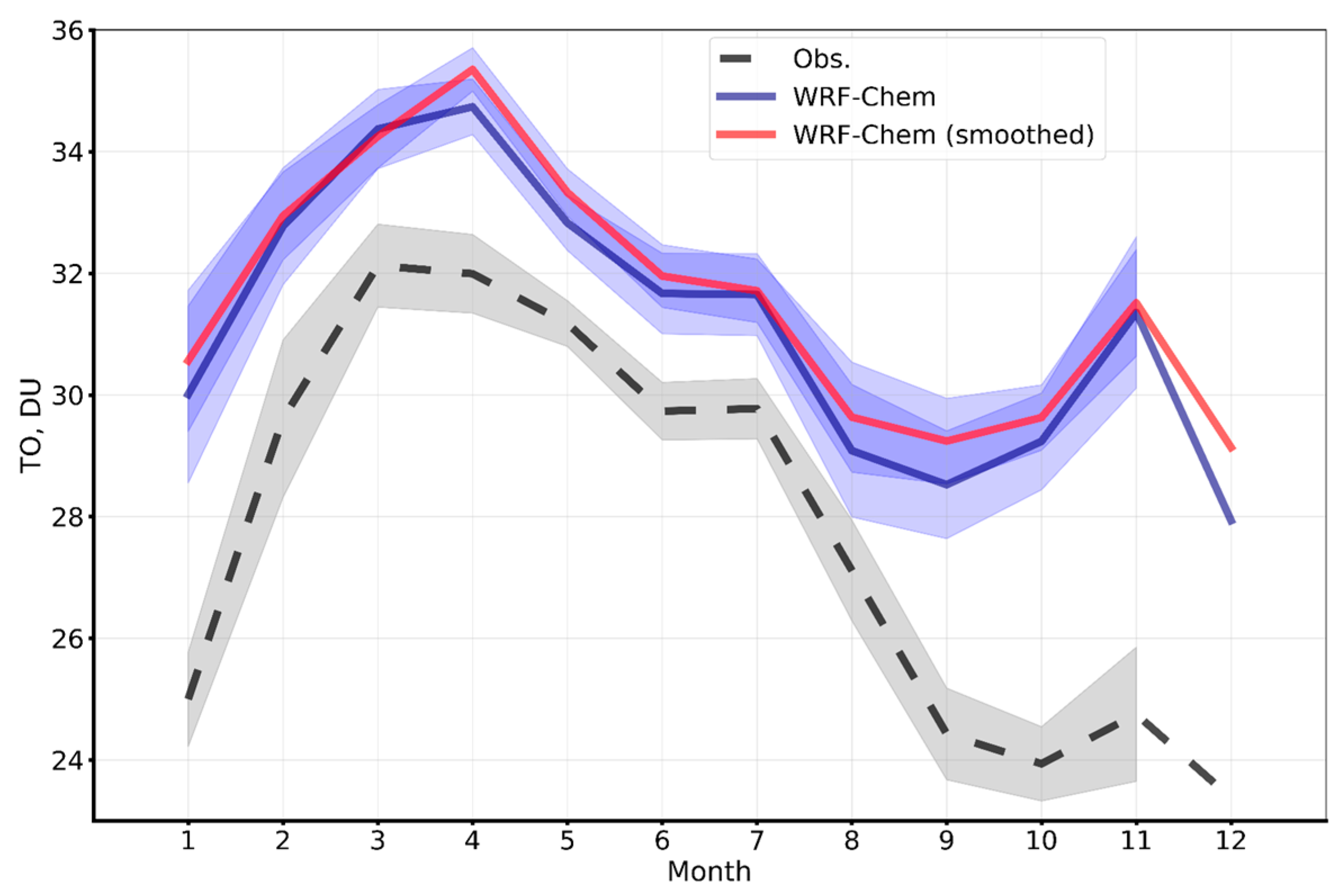
3.1.4. Tropospheric Ozone Content in St. Petersburg
0–8 km Layer
Total Tropospheric Layer
3.2. Analysis of WRF-Chem Modeling near the Gulf of Finland
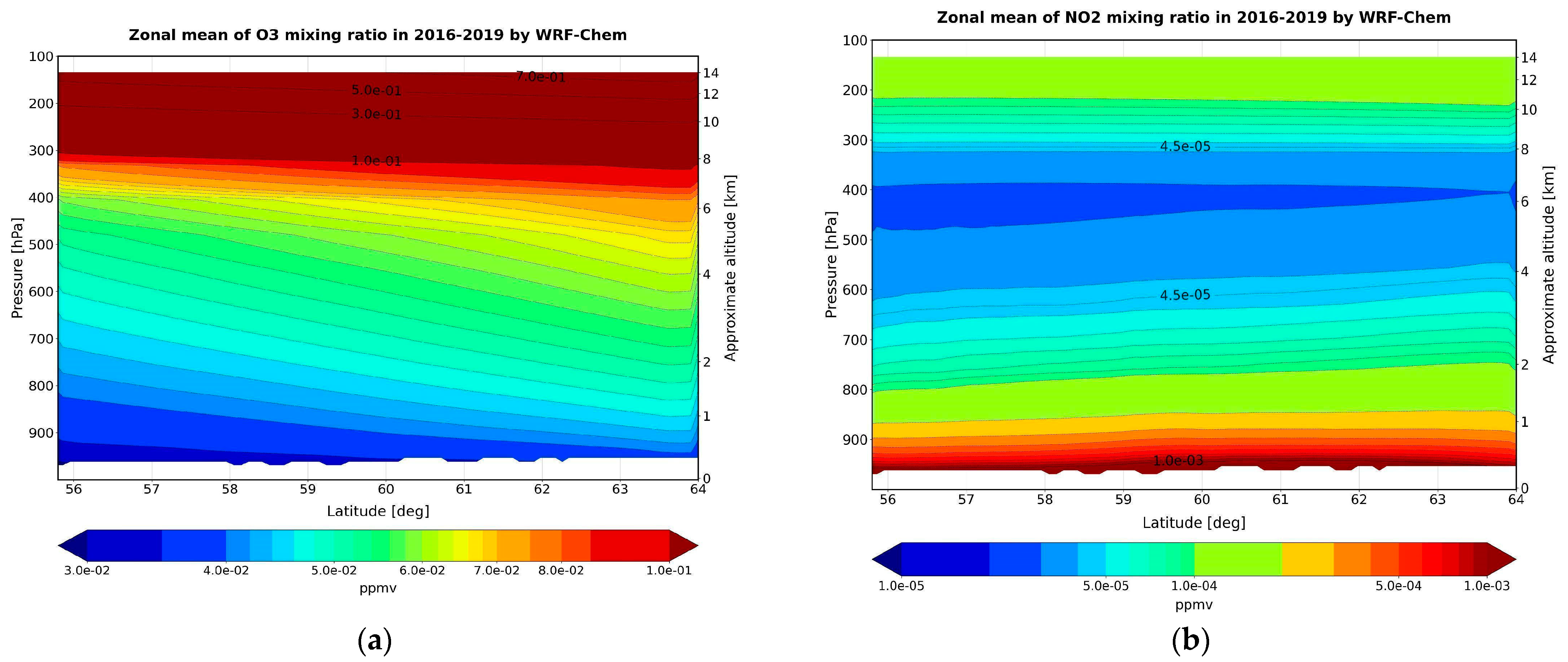
3.2.1. Zonal Distribution of Ozone and Its Precursors
H2O2 + OH → HO2 + H2O
3.2.2. Zonal Distribution of FNR
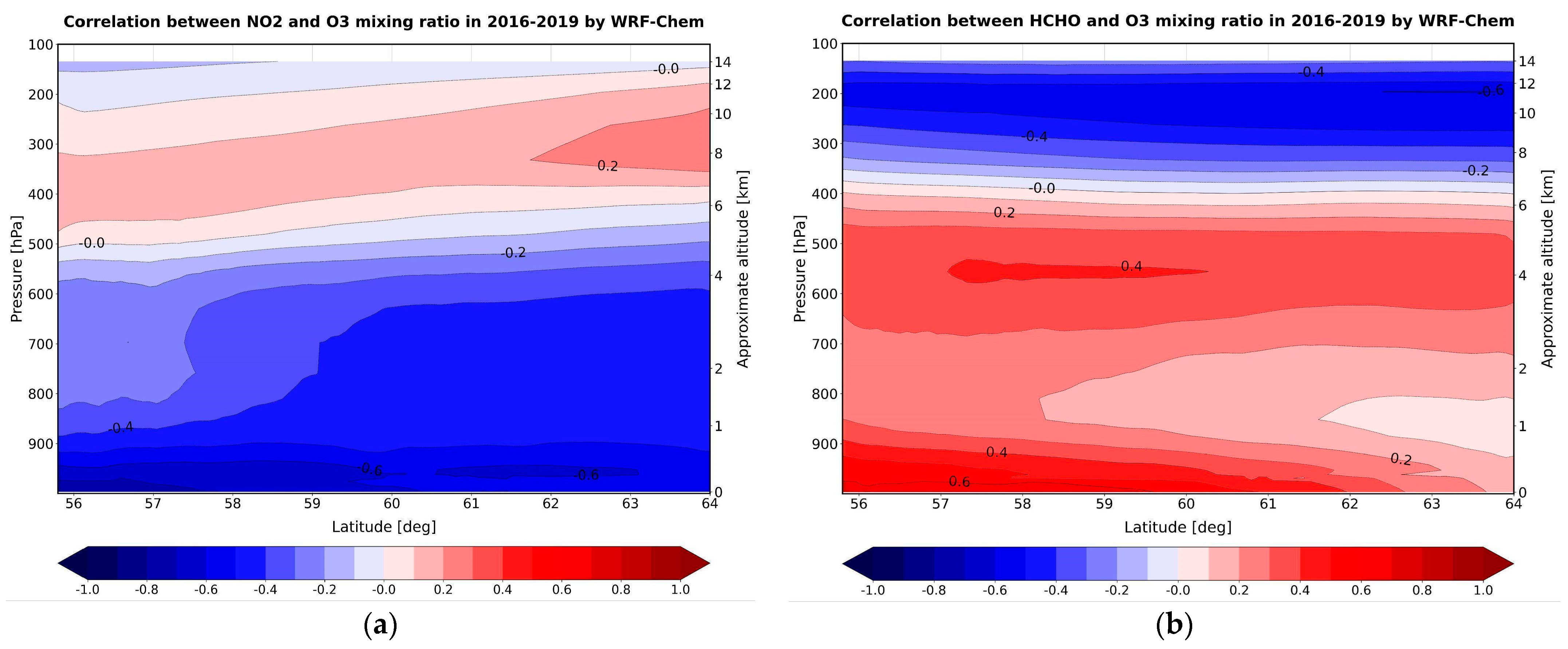
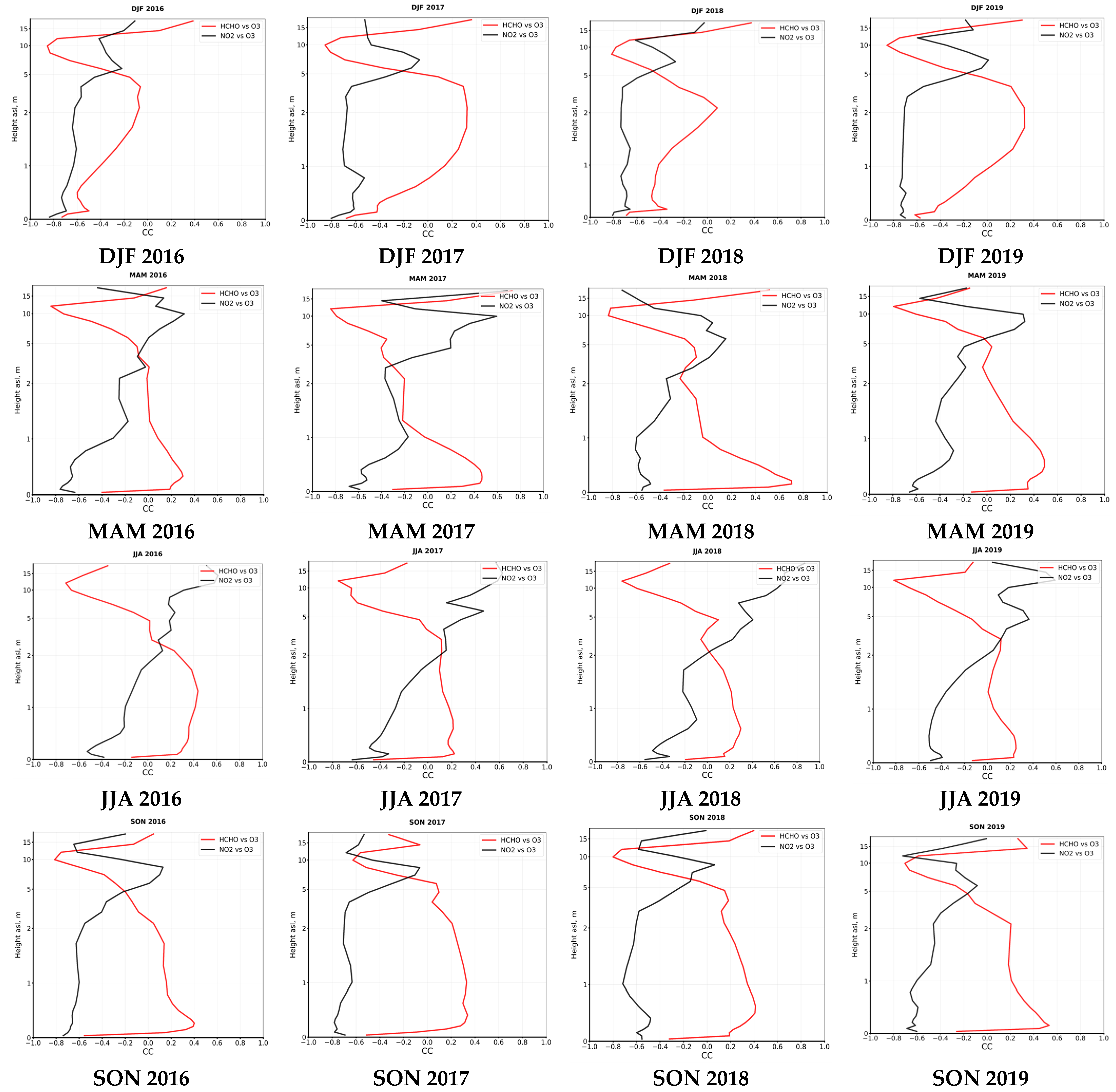
3.2.3. Vertical Correlations between Ozone and Its Precursors
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Determination of Integrated Tropospheric Ozone Content by WRF-Chem
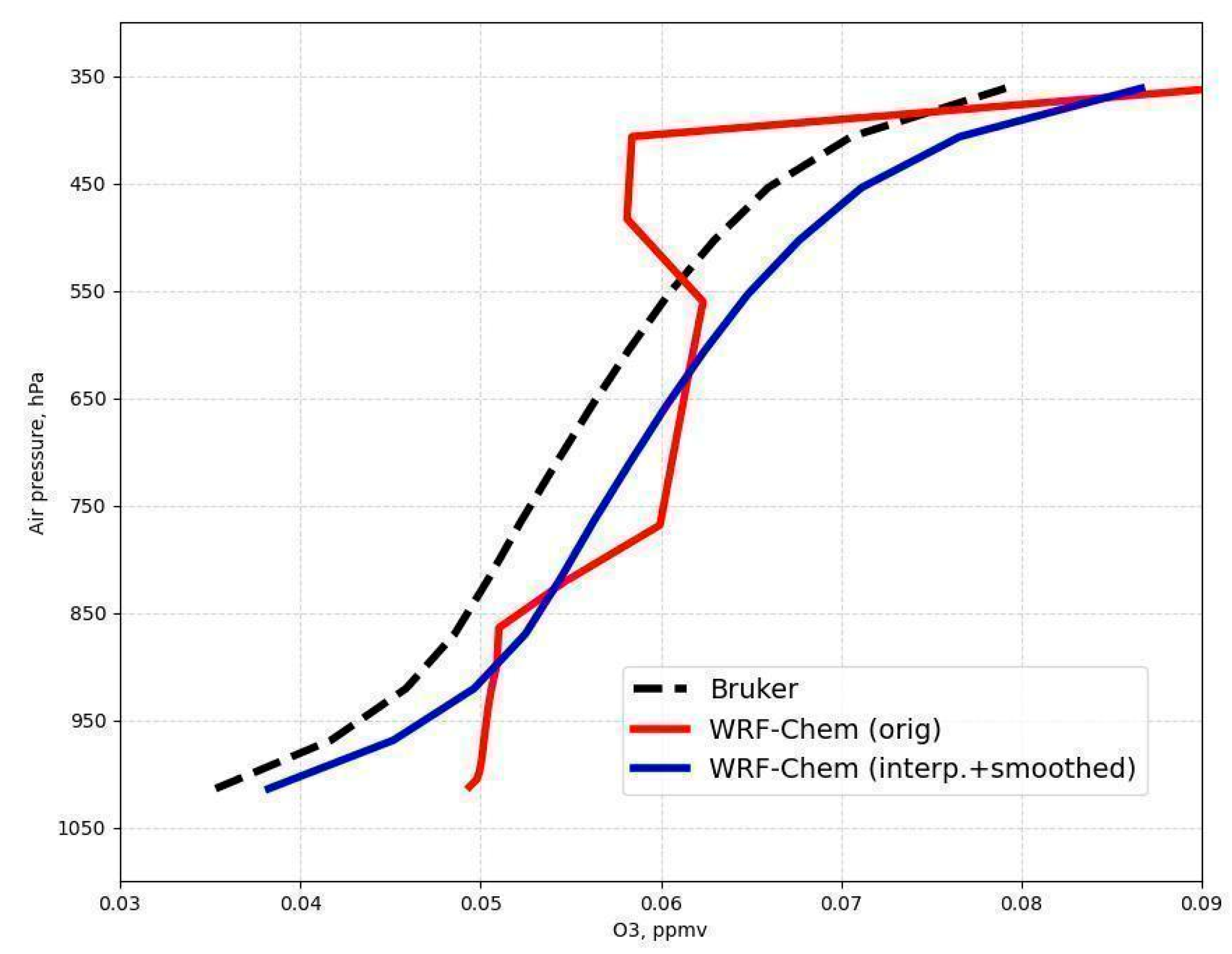
Appendix B
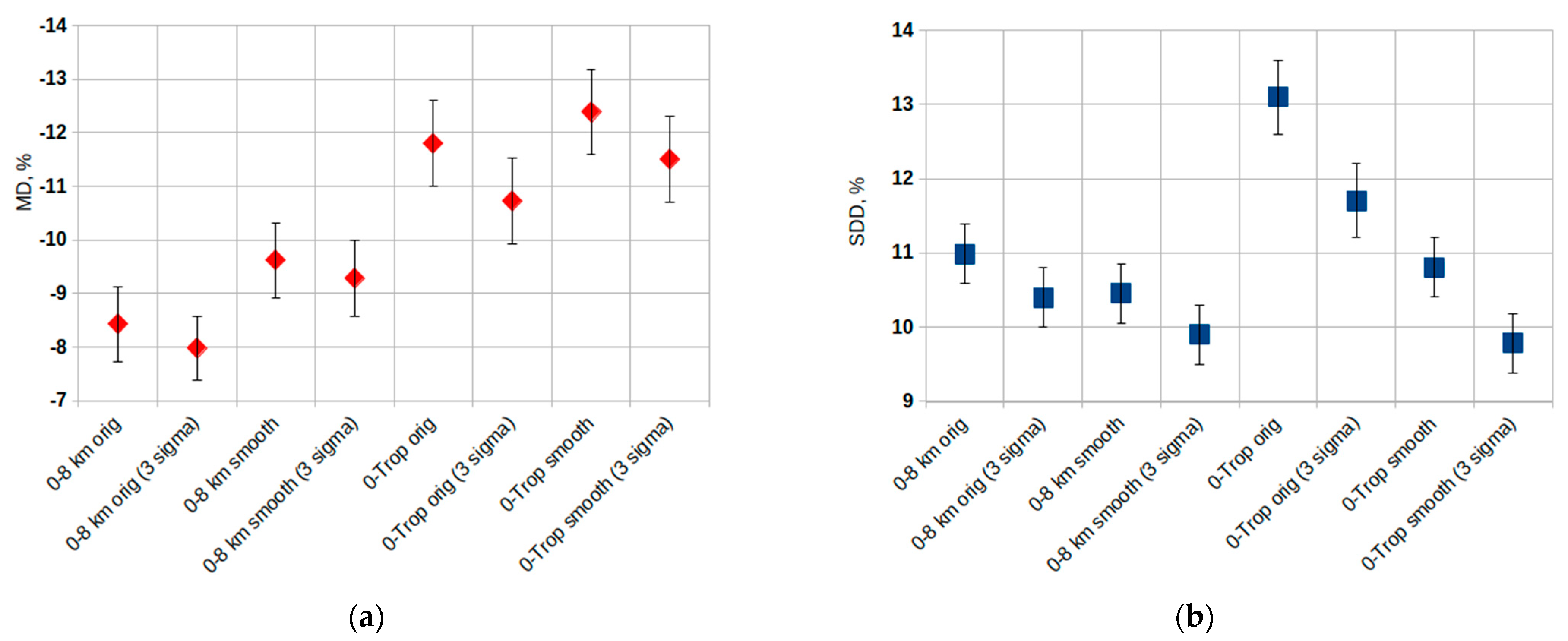
Appendix B.1. Statistical Characteristics
Appendix B.2. Confidence Intervals
Appendix C
Appendix C.1. Near-Surface Ozone Concentrations
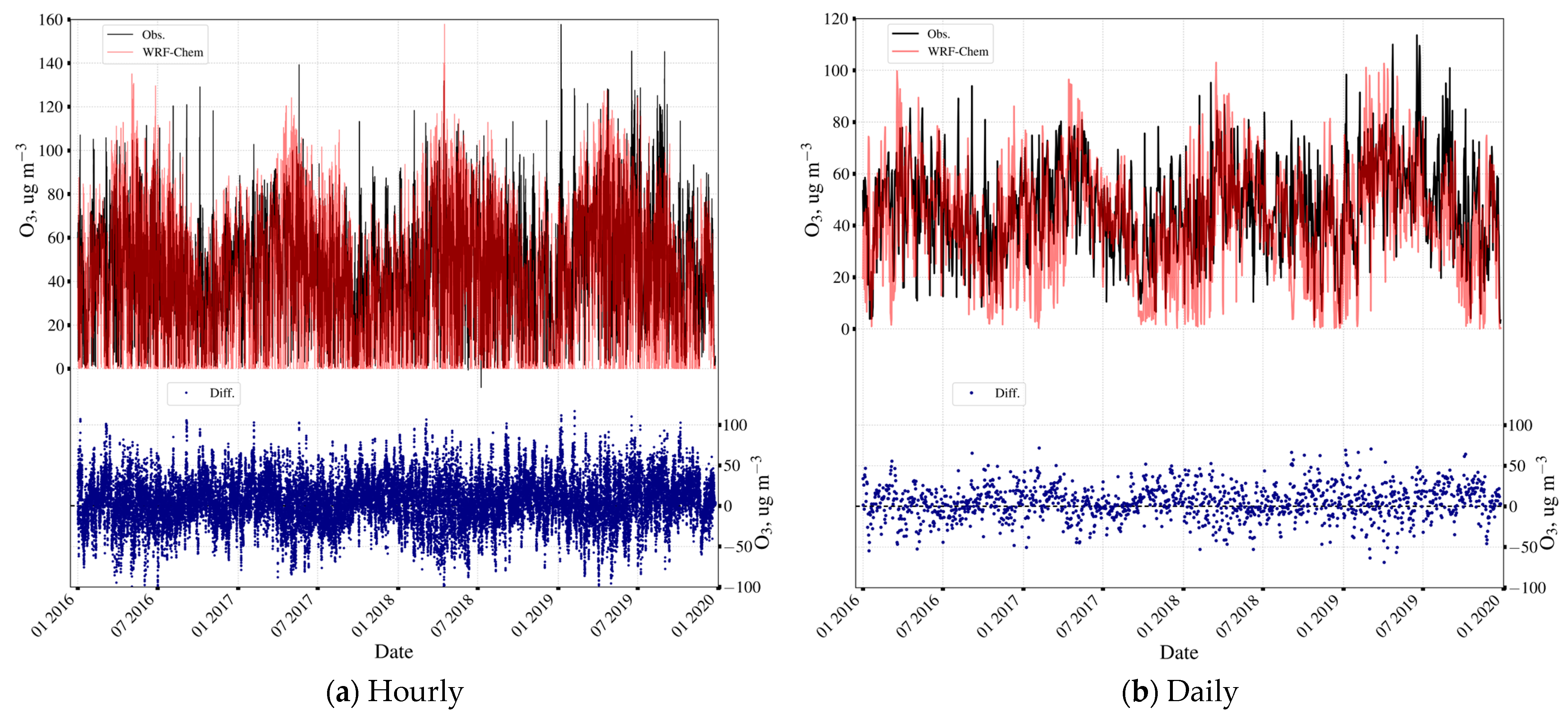
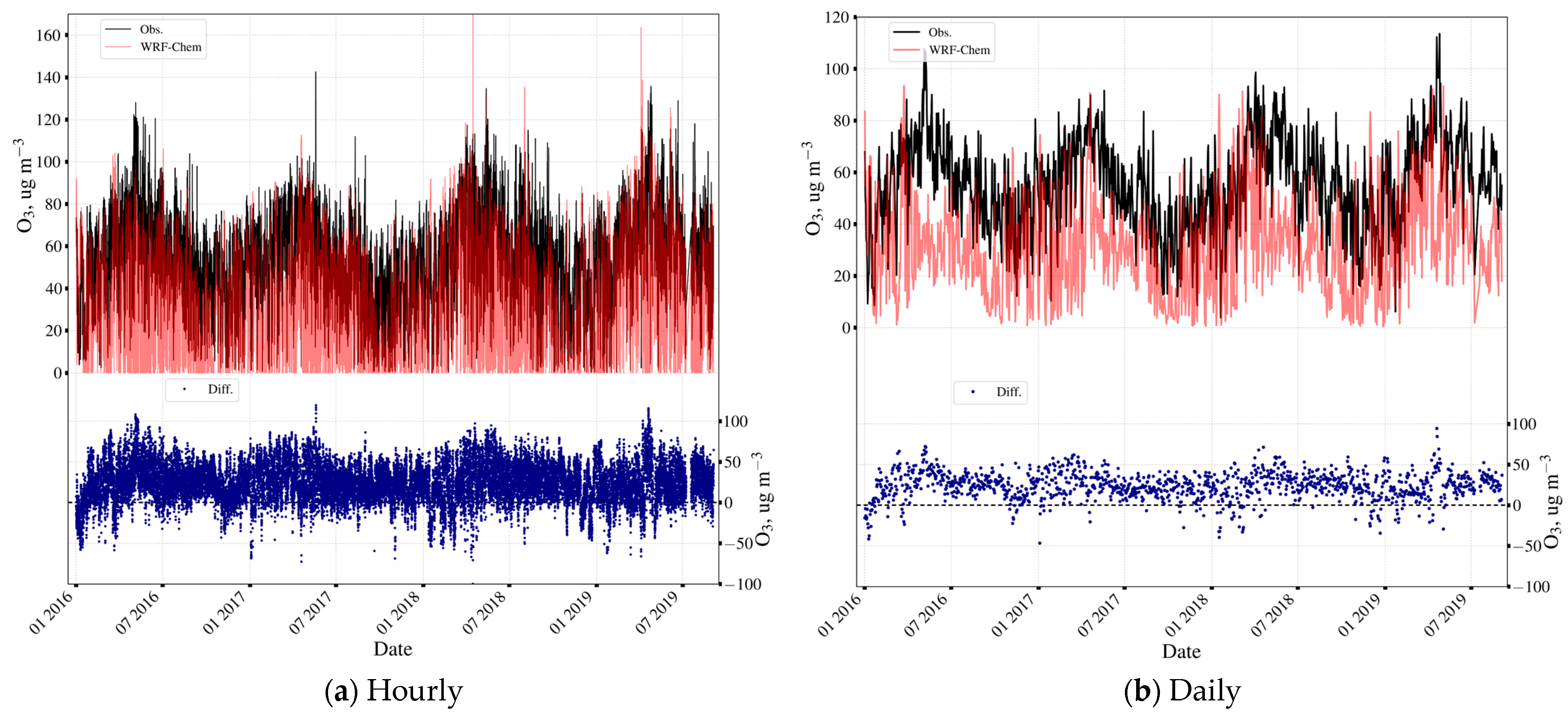
Appendix C.2. Tropospheric Ozone Content in St. Petersburg

References
- Stanek, L.W.; Brown, J.S.; Stanek, J.; Gift, J.; Costa, D.L. Air pollution toxicology—A brief review of the role of the science in shaping the current understanding of air pollution health risks. Toxicol. Sci. 2011, 120 (Suppl. S1), S8–S27. [Google Scholar] [CrossRef] [PubMed]
- Amann, M.; Derwent, D.; Forsberg, B.; Hänninen, O.; Hurley, F.; Krzyzanowski, M.; de Leeuw, F.; Liu, S.J.; Mandin, C.; Schneider, J.; et al. Health Risks of Ozone from Long-Range Transboundary Air Pollution; World Health Organization, Regional Office for Europe: Copenhagen, Denmark, 2008; Available online: https://apps.who.int/iris/handle/10665/326496 (accessed on 13 January 2024).
- Mills, G.; Pleijel, H.; Malley, C.S.; Sinha, B.; Cooper, O.R.; Schultz, M.G.; Neufeld, H.S.; Simpson, D.; Sharps, K.; Feng, Z.; et al. Tropospheric Ozone Assessment Report: Present-day tropospheric ozone distribution and trends relevant to vegetation. Elem. Sci. Anthr. 2018, 6, 47. [Google Scholar] [CrossRef]
- Forster, P.; Storelvmo, T.; Armour, K.; Collins, W.; Dufresne, J.-L.; Frame, D.; Lunt, D.J.; Mauritsen, T.; Palmer, M.D.; Watanabe, M.; et al. The Earth’s Energy Budget, Climate Feedbacks, and Climate Sensitivity. In Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Masson-Delmotte, V., Zhai, P., Pirani, A., Connors, S.L., Péan, C., Berger, S., Caud, N., Chen, Y., Goldfarb, L., Gomis, M.I., et al., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2021; pp. 923–1054. [Google Scholar] [CrossRef]
- Pope, R.J.; Rap, A.; Pimlott, M.A.; Barret, B.; Le Flochmoen, E.; Kerridge, B.J.; Siddans, R.; Latter, B.G.; Ventress, L.J.; Boynard, A.; et al. Quantifying the tropospheric ozone radiative effect and its temporal evolution in the satellite era. Atmos. Chem. Phys. 2024, 24, 3613–3626. [Google Scholar] [CrossRef]
- Tropospheric Ozone Assessment Report (TOAR): Global Metrics for Climate Change, Human Health and Crop/Ecosystem Research. Available online: https://igacproject.org/activities/TOAR (accessed on 22 December 2023).
- Liao, Z.; Gao, M.; Zhang, J.; Sun, J.; Quan, J.; Jia, X.; Pan, Y.; Fan, S. Mixing-layer-height-referenced ozone vertical distribution in the lower troposphere of Chinese megacities: Stratification, classification, and meteorological and photochemical mechanisms. Atmos. Chem. Phys. 2024, 24, 3541–3557. [Google Scholar] [CrossRef]
- Chen, Z.; Xie, Y.; Liu, J.; Shen, L.; Cheng, X.; Han, H.; Yang, M.; Shen, Y.; Zhao, T.; Hu, J. Distinct seasonality in vertical variations of tropospheric ozone over coastal regions of southern China. Sci. Total Environ. 2023, 874, 162423. [Google Scholar] [CrossRef] [PubMed]
- Li, D.; Liu, Z.; Zhou, M.; Zhao, Y.; Zhang, L. The influence of dry deposition on surface ozone simulations under different planetary boundary layer schemes over eastern China. Atmos. Environ. 2024, 327, 120514. [Google Scholar] [CrossRef]
- Ren, J.; Guo, F.; Xie, S. Diagnosing ozone–NOx–VOC sensitivity and revealing causes of ozone increases in China based on 2013–2021 satellite retrievals. Atmos. Chem. Phys. 2022, 22, 15035–15047. [Google Scholar] [CrossRef]
- Seinfeld, J.H.; Pandis, S.N. Atmospheric Chemistry and Physics: From Air Pollution to Climate Change, 2nd ed.; John Wiley & Sons: New York, NY, USA, 2006; p. 1225. [Google Scholar]
- Wallace, J.; Hobbs, P. Atmospheric Science—An Introductory Survey, 2nd ed.; Elsevier Academic Press: Amsterdam, The Netherlands, 2006; p. 484. [Google Scholar]
- Young, P.J.; Archibald, A.T.; Bowman, K.W.; Lamarque, J.-F.; Naik, V.; Stevenson, D.S.; Tilmes, S.; Voulgarakis, A.; Wild, O.; Bergmann, D.; et al. Pre-industrial to end 21st century projections of tropospheric ozone from the Atmospheric Chemistry and Climate Model Intercomparison Project (ACCMIP). Atmos. Chem. Phys. 2013, 13, 2063–2090. [Google Scholar] [CrossRef]
- Georgiou, G.K.; Christoudias, T.; Proestos, Y.; Kushta, J.; Hadjinicolaou, P.; Lelieveld, J. Air quality modelling in the summer over the eastern Mediterranean using WRF-Chem: Chemistry and aerosol mechanism intercomparison. Atmos. Chem. Phys. 2018, 18, 1555–1571. [Google Scholar] [CrossRef]
- Romero-Alvarez, J.; Lupaşcu, A.; Lowe, D.; Badia, A.; Archer-Nicholls, S.; Dorling, S.; Reeves, C.E.; Butler, T. Sources of surface O3 in the UK: Tagging O3 within WRF-Chem. Atmos. Chem. Phys. 2022, 22, 13797–13815. [Google Scholar] [CrossRef]
- Thorp, T.; Arnold, S.R.; Pope, R.J.; Spracklen, D.V.; Conibear, L.; Knote, C.; Arshinov, M.; Belan, B.; Asmi, E.; Laurila, T.; et al. Late-spring and summertime tropospheric ozone and NO2 in western Siberia and the Russian Arctic: Regional model evaluation and sensitivities. Atmos. Chem. Phys. 2021, 21, 4677–4697. [Google Scholar] [CrossRef]
- Federal State Statistics Service. Available online: https://eng.rosstat.gov.ru/ (accessed on 13 January 2024).
- Official Site of St. Petersburg Administration. Actualization of the Scheme of St. Petersburg Heat Supply. Available online: https://www.gov.spb.ru/ (accessed on 13 January 2024).
- Urbanica: 250 the Largest Industrial Centeres of Russia. Available online: http://urbanica.spb.ru/research/ratings/250-krupnejshih-promyshlennyh-tsentrov-ros-2/ (accessed on 13 January 2024).
- Federal State Statistics Service: The Number of Personal Automobiles per per Capita. Available online: https://rosstat.gov.ru/bgd/regl/b11_14p/isswww.exe/stg/d01/05-17.htm (accessed on 13 January 2024).
- Ionov, D.V.; Makarova, M.V.; Kostsov, V.S.; Foka, S.C. Assessment of the NOx integral emission from the St. Petersburg megacity by means of mobile DOAS measurements combined with dispersion modelling. Atmos. Pollut. Res. 2022, 13, 101598. [Google Scholar] [CrossRef]
- Pommier, M. Estimations of the NOx emissions, NO2 lifetime and their temporal variation over three British urbanised regions in 2019 using the TROPOMI NO2 observations. Environ. Sci. Atmos. 2023, 3, 408–421. [Google Scholar] [CrossRef]
- Shaiganfar, R.; Beirle, S.; Denier van der Gon, H.; Jonkers, S.; Kuenen, J.; Petetin, H.; Zhang, Q.; Beekmann, M.; Wagner, T. Estimation of the Paris NOx emissions from mobile MAX-DOAS observations and CHIMERE model simulations during the MEGAPOLI campaign using the closed integral method. Atmos. Chem. Phys. 2017, 17, 7853–7890. [Google Scholar] [CrossRef]
- Wang, S.; Zhou, B.; Wang, Z.; Yang, S.; Hao, N.; Valks, P.; Trautmann, T.; Chen, L. Remote sensing of NO2 emission from the central urban area of Shanghai (China) using the mobile DOAS technique. J. Geophys. Res. 2012, 117, D13305. [Google Scholar] [CrossRef]
- Virolainen, Y.A.; Ionov, D.V.; Polyakov, A.V. Analysis of Long-Term Measurements of Tropospheric Ozone at the St. Petersburg State University Observational Site in Peterhof. Izv. Atmos. Ocean. Phys. 2023, 59, 287–295. [Google Scholar] [CrossRef]
- Järvi, J.; Hannuniemi, H.; Hussein, T.; Junninen, H.; Aalto, P.P.; Hillamo, R.; Mäkelä, T.; Keronen, P.; Siivola, E.; Vesala, T.; et al. The urban measurement station smear iii: Continuous monitoring of air pollution and surface–atmosphere interactions in helsinki, Finland. Boreal Environ. Res. 2009, 14, 86–109. [Google Scholar]
- Grell, G.A.; Peckham, S.E.; Schmitz, R.; McKeen, S.A.; Frost, G.; Skamarock, W.C.; Eder, B. Fully coupled ‘online’ chemistry in the WRF model. Atmos. Environ. 2005, 39, 6957–6976. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Emmons, L.K.; Schwantes, R.H.; Orlando, J.J.; Tyndall, G.; Kinnison, D.; Lamarque, J.; Marsh, D.; Mills, M.J.; Tilmes, S.; Bardeen, C.; et al. The Chemistry Mechanism in the Community Earth System Model version 2 (CESM2). J. Adv. Model. Earth Syst. 2020, 12, e2019MS001882. [Google Scholar] [CrossRef]
- Buchholz, R.R.; Emmons, L.K.; Tilmes, S. The CESM2 Development Team. CESM2.1/CAM-chem Instantaneous Output for Boundary Conditions. UCAR/NCAR—Atmospheric Chemistry Observations and Modeling Laboratory. Subset used Lat: 50 to 70, Lon: 20 to 40, June 1–15, January 15–31 2019, Accessed 12 April 2022. [CrossRef]
- Janssens-Maenhout, G.; Crippa, M.; Guizzardi, D.; Dentener, F.; Muntean, M.; Pouliot, G.; Keating, T.; Zhang, Q.; Kurokawa, J.; Wankmüller, R.; et al. HTAP_v2.2: A mosaic of regional and global emission grid maps for 2008 and 2010 to study hemispheric transport of air pollution. Atmos. Chem. Phys. 2015, 15, 11411–11432. [Google Scholar] [CrossRef]
- Guenther, A.; Karl, T.; Harley, P.; Wiedinmyer, C.; Palmer, P.I.; Geron, C. Estimates of global terrestrial isoprene emissions using MEGAN (Model of Emissions of Gases and Aerosols from Nature). Atmos. Chem. Phys. 2006, 6, 3181–3210. [Google Scholar] [CrossRef]
- Wiedinmyer, C.; Kimura, Y.; McDonald-Buller, E.C.; Emmons, L.K.; Buchholz, R.R.; Tang, W.; Seto, K.; Joseph, M.B.; Barsanti, K.C.; Carlton, A.G.; et al. The Fire Inventory from NCAR version 2.5: An updated global fire emissions model for climate and chemistry applications. Geosci. Model Dev. 2023, 16, 3873–3891. [Google Scholar] [CrossRef]
- Gong, S.L. A parameterization of sea-salt aerosol source function for sub- and super-micron particles. Glob. Biogeochem. Cycles 2003, 17, 1097. [Google Scholar] [CrossRef]
- LeGrand, S.L.; Polashenski, C.; Letcher, T.W.; Creighton, G.A.; Peckham, S.E.; Cetola, J.D. The AFWA dust emission scheme for the GOCART aerosol model in WRF-Chem v3.8.1. Geosci. Model Dev. 2019, 12, 131–166. [Google Scholar] [CrossRef]
- Dudhia, J. Numerical study of convection observed during the Winter Monsoon Experiment using a mesoscale two–dimensional model. J. Atmos. Sci. 1989, 46, 3077–3107. [Google Scholar] [CrossRef]
- Mlawer, E.J.; Taubman, S.J.; Brown, P.D.; Iacono, M.J.; Clough, S.A. Radiative transfer for inhomogeneous atmospheres: RRTM, a validated correlated–k model for the longwave. J. Geophys. Res. 1997, 102, 16663–16682. [Google Scholar] [CrossRef]
- Mukul Tewari, N.C.A.R.; Tewari, M.; Chen, F.; Wang, W.; Dudhia, J.; LeMone, M.; Mitchell, K.; Ek, M.; Gayno, G.; Wegiel, J.; et al. Implementation and verification of the unified NOAH land surface model in the WRF model. In Proceedings of the 20th Conference on Weather Analysis and Forecasting/16th Conference on Numerical Weather Prediction, Seattle, WA, USA, 12–16 January 2004; pp. 11–15. [Google Scholar]
- Jiménez, P.A.; Dudhia, J.; González-Rouco, J.F.; Navarro, J.; Montávez, J.P.; García-Bustamante, E. A revised scheme for the WRF surface layer formulation. Mon. Weather Rev. 2012, 140, 898–918. [Google Scholar] [CrossRef]
- Song-You, H.; Noh, Y.; Dudhia, J. A new vertical diffusion package with an explicit treatment of entrainment processes. Mon. Weather Rev. 2006, 134, 2318–2341. [Google Scholar]
- Grell, G.A.; Freitas, S.R. A scale and aerosol aware stochastic convective parameterization for weather and air quality modeling. Atmos. Chem. Phys. 2014, 14, 5233–5250. [Google Scholar] [CrossRef]
- Morrison, H.; Thompson, G.; Tatarskii, V. Impact of Cloud Microphysics on the Development of Trailing Stratiform Precipitation in a Simulated Squall Line: Comparison of One– and Two–Moment Schemes. Mon. Weather Rev. 2009, 137, 991–1007. [Google Scholar] [CrossRef]
- Chen, F.; Kusaka, H.; Bornstain, R.; Ching, J.; Grimmond, C.S.B.; Grossman-Clarke, S.; Loridan, T.; Manning, K.; Martilli, A.; Miao, S.; et al. The integrated WRF/urban modeling system: Development, evaluation, and applications to urban environmental problems. Int. J. Climatol. 2011, 31, 273–288. [Google Scholar] [CrossRef]
- Emmons, L.K.; Walters, S.; Hess, P.G.; Lamarque, J.-F.; Pfister, G.G.; Fillmore, D.; Granier, C.; Guenther, A.; Kinnison, D.; Laepple, T.; et al. Description and evaluation of the Model for Ozone and Related chemical Tracers, version 4 (MOZART-4). Geosci. Model Dev. 2010, 3, 43–67. [Google Scholar] [CrossRef]
- Zaveri, R.A.; Easter, R.C.; Fast, J.D.; Peters, L.K. Model for Simulating Aerosol Interactions and Chemistry (MOSAIC). J. Geophys. Res. 2008, 113, D13204. [Google Scholar] [CrossRef]
- Ionov, D.V.; Poberovskii, A.V. Variability of Nitrogen Oxides in the Atmospheric Surface Layer near Saint Petersburg. Russ. Meteorol. Hydrol. 2020, 45, 720–726. [Google Scholar] [CrossRef]
- Crippa, M.; Guizzardi, D.; Muntean, M.; Schaaf, E. EDGAR v5.0 Global Air Pollutant Emissions; European Commission: Brussels, Belgium, 2021; p. JRC122516. [Google Scholar]
- Hase, F.; Hannigan, J.W.; Coffey, M.T.; Goldman, A.; Höpfner, M.; Jones, N.B.; Rinsland, C.P.; Wood, S.W. Inter-comparison of retrieval codes used for the analysis of high-resolution, ground-based FTIR measurements. J. Quant. Spectrosc. Radiat. Transfer. 2003, 87, 25–52. [Google Scholar] [CrossRef]
- Virolainen, Y.A.; Timofeev, Y.M.; Poberovskii, A.V.; Eremenko, M.; Dufour, G. Evaluation of ozone content in different atmospheric layers using ground-based Fourier transform spectrometry. Izv. Atmos. Ocean. Phys. 2015, 51, 167–176. [Google Scholar] [CrossRef]
- Virolainen, Y.A.; Nerobelov, G.M.; Polyakov, A.V. Comparison of Satellite and Ground-Based Measurements of Tropospheric Ozone Columns in the Vicinity of St. Petersburg. Izv. Atmos. Ocean. Phys. 2023, 59, 411–420. [Google Scholar] [CrossRef]
- García, O.E.; Schneider, M.; Redondas, A.; González, Y.; Hase, F.; Blumenstock, T.; Sepúlveda, E. Investigating the long-term evolution of subtropical ozone profiles applying ground-based FTIR spectrometry. Atmos. Meas. Technol. 2012, 5, 2917–2931. [Google Scholar] [CrossRef]
- Rodgers, C.D. Inverse Methods for Atmospheric Sounding (Oxford) Series on Atmospheric, Oceanic and Planetary Physics; World Scientific: Singapore, 2000; p. 256. [Google Scholar]
- Dekking, F.M.; Kraaikamp, C.; Lopuhaä, H.P.; Meester, L.E. A Modern Introduction to Probability and Statistics. Springer Texts in Statistics; Springer: London, UK, 2005; p. 488. [Google Scholar] [CrossRef]
- Fadeeva, L.N.; Lebedev, A.V. Theory of Probability and Mathematical Statistics; American Mathematical Society: Providence, RI, USA, 2011; p. 496. [Google Scholar]
- Matveev, L.G. The Course of General Meteorology—Atmospheric Physics; Gidrometizdat: Saint Petersburg, Russia, 1984; p. 752. [Google Scholar]
- Jacob, D.J. Introduction to Atmospheric Chemistry; Princeton University Press: Princeton, NJ, USA, 1999; p. 264. [Google Scholar]
- Teinilä, K.; Aurela, M.; Niemi, J.; Kousa, A.; Petäjä, T.; Järvi, L.; Hillamo, R.; Kangas, L.; Saarikoski, S.; Timonen, H. Concentration variation of gaseous and particulate pollutants in the Helsinki city centre—Observations from a two-year campaign from 2013–2015. Boreal Environ. Res. 2019, 24, 115–136. [Google Scholar]
- Peralta, A.H.D.; Gavidia-Calderón, M.; Andrade, M.d.F. Future Ozone Levels Responses to Changes in Meteorological Conditions under RCP 4.5 and RCP 8.5 Scenarios over São Paulo, Brazil. Atmosphere 2023, 14, 626. [Google Scholar] [CrossRef]
- Shith, S.; Ramli, N.A.; Awang, N.R.; Ismail, M.R.; Latif, M.T.; Zainordin, N.S. Does Light Pollution Affect Nighttime Ground-Level Ozone Concentrations? Atmosphere 2022, 13, 1844. [Google Scholar] [CrossRef]
- Laurila, T. Effects of environmental conditions and transport on surface ozone concentrations in Finland. Geophysica 1996, 32, 167–193. [Google Scholar]
- Sillanpää, S.; Fung, P.L.; Niemi, J.V.; Kousa, A.; Kangas, L.; Zaidan, M.A.; Timonen, H.; Kulmala, M.; Petäjä, T.; Hussein, T. Long-term air quality trends of regulated pollutants in the Helsinki metropolitan area from 1994–2019 and its implications to the Air Quality Index. Boreal Environ. Res. 2022, 27, 61–79. [Google Scholar] [CrossRef]
- Li, X.; Dong, Y.; Zhang, Y.; Shi, Z.; Yao, J. Climatology of Planetary Boundary Layer Height over Jiangsu, China, Based on ERA5 Reanalysis Data. Atmosphere 2023, 14, 1330. [Google Scholar] [CrossRef]
- WMO. GAW Report No. 209. Guidelines for Continuous Measurements of Ozone in the Troposphere; WMO: Geneva, Switzerland, 2013. [Google Scholar]
- Kuhn, L.; Beirle, S.; Kumar, V.; Osipov, S.; Pozzer, A.; Bösch, T.; Kumar, R.; Wagner, T. On the influence of vertical mixing, boundary layer schemes, and temporal emission profiles on tropospheric NO2 in WRF-Chem—Comparisons to in situ, satellite, and MAX-DOAS observations. Atmos. Chem. Phys. 2024, 24, 185–217. [Google Scholar] [CrossRef]
- Pancholi, P.; Kumar, A.; Bikundia, D.S.; Chourasiya, S. An observation of seasonal and diurnal behavior of O3–NOx relationships and local/regional oxidant (OX = O3 + NO2) levels at a semi-arid urban site of western India. Sustain. Environ. Res. 2018, 28, 79–89. [Google Scholar] [CrossRef]
- Safieddine, S.; Boynard, A.; Coheur, P.-F.; Hurtmans, D.; Pfister, G.; Quennehen, B.; Thomas, J.L.; Raut, J.-C.; Law, K.S.; Klimont, Z.; et al. Summertime tropospheric ozone assessment over the Mediterranean region using the thermal infrared IASI/MetOp sounder and the WRF-Chem model. Atmos. Chem. Phys. 2014, 14, 10119–10131. [Google Scholar] [CrossRef]
- Shah, V.; Jacob, D.J.; Dang, R.; Lamsal, L.N.; Strode, S.A.; Steenrod, S.D.; Boersma, K.F.; Eastham, S.D.; Fritz, T.M.; Thompson, C.; et al. Nitrogen oxides in the free troposphere: Implications for tropospheric oxidants and the interpretation of satellite NO2 measurements. Atmos. Chem. Phys. 2023, 23, 1227–1257. [Google Scholar] [CrossRef]
- Martin, R.V.; Fiore, A.M.; Van Donkelaar, A. Space-based diagnosis of surface ozone sensitivity to anthropogenic emissions. Geophys. Res. Lett. 2004, 31, L06120. [Google Scholar] [CrossRef]
- Jin, X.; Fiore, A.M.; Murray, L.T.; Valin, L.C.; Lamsal, L.N.; Duncan, B.; Boersma, K.F.; De Smedt, I.; Abad, G.G.; Chance, K.; et al. Evaluating a space-based indicator of surface ozone-NOx-VOC sensitivity over midlatitude source regions and application to decadal trends. J. Geophys. Res. Atmos. 2017, 122, 10,439–10,461. [Google Scholar] [CrossRef] [PubMed]
- Chang, C.-Y.; Faust, E.; Hou, X.; Lee, P.; Kim, H.C.; Hedquist, B.C.; Liao, K.-J. Investigating ambient ozone formation regimes in neighboring cities of shale plays in the Northeast United States using photochemical modeling and satellite retrievals. Atmos. Environ. 2016, 142, 152–170. [Google Scholar] [CrossRef]
- Irie, H.; Yonekawa, D.; Damiani, A.; Hoque, H.M.S.; Sudo, K.; Itahashi, S. Continuous multi-component MAX-DOAS observations for the planetary boundary layer ozone variation analysis at Chiba and Tsukuba, Japan, from 2013 to 2019. Prog. Earth Planet Sci. 2021, 8, 31. [Google Scholar] [CrossRef]


| Parameter | Description | |
|---|---|---|
| Horizontal extent and resolution | 960 × 960 km2, 10 km | |
| Dynamical, chemical and photochemical time steps | 1, 10, 30 min | |
| Vertical resolution | 25 hybrid levels, from the surface up to 50 hPa | |
| Initial and boundary conditions | Meteorology | ERA5 reanalysis, hor.res. 0.25°, up to ~80 km on 137 hybrid levels |
| Chemistry | CAM-chem model data, hor.res. 0.9 × 1.25°, up to ~45 km on 56 hybrid levels | |
| Emission sources | Anthropogenic emissions | EDGARv5.0 (2015), hor.res. 0.1°, monthly variation |
| Biogenic fluxes | Online biogenic model MEGAN, hor.res. ~1 km | |
| Biomass burning | FINN database v.2.4 and 2.5, hor.res. ~1 km | |
| Dust and sea salt | Online dust and sea salt emission preprocessors | |
| Chemistry scheme | MOZART | |
| Aerosol scheme | MOSAIC | |
| Simulation period and output frequency | 2016–2019, 1 h | |
| City | Parameter | MD | SDD | CC |
|---|---|---|---|---|
| St. Petersburg (2018–2019) | Air temperature, °C | 2.5 ± 0.05 | 2.2 ± 0.02 | 0.97 |
| Wind speed, m/s | −0.7 ± 0.02 | 1.0 ± 0.009 | 0.76 | |
| Wind direction, ° | 38.2 ± 0.6 | 29.3 ± 0.6 | 0.75 | |
| Helsinki (2016–2019) | Air temperature, °C | 3.2 ± 0.04 | 3.5 ± 0.02 | 0.93 |
| Wind speed, m/s | −2.2 ± 0.02 | 1.7 ± 0.009 | 0.75 | |
| Wind direction, ° | 9.7 ± 0.5 | 43.9 ± 0.2 | 0.78 |
| City | MD, µg/m3 (%) | SDD, µg/m3 (%) | CC |
|---|---|---|---|
| St. Petersburg | 5.0 ± 0.3 (10.7 ± 0.6) | 28.3 ± 0.15 (60.4 ± 0.3) | 0.44 |
| Helsinki | 24.1 ± 0.3 (43.5 ± 0.5) | 23.6 ± 0.14 (42.3 ± 0.25) | 0.52 |
| City | MD, µg/m3 (%) | SDD, µg/m3 (%) | CC |
|---|---|---|---|
| St. Petersburg | 5.1 ± 1.1 (10.8 ± 2.3) | 20.4 ± 0.16 (43.6 ± 1.2) | 0.48 |
| Helsinki | 24.1 ± 0.9 (43.5 ± 1.6) | 17.1 ± 0.5 (31.1 ± 0.9) | 0.56 |
| Time Scale | Number of Pairs | MD, DU (%) | SDD, DU (%) | CC |
|---|---|---|---|---|
| Hour | 833 | −2.5 ± 0.2 (−8.4 ± 0.7) | 3.3 ± 0.1 (11.0 ± 0.4) | 0.64 |
| Hour (3σ) | 821 | −2.4 ± 0.2 (−7.0 ± 0.6) | 3.1 ± 0.1 (10.4 ± 0.4) | 0.67 |
| Day | 248 | −2.7 ± 0.4 (−9.3 ± 1.4) | 3.1 ± 0.09 (10.5 ± 0.3) | 0.68 |
| Day (3σ) | 244 | −2.6 ± 0.4 (−8.8 ± 1.4) | 2.9 ± 0.2 (10.0 ± 0.8) | 0.71 |
| Time Scale | Number of Pairs | MD, DU (%) | SDD, DU (%) | CC |
|---|---|---|---|---|
| Hour | 833 | −2.9 ± 0.2 (−9.6 ± 0.7) | 3.1 ± 0.1 (10.5 ± 0.4) | 0.64 |
| Hour (3σ) | 821 | −2.8 ± 0.2 (−9.3 ± 0.7) | 3.0 ± 0.1 (9.9 ± 0.4) | 0.68 |
| Day | 248 | −3.1 ± 0.4 (−10.4 ± 1.3) | 3.0 ± 0.01 (10.1 ± 0.3) | 0.69 |
| Day (3σ) | 244 | −3.0 ± 0.4 (−10.1 ± 1.3) | 2.9 ± 0.2 (9.7 ± 0.7) | 0.71 |
| Time Scale | Number of Pairs | MD, DU (%) | SDD, DU (%) | CC |
|---|---|---|---|---|
| Hour | 833 | −4.5 ± 0.3 (−11.8 ± 0.8) | 5.0 ± 0.2 (13.1 ± 0.5) | 0.66 |
| Hour (3σ) | 808 | −4.1 ± 0.3 (−10.7 ± 0.8) | 4.5 ± 0.2 (11.7 ± 0.5) | 0.70 |
| Day | 248 | −4.8 ± 0.6 (−12.8 ± 1.6) | 4.8 ± 0.1 (12.8 ± 0.4) | 0.69 |
| Day (3σ) | 239 | −4.4 ± 0.5 (−11.6 ± 1.3) | 4.3 ± 0.3 (11.4 ± 0.9) | 0.74 |
| Time Scale | Number of Pairs | MD, DU (%) | SDD, DU (%) | CC |
|---|---|---|---|---|
| Hour | 833 | −4.7 ± 0.3 (−12.4 ± 0.8) | 4.1 ± 0.2 (10.8 ± 0.4) | 0.72 |
| Hour (3σ) | 807 | −4.4 ± 0.3 (−11.5 ± 0.8) | 3.8 ± 0.1 (9.8 ± 0.4) | 0.76 |
| Day | 248 | −5.0 ± 0.5 (−13.3 ± 1.3) | 4.0 ± 0.1 (10.6 ± 0.3) | 0.75 |
| Day (3σ) | 238 | −4.6 ± 0.5 (−12.3 ± 1.3) | 3.6 ± 0.3 (9.5 ± 0.7) | 0.79 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nerobelov, G.; Virolainen, Y.; Ionov, D.; Polyakov, A.; Rozanov, E. WRF-Chem Modeling of Tropospheric Ozone in the Coastal Cities of the Gulf of Finland. Atmosphere 2024, 15, 775. https://doi.org/10.3390/atmos15070775
Nerobelov G, Virolainen Y, Ionov D, Polyakov A, Rozanov E. WRF-Chem Modeling of Tropospheric Ozone in the Coastal Cities of the Gulf of Finland. Atmosphere. 2024; 15(7):775. https://doi.org/10.3390/atmos15070775
Chicago/Turabian StyleNerobelov, Georgii, Yana Virolainen, Dmitry Ionov, Alexander Polyakov, and Eugene Rozanov. 2024. "WRF-Chem Modeling of Tropospheric Ozone in the Coastal Cities of the Gulf of Finland" Atmosphere 15, no. 7: 775. https://doi.org/10.3390/atmos15070775
APA StyleNerobelov, G., Virolainen, Y., Ionov, D., Polyakov, A., & Rozanov, E. (2024). WRF-Chem Modeling of Tropospheric Ozone in the Coastal Cities of the Gulf of Finland. Atmosphere, 15(7), 775. https://doi.org/10.3390/atmos15070775







