Assessment of Atmospheric Particles Flux Variation on the Different Underlying Surfaces (Grasslands and Forest) in the Lake Baikal Region
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Conditions and Measurement Methods
2.2. Deposition Velocity Calculations
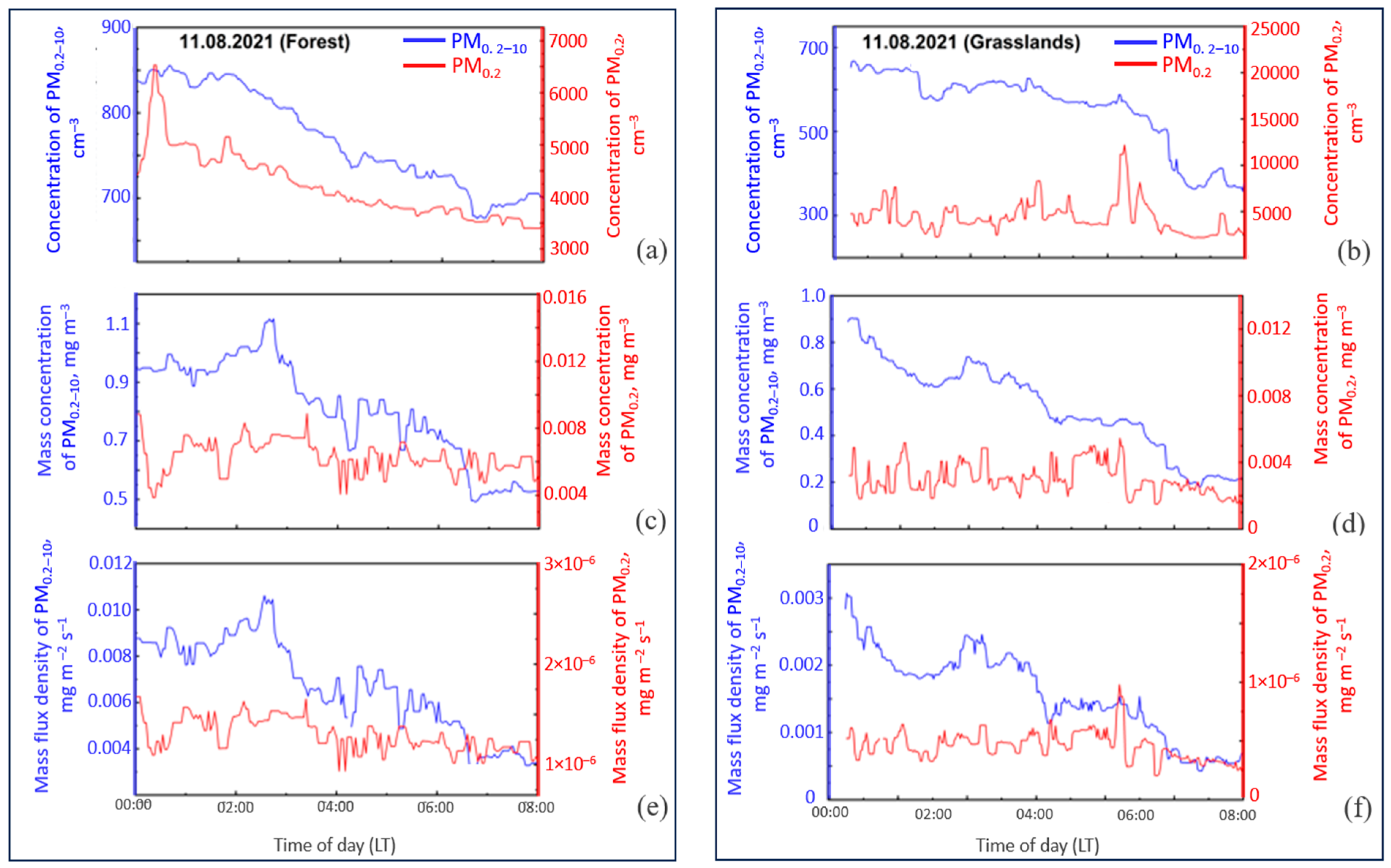
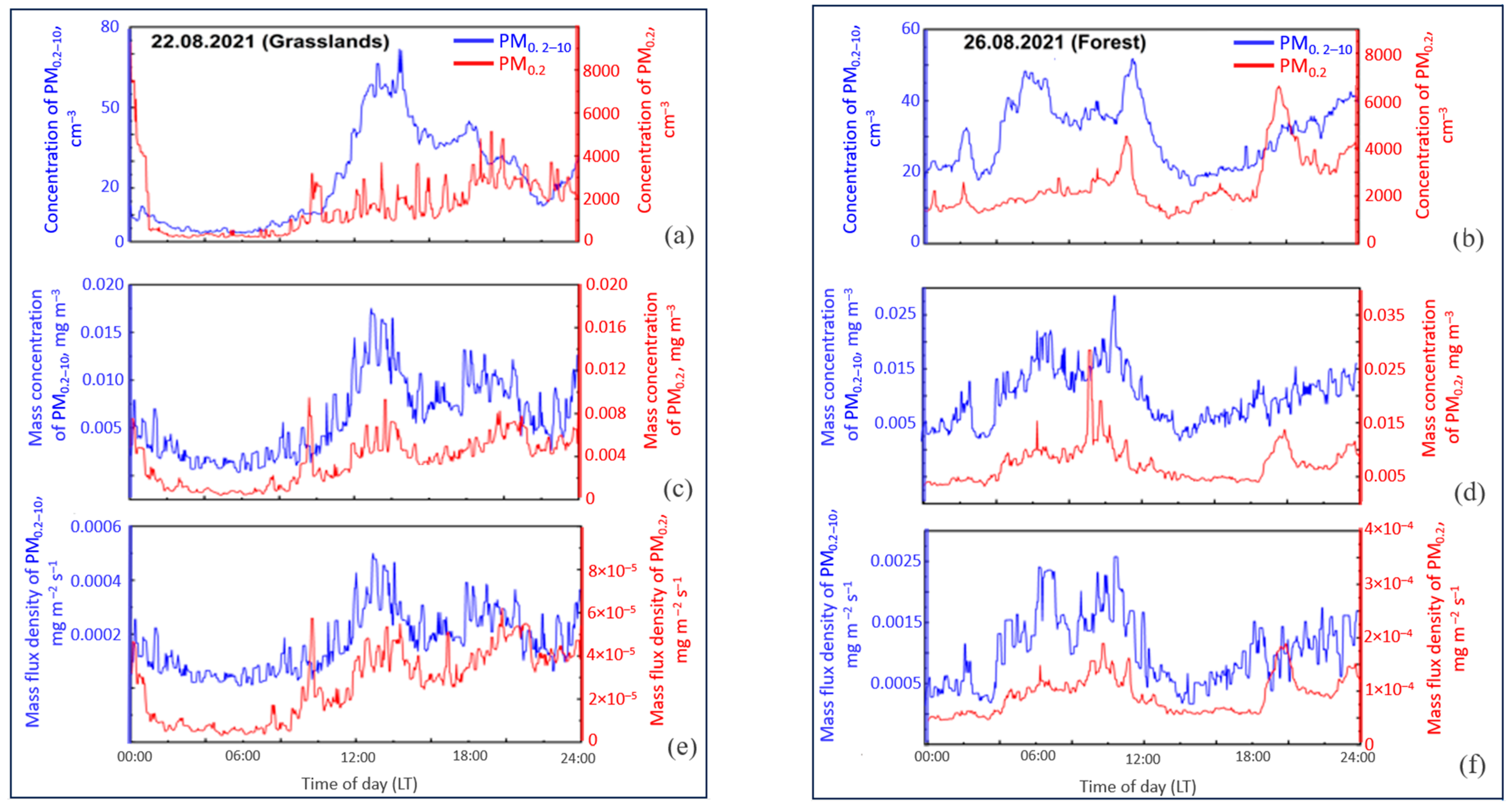
3. Results and Discussions
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, L.; Gong, S.; Padro, J.; Barrie, L. A size-segregated particle dry deposition scheme for an atmospheric aerosol model. Atmos. Environ. 2001, 35, 549–560. [Google Scholar] [CrossRef]
- Slinn, S.A.; Slinn, W.G.N. Predictions for particle deposition on natural waters. Atmos. Environ. 1980, 14, 1013–1016. [Google Scholar] [CrossRef]
- Slinn, W.G.N. Predictions for particle deposition to vegetative surfaces. Atmos. Environ. 1982, 16, 1785–1794. [Google Scholar] [CrossRef]
- Zhang, L.; Brook, J.R.; Vet, R. A revised parameterization for gaseous dry deposition in air-quality models. Atmos. Chem. Phys. 2003, 3, 2067–2082. [Google Scholar] [CrossRef]
- Wesely, M.L.; Cook, D.R.; Hart, R.L.; Speer, R.E. Measurements and parametrization of article sulfur deposition over grass. J. Geophys. 1985, 90, 2131–2143. [Google Scholar] [CrossRef]
- Giorgi, F. A particle dry deposition parameterization scheme for use in tracer transport models. J. Geophys. Res. 1986, 91, 9794–9806. [Google Scholar] [CrossRef]
- Padro, J.; Hartog, G.; Neumann, H.H. An investigation of the ADOM dry deposition module using summertime O3 measurements above a deciduous forest. Atmos. Environ. 1991, 25, 1689–1704. [Google Scholar] [CrossRef]
- Erisman, J.W.; Van Pul, A.; Wyers, P. Parametrization of surface resistance for the quantification of mospheric deposition of acidifying pollutants and ozone. Atmos. Environ. 1994, 28, 2595–2607. [Google Scholar] [CrossRef]
- Wesely, M.L.; Doskey, P.V.; Shannon, J. Deposition Parameterizations for the Industrial Source Complex (ISC3) Model; Report to U.S. EPA; Argonne National Laboratory: Du Page County, IL, USA, 2001. [Google Scholar]
- Kor, P.; Kharrat, R. Modelling of asphaltene particle deposition from turbulent oil flow in tubing: Model validation and a parametric study. Petroleum 2016, 2, 393–398. [Google Scholar] [CrossRef]
- Giardina, M.; Buffa, P. A new approach for modelling dry deposition velocity of particles. Atmos. Environ. 2018, 180, 11–22. [Google Scholar] [CrossRef]
- Pellerin, G.; Maro, D.; Damay, P.; Gehin, E.; Connan, O.; Laguionie, P.; Hébert, D.; Solier, L.; Boulaud, D.; Lamaud, E.; et al. Aerosol particle dry deposition velocity above natural surfaces: Quantification according to the particles diameter. J. Aerosol Sci. 2017, 114, 107–117. [Google Scholar] [CrossRef]
- Hofken, K.D.; Gravenhorst, G. Deposition of atmospheric aerosol particles to beech- and spruce forest. In Deposition of Atmospheric Pollutants, 2nd ed.; Georgii, H.W., Pankrath, J., Eds.; D. Reidel Publishing Company: Oberursel/Taunus, Germany, 1982; pp. 191–194. [Google Scholar]
- Pryor, S.C.; Gallagher, M.; Sievering, H.; Larsen, S.E.; Barthelmie, R.J.; Birsan, F.; Nemitz, E.; Rinne, J.; Kulmala, M.; Gronholm, T.; et al. Review of measurement and modelling results of particle atmosphere–surface exchange. Tellus B Chem. Phys. Meteorol. 2007, 60, 42–75. [Google Scholar] [CrossRef]
- Pryor, S. Size-resolved particle deposition velocities of sub-100 nm diameter particles over a forest. Atmos. Environ. 2006, 40, 6192–6200. [Google Scholar] [CrossRef]
- Gallagher, M.W.; Nemitz, E.; Dorsey, J.R.; Fowler, D.; Sutton, M.A.; Flynn, M.; Duyzer, J. Measurements and parameterizations of small aerosol deposition velocities to grassland, arable crops, and forest: Influence of surface roughness length on deposition. J. Geophys. Res. 2002, 107, 287–292. [Google Scholar] [CrossRef]
- Zhang, J.; Shao, Y.; Huang, N. Measurements of dust deposition velocity in a wind tunnel experiment. Atmos. Chem. Phys. 2014, 14, 8869–8882. [Google Scholar] [CrossRef]
- Frazer, G.W.; Canham, C.D.; Lertzman, K.P. Gap Light Analyzer (GLA), Version 2.0: Imaging Software to Extract Canopy Structure and Gap Light Transmission Indices from True-Colour Fisheye Photographs, User’s Manual and Program Documentation; Simon Fraser University: Burnaby, BC, Canada; Institute of Ecosystem Studies: Millbrook, NY, USA, 1999. [Google Scholar]
- Mason, E.G.; Diepstraten, M.; Pinjuv, G.L.; Lasserre, J.P. Comparison of direct and indirect leaf area index measurements of Pinus radiata D. Don. Agric. For. Meteorol. 2012, 166–167, 113–119. [Google Scholar] [CrossRef]
- Julanov, Y.V.; Lushnikov, A.A.; Zagaynov, V.A. Diffusion aerosol spectrometer. Atmos. Res. 2002, 62, 295–302. [Google Scholar] [CrossRef]
- Tikhomirov, A.A. Ultrasonic anemometers and thermometers for measuring fluctuations of air flux velocity and temperature. Review. Opt. Atmos. Okeana Pap. 2010, 7, 585–600. (In Russian) [Google Scholar]
- Seinfeld, J.H.; Pandis, S.N. Atmospheric Chemistry and Physics, 2nd ed.; John Wiley & Sons, Inc. Shapiro: New York, NY, USA, 1998; pp. 154–196. [Google Scholar]
- Venkatram, A.; Pleim, J. The electrical analogy does not apply to modelling dry deposition of particles. Atmos. Environ. 1999, 33, 3075–3076. [Google Scholar] [CrossRef]
- Csanady, G.T. Turbulent Diffusion in the Environment, 3rd ed.; D. Reidel Publisher: Dordrecht, The Netherlands, 1974. [Google Scholar]
- Wesely, M.L.; Hicks, B.B. Some factors that affect the deposition rates of sulfur dioxide and similar gases to vegetation. J. Air Polka. Control Ass. 1977, 27, 1110–1116. [Google Scholar] [CrossRef]
- Peters, K.; Eiden, R. Modelling the dry deposition velocity of aerosol particles to a spruce forest. Atmos. Environ. 1992, 26A, 2555–2564. [Google Scholar] [CrossRef]
- Pryor, S.C.; Barthelmie, R.J.; Spaulding, A.M.; Larsen, S.E.; Petroff, A. Size-resolved fluxes of sub-100-nm particles over forests. J. Geophys. Res. 2009, 114, D18. [Google Scholar] [CrossRef]
- Kumar, R.; Kumari, K.M. Experimental and parameterization method for evaluation of dry Deposition of S Compounds to natural surfaces. Atmos. Clim. Sci. 2012, 2, 492–500. [Google Scholar] [CrossRef]
- Liu, B.Y.H.; Agarwal, J.K. Experimental observation of aerosol deposition in turbulent flow. J. Aerosol Sci. 1974, 5, 145–155. [Google Scholar] [CrossRef]
- Chamberlain, A.C. Transport of Lycopodium Spores and Other Small Particles to Rough Surfaces. Proc. R. Soc. London. Ser. A Math. Phys. Sci. 1967, 296, 45–70. [Google Scholar]
- Bottalico, F.; Chirici, G.; Giannetti, F.; De Marco, A.; Nocentini, S.; Paoletti, E.; Salbitano, F.; Sanesi, G.; Serenelli, C.; Travaglini, D. Air pollution removal by green infrastructures and urban forests in the city of Florence. Agric. Sci. Procedia 2016, 8, 243–251. [Google Scholar] [CrossRef]
- Tiwari, A.; Kumar, P.; Baldauf, R.; Zhang, K.M.; Pilla, F.; Di Sabatino, S.; Brattich, E.; Pulvirenti, B. Considerations for evaluating green infrastructure impacts in microscale and macroscale air pollution dispersion models. Sci. Total Environ. 2019, 672, 410–426. [Google Scholar] [CrossRef] [PubMed]
- Huffman, J.A.; Prenni, A.J.; Demott, P.J.; Pöhlker, C.; Mason, R.H.; Robinson, N.H.; Fröhlich-Nowoisky, J.; Tobo, Y.; Després, V.R.; Garcia, E.; et al. High concentrations of biological aerosol particles and ice nuclei during and after rain. Atmos. Chem. Phys. 2013, 13, 6151–6164. [Google Scholar] [CrossRef]
- Jeanjean, A.; Buccolieri, R.; Eddy, J.; Monks, P.; Leigh, R. Air quality affected by trees in real street canyons: The case of Marylebone neighbourhood in central London. Urban Green 2017, 22, 41–53. [Google Scholar] [CrossRef]
- Kim, J.J.; Hann, T.; Lee, S.J. Effect of flow and humidity on indoor deposition of particulate matter. Environ. Pollut. 2019, 255, 113263. [Google Scholar] [CrossRef]
- Montgomery, J.F.; Rogak, S.N.; Green, S.I.; You, Y.; Bertram, A.K. Structural Change of Aerosol Particle Aggregates with Exposure to Elevated Relative Humidity. Environ. Sci. Technol. 2015, 49, 12054–12061. [Google Scholar] [CrossRef]
- Ryu, J.; Kim, J.J.; Byeon, H.; Go, T.; Lee, S.J. Removal of fine particulate matter (PM2.5) via atmospheric humidity caused by evapotranspiration. Environ. Pollut. 2019, 245, 253–259. [Google Scholar] [CrossRef] [PubMed]
- Shahid, M.; Dumat, C.; Khalid, S.; Schreck, E.; Xiong, T.; Niazi, N. Foliar heavy metal uptake, toxicity and detoxification in plants: A comparison of foliar and root metal uptake. J. Hazard. Mater. 2016, 325, 36–58. [Google Scholar] [CrossRef] [PubMed]
- Zhou, S.; Cong, L.; Liu, Y.; Xie, L.; Zhao, S.; Zhang, Z. Rainfall intensity plays an important role in the removal of PM from the leaf surfaces. Ecol. Indic. 2021, 128, 107778. [Google Scholar] [CrossRef]
- Pleim, J.E.; Ran, L.; Saylor, R.D.; Willison, J.; Binkowski, F.S. A new aerosol dry deposition model for air quality and climate modeling. J. Adv. Model. Earth Syst. 2022, 14, e2022MS003050. [Google Scholar] [CrossRef]
- Emerson, E.W.; Katich, J.M.; Schwarz, J.P.; McMeeking, G.R.; Farmer, D.K. Direct measurements of dry and wet deposition of black carbon over a grassland. J. Geophys. Res. Atmos. 2018, 123, 12277–12290. [Google Scholar] [CrossRef]
- Petroff, A.; Murphy, J.G.; Thomas, S.C.; Geddes, J.A. Size-resolved aerosol fluxes above a temperate broadleaf forest. Atmos. Environ. 2018, 190, 359–375. [Google Scholar] [CrossRef]
- Grönholm, T.; Aalto, P.P.; Hiltunen, V.; Rannik, U.; Rinne, J.; Laakso, L.; HyvöNen, S.; Vesala, I.; Kulmala, M. Measurements of aerosol particle dry deposition velocities using relaxed eddy accumulation technique. Tellus 2007, 59, 381–386. [Google Scholar] [CrossRef]
- Connan, O.; Pellerin, G.; Maro, D.; Damay, P.; Hébert, D. Dry deposition velocities of particles on grass: Field experimental data and comparison with models. J. Aerosol Sci. 2018, 126, 58–67. [Google Scholar] [CrossRef]
- Ahlm, L.; Krejci, R.; Nilsson, E.D.; Martensson, E.M.; Vogt, M.; Artaxo, P. Emission and dry deposition of accumulation mode particles in the Amazon Basin. Atmos. Chem. Phys. 2010, 10, 10237–10253. [Google Scholar] [CrossRef]
- Vong, R.J.; Vong, I.J.; Vickers, D.; Covert, D.S. Size-dependent aerosol deposition velocities during BEARPEX’07. Atmos. Chem. Phys. 2010, 10, 5749–5758. [Google Scholar] [CrossRef]
- Clough, W. The deposition of particles on moss and grass surfaces. Atmos. Environ. 1975, 9, 1113–1119. [Google Scholar] [CrossRef]
- Garland, J.; Cox, L. Deposition of small particles to grass. Atmos. Environ. 1982, 16, 2699–2702. [Google Scholar] [CrossRef]
- Dollard, G.; Unsworth, M. Field measurements of turbulent fluxes of wind-driven fog drops to a grass surface. Atmos. Environ. 1983, 17, 775–780. [Google Scholar] [CrossRef]
- Katen, P.C.; Hubbe, J.M. An evaluation of optical particle counter measurements of the dry deposition of atmospheric aerosol particles. J. Geophys. Res. Atmos. 1985, 90, 2145–2160. [Google Scholar] [CrossRef]
- Hicks, B.; Wesely, M.; Coulter, R.; Hart, R.; Durham, J. An experimental study of sulfur and NOX fluxes over grassland. Bound. Layer Meteorol. 1986, 34, 103–121. [Google Scholar] [CrossRef]
- Gallagher, M.; Choularton, T.; Morse, A.; Fowler, D. Measurements of the size dependence of cloud droplet deposition at a hill site. Q. J. R. Meteorol. Soc. 1988, 114, 1291–1303. [Google Scholar] [CrossRef]
- Fowler, D.; Morse, A.; Gallagher, M.; Choularton, T. Measurements of cloud water deposition on vegetation using a lysimeter and a flux gradient technique. Tellus B Chem. Phys. Meteorol. 1990, 42, 285–293. [Google Scholar] [CrossRef]
- Allen, A.; Harrison, R.; Nicholson, K. Dry deposition of fine aerosol to a short grass surface. Atmos. Environ. A 1991, 25, 2671–2676. [Google Scholar] [CrossRef]
- Nemitz, E.; Gallagher, M.W.; Duyzer, J.H.; Fowler, D. Micrometeorological measurements of particle deposition velocities to moorland vegetation. Q. J. R. Meteorol. Soc. 2002, 128, 2281–2300. [Google Scholar] [CrossRef]
- Vong, R.J.; Vickers, D.; Covert, D.S. Eddy correlation measurements of aerosol deposition to grass. Tellus B Chem. Phys. Meteorol. 2004, 56, 105–117. [Google Scholar] [CrossRef]
- Waraghai, A.; Gravenhorst, G. Dry deposition of atmospheric particles to an old spruce stand. In Proceedings of the Meeting on Mechanisms and Effects of Pollutant-Transfer into Forests, Oberursel, Germany, 24–25 November 1988. [Google Scholar]
- Lorenz, R.; Murphy, C. Dry deposition of particles to a pine plantation. Bound. Layer Meteorol. 1989, 46, 355–366. [Google Scholar] [CrossRef]
- Gallagher, M.; Beswick, K.; Duyzer, J.; Westrate, H.; Choularton, T.; Hummelshøj, P. Measurements of aerosol fluxes to Speulder forest using a micrometeorological technique. Atmos. Environ. 1997, 31, 359–373. [Google Scholar] [CrossRef]
- Buzorius, G.; Rannik, U.; Makela, J.M.; Vesala, T.; Kulmala, M. Vertical aerosol particle fluxes measured by eddy covariance technique using condensational particle counter. J. Aerosol Sci. 1998, 29, 157–171. [Google Scholar] [CrossRef]
- Gaman, A.; Rannik, Ü.; Aalto, P.; Pohja, T.; Siivola, E. Relaxed eddy accumulation system for size-resolved aerosol particle flux measurements. J. Atmos. Ocean. Technol. 2004, 21, 933–943. [Google Scholar] [CrossRef]
- Gordon, M.; Staebler, R.M.; Liggio, J.; Vlasenko, A.; Li, S.M.; Hayden, K. Aerosol flux measurements above a mixed forest at Borden, Ontario. Atmos. Chem. Phys. 2011, 11, 6773–6786. [Google Scholar] [CrossRef]
- Mammarella, I.; Rannik, Ü.; Aalto, P.; Keronen, P.; Vesala, T.; Kulmala, M. Long-term aerosol particle flux observations. Part II: Particle size statistics and deposition velocities. Atmos. Environ. 2011, 45, 3794–3805. [Google Scholar] [CrossRef]
- Lavi, A.; Farmer, D.K.; Segre, E.; Moise, T.; Rotenberg, E. Fluxes of fine particles over a semi-arid pine forest: Possible effects of a complex terrain. Aerosol Sci. Technol. 2013, 47, 906–915. [Google Scholar] [CrossRef][Green Version]


| Parameter | Unit | Parameter Values | |
|---|---|---|---|
| Grassland | Forest | ||
| Vegetation height (h) | m | 0.3 | 12 |
| Leaf area index (LAI) | - | 2.4 | 5.6 |
| Flat displacement (d) | m | 0.03 | 9.7 |
| Roughness length (z0) | m | 0.2 | 0.7 |
| Particle density (ρp) | kg m−3 | 1000 | 1000 |
| Parameter | Unit | Date | |
|---|---|---|---|
| 22 August | 26 August | ||
| Temperature | °C | 12 ± 1.5 | 12.5 ± 1.4 |
| Wind speed | m s−1 | 8.2 ± 3 | 8.1 ± 2.2 |
| Relative humidity | % | 90 ± 5 | 82 ± 8 |
| Wind direction | deg | 249.1 ± 5 | 248.4 ± 5 |
| Land Use Type | Site Location and Details | Method | Size Range (µm) | Vd (cm s−1) | Reference |
|---|---|---|---|---|---|
| Grassland | Present study (research station “Boyarsky”, Lake Baikal, Russia) | Gradient | 0.005–10 | 0.6 | Giardina et al., 2018 [11] |
| Grass and filter paper | Gradient | 0.08–32 | 0.01–7.2 | Chamberlain, 1967 [30] | |
| Moss (Hypnum cupressiforme) and Italian rye grass | Wind tunnel experiment | 0.5 | 0.024 | Clough, 1975 [47] | |
| Wood River refinery complex, Illinois, USA | Eddy covariance | 0.05–0.1 | 0.6 ± 0.4 | Wesely et al., 1977 [25] | |
| Grass | Gradient | 0.05–1 | 0.525 | Garland & Cox., 1982 [48] | |
| Mount St. Bernard Abbey near Coalville, Leicestershire, England | Gradient | 5–30 | 2.4–7.0 | Dollard & Unsworth, 1983 [49] | |
| Champaign, Illinois, USA | Eddy covariance | 0.15–2.5 | −0.05–−0.16 | Katen & Hubbe, 1985 [50] | |
| Champaign, Illinois, USA | Eddy covariance | ∼0.1–1 | 0.22 ± 0.06 | Wesely et al., 1985 [5] | |
| South Charleston, Ohio, USA | Eddy covariance | <1 | 0.4–0.8 | Hicks et al., 1986 [51] | |
| Moorland with Eriophorun and Juncus species, Great Dun Fell, England | Gradient | 5–31 | 0.5–8.9 | Gallagher et al., 1988 [52] | |
| Moorland with Eriophorun and Juncus species, Great Dun Fell, England | Gradient | 2–30 | 2.1–3.9 | Fowler et al., 1990 [53] | |
| Sports fields at the University of Essex, Colchester, England | Gradient | 0.1–2 | 0.10 ± 0.03 | Allen et al., 1991 [54] | |
| Transitional lowland raised bog, Sphagnum species, Auchencorth Moss field site, southeast Scotland | Eddy covariance | 0.1–3 | 0.007–1.2 | Nemitz et al., 2002 [55] | |
| Field of rye grass, Shedd, Oregon, USA | Eddy covariance | 0.52 | 0.16–0.44 | Vong et al., 2004 [56] | |
| Alfalfa (Medicago sativa) field, Southern Great Plains site, Lamont, Oklahoma, USA | Eddy covariance | 0.07–0.6 | 0.03 ± 0.02 | Emerson et al., 2018 [41] | |
| Grass cuttings and synthetic commercial grass | Gradient | 0.24–7.8 | 0.046–2.3 | Connan et al., 2018 [44] | |
| Forest | Present study (research station “Boyarsky”, Lake Baikal, Russia) | Gradient | 0.005–10 | 0.8 | Giardina et al., 2018 [11] |
| Solling forest (spruce and beech trees) | Gradient | 0.26–2.4 | 0.7–1.8 | Höfken & Gravenhorst, 1982 [13] | |
| Spruce forest | Gradient | 0.5–10 | 0.8–1.6 | Waraghai & Gravenhorst, 1989 [57] | |
| Pine plantation | Gradient | 0.5–5 | 0.34–0.92 | Lorenz & Murphy, 1989 [58] | |
| Douglas fir forest, Speulderbos, The Netherlands | Eddy covariance | 0.1–3 | 0.02–11 | Gallagher et al., 1997 [59] | |
| Scots pine forest (SMEAR II station), Hyytiäälä, Finland | Eddy covariance | 0.012–1 | NA | Buzorius et al., 1998 [60] | |
| Scots pine forest (SMEAR II station), Hyytiäälä, Finland | REA | 0.05 | 0.43 ± 0.06 | Gaman et al., 2004 [61] | |
| Beech forest (CarboEuroFlux experimental forest site), Sorø, Denmark | Eddy covariance | 0.02–0.07 | 0.15–0.45 | Pryor, 2006 [15] | |
| Scots pine forest (SMEAR II station), Hyytiäälä, Finland | REA | 0.008–0.15 | 0.6–2.1 | Grönholm et al., 2007 [43] | |
| Beech forest, Sorø, Denmark Scots pine forest (SMEAR II station), Hyytiälä, Finland | Eddy covariance and REA | 0.01–0.1 | 0.2–0.5 | Pryor et al., 2007 [14] | |
| Reserva Biológica do Cuieiras, Manaus, Brazil | Eddy covariance | 0.01–0.1 | NA | Ahlm et al., 2010 [45] | |
| Scots pine forest (SMEAR II station), Hyytiäälä, Finland | Eddy covariance | 0.01–0.06 | 0.06–0.5 | Grönholm et al., 2007 [43] | |
| Mixed deciduous forest: sugar maple, tulip poplar, sassafras, white oak, and black oak, Morgan-Monroe State Forest, Indiana, USA | Eddy covariance | 0.008–0.1 | 0.06–0.3 | Pryor et al., 2009 [27] | |
| Wet tropical rainforest, Amazonia, Brazil | Eddy covariance | 0.25–2.5 | NA | Ahlm et al., 2010 [45] | |
| Ponderosa pine plantation | Eddy covariance | 0.25–1.0 | 0.2–0.6 | Vong et al., 2010 [56] | |
| Mix of hardwood and coniferous trees, Borden Forest Research Station, Ontario, Canada | Eddy covariance | 0.018–0.452 | 0.08–0.6 | Gordon et al., 2011 [62] | |
| Scots pine forest (SMEAR II station), Hyytiäälä, Finland | Eddy covariance | 0.01–0.3 | 0.07–0.4 | Mammarella et al., 2011 [63] | |
| Aleppo pine trees (Yatir Forest Research Station), Israel | Eddy covariance | 0.25–0.65 | NA | Lavi et al., 2013 [64] | |
| Laboratory | Wind tunnel experiments | 0.5–200 | 0.9–13 | Zhang et al., 2014 [17] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Balzhanov, T.S.; Zayakhanov, A.S.; Zhamsueva, G.S.; Tcydypov, V.V.; Dementeva, A.L. Assessment of Atmospheric Particles Flux Variation on the Different Underlying Surfaces (Grasslands and Forest) in the Lake Baikal Region. Atmosphere 2024, 15, 737. https://doi.org/10.3390/atmos15060737
Balzhanov TS, Zayakhanov AS, Zhamsueva GS, Tcydypov VV, Dementeva AL. Assessment of Atmospheric Particles Flux Variation on the Different Underlying Surfaces (Grasslands and Forest) in the Lake Baikal Region. Atmosphere. 2024; 15(6):737. https://doi.org/10.3390/atmos15060737
Chicago/Turabian StyleBalzhanov, Tumen S., Alexander S. Zayakhanov, Galina S. Zhamsueva, Vadim V. Tcydypov, and Ayuna L. Dementeva. 2024. "Assessment of Atmospheric Particles Flux Variation on the Different Underlying Surfaces (Grasslands and Forest) in the Lake Baikal Region" Atmosphere 15, no. 6: 737. https://doi.org/10.3390/atmos15060737
APA StyleBalzhanov, T. S., Zayakhanov, A. S., Zhamsueva, G. S., Tcydypov, V. V., & Dementeva, A. L. (2024). Assessment of Atmospheric Particles Flux Variation on the Different Underlying Surfaces (Grasslands and Forest) in the Lake Baikal Region. Atmosphere, 15(6), 737. https://doi.org/10.3390/atmos15060737





