Long Short-Term Memory Recurrent Network Architectures for Electromagnetic Field Reconstruction Based on Underground Observations
Abstract
1. Introduction
2. Theory and Method
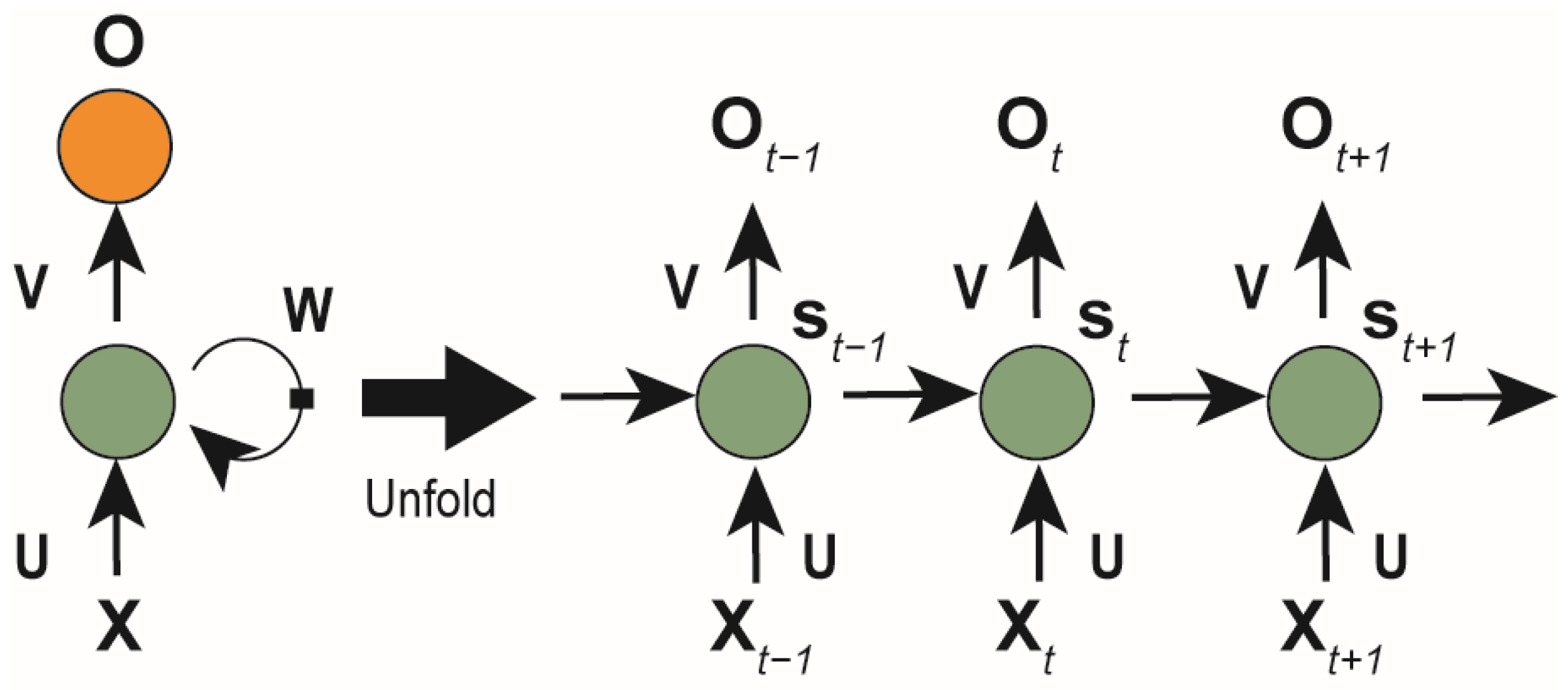
2.1. Recurrent Neural Network
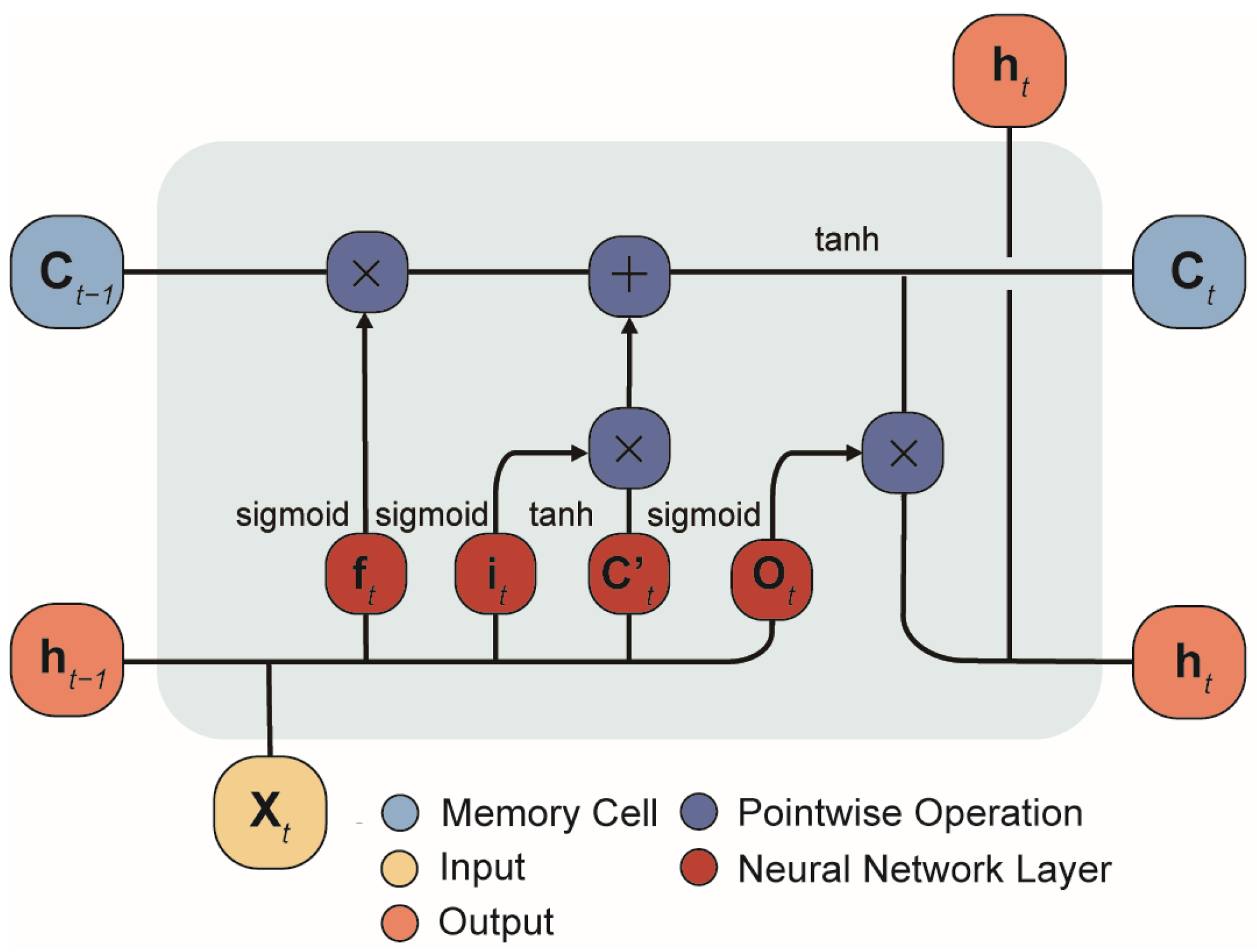
2.2. Long Short-Term Memory Neural Network
2.3. Reconstruction of Electromagnetic Data
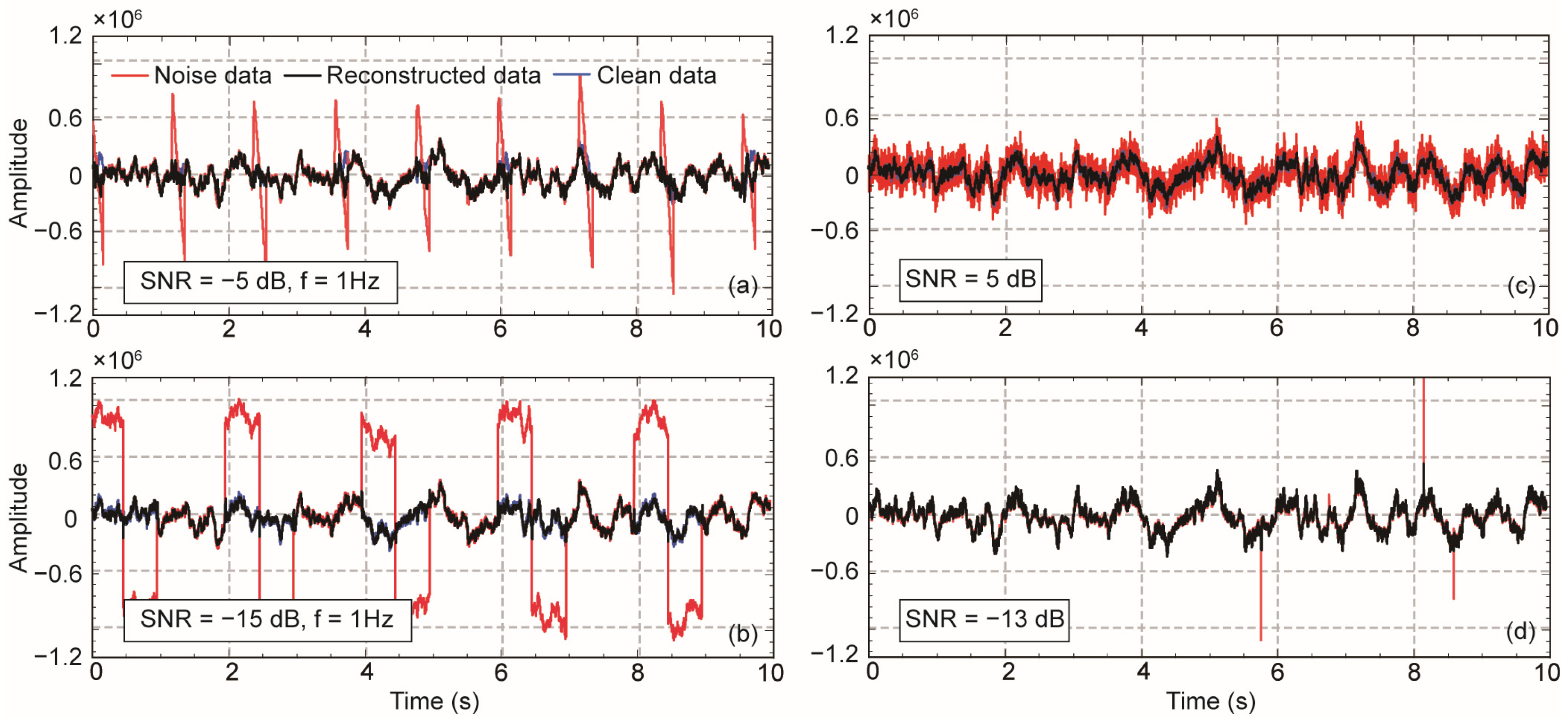
3. Synthetic Experiments
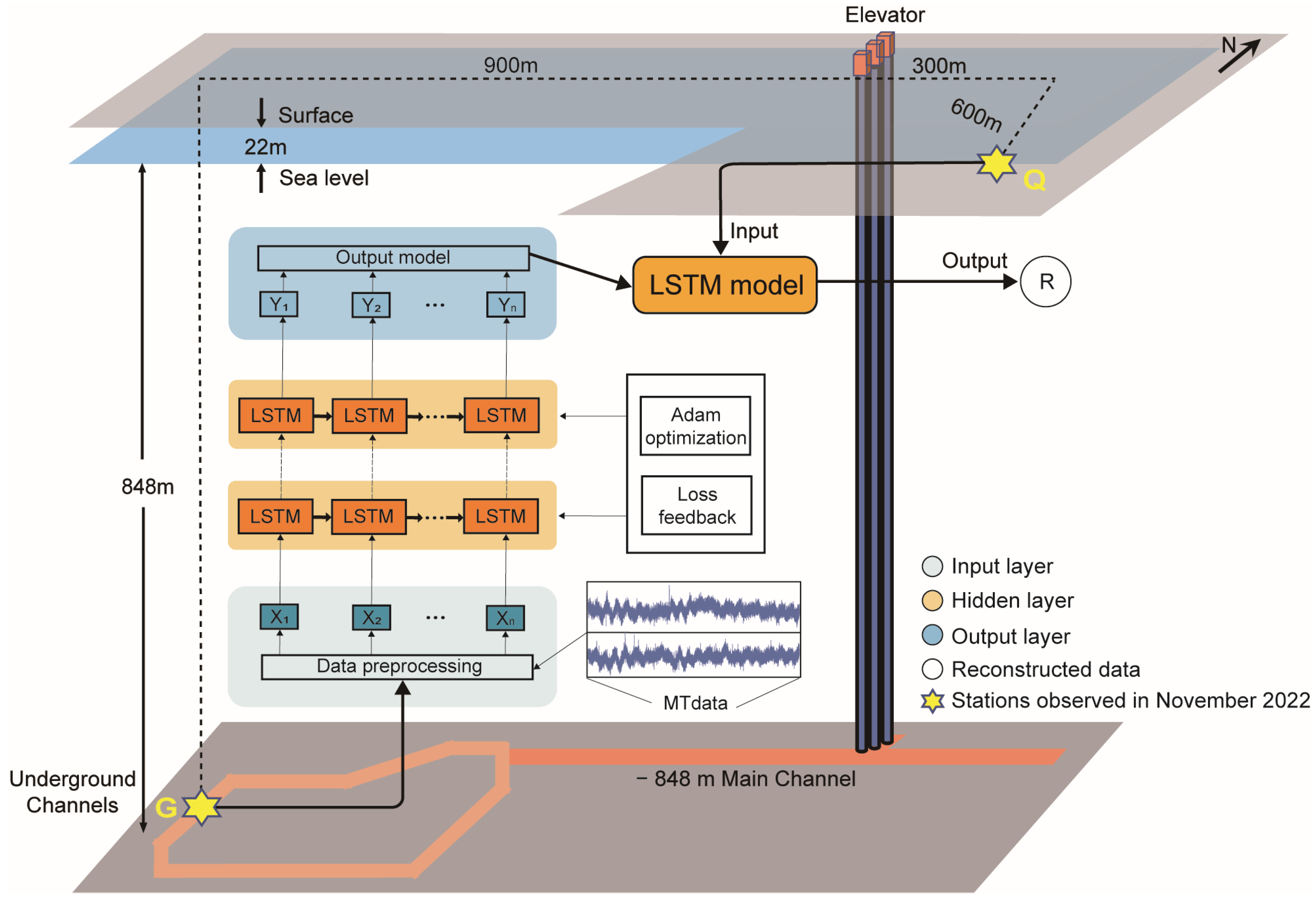
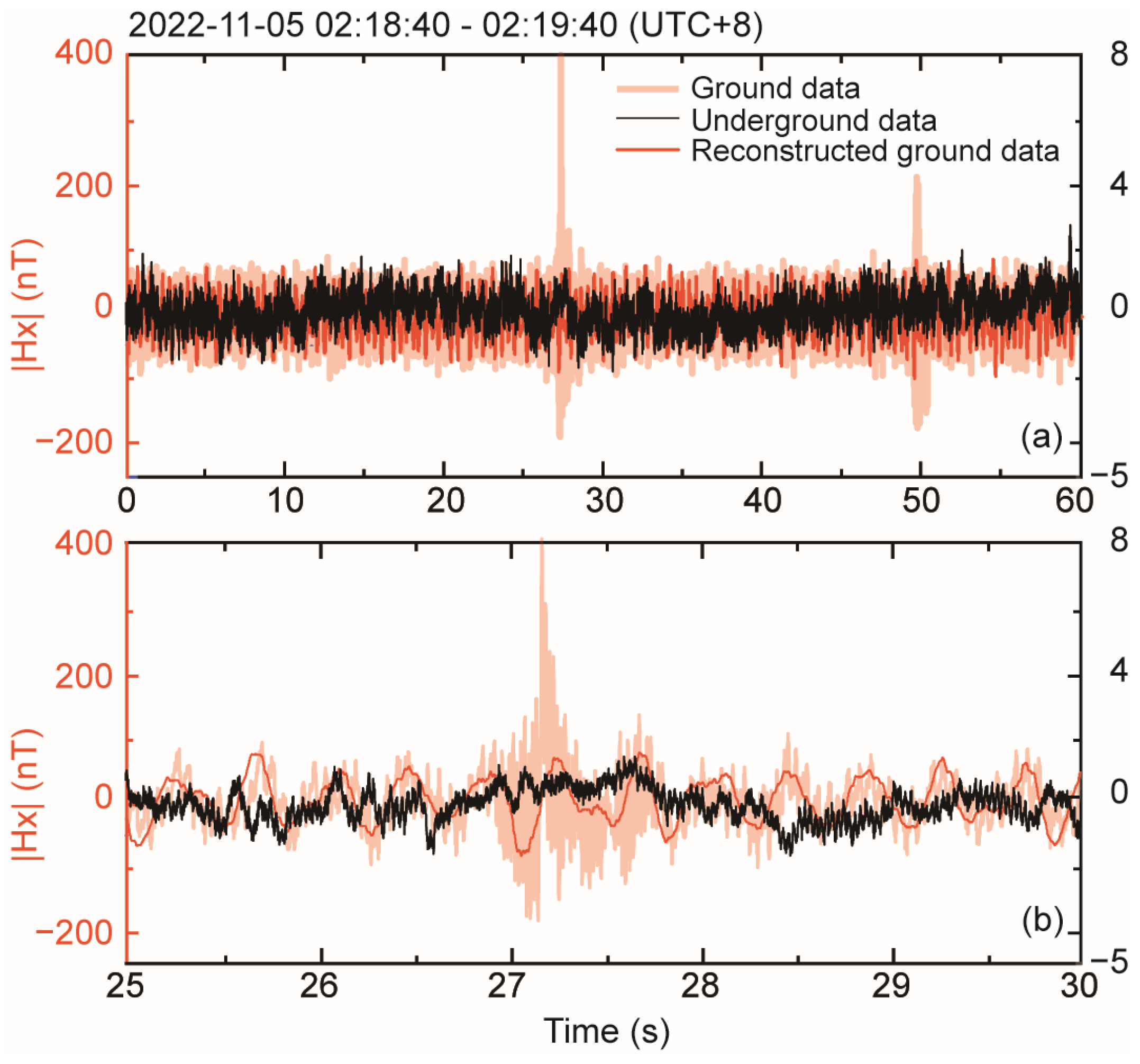
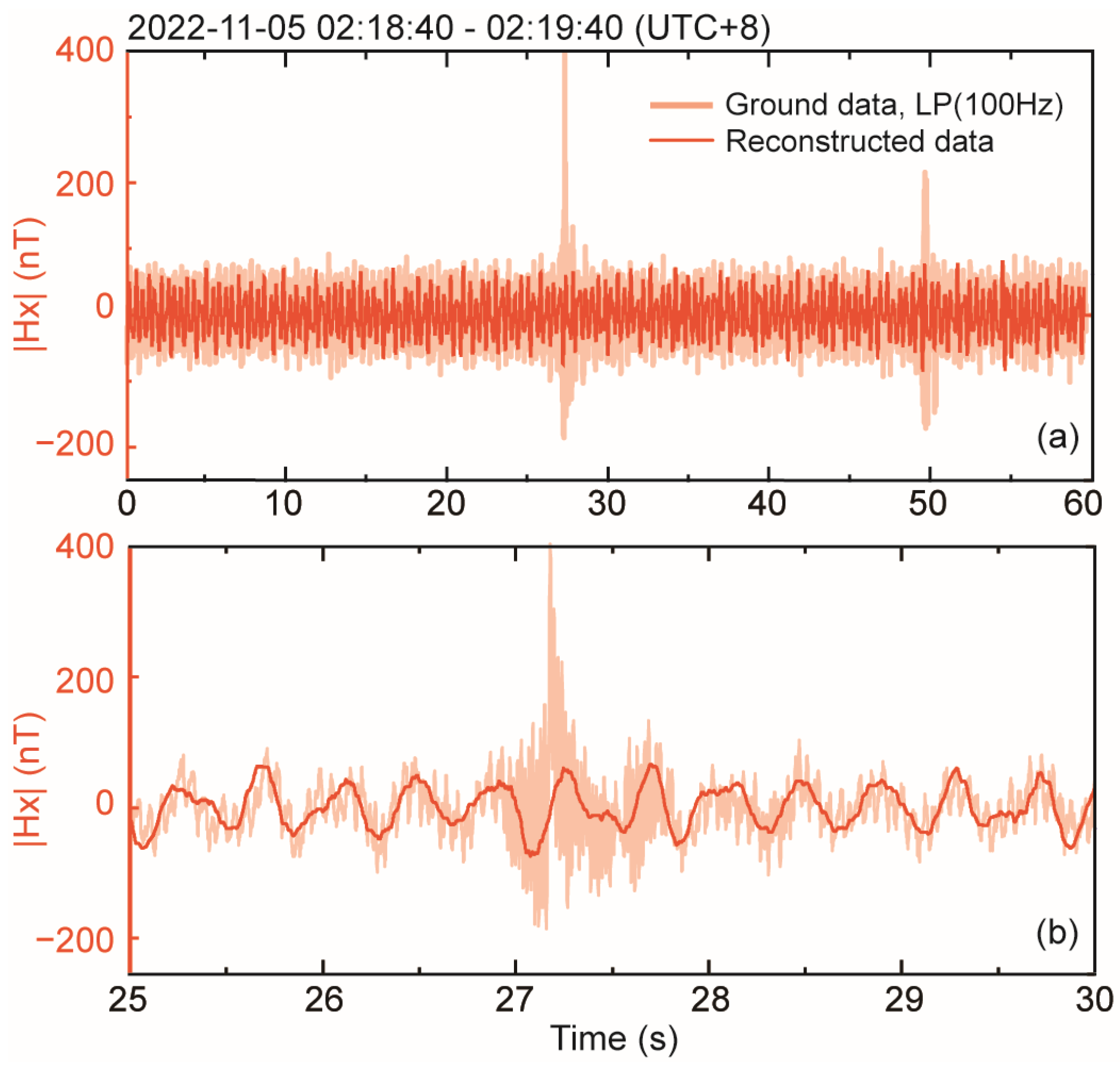
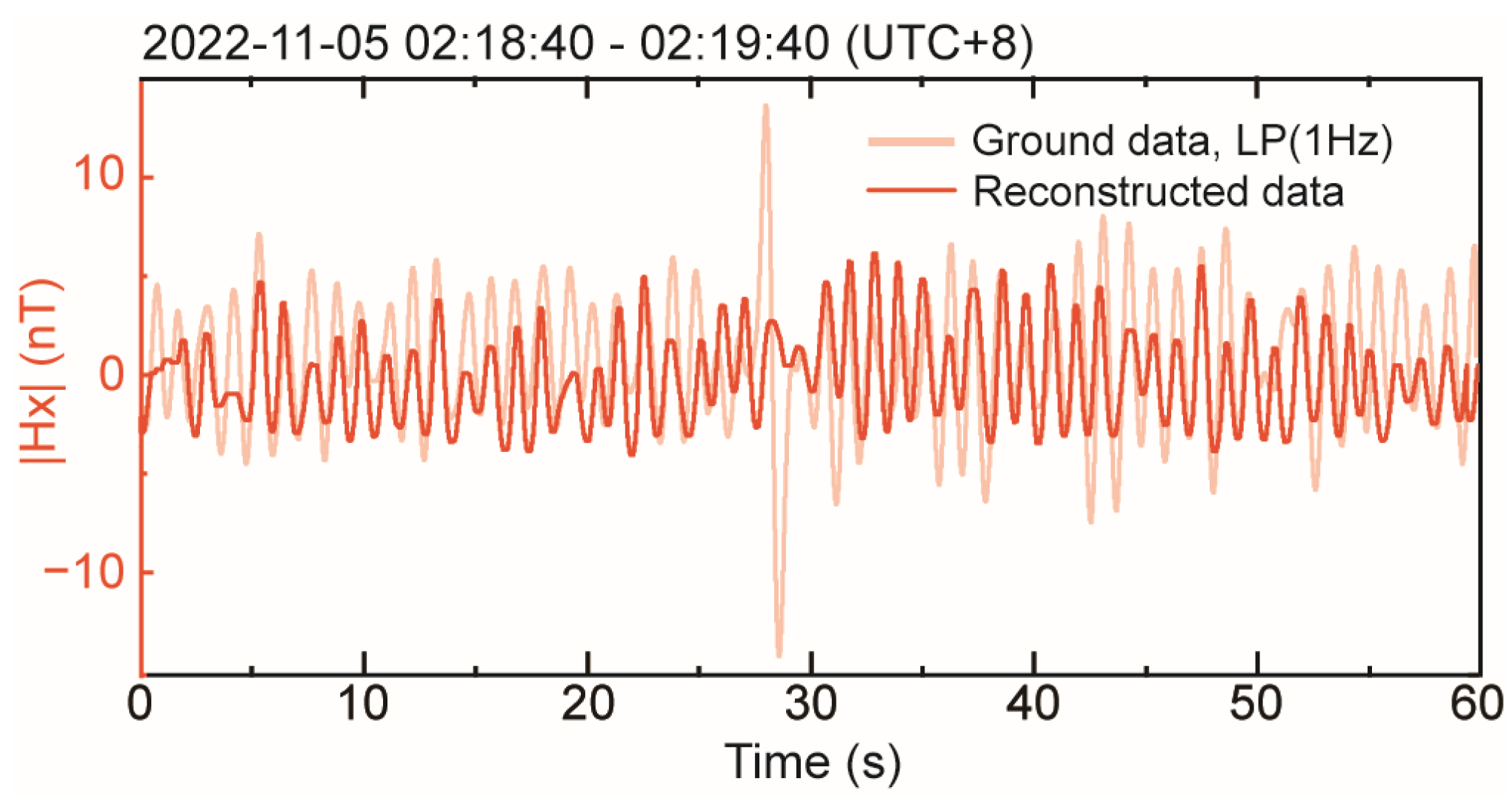
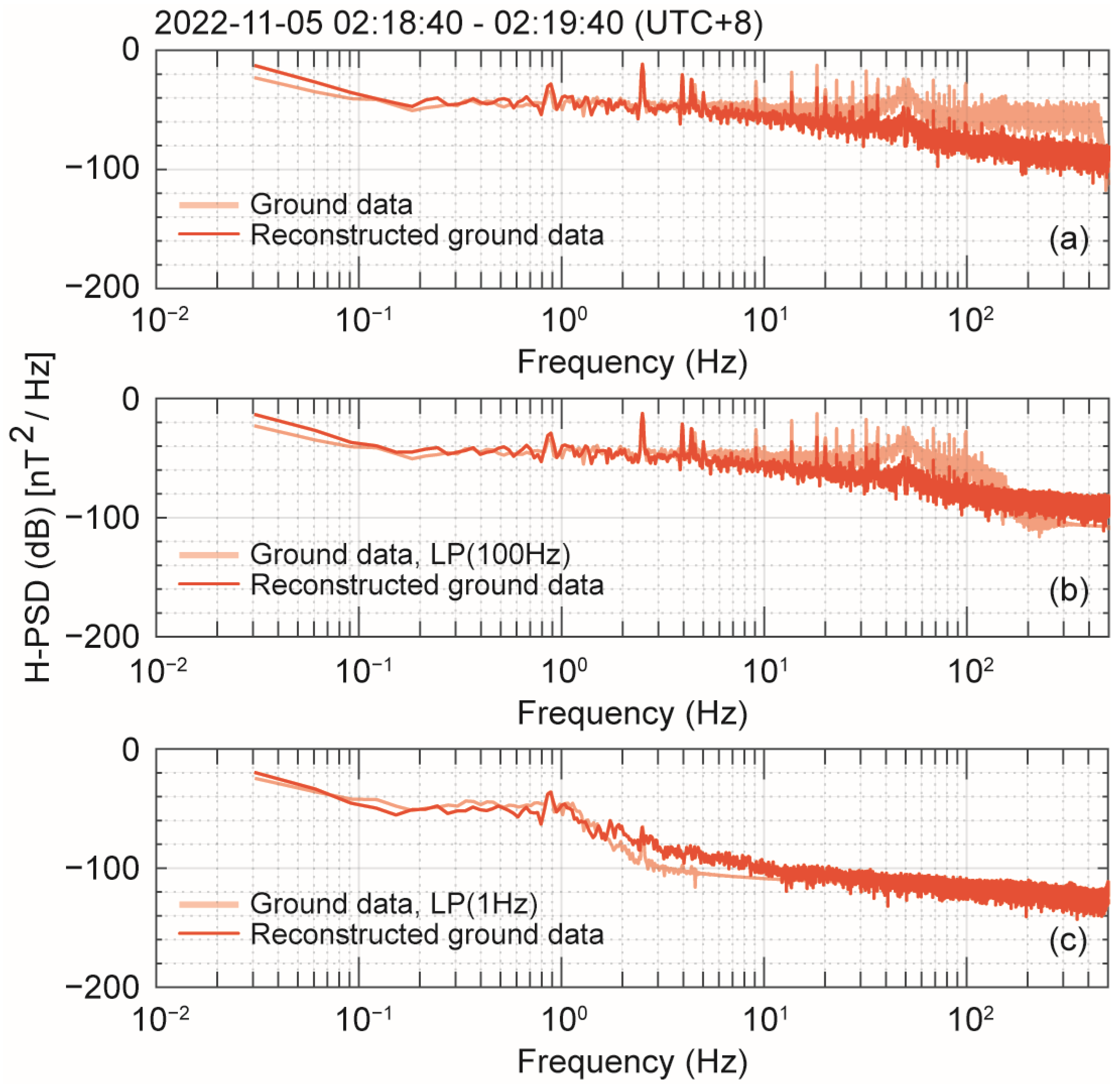
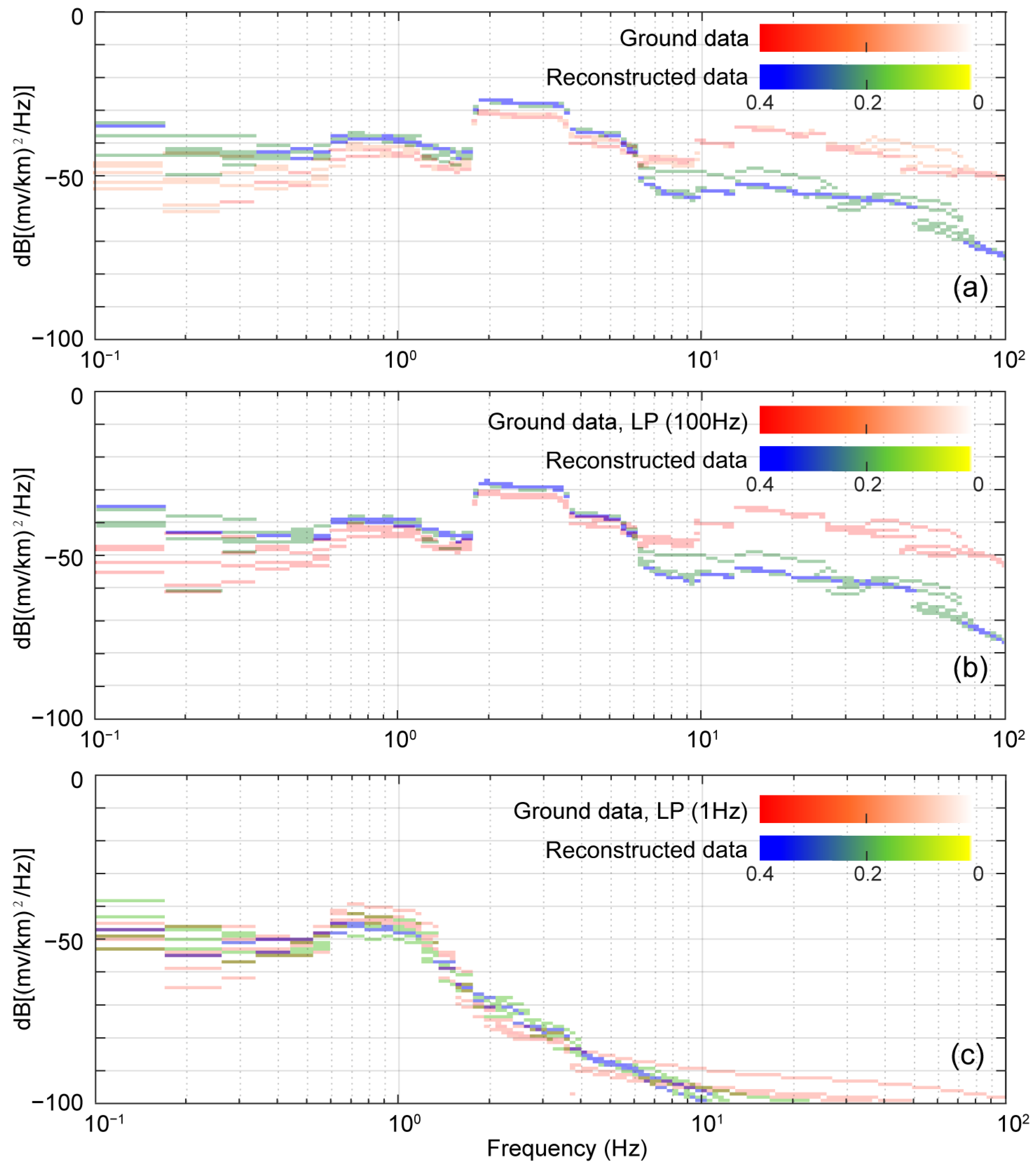
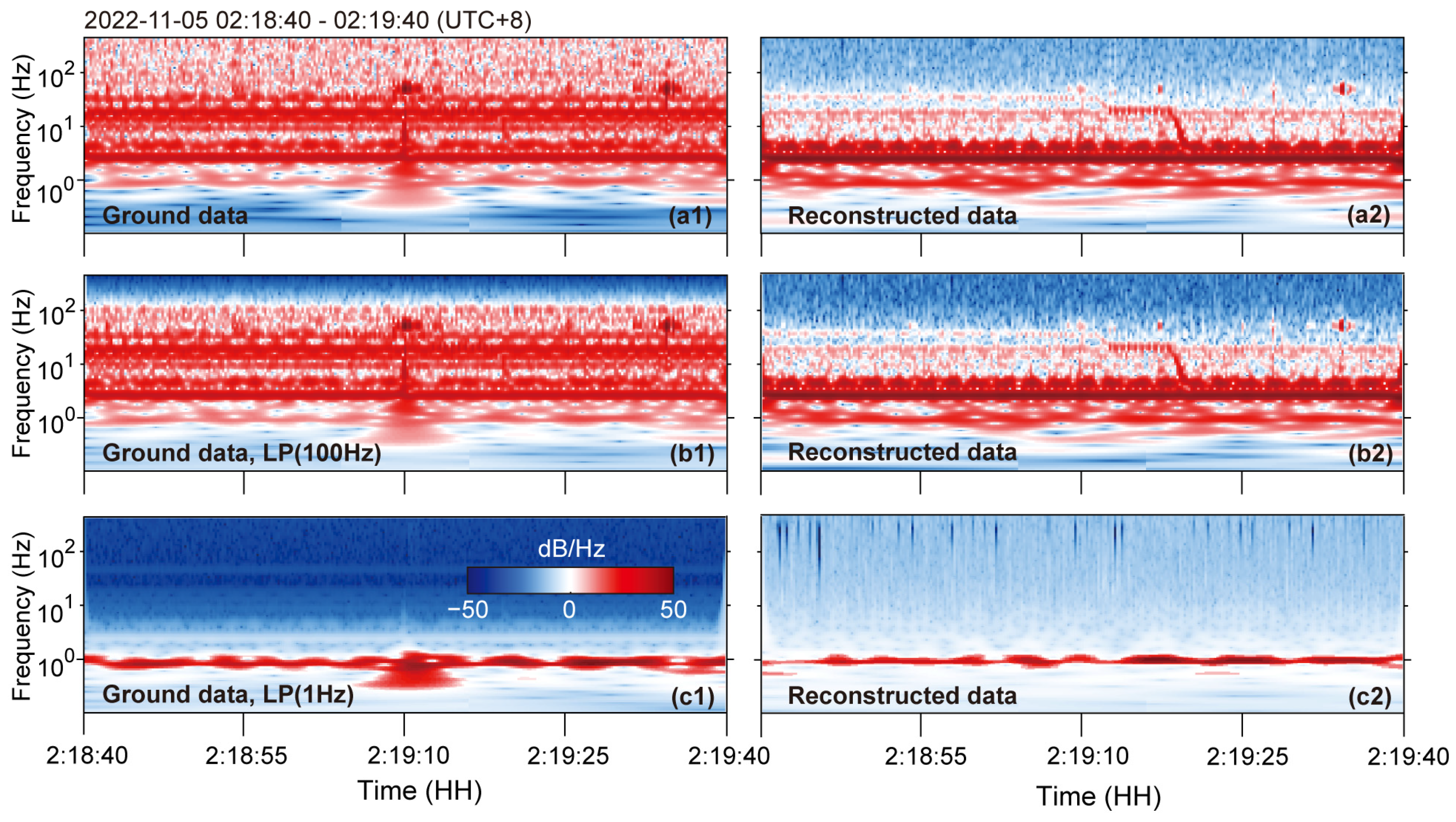
4. Application to Observed Datasets
4.1. Data
4.2. Processing and Results
5. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kang, K.J.; Cheng, J.P.; Chen, Y.H.; Li, Y.J.; Shen, M.B.; Wu, S.Y.; Yue, Q. Status and Prospects of a Deep Underground Laboratory in China. J. Phys. Conf. Ser. 2010, 203, 012028. [Google Scholar] [CrossRef]
- Smith, N.J.T. The SNOLAB Deep Underground Facility. Eur. Phys. J. Plus 2012, 127, 108. [Google Scholar] [CrossRef]
- Mizukoshi, K.; Taishaku, R.; Hosokawa, K.; Kobayashi, K.; Miuchi, K.; Naka, T.; Takeda, A.; Tanaka, M.; Wada, Y.; Yorita, K. Measurement of Ambient Neutrons in an Underground Laboratory at Kamioka Observatory and Future Plan. In Proceedings of the Journal of Physics: Conference Series, Toyama, Japan, 9–13 September 2019; IOP Publishing: Bristol, UK, 2020; Volume 1468, p. 012247. [Google Scholar]
- Palušová, V.; Breier, R.; Chauveau, E.; Piquemal, F.; Povinec, P.P. Natural Radionuclides as Background Sources in the Modane Underground Laboratory. J. Environ. Radioact. 2020, 216, 106185. [Google Scholar] [CrossRef]
- Waysand, G.; Bloyet, D.; Bongiraud, J.P.; Collar, J.I.; Dolabdjian, C.; Le Thiec, P. First Characterization of the Ultra-Shielded Chamber in the Low-Noise Underground Laboratory (LSBB) of Rustrel-Pays d’Apt. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2000, 444, 336–339. [Google Scholar] [CrossRef]
- Daniels, K.A.; Harrington, J.F.; Wiseall, A.C.; Shoemark-Banks, E.; Hough, E.; Wallis, H.C.; Paling, S.M. Battery Earth: Using the Subsurface at Boulby Underground Laboratory to Investigate Energy Storage Technologies. Front. Phys. 2023, 11, 1249458. [Google Scholar] [CrossRef]
- Pomansky, A.A. Underground Low Background Laboratories of the Baksan Neutrino Observatory. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. At. 1986, 17, 406–410. [Google Scholar] [CrossRef]
- Naticchioni, L.; Iudochkin, N.; Yushkin, V.; Majorana, E.; Perciballi, M.; Ricci, F.; Rudenko, V. Seismic Noise Background in the Baksan Neutrino Observatory. Eur. Phys. J. Plus 2022, 137, 124. [Google Scholar] [CrossRef]
- Naticchioni, L.; Perciballi, M.; Ricci, F.; Coccia, E.; Malvezzi, V.; Acernese, F.; Barone, F.; Giordano, G.; Romano, R.; Punturo, M. Microseismic Studies of an Underground Site for a New Interferometric Gravitational Wave Detector. Class. Quantum Gravity 2014, 31, 105016. [Google Scholar] [CrossRef]
- Naticchioni, L.; Boschi, V.; Calloni, E.; Capello, M.; Cardini, A.; Carpinelli, M.; Cuccuru, S.; D’Ambrosio, M.; De Rosa, R.; Di Giovanni, M. Characterization of the Sos Enattos Site for the Einstein Telescope. In Proceedings of the Journal of Physics: Conference Series, Toyama, Japan, 9–13 September 2019; IOP Publishing: Bristol, UK, 2020; Volume 1468, p. 012242. [Google Scholar]
- Gaffet, S.; Guglielmi, Y.; Virieux, J.; Waysand, G.; Chwala, A.; Stolz, R.; Emblanch, C.; Auguste, M.; Boyer, D.; Cavaillou, A. Simultaneous Seismic and Magnetic Measurements in the Low-Noise Underground Laboratory (LSBB) of Rustrel, France, during the 2001 January 26 Indian Earthquake. Geophys. J. Int. 2003, 155, 981–990. [Google Scholar] [CrossRef]
- Waysand, G.; Barroy, P.; Blancon, R.; Gaffet, S.; Guilpin, C.; Marfaing, J.; Di Borgo, E.P.; Pyée, M.; Auguste, M.; Boyer, D. Seismo-Ionosphere Detection by Underground SQUID in Low-Noise Environment in LSBB-Rustrel, France. Eur. Phys. J.-Appl. Phys. 2009, 47, 12705. [Google Scholar] [CrossRef][Green Version]
- Sun, H.; Chen, X.; Wei, Z.; Zhang, M.; Zhang, G.; Ni, S.; Chu, R.; Xu, J.; Cui, X.; Xing, L. A Preliminary Study on the Ultra-Wide Band Ambient Noise of the Deep Underground Based on Observations of the Seismometer and Gravimeter. Chin. J. Geophys. 2022, 65, 4543–4554. [Google Scholar]
- Wang, Z.; Wang, Y.; Xu, R.; Liu, T.; Fu, G.; Sun, H. Environmental Noise Assessment of Underground Gravity Observation in Huainan and the Potential Capability of Detecting Slow Earthquake. Chin. J. Geophys. 2022, 65, 4555–4568. [Google Scholar]
- Wang, Y.; Jian, Y.; He, Y.; Miao, Q.; Teng, J.; Wang, Z.; Rong, L.; Qiu, L.; Xie, C.; Zhang, Q. Underground Laboratories and Deep Underground Geophysical Observations. Chin. J. Geophys. 2022, 65, 4527–4542. [Google Scholar]
- Wang, Y.; Yang, Y.; Sun, H.; Xie, C.; Zhang, Q.; Cui, X.; Chen, C.; He, Y.; Miao, Q.; Mu, C.; et al. Observation and Research of Deep Underground Multi-Physical Fields—Huainan −848 m Deep Experiment. Sci. China Earth Sci. 2023, 66, 54–70. [Google Scholar] [CrossRef] [PubMed]
- Guo, L.; Wang, B.; Song, X.; Wang, Y.; Jin, C.; Yao, S.; Shi, Y. Continuous Observation of Geomagnetic Total-Field at the Underground Laboratory in Huainan City, China and Its Time-Varying Characteristics. Chin. J. Geophys. 2024, 67, 820–828. [Google Scholar]
- Wan, W.; Chen, C.; Wang, Y.; Mu, C.; He, Y.; Wang, C. Comparative Analysis of Surface and Deep Underground Seismic Ambient Noise. Chin. J. Geophys. 2024, 67, 793–808. [Google Scholar]
- Xie, C.; Chen, C.; Liu, C.; Wan, W.; Jin, S.; Ye, G.; Jing, J.; Wang, Y. Insights from Underground Laboratory Observations: Attenuation-Induced Suppression of Electromagnetic Noise. Eur. Phys. J. Plus 2024, 139, 218. [Google Scholar] [CrossRef]
- Wang, H.; Campanyà, J.; Cheng, J.; Zhu, G.; Wei, W.; Jin, S.; Ye, G. Synthesis of Natural Electric and Magnetic Time-series Using Inter-station Transfer Functions and Time-series from a Neighboring Site (STIN): Applications for Processing MT Data. JGR Solid Earth 2017, 122, 5835–5851. [Google Scholar] [CrossRef]
- Zhao, G.; Zhang, X.; Cai, J.; Zhan, Y.; Ma, Q.; Tang, J.; Du, X.; Han, B.; Wang, L.; Chen, X.; et al. A Review of Seismo-Electromagnetic Research in China. Sci. China Earth Sci. 2022, 65, 1229–1246. [Google Scholar] [CrossRef]
- Egbert, G.D.; Booker, J.R. Robust Estimation of Geomagnetic Transfer Functions. Geophys. J. R. Astron. Soc. 1986, 87, 173–194. [Google Scholar] [CrossRef]
- Chave, A.D.; Thomson, D.J. Some Comments on Magnetotelluric Response Function Estimation. J. Geophys. Res. Solid Earth 1989, 94, 14215–14225. [Google Scholar] [CrossRef]
- Jones, A.G.; Chave, A.D.; Egbert, G.; Auld, D.; Bahr, K. A Comparison of Techniques for Magnetotelluric Response Function Estimation. J. Geophys. Res. Solid Earth 1989, 94, 14201–14213. [Google Scholar] [CrossRef]
- Mebane, W.R., Jr.; Sekhon, J.S. Robust Estimation and Outlier Detection for Overdispersed Multinomial Models of Count Data. Am. J. Political Sci. 2004, 48, 392–411. [Google Scholar] [CrossRef]
- Goubau, W.M.; Gamble, T.D.; Clarke, J. Magnetotelluric Data Analysis: Removal of Bias. Geophysics 1978, 43, 1157–1166. [Google Scholar] [CrossRef]
- Gamble, T.D.; Goubau, W.M.; Clarke, J. Magnetotellurics with a Remote Magnetic Reference. Geophysics 1979, 44, 53–68. [Google Scholar] [CrossRef]
- Clarke, J.; Gamble, T.D.; Goubau, W.M.; Koch, R.H.; Miracky, R.F. Remote-Reference Magnetotellurics: Equipment and Procedures. Geophys. Prospect. 1983, 31, 149–170. [Google Scholar] [CrossRef]
- Egbert, G.D. Robust Multiple-Station Magnetotelluric Data Processing. Geophys. J. Int. 1997, 130, 475–496. [Google Scholar] [CrossRef]
- Egbert, G. Processing And Interpretation Of Electromagnetic Induction Array Data. Surv. Geophys. 2002, 23, 207–249. [Google Scholar] [CrossRef]
- Smirnov, M.Y.; Egbert, G.D. Robust Principal Component Analysis of Electromagnetic Arrays with Missing Data. Geophys. J. Int. 2012, 190, 1423–1438. [Google Scholar] [CrossRef]
- Zhou, C.; Tang, J.; Yuan, Y. Multi-Reference Array MT Data Processing Method. Oil Geophys. Prospect. 2020, 55, 1373–1382. [Google Scholar] [CrossRef]
- Garcia, X.; Jones, A.G. Robust Processing of Magnetotelluric Data in the AMT Dead Band Using the Continuous Wavelet Transform. Geophysics 2008, 73, 223–234. [Google Scholar] [CrossRef]
- Cai, J.-H.; Tang, J.-T.; Hua, X.-R.; Gong, Y.-R. An Analysis Method for Magnetotelluric Data Based on the Hilbert–Huang Transform. Explor. Geophys. 2009, 40, 197–205. [Google Scholar] [CrossRef]
- Chen, J.; Heincke, B.; Jegen, M.; Moorkamp, M. Using Empirical Mode Decomposition to Process Marine Magnetotelluric Data. Geophys. J. Int. 2012, 190, 293–309. [Google Scholar] [CrossRef]
- Tang, J.T.; Li, G.; Xiao, X. Strong Noise Separation for Magnetotelluric Data Based on a Signal Reconstruction Algorithm of Compressive Sensing. Chin. J. Geophys. 2017, 60, 3642–3654. (In Chinese) [Google Scholar]
- Kappler, K.N. A Data Variance Technique for Automated Despiking of Magnetotelluric Data with a Remote Reference. Geophys. Prospect. 2012, 60, 179–191. [Google Scholar] [CrossRef]
- Ogawa, H.; Asamori, K.; Negi, T.; Ueda, T. A Novel Method for Processing Noisy Magnetotelluric Data Based on Independence of Signal Sources and Continuity of Response Functions. J. Appl. Geophys. 2023, 213, 105012. [Google Scholar] [CrossRef]
- Zhou, Y.; Chang, Y.; Chen, H.; Zhou, Y.; Ma, Y.; XIE, C.; He, Z.; Katsumi, H.; Han, P. Application of Reference-Based Blind Source Separation Method in the Reduction of near-Field Noise of Geomagnetic Measurements. Chin. J. Geophys.-Chin. Ed. 2019, 62, 572–586. [Google Scholar]
- Dramsch, J. Chapter One—70 Years of Machine Learning in Geoscience in review. In Advance in Geophysics; Moseley, B., Krischer, L., Eds.; Elsevier: Amsterdam, The Netherlands, 2020; pp. 1–55. [Google Scholar] [CrossRef]
- Manoj, C.; Nagarajan, N. The Application of Artificial Neural Networks to Magnetotelluric Time-Series Analysis. Geophys. J. Int. 2003, 153, 409–423. [Google Scholar] [CrossRef]
- Li, J.; Liu, Y.; Tang, J.; Ma, F. Magnetotelluric Noise Suppression via Convolutional Neural Network. Geophysics 2023, 88, WA361–WA375. [Google Scholar] [CrossRef]
- Li, J.; Liu, Y.; Tang, J.; Peng, Y.; Zhang, X.; Li, Y. Magnetotelluric Data Denoising Method Combining Two Deep-Learning-Based Models. Geophysics 2023, 88, E13–E28. [Google Scholar] [CrossRef]
- Han, Y.; An, Z.; Di, Q.; Wang, Z.; Kang, L. Research on Noise Suppression of Magnetotelluric Signal Based on Recurrent Neural Network. Chin. J. Geophys. 2023, 66, 4317–4331. [Google Scholar]
- Li, G.; Gu, X.; Chen, C.; Zhou, C.; Xiao, D.; Wan, W.; Cai, H. Low-Frequency Magnetotelluric Data Denoising Using Improved Denoising Convolutional Neural Network and Gated Recurrent Unit. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5909216. [Google Scholar] [CrossRef]
- Li, G.; Zhou, X.; Chen, C.; Xu, L.; Zhou, F.; Shi, F.; Tang, J. Multi-Type Geomagnetic Noise Removal via an Improved U-Net Deep Learning Network. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5916512. [Google Scholar]
- Zhang, L.; Li, G.; Chen, H.; Tang, J.; Yang, G.; Yu, M.; Hu, Y.; Xu, J.; Sun, J. Identification and Suppression of Multicomponent Noise in Audio Magnetotelluric Data Based on Convolutional Block Attention Module. IEEE Trans. Geosci. Remote Sens. 2024, 62, 1–15. [Google Scholar] [CrossRef]
- Feng, C.; Li, Y.; Wu, Y.; Duan, S. A Noise Suppression Method of Marine Magnetotelluric Data Using K-SVD Dictionary Learning. Chin. J. Geophys. 2022, 65, 1853–1865. [Google Scholar]
- Li, J.; Peng, Y.; Tang, J.; Li, Y. Denoising of Magnetotelluric Data Using K-SVD Dictionary Training. Geophys. Prospect. 2021, 69, 448–473. [Google Scholar] [CrossRef]
- Li, G.; Gu, X.; Ren, Z.; Wu, Q.; Liu, X.; Zhang, L.; Xiao, D.; Zhou, C. Deep Learning Optimized Dictionary Learning and Its Application in Eliminating Strong Magnetotelluric Noise. Minerals 2022, 12, 1012. [Google Scholar] [CrossRef]
- Li, G.; Liu, X.; Tang, J.; Li, J.; Ren, Z.; Chen, C. De-Noising Low-Frequency Magnetotelluric Data Using Mathematical Morphology Filtering and Sparse Representation. J. Appl. Geophys. 2020, 172, 103919. [Google Scholar] [CrossRef]
- Li, G.; Wu, S.; Cai, H.; He, Z.; Liu, X.; Zhou, C.; Tang, J. IncepTCN: A New Deep Temporal Convolutional Network Combined with Dictionary Learning for Strong Cultural Noise Elimination of Controlled-Source Electromagnetic Data. Geophysics 2023, 88, E107–E122. [Google Scholar] [CrossRef]
- Li, G.; He, Z.; Tang, J.; Deng, J.; Liu, X.; Zhu, H. Dictionary Learning and Shift-Invariant Sparse Coding Denoising for Controlled-Source Electromagnetic Data Combined with Complementary Ensemble Empirical Mode Decomposition. Geophysics 2021, 86, E185–E198. [Google Scholar] [CrossRef]
- Li, G.; Liu, X.; Tang, J.; Deng, J.; Hu, S.; Zhou, C.; Chen, C.; Tang, W. Improved Shift-Invariant Sparse Coding for Noise Attenuation of Magnetotelluric Data, Earth. Planets Space 2020, 72, 45. [Google Scholar] [CrossRef]
- Liu, X.; Li, G.; Li, J.; Zhou, X.; Gu, X.; Zhou, C.; Gong, M. Self-Organizing Competitive Neural Network Based Adaptive Sparse Representation for Magnetotelluric Data Denoising. J. Phys. Conf. Ser. 2023, 2651, 012129. [Google Scholar] [CrossRef]
- Cunningham, P.; Cord, M.; Delany, S.J. Supervised Learning. In Machine Learning Techniques for Multimedia; Cord, M., Cunningham, P., Eds.; Cognitive Technologies; Springer: Berlin/Heidelberg, Germany, 2008; pp. 21–49. ISBN 978-3-540-75170-0. [Google Scholar]
- Schuster, M.; Paliwal, K.K. Bidirectional Recurrent Neural Networks. IEEE Trans. Signal Process. 1997, 45, 2673–2681. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep Learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Salehinejad, H.; Sankar, S.; Barfett, J.; Colak, E.; Valaee, S. Recent Advances in Recurrent Neural Networks. arXiv 2017, arXiv:1801.01078. [Google Scholar] [CrossRef]
- Graves, A. Supervised Sequence Labelling with Recurrent Neural Networks; Studies in Computational Intelligence; Springer: Berlin/Heidelberg, Germany, 2012; Volume 385, ISBN 978-3-642-24796-5. [Google Scholar]
- Van Houdt, G.; Mosquera, C.; Nápoles, G. A Review on the Long Short-Term Memory Model. Artif. Intell. Rev. 2020, 53, 5929–5955. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Malhotra, P.; Vig, L.; Shroff, G.; Agarwal, P. Long Short Term Memory Networks for Anomaly Detection in Time Series. In Proceedings of the 23rd European Symposium on Artificial Neural Networks, Bruges, Belgium, 22–24 April 2015; p. 89. [Google Scholar]
- Wan, S.; Qi, L.; Xu, X.; Tong, C.; Gu, Z. Deep Learning Models for Real-Time Human Activity Recognition with Smartphones. Mob. Netw. Appl. 2020, 25, 743–755. [Google Scholar] [CrossRef]
- Yang, J.; Yao, S.; Wang, J. Deep Fusion Feature Learning Network for MI-EEG Classification. IEEE Access 2018, 6, 79050–79059. [Google Scholar] [CrossRef]
- Staudemeyer, R.C.; Morris, E.R. Understanding LSTM—A Tutorial into Long Short-Term Memory Recurrent Neural Networks. arXiv 2019, arXiv:1909.09586. [Google Scholar]
- Huang, L.; Qin, J.; Zhou, Y.; Zhu, F.; Liu, L.; Shao, L. Normalization Techniques in Training Dnns: Methodology, Analysis and Application. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 10173–10196. [Google Scholar] [CrossRef]
- Chen, W.; Yang, L.; Zha, B.; Zhang, M.; Chen, Y. Deep Learning Reservoir Porosity Prediction Based on Multilayer Long Short-Term Memory Network. Geophysics 2020, 85, WA213–WA225. [Google Scholar] [CrossRef]
- Kingma, D.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar] [CrossRef]
- Bouktif, S.; Fiaz, A.; Ouni, A.; Serhani, M.A. Optimal Deep Learning LSTM Model for Electric Load Forecasting Using Feature Selection and Genetic Algorithm: Comparison with Machine Learning Approaches. Energies 2018, 11, 1636. [Google Scholar] [CrossRef]
- McNamara, D.E.; Buland, R.P. Ambient Noise Levels in the Continental United States. Bull. Seismol. Soc. Am. 2004, 94, 1517–1527. [Google Scholar] [CrossRef]
- Sokolova, E.; Varentsov, I. RRMC technique fights highly coherent em noise. In 21 Kolloquim EM Teifenforschung (Digitaliesiertes Protokoll); German Geophysical Society: Wohldenberg, Germany, 2005; pp. 124–136. [Google Scholar]
- Varentsov, I.; Sokolova, E.; Martanus, E.; Nalivaiko, K. Group System of Electromagnetic Field Transfer Operators for the BEAR Array of Simultaneous Soundings: Methods and Results. Izv. Phys. Solid Earth 2003, 39, 118–148. [Google Scholar]
- Dong, X.T.; Li, Y.; Yang, B.J. Desert Low-Frequency Noise Suppression by Using Adaptive DnCNNs Based on the Determination of High-Order Statistic. Geophys. J. Int. 2019, 219, 1281–1299. [Google Scholar] [CrossRef]
- Zhao, Y.; Li, Y.; Dong, X.; Yang, B. Low-Frequency Noise Suppression Method Based on Improved DnCNN in Desert Seismic Data. IEEE Geosci. Remote Sens. Lett. 2019, 16, 811–815. [Google Scholar] [CrossRef]
- Maiti, S.; Chiluvuru, R.K. A Deep CNN-LSTM Model for Predicting Interface Depth from Gravity Data over Thrust and Fold Belts of North East India. J. Asian Earth Sci. 2024, 259, 105881. [Google Scholar] [CrossRef]
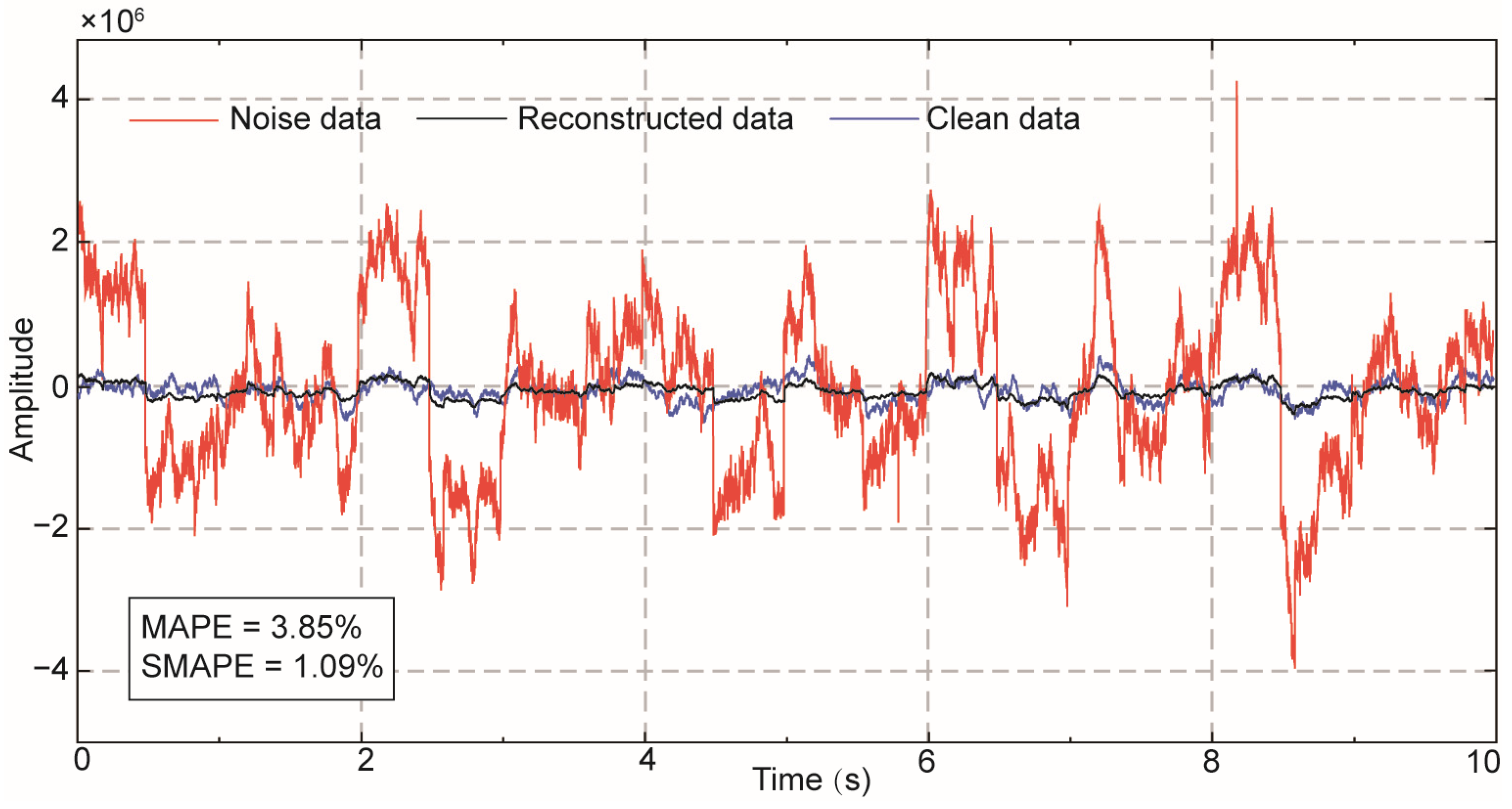
| Noise | MAPE (%) | SMAPE (%) |
|---|---|---|
| Charge and discharge triangle wave | 1.9222 | 0.6738 |
| Square wave | 1.7582 | 0.5977 |
| Gaussian noise | 2.0160 | 0.5724 |
| Peak noise | 1.6031 | 0.5099 |
| Combined noise | 3.8490 | 1.0905 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, Y.; Xie, C.; Wang, Y. Long Short-Term Memory Recurrent Network Architectures for Electromagnetic Field Reconstruction Based on Underground Observations. Atmosphere 2024, 15, 734. https://doi.org/10.3390/atmos15060734
Tian Y, Xie C, Wang Y. Long Short-Term Memory Recurrent Network Architectures for Electromagnetic Field Reconstruction Based on Underground Observations. Atmosphere. 2024; 15(6):734. https://doi.org/10.3390/atmos15060734
Chicago/Turabian StyleTian, Yixing, Chengliang Xie, and Yun Wang. 2024. "Long Short-Term Memory Recurrent Network Architectures for Electromagnetic Field Reconstruction Based on Underground Observations" Atmosphere 15, no. 6: 734. https://doi.org/10.3390/atmos15060734
APA StyleTian, Y., Xie, C., & Wang, Y. (2024). Long Short-Term Memory Recurrent Network Architectures for Electromagnetic Field Reconstruction Based on Underground Observations. Atmosphere, 15(6), 734. https://doi.org/10.3390/atmos15060734








