Development of X-Band Geophysical Model Function for Sea Surface Wind Speed Retrieval with ASNARO-2
Abstract
1. Introduction
2. Data and Basic Formulas for GMF
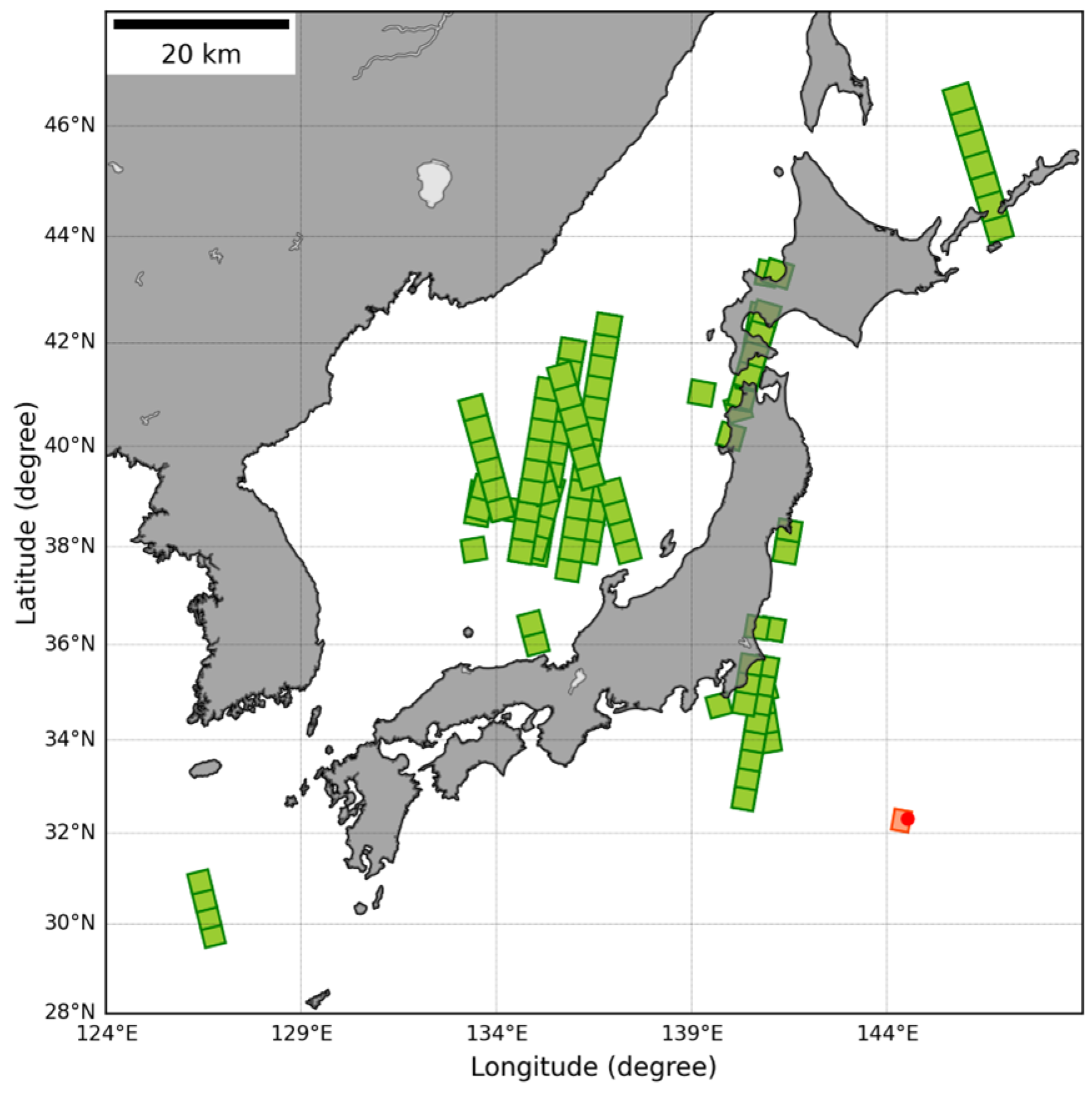
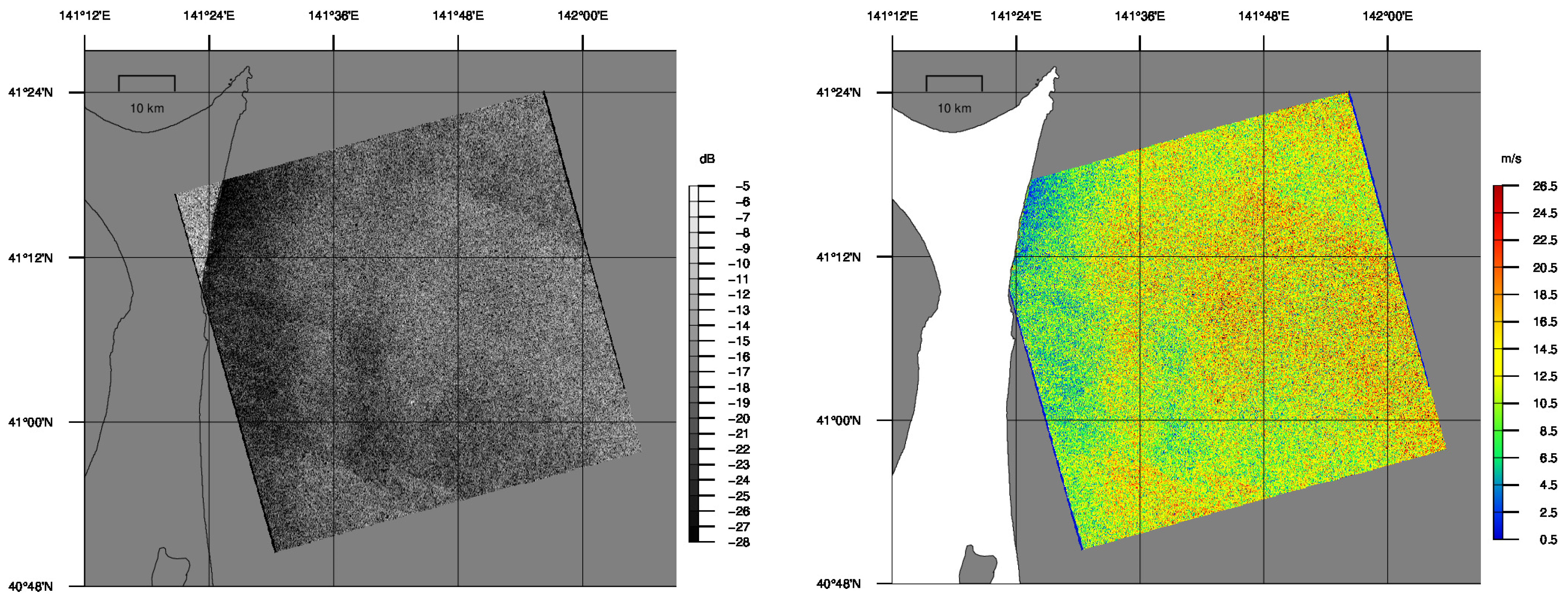
2.1. SAR Images Obtained by ASNARO-2
2.2. Local Forecast Model and Sea Surface Temperature
2.3. In Situ Wind Vectors Obserbed in the KEO Buoy
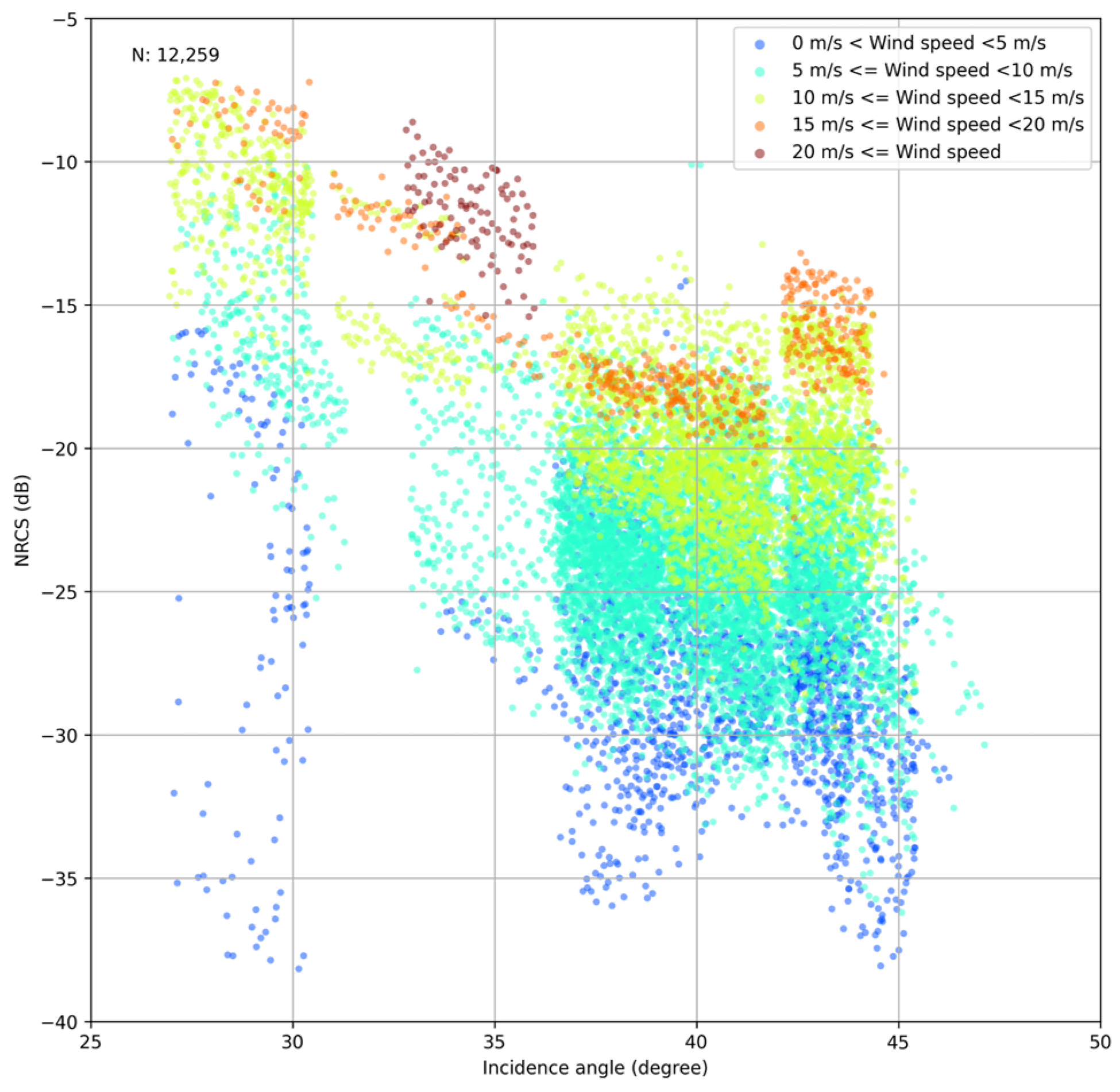
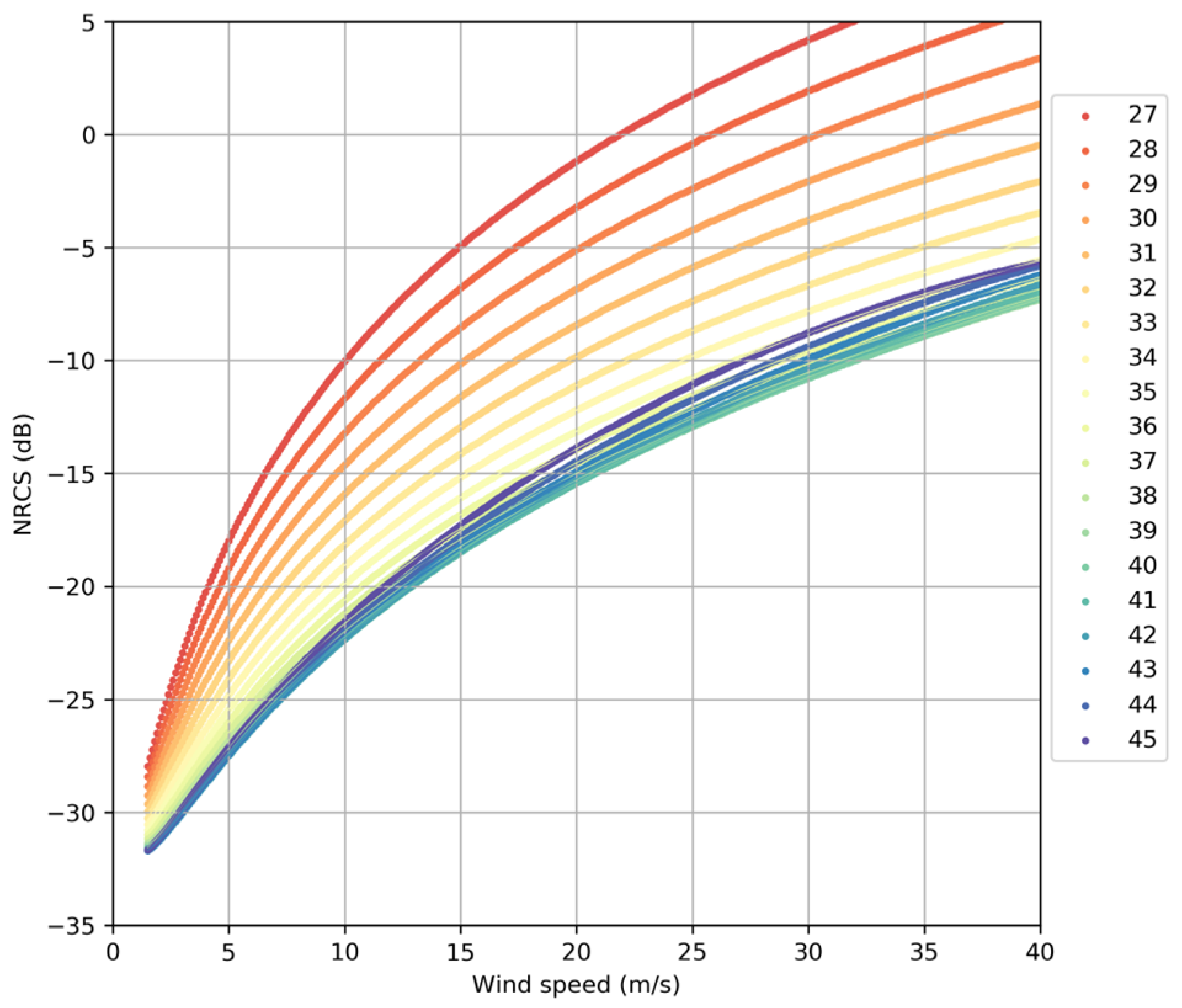
2.4. Formula for GMF
3. Development of the GMF
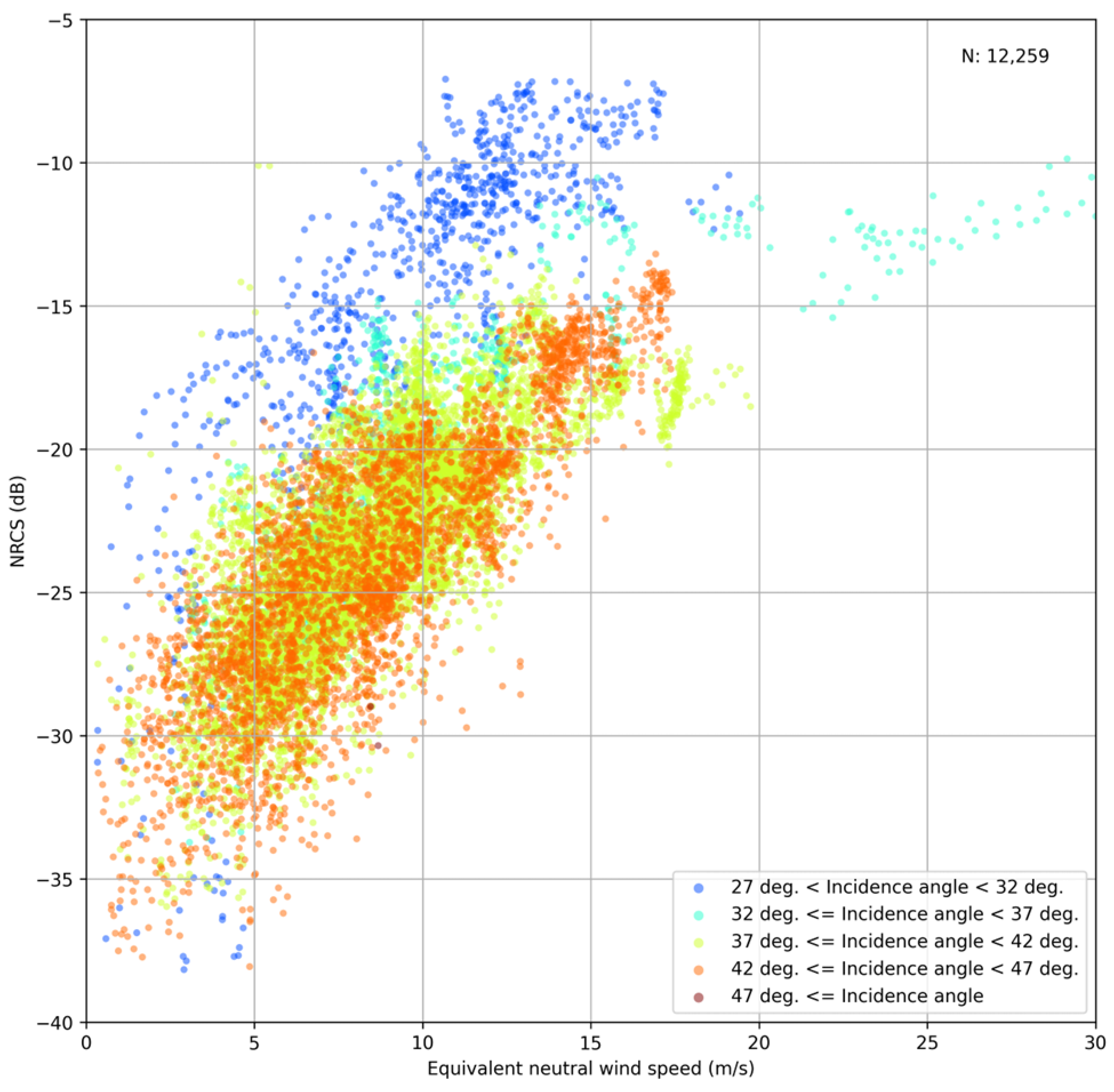
3.1. Determination of
3.2. Determination of and
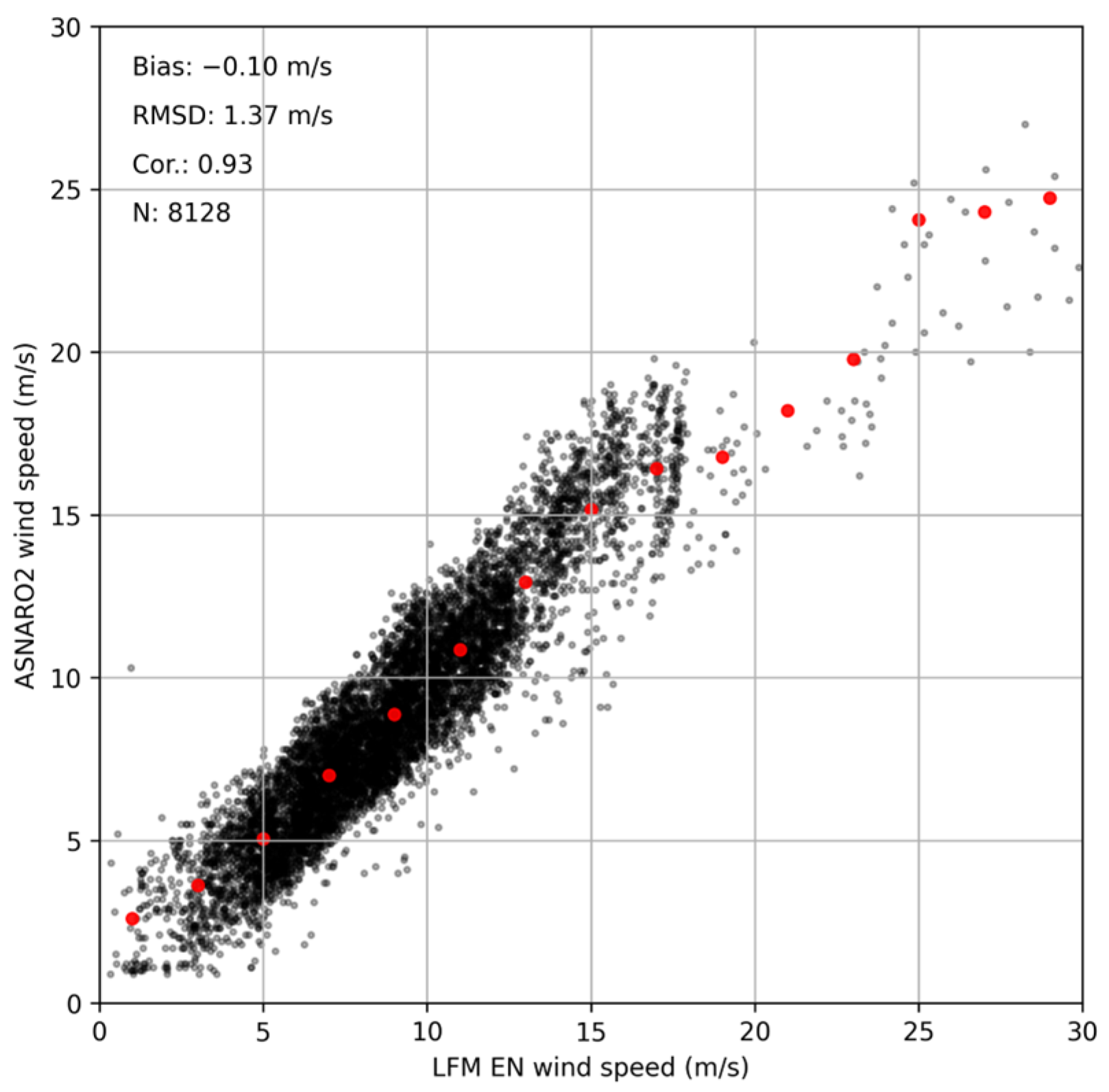
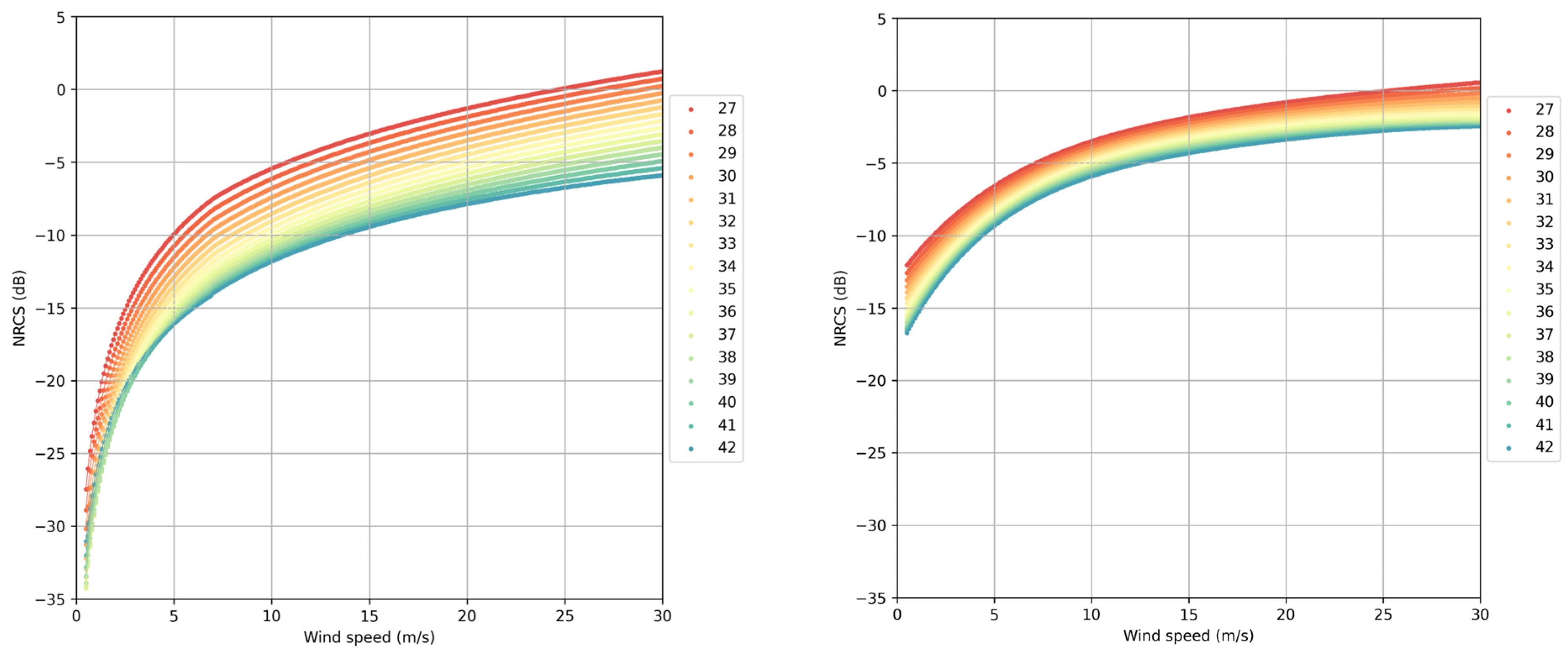
4. Evaluation of the GMF
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| A0 | a0 | c0 | 9.11336 |
| c1 | 6.49630 | ||
| c2 | −2.77146 | ||
| a1 | c3 | −12.73693 | |
| c4 | −7.61105 | ||
| c5 | 15.10509 | ||
| a2 | c6 | 25.45840 | |
| c7 | −6.41516 | ||
| c8 | −2.33088 | ||
| a3 | c9 | −3.85802 | |
| c10 | −30.61375 | ||
| A1 | B | c11 | −0.10040 |
| c12 | −0.00201 | ||
| c13 | 0.02240 | ||
| C | c14 | 0.65642 | |
| c15 | 0.11324 | ||
| c16 | −0.20075 | ||
| A2 | D | c17 | 0.02618 |
| c18 | 0.05286 | ||
| c19 | 0.01195 | ||
| E | c20 | −0.02781 | |
| c21 | −0.67547 | ||
| c22 | 0.03487 |
References
- Stoffelen, A.; Anderson, D. Scatterometer Data Interpretation: Estimation and Validation of the Tranfer Function CMOD4. J. Geophys. Res. 1997, 102, 5767–5780. [Google Scholar] [CrossRef]
- Quilfen, Y.; Chapron, B.; Elfouhaily, T.; Katsaros, K.; Tournadre, J. Observation of Tropical Cyclones by High-Resolution Scatterometry. J. Geophys. Res. 1998, 103, 7767–7786. [Google Scholar] [CrossRef]
- Hersbach, H.; Stoffelen, A.; Haan, S. An Improved C-Band Scatterometer Ocean Geophysical Model Function: CMOD5. J. Geophys. Res. 2007, 112, C03006. [Google Scholar] [CrossRef]
- Hersbach, H. Comparison of C-Band Scatterometer CMOD5.N Equivalent Neutral Winds with ECMWF. J. Atmos. Ocean. Technol. 2010, 27, 721–736. [Google Scholar] [CrossRef]
- Stoffelen, A.; Verspeek, J.A.; Vogelzang, J.; Verhoef, A. The CMOD7 Geophysical Model Function for ASCAT and ERS Wind Retrievals. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 2123–2134. [Google Scholar] [CrossRef]
- Lehner, S.; Horstmann, J.; Koch, W.; Rosenthal, W. Mesoscale Wind Measurements Using Recalibrated ERS SAR Images. J. Geophys. Res. 1998, 103, 7847–7856. [Google Scholar] [CrossRef]
- Christiansen, M.B.; Koch, W.; Horstmann, J.; Bayhasager, C.; Nielsen, M. Wind Resource Assessment from C-Band SAR. Remote Sens. Environ. 2006, 105, 68–81. [Google Scholar] [CrossRef]
- Hasager, C.B.; Badger, M.; Peña, A.; Larsén, X.G.; Bingöl, F. SAR-Based Wind Resource Statistics in the Baltic Sea. Remote Sens. 2011, 3, 117–144. [Google Scholar] [CrossRef]
- Takeyama, Y.; Ohsawa, T.; Kozai, K.; Hasager, C.B.; Badger, M. Comparison of Geophysical Model Functions for SAR Wind Speed Retrieval in Japanese Coastal Waters. Remote Sens. 2013, 5, 1956–1973. [Google Scholar] [CrossRef]
- Takeyama, Y.; Ohsawa, T.; Yamashita, T.; Kozai, K.; Muto, Y.; Baba, Y.; Kawaguchi, K. Estimation of Offshore Wind Resources in Coastal Waters off Shirahama Using ENVISAT ASAR Images. Remote Sens. 2013, 5, 2883–2897. [Google Scholar] [CrossRef]
- Takeyama, Y.; Ohsawa, T.; Kozai, K.; Hasager, C.B.; Badger, M. Effectiveness of WRF Wind Direction for Retrieving Coastal Sea Surface Wind from Synthetic Aperture Radar. Wind Energy 2013, 16, 865–878. [Google Scholar] [CrossRef]
- Chang, R.; Zhu, R.; Badger, M.; Hasager, C.B.; Xing, X.; Jiang, Y. Offshore Wind Resources Assessment from Multiple Satellite Data and WRF Modeling over South China Sea. Remote Sens. 2015, 7, 467–487. [Google Scholar] [CrossRef]
- Hasager, C.B.; Mouche, A.; Badger, M.; Bingöl, F.; Karagali, I.; Driesenaar, T.; Stoffelen, A.; Peña, A.; Longépé, N. Offshore Wind Climatology Based on Synergetic Use of Envisat ASAR, ASCAT and QuikSCAT. Remote Sens. Environ. 2015, 156, 247–263. [Google Scholar] [CrossRef]
- Ahsbahs, T.; Badger, M.; Karagali, I.; Larsén, X.G. Validation of Sentinel-1A SAR Coastal Wind Speeds against Scanning LiDAR. Remote Sens. 2017, 9, 552. [Google Scholar] [CrossRef]
- Kim, D.; Moon, W.M. Estimation of Sea Surface Wind Vector Using RADARSAT Data. Remote Sens. Environ. 2002, 80, 55–64. [Google Scholar] [CrossRef]
- Mouche, A.; Chapron, B. Global C-Band Envisat, RADARSAT-2 and Sentinel-1 SAR Measurements in Copolarization and Cross-Polarization. Nature 2015, 120, 7195–7207. [Google Scholar] [CrossRef]
- Zhang, B.; Mouche, A.; Lu, Y.; Perrie, W.; Zhang, G.; Wang, H. A Geophysical Model Function for Wind Speed Retrieval from C-Band HH-Polarized Synthetic Aperture Radar. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1521–1525. [Google Scholar] [CrossRef]
- Lu, Y.; Zhang, B.; Perrie, W.; Mouche, A.A.; Li, X.; Wang, H. A C-Band Geophysical Model Function for Determining Coastal Wind Speed Using Synthetic Aperture Radar. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 2417–2428. [Google Scholar] [CrossRef]
- Qin, T.; Jia, T.; Feng, Q.; Li, X. Sea Surface Wind Speed Retrieval from Sentinel-1 HH Polarization Data Using Conventional and Neural Network Methods. Acta Oceanol. Sin. 2021, 40, 13–21. [Google Scholar] [CrossRef]
- Isoguchi, O.; Shimada, M. An L-Band Ocean Geophysical Model Function Derived from PALSAR. IEEE Trans. Geosci. Remote Sens. 2009, 47, 1925–1936. [Google Scholar] [CrossRef]
- Ren, Y.; Lehner, S.; He, M. Study on X-Band Polarization Ratio with TerraSAR-X Images. In Proceedings of the SPIE—Remote Sensing and Modeling of the Atmosphere, Oceans, and Interactions III, Incheon, Republic of Korea, 13–14 October 2010; Volume 7856. [Google Scholar] [CrossRef]
- Li, X.M.; Lehner, S. Algorithm for Sea Surface Wind Retrieval from TerraSAR-X and TanDEM-X Data. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2928–2939. [Google Scholar] [CrossRef]
- Nirchio, F.; Venafra, S. XMOD2—An Improved Geophysical Model Function to Retrieve Sea Surface Wind Fields from Cosmo-SkyMed X-Band Data. Eur. J. Remote Sens. 2013, 46, 583–595. [Google Scholar] [CrossRef]
- Liu, W.T.; Tang, W. Equivalent Neutral Wind; JPL Publication 96-17; National Aeronautics and Space Administration, Jet Propulsion Laboratory: Pasadena, CA, USA; California Institute of Technology California: Pasadena, CA, USA, 1996. [Google Scholar]
- Good, S.; Fiedler, E.; Mao, C.; Martin, M.J.; Maycock, A.; Reid, R.; Roberts-Jones, J.; Searle, T.; Waters, J.; While, J.; et al. The Current Configuration of the OSTIA System for Operational Production of Foundation Sea Surface Temperature and Ice Concentration Analyses. Remote Sens. 2020, 12, 720. [Google Scholar] [CrossRef]
- De Kloe, J.; Stoffelen, A.; Verhoef, A. Improved Use of Scatterometer Measurements by Using Stress-Equivalent Reference Winds. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 2340–2347. [Google Scholar] [CrossRef]





| Satellite | Advanced Satellite with New System Architecture for Observation-2 (ASNARO-2) |
|---|---|
| Operation | NEC corporation |
| Launch date | 17 January 2018 |
| Orbit | Sun-synchronous circular orbit |
| Altitude | 817 km |
| Inclination | 98.7° |
| Local time of descending node | 9:30 |
| Orbital period | 107.1 min |
| Ground track repeat cycle | 29 days |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Takeyama, Y.; Kurokawa, S. Development of X-Band Geophysical Model Function for Sea Surface Wind Speed Retrieval with ASNARO-2. Atmosphere 2024, 15, 686. https://doi.org/10.3390/atmos15060686
Takeyama Y, Kurokawa S. Development of X-Band Geophysical Model Function for Sea Surface Wind Speed Retrieval with ASNARO-2. Atmosphere. 2024; 15(6):686. https://doi.org/10.3390/atmos15060686
Chicago/Turabian StyleTakeyama, Yuko, and Shota Kurokawa. 2024. "Development of X-Band Geophysical Model Function for Sea Surface Wind Speed Retrieval with ASNARO-2" Atmosphere 15, no. 6: 686. https://doi.org/10.3390/atmos15060686
APA StyleTakeyama, Y., & Kurokawa, S. (2024). Development of X-Band Geophysical Model Function for Sea Surface Wind Speed Retrieval with ASNARO-2. Atmosphere, 15(6), 686. https://doi.org/10.3390/atmos15060686






