Abstract
Potential evapotranspiration (PET) is a crucial parameter for forest development, having an important role in ecological, biometeorological, and hydrological assessments. Accurate estimations of PET using the FAO–56 Penman–Monteith (FAO–56 PM) benchmark method require a wide range of data parameters, which are not typically available at meteorological stations installed in forest environments. The aim of this study is to investigate the accuracy of various methods with low data requirements for assessing PET in a Mediterranean forest environment and propose appropriate alternatives for accurate PET estimation. Specifically, 50 temperature-based methods were evaluated against the FAO–56 PM method in a sub-humid forest in northern Greece, using high-quality daily meteorological data. The outcomes indicate that temperature-based methods offer a viable alternative for PET estimation when data availability is limited, with a considerable number of methods (22) presenting low deviations (up to 10%) compared to the benchmark method. Temperature-based models outperformed those incorporating water-related parameters (as relative humidity or precipitation) in Mediterranean forest environments. The top performing methods in the study site, based on several statistical indices, were the equations of Ravazzani et al., proposed in 2012, followed by Hargreaves–Samani in 1985 and Heydari and Heydari in 2014.
1. Introduction
Evapotranspiration (ET) is an essential part of the water cycle and plays a key role in several disciplines of geosciences, including climate classification and drought assessment, hydrological modeling, irrigation planning, water resources management, ecosystems’ adaptation to climate change, and accounting for ecosystem services [1,2,3,4,5,6,7,8,9]. Thus, accurate estimates of ET are necessary for implementing water management strategies and promoting efficient use of water resources, especially in regions facing water shortage, like the Mediterranean basin. Unfortunately, direct measurements of ET through techniques like lysimeters [10,11], eddy covariance [12,13], and the Bowen ratio energy balance (BREB) system are difficult due to the expensive equipment required and the practical difficulties involved. Therefore, several empirical mathematical models have been developed worldwide under various environments to estimate ET using meteorological data. Various models possess specific strengths and limitations, which are dependent on the methods’ applications and underlying assumptions [14]. In all these models, it is of paramount importance to note that the magnitude of ET is significantly influenced by the surface characteristics of the site [15].
The empirical ET models aim to provide reliable estimations of water demand solely driven by atmospheric conditions, regardless of crop or vegetation characteristics and soil factors. As a result, the output of these models is referred to as potential (PET) or reference evapotranspiration, which are different terms with different conceptual and physical bases for expressing water demand [16,17]. PET models can be classified into four major groups: mass-transfer, temperature-based, radiation-based, and combination methods. It is noteworthy that selection of the appropriate PET method for each specific site is of the utmost importance due to its impact on the computation of hydro-meteorological and climatic indices that are widely used for environmental monitoring [8,18,19,20].
The Food and Agriculture Organization of the United Nations (FAO) and the World Meteorological Organization (WMO) recommend the standardized FAO56 Penman–Monteith (FAO56–PM) equation for PET estimation [21]. The FAO56–PM equation is known for its accuracy across various climates and time periods [22] and serves as a standard for comparing other empirical or soft computing methods in most studies [23,24]. The advantage of this method lies in its ability to bypass the need for local calibration, as it encompasses both physiological and aerodynamic parameters. Moreover, the equation has undergone rigorous testing, making use of lysimeter data to validate its accuracy and reliability [25]. On the other hand, its application is not always feasible due to high data requirements, such as air temperature, relative humidity, wind speed, and solar radiation data, which are available in limited meteorological stations worldwide. Additionally, obtaining quality data from these parameters can also be challenging [26].
Thus, it is crucial to develop models that strike a balance between accuracy and simplicity, utilizing fewer meteorological parameters to allow more straightforward estimates of PET compared to the FAO56–PM method. Moreover, the adjustment or calibration of simpler original methods with reduced data requirements becomes essential to accurately estimate PET, particularly in regions where meteorological data are scarce [27].
In this context, several studies have evaluated the performance of PET methods against the FAO56–PM, considering a limited number of methods at a time [28,29,30,31,32,33,34,35], and conducted in low-humidity conditions at low altitudes, exclusively for urban and agricultural areas. In contrast, a recent thorough evaluation of 127 PET models was performed in two Mediterranean urban green sites [23]. Overall, previous studies conclude that combination-based methods (which are equally demanding with FAO56–PM) performed best for PET estimation, followed by radiation-based and temperature-based ones, whilst less accurate results are given by the mass-transfer-based method.
The temporal variability of PET is important especially for rainfed forest environments [36,37,38]. Exploring the performance of PET methods in forest ecosystems is particularly important for understanding water interactions and balance in forest ecosystems, as well as for assessing the water requirements and growth of forest vegetation [39,40]. Moreover, it becomes essential to assess model performance at high altitudes, where PET values exhibit distinctively higher levels, and models might display varying uncertainties. However, there is limited comparative evaluation of empirical PET models in forest ecosystems. This is due to the challenges associated with installing and maintaining meteorological stations at high elevations in mountainous regions. The most notable studies are analyzed below. Federer et al. [41] compared five reference surface PET methods to four surface-dependent PET methods in different forest types at seven locations. Another study, conducted at a coniferous forest site in northern California [42] compared five models and proposed a modified Priestley–Taylor model. Rao et al. [43] compared the estimates of three PET models with measured actual ET in two forested watersheds (Appalachian Mountains, North America), with one dominated by a conifer plantation and one dominated by native naturally regenerated deciduous hardwoods. Ha et al. [44] compared five PET models with ET measurements with the eddy covariance method in three ponderosa pine forests in Arizona. In Greece, Gebhart et al. [45] evaluated the performance of 13 PET methods against FAO56–PM in forest sites of northern Greece. Bourletsikas et al. [46] published a comparative evaluation of 24 PET equations applied on an evergreen-broadleaved forest in central Greece. More recently, Markos and Radoglou (2021) conducted a study comparing FAO56–PM PET values with eddy covariance measurements from a Robinia pseudoacacia site in northern Greece.
Understanding the behavior of PET models in such environments is crucial for ensuring accurate estimations and reliable predictions in specific climatic conditions. Hence, conducting evaluations in high-altitude regions can lead to valuable insights and improve the overall reliability of PET models in challenging terrains. Therefore, thorough evaluation of a wide range of PET methods in forest environments is of high importance.
This study follows the work by Proutsos et al. [23] who evaluated the performance of empirical PET methods in urban green spaces in Greece. The present study aims at investigating the performance of 50 temperature-based PET methods against the benchmark FAO56–PM method, in a mountainous forest site in northern Greece, to evaluate the applicability of methods with limited data requirements in the Mediterranean forest environment. Daily data from an automatic forest meteorological station were employed to produce the PET estimates for 5389 days over the period from 2008 to 2023. The findings of this work can contribute to improving our understanding of water dynamics in forest ecosystems and provide valuable tools for assessing forest vegetation water requirements and growth under specific climatic and geographical conditions.
Based on the previous work by Proutsos et al. [23] in urban green spaces in Greece, the present study aims at investigating the performance of 50 temperature-based PET methods against the benchmark FAO56–PM method, in a mountainous forest site in northern Greece. Daily data from an automatic forest meteorological station were employed to produce the PET estimates for 5389 days over the period from 2008 to 2023. The results can contribute to improving our understanding of water dynamics in forest ecosystems and provide valuable tools for assessing forest vegetation water requirements and growth under specific climatic and geographical conditions. In addition, the evaluation of low-demand temperature-based PET methods can support the applicability of the appropriate methods in mountainous Mediterranean forest environments with limited data availability.
2. Materials and Methods
2.1. Study Site
The study site is located in the area of Chrysopigi village (Figure 1), about 13 km northeast from the Serres Municipality. The forest meteorological station was installed at 605m a.s.l., at the Research Center of the Forest Research Institute (41°10′ N, 23°34′ E) in 1978. In 2008, the station was upgraded to automatic and monitoring of radiation fluxes was added.

Figure 1.
Map of Greece, where the study site of Chrysopigi is indicated.
Based on the long-term meteorological data of the 45-year period from 1978 to 2023 from the same station, the climate of the region is characterized by an average annual air temperature of 13.3 °C (with a standard deviation SD = 0.7) ranging seasonally from 4.4 °C (SD = 1.2) in winter to 22.8 °C (SD = 1.0) in summer, with intermediate values at the transitional seasons of spring (12.0 °C, SD = 1.2) and autumn (14.2 °C, SD = 1.1). The warmest month of the year is August (23.6 °C, SD = 1.5) and the coolest is January (3.6 °C, SD = 1.7). The annual precipitation in Chrysopigi is 623 mm, almost uniformly distributed between seasons (27% in winter, 27% in spring, 22% in summer, and 24% in autumn), which is not typical of the Mediterranean climate of Greece which is characterized by wet winters and dry summers.
The above patterns result in the classification of the area in the sub-humid climatic type with very cold winters, according to Emberger’s [47] bioclimatic classification, with a Q2 index of 77.0. The dry summer conditions last about 2 months (from the beginning of July to the end of August) as depicted in the Bagnouls and Gaussen [48] pluviometric diagram of the area (Figure 2).
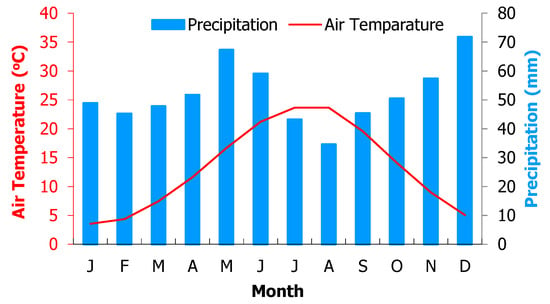
Figure 2.
Pluviometric diagram of Chrysopigi, produced by long-term data (period 1978–2023).
The broader area belongs to the Quercetalia pubescentis vegetation zone with the presence of Quercus pubescens, Q. coccifera, Caprinus orientalis, Fraxinus ornus, Cistus incanus, and Colutea arborescens. Its larger part is occupied by a 60-year-old planted Pinus brutia forest. Kermes oak (Q. coccifera) dominates especially in the forest openings [49]. The soil is, generally, sandy loam, with shallow depth and pH of about 6 and organic matter content of 1.47% [49].
In a forest opening, a fully equipped meteorological station recorded data on a 60 min timestep. Air temperature and relative humidity (E+E sensor, model EE08; E+E Elektronik Ges.m.b.H., Engerwitzdorf, Austria, with accuracy less than ±3% for relative humidity and less than 0.2 °C at 23 °C), windspeed (Thies Clima Small Wind transmitter, Adolf Thies GmbH & Co. KG, Göttingen, Germany, with accuracy ±0.5 m s−1) and wind direction (NRG 200P; Kintech Engineering, Zaragoza, Spain), precipitation PR (Pronamic ApS rain gauge; Skjern, Denmark, with accuracy ±2%), and global solar radiation (SP110 Apogee Pyranometer; Apogee Instruments Inc., Logan, UT, USA, with typical absolute calibration error of less than 3% ± 5% cosine error) were measured with a Symmetron Stylitis–10 datalogger (Symmetron Electronic Applications, Gerakas, Athens, Greece).
Meteorological data of the period from January 2008 to May 2023 were employed to produce estimates of potential daily evapotranspiration (PET) by different empirical models. Specifically, air temperature T and relative humidity RH (average, minimum, and maximum), precipitation, wind speed, and global solar radiation daily values were used to produce the daily PET values. The analysis was performed on the PET estimates. A total number of 5389 daily values were assessed based on the PET estimates with the FAO56 Penman Monteith (FAO56–PM). The values are almost evenly distributed among seasons: 26% in winter, 26% in spring, 24% in summer, and 24% in autumn.
2.2. Potential Evapotranspiration Empirical Models Temperature-Based Potential Evapotranspiration (PET) Methods
In this study several temperature-based empirical models were applied to estimate PET. In general, the models can be grouped into three main categories based on the data input requirements. The two groups of equations, along with the mathematical expression for each equation, are presented below.
- PET = f (T), 36 methods presented in Equations (1)–(36) in Table 1.
 Table 1. Temperature-based methods. General form PET = f (T).
Table 1. Temperature-based methods. General form PET = f (T). - PET = f (T, RH), 13 methods presented in Equations (37)–(49) in Table 2.
 Table 2. Temperature-based methods. General forms PET = f (T, RH) and PET = f (T, PR).
Table 2. Temperature-based methods. General forms PET = f (T, RH) and PET = f (T, PR). - PET = f (T, PR), 1 method presented in Equation (50) in Table 2.
The above-presented empirical models were then compared with the benchmark method FAO56–PM [21]:
2.3. Statistical Indices and Ranking
To compare the estimations of PET by the different models against the estimates by FAO56–PM, the commonly used coefficients of the linear regression y = ax + b were employed as follows: slope a, intercept b, and coefficient of determination R2. Four additional statistical measures, recommended by Fox [82], were applied: the mean bias error (MBE) to assess the bias, the variance of the differences distribution to evaluate the variability of the differences between the PET values around the MBE, the mean absolute error (MAE), and the root mean square error (RMSE) to express the average difference. The index of agreement (d) was also used to make the cross-comparison between the models [83,84,85]. The analytic equations for the estimation of the indices are:
where Oi is the estimated PET by FAO56–PM, Pi is the PET by the compared methods, , and .
To rank the methods, the above indices were used and through a standardization procedure proposed by Aschonitis et al. [86] and also described in Rahimikhoob et al. [87]. The standardized ranking performance index (sRPI) was estimated by the following equations:
where Vi is each statistical index and k is the number of the statistical indices used for the RPI and sRPI estimations.
3. Results
3.1. Meteorological Conditions
For the recording period (1 January 2008 to 16 May 2023), the monthly average patterns of the main meteorological attributes in Chrysopigi are depicted in Figure 3. The average air temperature presented a mean annual value of 13.9 °C, ranging seasonally from 5.2 °C in winter to 23.3 °C in summer. However, there were temperature extremes on the hourly values. The absolute minimum was −11.7 °C, recorded on 8 January 2017, whereas an absolute maximum of 46.8 °C was recorded on 10 June 2015. The annual relative humidity is relatively high (60.6%) with a seasonal variation from 50.7% in summer to 68.8% in winter. The solar radiation pattern, which is the most determinant factor for the formation of PET, follows the distribution of air temperature and presents an annual value of 157 W m−2, being lower in winter (76 W m−2) and maximum in summer (243 W m−2). The sky conditions at the site assessed by the values of atmospheric clearness (Kt, which is defined as the ratio of global solar to extraterrestrial radiation), suggest that at Chysopigi, intermediate skies generally prevail, with Kt values ranging seasonally from 0.40 in winter to 0.51 in summer.
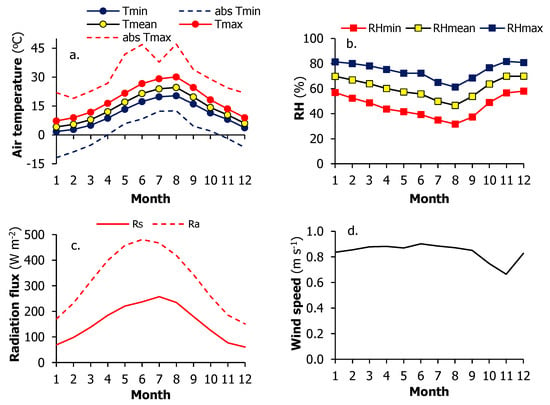
Figure 3.
Monthly averages of (a) the mean, Tmean, maximum, Tmax, minimum, Tmin temperatures, and absolute values of Tmin and Tmax; (b) the mean, RHmean, maximum, RHmax, and minimum, RHmin relative humidity; (c) the global solar Rs and the extraterrestrial Ra radiation flux densities; and (d) the wind speed, WS, for the site of Chrysopigi in the period 2008–2023.
Under such atmospheric conditions, PET rates by the FAO56–PM model were high in summer (4.43 mm d−1), maximized in July (4.72 mm d−1), and low in winter (0.81 mm d−1), becoming minimum in December (0.63 mm d−1). Moderate rates were estimated for the transitional seasons of spring (2.65 mm d−1) and autumn (1.86 mm d−1), as depicted in Figure 4. The annual average daily PET was 2.44 mm d−1.
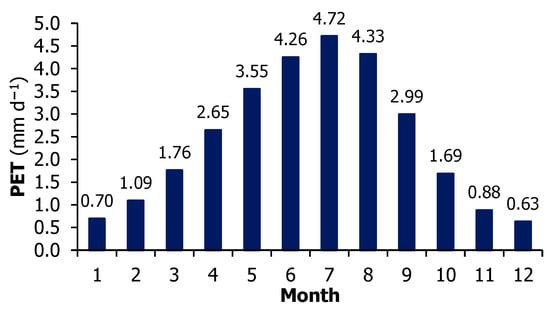
Figure 4.
Average monthly values of potential evapotranspiration (PET) estimated by the FAO56–PM benchmark method for the study site of Chrysopigi, for the period 2008–2023.
It is notable that most of the daily data (55.5%) are associated with relatively clear sky conditions (Kt greater than 0.5), whereas about 56.8% of the estimated PET values refer to average daily temperatures less than 15 °C (Figure 5). Such a distribution indicates that the PET estimates might be influenced by the local atmospheric clearness conditions and global solar radiation to a high degree. Specifically, the Pearson correlation assessment between the PET estimates by the FAO56–PM and the input parameters produced high and positive r values for Rs (0.928) and for the temperature attributes (0.855 for Tmean, 0.806 for Tmin, 0.878 for Tmax), and lower and negative r values for the relative humidity (−0.549 for RHmean, −0.578 for RHmin and −0.468 for RHmax), whereas the effect of wind speed appears to be weaker (r = +0.226).
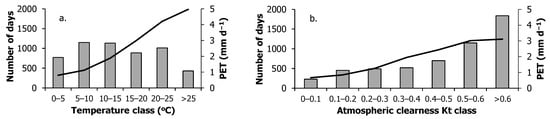
Figure 5.
Frequency distributions (bars) and average potential evapotranspiration PET values (lines) for different (a) daily mean air temperatures and (b) atmospheric clearness conditions in Chrysopigi, for the period 2008–2023.
The above patterns suggest that solar radiation is the main attribute determining PET; however, in regions with low meteorological data availability, the estimations of PET by using temperature data might be a meaningful alternative. In conjunction with the estimates of the daily extraterrestrial radiation Ra (which is estimated by only the geographical latitude of each site), PET can be estimated with accuracy, also considering the strong correlation between Ra and PET (r = +0.863).
3.2. PET Estimates and Comparisons
The estimation of daily PET by models incorporating only temperature attributes (Equations (1)–(36)) is presented comparatively with the estimates of the FAO56–PM benchmark method in Figure 6. Most PET = f(T) equations presented high R2 values (higher than 0.85), and two of them, Equation (19), Droogers & Allen 2002 (1), and Equation (26), Trajkovic 2007, presented the best R2 (0.902).
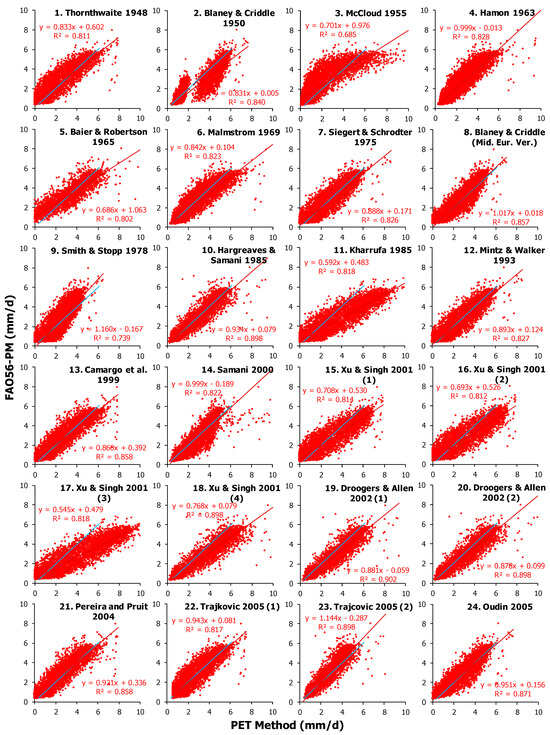
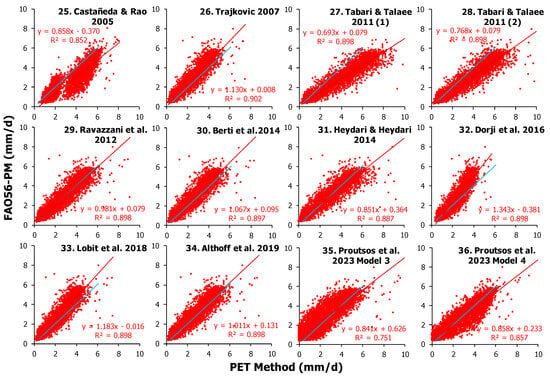
Figure 6.
Correlation between daily PET values estimated by different temperature (T)-based methods (x–axis) of the general form PET = f (T) against the benchmark FAO56–PM method (y–axis) for the forest site of Chrysopigi, Greece, along with the linear regression statistics. The blue line indicates the 1:1 regression.
The inclusion of water-related attributes as relative humidity or precipitation does not affect the accuracy of PET in Chrysopigi (Figure 7). The dispersion of values against the benchmark method indicates the good performance of the tested models. However, the R2 values are, in general, lower, ranging from 0.682 (Equation (38), Schendel 1967) to 0.885 (Equation (47), Ahooghalaandari et al. 2016 (4)), while none of the models showed R2 higher than 0.9. It should be stated, however, that six out of the 14 tested PET = f(T, RH or PR) models presented R2 higher than 0.85.
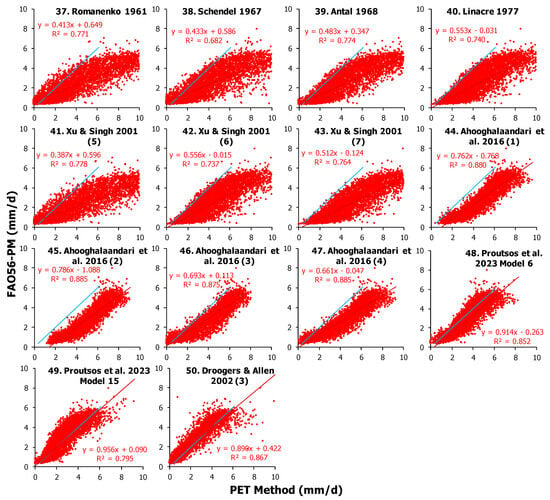
Figure 7.
Correlation between daily PET values estimated by different temperature-based methods (x–axis) corrected with relative humidity (RH) or precipitation (PR) attributes, following the general forms PET = f (T, RH) (Equations (37)–(49)) and PET = f (T, PR) (Equation (50)) against the benchmark FAO56–PM method (y–axis) for the forest sites of Chrysopigi, Greece, along with the linear regression statistics. The blue line indicates the 1:1 regression.
More statistical indices to perform an accurate evaluation of the performance of the 50 tested models, along with their overall ranking, are presented in Table 3 and Table 4. For the group of the PET = f(T) estimates, the average values range from 1.988 mm d−1 (Equation (3), McCloud 1955) to 3.676 mm d−1 (Equation (17), Xu & Singh 2001 (3)), which correspond to −18.1% and +51.4% deviations from the FAO56–PM average value (2.428 mm d−1), respectively. It is worth noting that most methods (20 out of the 36) of the general form PET = f(T) produced accurate averages with less than 10% difference from the benchmark method, and two of them, i.e., Equation (4), Hamon 1963, and Equation (31), Heydari & Heydari 2014, had averages with differences less than 1%. In addition, Equation (36), Proutsos et al. 2023, Model 4, had the best slope value (1.000), whereas Equation (35), Proutsos et al. 2023, Model 3, showed the best offset (−0.009). Similarly, Equation (31), Heydari & Heydari 2014, presented the best MBE (−0.004) and Equation (29), Ravazzani et al. 2012, had the best RMSE (0.519), MAE (0.346), and d (0.979).

Table 3.
Statistical indices (mean, slope a, intercept b, coefficient of determination R2, of the linear regression y = ax + b; mean bias error MBE; root mean square error RMSE; mean absolute error MAE; standard deviation square sd2; and index of agreement d) for the 36 models of the PET = f(T) group compared to the FAO56–PM benchmark method, at the forest site of Chrysopigi. The ranking (sRPI score and Rank) is based on the optimum values of the indices for all tested 50 PET models.

Table 4.
Statistical indices (mean, slope a, intercept b, and coefficient of determination R2, of the linear regression y = ax + b; mean bias error MBE; root mean square error RMSE; mean absolute error MAE; standard deviation square sd2; and index of agreement d) for the 36 models of the PET = f (RH or PR) groups compared to the FAO56–PM benchmark method, at the forest site of Chrysopigi. The ranking (sRPI score and Rank) is based on the optimum values of the indices for all tested 50 PET models.
The statistics for the PET = f (RH or PR) group are overall worse than the PET = f(T) group, as shown in Table 3 and Table 4. However, Equation (49), Proutsos et al. 2023, Model 15, and Equation (50), Droogers & Allen 2002 (3), produced PET averages that were less than 10% different from the benchmark method (+0.7 and +6.8%, respectively). In this category, Equation (47), Ahooghalaandari et al. 2016 (4), presented the best R2 (0.885), and Equation (49), Proutsos et al. 2023, Model 15, the best MBE (0.017), but Equation (50), Droogers & Allen 2002 (3), showed the best statistics in the slope (0.974) and the offset (−0.109) of the linear regression, the RMSE (0.643), MAE (0.421), sd2 (0.383), and d (0.976).
3.3. PET Methods Ranking
The overall assessment of all indices and the ranking of all the tested models for the forest site of Chrysopigi is presented in Table 3 and in Figure 8. Twelve out of the 50 tested methods showed sRPI scores higher than 0.90 and four of them reached scores higher than 0.95 as follows: Equation (29), Ravazzani et al. 2012; Equation (10), Hargreaves & Samani 1985; Equation (31) Heydari & Heydari 2014; Equation (20) Droogers & Allen 2002 (2); and Equation (34) Althoff et al., 2019. On the contrary, Equation (39), Antal 1968; Equation (42), Xu & Singh 2001 (6); Equation (40), Linacre 1977; Equation (38), Schendel 1967; Equation (43), Xu & Singh 2001 (7); Equation (37), Romanenko 1961; and Equation (41), Xu & Singh 2001 (5) performed worse at the studied forest site and presented very low sRPI scores (less than 0.500).
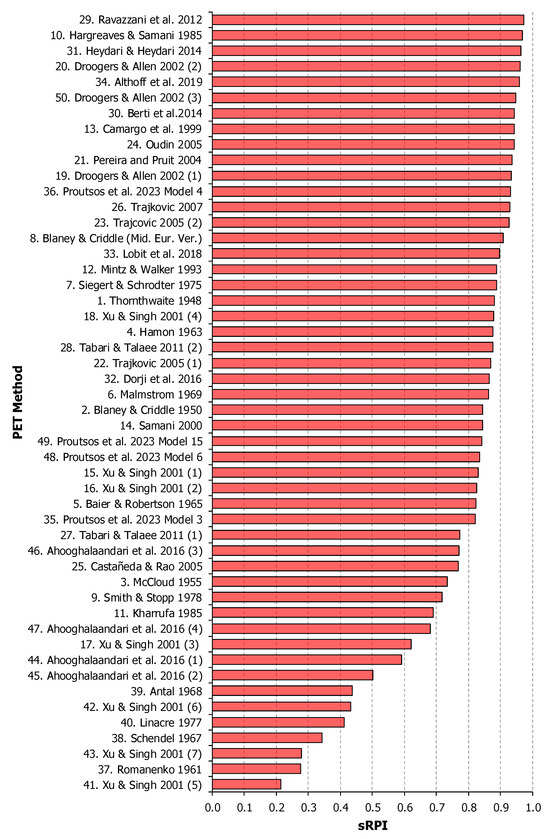
Figure 8.
Rank scores based on the sRPI index and ranking of the 50 temperature-based PET methods at the forest site of Chrysopigi, Greece.
The best performing method (Equation (29), Ravazzani et al. 2012) showed an average PET of 2.349 mm d−1 and was only by −1.4% different compared to the benchmark method. Worth noting is the performance of the widely used Equation (10), Hargreaves and Samani, method, which is ranked 2nd among all the 50 models, with an average PET (2.514 mm d−1) that was 3.5% higher than the benchmark.
4. Discussion
The superior performance of radiation-based methods compared to temperature-based ones for the estimation of PET is widely acknowledged [88]. However, temperature-based models also exhibit adequate behavior and are preferred in many studies due to their lower data requirements and the greater availability of temperature data compared to radiation.
In our forest site, various temperature-based methods demonstrated differing performance. The calculated PET average values ranged from 1.988 mm/d to 4.975 mm/d, resulting in differences with the FAO–56 PM benchmark method (2.428 mm–d). These differences suggest either underestimation or overestimation of PET values by percentages ranging from −18% to +105%. Specifically, 33 out of the 50 tested methods overestimated PET, while the remaining 17 underestimated it. However, 22 methods produced average PET values with less than a 10% difference from the benchmark method’s average. The five best-performing methods exhibited PET averages that differed from −6% (Equation (34), Althoff et al. 2019) to +9% (Equation (20), Droogers & Allen 2002 (2)) from the benchmark method’s mean PET, while Equation (31), Heydari & Heydari 2014, showed the smallest difference (−0.2%).
The equation proposed by Ravazzani et al. 2012 demonstrates an overall superior performance compared to all other temperature-based models, followed by the original Equation (31), Hargreaves–Samani model 1985; Equation (20), Heydari & Heydari 2014; Equation (20), Droogers & Allen 2002 (2); and Equation (34), Althoff et al. 2019 methods, all of which exhibited high rank scores (sRPI > 0.95). Ravazzani et al. (2012) along with all the aforementioned models are actually modifications of the Hargreaves–Samani 1985 model. Notably, Ravazzani et al. 2012 incorporated an altitude-related term into the original Hargreaves–Samani equation. The commendable performance of the original Hargreaves–Samani model aligns with the findings of Lang et al. (2017), who investigated the performance of eight PET methods in southwest China and recommended this specific method as the best temperature-based method for the area. It should be highlighted that the aforementioned five best-performing methods are solely temperature-related, classified into the PET = f(T) group, without incorporating any water-related (RH or precipitation) factors. This suggests that an increase in the number of input parameters does not necessarily lead to more accurate PET estimates, at least not in the specific Mediterranean forest environment.
Among the group of models incorporating temperature and relative humidity, or precipitation (PET = f(T, RH or PR)), Proutsos et al. 2023, Model 15 and Model 6, along with the equations by Ahooghalaandari et al. 2016 (3), (4), and (1), produced the most accurate PET estimates, exhibiting relatively higher rank scores compared to other equations in this category. However, PET estimates from this group of methods differed, on average, by +60%, ranging from −7% (Droogers and Allen 2002 (3)) to +105% (Xu and Singh 2001 (7)). Notably, the models by Droogers and Allen 2002 (3) and Proutsos et al. 2023, Model 15, emerged as the top performers in this category, ranking 6th and 28th among all examined methods, with average PET differences of −7% and +0.7%, respectively.
The method proposed by Ravazzani et al. 2012 was identified as the overall best-performing method, with an average PET of 2.394, being only by −1.4% different from the benchmark method. However, this method exhibited poorer performance when applied in urban green areas. In the study of Proutsos et al. [23], Ravazzani et al. 2012 ranked 32nd among 52 examined temperature-based methods, indicating that urban environments or variations in latitude and altitude may affect its accuracy. Similar discrepancies were observed for other top-performing methods at the forest site of Chrysopigi, such as the original Hargreaves–Samani 1985 model, which ranked 2nd in this study but 25th among 52 methods in urban sites. Similarly, Heydari & Heydari 2014, Droogers & Allen 2002 (2), and Althoff et al. 2019, ranked 3rd, 4th, and 5th, respectively, in this study, but were 21st, 31st, and 26th among temperature-based methods in urban sites.
Previous studies suggest that the best-performing temperature-based methods in urban sites differ from those in forest environments. For example, Ahooghalaandari et al. 2016 (3), Oudin 2005, and Xu & Singh 2001 (2) and (1) were ranked 12th, 35th, 9th, 31st, and 30th, respectively, when applied to the studied forest site. In the forest site studied by Bourletsikas et al. [46] in central Greece, almost all temperature-based models showed good performance with slight underestimation of PET. The original Hargreaves–Samani method and its modifications performed well, consistent with the findings of Valipour and Eslamian [34] and Valipour [89] at various Iranian provinces. Our results are also in line with the findings of Tabari et al. [27] and Trajkovic and Kolakovic [90], using, though, monthly data, who also found that the equation of Hargreaves–Samani and its modifications overestimate PET under humid conditions, but identified poor performance of the Thornthwaite model. A systematic overestimation of Hargreaves–Samani, was also addressed by Alexandris et al. [91], who estimated PET by five empirical models, above rainfed grass in central Serbia and compared the results against the FAO–56 PM benchmark method.
Gebhart et al. [45] evaluated the performance of 13 PET models in Greek forest sites and confirmed an overall better performance of the radiation-based methods against the temperature-based ones, attributing it to the large influence of solar radiation on the determination of the PET fluxes. Regarding the temperature-based models the authors suggested Hammon, McGuiness, and Hargreaves as best performing with regard to their latitudinal distribution. Forest type may also influence evapotranspiration fluxes. Rao et al. [43] compared the monthly measured actual evapotranspiration in two small forested watersheds (conifer plantation and naturally regenerated deciduous hardwoods) in the humid Appalachians in the southeastern U.S. with the PET estimates from three empirical methods (FAO–56 PM, Priestley–Taylor, and Hamon) and found that the annual PET of conifers was higher than of deciduous hardwoods and that Hamon’s and the FAO–56 PM equations generally underestimate the forest PET.
5. Conclusions
In the present study, 50 temperature-based methods for estimating potential evapotranspiration (PET) were compared against the widely used FAO–56 PM benchmark method, known for producing accurate PET estimates. Daily meteorological data from a forest sub-humid site in Chrysopigi (northern Greece) spanning 16 years (2008–2023) were utilized. The resulting PET estimates were evaluated using several statistical indices and were ranked accordingly.
The findings suggest that temperature-based methods can serve as suitable alternatives for PET estimation in forest environments. The performance of the original Hargreaves–Samani model and its modifications was quite efficient for estimating PET in the Mediterranean forest environment. The average daily PET at the studied forest was 2.428 mm, while the tested models produced averages ranging from 1.988 mm/d to 4.975 mm/d, indicating potential overestimation of PET by up to +105% or underestimation by −18%. Among the tested models, 33 overestimated PET and 17 underestimated PET, with 22 showing deviations of less than 10% from the average PET estimated by the benchmark method.
Temperature-based models relying solely on temperature appear to be more suitable for use in Mediterranean forest environments compared to methods incorporating water-related parameters, such as relative humidity or precipitation. The equations of Ravazzani et al., proposed in 2012, followed by Hargreaves–Samani in 1985, Heydari & Heydari in 2014, Droogers & Allen in 2002, model 2, and Althoff et al. in 2019, emerged as the top five performing methods with rank (sRPI index) scores exceeding 0.95, recommending their application in Mediterranean forest areas with limited data. However, further research is necessary at various sites to evaluate the models’ performance. Future work should include assessing the performance of radiation-based and combination methods for PET estimation in natural and urban forests and other green areas, as well as testing temperature and mass-transfer PET methods in different forest areas in Greece.
Author Contributions
Conceptualization, N.D.P.; data curation, N.D.P. and M.N.F.; formal analysis, N.D.P., M.N.F., S.P.S. and D.T.; funding acquisition. N.D.P. and M.N.F.; investigation, N.D.P., M.N.F., S.P.S. and D.T.; methodology, N.D.P., M.N.F., S.P.S. and D.T.; resources, N.D.P., M.N.F., S.P.S. and D.T.; supervision, N.D.P.; validation, N.D.P., M.N.F. and D.T.; visualization, S.P.S. and D.T.; writing—original draft, N.D.P. and S.P.S.; writing—review and editing, N.D.P., M.N.F., S.P.S. and D.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the research project “Meteo–FRI” of the Forest Research Institute, as well as by the project “Bioclima and natural vegetation in Greece” of the Institute of Mediterranean Forest Ecosystems, both funded by the Hellenic Agricultural Organization—DIMITRA, for maintaining the operation of Chrysopigi’s meteorological station and for conducting this research.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author due to privacy.
Acknowledgments
We acknowledge John Mamanis and Spyros Patropoulos from Scientact S.A. for their support in data acquisition from the studied meteorological station. We would also like to thank Kalliopi Radoglou and George Halivopoulos for the maintenance of the station during part of the study period. The authors highly acknowledge the meaningful comments and suggestions of the four anonymous reviewers that enhanced the quality of the present study.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Fotelli, M.N.; Korakaki, E.; Paparrizos, S.A.; Radoglou, K.; Awada, T.; Matzarakis, A. Environmental controls on the seasonal variation in gas exchange and water balance in a near-coastal Mediterranean Pinus halepensis forest. Forests 2019, 10, 313. [Google Scholar] [CrossRef]
- Fotelli, M.N.; Nahm, M.; Radoglou, K.; Rennenberg, H.; Halyvopoulos, G.; Matzarakis, A. Seasonal and interannual ecophysiological responses of beech (Fagus sylvatica) at its south-eastern distribution limit in Europe. For. Ecol. Manag. 2009, 257, 1157–1164. [Google Scholar] [CrossRef]
- Jayathilake, D.I.; Smith, T. Understanding the role of hydrologic model structures on evapotranspiration-driven sensitivity. Hydrol. Sci. J. 2020, 65, 1474–1489. [Google Scholar] [CrossRef]
- Jia, W.; Zhang, Y.; Wei, Z.; Zheng, Z.; Xie, P. Daily reference evapotranspiration prediction for irrigation scheduling decisions based on the hybrid PSO-LSTM model. PLoS ONE 2023, 18, e0281478. [Google Scholar] [CrossRef] [PubMed]
- Nedkov, S.; Campagne, S.; Borisova, B.; Krpec, P.; Prodanova, H.; Kokkoris, I.P.; Hristova, D.; Le Clec’h, S.; Santos-Martin, F.; Burkhard, B. Modeling water regulation ecosystem services: A review in the context of ecosystem accounting. Ecosyst. Serv. 2022, 56, 101458. [Google Scholar] [CrossRef]
- Proutsos, N.D.; Tsiros, I.X.; Nastos, P.; Tsaousidis, A. A note on some uncertainties associated with Thornthwaite’s aridity index introduced by using different potential evapotranspiration methods. Atmos. Res. 2021, 260, 105727. [Google Scholar] [CrossRef]
- Roy, D.K. Long short-term memory networks to predict one-step ahead reference evapotranspiration in a subtropical climatic zone. Environ. Process. 2021, 8, 911–941. [Google Scholar] [CrossRef]
- Stefanidis, S.; Rossiou, D.; Proutsos, N. Drought Severity and Trends in a Mediterranean Oak Forest. Hydrology 2023, 10, 167. [Google Scholar] [CrossRef]
- Tsiros, I.X.; Nastos, P.; Proutsos, N.D.; Tsaousidis, A. Variability of the aridity index and related drought parameters in Greece using climatological data over the last century (1900–1997). Atmos. Res. 2020, 240, 104914. [Google Scholar] [CrossRef]
- Boast, C.; Robertson, T. A “micro-lysimeter” method for determining evaporation from bare soil: Description and laboratory evaluation. Soil. Sci. Soc. Am. J. 1982, 46, 689–696. [Google Scholar] [CrossRef]
- Jia, X.; Dukes, M.D.; Jacobs, J.M.; Irmak, S. Weighing lysimeters for evapotranspiration research in a humid environment. Trans. ASABE 2006, 49, 401–412. [Google Scholar] [CrossRef]
- Hirschi, M.; Michel, D.; Lehner, I.; Seneviratne, S.I. A site-level comparison of lysimeter and eddy covariance flux measurements of evapotranspiration. Hydrol. Earth Syst. Sci. 2017, 21, 1809–1825. [Google Scholar] [CrossRef]
- Liu, S.; Xu, Z.; Zhu, Z.; Jia, Z.; Zhu, M. Measurements of evapotranspiration from eddy-covariance systems and large aperture scintillometers in the Hai River Basin, China. J. Hydrol. 2013, 487, 24–38. [Google Scholar] [CrossRef]
- Xiang, K.; Li, Y.; Horton, R.; Feng, H. Similarity and difference of potential evapotranspiration and reference crop evapotranspiration–a review. Agric. Water Manag. 2020, 232, 106043. [Google Scholar] [CrossRef]
- Alexandris, S.; Proutsos, N. How significant is the effect of the surface characteristics on the Reference Evapotranspiration estimates? Agric. Water Manag. 2020, 237, 106181. [Google Scholar] [CrossRef]
- Doorenbos, J.; Pruitt, W. Crop water requirements. In FAO Irrigation and Drainage Paper 24; Land and Water Development Division; FAO: Rome, Italy, 1977; p. 144. [Google Scholar]
- Penman, H.L. Natural evaporation from open water, bare soil and grass. Proc. R. Soc. London. Ser. A. Math. Phys. Sci. 1948, 193, 120–145. [Google Scholar] [CrossRef]
- Proutsos, N.; Tigkas, D.; Tsevreni, I.; Tsevreni, M. Drought Assessment in Nestos River Basin (N. Greece) for the Period 1955–2018. In Proceedings of the 10th International Conference on Information and Communication Technologies in Agriculture, Food and Environment, HAICTA 2022, Athens, Greece, 22–25 September 2022; pp. 429–437. [Google Scholar]
- Tegos, A.; Stefanidis, S.; Cody, J.; Koutsoyiannis, D. On the Sensitivity of Standardized-Precipitation-Evapotranspiration and Aridity Indexes Using Alternative Potential Evapotranspiration Models. Hydrology 2023, 10, 64. [Google Scholar] [CrossRef]
- Vangelis, H.; Tigkas, D.; Tsakiris, G. The effect of PET method on Reconnaissance Drought Index (RDI) calculation. J. Arid. Environ. 2013, 88, 130–140. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration-Guidelines for Computing Crop Water Requirements-FAO Irrigation and Drainage Paper 56; FAO: Rome, Italy, 1998; Volume 300, p. D05109. [Google Scholar]
- Allen, R.G.; Clemmens, A.J.; Burt, C.M.; Solomon, K.; O’Halloran, T. Prediction accuracy for projectwide evapotranspiration using crop coefficients and reference evapotranspiration. J. Irrig. Drain. Eng. 2005, 131, 24–36. [Google Scholar] [CrossRef]
- Proutsos, N.; Tigkas, D.; Tsevreni, I.; Alexandris, S.G.; Solomou, A.D.; Bourletsikas, A.; Stefanidis, S.; Nwokolo, S.C. A Thorough Evaluation of 127 Potential Evapotranspiration Models in Two Mediterranean Urban Green Sites. Remote Sens. 2023, 15, 3680. [Google Scholar] [CrossRef]
- Xu, L.; Shi, Z.; Wang, Y.; Zhang, S.; Chu, X.; Yu, P.; Xiong, W.; Zuo, H.; Wang, Y. Spatiotemporal variation and driving forces of reference evapotranspiration in Jing River Basin, northwest China. Hydrol. Process. 2015, 29, 4846–4862. [Google Scholar] [CrossRef]
- Trajkovic, S. Comparison of radial basis function networks and empirical equations for converting from pan evaporation to reference evapotranspiration. Hydrol. Process. Int. J. 2009, 23, 874–880. [Google Scholar] [CrossRef]
- Droogers, P.; Allen, R.G. Estimating reference evapotranspiration under inaccurate data conditions. Irrig. Drain. Syst. 2002, 16, 33–45. [Google Scholar] [CrossRef]
- Tabari, H.; Talaee, P.H. Local calibration of the Hargreaves and Priestley-Taylor equations for estimating reference evapotranspiration in arid and cold climates of Iran based on the Penman-Monteith model. J. Hydrol. Eng. 2011, 16, 837–845. [Google Scholar] [CrossRef]
- Islam, S.; Alam, A.R. Performance evaluation of FAO Penman-Monteith and best alternative models for estimating reference evapotranspiration in Bangladesh. Heliyon 2021, 7, e07487. [Google Scholar] [CrossRef]
- Kisi, O. Comparison of different empirical methods for estimating daily reference evapotranspiration in Mediterranean climate. J. Irrig. Drain. Eng. 2014, 140, 04013002. [Google Scholar] [CrossRef]
- Li, S.; Kang, S.; Zhang, L.; Zhang, J.; Du, T.; Tong, L.; Ding, R. Evaluation of six potential evapotranspiration models for estimating crop potential and actual evapotranspiration in arid regions. J. Hydrol. 2016, 543, 450–461. [Google Scholar] [CrossRef]
- Paparrizos, S.; Maris, F.; Matzarakis, A. Sensitivity analysis and comparison of various potential evapotranspiration formulae for selected Greek areas with different climate conditions. Theor. Appl. Climatol. 2017, 128, 745–759. [Google Scholar] [CrossRef]
- Samaras, D.A.; Reif, A.; Theodoropoulos, K. Evaluation of radiation-based reference evapotranspiration models under different Mediterranean climates in central Greece. Water Resour. Manag. 2014, 28, 207–225. [Google Scholar] [CrossRef]
- Sharafi, S.; Mohammadi Ghaleni, M. Calibration of empirical equations for estimating reference evapotranspiration in different climates of Iran. Theor. Appl. Climatol. 2021, 145, 925–939. [Google Scholar] [CrossRef]
- Valipour, M.; Eslamian, S. Analysis of potential evapotranspiration using 11 modified temperature-based models. Int. J. Hydrol. Sci. Technol. 2014, 4, 192–207. [Google Scholar] [CrossRef]
- Xystrakis, F.; Matzarakis, A. Evaluation of 13 empirical reference potential evapotranspiration equations on the island of Crete in southern Greece. J. Irrig. Drain. Eng. 2011, 137, 211–222. [Google Scholar] [CrossRef]
- Chen, X.; Liu, X.; Zhou, G.; Han, L.; Liu, W.; Liao, J. 50-year evapotranspiration declining and potential causations in subtropical Guangdong province, southern China. Catena 2015, 128, 185–194. [Google Scholar] [CrossRef]
- Stefanidis, S.; Alexandridis, V. Precipitation and potential evapotranspiration temporal variability and their relationship in two forest ecosystems in Greece. Hydrology 2021, 8, 160. [Google Scholar] [CrossRef]
- Yassen, A.; Nam, W.; Hong, E. Impact of climate change on reference evapotranspiration in Egypt. Catena 2020, 194, 104711. [Google Scholar] [CrossRef]
- Proutsos, N.; Tigkas, D. Growth response of endemic black pine trees to meteorological variations and drought episodes in a Mediterranean region. Atmosphere 2020, 11, 554. [Google Scholar] [CrossRef]
- Sun, G.; Wei, X.; Hao, L.; Sanchis, M.G.; Hou, Y.; Yousefpour, R.; Tang, R.; Zhang, Z. Forest hydrology modeling tools for watershed management: A review. For. Ecol. Manag. 2023, 530, 120755. [Google Scholar] [CrossRef]
- Federer, C.; Vörösmarty, C.; Fekete, B. Intercomparison of methods for calculating potential evaporation in regional and global water balance models. Water Resour. Res. 1996, 32, 2315–2321. [Google Scholar] [CrossRef]
- Fisher, J.B.; DeBiase, T.A.; Qi, Y.; Xu, M.; Goldstein, A.H. Evapotranspiration models compared on a Sierra Nevada forest ecosystem. Environ. Model. Softw. 2005, 20, 783–796. [Google Scholar] [CrossRef]
- Rao, L.; Sun, G.; Ford, C.; Vose, J. Modeling potential evapotranspiration of two forested watersheds in the southern Appalachians. Trans. ASABE 2011, 54, 2067–2078. [Google Scholar] [CrossRef]
- Ha, W.; Kolb, T.E.; Springer, A.E.; Dore, S.; O’Donnell, F.C.; Martinez Morales, R.; Masek Lopez, S.; Koch, G.W. Evapotranspiration comparisons between eddy covariance measurements and meteorological and remote-sensing-based models in disturbed ponderosa pine forests. Ecohydrology 2015, 8, 1335–1350. [Google Scholar] [CrossRef]
- Gebhart, S.; Radoglou, K.; Chalivopoulos, G.; Matzarakis, A. Evaluation of potential evapotranspiration in central Macedonia by EmPEst. In Advances in Meteorology, Climatology and Atmospheric Physics; Springer: Berlin/Heidelberg, Germany, 2013; pp. 451–456. [Google Scholar]
- Bourletsikas, A.; Argyrokastritis, I.; Proutsos, N. Comparative evaluation of 24 reference evapotranspiration equations applied on an evergreen-broadleaved forest. Hydrol. Res. 2018, 49, 1028–1041. [Google Scholar] [CrossRef]
- Emberger, L. Un projet d’une classification des climats du point de vue phytogéographique. Bul. Soc. D’ Hist. Nat. Toulouse 1942, 77, 97–124. [Google Scholar]
- Bagnouls, F.; Gaussen, H. Les climats biologiques et leur classification. Ann. Géographie 1957, 355, 193–220. [Google Scholar] [CrossRef]
- Mantratzis, P. The Influence of Canopy Architecture on Kermes oak (Quercus coccifera L.) Ecophysiology; Aristotle University of Thessaloniki: Thessaloniki, Greece, 2003. (In Greek) [Google Scholar]
- Pereira, A.R.; Pruitt, W.O. Adaptation of the Thornthwaite scheme for estimating daily reference evapotranspiration. Agric. Water Manag. 2004, 66, 251–257. [Google Scholar] [CrossRef]
- Thornthwaite, C.W. An approach toward a rational classification of climate. Geogr. Rev. 1948, 38, 55–94. [Google Scholar] [CrossRef]
- Blaney, H.; Criddle, W. Determining Water Requirements in Irrigated Area from Climatological Irrigation Data; USDA, Soil Conservation Service: Washington, DC, USA, 1950; p. 48. [Google Scholar]
- McCloud, D. Water requirements of field crops in Florida as influenced by climate. Proc. Soil. Sci. Soc. Fla. 1955, 15, 165–172. [Google Scholar]
- Dingman, S. Physical Hydrology, 2nd ed.; Waveland Pr Inc.: Salem, WI, USA, 2008; p. 656. [Google Scholar]
- Hamon, W.R. Computation of direct runoff amounts from storm rainfall. Int. Assoc. Sci. Hydrol. Publ. 1963, 63, 52–62. [Google Scholar]
- Baier, W.; Robertson, G.W. Estimation of latent evaporation from simple weather observations. Can. J. Plant Sci. 1965, 45, 276–284. [Google Scholar] [CrossRef]
- Siegert, E.; Schrödter, H. Erfahrungen mit dem Wasserbilanzschreiber nach Klausing. Dtsch. Gewasserkdl. Mitteilungen 1975, 19, 167–171. [Google Scholar]
- Smith, D.I.; Stopp, P. The River Basin: An Introduction to the Study of Hydrology; Cambridge University Press: Cambridge, UK, 1978. [Google Scholar]
- Hargreaves, G.H.; Samani, Z.A. Reference crop evapotranspiration from temperature. Appl. Eng. Agric. 1985, 1, 96–99. [Google Scholar] [CrossRef]
- Kharrufa, N. Simplified equation for evapotranspiration in arid regions. Beiträge Zur. Hydrol. 1985, 5, 39–47. [Google Scholar]
- Mintz, Y.; Walker, G. Global fields of soil moisture and land surface evapotranspiration derived from observed precipitation and surface air temperature. J. Appl. Meteorol. Climatol. 1993, 32, 1305–1334. [Google Scholar] [CrossRef]
- Camargo, Â.P.d.; Marin, F.R.; Sentelhas, P.C.; Picini, A.G. Ajuste da equação de Thornthwaite para estimar evapotranspiração potencial em climas áridos e superúmidos, com base na ampliturde térmica diária. Rev. Bras. Agrometeorol. 1999, 7, 251–257. [Google Scholar]
- Hargreaves, G.; Samani, Z. Estimating potential evapotranspiration. J. Irrig. Drain. Engr. ASCE 1982, 108, 223–230. [Google Scholar] [CrossRef]
- Samani, Z. Estimating solar radiation and evapotranspiration using minimum climatological data. J. Irrig. Drain. Eng. 2000, 126, 265–267. [Google Scholar] [CrossRef]
- Xu, C.Y.; Singh, V. Evaluation and generalization of temperature-based methods for calculating evaporation. Hydrol. Process. 2001, 15, 305–319. [Google Scholar] [CrossRef]
- Trajkovic, S. Temperature-based approaches for estimating reference evapotranspiration. J. Irrig. Drain. Eng. 2005, 131, 316–323. [Google Scholar] [CrossRef]
- Oudin, L.; Hervieu, F.; Michel, C.; Perrin, C.; Andréassian, V.; Anctil, F.; Loumagne, C. Which potential evapotranspiration input for a lumped rainfall–runoff model? Part 2—Towards a simple and efficient potential evapotranspiration model for rainfall–runoff modelling. J. Hydrol. 2005, 303, 290–306. [Google Scholar] [CrossRef]
- Castaneda, L.; Rao, P. Comparison of methods for estimating reference evapotranspiration in Southern California. J. Environ. Hydrol. 2005, 13, 1–10. [Google Scholar]
- Trajkovic, S. Hargreaves versus Penman-Monteith under humid conditions. J. Irrig. Drain. Eng. 2007, 133, 38–42. [Google Scholar] [CrossRef]
- Ravazzani, G.; Corbari, C.; Morella, S.; Gianoli, P.; Mancini, M. Modified Hargreaves-Samani equation for the assessment of reference evapotranspiration in Alpine river basins. J. Irrig. Drain. Eng. 2012, 138, 592–599. [Google Scholar] [CrossRef]
- Berti, A.; Tardivo, G.; Chiaudani, A.; Rech, F.; Borin, M. Assessing reference evapotranspiration by the Hargreaves method in north-eastern Italy. Agric. Water Manag. 2014, 140, 20–25. [Google Scholar] [CrossRef]
- Heydari, M.M.; Heydari, M. Calibration of Hargreaves–Samani equation for estimating reference evapotranspiration in semiarid and arid regions. Arch. Agron. Soil. Sci. 2014, 60, 695–713. [Google Scholar] [CrossRef]
- Dorji, U.; Olesen, J.E.; Seidenkrantz, M.S. Water balance in the complex mountainous terrain of Bhutan and linkages to land use. J. Hydrol. Reg. Stud. 2016, 7, 55–68. [Google Scholar] [CrossRef]
- Lobit, P.; López Pérez, L.; Lhomme, J.-P. Retrieving air humidity, global solar radiation, and reference evapotranspiration from daily temperatures: Development and validation of new methods for Mexico. Part II: Radiation. Theor. Appl. Climatol. 2018, 133, 799–810. [Google Scholar] [CrossRef]
- Althoff, D.; Santos, R.A.d.; Bazame, H.C.; Cunha, F.F.d.; Filgueiras, R. Improvement of Hargreaves–Samani reference evapotranspiration estimates with local calibration. Water 2019, 11, 2272. [Google Scholar] [CrossRef]
- Romanenko, V. Computation of the Autumn Soil Moisture Using a Universal Relationship for a Large Area; Ukrainian Hydrometeorological Research Institute: Kyiv, Ukraine, 1961; pp. 12–25. [Google Scholar]
- Schendel, U. Vegetationswasserverbrauch und-wasserbedarf. Habilit. Kiel. 1967, 137, 1–11. [Google Scholar]
- Antal, E. Új Módszer a Potenciális Evapotranspiráció Számítására; Beszámolók az 1968-ban Végzett Tudományos Kutatásokró; OMI Hiv. Kiadványa: Budapest, Hungary, 1968; Volume XXXIV, pp. 414–423. [Google Scholar]
- Müller, J.; Jörn, P.; Wendling, U. Untersuchungen zur Eignung des ANTAL-Verfahrens für die Bestimmung der potentiellen Evapotranspiration von Gras auf Flachlandstandorten. Z. Für Meteorol. 1990, 40, 189–191. [Google Scholar]
- Linacre, E.T. A simple formula for estimating evaporation rates in various climates, using temperature data alone. Agric. Meteorol. 1977, 18, 409–424. [Google Scholar] [CrossRef]
- Ahooghalandari, M.; Khiadani, M.; Jahromi, M.E. Developing equations for estimating reference evapotranspiration in Australia. Water Resour. Manag. 2016, 30, 3815–3828. [Google Scholar] [CrossRef]
- Fox, D.G. Judging air quality model performance: A summary of the AMS workshop on dispersion model performance, woods hole, Mass., 8–11 September 1980. Bull. Am. Meteorol. Soc. 1981, 62, 599–609. [Google Scholar] [CrossRef]
- Willmott, C.J. On the validation of models. Phys. Geogr. 1981, 2, 184–194. [Google Scholar] [CrossRef]
- Willmott, C.J. Some comments on the evaluation of model performance. Bull. Am. Meteorol. Soc. 1982, 63, 1309–1313. [Google Scholar] [CrossRef]
- Willmott, C.J.; Wicks, D.E. An empirical method for the spatial interpolation of monthly precipitation within California. Phys. Geogr. 1980, 1, 59–73. [Google Scholar] [CrossRef]
- Aschonitis, V.G.; Lekakis, E.; Tziachris, P.; Doulgeris, C.; Papadopoulos, F.; Papadopoulos, A.; Papamichail, D. A ranking system for comparing models’ performance combining multiple statistical criteria and scenarios: The case of reference evapotranspiration models. Environ. Model. Softw. 2019, 114, 98–111. [Google Scholar] [CrossRef]
- Rahimikhoob, H.; Sohrabi, T.; Delshad, M. Assessment of reference evapotranspiration estimation methods in controlled greenhouse conditions. Irrig. Sci. 2020, 38, 389–400. [Google Scholar] [CrossRef]
- Lang, D.; Zheng, J.; Shi, J.; Liao, F.; Ma, X.; Wang, W.; Chen, X.; Zhang, M. A comparative study of potential evapotranspiration estimation by eight methods with FAO Penman–Monteith method in southwestern China. Water 2017, 9, 734. [Google Scholar] [CrossRef]
- Valipour, M. Temperature analysis of reference evapotranspiration models. Meteorol. Appl. 2015, 22, 385–394. [Google Scholar] [CrossRef]
- Trajkovic, S.; Kolakovic, S. Evaluation of reference evapotranspiration equations under humid conditions. Water Resour. Manag. 2009, 23, 3057–3067. [Google Scholar] [CrossRef]
- Alexandris, S.; Stricevic, R.; Petkovic, S. Comparative analysis of reference evapotranspiration from the surface of rainfed grass in central Serbia, calculated by six empirical methods against the Penman-Monteith formula. Eur. Water 2008, 21, 17–28. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).