Abstract
The high complexity of the parameter–simulation problem in land surface models over semiarid areas makes it difficult to reasonably estimate the surface simulation conditions that are important for both weather and climate in different regions. In this study, using the dense site datasets of a typical semiarid region over Tibet and the Noah land surface model with the constrained land parameters of multiple sites, an enhanced Kling–Gupta efficiency criterion comprising multiple objectives, including variable and layer dimensions, was obtained, which was then applied to calibration schemes based on two global search algorithms (particle swarm optimization and shuffled complex evaluation) to investigate the site-scale spatial complexities in soil temperature simulations. The calibrations were then compared and further validated. The results show that the Noah land surface model obtained reasonable simulations of soil moisture against the observations with fine consistency, but the negative fit and huge spatial errors compared with the observations indicated its weak ability to simulate the soil temperature over regional semiarid land. Both calibration schemes significantly improved the soil moisture and temperature simulations, but particle swarm optimization generally converged to a better objective than shuffled complex evaluation, although with more parameter uncertainties and less heterogeneity. Moreover, simulations initialized with the optimal parameter tables for the calibrations obtained similarly sustainable improvements for soil moisture and temperature, as well as good consistency with the existing soil reanalysis. In particular, the soil temperature simulation errors for particle swarm optimization were unbiased, while those for the other method were found to be biased around −3 K. Overall, particle swarm optimization was preferable when conducting soil temperature simulations, and it may help mitigate the efforts in surface forecast improvement over semiarid regions.
1. Introduction
Soil temperature (ST) can significantly affect weather and climate by controlling land–atmosphere interactions and land biochemical processes [1,2,3]. However, while land surface models (i.e., LSMs) with efficient calibrations can achieve their various desired land surface objectives (i.e., soil moisture, runoff, fluxes, etc.) over semiarid regions [4,5,6,7], due to the great complexity of land surface physics and limited observations, the soil temperature forecast directly produced by LSMs has received little attention. Research efforts have been made recently in demonstrating surface ST improvement over greater time scales through semi-manually corrected LSMs with several key sensitive land surface parameters (i.e., leaf area index, known as LAI, and the coefficient of the roughness length of heat, known as CZIL) [8,9], but many other LSM land parameters that could affect medium-range ST simulations are still unaddressed, e.g., the varied flux physics related to thermal and/or hydraulic diffusion and conductivity over arid and semiarid lands can determine STs’ tendencies. Therefore, identifying the most robust corrected LSM by comparing different calibration schemes could be of great significance for mitigating efforts in ST forecast improvement over semiarid regions.
LSM performance over semiarid regions could be improved by reducing land surface parameter uncertainties through calibration at a soil moisture (SM)-controlled scale (which is usually climatological); therefore, the available SM datasets and the high LSM complexity dimension related to the land surface parameters have played decisive roles in improving most land simulations at greater time scales [10,11]. Nevertheless, the significant temporal scale differences between different soil layers (i.e., the diurnally varied surface but the seasonally varied subsurface) [12], the demand for finer spatiotemporal-scale surface conditions (as indicated by their high sensitivity to weather forecasts) [13,14,15,16], and the complexities of interaction scales between SM and ST [17], etc., demand the establishment of comprehensive objectives (i.e., SM and ST joint evaluation) for robust calibration. Meanwhile, frequently updated LSM systems are often subject to multiple factors that cannot be quantified (i.e., the heterogeneity of spatial errors) [18,19,20], which could be critical for medium-range forecast improvement against the high-spatiotemporal-resolution soil observation development [21]. Moreover, the spatial differences in surface simulations caused by the surface heterogeneity of land surface parameters could be great [22,23], and multi-site applications with multiple land parameter tables (or multi-corrected LSMs) could be more suitable for regional high-resolution simulation. Generally, the comprehensive calibration objectives, high LSM parameter update frequency, and high spatial heterogeneity among sites demand more efficient and effective calibration.
Automatic calibration with a global search algorithm (GSA) is preferred to address the inefficient convergence caused by high-dimensional parameters in LSMs, e.g., the well-known shuffled complex evaluation (SCE) and particle swarm optimization (PSO) have been significantly developed for LSM calibration over the decades [24,25]. SCE considering a conservative evolutionary strategy (i.e., the population advantage retention mechanism as complex shuffling) [26,27] was first introduced in hydrological model calibration with flexible multi-objectives [28] and further developed for calibrating complex LSM simulations by reducing the LSM parameter-related model complexities and noncommensurable information [29,30]. Meanwhile, PSO considering a radical evolutionary strategy (i.e., the population disadvantage elimination mechanism as swarm flying) [31,32,33] was first expanded with additional internal parameters (i.e., weight and constraint factors for a desired general searching space) [33,34], and has been further recommended for broader applications [35,36,37,38]. Furthermore, PSO and SCE have been widely compared for various calibrations during hydrological applications, and both have advantages over each other for different goals (i.e., the efficiency of PSO is preferable for relatively deterministic objectives but the convenience of SCE is preferable for relatively flexible objectives, and the effectiveness of PSO is preferable for the constrained LSM parameter space but the determinacy of SCE is preferable for determining relatively more general LSMs) [39,40,41,42,43].
For calibration schemes based on GSAs (i.e., PSO and/or SCE), the parameter–simulation problem in LSM was addressed by searching for the optimal LSM parameters and/or simulations that minimized or maximized an objective function, which was used to measure the distances between simulations (SIM) and observations (OBS), while the search strategy and comprehensive criteria used in GSAs can be sensitive to the global optima, including the LSM parameters, objectives, and simulations [24,25,29,30,39,40,41,42,43]. The comprehensive multi-objective criteria in GSAs considering multiple variables and/or multiple criteria require various transformations of different dimensions [28,35,36,37,38]. In particular, the Kling–Gupta efficiency (KGE) criterion can consider the correlations and error information related to a single variable [44], which are suitable for solving various medium-scale LSM problems [37,41]. Generally, the comprehensive objective of expanding KGE into multiple objectives could be pursued to hopefully meet the various demands during medium-range ST forecast calibration over semiarid regions [12,13,14,15,16,17,18,19,20,21,22,23], while a comparison of the GSA embedded with this comprehensive objective could determine whether they are preferable or not [39,40,41,42,43].
Note that Tibet boasts a diverse climate, featuring a distinct southeast–northwest gradient from humid to arid lands, while the land use change transitions induced by climate variations [45,46,47,48] in arid and semiarid lands (ASALs) have led to varied soil characteristics (i.e., texture and thickness) through pedotransfer, and this has given rise to complexities in observational soil water and heat flow interactions [49,50], e.g., the missing mechanism of vapor transfer (such as the modulation uncertainties of SM—ST on soil fluxes) [17] has caused unaccountable instances of globally applicable LSM parameterization physics [51,52,53]. Consequently, this has increased the distinguished soil thermal and hydraulic parameter configurations (such as the diffusion and conductivity functions) that are used to estimate various fluxes (which can determine the SM and ST tendencies) in LSMs over regional ASALs [54,55,56], which usually need these experiential LSM parameter uncertainties (configured into an LSM parameter lookup table) to be addressed or reduced through various observation-based specific simulation-objective calibrations [4,5,6,7,10,11,26,27,28,29,30]. Notably, though the dense soil observation network over northwest Nagqu had been established for finer dynamic SM and ST objectives with predominant land cover (grassland) and soil type (silt) [21,56,57,58,59], the generally varied LSM parameter uncertainties’ complexities within regional surface forecasting are highly challenged [18,19,20,49,50].
Overall, due to the high complexities of LSM parameter–simulation problems over semiarid land, medium-range calibration lacks the investigation of the comprehensive SM—ST objectives for solving spatial complexities in regional surface forecasting. To fill this gap, this study introduced an enhanced KGE objective that was applied for joint SM—ST calibration, which aimed to improve the medium-scale high-resolution ST forecast over Tibet’s typical semiarid region (such as northwest Naqu). Based on the GSAs that comprise high-density soil observations, the Noah LSM, two global optimizers (i.e., PSO and SCE), and the constrained space of the full land parameter table, two calibration schemes were introduced and further compared with the LSM parameters’ spatial complexes within heterogeneity and uncertainties, as well as calibration efficiency, effectiveness, and robustness, with the intention to explore the calibration’s ability to solve the parameter complexities in regional surface forecasts, and further highlight their general performance for potential applications.
2. Data and Model
2.1. Datasets
2.1.1. Soil Observation
The multi-scale observation network constructed by the Institute of Tibetan Plateau Research, Chinese Academy of Sciences (ITPCAS), comprises 57 stations in the central Tibetan Plateau region adjacent to Nagqu City for measuring the SM and ST at four soil depths, 0–5, 10, 20, and 40 cm. As the highest soil moisture network above sea level in the world (the elevations of these stations vary in the range of 4470~4950 m) (Figure 1a), the experimental area is characterized by a high soil moisture dynamic range and semiarid climate, and the available datasets cover the period from 2008 to 2016 [21,57]. All the sensors of each station were calibrated by taking into account the impact of soil texture and soil organic carbon content on the measurements.
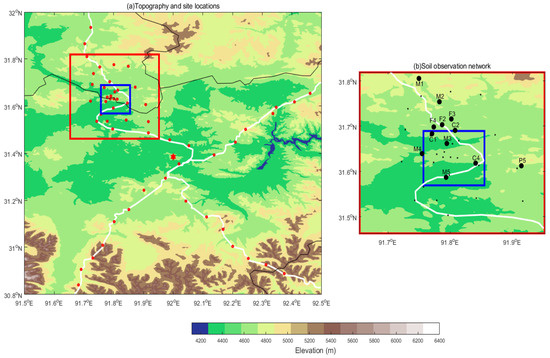
Figure 1.
(a) Topography (shaded) and site locations (filled dots) in Tibet (inset), with three types of observation networks (rectangular boxes), roads (white lines), and sites (red dots). (b) Topography (shaded) and soil sampling sites (filled dots) in the study area (bold black dots are our study sites).
To avoid the high complexities caused by local freeze–thaw processes, this study chose mesoscale soil network (which has a dense spatiotemporal resolution of around 0.1° and 0.5 h intervals) datasets from the local warm season period that covered from 1 April to 31 July 2014 (when local ice and snow were absent) to assemble the targeted dense soil observations over the typically semiarid region. Moreover, due to temporal discontinuity in the raw soil datasets, simple quality control using inverse time–distance-weighted linear interpolation was conducted to fill missing observations with 0.5 h intervals as follows.
In Equation (1), and represent the starting and ending time values (in hours measured since 1 April, i.e., 03:30 on 1 April equals 3.5) of the missing period range, respectively, where represents one time value during the missing period, and represents the soil value.
This simple linearly weighted interpolation was conducted when the soil observations had missing periods of less than 3 h (which equals the meteorological forcing interval; see Section 2.1.2), and several stations with missing periods of more than 3 h were rejected. After this simple quality control, there were 12 stations with full temporal continuity and a spatial resolution of around 0.1° left for this study (Figure 1b). The elevations of these selected sites varied around 4700 m, and their main vegetation types were grassland. Note that the main soil texture (the highest percentage of the top-soil texture) was chosen as the soil type required by the Noah LSM, and the main soil type of our study region was silt, except for the C4 and and M3 sites (Table 1), whose sand percentages were larger than the sum of the remaining percentages.

Table 1.
Description of the available soil stations.
In addition, to compare the site simulation performance against the existing high-resolution soil product during our study period, GLDAS [58] and ERA5 [59] grid soil reanalysis data with resolutions of 3 h/0.25°and 1 h/0.1°, respectively, were collected for intercomparison with the surface simulations during this study.
2.1.2. Meteorological Forcing
The surface forcing datasets developed by ITPCAS, with a 3 h interval (3 h) and a resolution of 0.1° × 0.1°, were produced by merging a variety of data sources [60,61], including the China Meteorological Administration (CMA) weather station observation data (i.e., wind, air temperature, relative humidity, sunshine duration, precipitation, and surface pressure), TRMM 3B42 satellite precipitation analysis data, GEWEX-SRB downward shortwave radiation data, the Modern Era-Retrospective Analysis for Research and Applications (MERRA) pressure data, and global land data assimilation system (GLDAS) data (i.e., wind, air temperature, and relative humidity). Moreover, this dataset covers the period 1979–2018, and the surface air temperature and wind were reassembled at screen levels of 2 and 10 m, respectively.
To match the selected stations that passed through simple quality control (QC), grid forcing was simply interpolated for the available station points and data periods (from 1 April to 31 July 2014) by using the inverse distance-weighted quadratic spline interpolation method. As the difference in the spherical distance between different stations over a small region was too small for calculation, the ongoing mentioned distance was measured with the differences in longitude and latitude. Then, the multi-site forcing datasets were assembled to drive the Noah LSM.
2.2. Model
The Unified Noah LSM was designed to understand the complex biophysical, hydrological, and bio-geochemical interactions between the land surface and the atmosphere at micro- and mesoscales, and has been widely used in numerical mesoscale weather prediction and regional climate models to improve the prediction of the impacts of land surface processes on regional weather, climate, and hydrology [12].
The Noah LSM uses a simple time driver for site simulations, and it can link to predefined external data such as a land surface parameter table, forcing, initial conditions, various physical–dynamic-specific controllers (i.e., the forcing interval time step size, the model integral step size, and soil texture characteristics), etc., through universally embedded interfaces. In addition, to fulfill the multi-point applications with running efficiency in this work, the read and write in- and/or output interfaces for Noah LSM, such as forcing, land surface parameter tables, soil textures, and simulations, were simply extended in a distributed manner.
To reduce the complexities caused by the land surface characteristic and dataset uncertainties in the regional site-scale-specific soil temperature simulations, except where soil textures were slightly varied for different sites in this study (i.e., the silt or sand soil type), the model for all sites was initialized with the same soil/surface textures, including the vegetation and slope types, the same soil depths of 5, 10, 20, and 40 cm, respectively, a 30-min runtime step (equal to the soil observation network), and the same screen levels at a 3 h interval step for forcing (equal to the forcing data interval).
3. Methods
3.1. Calibration Scheme
The general process of calibration can be described as considering that Noah LSM, based on physical concepts, has an -dimensional parameter space () that needs to be calibrated by using observations and corresponding model simulations to respond to the parameters, or the objective function , which was used to measure the distance between the simulation and observations. Then, calibration can be described as solving the following problem: . The ideal solution to this problem was to find the parameter (or the optimal parameters) in the parameter space that minimizes or maximizes the objective function (or the optimal objective), and the potentially least biased simulation (or the optimal simulation) can be achieved alongside this.
Due to the high nonlinearity (i.e., the high-dimensional parameter space and the multi-objective simulations), intelligent evolution considering a stochastic searching strategy based on both population (or global) and individual (or local) evolution was desired to find the global optimal solution, which is also known a the GSA. The GSA of this study, described in Figure 2, used a general framework considering broader flexibility to encourage various global optimizers and/or LSMs updates. It had three sequential modules as follows: Firstly, the optimizer parameter and population were initialized sequentially. Then, global searching that compared the LSM and observations was conducted to find the ongoing mentioned solution with potentially global optima. Finally, the optima were output when the GSA stop criteria were met.
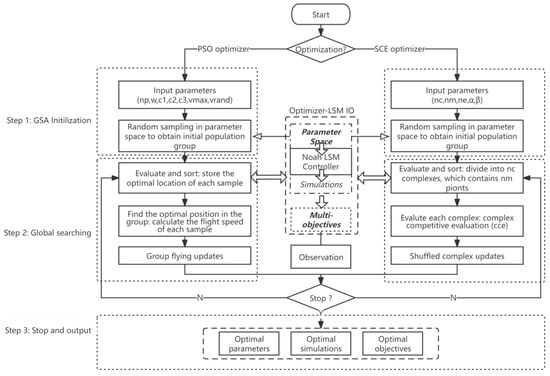
Figure 2.
Flowchart of the GSA framework used in this study.
To insert the LSMs (i.e., the Noah LSM) into the GSA framework, the optimizer–LSM interface (the Optimizer-LSM IO in Figure 2) was designed with flexibly corresponding modules including a land parameter space, an LSM time integration controller, multi-objective metrics, and the observations. Moreover, the global and local searching during both PSO (i.e., group and particle moving) and SCE (i.e., complex shuffling and individual mutation) were designed based on the group–individual interaction proceeding the modules and the quasi-Monte Carlo perturbations [31,32,33].
It should be noted that the stop criterion (maximum search time) of the GSA was set to 105 to improve the efficiency of the GSA runs. In addition to the optimizer input parameters, the local searching strategy that controls the stochastic update (i.e., the individual flying speed of PSO or the individual mutation of SCE) was based on those given by [26,27,33,34,41] to keep the generality of PSO and SCE. Moreover, to ensure a relatively fair optimizer difference comparison, the population size (i.e., the particle number in PSO and/or the individual number in SCE) of both PSO and SCE should be equally considered.
3.1.1. Particle Swarm Optimization
The basic PSO algorithm process adopts the concept of group social behavior. It uses a comparison between individuals and their previous positions to obtain local solutions, and a comparison between individuals and groups to obtain the global optimal solution, using few parameters [31,32].
The algorithm first randomly selected an initial population consisting of particles, (here,)) which represent the candidate optimal solution and contain empirical information or the position. The position includes both particle and population parts. The former includes the individual’s objective function value and velocity (i.e., the rate of change in position); the latter includes the optimal objective function value and optimal speed of the group. Then, the following three steps are carried out: (1) optimizing individuals by comparing their current and previous objective function values to obtain the current optimal position; (2) population optimization to find the optimal position of the population by sorting all particles; (3) each particle obtains its own evolutionary selection based on the weight information of individual and group experiences. When all particles were updated to a new position based on their evolutionary selection, the group update was completed. The above three steps were repeated until the stop condition was met (Figure 2). PSO also required additional parameter settings in the group update step, where each particle in the group was updated using the following equation:
In Equation (2), is the current position of the particle, and . is the optimal position before the particle, and . is the velocity of the particle, and . represents the optimal particle of the population. , , and are three stochastic equations with a range of variation of [0, 1]. and are two parameters that limit the degree of the velocity vector and the random search speed (i.e., 0.5 and 0.15) [34], respectively, and and are the two corresponding numbers. represents the variation in internal weight between 0 and 1 (i.e., 0.9) [33,41]. , , and are positive constants (i.e., 2.0, 2.0, and 10−7) [31,32]. Except , all the parameters that can affect the generality of PSO are vaguely related to the dimension of the parameter space.
3.1.2. Shuffled Complex Evaluation
The process of the SCE algorithm includes a gradient search to obtain local solutions, and complex dragging to obtain the global optimal solution. During the search process, complex shuffling allows for information sharing among each complex, thus avoiding local solutions. The gradient algorithm ensures that SCE can quickly find every local solution [26].
The algorithm randomly selects the initial population, which includes communities ( was affected by the number of approximate conditions in the search, and ), and each community contains individuals (). Then, the following three steps are carried out: (1) calculating the objective equation value for each point, and based on these values, the original population is reorganized into communities; (2) based on the simple gradient search algorithm, after a period of independent evolution (i.e., complex competitive evaluation, CCE [24,26]), new individuals from each community are mixed to form a new population; (3) reordering the individuals to form new communities. The first to third steps are repeated until the stop iteration condition is met (Figure 2). In the competitive evolution step, the individuals in each community were determined by the following triangular probability distribution () to determine the previous generation or select elimination:
SCE requires necessary settings to complete the steps of competitive evolution (CCE), where was and was 2 [26]. The number of training sessions required for the CCE algorithm () and the number of internal and external iterations ( and ) were , , and , respectively. Except and , all five parameters that can affect the generality of SCE were only related to the dimension of the parameter space. Thus, the total individual number of SCEs was , which equals the total particle number () of PSO.
3.1.3. The Multi-Objective Metrics
For calibration schemes based on global stochastic search algorithms (i.e., PSO and/or SCE), the parameter–simulation problem in LSMs was addressed by searching for the optimal parameters and/or simulations that minimized an objective function, which was used to measure the distances between simulations () and observations (). In the present study, the KGE value (KGE09; [44]) was used as an objective criterion to evaluate the Noah LSM. KGE09 was defined as follows:
In Equation (4), KGE09 is a function of three factors (), is the time index, represents the total time numbers, and and represent the mean values. is the correlation coefficient, where is the relative ratio between the standard deviation of and standard deviation of , and is the relative ratio of the mean values.
KGE09 was derived through decomposition of the mean square errors, so it considers both the error and correlation information between and , but only in the temporal dimension. However, evaluating the LSM by considering the temporal, variable, and soil layer dimensions requires and o values in a temporal sequence for multi-dimensional applications. The three factors () can be calculated from the variable and layer dimensions simply by using the average, which was similar to the Pareto set [28,30], but the multi-objective transform of the criteria KGE09 can be derived with a linear factor weighted by the overall objective dimension. The calculation uses the following functions:
In Equations (5) and (6), and are the variable and layer indexes, respectively, and and are the total numbers of variables and layers. Therefore, the factors and indicate overall statistics related to the vector objectives and , respectively. KGE09 was then calculated as an enhanced KGE with Equation (6), which considers multi-variable and multi-layer objectives. The second term on the right-hand side of Equation (6) is always greater than 0, KGE then varies between and 1. Note that due to the unsolved vertical and/or thickness heterogeneity (i.e., one parameter but multiple layers) in LSM’s soil layer configuration as a former study suggested [62], here, the two surface soil layers () were chosen to fulfill the KGE objective for solving the land parameters’ horizontal complexities that account for the reduction in the regional surface forecast’s spatial errors and neglect the land parameters’ vertical complexities.
3.2. Land Parameters
3.2.1. Parameter Space
As shown in Table 2, the land surface parameter ranges were the same as those given by [4,5,37,41]. Moreover, the default unobserved parameter values, including the vegetation, soil, and general and partial initial types, were initialized as the default Noah LSM parameter lookup table (https://ral.ucar.edu/solutions/products/unified-wrf-noah-lsm, accessed on 25 March 2024), while the rest of the initial types were initialized with the soil observations (i.e., SM and ST) for the LSM’s preparation at the very beginning (see Section 4). Therefore, it should be noted that all the sites, simulations were initialized with the same physical parameter values but different initial parameter values. And this could determine the observed and/or unobserved parameter uncertainty during the soil temperature calibrated simulation.

Table 2.
Ranges of Noah LSM parameters.
Note that the land surface model parameter ranges were quite irregular. To ensure rapid convergence of the GSA, threshold normalization was conducted in the GSA as follows:
where , , , and represent the default, minimum, maximum, and normalized parameter values, respectively. Moreover, all the default parameter values of this study were obtained from a 90-day warm-up run. The default parameters (whose dimension was n) were normalized to generate the first-generation population of GSA in the parameter space.
3.2.2. Physical Constraints
Due to the physical relationships between different parameters of the same soil type (see Table 1), i.e., whose texture differences could influence the soil evaporation rate, hydraulic conductivity, etc., necessary constraints can help avoid ineffective searches by the optimizer. However, excessive constraints can lead to inefficient optimizers. Therefore, here, we consider that the soil moisture of the first two surface soil layers ( and ) only varies between the wilting point () and the soil moisture where transpiration stress begins () [28], which can be written as follows:
Note that the two constraints and the multi-objective metrics comprise the multi-objective evaluator. And the multi-objective metric of the LSM only corresponds to the optimizer if this specific LSM parameter space has passed through the constraints; otherwise, the optimizer will retain fewer features of the previous generation’s population and expand the search domain of the next generation.
3.3. Performance Evaluation
3.3.1. Heterogeneity and Uncertainty
The parameter heterogeneity during this work was defined as the land parameter differences among sites or the parameter sensitivities against the sites. Since the parameter and site numbers (i.e., 46 and 12, respectively) were large, the dimensionality of the parameter–site sensitivities could be huge (i.e., far greater than 46 × 12). To fulfill this objective, the relative sensitivities among parameters were compared by using the predefined reference in the parameter space [11,29]. Two thresholds of the parameter space, 0.67 and 0.33, were taken as the upper and lower limits. For one land parameter compared to the others, more (or fewer) sites can reach (or not) its one limit; thus, sites were relatively sensitive to this parameter at the confidence of this limit. Moreover, the parameter uncertainty during this work was defined as the land parameter range and outlier against the sites. For all sites, smaller parameter ranges of the upper- and lower-limit intervals (such as the parameter’s interquartile range) indicated fewer uncertainties, while fewer parameter outliers indicated fewer unaccountable factors during parameter uncertainties.
3.3.2. Regional Overall Evaluation
To qualify the regional performance of surface conditions, the spatiotemporal differences among the control simulations, the calibrated simulations, the validated simulations of the calibrated models, the site observations, and the available surface reanalysis were compared using the following equations.
In Equations (9) and (10), and represent the time and the site, respectively. and represent for the root-mean-square errors and the correlation coefficient, respectively, in temporal sequence, while and represent those in the spatial sequence.
To determine the overall spatial performance of one datapoint, the quantitative regional horizontal and vertical errors (i.e., the averaged value on a certain dimension of the overall root-mean-square errors) were defined as
where the superscripts T and L represent the temporal and the soil layer dimension, respectively.
Moreover, besides the spatial average, linear fitting between the observations and simulations for all sites was conducted in this work to simplify the complexity (i.e., linear relation, coefficient of determination, etc.) among regional datasets. In addition, to determine the main spatial characteristics of the errors among two different datasets (i.e., OBS and SIM), the errors were resampled into 100 bins and then fitted by a 2-peak Gaussian function (describing the distributions with centroid, peak width, peak, etc.) to generate at most two main signals on the errors.
3.3.3. Efficiency and Effectiveness
The calibration efficiency of this work was defined as the fitness values (or the best population location, Pb) against the number of LSM runs (or the convergence speed). Better fitness values (i.e., larger KGE values) with fewer LSM runs indicated more efficiency. However, because it was often not possible to have both because of the physical constraints of the LSM parameters, the success rate (i.e., the ratio between the constrained individual numbers and the population size during one generation) was usually assessed at the same time to explain this during the calibration comparison. A larger success rate indicated eliminating more individuals, or a larger searching domain, with stronger evolution ability.
The calibration effectiveness could be simply defined as the optimal objectives (i.e., the final KGE values). Larger optimal KGE values indicated more effective calibration. Nevertheless, since the multi-objective KGE vector was designed in one single metric for one single site during this work, the layer-dimension averaged value of the overall root-mean-square errors in a temporal sequence (i.e.,) was also applied in evaluating the overall calibration effectiveness for one site. Smaller values indicated better effectiveness. Moreover, a Taylor diagram [63] that could assemble the comprehensive statistics (i.e., standard deviation, root-mean-square difference, and correlation) in a temporal sequence between the simulations and observations was also created for comparison with the method’s relative effectiveness. Usually, a smaller distance away from the observation location (where there is a zero root-mean-square difference, a correlation coefficient of 1, and the observed standard deviation) indicated better effectiveness.
In addition, the calibration robustness of this study was simply defined as the performance of the various regional evaluation metrics (as described in Section 3.3.2) for the simulation of the calibrated models. Smaller spatiotemporal differences and overall spatial errors, a larger fitting slope and coefficient of determination, and a closer error distribution to normal indicated more robustness. Note that the spatial resolution of the existing high-resolution soil reanalysis was 3 h, while that of the soil simulations was 30 min. The simulation datasets were linearly interpolated into 3 h for a broad comparison during this study.
4. Experiments
The experimental design is shown in Figure 3, and four steps were conducted as follows. (1) Data preparation: Simple quality control was conducted first for the raw soil observations to ensure that the selected datasets with a four-month-long period were temporally consistent. When preparing the reformatted forcing and the multi-site land static parameters, three-month-long controlled LSM runs were conducted to achieve the multi-site default parameter values. (2) Control run: A one-month-long (the controlled period) run with the default parameter values was conducted to determine the controlled parameters and simulations that can describe the problematical or biased relations between land parameters and soil temperature simulations. (3) LSM calibration: For the first fifteen days of the controlled period, two calibrations (based on PSO and SCE) with the same parameters as the control run were conducted to achieve the multiple optima of the GSA. A comparison of the different optimizers in the multiple optima was conducted to determine the optimizer’s ability to perform soil temperature calibration, and simulation differences among the control run, calibrations, and observations were assessed to determine the overall advantages and weaknesses of the GSA in soil temperature calibration. (4) Calibration validation: For the following fifteen days of the controlled period, two verification simulations with the optimal parameters derived from the calibration runs were conducted to achieve the optimized simulations. The various simulation differences among control run, calibration, and validation were compared to identify the calibration performance on the medium-range soil temperature forecast.
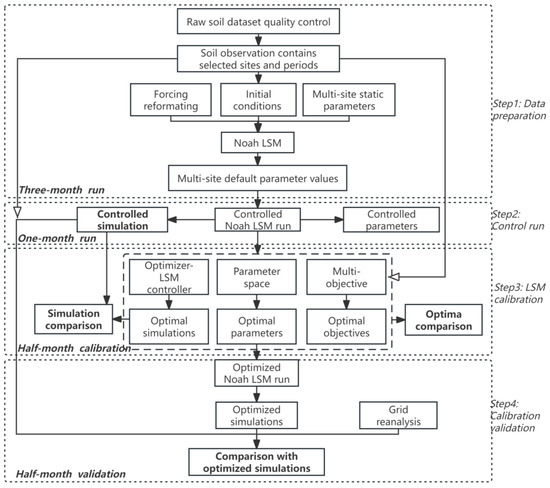
Figure 3.
The experimental design of this study. LSM = land surface model.
Moreover, due to the covering period of the forcing (covering 1979–2018) and soil (covering 2008–2016) datasets being different, the recent cross-time period (2014) with more available dense soil sites (Figure 1b) in both datasets was chosen as the study period. Considering the well-verified accuracy of both datasets [21,57,60,61] and the few surface transfers of northwest Naqu, the various unaddressed influences of climatic variation uncertainties (i.e., forcing and soil texture uncertainties) could be neglected; thus, the experimental design mainly concentrates on the objective of regional parameter–simulation issues over semiarid land during potential regional forecast scenarios.
It should be noted that the multi-site static land parameters and initial conditions during the data preparation step were derived from the original Noah LSM parameter tables and observations, respectively. As shown in Table 3, all the parameters of the control run (CTR) were initialized from the 3-month multi-site LSM warm-up run, and this was the same with the two calibration runs (i.e., PSOC and/or SCEC). Thus, the simulation differences between CTR and calibration can be attributed to the GSA’s performances. Meanwhile, all the parameters of the validation run (i.e., PSOO and/or SCEO) were initialized from the calibration runs. Thus, the differences between the validation simulations and observations should directly account for the GSA’s optimal parameter differences, while the simulation differences between the validation and CTR should account for the GSA’s performance robustness.

Table 3.
Experiments conducted in this study.
All the experiments were run at the 30 min step of the soil layers and the 3 h step of meteorological forcing. Nevertheless, due to the observation limits, the objectives of the calibration during this study only consider the soil moisture and temperature variables. Moreover, the same individual case duration for both the calibration and validation runs and the sum of their duration was equal to the CTR run, which should lay a foundation for GSA’s potential application during the high-frequency updating of soil simulations of medium-range forecasts.
5. Results
5.1. Case Description
The site-averaged 3 h meteorological forcing values against time during the study period are shown in Figure 4. During July 2014, the diurnal temperature variation mostly ranged between 5 and 15 °C, with an extremely dry atmosphere and relative humidity values mostly below 1%. The relatively low wind speed generally varied between 0 and 6 m.s−1, and the wind direction was mostly dominated by southern flow (between 180° and 270°) from 1 July to 10 July and from 16 July to 21 July, respectively, but the opposite was true in other periods. The incoming shortwave radiation exhibited strong diurnal variation between 0 and 600 W.m−2, and the incoming longwave radiation varied between 250 and 350 W.m−2. The pressure was generally around 586 hPa and the maximum 1 h precipitation was about 5 mm (in Figure 4d) around 10 July.

Figure 4.
Site−averaged forcing datasets for the study area from 1 July to 31 July 2014: (a) temperature (blue) and humidity (red), (b) wind speed (blue) and wind direction (red), (c) shortwave (blue) and longwave (red) radiation, and (d) pressure (blue) and precipitation (red).
The CTR simulations and OBS for the surface layer are compared in Figure 5. The linear fit for SM exhibited a small increasing slope (about 0.21) with weak consistency, and ST had a larger decreasing slope (about −0.46) with strong differences (Figure 5a). The spatial root-mean-square error (RMSES) for soil moisture was generally around 0.15 m3 m−3 and it increased slowly with time. The CCS decreased with time, and the RMSES and CCS for soil temperature exhibited diurnal differences. The Gaussian histogram fits for the errors of SM and ST had bimodal distributions, where the RMSES and CCS for soil moisture were about 0.17 m3 m−3 and 0.58, respectively, and the RMSES for the soil temperature was quite large and the CCS was even negative.
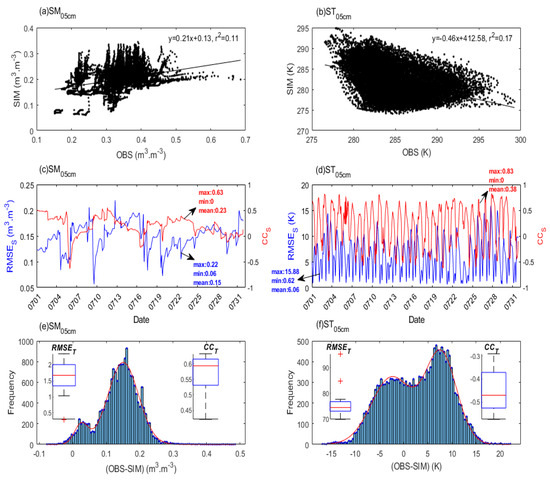
Figure 5.
Comparison of CTR simulations and observations of the surface layer for all sites during July 2014. (a,b) Fit between simulations and observations for surface soil moisture and temperature, respectively. (c,d) Spatial difference (RMSES, blue line; CCS, red line) versus time for surface soil moisture and temperature, respectively. Statistics for RMSES and absolute CCS are also shown. (e,f) Gaussian histogram fits (bar, frequency; red line, best fit; RMSET and CCT among all sites are shown in the box plot) for errors between simulations and observations of surface soil moisture and temperature, respectively.
A previous study suggested using either the ITPCAS forcing datasets or the improved heat-sensitive parameter Z0h (the same as CZIL in Table 2) to improve soil temperature simulations with the Noah LSM over a surface near our study area [8], and the non-negligible biased soil temperature in CTR indicated a more effective soil temperature calibration scheme in the present study.
In general, the surface soil moisture in CTR exhibited better temporal and spatial consistency with OBS than the soil temperature. The spatial differences in the soil moisture increased slightly with time, whereas those in the soil temperature exhibited strong diurnal variation. Thus, the LSM was not effective at simulating the multi-site soil temperature under forcing over a typical semiarid region.
5.2. Calibration Performance
5.2.1. Parameter Heterogeneity and Uncertainty
The optimal parameters of different sites for different types and optimizers are shown in Figure 6. For the “Vegetation” type in the PSO’s optimal parameter space (Figure 6a), the upper reference limit (i.e., 0.67) for RGL, RSMIN, CFACTR, TOPT, and Z0 was quite frequently crossed against the sites, while LAIMAX and RSMAX behaved oppositely (i.e., could only mostly reach 0.67). For the “Soil” and “General” types, except QTZ and SBETA, the upper limits for all other parameters could be frequently crossed against the sites. Nevertheless, for the “Initial” type (Figure 6d), except STC1, STC2, and STC4, the upper limits for all other parameters could be frequently crossed against the sites, and this was quite pronounced for ALBEDO, EMISSI, CMC, T1, STC3, SH2O3, and SH2O1. In general, 10 optimal land parameters in the optimal parameter space (including 46 parameters) of PSO seem to be less sensitive to sites indicated by fewer sites crossing with the upper reference limit when compared to other land parameters.
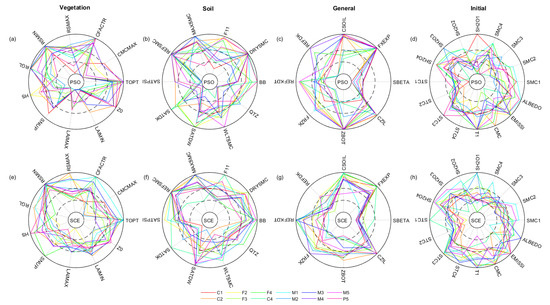
Figure 6.
The optimal vegetation (a), soil (b), general (c), and initial (d) land surface parameters of the twelve sites for the PSO optimizer. (e–h) are the same as (a–d), but for the SCE optimizer. The two dashed circles represent the reference limits of 0.33 (inner) and 0.67 (outer) in the parameter space.
For the optimal parameter space of SCE, LAIMAX of the “Vegetation” type, REFDK and SBETA of the “General” type, and STC2 and SMC3 of the “Initial” type could mostly reach 0.67 but were not crossed for most sites. In general, six optimal land parameters in the SCE’s optimal parameter space seemed to be less sensitive to sites. And the SCE’s optimal parameter space was more sensitive to sites when compared to PSO. This indicates that SCE calibrations have larger LSM parameter heterogeneity over typical semiarid land, which is consistent with a previous study [64].
Moreover, the optimal parameter ranges and outliers against sites between PSO and SCE are shown in Figure 7. For the “Vegetation” type, except the CFACTR, SNUP, LAIMIN, and Z0 parameters, all other PSO optimal parameters have smaller ranges than SCE. For the “Soil” and “General” types, except WLTSMC and FXEXP, all the other SCE optimal parameters have smaller ranges than PSO. Meanwhile, for the “Initial” type, except SH2O2 and SH2O3, all the other SCE optimal parameters also have smaller ranges than PSO. Thus, except for the “Vegetation” type, most of the optimal parameters for PSO exhibited more spatial differences than those for SCE. Nevertheless, the optimal parameters of the “Initial” type for SCE have more outliers than PSO. This indicates that SCE achieved small ranges for the “Soil” and “General” types, but possibly at the cost of large “Vegetation” uncertainties and more unaccountable initial parameters.

Figure 7.
Box plot of optimal vegetation (a), soil (b), general (c), and initial (d) land surface parameters against stations (SCEC in light blue and PSOC in dark blue). Red crosses indicate outliers.
PSO achieved larger parameter ranges with less sensitivity against sites compared to SCE; this can be mostly attributed to more outliers of SCE. Since the land parameter‘s sensitivity and/or uncertainties against sites over a small region can reflect the surface characteristic heterogeneity to some extent, the opposite parameter sensitivity and uncertainties between PSO and SCE indicate the unaccountable dimensions in surface heterogeneity to some extent. For regional calibration considering a multi-point application, fewer outliers and sensitivities against sites can fulfill more stable operational processes while considering the acceptable uncertainties. In general, for the typical semiarid region studied in this work, PSO converged better to the optimal parameters than SCE, but with more parameter uncertainties.
Overall, for both PSO and SCE, the Noah LSM parameters obtained in this study were generally characterized by great uncertainties against sites, but not for the “Initial” type. These findings indicate the need for robust LSM calibration schemes where the LSM parameters should be determined for specific applications, as suggested in previous studies [4,5,64,65]. The effectiveness of these optimal land parameters can be promptly verified in their corresponding simulations to highlight their potential applications in the frequently updated numerical systems.
5.2.2. Calibration Efficiency and Effectiveness
Figure 8 shows various efficiency and effectiveness performances against the sites. The fitness (the best population estimation during global searching; or Pb) curves show that PSOC and SCEC mostly converged at around 10,000 and 3000 Noah runs, respectively, for almost all the sites, but PSOC achieved higher final fitness (or objective, KGE) than the latter (Figure 8a). However, the fitness curves of both PSOC and SCEC for the C4 site (yellow lines) converged at a high negative value (i.e., around −10) that was far from the other sites. Slower convergence (i.e., larger Noah runs) and a higher converged Pb value of PSOC when compared to SCEC indicated PSO’s worse efficiency but better effectiveness than the latter for multi-objective simulation calibration. Nevertheless, the extremely low Pb of both SCE and PSO for site C4 when compared to the other sites indicated that the calibration’s effectiveness was highly dependent on non-self factors (i.e., LSM or forcing datasets uncertainties) that cannot be neglected.
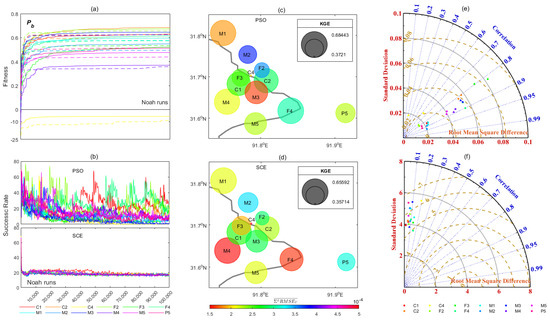
Figure 8.
Calibration efficiency and effectiveness comparison. (a) Fitness curves the of PSO (solid) and SCE (dashed) against sites (colored), and (b) success rate for PSO and SCE against sites (colored). (c,d) Optimal objectives (KGE, units: 1; bubble size) and layer dimensionally averaged root−mean−square errors (RMSET, units: 1; shaded) against sites for PSO and SCE, respectively. (e,f) Taylor diagrams of PSO (circle) and SCE (triangle) against sites (colored) for SMC1 (units: m3.m−3) and STC1 (units: K), respectively. In the Taylor diagram, the tawny dashed, blue dotted, and gray lines represent the referenced root-mean-square difference (RMSD), correlation (CCT), and standard deviation (STD), respectively.
For almost all sites, the success rate of PSO showed a sharp decrease (to 20) at around 3000 Noah runs, and then, it seemed to be varied in a disorderly manner from 80 to 10 during the following runs, while that of SCE showed a relatively sharper decrease (to 20) at around 3000 Noah runs, and then, it stably varied around 20 during the following period (Figure 8b). Since the success rates indicate the constraint rate of the searching space of one generation (i.e., swarms or complexes) during the optimization process, the relatively higher success rate of PSO indicated a more comprehensive evolutionary selection when compared to SCE. This can also explain why PSO usually found a better objective at the cost of lower efficiency with a more competitive evaluation space than SCE to some extent.
The KGE values (or the optimal objective) for PSOC varied between about 0.37 (site C4) and 0.68 (site F4), while those for SCEC varied from about 0.36 (site C4) to 0.66 (site M1) (Figure 8c,d). PSOC obtained better optimal objectives (closer to 1) than SCEC for most sites. Meanwhile, the RMSEO values of both PSOC and SCEC were extremely small (i.e., at the level of 10−4) for all sites, and their differences can be neglected. Nevertheless, the value ranges (i.e., 0.0002~0.0004) for PSOC were smaller than those (i.e., 0.0001~0.0005) for SCEC. The larger KGE and smaller RMSEO ranges when compared to SCE indicate that PSO achieved better objectives with slightly more stability than SCE.
As seen from the Taylor diagrams for SMC1 (Figure 8e), the CCT of most sites (except C4) was larger than 0.8 for both PSO and SCE, while PSO achieved slightly larger CCT than the latter for all the sites except M4. RMSD and STD for PSO and SCE were quite varied with a relatively minor magnitude, i.e., 0~0.06 m3.m−3 for RMSD, and 0.02~0.08 m3.m−3 for STD. For STC1 (Figure 8f), the CCT of most sites was smaller than 0.1 for both PSO and SCE, while PSO achieved a larger CCT than the latter for most sites (i.e., only four sites for SCE had a positive CCT). RMSD for both PSO and SCE varied around 6 K, while STD varied around 5 K. The relatively larger positive CCT of both STC1 and SMC1 for PSO, when compared to SCE, indicated that the former was more effective than the latter. Note that though the varied range magnitude of RMSD almost equals the STD for both STC1 and SMC1, all the CCT, RMSD, and STD values of SMC1 were considerably smaller than those of STC1. These positive Taylor diagram skills indicated that although the soil temperature simulation was highly biased, the two calibrations could be effective in calibrating both simulations, and this was more pronounced for SMC1.
5.2.3. Evaluation of Optimal Simulations
The optimal simulations and CTR were compared in Figure 9. The linear fit for the surface soil moisture (SM05cm) showed that SCEC had a slope of about 0.6 with a goodness of fit of about 0.6, which was highly consistent with the observations, while PSOC had a slope of about 0.4 with a goodness of fit of about 0.4, and CTR had a slope of about 0.2 with a goodness of fit of about 0.2 (Figure 9a). However, for the surface soil temperature (ST05cm), the best slope was about 0.2 for PSOC, followed by about 0.05 for SCEC, and the slope was negative for CTR at about −0.5 with a goodness of fit of about 0.2, while PSOC and SCEC both had zero goodness of fit (Figure 9b). Both PSO and SCE optimizers were able to calibrate the soil moisture and temperature simulations, and SCE seems to be better than PSO for soil moisture, while it behaves oppositely for soil temperature.
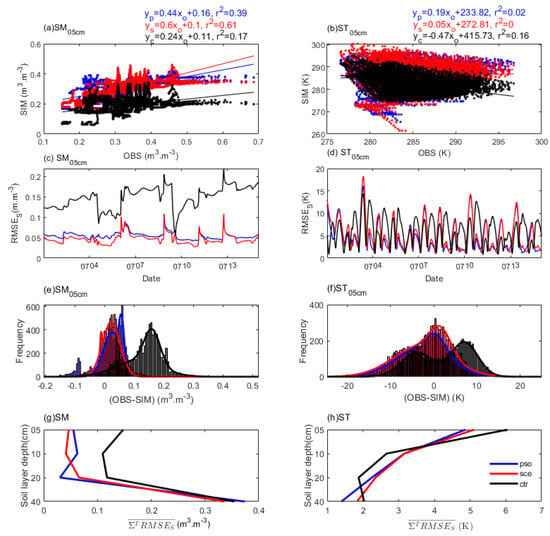
Figure 9.
Comparison of two optimal simulations (PSOC and SCEC in blue and red, respectively) and CTR (in black) with observations for selected soil variables. Goodness of fit for surface (a) soil moisture (SM05cm) and (b) soil temperature (ST05cm). RMSES values against time for (c) SM05cm and (d) ST05cm. Histogram fits of simulation errors for (e) SM05cm and (f) ST05cm. Vertical profile of temporally averaged RMSES values for (g) SM and (h) ST.
The RMSES values for SM05cm in CTR were around 0.15 m3.m−3 during most of the calibration period, but the values were around 0.05 m3.m−3 for both SCEC and PSOC (Figure 9c), and the values of SCEC were relatively smaller than PSOC. However, the RMSES values for ST05cm exhibited significant diurnal variation (Figure 9d), where the values for PSOC (i.e., varied around 4 K) were smaller than the other two (i.e., they varied around 7 K) during most periods. In particular, the RMSES values for SCE were sometimes even larger than those in CTR (i.e., around 4 in July). Both PSO and SCE could achieve smaller RMSES than CTR for SM05cm, and SCE seemed preferable, which was consistent with the linear fit slopes. However, PSO showed more significant advantages in reducing the spatial errors of ST05cm than SCE.
The simulation errors of SCEC for SM05cm showed a narrow distribution centered around 0.02 m3.m−3 with a frequency of around 420, and those of PSOC showed a distribution of bimodal adjacency, whose centers were located around 0.02 m3.m−3 with a frequency of around 400, and around 0.05 m.m−3 with a frequency of around 500, respectively (Figure 9c). Meanwhile, the errors of CTR had a broadly biased distribution centered around 0.15 m3.m−3 with a frequency of around 400. For the ST05cm simulation errors, CTR showed a broadly bimodal distribution centered around −5 K with a frequency of around 100, and around 9 K with a frequency of around 200, while PSOC and SCEC showed relatively narrow distributions that centered around 0 K with a frequency of around 250, and around 2 K with a frequency of around 300, respectively (Figure 9d). The Gaussian histogram fit comparison showed that the biased simulation error distribution in CTR could be significantly adjusted by both SCEC and PSOC for both the soil moisture and soil temperature, where SCEC performed better than PSOC for soil moisture, whereas the opposite was the case for the soil temperature, and this was consistent with the RMSES performance.
The temporally averaged RMSES () values against the vertical soil layers were further compared. For soil moisture (SM, Figure 9g), the values for the top three layers in CTR at around 0.15 m3.m−3 were reduced to 0.05 m3.m−3 after calibration. For soil temperature (ST), the values of the calibrations were decreased by 1 K in the surface layer when compared to CTR (Figure 9h). In particular, the calibrated ST of the middle two layers for both PSO and SCE were even worse than those for CTR (i.e., 2 K for CTR, but 2.5 K for the others). Nevertheless, both SM and ST of the bottom layer for PSO (whose RMSES was around 1.3 K) and SCE (whose RMSES was around 1.9 K) were slightly more improved when compared to the surface layer. This could be attributed to the different scales between surface and bottom soil layers. Generally, both PSO and SCE could effectively calibrate SM simulations of all soil layers; however, they can likely improve surface- and bottom-layer ST simulations when PSO behaves more preferably than SCE.
In general, the multi-objective GSA including SCE and PSO greatly improved the consistency of the soil moisture and soil temperature simulations both temporally and spatially. In particular, PSO was more effective than SCE for calibrating the soil temperature. Thus, the GSA conducted by PSO with the enhanced KGE was more suitable for regional multi-site and multi-variable applications.
5.3. Robustness Performance
5.3.1. Continuity in Improving Soil Forecasts
By using the optimal parameters derived from the calibration comprising PSOC and SCEC (or the calibrated LSM model), the experimental verification results with PSOO and SCEO were compared with CTR, as shown in Figure 10. For SM05cm (Figure 10a), the linear fitness for PSOO, SCEO, and CTR were about 0.14, 0.54, and 0.01, respectively, and the goodness of fit values for them were 0.04, 0.59, and 0, respectively. The optimal parameters of both SCEC and PSOC greatly improved the SM05cm simulations, and the former performed better than the latter. For ST05cm (Figure 10b), the linear fitness values for PSOO, SCEO, and CTR were about 0.17, 0.06, and −0.45, respectively, and the goodness of fit values for them were 0.04, 0, and 0.15, respectively. The optimal parameters of PSO significantly improved the ST05cm simulations when compared to the others. These were similar to the simulation performance of the calibration period (Figure 9a,b). The optimal parameters for both PSOC and SCEC significantly improved the consistency of the soil moisture and soil temperature simulations relative to CTR. SCEO performed better at simulating soil moisture, whereas PSOO performed better at simulating soil temperature.
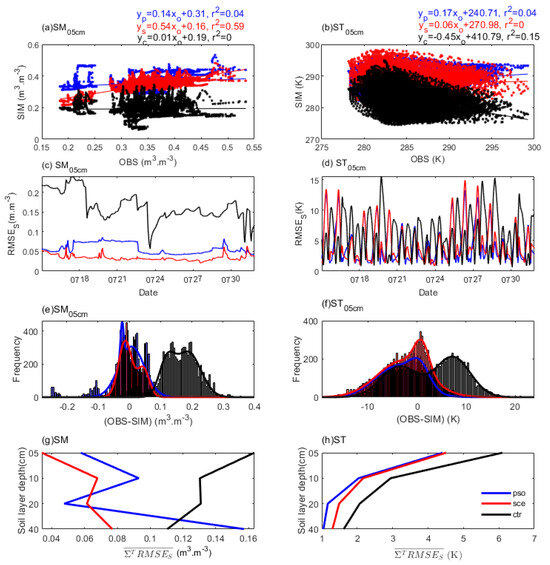
Figure 10.
Similar to the results shown in Figure 9, but with comparisons of the simulation of the calibrated models (PSOO in blue and SCEO in red).
The RMSES values of SM05cm for both PSOO and SCEO (i.e., varied around 0.05 m3.m−3) improved greatly when compared to CTR (i.e., varied around 0.15 m3.m−3) (Figure 10c). This was quite similar to the calibration performance (Figure 9c). Meanwhile, the RMSES values of ST05cm for PSOO, SCEO, and CTR over the validation period varied around 3, 6, and 7 K, respectively (Figure 10d). The reduction range of RMSES for validation was even larger than that for calibration (Figure 9d). The parameters of PSOC were also more effective at reducing the RMSES values for the soil temperature than those of SCEC.
The simulation errors of SM05cm for CTR showed a broad distribution centered around 0.17 m3.m−3 with a frequency of around 300, while those for both SCE and PSO showed a narrow distribution centered around 0 m3.m−3 with a frequency of around 375 (Figure 10e). Meanwhile, the simulation ST05cm for CTR showed a broadly bimodal distribution with two distinguished centers located around −5 K at a frequency of around 180 and around 8 K at a frequency of around 200, respectively (Figure 10f); nevertheless, those for PSOO and SCEO showed relatively narrow distributions with two adjacent centers located around 0 K at a frequency of around 200 and around 3 K at a frequency of around 250, respectively. The simulation errors with both SCEO and PSOO followed a consistent quasi-zero-centered Gaussian distribution (or a normal distribution), thereby demonstrating great improvement compared with those in CTR, and PSO seemed to be more robust for both SM and ST than SCE.
For the SM of the first three layers, the values for both PSOO and SCEO were mostly varied around 0.07 m3.m−3, and were much smaller than those of CTR (i.e., around 0.15 m3.m−3) (Figure 10g). For ST, the differences between PSO and CTR increased from 0.8 K to 1.8 K against the soil layer depth reduction (Figure 10h), and this was similar to the differences between SCE and CTR. In particular, PSOO obtained the smallest values for ST in all layers during the validation period. In general, the two types of calibrated parameters significantly improved both the SM and ST simulations of the validation period, where the optimal parameters with PSOC performed better than those with SCEC for the ST simulations.
Generally, the above-mentioned soil layer simulation advantages using the optimized parameters could demonstrate the robustness of both PSO and SCE schemes. In particular, the values of both SM and ST for the two schemes during validation were smaller than those during the calibration period (Figure 9g), this could demonstrate the advantages of calibration under month-long scaled systems (or medium-range parameter updates) to some extent.
5.3.2. Intercomparison with Surface Simulations
To identify the overall performance of the surface simulations with the calibrated model, domain-averaged surface soil moisture and temperature comparisons among CTR, PSOO, SCEO, ERA5, GLDAS, and OBS during the validation period were conducted and the results are shown in Figure 11.
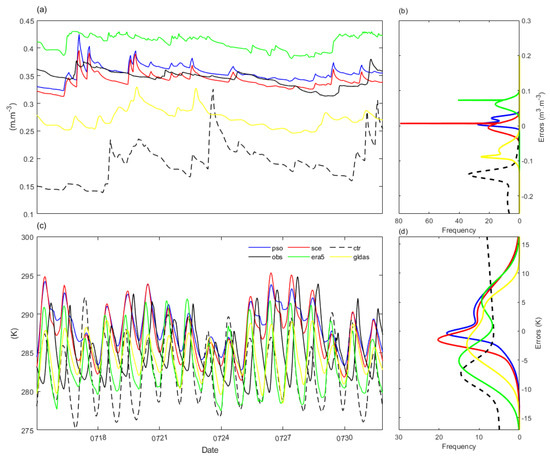
Figure 11.
Comparison among simulations (PSOO, SCEO, and CTR are shown as blue, red, and dashed lines, respectively), ERA5 (green), GLDAS (yellow), and observations (black) against time. (a) SM05cm and (c) ST05cm; (b,d) Gaussian fits of the errors of the datasets when compare to the observations.
The observed SM05cm was shown to be mostly varied around 0.35 m3.m−3 against time (Figure 11a). In CTR, SM05cm was severely underestimated (i.e., varied around 0.2 m3.m−3), with an abnormal increase around July 24 (which reached 0.33 m3.m−3). ERA5 clearly overestimated SM05cm (i.e., varied around 0.4 m3.m−3) with a smooth variation against time, whereas the opposite behavior (i.e., varied around 0.27 m3.m−3) was obtained with GLDAS. Obviously, the two simulations with calibrated land parameters were more consistent with the observed SM05cm than the other datasets; nevertheless, except for ERA5, consistent rhythmic temporal variations were observed in all other datasets.
The SM05cm error distribution of SCEO showed a narrow distribution, with the center located around 0 m3.m−3 at a frequency of around 80 (Figure 11b). For PSOO, the error distribution had a center located around 0 m3.m−3, similar to SCEO, but at a frequency of around 30. However, for ERA and GLDAS, the error distribution centers were located around 0.06 m3.m−3 with frequencies of around 40 and –0.07 m3.m−3, respectively, with a frequency of around 30. Nevertheless, for CTR, the errors were broadly distributed, with the center located around –0.15 m3.m−3 at a frequency of around 40. Obviously, almost unbiased errors of SM05cm could be found for the two runs with calibrated parameters, while CTR and GLDAS both had negative deviations, and ERA5 was positively biased. Moreover, the error with SCEO at a frequency of almost 80 around the mean (around zero) was twice that with the others, which possibly indicated overfitting of the surface soil moisture.
The observed ST05cm showed significant diurnal variation, which mostly ranged from 281 to 295 K (Figure 11c). In CTR, ST05cm had both the lowest upper and lower limits among all datasets (i.e., around 293 K and 275 K); thus, it was negatively biased. For ERA5, ST05cm was shown to vary from 279 to 293 K, while it was shown to vary from 280 to 289 K for GLDAS. Nevertheless, PSOO varied from 285 to 294 K, and SCEO varied from 283 to 295 K. Moreover, except PSOO and SCEO, all of the other ST05cm candidates exhibited more-or-less opposite variations compared with OBS. And CTR, ERA5, and GLDAS underestimated the minimum daily soil temperature.
The error fits for ST05cm for CTR showed a broad distribution centered around −7 K with a frequency of around 15. For PSOO and SCEO, the relatively narrow error distributions had centers located around 0 K with a frequency of around 18, and around −3 K with a frequency of around 20, respectively. However, for both ERA5 and GLDAS, broad bimodal distributions were observed, i.e., the centers were located around −6 K and 5 K, respectively, for ERA5, and the centers were located around −3 K and 4 K, respectively, for GLDAS. The ST05cm of ERA5 and GLDAS datasets during this study had multiple bias factors. Meanwhile, the error distributions showed negatively biased ST05cm for CTR and SCEO, and notably, almost unbiased ST05cm for PSOO.
Due to the observed non-site fluxes and null ERA5 fluxes in our study area, comparisons of diurnally varied surface sensible heat and latent flux during the validation period among CTR, PSOO, SCEO, and GLDAS were further conducted (Figure 12). For surface sensible heat flux, CTR varied from −200 to 430 W.m2, GLDAS varied from −50 to 280 W.m2, SCEO varied from −50 to 350 W.m2, and PSOO varied from −50 to 400 W.m2 (Figure 12a). However, for surface latent heat flux, CTR varied from 0 to 550 W.m2, GLDAS varied from 0 to 450 W.m2, SCEO varied from 0 to 300 W.m2, and PSOO varied from 0 to 200 W.m2 (Figure 12b). CTR likely produced the sharpest diurnal variations in surface fluxes, and it was more consistent with GLDAS when compared to the simulations of the calibrated models. Moreover, the two calibrated models led to more sensible heat fluxes but fewer latent heat fluxes in the temporal mean statistics when compared to the other two, and the diurnal flux variations of the two calibrated models were smoother.
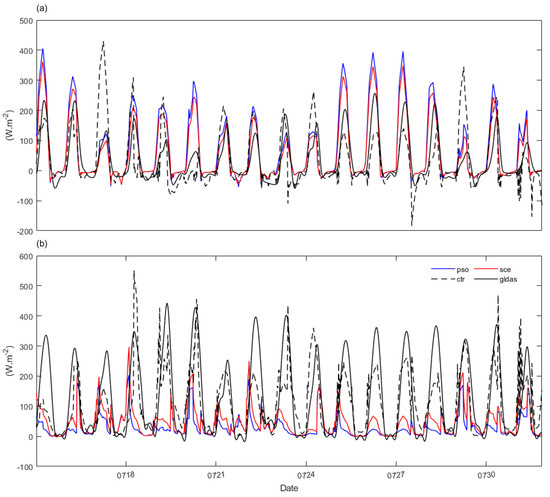
Figure 12.
Comparison among simulations (PSOO, SCEO, and CTR are shown as blue, red, and dashed lines, respectively), and GLDAS (black) against time. (a) Surface sensible heat flux and (b) latent heat flux averaged over our study area.
The consistent diurnal variations in fluxes between CTR and GLDAS are likely due to the forcing datasets, whose values (i.e., air temperature, winds, and humidity) were the same as GLDAS [21]. The difference between CTR and the calibrated models can mostly be attributed to the advantages of the calibration schemes. Moreover, recall the fact that the significantly negatively biased SM05cm and ST05cm in CTR and GLDAS (Figure 11) when compared to OBS, and their more significant latent fluxes but weaker sensible fluxes compared to the simulations of the calibrated models, could be biased because of the limitations of the evapotranspiration of grassland (i.e., weaker latent fluxes but stronger sensible fluxes were usually observed over drier soils).
In general, the biased ST in model simulations and reanalysis in regional studies need to be addressed, and the improvements in the consistency of soil temperature errors obtained in the simulations in the present study indicate the advantages of multi-objective optimization for calibration. In particular, PSO was preferable because it could obtain unbiased SM and ST simulation errors, while the ST simulation errors for SCE were biased around −3 K. These continuous improvements and effectiveness differences during validation indicated the robust calibration of both PSO and SCE and the preferable significance of PSO in promoting ST forecasting in frequent land parameter update systems.
6. Discussion
Though the multi-objective PSO and SCE optimizers greatly improved the significantly biased Noah LSM forecast over the semiarid region when considering that the land parameters were both unobserved and physically biased over a highly heterogeneous surface, there were still limitations to this study because of the imperfect observations (i.e., the simultaneous soil and meteorological observation data of high-density stations were unavailable) [21,57,61] and the unsolved highly dimensional non-linearity (i.e., the occasional outliers of both the optimal parameter space (i.e., the “Initial” parameter type) and the optimal objective (i.e., the final negative KGE values of site C4) against sites, which could be likely attributed to surrounding human activities (such as nearby road hardening) and/or the possibly unfixed soil classification parameter (i.e., soil type) in the LSM’s configuration (such as one soil type against different percentages and soil textures; see Table 1).
For land parameter complexity recognition in medium-range SM—ST calibration over ASALs through default LSM configuring, compared to the default or globally applicable parameters that are induced from limited benchmark optimizations [4,5,65], the optimized parameters of each site in this study gained considerable improvements in the objective-informed forecasts (see Section 5.3), and indicated that the sowed calibration objective always reaps better (or more favorable) parameters for multi-site or distributed LSMs, highlighting the benefits of necessary LSM configuration updates (i.e., dynamically updated LSMs lookup table). And this could be in line with the suggestion that PSO could be a better solver, as many previous medium-range scale studies have suggested [39,40,41,42,43]. Nevertheless, the greatly desired regional soil temperature improvement, which could account for the land parameter uncertainties during this work, could be affected by bimodal scales, which can be attributed to the scale-distinguished physics that dictate that water has a larger heat capacity than soil [12].
The great heterogeneity and uncertainty of the optimal parameters against the sites for both PSO and SCE, (see Section 5.2.1) showed large spatial complexities for globally applicable LSMs parameters over ASALs and highlight the necessity for future extensive work efforts in model physics and observations. In particular, the optimal CZIL in “General” was more sensitive to the site compared to LAIMAX and LAIMIN in “Vegetation” (Figure 6), and the high spatial heterogeneity of CZIL could support possible larger-scale ST improvement by promoting the thermal physics related to CZIL, as previous studies have suggested [8,54,56,66,67]. Meanwhile, the combination of the land’s physical configuration with a few parameters could reduce the complexity dimensions of the global LSM’s parameter–simulation problem itself [7,68], and SCE that achieves fewer spatial parameter uncertainties could be more favorable to meet the global land parameter solution demand.
For real-world applications, the enhanced KGE evaluator showed robust generality in maintaining the optimizers’ efficiency and effectiveness for most sites, and the use of this multi-dimensional combined evaluator could be suggested for further regional LSM multi-objective calibration studies for solving high dimensional non-linearity problems; the robust performance of PSO with the mostly unbiased soil simulation errors indicated its advantageous ability to solve medium-scale ranged multi-objective LSM forecasts, especially when considering that the LSM parameter uncertainties were both spatially and temporally distinguished, accompanied by the great spatial accuracy demand in local forecasts [18,49,50].
Note that the validation results were highly consistent with the soil moisture reanalysis at 3 h and 0.25° scales for GLDAS and 1 h and 0.1° scales for ERA5, but opposite variations in the soil temperature were observed between the reanalysis results and observations (Figure 11); also, the sensible heat fluxes were highly consistent but the latent heat fluxes were underestimated using the calibration methods compared with GLDAS (Figure 12). As the differences in the latent heat fluxes over dry surfaces should be measured by using more reliable flux observations [4], these datasets’ inconsistencies can be mostly attributed to the ST modeling deficits [21,57,58,59,60,61].
Overall, due to the LSM’s high complexity, continuous efforts in both ST modeling physics and configuration should be equally emphasized to meet the demand for surface accuracy, and the calibration schemes introduced in this study could provide a clue to addressing the unsolved complexity between parameters and ST forecasts. Nevertheless, due to the quite different searching strategies (i.e., the survival and searching space) for quite different applications, SCE and PSO were preferable for the LSM’s optimal parameter and simulation determinations, respectively. In particular, with the gradual improvement in high-spatiotemporal-density-land remote sensing observation network [69,70], comprehensive comparisons of different multi-objective evaluators in improving regional semiarid surface forecasts, as well as calibrations with relatively low resource consumption based on machine learning [71,72,73,74], should be carried out in the future to enhance the knowledge of the LSM’s unaccountable biases caused by highly dimensional surface heterogeneity.
7. Conclusions
Surface conditions are important for regional weather and hydrology. In the present study, by using ITPCAS point-scale datasets from 1 April to 31 July 2014, an enhanced multi-objective KGE and Noah LSM multi-parameter tables were introduced into a GSA as the optimal criteria for PSO and SCE, and the improvements in regional surface simulations were compared and further validated. The results showed the following:
Under the typical semiarid climate background, the Noah LSM simulations had a positive fit (0.21), with small spatial differences, and a positively biased error distribution compared with the soil moisture observations. In addition, significantly biased soil temperature simulations were obtained, with a negative fit (−0.46), high spatial differences, and both positive and negative bimodal differences in errors. The results demonstrated the poor performance of the LSM at simulating multiple sites in our study area, possibly due to imperfect land physics and/or many land parameters.
Two calibrations obtained significant improvements in the soil simulations for different layers and variables, and they indicated the advantage of the GSA with multi-objective KGE and multi-site parameter tables. In general, PSO converged better to the objective compared with SCE, but with relatively larger parameter uncertainties and less parameter heterogeneity. In particular, PSO performed better than SCE at calibration for soil temperature simulations. In addition, the significant heterogeneity and uncertainties against the sites in the optimal parameter space for both PSO and SCE (Figure 6 and Figure 7) indicated that frequent calibration of the LSM is required for regional applications.
The simulations initialized with the optimal parameters in the validation period behaved similarly to those in the calibration period, i.e., a linear fit increase and a spatial error reduction (Figure 10 and Figure 11), thereby demonstrating that the calibration methods could obtain sustainable improvements in the simulation, which could be helpful for regional forecasting. Moreover, PSO could obtain unbiased SM and ST simulation errors, while the ST simulation errors for SCE were biased around −3 K.
Overall, the GSA with the multi-objective KGE and multi-site parameter tables significantly improved the soil moisture and temperature simulations, but PSO was preferable when considering soil temperature. This robust calibration scheme could be helpful for research related to the land surface on the Tibet Plateau, as well as allowing producers of datasets and researchers to recognize the spatial complexities in regional surface applications.
Author Contributions
Conceptualization, methodology, validation, and formal analysis, Y.G. (Yakai Guo); investigation, resources, and data curation, Y.G. (Yakai Guo), C.S., and Y.G. (Yong Gao); writing—original draft preparation, Y.G. (Yakai Guo) and C.S.; writing—review and editing, Y.G. (Yakai Guo), C.S., and Y.G. (Yong Gao); visualization, C.S.; supervision, B.Y. and A.S.; project administration, A.S. and B.Y.; funding acquisition, B.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Henan Provincial Natural Science Foundation Project (grant numbers: 242300421367, 222300420468), the Science and Technology Project on Innovation Ecosystem Construction at Zhengzhou Supercomputing Center in Henan province (grant number: 201400210800), and the Application Technology Research Fund Project at CMA Henan Provincial Key Laboratory of Agricultural Meteorological Research Institute (grant number: KQ202204).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to privacy concerns and ongoing research using the dataset.
Acknowledgments
We would like to express our gratitude to the Henan Meteorological Bureau and the China Meteorological Administration Meteorological Observation Centre for their support in carrying out this study. We would like to thank the anonymous reviewers for their valuable feedback, which greatly improved the quality of this article. And we would like to give our many thanks to those who made efforts to advance this work, and the fellow travelers encountered along the way.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Edmondson, J.; Stott, I.; Davies, Z.; Gaston, K.J.; Leake, J.R. Soil surface temperatures reveal moderation of the urban heat island effect by trees and shrubs. Sci. Rep. 2016, 6, 33708. [Google Scholar] [CrossRef] [PubMed]
- Li, K.; Zhang, J.; Wu, L.; Yang, K.; Li, S. The role of soil temperature feedbacks for summer air temperature variability under climate change over East Asia. Earth’s Future 2022, 10, e2021EF002377. [Google Scholar] [CrossRef]
- García-García, A.; Cuesta-Valero, F.J.; Miralles, D.G.; Mahecha, M.D.; Quaas, J.; Reichstein, M.; Zscheischler, J.; Peng, J. Soil heat extremes can outpace air temperature extremes. Nat. Clim. Chang. 2023, 13, 1237–1241. [Google Scholar] [CrossRef]
- Hogue, T.; Bastidas, L.; Gupta, H.; Sorooshian, S.; Mitchell, K.; Emmerich, W. Evaluation and transferability of the Noah Land Surface Model in semiarid environments. J. Hydrometeor. 2005, 6, 68. [Google Scholar] [CrossRef]
- Rosero, E.; Yang, Z.; Gulden, L.; Niu, G.; Gochis, D.J. Evaluating enhanced hydrological representations in Noah LSM over transition zones, implications for model development. J. Hydrometeor. 2009, 10, 600–622. [Google Scholar] [CrossRef]
- Liu, Y.; Guo, W.; Song, Y. Estimation of key surface parameters in semi-arid region and their impacts on improvement of surface fluxes simulation. Sci. China Earth Sci. 2015, 45, 1524–1536. (In Chinese) [Google Scholar] [CrossRef]
- Li, J.; Chen, F.; Zhang, G.; Barlage, M.; Gan, Y.; Xin, Y.; Wang, C. Impacts of land cover and soil texture uncertainty on land model simulations over the Central Tibetan Plateau. J. Adv. Model Earth Sys. 2018, 10, 2121–2146. [Google Scholar] [CrossRef]
- Chen, Y.; Yang, K.; He, J.; Qin, J.; Shi, J.; Du, J.; He, Q. Improving land surface temperature modeling for dry land of China. J. Geophys. Res. Atmos. 2011, 116, D20104. [Google Scholar] [CrossRef]
- He, Q.; Lu, H.; Yang, K.; Zhao, L.; Zou, M. Improving Land Surface Temperature Simulation of NOAH-MP on the Tibetan Plateau. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 11–16 July 2021; pp. 6217–6220. [Google Scholar]
- Xia, Y.; Yang, Z.L.; Charles, J.; Stoffa, P.L.; Sen, M.K. Impacts of data length on optimal parameter and uncertainty estimation of a land surface model. J. Geophys. Res. Atmos. 2004, 109, D07101. [Google Scholar] [CrossRef]
- Xia, Y.; Yang, Z.; Stoffa, P.L.; Sen, M.K. Optimal parameter and uncertainty estimation of a land surface model, Sensitivity to parameter ranges and model complexities. Adv. Atmos. Sci. 2005, 22, 142–157. [Google Scholar] [CrossRef]
- Chen, F.; Dudhia, J. Coupling an advanced land-surface/hydrology model with the Penn State/NCAR MM5 modeling system. Part I, Model implementation and sensitivity, Mon. Weather. Rev. 2001, 129, 569–585. [Google Scholar]
- Trigo, I.F.; Boussetta, S.; Viterbo, P.; Balsamo, G.; Beljaars, A.; Sandu, I. Comparison of model land skin temperature with remotely sensed estimates and assessment of surface-atmosphere coupling. J. Geophys. Res. Atmos. 2016, 120, D023812. [Google Scholar] [CrossRef]
- Santanello, J.A.; Kumar, S.; Peters-Lidard, C.D.; Harrison, K.; Zhou, S. Impact of land model calibration on coupled land-atmosphere prediction. J. Hydrometeor. 2013, 14, 1373–1400. [Google Scholar] [CrossRef][Green Version]
- Li, D.; Zhang, S.; Wen, X.; He, H. Soil Moisture Parameterization and Its Influences in Weather and Climate Simulation: A Review. Adv. Earth Sci. 2016, 31, 236–247. (In Chinese) [Google Scholar]
- Santanello, J.A.; Lawston, P.; Kumar, S.; Dennis, E. Understanding the impacts of soil moisture initial conditions on NWP in the context of land–atmosphere coupling. J. Hydrometeor. 2019, 20, 793–819. [Google Scholar] [CrossRef]
- Gevaert, A.I.; Miralles, D.G.; de Jeu, R.A.M.; Schellekens, J.; Dolman, A.J. Soil moisture-temperature coupling in a set of land surface models. J. Geophys. Res. Atmos. 2018, 123, 1481–1498. [Google Scholar] [CrossRef]
- Kumar, S.; Kolassa, J.; Reichle, R.; Crow, W.; Lannoy, G.; Rosnay, P.; MacBean, N.; Girotto, M.; Fox, A.; Quaife, T.; et al. An agenda for land data assimilation priorities, Realizing the promise of terrestrial water, energy, and vegetation observations from space. J. Adv. Model Earth Sys. 2022, 14, c2022MS003259. [Google Scholar] [CrossRef]
- Kumar, S.; Peters-Lidard, C.; Eastman, J.; Tao, W. An integrated high-resolution hydrometeorological modeling testbedusing LIS and WRF. Environ. Model. Soft. 2008, 23, 169–181. [Google Scholar] [CrossRef][Green Version]
- Kumar, S.; Reichle, R.; Peters-Lidard, C.; Koster, R.; Zhan, X.; Crow, W.; Eylander, J.; Houser, P. A land surface data assimilation framework using the land information system: Description and applications. Adv. Water Res. 2008, 31, 1419–1432. [Google Scholar] [CrossRef]
- Yang, K.; Qin, J.; Zhao, L.; Chen, Y.; Tang, W.; Han, M.; Lazhu; Chen, Z.; Lv, N.; Ding, B.; et al. A multi-scale soil moisture and freeze-thaw monitoring network on the third pole. Bull. Amer. Meteor. Soc. 2013, 94, 1907–1916. [Google Scholar] [CrossRef]
- Thorstensen, A.; Nguyen, P.; Hsu, K.; Sorooshian, S. Using densely distributed soil moisture observations for calibration of a hydrologic model. J. Hydrometeor. 2016, 17, 571–590. [Google Scholar] [CrossRef]
- Rajib, M.A.; Merwade, V.; Yu, Z. Multi-objective calibration of a hydrologic model using spatially distributed remotely sensed/in-situ soil moisture. J. Hydro. 2016, 536, 192–207. [Google Scholar] [CrossRef]
- Naeini, M.R.; Analui, B.; Gupta, H.V.; Duan, Q.; Sorooshian, S. Three decades of the shuffled complex evolution (sce-ua) optimization algorithm, review and applications. Sci. Iran. 2019, 26, 2015–2031. [Google Scholar]
- Jahandideh-Tehrani, M.; Bozorg-Haddad, O.; Loáiciga, H.A. Application of particle swarm optimization to water management: An introduction and overview. Environ. Monit. Assess. 2020, 192, 28. [Google Scholar] [CrossRef] [PubMed]
- Duan, Q.; Gupta, V.; Sorooshian, S. Shuffled complex evolution approach for effective and efficient global minimization. J. Optimiz. Theroy App. 1993, 76, 501–521. [Google Scholar] [CrossRef]
- Yapo, P.O.; Gupta, H.V.; Sorooshian, S. Multi-objective global optimization for hydrologic models. J. Hydro. 1998, 204, 83–97. [Google Scholar] [CrossRef]
- Crow, W.; Wood, E.; Pan, M. Multiobjective calibration of land surface model evapotranspiration predictions using streamflow observations and spaceborne surface radiometric temperature retrievals. J. Geophys. Res. Atmos. 2003, 108, 4725. [Google Scholar] [CrossRef]
- Xia, Y.; Pitman, A.; Gupta, H.; Leplastrier, M.; Henderson-Sellers, A.; Bastidas, L. Calibrating a land surface model of varying complexity using multicriteria methods and the Cabauw Dataset. J. Hydrometeor. 2009, 3, 181–194. [Google Scholar] [CrossRef]
- Gupta, H.V.; Sorooshian, S.S.; Yapo, P.O. Toward improved calibration of hydrologic models, Multiple and noncom-mensurable measures of information. Water Resour. Res. 1998, 34, 751–763. [Google Scholar] [CrossRef]
- Eberhart, R.; Kennedy, J. A new optimizer using particle swarm theory. In Proceedings of the Sixth International Symposium on Micro Machine and Human Science, Nagoya, Japan, 4–6 October 1995; pp. 39–43. [Google Scholar]
- Kennedy, J.; Eberhart, R.C. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Shi, Y.; Eberhart, R.C. A modified particle swarm optimizer. In Proceedings of the 1998 IEEE International Conference on Evolutionary Computation Proceedings. IEEE World Congress on Computational Intelligence (Cat. No.98TH8360), Anchorage, AK, USA, 4-9 May 1998; pp. 69–73. [Google Scholar]
- Eberhart, R.C.; Shi, Y. Comparing inertia weights and constriction factors in particle swarm optimization. Proc. IEEE 2000, 1, 84–88. [Google Scholar]
- Hinchey, M.G.; Sterritt, R.; Rouff, C. Swarms and Swarm Intelligence. Computer 2007, 40, 111–113. [Google Scholar] [CrossRef]
- Wang, D.; Tan, D.; Liu, L. Particle swarm optimization algorithm, an overview. Soft. Comput. 2017, 22, 387–408. [Google Scholar] [CrossRef]
- Guo, Y.; Wang, G.; Shen, F.; Min, J. Comparison of two correction schemes on soil moisture assimilation based on the ensemble square root filter. Jiangsu Agric. Sci. 2018, 46, 210–218. (In Chinese) [Google Scholar]
- Cheonga, K.H.; Jonesa, M.C. Swarm intelligence begins now or never. Proc. Natl. Acad. Sci. USA 2021, 118, e2113678118. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Srinivasan, R.; Zhao, K.; Liew, M.V. Evaluation of global optimization algorithms for parameter calibration of a computationally intensive hydrologic model. Hydro. Proc. 2009, 23, 430–441. [Google Scholar] [CrossRef]
- Ketabchi, H.; Ataie-Ashtiani, B. Evolutionary algorithms for the optimal management of coastal groundwater, A comparative study toward future challenges. J. Hydro. 2015, 520, 193–213. [Google Scholar] [CrossRef]
- Guo, Y. Study on Soil Moisture Sensitivity and Assimilation Based on Noah Land Surface Model. Ph.D. Dissertation, NUIST, Nanjing, China, 2017; pp. 1–128. (In Chinese). [Google Scholar]
- Adeyeri, O.E.; Laux, P.; Arnault, J.; Lawin, A.E.; Kunstmann, H. Conceptual hydrological model calibration using multi-objective optimization techniques over the transboundary Komadugu-Yobe basin, Lake Chad Area, West Africa. J. Hydro. Reg. Stud. 2020, 27, 100655. [Google Scholar] [CrossRef]
- Masoumi, F.; Masoumzadeh, S.; Zafari, N.; Emami-Skardi, M.J. Optimal operation of single and multi-reservoir systems via hybrid shuffled grey wolf optimization algorithm (SGWO). Water Supply 2022, 22, 1663–1675. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria, Implications for improving hydrological modelling. J. Hydro. 2009, 377, 80–91. [Google Scholar] [CrossRef]
- Yu, Y.; Chen, X.; Huttner, P.; Hinnenthal, M.; Brieden, A.; Sun, L.X.; Disse, M. Model based decision support system for land use changes and socio-economic assessments. J. Arid Land 2018, 10, 169–182. [Google Scholar] [CrossRef]
- Yu, Y.; Pi, Y.; Yu, X.; Ta, Z.; Sun, L.; Disse, M.; Zeng, F.; Li, Y.; Chen, X.; Yu, R. Climate change, water resources and sustainable development in the arid and semi-arid lands of Central Asia in the past 30 years. J. Arid Land 2018, 11, 1–14. [Google Scholar] [CrossRef]
- Yu, Y.; Chen, X.; Disse, M.; Cyffka, B.; Lei, J.Q.; Zhang, H.Y.; Brieden, A.; Welp, M.; Abuduwaili, J.; Li, Y.M.; et al. Climate change in Central Asia: Sino-German cooperative research findings. Sci. Bull. 2020, 65, 689–692. [Google Scholar] [CrossRef] [PubMed]
- Yu, Y.; Chen, X.; Malik, I.; Wistuba, M.; Cao, Y.G.; Hou, D.D.; Ta, Z.J.; He, J.; Zhang, L.Y.; Yu, R.D.; et al. Spatiotemporal changes in water, land use, and ecosystem services in Central Asia considering climate changes and human activities. J. Arid Land 2021, 13, 881–890. [Google Scholar] [CrossRef]
- Li, X.; Liu, F.; Ma, C.; Hou, J.; Zheng, D.; Ma, H.; Bai, Y.; Han, X.; Vereecken, H.; Yang, K.; et al. Land Data Assimilation: Harmonizing Theory and Data in Land Surface Process Studies. Rev. Geophys. 2024, 62, e2022RG000801. [Google Scholar] [CrossRef]
- Stephens, G.; Polcher, J.; Zeng, X.B.; van Oevelen, P.; Poveda, G.; Bosilovich, M.; Ahn, M.H.; Balsamo, G.; Duan, Q.Y.; Hegerl, G.; et al. The First 30 Years of GEWEX. Bull. Amer. Meteor. Soc. 2023, 104, E126–E157. [Google Scholar] [CrossRef]
- Gudmundsson, L.; Cuntz, M. Soil Parameter Model Intercomparison Project (SP-MIP): Assessing theinfluence of soil parameters on the variability of Land Surface Models; GEWEX–SoilWat workshop, Leipzig, German, 28–30 June, 2016; pp. 1–6. Available online: https://www.gewexevents.org/wp-content/uploads/GLASS2017_SP-MIP_Protocol.pdf (accessed on 30 April 2024).
- Zeng, Y.; Anne, V.; Or, D.; Cuntz, M.; Gudmundsson, L.; Weihermueller, L.; Kollet, S.; Vanderborght, J.; Vereecken, H. GEWEX-ISMC SoilWat Project: Taking Stock and Looking Ahead; GEWEX GLASS Meeting, USA, 23–25 November, 2020; GEWEX QUARTERLY II 2021, 31(2); pp. 4–9. Available online: https://gewex.org/gewex-content/files_mf/1633983474Q22021.pdf (accessed on 30 April 2024).
- Fang, X.W.; Lyu, S.H.; Cheng, C.; Li, Z.G.; Zhang, S.B. Numerical modelling of the responses of soil temperature and soil moisture to climate change over the Tibetan Plateau, 1961-2010. Int. J. Climatol. 2021, 41, 4134–4150. [Google Scholar] [CrossRef]
- Zhao, X.; Liu, C.; Tong, B.; Li, Y.; Wang, L.; Ma, Y.; Gao, Z. Study on Surface Process Parameters and Soil Thermal Parameters at Shiquanhe in the Western Qinghai-Xizang Plateau. Plateau Meteorol. 2021, 40, 711–723. (In Chinese) [Google Scholar]
- Sun, S.; Chen, B.; Che, T.; Zhang, H.; Chen, J.; Che, M.; Lin, X.; Guo, L. Simulating the Qinghai—Tibetan Plateau seasonal frozen soil moisture and improving models parameters—A case study in the upper reaches of Heihe River. Plateau Meteorol. 2017, 36, 643–656. (In Chinese) [Google Scholar]
- Ma, Y.M.; Yao, T.D.; Zhong, L.; Wang, B.B.; Xu, X.D.; Hu, Z.Y.; Ma, W.Q.; Sun, F.L.; Han, C.B.; Li, M.S.; et al. Comprehensive study of energy and water exchange over the Tibetan Plateau: A review and perspective: From GAME/Tibet and CAMP/Tibet to TORP, TPEORP, and TPEITORP. Earth-Sci. Rev. 2023, 237, 104312. [Google Scholar] [CrossRef]
- Bob, S.; Yang, K. Time-Lapse Observation Dataset of Soil Temperature and Humidity on the Tibetan Plateau (2008–2016). TPDC. 2019. Available online: https://data.tpdc.ac.cn/en/data/ef949bb0-26d4-4cb6-acc2-3385413b91ee/ (accessed on 30 April 2024).
- Rodell, M.; Houser, P.R.; Jambor, U.; Gottschalck, J.; Mitchell, K.; Meng, C.; Arsenault, K.; Cosgrove, B.; Radakovich, J.; Bosilovich, M.; et al. The Global Land Data Assimilation System. Bull. Amer. Meteor. Soc. 2004, 85, 381–394. [Google Scholar] [CrossRef]
- Muñoz, S.J. ERA5-Land Hourly Data from 1950 to Present. Copernicus Climate Change Service (C3S) Climate Data Store (CDS). 2021. Available online: https://cds.climate.copernicus.eu/cdsapp#!/dataset/10.24381/cds.e2161bac?tab=overview (accessed on 30 April 2024).
- Yang, K.; He, J.; Tang, W.; Qin, J.; Cheng, C. On downward shortwave and longwave radiations over high altitude regions, Observation and modeling in the Tibetan Plateau. Agric. Forest. Meteorol. 2010, 150, 38–46. [Google Scholar] [CrossRef]
- Yang, K.; He, J.; Tang, W.; Lu, H.; Qin, J.; Chen, Y.; Li, X. China Meteorological Forcing Dataset (1979–2018). TPDC. 2019. Available online: https://data.tpdc.ac.cn/en/data/8028b944-daaa-4511-8769-965612652c49 (accessed on 30 April 2024).
- Yang, K.; Koike, T.; Ye, B.S.; Bastidas, L. Inverse analysis of the role of soil vertical heterogeneity in controlling surface soil state and energy partition. J. Geophys. Res. Atmos. 2005, 110, D08101. [Google Scholar]
- Taylor, K.E. Summarizing multiple aspects of model performance in a single diagram. J. Geophys. Res. Atmos. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]
- Zhang, Q.; Cao, X.; Wei, G.; Huang, R. Observation and study of land surface parameters over Gobi in typical arid region. Adv. Atmos. Sci. 2002, 19, 121–135. [Google Scholar]
- Hogue, T.S.; Bastidas, L.A.; Gupta, H.V.; Sorooshian, S. Evaluating model performance and parameter behavior for varying levels of land surface model complexity. Water Resour. Res. 2006, 42, W08430. [Google Scholar] [CrossRef]
- Yang, K.; Chen, Y.Y.; Qin, J. Some practical notes on the land surface modeling in the Tibetan Plateau. Hydrol. Earth Sys. Sci. 2009, 13, 687–701. [Google Scholar] [CrossRef]
- Chen, Y.Y.; Yang, K.; Zhou, D.G.; Qin, J.; Guo, X.F. Improving the Noah Land Surface Model in Arid Regions with an Appropriate Parameterization of the Thermal Roughness Length. J. Hydrometeor. 2010, 11, 995–1006. [Google Scholar] [CrossRef]
- Zhang, G.; Chen, F.; Gan, Y.J. Assessing uncertainties in the Noah-MP ensemble simulations of a cropland site during the Tibet Joint International Cooperation program field campaign. J. Geophys. Res. Atmos. 2016, 121, 9576–9596. [Google Scholar] [CrossRef]
- Li, C.; Lu, H.; Yang, K.; Han, M.; Wright, J.S.; Chen, Y.; Yu, L.; Xu, S.; Huang, X.; Gong, W. The Evaluation of SMAP Enhanced Soil Moisture Products Using High-Resolution Model Simulations and In-Situ Observations on the Tibetan Plateau. Remote Sens. 2018, 10, 535. [Google Scholar] [CrossRef]
- Li, M.; Wu, P.; Ma, Z. A comprehensive evaluation of soil moisture and soil temperature from third-generation atmospheric and land reanalysis data sets. Int. J. Climatol. 2020, 40, 5744–5766. [Google Scholar] [CrossRef]
- Chaney, N.W.; Herman, J.D.; Ek, M.B.; Wood, E.F. Deriving global parameter estimates for the Noah land surface model using FLUXNET and machine learning. J. Geophys. Res. Atmos. 2016, 121, 13218–13235. [Google Scholar] [CrossRef]
- Bastrikov, V.; MacBean, N.; Bacour, C.; Santaren, D.; Kuppel, S.; Peylin, P. Land surface model parameter optimisation using in situ flux data: Comparison of gradient-based versus random search algorithms (a case study using ORCHIDEE v1.9.5.2). Geosci. Model Dev. 2018, 11, 4739–4754. [Google Scholar] [CrossRef]
- Sawada, Y. Machine Learning Accelerates Parameter Optimization and Uncertainty Assessment of a Land Surface Model. J. Geophys. Res. Atmos. 2020, 125, e2020JD032688. [Google Scholar] [CrossRef]
- Yu, Y.; Cao, Y.G.; Hou, D.D.; Disse, M.; Brieden, A.; Zhang, H.Y.; Yu, R.D. The study of artificial intelligence for predicting land use changes in an arid ecosystem. J. Geogr. Sci. 2022, 32, 717–734. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).