Meteor Radar for Investigation of the MLT Region: A Review
Abstract
1. Introduction
1.1. Meteor Source Regions
1.2. Radar Detection of Meteors
1.3. Brief History of Meteor Observations
1.3.1. Optical Observations
1.3.2. Radio Observations
1.4. Meteor Wind Radars
1.4.1. CW Doppler Radars
1.4.2. Pulsed Doppler Radars
1.4.3. Narrow-Beam ST and MST Radars
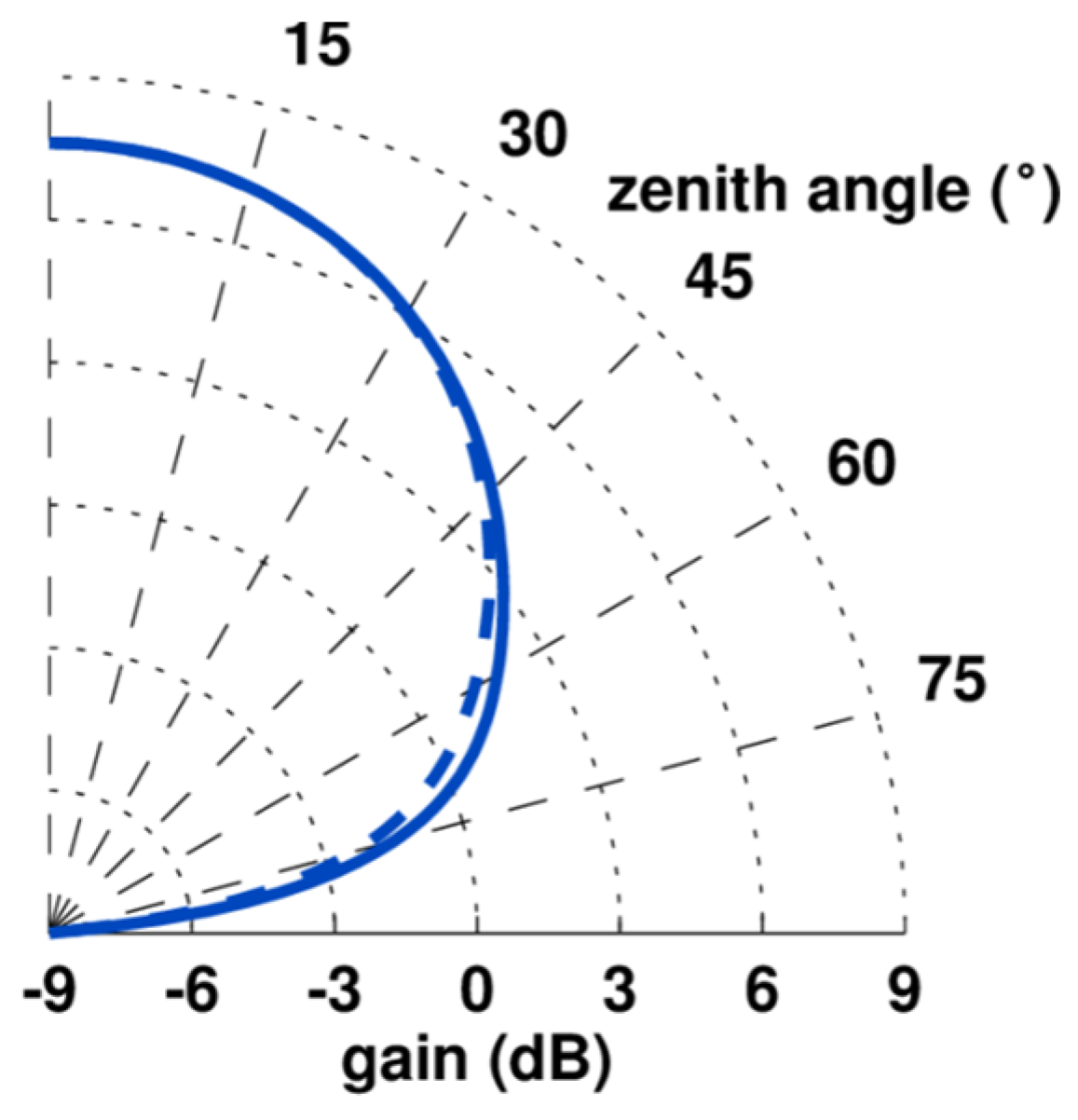
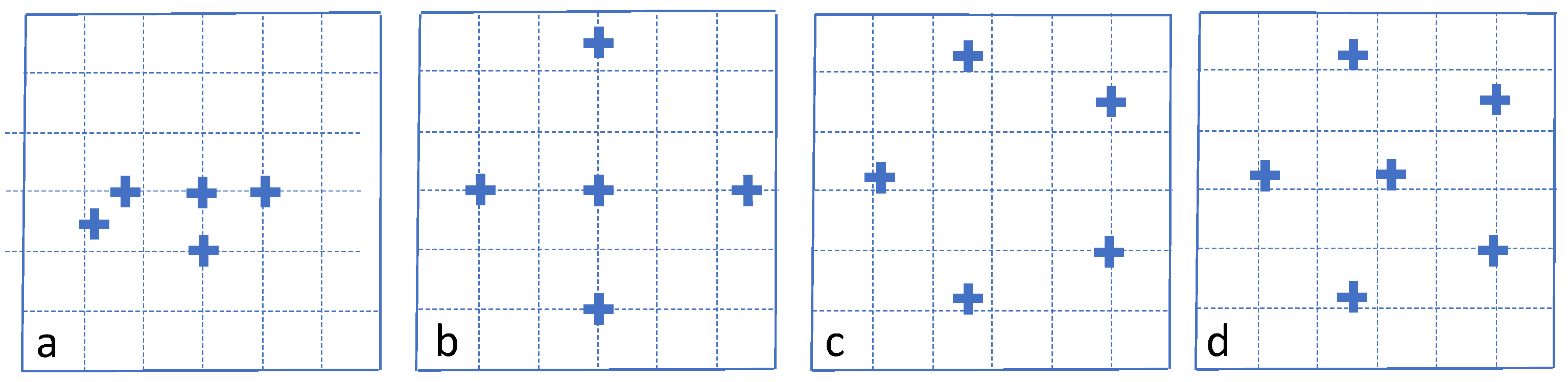
2. ‘All-Sky’ Meteor Wind Radars
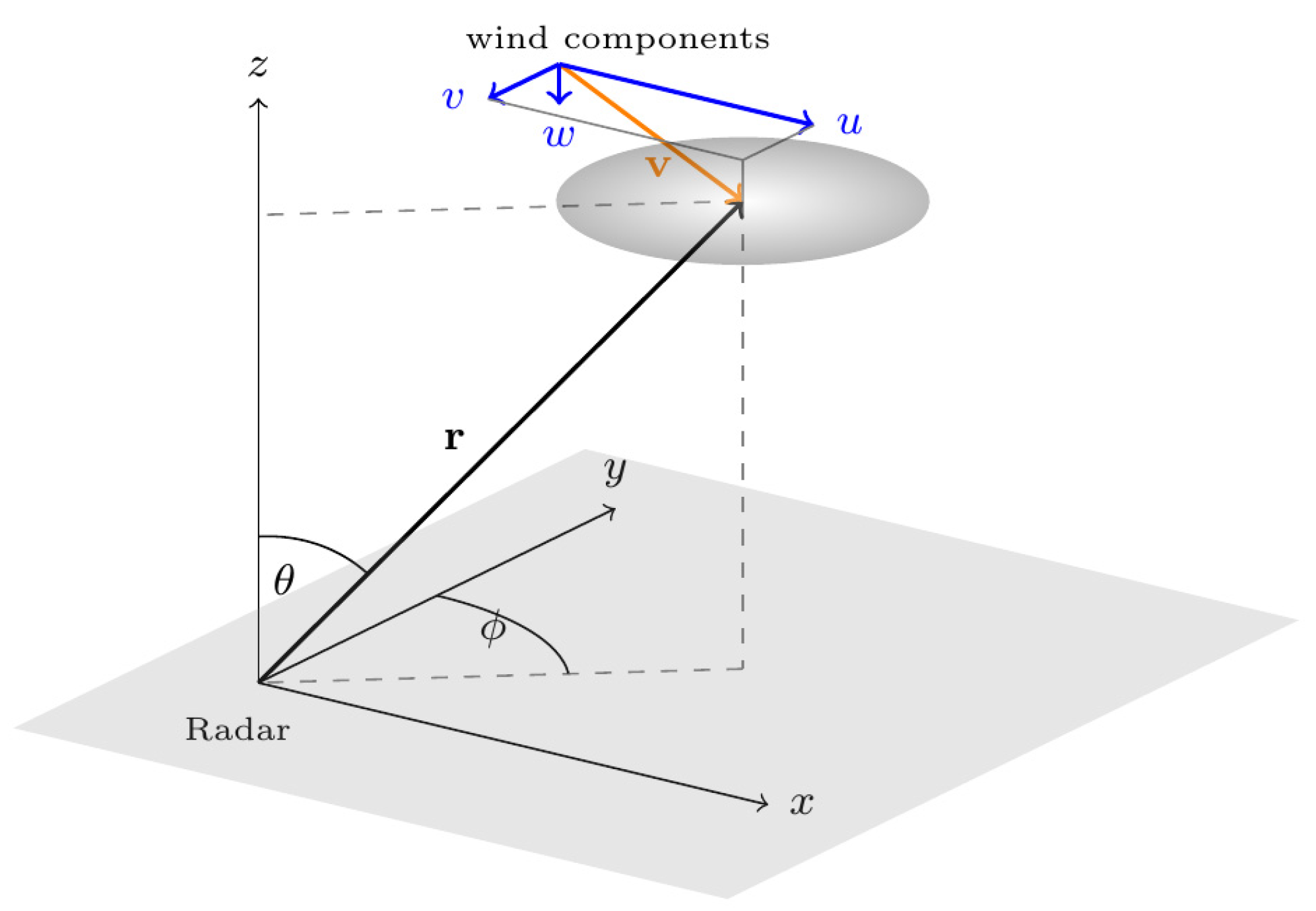
3. Measuring Wind Velocities
3.1. Mean Wind Components
3.2. Gravity Wave and Turbulence Parameters
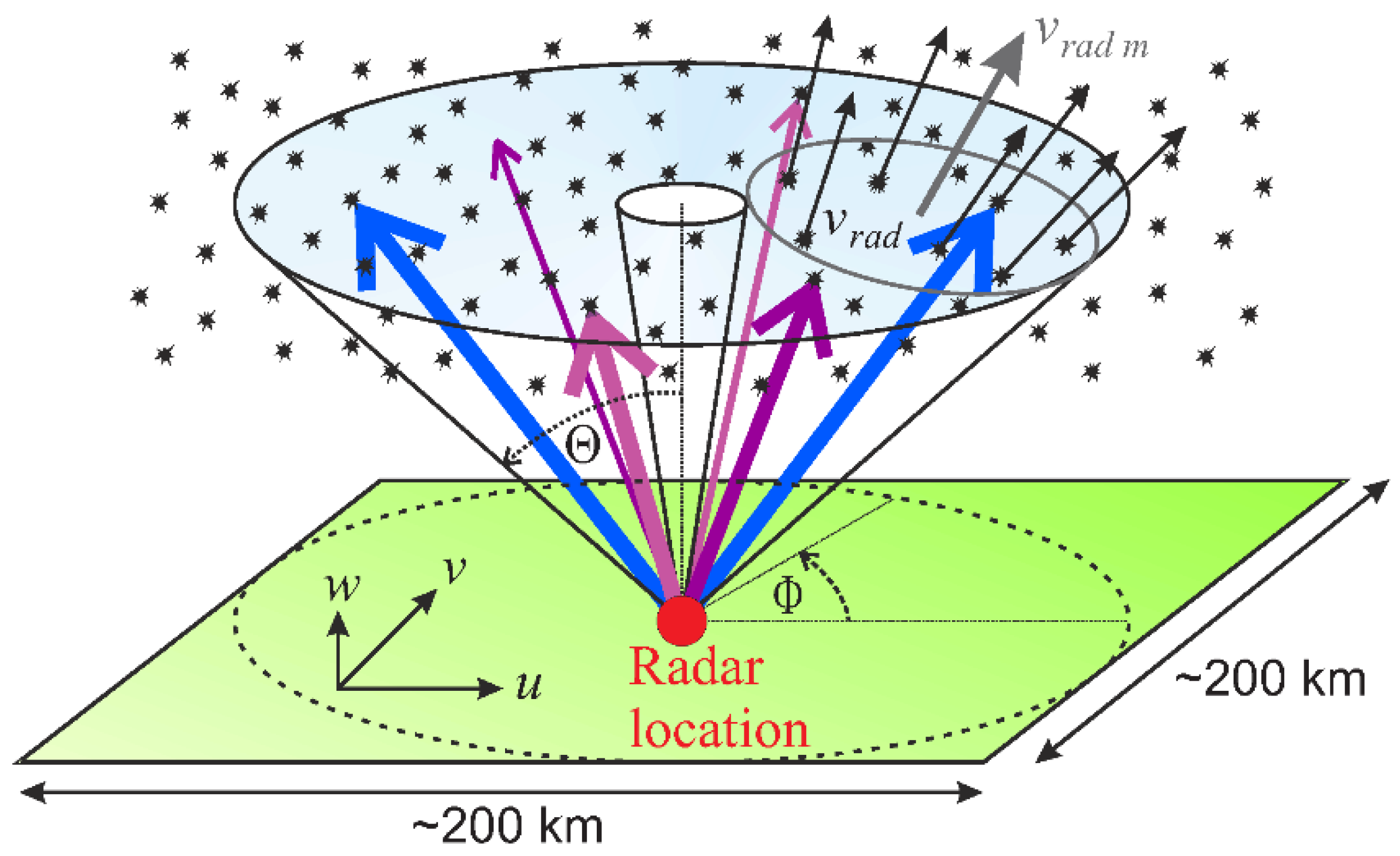
4. Multistatic Meteor Radar and Radar Networks
4.1. Mean Wind Components: Winds Bistatic Case
4.2. Radar Networks
5. Measuring Density and Temperature: Anomalous Diffusion
6. Conclusions
Supplementary Materials
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- International Astronomical Union. Definitions of Terms in Meteor Astronomy. Available online: https://www.iau.org/static/science/scientific_bodies/commissions/f1/meteordefinitions_approved.pdf (accessed on 13 February 2023).
- Borovička, J. About the definition of meteoroid, asteroid, and related terms. WGN J. Int. Meteor Organ. 2016, 44, 31–34. Available online: https://ui.adsabs.harvard.edu/abs/2016JIMO...44...31B/abstract (accessed on 10 January 2024).
- Taylor, A.D.; Elford, W.G. Meteoroid orbital element distributions at 1 AU deduced from the Harvard Radio Meteor Project observations. Earth Planets Space 1998, 50, 569–575. [Google Scholar] [CrossRef]
- Drolshagen, E.; Ott, T.; Koschny, D.; Drolshagen, G.; Schmidt, A.K.; Poppe, B. Velocity distribution of larger meteoroids and small asteroids impacting. Planet. Space Sci. 2020, 184, 104869. [Google Scholar] [CrossRef]
- Steel, D. Meteoroid Orbits. Space Sci. Rev. 1996, 78, 507–553. [Google Scholar] [CrossRef]
- Baggaley, W.J.; Bennett, R.G.T.; Steel, D.I.; Taylor, A.D. The advanced meteor orbit radar facility-AMOR. Q. J. R. Astron. Soc. 1994, 35, 293. Available online: https://articles.adsabs.harvard.edu//full/1994QJRAS..35..293B/0000293.000.html (accessed on 10 January 2024).
- Younger, J.P. Theory and Applications of VHF Meteor Radar Observations. Ph.D. Thesis, University of Adelaide, Adelaide, Australia, 2011. Available online: https://hdl.handle.net/2440/86566 (accessed on 11 January 2024).
- Ceplecha, Z.; Borovička, J.; Elford, W.G.; ReVelle, D.O.; Hawkes, R.L.; Porubčan, V.; Šimek, M. Meteor Phenomena and Bodies. Space Sci. Rev. 1998, 84, 327–471. [Google Scholar] [CrossRef]
- Galligan, D.P.; Baggaley, W.J. The orbital distribution of radar-detected meteoroids of the Solar system dust cloud. Mon. Not. R. Astron. Soc. 2004, 353, 422–446. [Google Scholar] [CrossRef]
- Campbell-Brown, M.D.; Jones, J. Annual variation of sporadic radar meteor rates. Mon. Not. R. Astron. Soc. 2006, 367, 709–716. [Google Scholar] [CrossRef]
- McIntosh, D.L. Comparisons of VHF Meteor Radar Observations in the Middle Atmosphere with Multiple Independent Remote Sensing Techniques. Ph.D. Thesis, University of Adelaide, Adelaide, Australia, 2010. Available online: https://hdl.handle.net/2440/60068 (accessed on 11 December 2023).
- Reid, I.M.; McIntosh, D.L.; Murphy, D.J.; Vincent, R.A. Mesospheric Radar Wind Comparisons at High and Middle Southern Latitudes. Earth Planets Space 2018, 70, 84. [Google Scholar] [CrossRef]
- Olsson-Steel, D.; Elford, W.G. The height distribution of radio meteors: Observations at 2 MHz. J. Atmos. Terr. Phys. 1987, 49, 243–258. [Google Scholar] [CrossRef]
- Steel, D.I.; Elford, W.G. The height distribution of radio meteors: Comparison of observations at different frequencies on the basis of standard echo theory. J. Atmos. Terr. Phys. 1991, 53, 409–417. [Google Scholar] [CrossRef]
- Cervera, M.A.; Elford, W.G. The meteor radar response function: Theory and application to narrow beam MST radar. Planet. Space Sci. 2004, 52, 591–602. [Google Scholar] [CrossRef]
- McKinley, D.W.R. Meteor Science and Engineering; McGraw-Hill: New York, NY, USA, 1961; 309p. [Google Scholar]
- Cervera, M.A. Meteor Observations with a Narrow Beam VHF Radar. Ph.D. Thesis, University of Adelaide, Adelaide, Australia, 1996. Available online: https://hdl.handle.net/2440/18710 (accessed on 12 December 2023).
- Elford, W.G. Novel applications of MST radars in meteor studies. J. Atmos. Sol.-Terr. Phys. 2001, 63, 143–153. [Google Scholar] [CrossRef]
- Holdsworth, D.A.; Elford, W.G.; Vincent, R.A.; Reid, I.M.; Murphy, D.J.; Singer, W. All-sky interferometric meteor radar meteoroid speed estimation using the Fresnel transform. Ann. Geophys. 2007, 25, 385–398. [Google Scholar] [CrossRef][Green Version]
- Roy, A.; Doherty, J.F.; Mathews, J.D. Analyzing Radar Meteor Trail Echoes using the Fresnel Transform Technique: A Signal Processing Viewpoint. Earth Moon Planets 2007, 101, 27–39. [Google Scholar] [CrossRef]
- ATRAD Results. Available online: https://www.atrad.com.au/results/resplot.php?p=BP_ST-MET/bp_st-met_decay (accessed on 17 September 2023).
- Poulter, E.; Baggaley, W. Radiowave scattering from meteoric ionization. J. Atmos. Terr. Phys. 1977, 39, 757–768. [Google Scholar] [CrossRef]
- Stober, G.; Weryk, R.; Janches, D.; Dawkins, E.C.; Günzkofer, F.; Hormaechea, J.L.; Pokhotelov, D. Polarization dependency of transverse scattering and collisional coupling to the ambient atmosphere from meteor trails—Theory and observations. Planet. Space Sci. 2023, 237, 105768. [Google Scholar] [CrossRef]
- Stober, G.; Brown, P.; Campbell-Brown, M.; Weryk, R.J. Triple-frequency meteor radar full wave scattering—Measurements and comparison to theory. Astron. Astrophys. 2021, 654, A108. [Google Scholar] [CrossRef]
- Valentic, T.A.; Avery, J.P.; Avery, S.K.; Cervera, M.A.; Elford, W.G.; Vincent, R.A.; Reid, I.M. A comparison of meteor radar systems at Buckland Park. Radio Sci. 1996, 31, 1313–1329. [Google Scholar] [CrossRef]
- Malhotra, A.; Mathews, J.D.; Urbina, J.A. radio science perspective on long-duration meteor trails. J. Geophys. Res. 2007, 112, A12303. [Google Scholar] [CrossRef]
- Hey, J.S.; Stewart, G.S. Radar observations of meteors. Phys. Soc. 1947, 59, 858. [Google Scholar] [CrossRef]
- Li, G.; Xie, H.; Wang, Y.; Yang, S.; Hu, L.; Sun, W.; Wu, Z.; Ning, B.; Li, Y.; Zhao, X.; et al. Design of Meteor and ionospheric Irregularity Observation System and First Results. J. Geophys. Res. Space 2022, 127, e2022JA030380. [Google Scholar] [CrossRef]
- Li, G.; Ning, B.; Hu, L.; Chu, Y.-H.; Reid, I.M.; Dolman, B.K. A comparison of lower thermospheric winds derived from range spread and specular meteor trail echoes. J. Geophys. Res. 2012, 117, A03310. [Google Scholar] [CrossRef]
- Benzenberg, J.F. Versuche die Entfernung, die Geschwindigkeit und die Bahnen der Sternschnuppen zu Bestimmen; F. Perthes: Hamburg, Germany, 1800. [Google Scholar]
- Rendtel, J. Review of amateur meteor research. Planet. Space Sci. 2017, 143, 7–11. [Google Scholar] [CrossRef]
- Hart, P. Mount Glasgow Meteor Train. 2017. Available online: https://vimeo.com/217986931 (accessed on 13 February 2023).
- Whipple, F.L. Evidence for winds in the outer atmosphere. Proc. Natl. Acad. Sci. USA 1954, 40, 966–972. Available online: https://www.pnas.org/doi/pdf/10.1073/pnas.40.10.966 (accessed on 13 February 2023). [CrossRef][Green Version]
- Hines, C.O. Earlier days of gravity waves revisited. Pure Appl. Geophys. 1989, 130, 151–170. [Google Scholar] [CrossRef]
- Barnard, E.E. “Drifting Meteor Trains”. Sidereal Messenger 1882, 1, 174–180. Available online: https://adsabs.harvard.edu/full/1882SidM....1..174B (accessed on 15 December 2023).
- Trowbridge, C.C. Physical nature of meteor trains. Astrophys. J. 1907, 26, 95. Available online: https://adsabs.harvard.edu/full/1907ApJ....26...95T (accessed on 15 December 2023). [CrossRef]
- Jarrell, R.A. Canadian Meteor Science: The first phase. J. Astron. Hist. Herit. 2009, 12, 224–234. Available online: https://adsabs.harvard.edu/full/2009JAHH...12..224J (accessed on 15 December 2023). [CrossRef]
- Springer. Meteor Groups and Organizations. In Meteors and How to Observe Them; Astronomers’ Observing Guides; Lunsford, R., Ed.; Springer: New York, NY, USA, 2009. [Google Scholar] [CrossRef]
- MeteorNews. Available online: https://www.meteornews.net (accessed on 9 January 2023).
- Howie, R.M.; Paxman, J.; Bland, P.A.; Towner, M.C.; Cupak, M.; Sansom, E.K.; Devillepoix, H.A.R. How to build a continental scale fireball camera network. Exp. Astron. 2017, 43, 237–266. [Google Scholar] [CrossRef]
- Jenniskens, P.; Moskovitz, N.; Garvie, L.A.J.; Yin, Q.; Howell, J.A.; Free, D.L.; Albers, J.; Samuels, D.; Fries, M.D.; Mane, P.; et al. Orbit and origin of the LL7 chondrite Dishchii’bikoh (Arizona). Meteorit. Planet Sci. 2020, 55, 535–557. [Google Scholar] [CrossRef]
- Kelley, M.C.; Alcala, C.; Cho, J.Y.N. Detection of a meteor contrail and meteoric dust in the Earth’s upper mesosphere. J. Atmos. Sol.-Terr. Phys. 1998, 60, 359–369. [Google Scholar] [CrossRef]
- Hey, J.S.; Parsons, S.J.; Stewart, G.S. Radar Observations of the Giacobinid Meteor Shower. Mon. Not. R. Astron. Soc. 1946, 107, 176–183. [Google Scholar] [CrossRef]
- Eshleman, V.R. 4. Meteor Scatter. In The Radio Noise Spectrum; Menzel, D.H., Ed.; Harvard University Press: Cambridge, MA, USA, 1960; pp. 49–78. [Google Scholar] [CrossRef]
- Hey, J.S. The Evolution of Radio Astronomy; Paul Elek (Scientific Books): London, UK, 1973; 214p. [Google Scholar]
- Muller, H.G. Winds and Turbulence in the Meteor Zone. In Structure and Dynamics of the Upper Atmosphere. Developments in Atmospheric in Science; Verniani, F., Ed.; Elsevier: Amsterdam, The Netherlands, 1974; Volume 1, pp. 347–388. [Google Scholar]
- Gilbert, N.G. Growth and decline of a scientific specialty: The case of radar meteor research. Eos Trans. Am. Geophys. Union 1977, 58, 273–277. [Google Scholar] [CrossRef]
- Roper, R.G. MWR, Meteor Wind Radars. In Handbook for MAP, International Council of Scientific Unions Middle Atmosphere Program; Vincent, R.A., Ed.; SCOSTEP Secretariat: Chicago, IL, USA, 1984; Volume 13, pp. 124–134. [Google Scholar]
- Butrica, A.J. To See the Unseen: A History of Planetary Radar Astronomy; NASA History Series, SP4218; National Aeronautics and Space Administration: Washington, DC, USA, 1996. Available online: https://history.nasa.gov/SP-4218/ch1.htm (accessed on 15 November 2023).
- Reid, I.M.; Younger, J. 65 years of meteor radar research at Adelaide. In Proceedings of the 35th International Meteor Conference, Egmond, The Netherlands, 2–5 June 2016; International Meteor Organization: Mechelen, Belgium, 2016; p. 242. Available online: https://hdl.handle.net/2440/109534 (accessed on 16 November 2023).
- Hocking, W.K.; Kolomiyets, S.V. Radio meteor physics—A comparison between techniques from 1945 to the mid-1970’s. Radiotekhnika 2020, 201, 78–90. Available online: http://openarchive.nure.ua/handle/document/13985 (accessed on 17 November 2023). [CrossRef]
- Baggaley, J. Meteoric ionization: The interpretation of radar trail echoes. URSI Radio Sci. Bull. 2009, 2009, 6–20. [Google Scholar] [CrossRef]
- Manning, L.; Villard, O.; Peterson, A. Meteoric Echo Study of Upper Atmosphere Winds. Proc. IRE 1950, 38, 877–883. [Google Scholar] [CrossRef]
- Greenhow, J.S. A radio echo method for the investigation of atmospheric winds at altitudes of 80 to 100 km. J. Atmos. Terr. Phys. 1952, 2, 22–29. [Google Scholar] [CrossRef]
- Elford, W.G.; Robertsson, D.S. Measurements of winds in the upper atmosphere by means of drifting meteor trails II. J. Atmos. Terr. Phys. 1953, 4, 271–284. [Google Scholar] [CrossRef]
- Revah, I.; Spizzichino, A. A Continuous Wave Radar for lonospheric Wind Measurements. In Proceedings of the Workshop on Methods of Obtaining Winds and Densities from Radar Meteor Trail Returns, Waltham, MA, USA, 16–19 August 1966; (No. 75, p. 83); AFCRL-68-0228; Air Force Cambridge Research Laboratories, Office of Aerospace Research, United States Air Force: Cambridge, MA, USA, 1968. [Google Scholar]
- Balis, J.; Lamy, H.; Anciaux, M.; Jehin, E. Reconstructing meteoroid trajectories using forward scatter radio observations from the BRAMS network. Radio Sci. 2023, 58, e2023RS007697. [Google Scholar] [CrossRef]
- Lamy, H.; Balis, J. Mesosphere and Lower Thermosphere wind speed determination using data from the radio forward scatter BRAMS network. In Proceedings of the EGU General Assembly 2023, Vienna, Austria, 23–28 April 2023. [Google Scholar] [CrossRef]
- Clark, R.R. Upper atmosphere wind observations of waves and tides with the UNH Meteor Radar System at Durham 43° N (1977, 1978 and 1979). J. Atmos. Terr. Phys. 1983, 45, 621–627. [Google Scholar] [CrossRef]
- Tsuda, T.; Yamamoto, M.; Sato, T.; Kato, S.; Fukao, S. Comparison observations between the MU radar and the Kyoto meteor radar. Radio Sci. 1985, 20, 1241–1246. [Google Scholar] [CrossRef]
- Roper, R.G. Global meteor observation system (GLOBMET). In International Council of Scientific Unions Middle Atmosphere Program, Handbook for MAP; SCOSTEP Secretariat: Chicago, IL, USA, 1982; Volume 7, pp. 21–33. [Google Scholar]
- Bowhill, S.A. Introduction and New International Equatorial Observatory (NIEO): The middle atmosphere program; an overview. In International Council of Scientific Unions, Middle Atmosphere Program. Handbook for MAP; SCOSTEP Secretariat: Chicago, IL, USA, 1989; Volume 27. [Google Scholar]
- Roper, R.G. Globmet—The contributions of radio meteor measurements to the middle atmosphere program. Adv. Space Res. 1990, 10, 189–192. [Google Scholar] [CrossRef]
- Manson, A.H.; Meek, C.E.; Avery, S.; Clark, R.R.; Schminder, R.; Kurschner, D.; Vincent, R.A. Radars of the mesosphere, lower thermosphere network: Their capability to measure winds and waves, and their role in step. Adv. Space Res. 1992, 12, 277–287. [Google Scholar] [CrossRef]
- Reid, I.M. MF and HF Spaced Antenna radar techniques for investigating the dynamics and structure of the 50 to 110 km height region: A review. Prog. Earth Planet. Sci. 2015, 2, 33. [Google Scholar] [CrossRef]
- Jacobi, C.; Arras, C.; Kürschner, D.; Singer, W.; Hoffmann, P.; Keuer, D. Comparison of mesopause region meteor radar winds, medium frequency radar winds and low frequency drifts over Germany. Adv. Space Res. 2009, 43, 247–252. [Google Scholar] [CrossRef]
- Wilhelm, S.; Stober, G.; Chau, J.L. A comparison of 11-year mesospheric and lower thermospheric winds determined by meteor and MF radar at 69° N. Ann. Geophys. 2017, 35, 893–906. [Google Scholar] [CrossRef]
- Avery, S.K. Meteor detection on ST (MST) radars. In International Council of Scientific Unions, Middle Atmosphere Program, Handbook for MAP; SCOSTEP Secretariat: Chicago, IL, USA, 1987; Volume 25. Available online: https://ntrs.nasa.gov/api/citations/19880005172/downloads/19880005172.pdf (accessed on 13 February 2023).
- Nakamura, T.; Tsuda, T.; Tsutsumi, M.; Kita, K.; Uehara, T.; Kato, S.; Fukao, S. Meteor wind observations with the MU radar. Radio Sci. 1991, 26, 857–869. [Google Scholar] [CrossRef]
- Ruey-Ming, K.; Chu, Y.-H.; Su, S.-Y.; Su, C.-L. The Chung-Li VHF radar as a meteor radar: System phase bias estimation and experimental results. Terr. Atmos. Ocean. Sci. 2003, 14, 113–132. [Google Scholar]
- Schult, C.; Kero, J.; Stober, G.; Brown, P. Dual frequency measurements of meteor head echoes simultaneously detected with the MAARSY and EISCAT radar systems. Icarus 2021, 355, 114137. [Google Scholar] [CrossRef]
- Elford, W.G.; Taylor, A.D. Measurement of Faraday rotation of radar meteor echoes for the modelling of electron densities in the lower ionosphere. J. Atmos. Sol.-Terr. Phys. 1997, 59, 1021–1024. [Google Scholar] [CrossRef]
- Pellinen-Wannberg, A. Even a blind chicken sometimes finds a grain of corn—In my case in space. Perspect. Earth Space Sci. 2023, 4, e2022CN000176. [Google Scholar] [CrossRef]
- Kero, J.; Campbell-Brown, M.D.; Stober, G.; Chau, J.L.; Mathews, J.D.; Pellinen-Wannberg, A. Radar Observations of Meteors. In Meteoroids: Sources of Meteors on Earth and Beyond; Cambridge Planetary Science; Ryabova, G., Asher, D., Campbell-Brown, M., Eds.; Cambridge University Press: Cambridge, UK, 2019; pp. 65–89. [Google Scholar] [CrossRef]
- Janches, D.; Hocking, W.; Pifko, S.; Hormaechea, J.L.; Fritts, D.C.; Brunini, C.; Michell, R.; Samara, M. Interferometric meteor head echo observations using the Southern Argentina Agile Meteor Radar. J. Geophys. Res. Space Phys. 2014, 119, 2269–2287. [Google Scholar] [CrossRef]
- Hocking, W.K.; Fuller, B.; Vandepeer, B. Real-time determination of meteor-related parameters utilizing modern digital technology. J. Atmos. Sol.-Terr. Phys. 2001, 63, 155–169. [Google Scholar] [CrossRef]
- Holdsworth, D.A.; Reid, I.M. The Buckland Park meteor radar—Description and initial results. In Proceedings of the Workshop on Applications of Radio Science (WARS02), Leura, NSW, Australia, 20–22 February 2002; Available online: https://www.researchgate.net/publication/378128996_The_Buckland_Park_meteor_radar_-_description_and_initial_results (accessed on 5 January 2024).
- Holdsworth, D.A.; Reid, I.M.; Cervera, M.A. The Buckland Park all-sky interferometric meteor radar—Description and first results. Radio Sci. 2004, 39, RS5009. [Google Scholar] [CrossRef]
- Holdsworth, D.A.; Tsutsumi, M.; Reid, I.M.; Nakamura, T.; Tsuda, T. Interferometric meteor phase calibration using meteor echoes. Radio Sci. 2004, 39, RS5012. [Google Scholar] [CrossRef]
- Yi, W.; Xue, X.; Zeng, J.; Wang, J.; Zhou, B.; Hailun, Y.; Chen, T.; Dou, X. Observation of MLT region winds, tides, temperatures, and relative densities by the USTC Mengcheng meteor radar. JUSTC 2023, 53, 0501. [Google Scholar] [CrossRef]
- Spargo, A.J.; Reid, I.M.; MacKinnon, A.D. Multistatic meteor radar observations of gravity wave-tidal interaction over Southern Australia. Atmos. Meas. Tech. 2019, 12, 4791–4812. [Google Scholar] [CrossRef]
- Stober, G.; Chau, J. A multistatic and multifrequency novel approach for specular meteor radars to improve wind measurements in the MLT region. Radio Sci. 2015, 50, 431–442. [Google Scholar] [CrossRef]
- Jones, J.; Webster, A.R.; Hocking, W.K. An improved interferometer design for use with meteor radars. Radio Sci. 1998, 33, 55–65. [Google Scholar] [CrossRef]
- Younger, J.; Reid, I.; Adami, C.; Hall, C.; Tsutsumi, M. Meteor radar observations of polar mesospheric summer echoes over Svalbard. Atmos. Meas. Tech. 2021, 14, 5015–5027. [Google Scholar] [CrossRef]
- Xu, Q.; Reid, I.M.; Cai, B.; Adami, C.; Zhang, Z.; Zhao, M.; Li, W. A New Dual-Frequency Stratospheric Tropospheric/Meteor Radar: System Description and First Results. Atmos. Meas. Tech. Discuss. 2023. [Google Scholar] [CrossRef]
- Weryk, R.J.; Brown, P.G. Simultaneous radar and video meteors—I: Metric comparisons. Planet. Space Sci. 2012, 62, 132–152. [Google Scholar] [CrossRef]
- Younger, J.P.; Reid, I.M. Interferometer angle-of-arrival determination using pre-calculated phases. Radio Sci. 2017, 52, 1058–1066. [Google Scholar] [CrossRef]
- Chau, J.L.; Urco, J.M.; Vierinen, J.; Harding, B.J.; Clahsen, M.; Pfeffer, N.; Kuyeng, K.M.; Milla, M.A.; Erickson, P.J. Multistatic specular meteor radar network in Peru: System description and initial results. Earth Space Sci. 2021, 8, e2020EA001293. [Google Scholar] [CrossRef]
- Conte, J.F.; Chau, J.L.; Liu, A.; Qiao, Z.; Fritts, D.C.; Hormaechea, J.L.; Salvador, J.O.; Milla, M.A. Comparison of MLT momentum fluxes over the Andes at four different latitudinal sectors using multistatic radar configurations. J. Geophys. Res. Atmos. 2022, 127, e2021JD035982. [Google Scholar] [CrossRef]
- Kumar, K.K.; Rankumar, G.; Shelbi, S.T. Initial results from SKiYMET meteor radar at Thumba (8.5° N, 77° E): 1. Comparison of wind measurements with MF spaced antenna radar system. Radio Sci. 2007, 42, RS6008. [Google Scholar] [CrossRef]
- Fritts, D.C.; Janches, D.; Iimura, H.; Hocking, W.K.; Mitchell, N.J.; Stockwell, R.G.; Fuller, B.; Vandepeer, B.; Hormaechea, J.; Brunini, C.; et al. Southern Argentina Agile Meteor Radar: System design and initial measurements of large-scale winds and tides. J. Geophys. Res. 2010, 115, D18112. [Google Scholar] [CrossRef]
- Rainville, N.; Palo, S.; Marino, J.; Volz, R. Multistatic Radar Development for the Colorado Zephyr Meteor Radar Network. URSI Radio Sci. Lett. 2023, 4, 61. Available online: https://www.ursi.org/Publications/RadioScienceLetters/Volume4/RSL22-0061-final.pdf (accessed on 15 November 2023).
- Placke, M. Gravity Waves and Momentum Fluxes in the Mesosphere and Lower Thermosphere Region. Ph.D. Thesis, Leibniz-Institut für Atmosphärenphysik, Kuhlungsborn, Germany, 2014. IAP Nr. 36/2014 ISSN 1615–8083. [Google Scholar]
- Wang, J.; Yi, W.; Wu, J.; Chen, T.; Xue, X.; Zeng, J.; Vincent, R.A.; Reid, I.M.; Batista, P.P.; Buriti, R.A.; et al. Coordinated observations of migrating tides by multiple meteor radars in the equatorial mesosphere and lower thermosphere. J. Geophys. Res. Space Phys. 2022, 127, e2022JA030678. [Google Scholar] [CrossRef]
- Hagen, J.; Hocke, K.; Stober, G.; Pfreundschuh, S.; Murk, A.; Kämpfer, N. First measurements of tides in the stratosphere and lower mesosphere by ground-based Doppler microwave wind radiometry. Atmos. Chem. Phys. 2020, 20, 2367–2386. [Google Scholar] [CrossRef]
- Stober, G.; Liu, A.; Kozlovsky, A.; Qiao, Z.; Krochin, W.; Shi, G.; Kero, J.; Tsutsumi, M.; Gulbrandsen, N.; Nozawa, S.; et al. Identifying gravity waves launched by the Hunga Tonga–Hunga Ha′apai volcanic eruption in mesosphere/lower-thermosphere winds derived from CONDOR and the Nordic Meteor Radar Cluster. Ann. Geophys. 2023, 41, 197–208. [Google Scholar] [CrossRef]
- Stober, G.; Liu, A.; Kozlovsky, A.; Qiao, Z.; Kuchar, A.; Jacobi, C.; Meek, C.; Janches, D.; Liu, G.; Tsutsumi, M.; et al. Meteor radar vertical wind observation biases and mathematical debiasing strategies including the 3DVAR+DIV algorithm. Atmos. Meas. Tech. 2022, 15, 5769–5792. [Google Scholar] [CrossRef]
- Stober, G.; Kozlovsky, A.; Liu, A.; Qiao, Z.; Tsutsumi, M.; Hall, C.; Nozawa, S.; Lester, M.; Belova, E.; Kero, J.; et al. Atmospheric tomography using the Nordic Meteor Radar Cluster and Chilean Observation Network De Meteor Radars: Network details and 3D-Var retrieval. Atmos. Meas. Tech. 2021, 14, 6509–6532. [Google Scholar] [CrossRef]
- Reid, I.M. Some aspects of Doppler radar measurements of the mean and fluctuating components of the wind field in the upper middle atmosphere. J. Atmos. Terr. Phys. 1987, 49, 467–484. [Google Scholar] [CrossRef]
- Thorsen, D.; Franke, S.J.; Kudeki, E. A new approach to MF radar interferometry for estimating mean winds and momentum flux. Radio Sci. 1997, 32, 707–726. [Google Scholar] [CrossRef]
- Vincent, R.A.; Reid, I.M. HF Doppler measurements of mesospheric gravity wave momentum fluxes. J. Atmos. Sci. 1983, 40, 1321–1333. [Google Scholar] [CrossRef]
- Hocking, W.K. A new approach to momentum flux determinations using SKiYMET meteor radars. Ann. Geophys. 2005, 23, 2433–2439. [Google Scholar] [CrossRef]
- Placke, M.; Hoffmann, P.; Latteck, R.; Rapp, M. Gravity wave momentum fluxes from MF and meteor radar measurements in the polar MLT region. J. Geophys. Res. Space Phys. 2015, 120, 736–750. [Google Scholar] [CrossRef]
- De Wit, R.J.; Hibbins, R.E.; Espy, P.J. The seasonal cycle of gravity wave momentum flux and forcing in the high latitude northern hemisphere mesopause region. J. Atmos. Sol.-Terr. Phys. 2014, 127, 21–29. [Google Scholar] [CrossRef]
- Andrioli, V.F.; Fritts, D.C.; Batista, P.P.; Clemesha, B.R. Improved analysis of all-sky meteor radar measurements of gravity wave variances and momentum fluxes. Ann. Geophys. 2013, 31, 889–908. [Google Scholar] [CrossRef]
- Liu, A.Z.; Lu, X.; Franke, S.J. Diurnal variation of gravity wave momentum flux and its forcing on the diurnal tide. J. Geophys. Res.-Atmos. 2013, 118, 1668–1678. [Google Scholar] [CrossRef]
- Fritts, D.C.; Janches, D.; Hocking, W.K. Southern Argentina Agile Meteor Radar: Initial assessment of gravity wave momentum fluxes. J. Geophys. Res. 2010, 115, D19123. [Google Scholar] [CrossRef]
- Fritts, D.C.; Janches, D.; Hocking, W.K.; Mitchell, N.J.; Taylor, M.J. Assessment of gravity wave momentum flux measurement capabilities by meteor radars having different transmitter power and antenna configurations. J. Geophys. Res.-Atmos. 2012, 117, D10. [Google Scholar] [CrossRef]
- Vincent, R.A.; Kovalam, S.; Reid, I.M.; Younger, J.P. Gravity wave flux retrievals using meteor radars. Geophys. Res. Lett. 2010, 37, L14802. [Google Scholar] [CrossRef]
- Stober, G.; Janches, D.; Matthias, V.; Fritts, D.; Marino, J.; Moffat-Griffin, T.; Baumgarten, K.; Lee, W.; Murphy, D.; Kim, Y.H.; et al. Seasonal evolution of winds, atmospheric tides, and Reynolds stress components in the Southern Hemisphere mesosphere–lower thermosphere in 2019. Ann. Geophys. 2021, 39, 1–29. [Google Scholar] [CrossRef]
- Jones, J.; Brown, P.; Ellis, K.; Webster, A.; Campbell-Brown, M.; Krzemenski, Z.; Weryk, R. The Canadian Meteor Orbit Radar: System overview and preliminary results. Planet. Space Sci. 2005, 53, 413–421. [Google Scholar] [CrossRef]
- Stober, G.; Chau, J.L.; Vierinen, J.; Jacobi, C.; Wilhelm, S. Retrieving horizontally resolved wind fields using multi-static meteor radar observations. Atmos. Meas. Tech. 2018, 11, 4891–4907. [Google Scholar] [CrossRef]
- Conte, J.F.; Chau, J.L.; Urco, J.M.; Latteck, R.; Vierinen, J.; Salvador, J.O. First studies of mesosphere and lower thermosphere dynamics using a multistatic specular meteor radar network over southern Patagonia. Earth Space Sci. 2021, 8, e2020EA001356. [Google Scholar] [CrossRef]
- Yi, W.; Zeng, J.; Xue, X.; Reid, I.; Zhong, W.; Wu, J.; Chen, T.; Dou, X. Multistatic meteor radar observations of two-dimensional horizontal MLT wind. Atmos. Meas. Tech. Discuss. 2022. preprint. [Google Scholar] [CrossRef]
- Wilson, D.A.; Miller, L.J. Chapter 13. In Remote Sensing of the Troposphere; Derr, V.E., Ed.; U.S. National Oceanic and Atmospheric Administration, U.S. Government Publishing Office: Washington, DC, USA, 1972. [Google Scholar]
- Chau, J.L.; Stober, G.; Hall, C.M.; Tsutsumi, M.; Laskar, F.I.; Hoffmann, P. Polar mesospheric horizontal divergence and relative vorticity measurements using multiple specular meteor radars. Radio Sci. 2017, 52, 811–828. [Google Scholar] [CrossRef]
- Volz, R.; Chau, J.L.; Erickson, P.J.; Vierinen, J.P.; Urco, J.M.; Clahsen, M. Four-dimensional mesospheric and lower thermospheric wind fields using Gaussian process regression on multistatic specular meteor radar observations. Atmos. Meas. Tech. 2021, 14, 7199–7219. [Google Scholar] [CrossRef]
- Zhong, W.; Xue, X.; Yi, W.; Reid, I.M.; Chen, T.; Dou, X. Error analyses of a multistatic meteor radar system to obtain a three-dimensional spatial-resolution distribution. Atmos. Meas. Tech. 2021, 14, 3973–3988. [Google Scholar] [CrossRef]
- Geller, M.A.; Alexander, M.J.; Love, P.T.; Bacmeister, J.; Ern, M.; Hertzog, A.; Manzini, E.; Preusse, P.; Sato, K.; Scaife, A.A.; et al. A comparison between gravity wave momentum fluxes in observations and climate models. J. Clim. 2013, 26, 6383–6405. [Google Scholar] [CrossRef]
- Stober, G.; Sommer, S.; Rapp, M.; Latteck, R. Investigation of gravity waves using horizontally resolved radial velocity measurements. Atmos. Meas. Tech. 2013, 6, 2893–2905. [Google Scholar] [CrossRef]
- Browning, K.A.; Wexler, R. The Determination of Kinematic Properties of a Wind Field Using Doppler Radar. J. Appl. Meteor. Climatol. 1968, 7, 105–113. [Google Scholar] [CrossRef]
- Waldteufel, P.; Corbin, H. On the Analysis of Single-Doppler Radar Data. J. Appl. Meteor. Climatol. 1979, 18, 532–542. [Google Scholar] [CrossRef]
- Vierinen, J.; Chau, J.L.; Charuvil, H.; Urco, J.M.; Clahsen, M.; Avsarkisov, V.; Marino, R.; Volz, R. Observing mesospheric turbulence with specular meteor radars: A novel method for estimating second-order statistics of wind velocity. Earth Space Sci. 2019, 6, 1171–1195. [Google Scholar] [CrossRef]
- Mason, E.A.; McDaniel, E.W. Transport Properties of Ions in Gases; Wiley: New York, NY, USA, 1988; Volume 26. [Google Scholar]
- Tsutsumi, M.; Tsuda, T.; Nakamura, T.; Fukao, S. Temperature fluctuations near the mesopause inferred from meteor observations with the middle and upper atmosphere radar. Radio Sci. 1994, 29, 599–610. [Google Scholar] [CrossRef]
- Cervera, M.A.; Reid, I.M. Comparison of atmospheric parameters derived from meteor observations with CIRA. Radio Sci. 2000, 35, 833–843. [Google Scholar] [CrossRef]
- Hocking, W.K. Temperatures using radar-meteor decay times. Geophys. Res. Lett. 1999, 26, 3297–3300. [Google Scholar] [CrossRef]
- Stober, G.; Jacobi, C.; Matthias, V.; Hoffmann, P.; Gerding, M. Neutral air density variations during strong planetary wave activity in the mesopause region derived from meteor radar observations. J. Atmos. Sol.-Terr. Phys. 2012, 74, 55–63. [Google Scholar] [CrossRef]
- Holdsworth, D.A. (Adelaide, SA, Australia). Private communication, 2005.
- Kim, J.-H.; Kim, Y.H.; Lee, C.S.; Jee, G. Seasonal variation of meteor decay times observed at King Sejong Station (62.22° S, 58.78° W), Antarctica. J. Atmos. Sol.-Terr. Phys. 2010, 72, 883–889. [Google Scholar] [CrossRef]
- Yi, W.; Xue, X.; Reid, I.M.; Younger, J.P.; Chen, J.; Chen, T.; Li, N. Estimation of mesospheric densities at low latitudes using the Kunming meteor radar together with SABER temperatures. J. Geophys. Res. Space Phys. 2018, 123, 3183–3195. [Google Scholar] [CrossRef]
- Dyrud, L.P.; Oppenheim, M.M.; vom Endt, A.F. The anomalous diffusion of meteor trails. Geophys. Res. Lett. 2001, 28, 2775–2778. [Google Scholar] [CrossRef]
- Choi, J.-M.; Kwak, Y.-S.; Kim, Y.H.; Lee, C.; Kim, J.-H.; Jee, G.; Yang, T.-Y. Anisotropic diffusion of meteor trails due to the geomagnetic field over King Sejong Station (62.2° S, 58.8° W), Antarctica. Astrophys. Space Sci. 2018, 363, 111. [Google Scholar] [CrossRef]
- Lee, C.S.; Younger, J.P.; Reid, I.M.; Kim, Y.H.; Kim, J.-H. The effect of recombination and attachment on meteor radar diffusion coefficient profiles. J. Geophys. Res. Atmos. 2013, 118, 3037–3043. [Google Scholar] [CrossRef]
- Younger, J.P.; Lee, C.S.; Reid, I.M.; Vincent, R.A.; Kim, Y.H.; Murphy, D.J. The effects of deionization processes on meteor radar diffusion coefficients below 90 km. J. Geophys. Res. Atmos. 2014, 119, 10027–10043. [Google Scholar] [CrossRef]
- Southworth, R.B. Density Measurements at Havana. In Proceedings of the Workshop on Methods of Obtaining Winds and Densities from Radar Meteor Trail Returns, Waltham, MA, USA, 16–19 August 1966; (No. 75, p. 251). AFCRL-68-0228; Air Force Cambridge Research Laboratories, Office of Aerospace Research, United States Air Force: Washington, DC, USA, 1968. [Google Scholar]
- Yi, W.; Xue, X.; Reid, I.M.; Murphy, D.J.; Hall, C.M.; Tsutsumi, M.; Ning, B.; Li, G.; Yang, G.; Li, N.; et al. Climatology of Interhemispheric mesopause temperatures using the high-latitude and middle-latitude meteor radars. J. Geophys. Res. Atmos. 2021, 126, e2020JD034301. [Google Scholar] [CrossRef]
- Yi, W.; Xue, X.; Reid, I.M.; Murphy, D.J.; Hall, C.M.; Tsutsumi, M.; Ning, B.; Li, G.; Vincent, R.A.; Chen, T.; et al. Climatology of the mesopause density using a global distribution of meteor radars. Atmos. Chem. Phys. Discuss. 2018, 595, 1–31. Available online: https://acp.copernicus.org/preprints/acp-2018-1040/acp-2018-1040.pdf (accessed on 15 December 2023). [CrossRef]
- Younger, J.P.; Reid, I.M.; Vincent, R.A.; Murphy, D.J. A method for estimating the height of a mesospheric density level using meteor radar. Geophys. Res. Lett. 2015, 42, 6106–6111. [Google Scholar] [CrossRef]
- Reid, I.M.; Spargo, A.J.; Woithe, J.M.; Klekociuk, A.R.; Younger, J.P.; Sivjee, G.G. Seasonal MLT-region nightglow intensities, temperatures, and emission heights at a Southern Hemisphere midlatitude site. Ann. Geophys. 2017, 35, 567–582. [Google Scholar] [CrossRef]
- Schwartz, M.J.; Lambert, A.; Manney, G.L.; Read, W.G.; Livesey, N.J.; Froidevaux, L.; Ao, C.O.; Bernath, P.F.; Boone, C.D.; Cofield, R.E.; et al. Validation of the Aura Microwave Limb sounder temperature and geopotential height measurements. J. Geophys. Res. 2008, 113, D15S11. [Google Scholar] [CrossRef]
- Zhou, B.; Yi, W.; Xue, X.; Ye, H.; Zeng, J.; Li, G.; Tsutsumi, M.; Gulbrandsen, N.; Chen, T.; Dou, X. Impact of sudden stratospheric warmings on the neutral density, temperature, and wind in the MLT region. Front. Astron. Space Sci. 2023, 10, 1–9. [Google Scholar] [CrossRef]
- Clemesha, B.; Batista, P. The quantification of long-term atmospheric change via meteor ablation height measurements. J. Atmos. Sol.-Terr. Phys. 2006, 68, 1934–1939. [Google Scholar] [CrossRef]
- Jacobi, C. Meteor heights during the recent solar minimum. Adv. Radio Sci. 2014, 12, 161–165. [Google Scholar] [CrossRef]
- Lima, L.; Araújo, L.; Alves, E.; Batista, P.; Clemesha, B. Variations in meteor heights at 22.7° S during solar cycle 23. J. Atmos. Sol.-Terr. Phys. 2015, 133, 139–144. [Google Scholar] [CrossRef]
- Stober, G.; Matthias, V.; Brown, P.; Chau, J.L. Neutral density variation from specular meteor echo observations spanning one solar cycle. Geophys. Res. Lett. 2014, 41, 6919–6925. [Google Scholar] [CrossRef]
- Dawkins, E.C.M.; Stober, G.; Janches, D.; Carrillo-Sánchez, J.D.; Lieberman, R.S.; Jacobi, C.; Moffat-Griffin, T.; Mitchell, N.J.; Cobbett, N.; Batista, P.P.; et al. Solar cycle and long-term trends in the observed peak of the meteor altitude distributions by meteor radars. Geophys. Res. Lett. 2023, 50, e2022GL101953. [Google Scholar] [CrossRef]
- Xie, H.; Li, G.; Ning, B.; Reid, I.; Hu, L.; Wu, B.; Yu, Y.; Yang, S. The possibility of using all-sky meteor radar to observe ionospheric E-region field-aligned irregularities. Sci. China Technol. Sci. 2019, 62, 1431–1437. [Google Scholar] [CrossRef]
- Tsutsumi, M.; Holdsworth, D.; Nakamura, T.; Reid, I. Meteor observations with an MF radar. Earth Planet Space 1999, 51, 691–699. [Google Scholar] [CrossRef]
- Tsutsumi, M.; Aso, T. MF radar observations of meteors and meteor-derived winds at Syowa (69° S, 39° E), Antarctica: A comparison with simultaneous spaced antenna winds. J. Geophys. Res. 2005, 110, D24111. [Google Scholar] [CrossRef]
- Cai, B.; Xu, Q.; Hu, X.; Yang, J. Initial Results of Meteor Wind with Langfang Medium Frequency Radar. Atmosphere 2020, 11, 507. [Google Scholar] [CrossRef]
- Tsutsumi, M. High resolution wind observations in the mesosphere to lower thermosphere based on MF radar meteor echo measurements. In Proceedings of the XXVIII General Assembly of the International Union of Geodesy and Geophysics (IUGG) (Berlin 2023), Berlin, Germany, 11–20 July 2023. [Google Scholar] [CrossRef]
- Younger, J.P.; Reid, I.M.; Vincent, R.A.; Holdsworth, D.A.; Murphy, D.J. A southern hemisphere survey of meteor shower radiants and associated stream orbits using single station radar observations. Mon. Not. R. Astron. Soc. 2009, 398, 350–356. [Google Scholar] [CrossRef]
- Younger, J.P.; Reid, I.M.; Vincent, R.A.; Murphy, D.J. Meteor shower velocity estimates from single-station meteor radar: Accuracy and precision. Mon. Not. R. Astron. Soc. 2012, 425, 1473–1478. [Google Scholar] [CrossRef][Green Version]
- Li, Y.; Li, G.; Hu, L.; Zhao, X.; Sun, W.; Xie, H.; Yang, S.; Ning, B. Observations of the October Draconid outburst at different latitudes along 120° E. Mon. Not. R. Astron. Soc. 2022, 516, 5538–5543. [Google Scholar] [CrossRef]
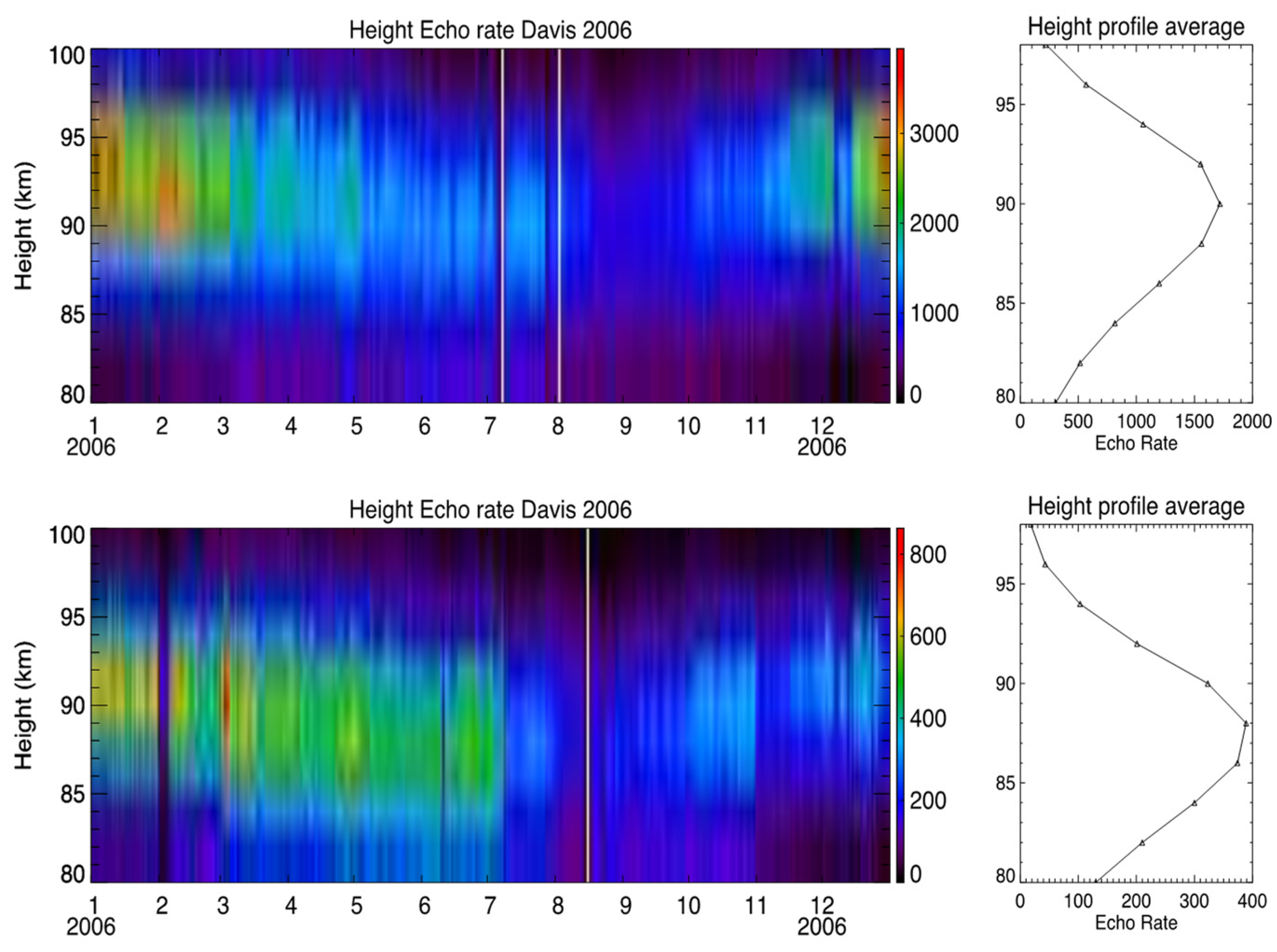
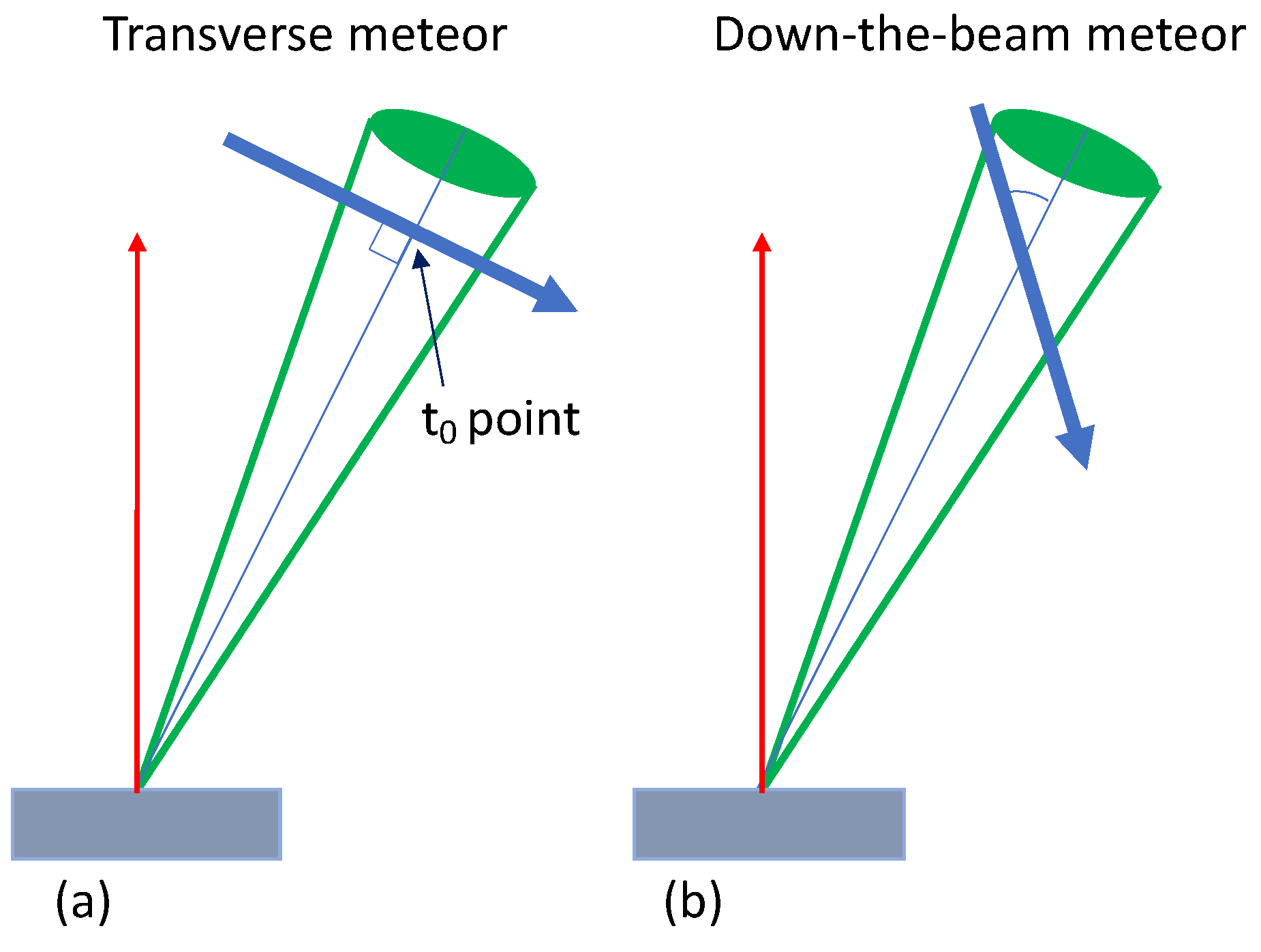
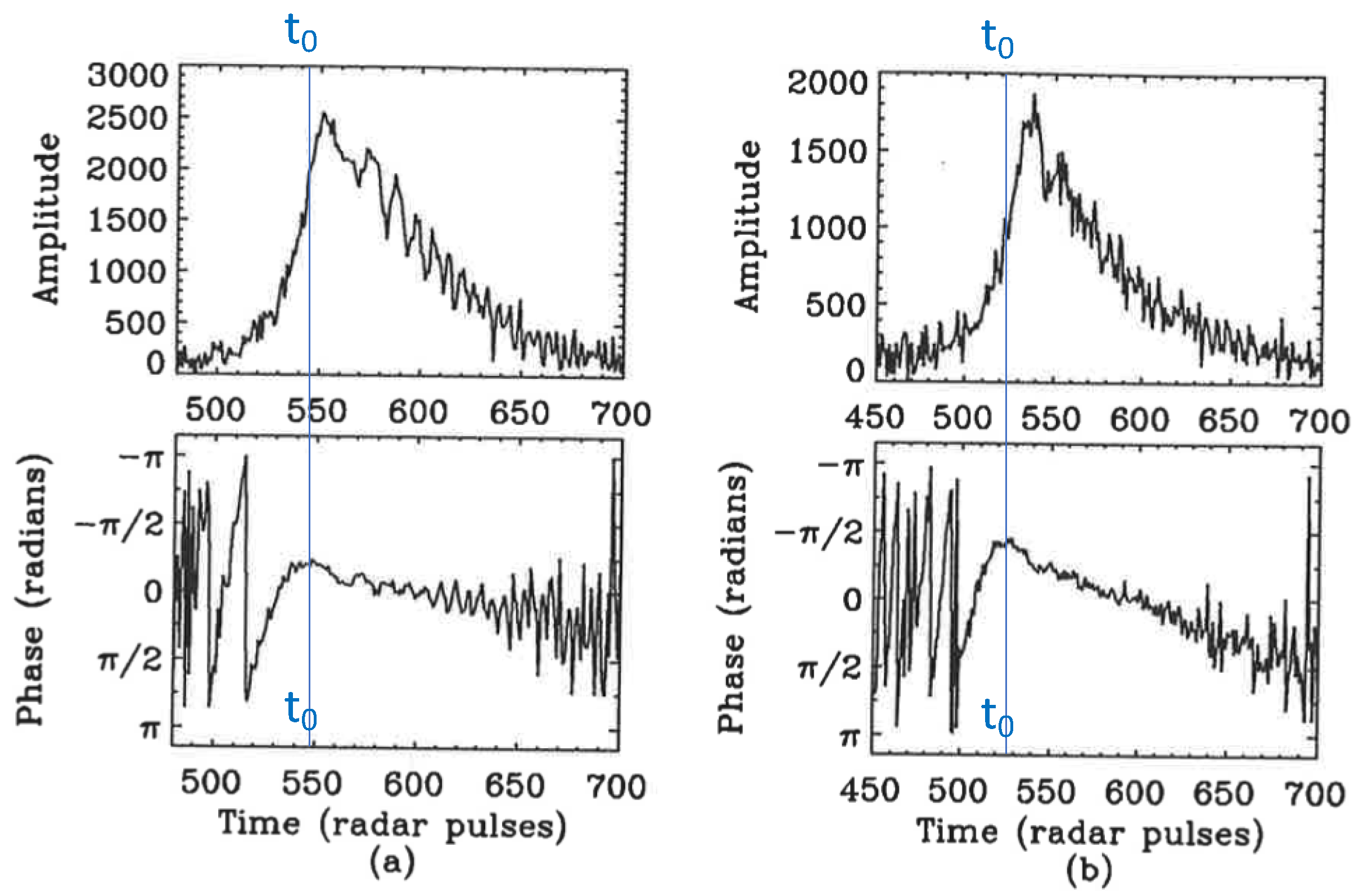
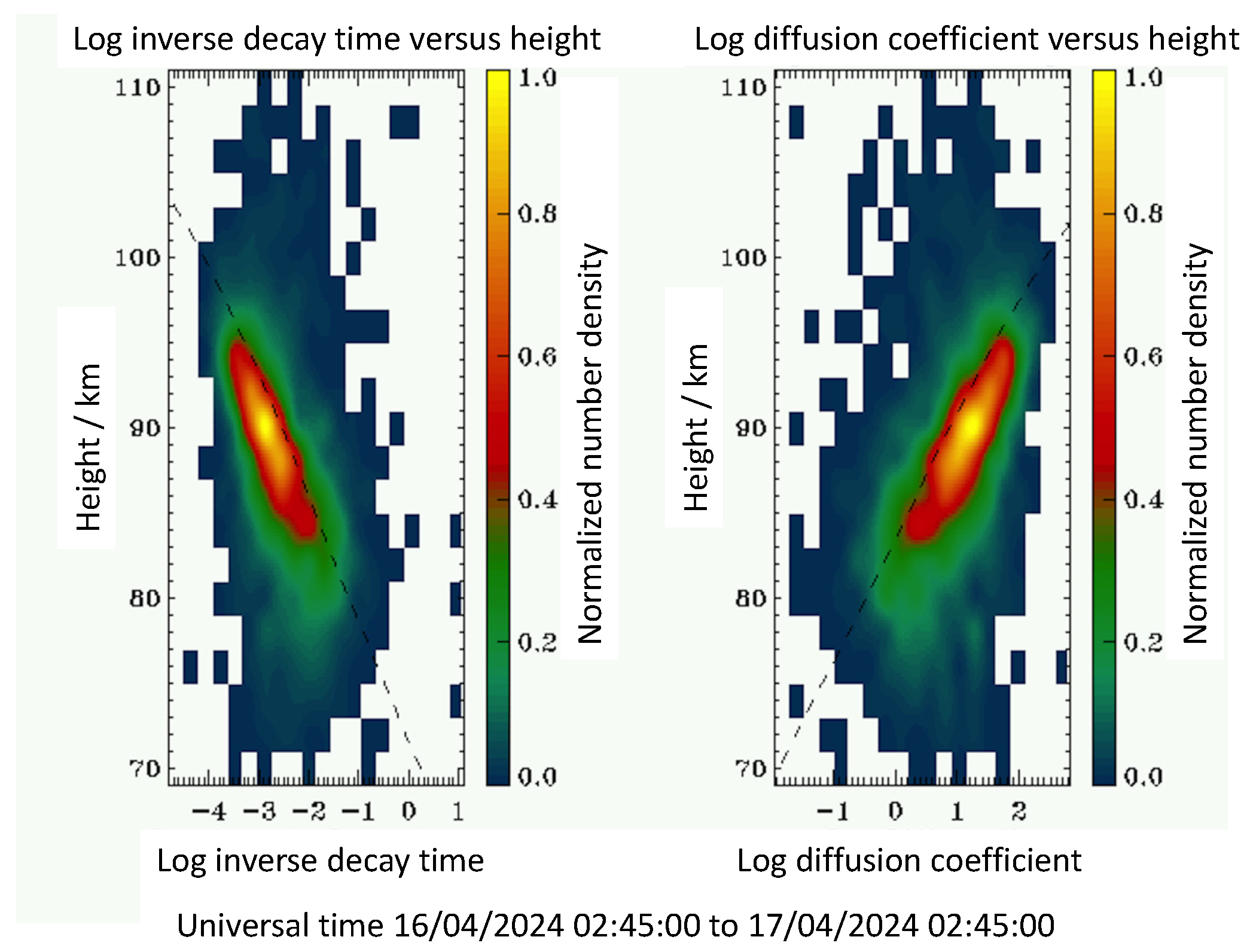
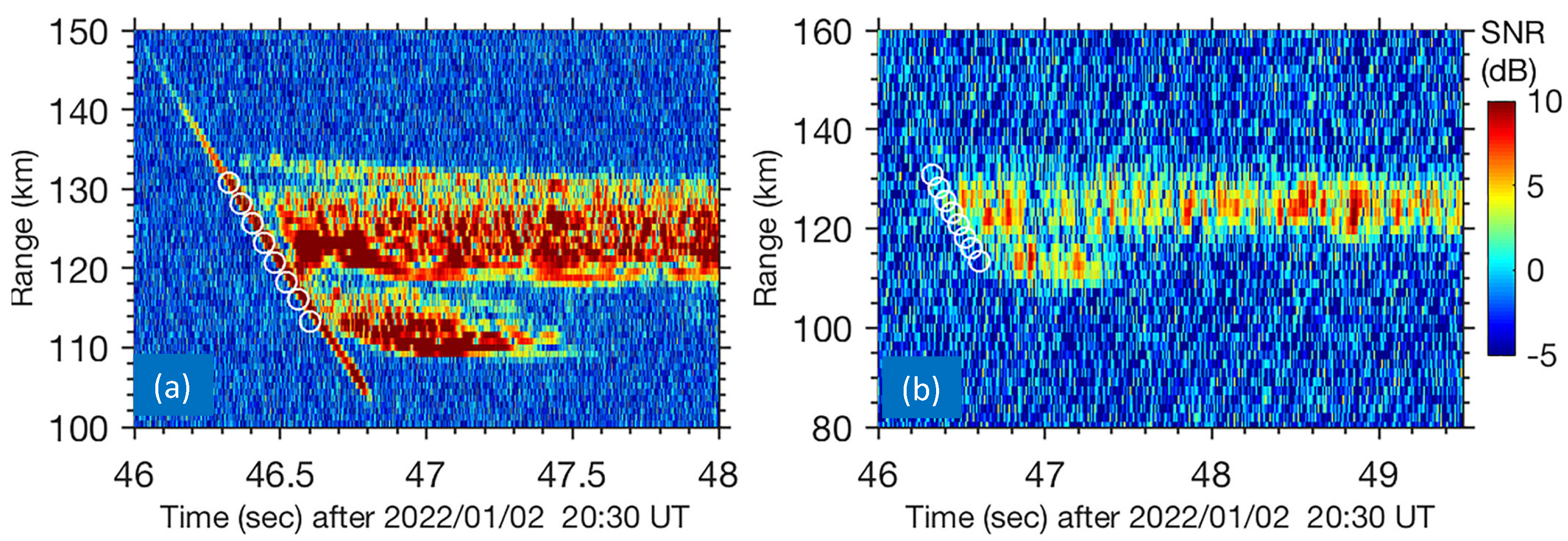
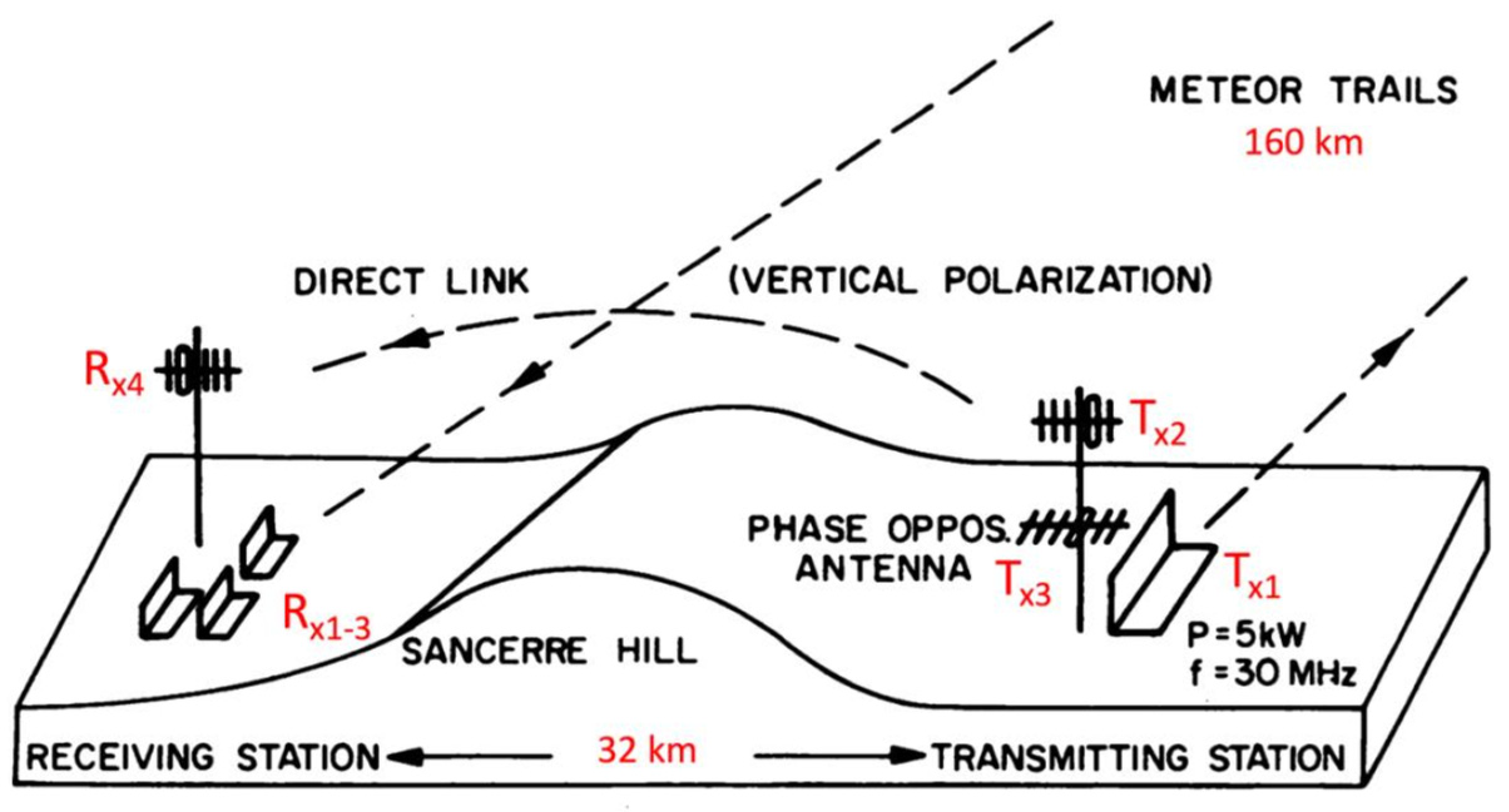
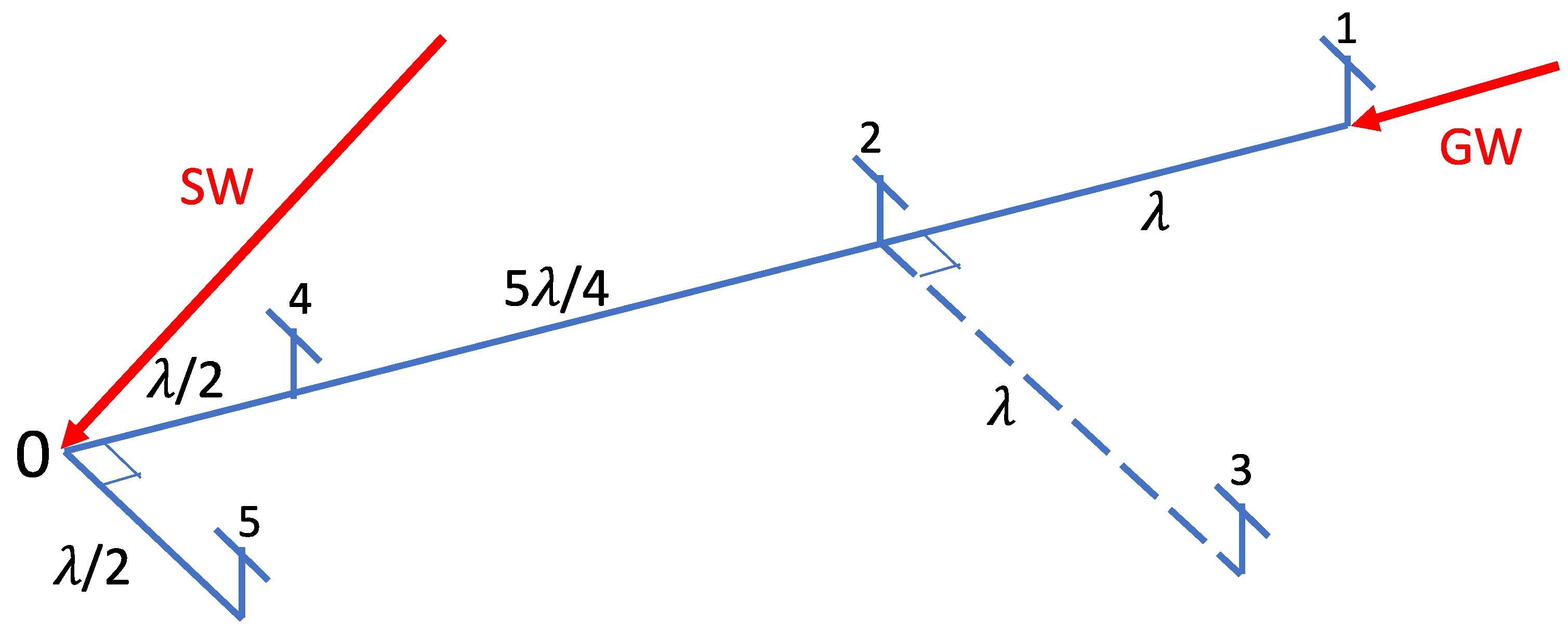
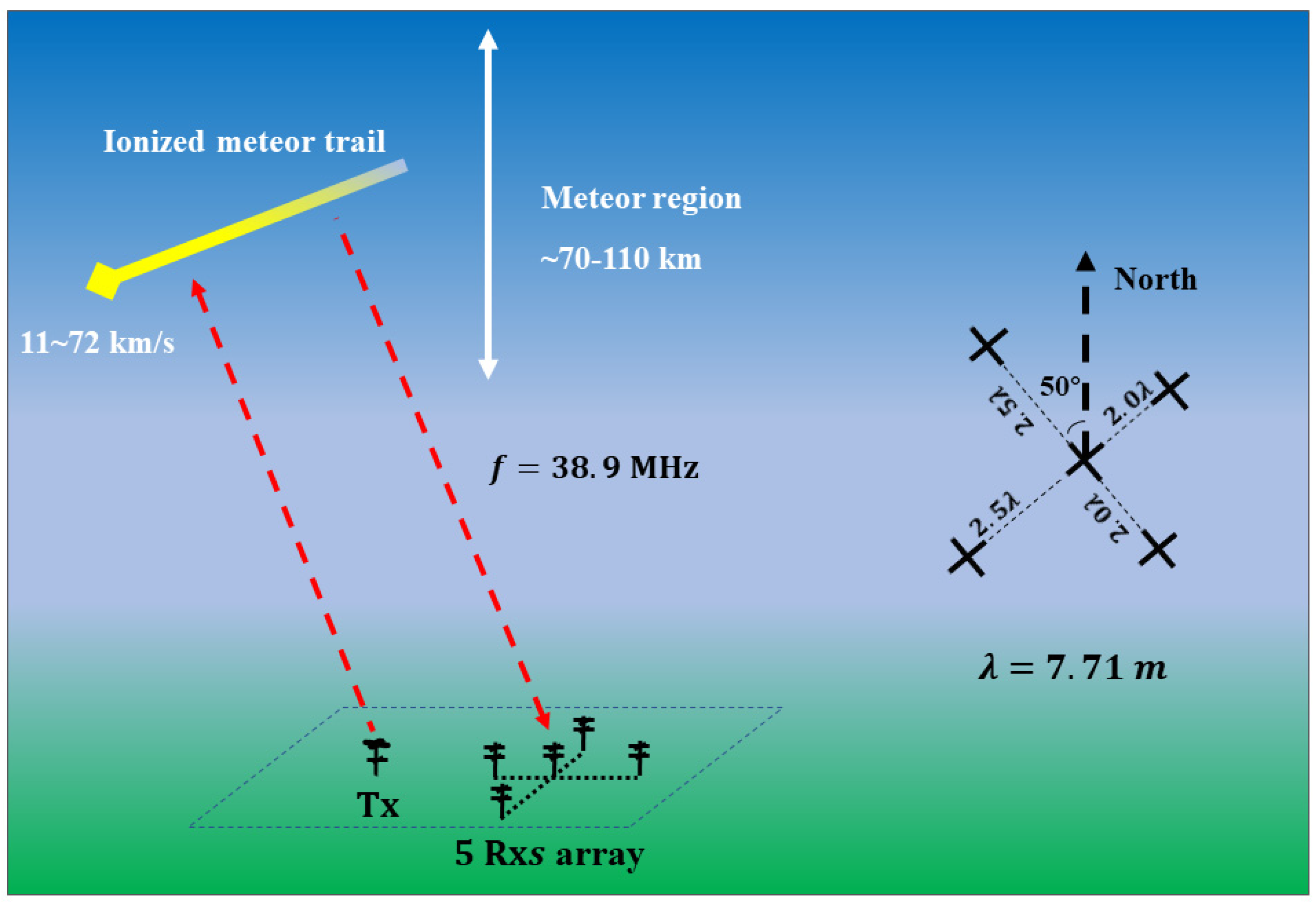
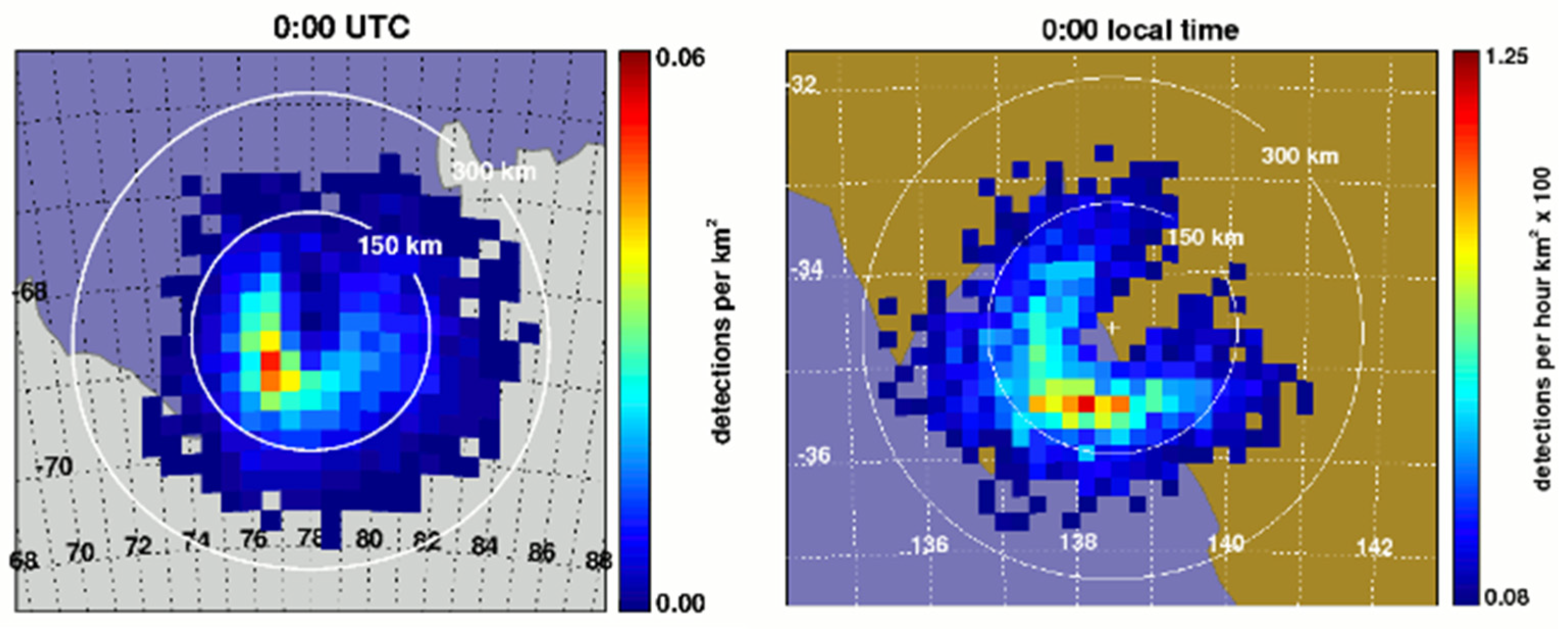
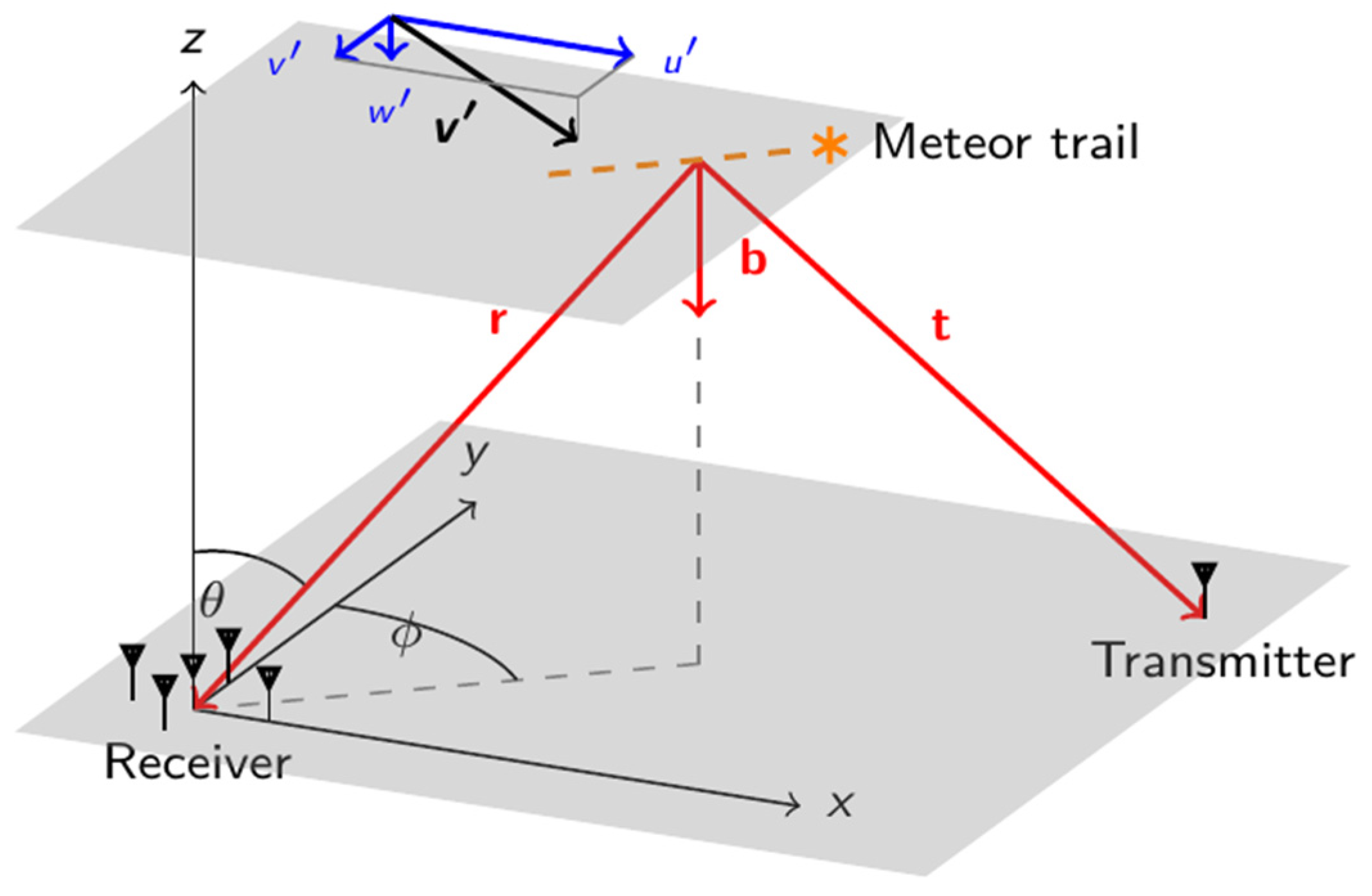
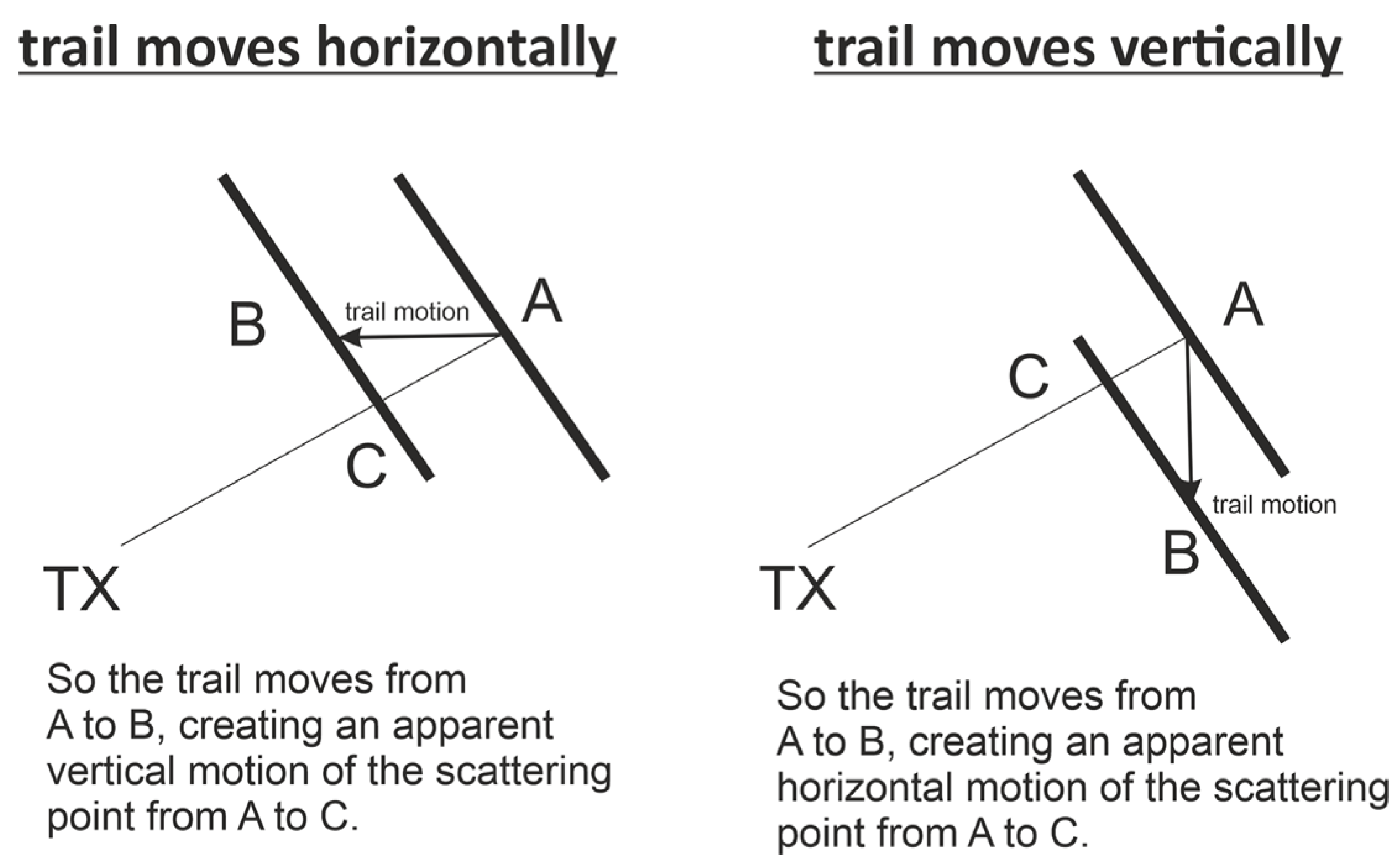
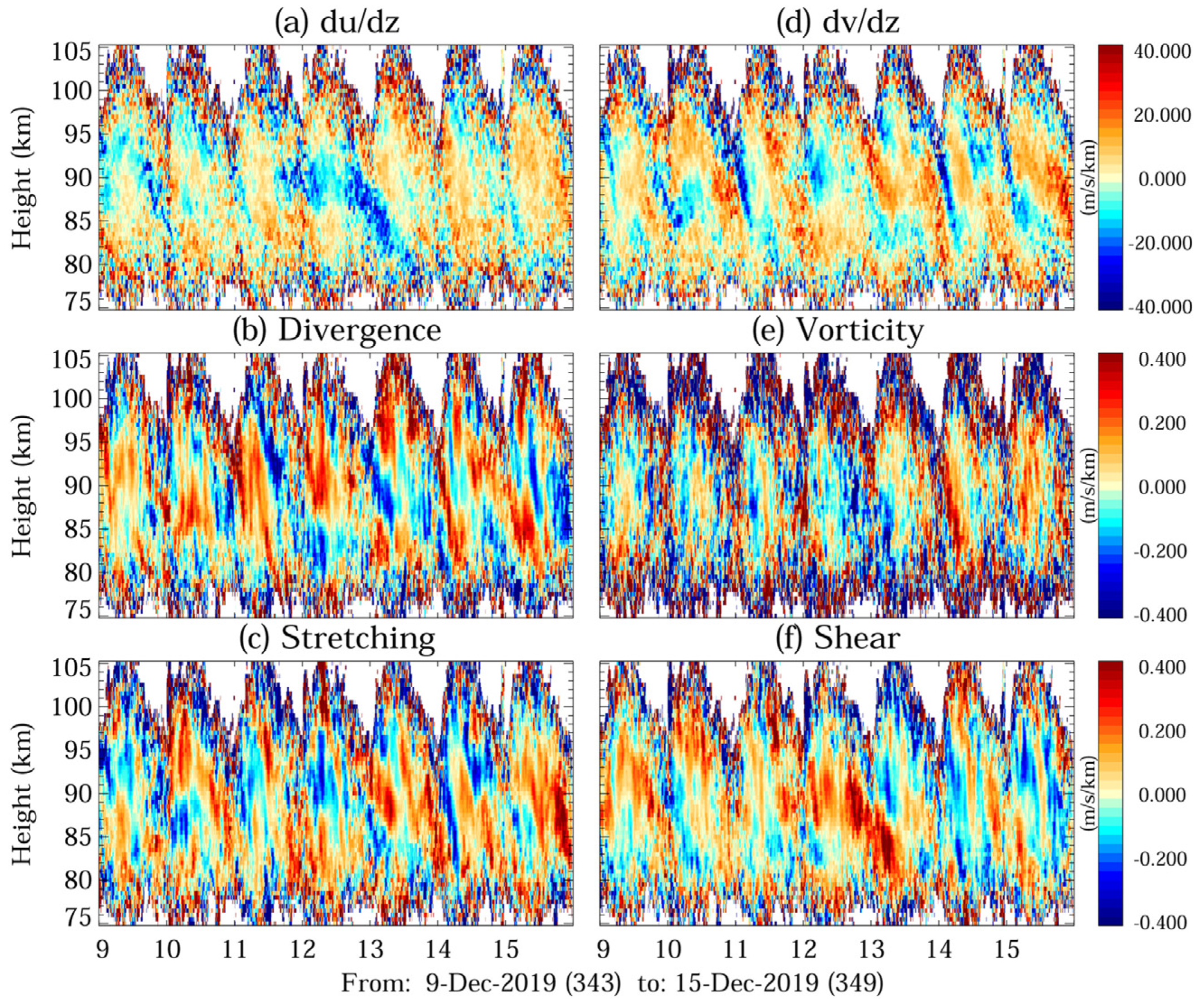
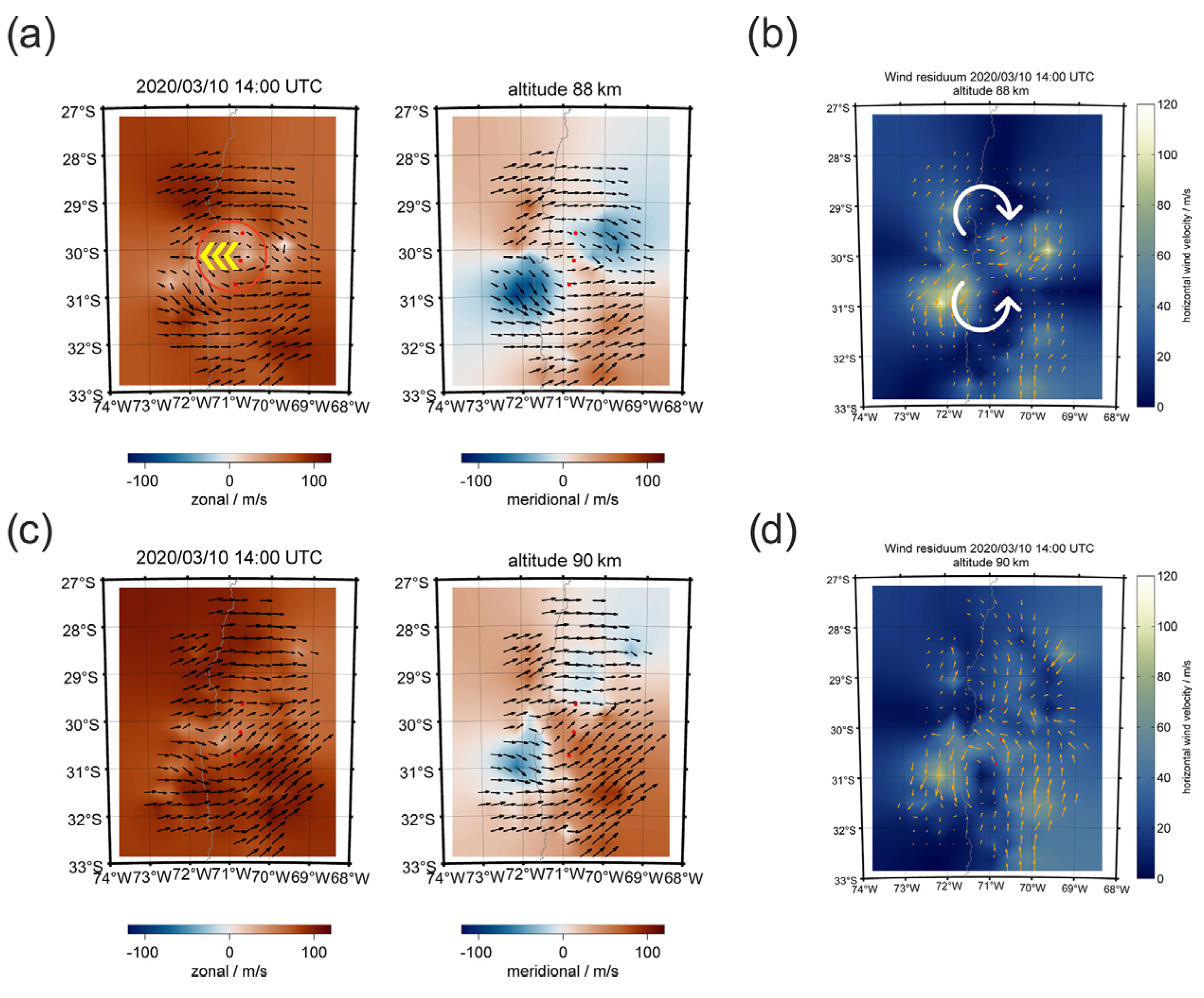
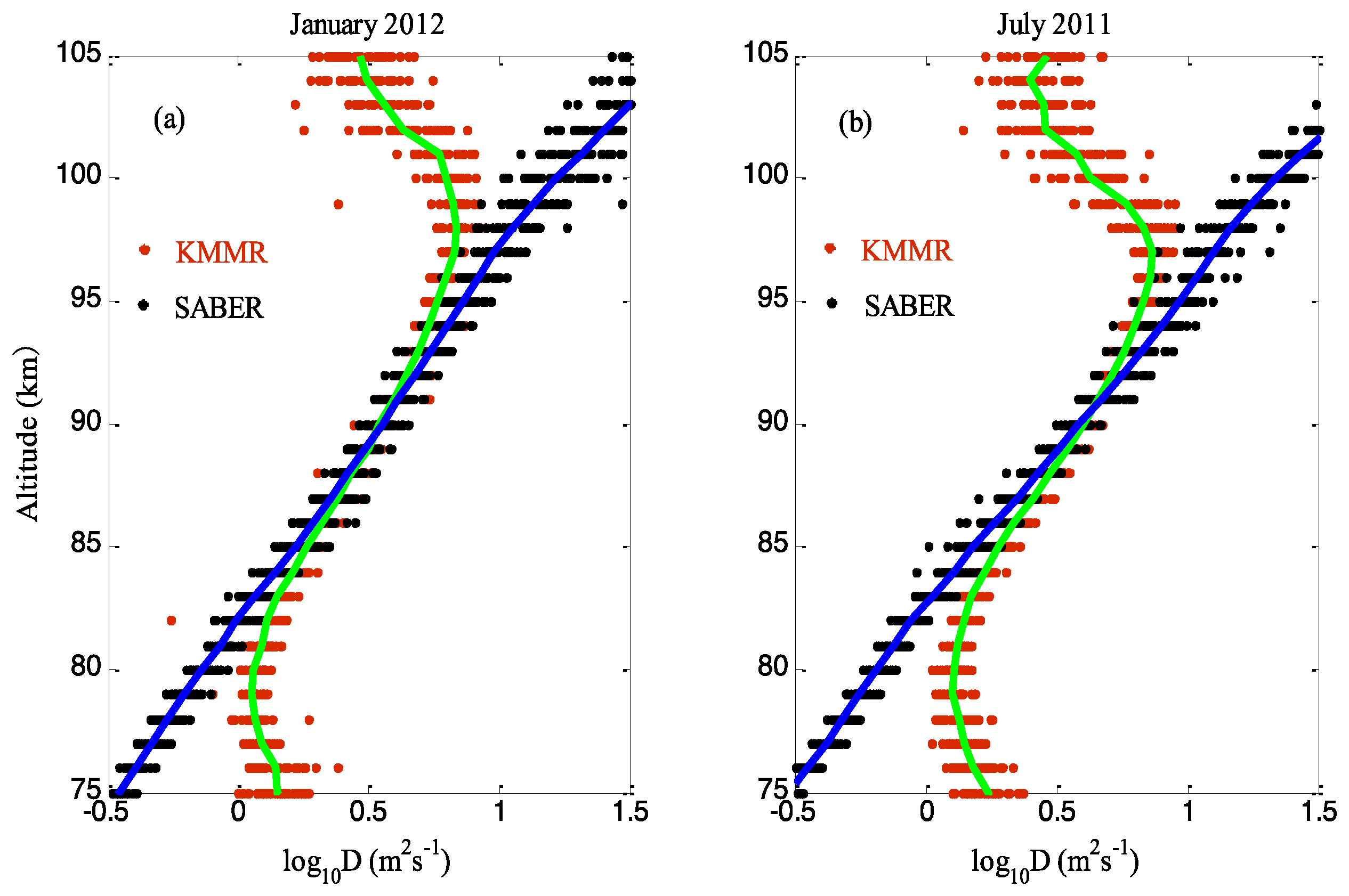
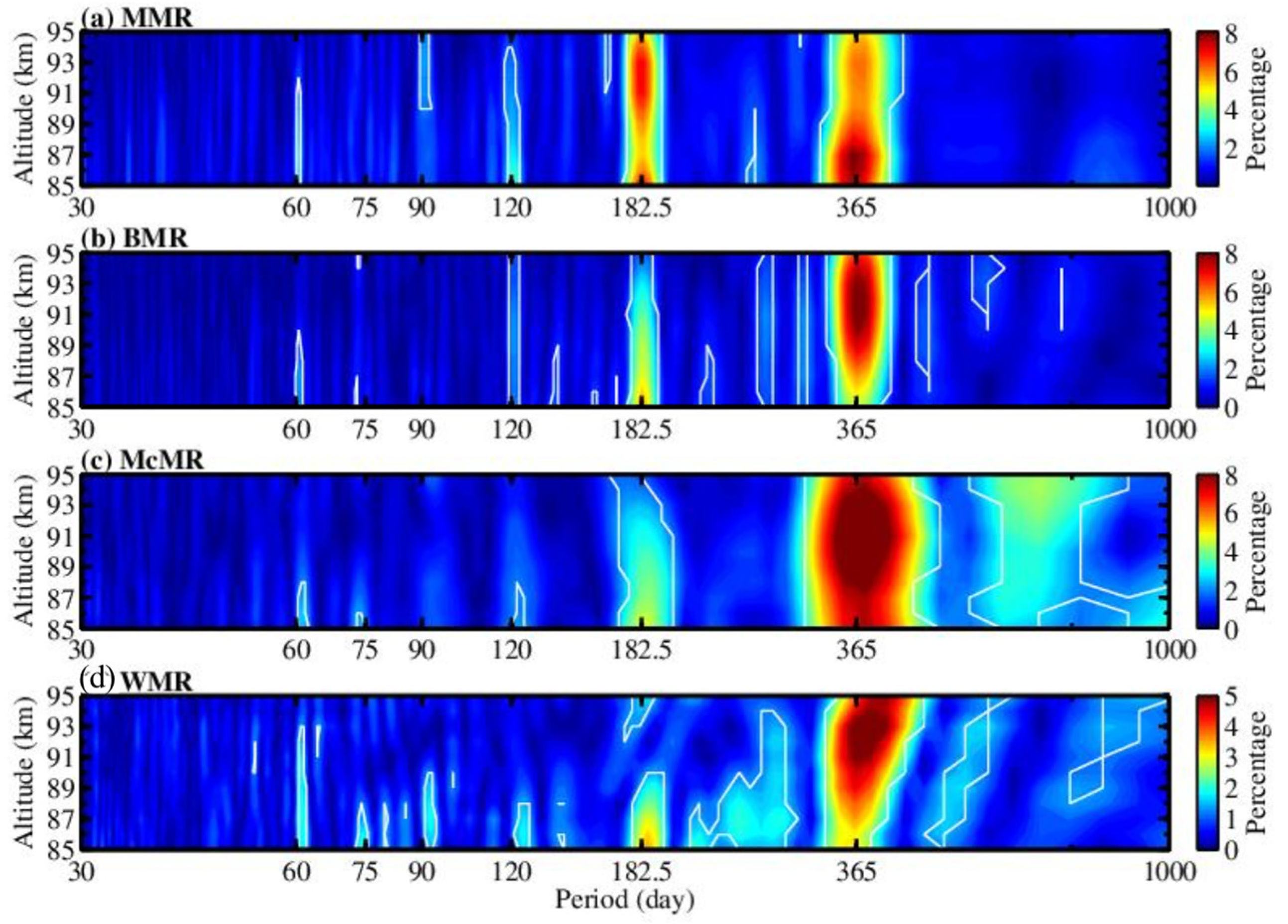
| Parameter | Mengcheng [80] | Langfang [85] |
|---|---|---|
| Location | USTC Observatory, Mengcheng (33.4° N, 116.5° E), China | NSSC Langfang Observatory (39.39° N, 116.66° E), China |
| Frequency | 38.9 MHz | 35.0 MHz in Meteor Mode; 53.8 MHz in ST Mode |
| Receive Channels | Six (Five used) | Six (Five used); Six (One used) |
| Peak power | 24 kW | 48 kW |
| Antennas | One crossed two-element folded dipole for Tx, and five two-element crossed Yagis for Rx | One crossed two-element folded dipole for Tx, and five two-element crossed Yagis for Rx; 144 (12 × 12) three-element linear Yagis for Tx/Rx, tuned |
| Pulse repetition frequency | 430 Hz | 430 Hz; user selected |
| Transmission mode | Circular | Circular; linear |
| Coherent integrations | Four | Four; user-selected |
| Range resolution | 1.8 km | 1.8 km; from 100 m |
| Pulse type | Gaussian | Gaussian; Raised cosine |
| Pulse width | 24 μs | 24 μs; user-selected |
| Duty cycle | 8.3% | 8.3%; 2.4% @ 600 m |
| Detection range | 70–110 km | 70–110 km; 0.5–20 km |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Reid, I.M. Meteor Radar for Investigation of the MLT Region: A Review. Atmosphere 2024, 15, 505. https://doi.org/10.3390/atmos15040505
Reid IM. Meteor Radar for Investigation of the MLT Region: A Review. Atmosphere. 2024; 15(4):505. https://doi.org/10.3390/atmos15040505
Chicago/Turabian StyleReid, Iain M. 2024. "Meteor Radar for Investigation of the MLT Region: A Review" Atmosphere 15, no. 4: 505. https://doi.org/10.3390/atmos15040505
APA StyleReid, I. M. (2024). Meteor Radar for Investigation of the MLT Region: A Review. Atmosphere, 15(4), 505. https://doi.org/10.3390/atmos15040505






