Abstract
To ensure water use and water resource security along “the Belt and Road”, the runoff and hydrological droughts and floods under future climate change conditions in the upper Heihe River Basin were projected in this study, based on the observed meteorological and runoff data from 1987 to 2014, and data from 10 GCMs from 1987 to 2014 and from 2026 to 2100, using the SWAT model, the Standardized Runoff Index, run length theory, and the entropy-weighted TOPSIS method. Both the multi-GCM ensemble (MME) and the optimal model were used to assess future hydrological drought and flood responses to climate change. The results showed that (1) the future multi-year average runoff from the MME was projected to be close to the historical period under the SSP245 scenario and to increase by 2.3% under the SSP585 scenario, and those from the optimal model CMCC-ESM2 were projected to decrease under both scenarios; (2) both the MME and the optimal model showed that drought duration and flood intensity in the future were projected to decrease, while drought intensity, drought peak, flood duration, and flood peak were projected to increase under both scenarios in their multi-year average levels; (3) drought duration was projected to decrease most after 2080, and drought intensity, flood duration, and flood peak were projected to increase most after 2080, according to the MME. The MME and the optimal model reached a consensus on the sign of hydrological extreme characteristic responses to climate change, but showed differences in the magnitude of trends.
1. Introduction
The Sixth Assessment Report of the Intergovernmental Panel on Climate Change (IPCC) points out that climate change is affecting every region on Earth in various ways, and that global average temperature is expected to increase by 1.5 °C or more in the next 20 years. The intensified water cycle caused by climate change leads to some areas facing stronger rainfall and floods, and others facing more severe droughts. Strong evidence shows that climate change will increase drought and flood risk and severity, although these conclusions depend on the regions, seasons, and drought or flood metrics being considered [1,2]. In contrast with the changes in the mean state of water resources, changes in their extreme states often have more devastating social and economic impacts on natural resources and ecosystems. Therefore, extreme states, including droughts and floods, have become one of the most concerning hydrological phenomena for research (e.g., [3,4,5,6,7]).
The Heihe River Basin (HRB), the second-largest inland river basin in the northwest of China, belongs to a typical continental arid climate with low precipitation, high evaporation, and large temperature differences [8]. This basin has attracted much attention from scholars from various fields so far (e.g., [8,9,10,11,12,13]), due to its vulnerability to climate change, fragile ecological environments, water resource shortages, and some problems arising therefrom like prominent water conflicts between the upper reach and middle and lower reaches.
Large numbers of glaciers, as well as snow and permafrost, makes the basin sensitive and vulnerable to global climate change. Research has shown that the impact of climate change on runoff changes in the basin is significant, with contributions reaching 56% in 1980, increasing to 61% in 1990, and reaching as high as 93% in 2000 [14,15]. Against a background of climate warming, Shang et al. [16] assessed the runoff in the basin and showed an increasing trend from 1958 to 2014; Yin et al. [17] revealed that the total runoff during the period from 1964 to 2013 increased by 30.5%; Yang et al. [18] concluded that the runoff exhibited an upward trend between 1980 and 2010, and found that climate factors accounted for notable effects on hydrological processes in the upper HRB. In the coming decades, climate change may further intensify. How the runoff will change, especially how the runoff extremes will change in the future, is still a matter of great concern.
Much attention has been given to future runoff in this basin. For example, Wu et al. [19] concluded that the water yield would increase by 9.8% from 2006 to 2030. Zhang et al. [14] projected that the runoff would increase by 11.4% under the RCP4.5 scenario and increase by 12.5% under the RCP8.5 scenario in the near future from 2021 to 2050. Li et al. [20] estimated that projected runoff would increase by 5.6% from 2021 to 2050 and increase by 6.7% from 2051 to 2080. Note that not all the future runoff in this basin was projected to increase compared to historical periods. Wang et al. [21] investigated the simulated runoff changes under global warming by using the Soil and Water Assessment Tool (SWAT) and concluded that the simulated annual runoff in this basin would decrease by 3% and 4% under 1.5 °C and 2.0 °C of global warming, compared with the period from 1976 to 2005. It is clear from previous studies that more researchers focused on total runoff projection under climate change scenarios [14,19,20,21], while there is a significant lack of research on the response of extreme runoff to future climate change [8,12].
This basin is a high-risk area for natural disasters such as drought, floods, hail, and frost [22,23]. Research showed that, in the 20th century, drought and floods were more frequent than in other centuries, with an average of 4.2 droughts and 1.8 floods every 10 years [23]. In 2001, the basin experienced the most severe successive drought in nearly 60 years, starting in the autumn of 2001 and ending in the next spring [22]. Drought can aggravate water scarcity and challenges to food security, and may sometimes induce other natural disasters, such as sandstorms, forest fires, and insect infestations [24]. Floods are prone to cause life-threatening damage to infrastructure and property (such as houses, buildings, farmland, roads, bridges, etc.), and even to ecosystems. Therefore, in this paper, we aim to explore how runoff extremes, including both hydrological droughts and floods, are expected to change in the future as a result of climate change in the upper HRB.
As numerical models describing natural mechanisms in the atmosphere, land surface and ocean, Global Climate Models (GCMs) are widely used in research in many fields related to global warming such as climatology and hydrology [25,26,27]. GCMs can provide an important data basis for hydrological process simulation and prediction under climate change conditions. Many factors like initial and boundary conditions, parameters, model structures, etc., could lead to variability across GCM outputs of future climate data [28], and thus single GCM–driving may bring large errors to the simulation and prediction results. Some research prefers to use a multi-model ensemble (MME) as a potential solution for reducing the reliance of climate projections on a single model and the possible errors caused by an inferior choice of GCM (e.g., [2,29,30,31]). Some believe that to abandon some GCMs with poor performance in projections and to select a few optimal GCMs from a pool is very necessary [32], and they regard the optimal GCM as generally corresponding to the best performance and less uncertainty [33,34]. However, undeniably, the selection of the optimal GCM usually depends on many factors such as evaluation methods and evaluation indicators [34,35]. Since not much evidence suggests that the MME and the optimal GCM will agree on the sign and magnitude of hydrological extreme responses, we will use both of them to assess the future drought and flood responses to climate change in this study, and then visit the similarities and differences on the conclusions arising therefrom.
Consequently, this study will probe into the following two issues: (1) How do runoff and hydrological extremes (drought and flood) change under future (from 2026 to 2100) climate change conditions? and (2) What are the similarities and differences between the hydrological extreme characteristics obtained from the MME and the optimal GCM?
As many as 10 GCMs were used to provide information, to avoid possible large errors caused by a single model or inferior model, and to help to reduce the uncertainty caused by data deviation. The entropy-weighted TOPSIS method was used to select the optimal GCM from the 10 alternatives. Future runoff and hydrological drought and floods were projected using the SWAT model and the Standardized Runoff Index (SRI). Based on the SRI series, the duration, intensity, and the peak of hydrological drought and flood events were mainly focused on.
2. Study Area and Data Description
2.1. Study Area
The HRB is located in the central part of the Hexi Corridor, between 98°–102° E and 38°–42° N, with an area of approximately 14.29 × 104 km2. Geographically, it includes the Yingluoxia watershed (i.e., the upper reach of the basin, above the Yingluoxia hydrological station), the middle Hexi Corridor (i.e., the middle reach), and the northern Alxa high plain (i.e., the lower reach) from south to north. The climate of the basin is characterized by cold and dry winters and hot and arid summers. The Yingluoxia watershed, with an area of approximately 10,000 km2, is the main runoff-producing area of the basin (Figure 1), and thus was selected as our study area. The upper reach has an altitude of 2000–5500 m, an annual average temperature of less than 2 °C, and an annual precipitation of 200–500 mm, gradually decreasing from east to west spatially, and mainly concentrated from June to August temporally (accounting for more than half of the total annual precipitation).
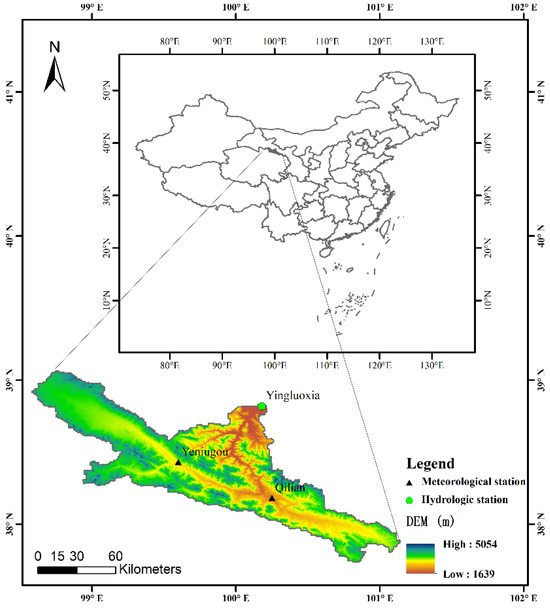
Figure 1.
The location of the upper Heihe River Basin.
The Heihe River and its tributaries are primarily fed by precipitation and snowmelt in mountainous areas of the upper reach. According to the observed runoff data from the Yingluoxia station, the multi-year average annual runoff of the upper reach is 1.61 billion m3. The inner annual distribution of runoff is uneven, with over half concentrated in the flood season (from July to September) and about 10% in the dry season (from November to the next February) [20].
2.2. Data Description
Three types of data were used in this study: geographic information data, meteorological and runoff observation data, and GCM simulation data.
The geographic information data includes the DEM data, land use type data, and soil data, with detailed descriptions shown in Table 1. The meteorological and runoff observation data include the daily precipitation, relative humidity, average wind speed, and maximum and minimum temperatures from the Tuole, Yeniugou, and Qilian stations from 1987 to 2014, as well as daily runoff data from the Yingluoxia hydrological station at the outlet of the watershed during the same period. The locations of the stations are presented in Figure 1 and Table 2. The GCM data include the daily precipitation, relative humidity, average wind speed, and maximum and minimum temperatures derived from 10 GCMs provided by CMIP6 during two periods, 1987–2014 and 2026–2100, under two scenarios, SSP245 and SSP585. The details are shown in Table 3. The above data are all released by official international or domestic institutions.

Table 1.
The data used in this study and their sources.

Table 2.
Locations of meteorological and hydrological stations in the study area.

Table 3.
List of GCMs selected in this study.
3. Study Methods
3.1. SWAT Model and Performance Evaluation
The SWAT model is a watershed hydrological model with strong physical mechanisms, suitable for simulating the impacts of climate change and human activities on watershed hydrological cycles. This study used the SCS runoff curve method for surface runoff estimation, the Muskingum algorithm for river flow calculation, and the Penman–Monteith method for potential evapotranspiration estimation. The runoff series of the Yingluoxia station was divided into three periods: a warmup period from 1987 to 1989, a calibration period from 1990 to 2000, and a validation period from 2001 to 2014. The coefficient of determination (Equation (1)) and the Nush efficiency coefficient (Equation (2)) were used to evaluate the simulation performance of the model.
Here, and mean the observed and simulated values of the runoff at the time, , , and mean the average observed and simulated runoff over many years, and means the length of the time series. Moriasi et al. [36] provided the specific performance evaluation criteria, as detailed in Table 4.

Table 4.
Model performance evaluation criteria (Moriasi et al. 2007 [36]).
3.2. Data Bias Correction
It is necessary to perform bias correction on GCM output data before using them. The commonly used methods for the bias correction of such data include the Delta method, the linear scaling method, and the QM family of methods [37,38,39,40,41]. The QM family of methods are considered to be the most important, popular, and promising bias-correction methods [40].
The QM methods implement statistical transformations for the post-processing of GCM outputs. The statistical transformations involve transforming the distribution functions of the modeled variables into the observed ones using a mathematical function. Both parametric and nouppln-parametric transformation functions have been proposed. A typical non-parametric QM method is the Empirical quantile mapping method (EQM), which uses a non-parametric transformation function. EQM estimates the values of the empirical cumulative distribution functions of observed and modeled time series for regularly spaced quantiles. Accordingly, EQM uses interpolations to adjust a datum with unavailable quantile values [40,41]. EQM uses the empirical distributions of the data and does not require any initial assumptions of specific theoretical distributions about the data, and is not bound by any predetermined functions, which makes this method more flexible. Hence, this method was chosen in this study for the bias correction of the GCM outputs. Details about this method can be found in the references (see Enayati et al. [40] and Li et al. [41]). The indicator (Equation (3)) was used for evaluating the performance of bias correction,
where and indicate the simulated values from GCMs and the observed values of the variable, and is the sample size of the data series.
3.3. Optimal GCM Selection and MME
The Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS) is a decision technique used in the multi-objective decisional analysis of finite schemes, proposed by Rau and Wassenberg [35]. The method is based on the principle that the chosen alternative should have the shortest distance from the ideal solution and the furthest distance from the anti-ideal solution. In this study, we use the entropy-weighted TOPSIS method to prioritize the 10 bias-corrected GCM outputs [34,35] according to their performances in simulating the observed precipitation and the maximum and minimum temperatures from 1987 to 2014. The procedures are as follows [34]:
I. Build the original decision matrix according to the selected indicators which are evaluated, and then normalize it based on Equation (4) to form the normalized decision matrix ,
where represents the value of indicator for the GCM (, and and represent the maximum and minimum values of indicator for all GCMs, respectively.
II. The weight of each indicator is determined by the information entropy, namely, based on the evaluation of the variation degree of each indicator value, and then forms the weighted normalized decision matrix , where , and is given by:
III. The distance of positive and negative ideal solutions and are calculated following the ideal value () and anti-ideal values () of each indicator for GCM :
This technique is designed to minimize the distance of a data object from the positive ideal solution () and maximize the distance from the negative ideal solution ().
IV. The relative closeness degree () of each GCM is calculated as follows:
The performance of bias-corrected GCMs can be ranked according to . The larger the values of , the better the performance of the GCM. Five evaluation indicators, including the mean, standard deviation, coefficient of variation, normalized root mean square error, and the Pearson correlation coefficient are used to evaluate the performance of bias-corrected GCMs in simulating the monthly precipitation and maximum and minimum temperatures [35].
The MME was constructed using the simple arithmetic averaging approach; i.e., the arithmetic mean of a climate variable given by all the alternative GCMs is used as the output of the MME.
3.4. Standardized Runoff Index and Drought/Flood Characteristic Variables
The Standardized Runoff Index (SRI) proposed by Shukla and Wood was selected to analyze the hydrological drought and flood characteristics of the study area. Many studies have shown the efficacy of this index in depicting hydrological droughts (e.g., [42,43,44]). To obtain this index, fit the runoff series for a certain period by first using Gamma distribution, and then transform it into a standard normal distribution through an equal probability transformation.
According to the rating standard of the SRI, when the index is between −0.5 and 0.5, it indicates a normal state. When the SRI ≤ −0.5, it indicates drought, and the smaller the value, the stronger the degree of drought. When the SRI ≥ 0.5, it indicates flood, and the larger the value, the stronger the degree of flood [43].
In terms of the SRI series, the drought and flood events and their characteristics (i.e., duration, intensity, and peak) were identified using run length theory [43]. Taking drought as an example, set the threshold R0 as −0.5, where a positive run occurs when the SRI value is greater than this threshold, and a negative run occurs when it is lower. One negative run represents one drought event. Drought duration, indicating the duration of one drought event, refers to the length of a negative run. Drought intensity, representing the cumulative value of the SRI in one drought event, refers to the area of a negative run. Drought peak, representing the minimum value of the SRI in one drought event, refers to the extreme value of a negative run. The three characteristics are shown in Figure 2. Similarly, the flood events and their corresponding characteristics were determined as well, with a threshold of +0.5 for flood events.
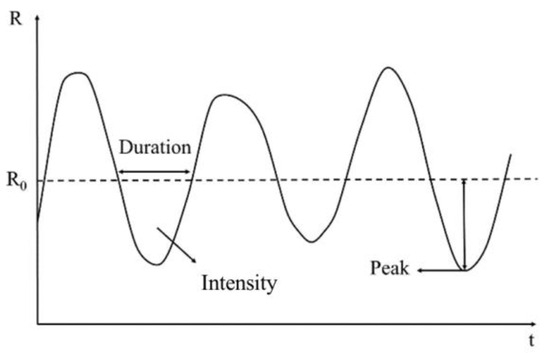
Figure 2.
The definition of drought characteristics based on run length theory.
Drought duration, intensity, and peak in one year was defined as the total duration, the average intensity, and the minimum peak of all drought events within this year, respectively. Flood duration, intensity, and peak in one year was defined similarly to above, corresponding to the total duration, the average intensity, and the maximum peak of all flood events within this year, respectively.
4. Results and Analysis
4.1. Historical Runoff Simulation and Hydrological Drought and Flood Assessment
4.1.1. Historical Runoff Simulation
Figure 3 shows the simulated daily runoff from the calibrated SWAT model and the observed values at Yingluoxia station. It can be seen that the simulated values are in good agreement with the observed ones. The R2 reaches 0.87 and the NSE reaches 0.68 in the calibration period, showing good performance in the simulation according to Table 3. The R2 reaches 0.89 and the NSE reaches 0.71 in the validation period, showing very good performance in the simulation. This indicates that the model achieved high accuracy in simulating the runoff process in the study area, and the simulation performance is good. Hence, the model can be used for predicting future runoff processes.
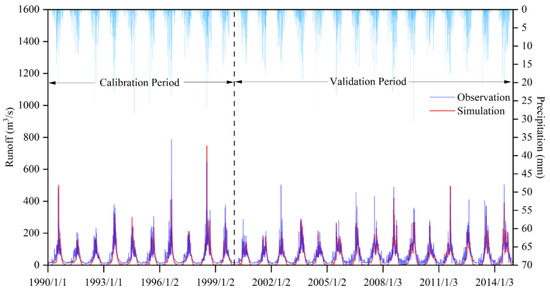
Figure 3.
Runoff observation at the Yingluoxia station and its simulation from the SWAT model.
4.1.2. Historical Hydrological Drought and Flood Assessment
According to the measured runoff data, the SRI series was calculated and then the duration, intensity, and peak values of hydrological drought and flood events were extracted based on run length theory. The multi-year average hydrological drought duration in the basin was 2.83 months, the drought intensity was −0.83, and the drought peak was −1.01 from 1987 to 2014. The multi-year average flood duration was a little longer, 5.15 months, the flood intensity was 1.23, and the flood peak was 1.87.
Figure 4 shows the hydrological drought and flood characteristics during the historical periods in detail. It can be seen that, after 2000, the drought duration became shorter, and the drought peak also decreased, but the flood duration increased, and the flood peak also increased. That is, after 2000, hydrological drought in the study area was alleviated, while floods were enhanced.
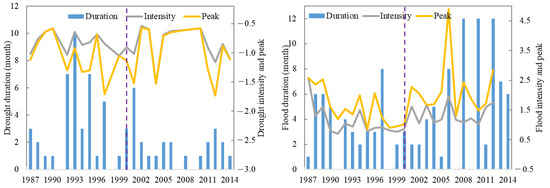
Figure 4.
Hydrological drought and flood characteristics in historical period (1987–2014) in the upper HRB (the purple dashed line corresponds to the year 2000).
4.2. Future Runoff Projection and Analysis
4.2.1. Bias Correction of GCM Output
Figure 5 shows the box plot of the GCM output from 1987 to 2014, before and after the bias correction. Before the bias correction, the meteorological variables from the GCMs were largely overestimated; especially for precipitation, the simulated values reach about four times the observed ones. After the bias correction, all data deviations were significantly reduced.
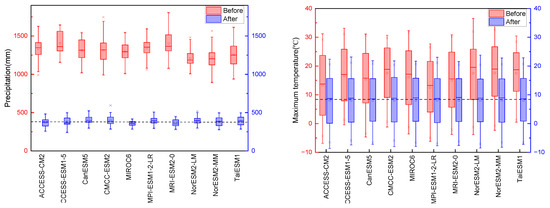
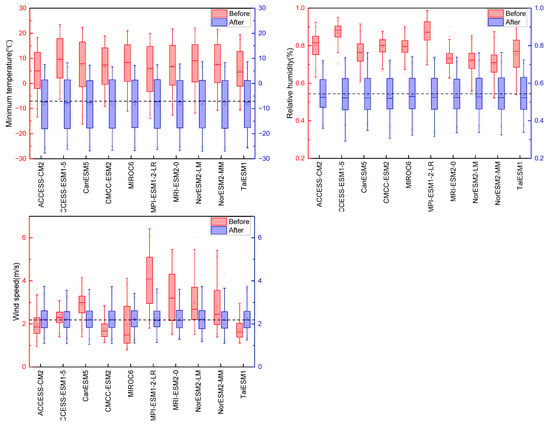
Figure 5.
Box plots of comparisons of GCM output from 1987 to 2014 before and after bias correction (the dashed lines indicate the multi-year average observed values).
Table 5 shows the values of indicator . All the values decreased after the bias correction. For example, the decreased from 2.45 to −0.04 for the precipitation data from ACCESS-CM2, decreased from 1.18 to 0.00 for the maximum temperature from CMCC-ESM2, and decreased from 2.18 to 0.00 for the minimum temperature from ACCESS-ESM1-5. After the bias correction, the multi-year average values of all variables simulated by each GCM were closer to the measured ones (Figure 5).

Table 5.
Comparisons of indicator PBIAS for GCM output before and after bias correction (%).
4.2.2. Optimal GCM Selection
From Figure 5, it can also be seen that the performance of different GCMs in simulating the meteorological variables varies, even after the bias correction. Thus, the optimal model was selected from the 10 models using the entropy-weighted TOPSIS method.
The monthly precipitation, maximum temperature, and minimum temperature, from 1987 to 2014, was selected as the basic data to be analyzed. For the indicators of mean, standard deviation, and the coefficient of variation, the absolute value of the difference between the bias-corrected GCM output and the measured data was taken for better comparison. The results of the evaluation indicators are shown in Table 6. After normalizing each indicator, the entropy-weighted method was applied to determine the weight of each indicator, and the results are shown in Table 7. By taking the set of evaluation indicators from the measured data as the positive ideal solution, and that farthest from the measured data as the negative ideal solution, the relative closeness degree between different GCMs and the ideal solution can be obtained from Formulas (6) and (7), which is shown in Table 8. The larger the value of , the better the simulation performance and the higher the ranking of the model. According to Table 8, CMCC-ESM2 has the best performance in simulating monthly precipitation, maximum temperature, and minimum temperature in the study area, followed by the NorESM2-MM model and the MRI-ESM2-0 model.

Table 6.
Evaluation indicators of bias-corrected GCMs in simulating monthly precipitation and temperatures in the study area.

Table 7.
The weights of evaluation indicators determined by the entropy-weighted method.

Table 8.
Performance ranking of different GCMs in simulating monthly precipitation and maximum and minimum temperatures based on the entropy-weighted TOPSIS method.
4.2.3. Future Projected Runoff
After inputting the future bias-corrected meteorological variables into the calibrated SWAT model, the future runoff was then projected. Table 9 gives the multi-year average projected runoff and its comparison with the historical period. The projected runoff from 2026 to 2100 from different GCMs varies significantly. Under the SSP245 scenario, five GCMs (ACCESS-CM2, MIROC6, MRI-ESM2-0, NorESM2-LM, and TaiESM1) projected an increase in the future runoff compared to the historical period, with increases of 1.6% to 10.8%. The other five GCMs projected a decreased future runoff, decreasing by 0.9% to 13.0%. Under the SSP585 scenario, six GCMs (ACCESS-CM2, CanESM5, MIROC6, MRI-ESM2-0, NorESM2-LM, and TaiESM1) projected an increased future runoff, increasing by 1.0% to 19.8%, and the other four models projected a decreased runoff, decreasing by 0.9% to 11.0%.

Table 9.
Multi-year average future runoff projection (2026–2100) and the changes compared to historical period (1987–2014).
Figure 6 shows the ranges of annual runoff projected by all the GCMs, the annual runoff projected by the MME and by the optimal model CMCC-ESM2, and their multi-year average values. It is clear that the ranges of projected annual runoff are large and vary a lot in their multi-year average level, from 27.5 m3/s to 57.2 m3/s under the SSP245 scenario and from 27.0 m3/s to 59.8 m3/s under the SSP585 scenario, indicating that the projected runoff has great uncertainty. The MME, combining the projections of large numbers of GCMs, may reduce this uncertainty to a certain extent. Under the SSP245 scenario, the multi-year average annual runoff projected by the MME is 40.5 m3/s, close to the historical period. Under the SSP585 scenario, the projected runoff is 41.5 m3/s, an increase of 2.3% compared to the historical period. The optimal model CMCC-ESM2 projected a lower runoff than the MME, with a multi-year average of 37.7 m3/s under the SSP245 scenario and 37.3 m3/s under the SSP585 scenario, which is a decrease of 7.1% (SSP245) and 8.1% (SSP585), respectively.
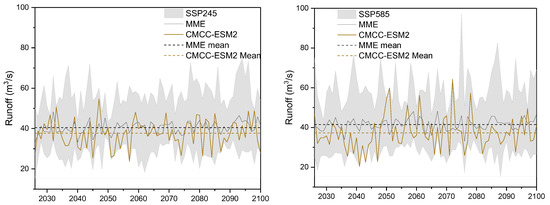
Figure 6.
Future runoff projection under SSP245 and SSP585 scenarios in the study area (2026–2100).
4.3. Future Hydrological Drought and Flood Projection and Analysis
The SRI series was calculated based on the future runoff series, and then the drought and flood events and characteristics were derived from the SRI series using run length theory. Figure 7, taking the results of the SSP245 scenario as an example, shows the projections of drought/flood duration, intensity, and peak from 2026 to 2100. It shows that the variations of all characteristics are great, indicating that large differences exist in the projections given by different GCMs. Figure 8 shows the changes in the projected characteristics compared to the historical period. Table 10 and Table 11 show the changes in future runoff and hydrological drought and flood characteristic projections compared to the historical period.
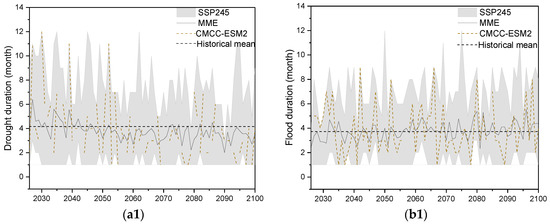
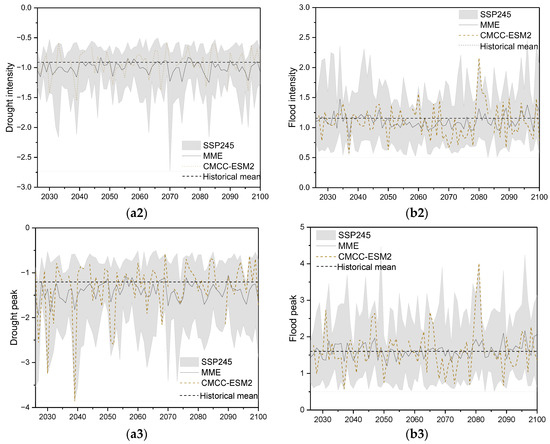
Figure 7.
Future hydrological drought and flood characteristic ((a1): Drought duration, (a2): Drought intensity, (a3): Drought peak, (b1): Flood duration, (b2): Flood intensity, (b3): Flood peak) projection under SSP245 scenario (2026–2100) and the comparison with the historical period (1987–2014).
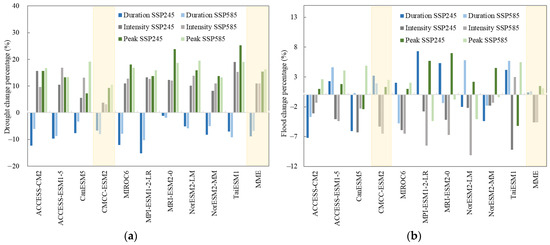
Figure 8.
Changes in future hydrological drought (a) and flood (b) characteristic projections (2026–2100) compared to the historical period (1987–2014).

Table 10.
Percentages of changes in the multi-year average future runoff and hydrological extreme characteristic projections (2026–2100) compared to the historical period (1987–2014) (%).

Table 11.
Percentages of changes in future runoff and hydrological extreme characteristic projections in different periods compared to the historical period (1987–2014) (%).
4.3.1. Hydrological Drought
Drought Duration
According to Figure 7 and Figure 8, all the GCMs projected a shorter drought duration in multi-year average value than the historical period (blue bars in Figure 8a) and, among them, model MPI-ESM1-2-LR projected the shortest multi-year average duration, which decreased by 15.2% and 10.3% under the SSP245 and SSP585 scenarios, respectively. In terms of the result of the MME, although some years before 2050 were projected to have a longer drought duration than the historical period, after 2050 they were basically shorter (Figure 7(a1) and Table 11). The MME projected the multi-year average drought duration to be 3.77 months under the SSP245 scenario and 3.86 months under the SSP585 scenario, a decrease of 0.39 months (8.8%) and 0.30 months (6.8%) under the two scenarios, respectively. The optimal model CMCC-ESM2 projected a multi-year average drought duration of 3.86 months and 3.81 months, a decrease of 0.28 months (6.7%) and 0.33 months (8.0%) under the SSP 245 and SSP585 scenarios compared to the historical period (Table 10). In addition, the annual drought duration projected by the optimal model CMCC-ESM2 shows a decreasing trend over time overall (Figure 7(a1)). The above results indicate that the average duration of drought events in the study area will be shortened in the future.
Drought Intensity
Contrary to drought duration, the drought intensity projected by all the GCMs increased in multi-year average value compared to the historical period (gray bars in Figure 8a), with an increasing rate from 3.8% to 19% under the SSP245 scenario and a lower rate from 3.2% to 16.8% under the SSP585 scenario. Model TaiESM1 projected the largest increases (19%) under the SSP245 scenario, and model ACCESS-ESM1-5 projected the largest increases (16.8%) under the SSP585 scenario. The optimal model CMCC-ESM2 projected the least increases (3.8% and 3.2%) under both scenarios. The MME projected the multi-year average drought intensity to be −1.0, an 11% increase compared to the historical period (Table 10). From Figure 7(a2), it can also be observed that most of the annual drought intensity projected by the MME was greater than the historical mean value (black curve basically lower than the horizontal dashed line). The increase in drought intensity can reflect that drought in the future will become more severe to some extent.
Drought Peak
Similar to drought intensity, the multi-year average drought peak projected by all the GCMs also increased compared to the historical period (green bars in Figure 8a), with a greater increasing rate than drought intensity, ranging from 7.3% (CanESM5) to 25.3% (TaiESM1) under the SSP245 scenario, and 10.5% (CMCC-ESM2) to 19.5% (NorESM2-LM) under the SSP585 scenario. The multi-year average drought peak projected by the MME showed an increase of 15.4% under the SSP245 scenario and 16.2% under the SSP585 scenario (Table 10). The annual drought peak projected by the MME was also greater than the historical mean value in most years (black curve basically lower than the horizontal dashed line in Figure 7(a3)). The increase in drought peak indicates that the severity of extreme drought will strengthen in the future.
4.3.2. Flood
Flood Duration
Unlike drought characteristics, flood characteristics projected by the different GCMs are not so consistent in trends. For flood duration, four GCMs projected a decreased multi-year average flood duration, and six GCMs projected the opposite under both scenarios (blue bars in Figure 8b). Due to great differences between them, we mainly analyzed the results from the MME and the optimal model.
The multi-year average flood duration projected using the MME was 3.77 months and 3.78 months under the SSP245 and SSP585 scenarios, very close to the historical period. However, as shown in Figure 7(b1), differences exist in different time periods. The multi-year average flood duration was projected to reduce by 8.6% (SSP245) and 11.5% (SSP585) before 2050, to increase after 2050 by 4.6% (SSP245) and 6.3% (SSP585), and to increase more after 2080, by 7.6% (SSP245) and 14.8% (SSP585) (Table 11). Those projected by the optimal model CMCC-ESM2 were a little larger than the results of the MME for the multi-year average values, showing increases of 3.2% and 1.9% under the SSP245 and SSP585 scenarios, respectively (Table 10). From different time periods, the optimal model projected the highest increase (9.2%) after 2080 under the SSP245 scenario, and the highest increase (7.5%) from 2050 to 2079 under the SSP585 scenario (Table 11). Both the MME and the optimal model show the projected duration of flood events will be extended as a whole.
Flood Intensity
The flood intensity was projected to decrease in almost all time periods compared to historical periods, and the MME and the optimal model CMCC-ESM2 produced the same trends in the projections overall (Figure 7(b2)). The multi-year average flood intensity was projected to decrease by 4.6% under both scenarios based on the MME, and decrease by 5.3% and 6.5% based on the optimal model under the SSP245 and SSP585 scenarios, respectively (Table 10). The most significant decline was projected to occur during the period 2050–2079 under the SSP245 scenario, and during the period 2026–2049 under the SSP585 scenario (Table 11). This indicates that the floods in the study area will alleviate in the future overall; however, the changes in flood intensity vary in different future periods, decreasing more after 2050 under the SSP245 scenario while decreasing more before 2050 under the SSP585 scenario.
Flood Peak
There was a slight increase in the trend for the projected multi-year average flood peak based on the results of the MME and the optimal model, but the trends were different in different time periods (Figure 7(b3) and Table 11). For example, under the SSP245 scenario, increases were projected during the periods 2026–2049 and 2080–2100, whereas decreases were predicted during the period 2050–2079 (Table 11). In addition, based on the results of the MME, the flood peak was projected to increase most (by 7.8% under the SSP245 scenario and 6.8% under the SSP585 scenario) after 2080 in its multi-year average value. Based on the optimal model, it was projected to increase most (10.4%) after 2080 under the SSP245 scenario, and increase most (10.6%) during the period 2050–2079 under the SSP585 scenario (Table 11). But overall, the severity of extreme flood events after 2080 will be enhanced, which will lead to a rise in flood risk.
4.4. Discussion
4.4.1. Historical Hydrological Drought and Floods
As mentioned above, by analyzing the drought and flood characteristics from 1978 to 2014, it was found that, after 2000, hydrological drought was eased while floods intensified. This should be closely related to precipitation. According to the measured precipitation data from the three stations (Tuole, Yeniugou, and Qilian), higher precipitation (an increase of about 9%) occurred after 2000 (2000–2014) than before (1978–2009). The increase in precipitation led to a reduction in drought and an intensification of floods. At the same time, it would also be affected by changes in other climate factors such as temperature. The measured temperature was found to increase after 2000. Climate warming can cause an increase in snowmelt runoff, thereby resulting in an increase in total runoff and in floods. In addition, Zan [45] concluded that the meteorological drought situation in this study area was alleviated from 1967 to 2009 based on the standardized precipitation evapotranspiration index. The alleviation of meteorological drought would restrict the occurrence of hydrological drought, so the hydrological drought would be alleviated to some extent.
4.4.2. Future Runoff
The future runoff projected by the MME slightly increased compared to the historical periods under the SSP585 scenario. It is the result of the combined effects of various factors, including climatic ones. Table 12 shows the multi-year average values of future meteorological variables. It shows that the future precipitation and temperatures were projected to increase, and relative humidity and wind speed were projected to decrease overall. The increases in future precipitation will have a promoting effect on the increases in runoff, and the changes in evapotranspiration caused by rising temperatures and other climate factors will largely offset the impact of increased precipitation on runoff. Some previous studies also concluded that the future runoff in the upper HRB will increase. For example, Zhang et al. [14] projected that the future runoff would increase by 11.4% and 12.5% under the RCP4.5 and RCP8.5 scenarios, respectively, during the period from 2021 to 2050. Li et al. [20] estimated that the runoff would increase by 5.6% and 6.7% during the periods from 2021 to 2050 and from 2051 to 2080, respectively. Conversely, some studies found decreasing trends in the future runoff over the study area. For example, Wang et al. [21] estimated that the annual runoff in this basin would decrease by 3% and 4% under 1.5 °C and 2.0 °C of global warming compared with the period from 1976 to 2005. The optimal model in our study also projected a decreasing trend in the future runoff, and so did the second optimal model, NorESM2-MM.

Table 12.
Future meteorological variable projection (2026–2100) and the changes compared to historical period (1987–2014).
It should be noted that, for the contrary trends in the future runoff projections from the MME and the optimal model, it is hard to say which one is more accurate, since both of them have uncertainty. The MME may involve inferior GCMs and thus reduce the reliability of climate projections, and the optimal model depends on many factors such as evaluation methods, evaluation indicators, and so forth, which result in the optimal model not being uniquely determined [2,29,30,31,32,33,34]. In addition to the uncertainty involved in the GCM selection process, we assumed that the optimal model selected based on historical data would be applicable to future periods, which also carries some uncertainties since we cannot judge whether the meteorological elements in the future will still follow the laws of historical periods.
In terms of the results of the MME, the projected runoff will increase in the future, which can to some extent alleviate the occurrence of hydrological drought and alleviate the contradiction of water resource shortages in the study area. The increased future runoff will result in higher water availability, which is beneficial for agricultural production in the middle reach and the natural ecosystems in the lower reach.
4.4.3. Future Hydrological Drought and Flood
By projecting hydrological drought and floods in the study area in the future, both the MME and the optimal model reveal that, under the SSP245 and SSP585 scenarios, although the multi-year average duration of hydrological drought in the future was projected to shorten compared to the historical period, especially after 2050 (decreased by 15.4% and 12.7% under the SSP245 and SSP585 scenarios from the MME, and by 20.6% and 19.3% under both scenarios from the optimal model, Table 11), the multi-year average intensity and peak of drought were both projected to increase. Although the multi-year average intensity of floods was projected to decrease (decreasing most during the period 2050–2079 under SSP245 and during the period 2026–2049 under SSP585), the flood duration and peak were projected to increase, and increase most after 2080 overall under both scenarios (except those projected by the optimal model under the 585 scenario).
By comparing the results of the MME and the optimal model in the multi-year average level, the trends they projected present the same in the duration, intensity, and peak of both hydrological drought and floods, although the magnitudes of the trends they projected vary; in specific time periods (i.e., 2026–2049, 2050–2079, 2080–2100, and 2050–2100), most of the trends they projected also present the same (Table 11). Comparatively speaking, the optimal model predicted a greater reduction in drought duration under both scenarios, and the MME predicted a greater increase in drought intensity and peak, no matter the multi-year average level or the specific time period (Table 11). The above indicates that the MME and the optimal model reached a consensus on the sign of the hydrological extreme characteristic response to climate change, but showed differences in the magnitude of the trends.
To sum up, in the future, the study area tends to suffer from hydrological drought with short duration, high intensity, and high peak value, and floods with low intensity but long duration and high peak value. This indicates that water resources in the study area will be more uneven in temporal distribution in the future, and will occur in a more extreme form (e.g., rainstorm after a long drought, or continuous drought after a rainstorm).
The uneven distribution of future runoff in the study area means that the water resource development, utilization, management, and allocation in the basin will face some new challenges. Therefore, it is necessary on one hand to adjust water use behavior and water resource development and utilization strategies in the middle and lower reaches to adapt to the changes in the total amount and the spatiotemporal distribution of water resources in the future and, on the other hand, to strengthen defenses against extreme hydrological risks, such as by fully leveraging the regulating capacity (e.g., the water storage and replenishment) of water conservancy projects such as reservoirs.
5. Conclusions
This paper projected and analyzed the future runoff (from 2026 to 2100) in the upper HRB under climate change scenarios by using 10 GCMs. Based on this, it projected and investigated the changes in the duration, intensity, and peak of future hydrological droughts and floods in the basin. The main conclusions are as follows:
- (1)
- Large differences exist in future runoff projections by different GCMs. The multi-year average runoff projected by the MME was close to the historical period (1987–2014) under the SSP245 scenario, and increased by 2.3% under the SSP585 scenario. The optimal model CMCC-ESM2, which was determined by the entropy-weighted TOPSIS method, projected a decreased runoff in the future, decreasing by 7.1% and 8.1% under the SSP245 and SSP585 scenarios, respectively.
- (2)
- Both the MME and the optimal model projected that the drought duration in the study area would decrease, especially after 2050, while the drought intensity and drought peak would increase overall under both scenarios, no matter the multi-year average level or the specific time period. It indicates that the duration of drought events in the future will be shortened, but drought will become more severe, and the magnitude of extreme drought will increase.
- (3)
- Both the MME and the optimal model projected the multi-year average flood intensity would decrease, while the flood duration and flood peak would increase on the whole under both scenarios, and that the increase magnitudes would be greater after 2080. It indicates that floods will become more severe after the mid- to late 21st century, with longer durations and a higher peak for flood events.
- (4)
- The MME and the optimal model projected the most similar trends for the duration, intensity, and peak of hydrological drought and floods in either the multi-year average level or in the specific time periods, although the magnitudes of the trends they projected vary.
We discussed the similarities and differences between the sign and magnitude of hydrological extreme responses obtained from both the MME and the optimal GCM. It is hoped that the relevant findings can provide ideas for the selection of GCM data in related research. However, the MME generated here was based just on the simple arithmetic averaging approach, without considering the weights of different models and the impacts of inferior models, which may lead to bias and uncertainty. Han et al. (2023) [34] found in their research that such an MME may severely compress the interannual variability of precipitation data. Thus, in future research, efforts can be made to construct a more accurate MME by using techniques such as random forest and machine learning.
Author Contributions
Conceptualization, Z.L. (Zhanling Li) and Y.Y.; methodology, Z.L. (Zhanling Li) and Y.Y.; software, Y.Y., X.L. and M.B.; validation, Z.L. (Zhanling Li) and Z.L. (Zhanjie Li); formal analysis, Z.L. (Zhanling Li) and Z.L. (Zhanjie Li); investigation, X.L. and M.B.; resources, Z.L. (Zhanling Li) and Y.Y.; data curation, Y.Y., X.L. and M.B.; writing—original draft preparation, Z.L. (Zhanling Li); writing—review and editing, Z.L. (Zhanling Li); visualization, Z.L. (Zhanling Li); supervision, Z.L. (Zhanling Li) and Z.L. (Zhanjie Li); project administration, Z.L. (Zhanling Li); funding acquisition, Z.L. (Zhanling Li). All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the Belt and Road Special Foundation of the State Key Laboratory of Hydrology-Water Resources and Hydraulic Engineering (2021nkms03) and the National Natural Science Foundation of China (No. 41101038).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The GCM datasets used in this study can be downloaded from http://www.ceda.ac.uk (accessed on 15 October 2022). The runoff datasets in the study area are unavailable due to privacy.
Acknowledgments
The authors thank the anonymous referees for their comments and suggestions that have led to the quality of this paper being improved.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Alfieri, L.; Bisselink, B.; Dottori, F.; Naumann, G.; de Roo, A.; Salamon, P.; Wyser, K.; Feyen, L. Global projections of river flood risk in a warmer world. Earth’s Future 2017, 5, 171–182. [Google Scholar] [CrossRef]
- Cook, B.I.; Mankin, J.S.; Marvel, K.; Williams, A.P.; Smerdon, J.E.; Anchukaitis, K.J. Twenty-first century drought projections in the CMIP6 forcing scenarios. Earth’s Future 2020, 8, e2019EF001461. [Google Scholar] [CrossRef]
- Zhang, R.; Qu, Y.; Zhang, X.; Wu, X.; Zhou, X.; Ren, B.; Zeng, J.; Wang, Q. Spatiotemporal variability in annual drought severity, duration, and frequency from 1901 to 2020. Clim. Res. 2022, 87, 81–97. [Google Scholar] [CrossRef]
- Xu, Y.; Zhu, X.; Cheng, X.; Gun, Z.; Lin, J.; Zhao, J.; Yao, L.; Zhou, C. Drought assessment of China in 2002–2017 based on a comprehensive drought index. Agric. For. Meteorol. 2022, 319, 108922. [Google Scholar] [CrossRef]
- Bi, W.; Li, M.; Weng, B.; Yan, D.; Dong, Z.; Feng, J.; Wang, H. Drought-flood abrupt alteration events over China. Sci. Total Environ. 2023, 875, 162529. [Google Scholar] [CrossRef] [PubMed]
- Rezvani, R.; RahimiMovaghar, M.; Na, W.; Najafi, M.R. Accelerated lagged compound floods and droughts in northwest North America under 1.5 °C–4 °C global warming levels. J. Hydrol. 2023, 624, 129906. [Google Scholar] [CrossRef]
- Pavur, G.; Lakshmi, V. Observing the recent floods and drought in the Lake Victoria Basin using Earth observations and hydrological anomalies. J. Hydrol. Reg. Stud. 2023, 46, 101347. [Google Scholar] [CrossRef]
- Ye, Y.; Li, Z.; Li, X.; Li, Z. Projection and analysis of floods in the upper Heihe River basin under climate change. Atmosphere 2023, 14, 1083. [Google Scholar] [CrossRef]
- Tian, Q.; Li, Z.; Sun, X. Frequency analysis of precipitation extremes under a changing climate: A case study in Heihe River basin, China. J. Water Clim. Chang. 2021, 12, 772–786. [Google Scholar] [CrossRef]
- Gao, N.N.; Li, F.; Zeng, H.; Zheng, Y.R. The impact of human activities, natural factors, and climate time-lag effects over 33 years in the Heihe River Basin, China. Appl. Ecol. Environ. Res. 2021, 19, 1589–1606. [Google Scholar] [CrossRef]
- Hu, J.; Wu, Y.; Zhao, W.; Wang, F.; Zhang, G.; Qiu, L.; Hui, J.; Yin, X. Assessment and projection of ground freezing–thawing responses to climate change in the Upper Heihe River Basin, Northwest China. J. Hydrol. Reg. Stud. 2022, 42, 101137. [Google Scholar] [CrossRef]
- Li, Z.; Li, W.; Li, Z.; Lv, X. Responses of Runoff and Its Extremes to Climate Change in the Upper Catchment of the Heihe River Basin, China. Atmosphere 2023, 14, 539. [Google Scholar] [CrossRef]
- Yang, H.; Ma, F.; Yuan, X. The role of human activities in the weakening of the propagation relationship between meteorological and hydrological droughts in the Heihe River Basin. Hydrol. Process. 2023, 37, e14946. [Google Scholar] [CrossRef]
- Zhang, A.; Liu, W.; Yin, Z.; Fu, G.; Zheng, C. How will climate change affect the water availability in the Heihe River Basin, Northwest China? J. Hydrometeorol. 2016, 17, 1517–1542. [Google Scholar] [CrossRef]
- Luo, K.; Tao, F.; Moiwo, J.P.; Xiao, D. Attribution of hydrological change in Heihe River Basin to climate and land use change in the past three decades. Sci. Rep. 2016, 6, 33704. [Google Scholar] [CrossRef] [PubMed]
- Shang, X.; Jiang, X.; Jia, R.; Wei, C. Land use and climate change effects on surface runoff variations in the upper Heihe River basin. Water 2019, 11, 344. [Google Scholar] [CrossRef]
- Yin, Z.; Feng, Q.; Zou, S.; Yang, L. Assessing variation in water balance components in mountainous inland river basin experiencing climate change. Water 2016, 8, 472. [Google Scholar] [CrossRef]
- Yang, L.; Feng, Q.; Yin, Z.; Wen, X.; Si, J.; Li, C.; Deo, R.C. Identifying separate impacts of climate and land use/cover change on hydrological processes in upper stream of Heihe River, Northwest China. Hydrol. Process. 2017, 31, 1100–1112. [Google Scholar] [CrossRef]
- Wu, F.; Zhan, J.; Su, H.; Yan, H.; Ma, E. Scenario-based impact assessment of land use/cover and climate changes on watershed hydrology in Heihe River Basin of northwest China. Adv. Meteorol. 2015, 2015, 410198. [Google Scholar] [CrossRef]
- Li, Z.; Li, Q.; Wang, J.; Feng, Y.; Shao, Q. Impacts of projected climate change on runoff in upper reach of Heihe River basin using climate elasticity method and GCMs. Sci. Total Environ. 2020, 716, 137072. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, Y.; Xu, H. Impacts of 1.5 °C and 2.0 °C global warming on runoff of three inland rivers in the Hexi Corridor, Northwest China. J. Meteorol. Res. 2020, 34, 1082–1095. [Google Scholar] [CrossRef]
- Cao, L.; Dou, Y.X.; Zhang, D.Y. Effect of Climate Change on Ecological Environment of Heihe Field. Arid Meteorol. 2003, 21, 45. [Google Scholar]
- Ren, Z.; Lu, Y.; Yang, D. Study on drought and flood changes in recent 2000 years in Heihe River Basin. J. Arid Land Resour. Environ. 2009, 23, 90–93. [Google Scholar]
- Li, M.-J.; Shi, P.-J. Climate Changing Characteristics of Zhangye City in Heihe River Basin During 1968–2005. J. Desert Res. 2007, 2007, 1048–1054. [Google Scholar] [CrossRef]
- Van Huijgevoort, M.H.J.; Van Lanen, H.A.J.; Teuling, A.J.; Uijlenhoet, R. Identification of changes in hydrological drought characteristics from a multi-GCM driven ensemble constrained by observed discharge. J. Hydrol. 2014, 512, 421–434. [Google Scholar] [CrossRef]
- Kamruzzaman, M.; Jang, M.W.; Cho, J.; Hwang, S. Future changes in precipitation and drought characteristics over Bangladesh under CMIP5 climatological projections. Water 2019, 11, 2219. [Google Scholar] [CrossRef]
- Yao, N.; Li, L.; Feng, P.; Feng, H.; Li Liu, D.; Liu, Y.; Jiang, K.; Hu, X.; Li, Y. Projections of drought characteristics in China based on a standardized precipitation and evapotranspiration index and multiple GCMs. Sci. Total Environ. 2020, 704, 135245. [Google Scholar] [CrossRef]
- Raje, D.; Mujumdar, P.P. Hydrologic drought prediction under climate change: Uncertainty modeling with Dempster–Shafer and Bayesian approaches. Adv. Water Resour. 2010, 33, 1176–1186. [Google Scholar] [CrossRef]
- Akhter, J.; Das, L.; Deb, A. CMIP5 ensemble-based spatial rainfall projection over homogeneous zones of India. Clim. Dyn. 2017, 49, 1885–1916. [Google Scholar] [CrossRef]
- Bisht, D.S.; Sridhar, V.; Mishra, A.; Chatterjee, C.; Raghuwanshi, N.S. Drought characterization over India under projected climate scenario. Int. J. Climatol. 2019, 39, 1889–1911. [Google Scholar] [CrossRef]
- Sung, J.H.; Park, J.; Jeon, J.J.; Seo, S.B. Assessment of inter-model variability in meteorological drought characteristics using CMIP5 GCMs over South Korea. KSCE J. Civ. Eng. 2020, 24, 2824–2834. [Google Scholar] [CrossRef]
- Shiru, M.S.; Chung, E.S.; Shahid, S.; Alias, N. GCM selection temperature projection of Nigeria under different RCPs of the CMIP5 GCMS. Theor. Appl. Climatol. 2020, 141, 1611–1627. [Google Scholar] [CrossRef]
- Chhin, R.; Oeurng, C.; Yoden, S. Drought projection in the Indochina Region based on the optimal ensemble subset of CMIP5 models. Clim. Chang. 2020, 162, 687–705. [Google Scholar] [CrossRef]
- Han, R.C.; Li, Z.L.; Han, Y.Y.; Huo, P.Y. A comparative study of TOPSIS-based GCMs selection and multi-model ensemble. Int. J. Climatol. 2023, 43, 5348–5368. [Google Scholar] [CrossRef]
- Wang, J.; Li, Z.L. Application of entropy weighted TOPSIS method for selection of general circulation models. South-North Water Transf. Water Sci. Technol. 2020, 18, 14–21. (In Chinese) [Google Scholar]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Piani, C.; Haerter, J.O.; Coppola, E. Statistical bias correction for daily precipitation in regional climate models over Europe. Theor. Appl. Climatol. 2010, 99, 187–192. [Google Scholar] [CrossRef]
- Teutschbein, C.; Seibert, J. Bias correction of regional climate model simulations for hydrological climate-change impact studies: Review and evaluation of different methods. J. Hydrol. 2012, 456, 12–29. [Google Scholar] [CrossRef]
- Ghimire, U.; Srinivasan, G.; Agarwal, A. Assessment of rainfall bias correction techniques for improved hydrological simulation. Int. J. Climatol. 2019, 39, 2386–2399. [Google Scholar] [CrossRef]
- Enayati, M.; Bozorg-Haddad, O.; Bazrafshan, J.; Hejabi, S.; Chu, X. Bias correction capabilities of quantile mapping methods for rainfall and temperature variables. J. Water Clim. Chang. 2021, 12, 401–419. [Google Scholar] [CrossRef]
- Li, X.T.; Li, Z.L.; Han, R.C. Evaluations of Different Bias Correction Methods on the GCM Precipitation Data. J. China Hydrol. 2023, 43, 93–111. (In Chinese) [Google Scholar]
- Wu, J.; Miao, C.; Tang, X.; Duan, Q.; He, X. A nonparametric standardized runoff index for characterizing hydrological drought on the Loess Plateau, China. Glob. Planet. Chang. 2018, 161, 53–65. [Google Scholar] [CrossRef]
- Sun, X.; Li, Z.; Tian, Q. Assessment of hydrological drought based on nonstationary runoff data. Hydrol. Res. 2020, 51, 894–910. [Google Scholar] [CrossRef]
- Porhemmat, J.; Altafi Dadgar, M. Analysis of hydrological drought indices in Alpine Zagros Mountains of Iran. Arab. J. Geosci. 2023, 16, 594. [Google Scholar] [CrossRef]
- Zan, D.W. Spatial-temporal variation characteristics of meteorological drought during 1967–2009 in the Heihe River Basin. J. Water Resour. Water Eng. 2019, 3, 92–99. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).