Improving the Estimation of PM2.5 Concentration in the North China Area by Introducing an Attention Mechanism into Random Forest
Abstract
1. Introduction
2. Materials and Methods
2.1. Datasets and Preprocessing
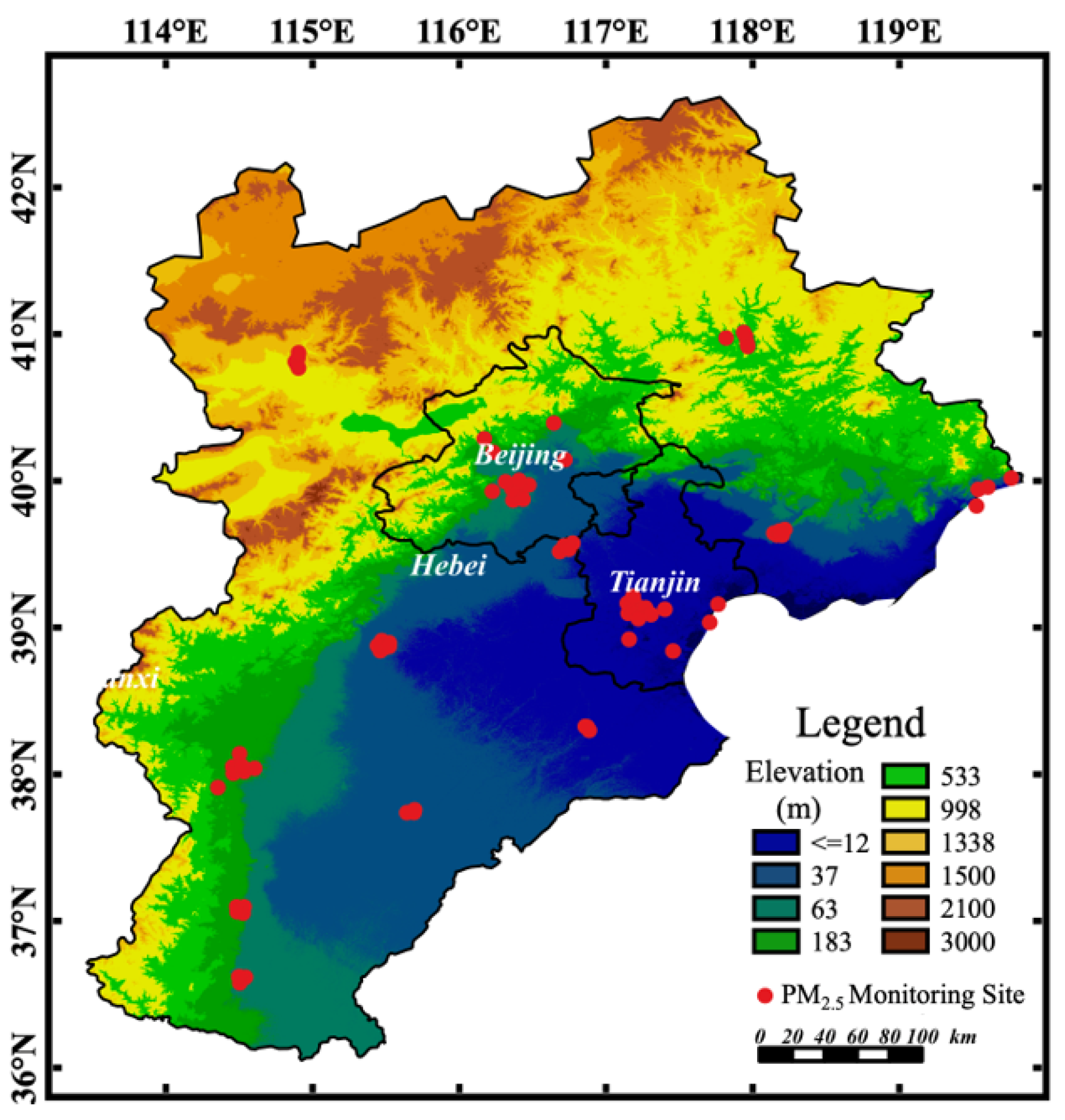
2.1.1. Ground-Level Measurements
2.1.2. AOD Data
2.1.3. Auxiliary Data
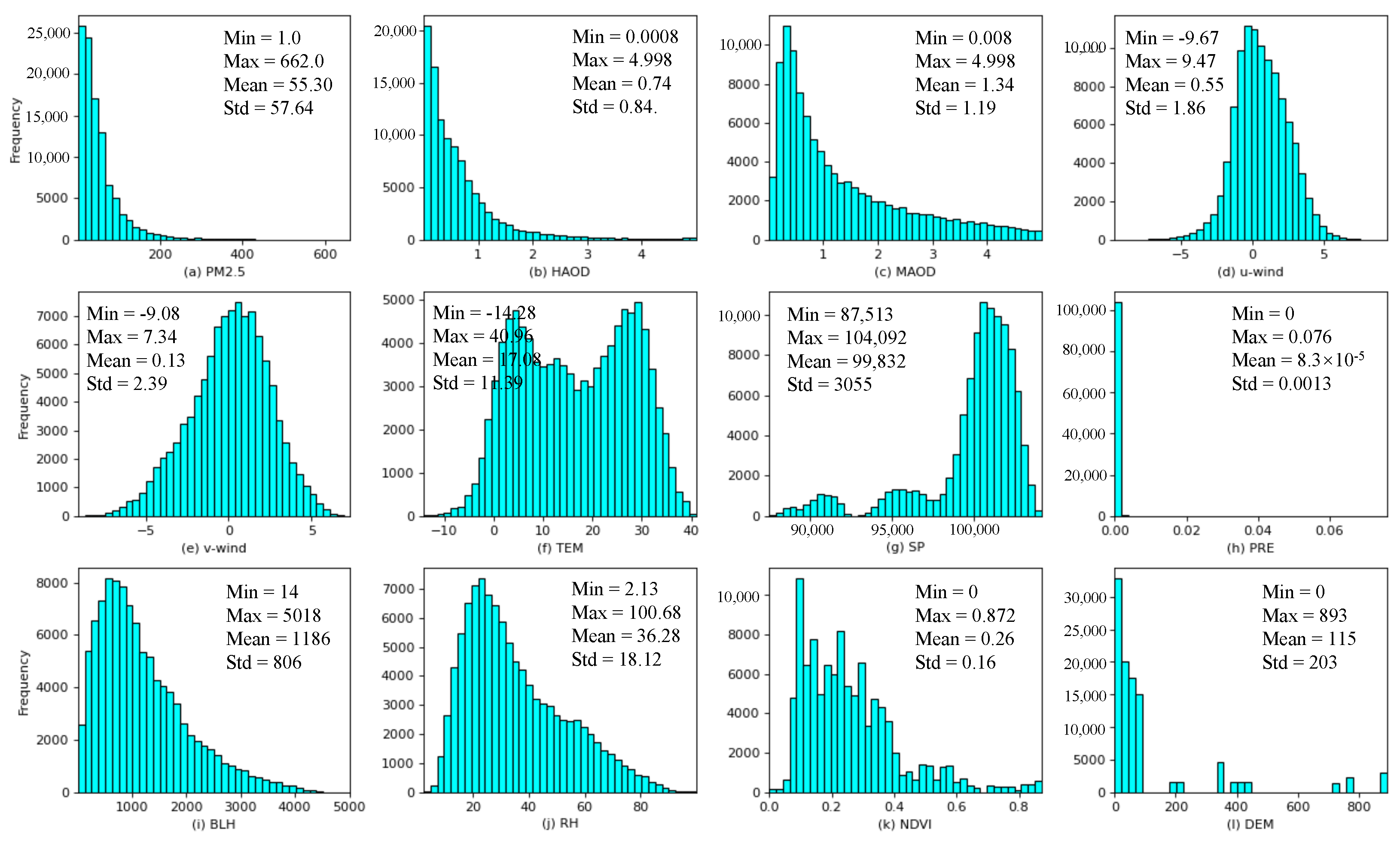
2.1.4. Processing of Data
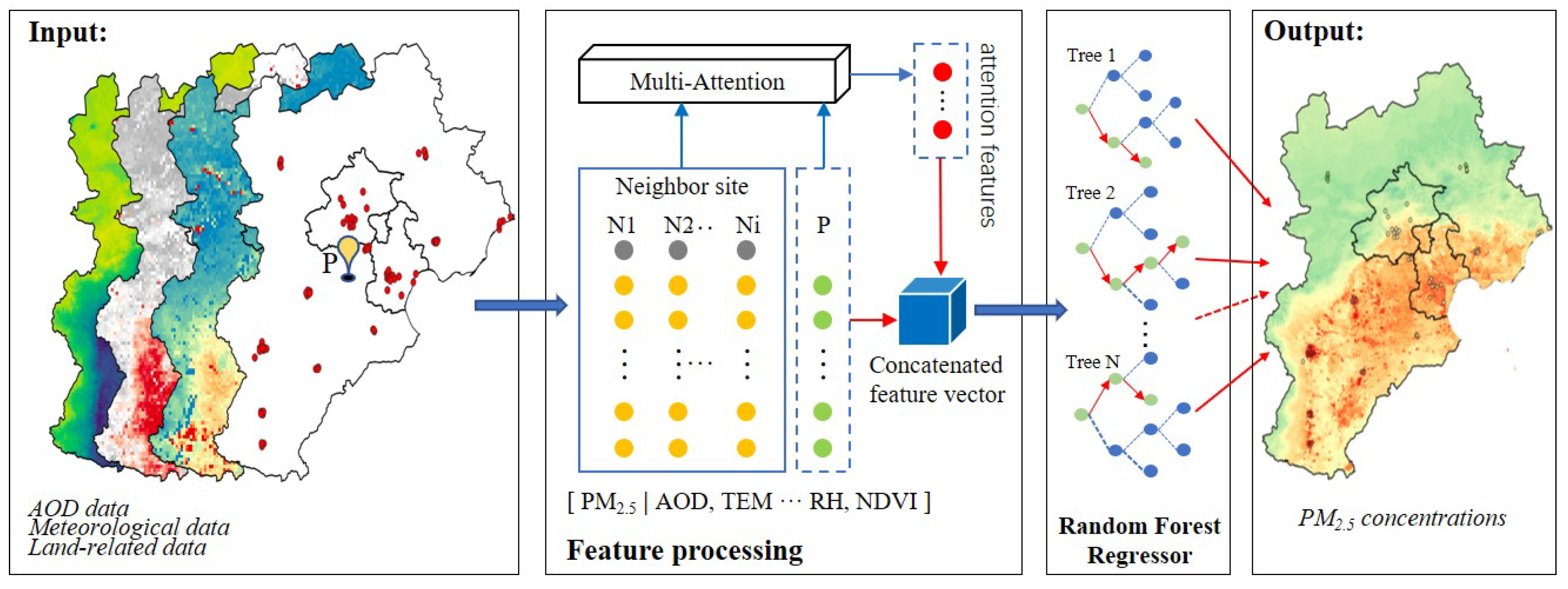
2.2. Methods
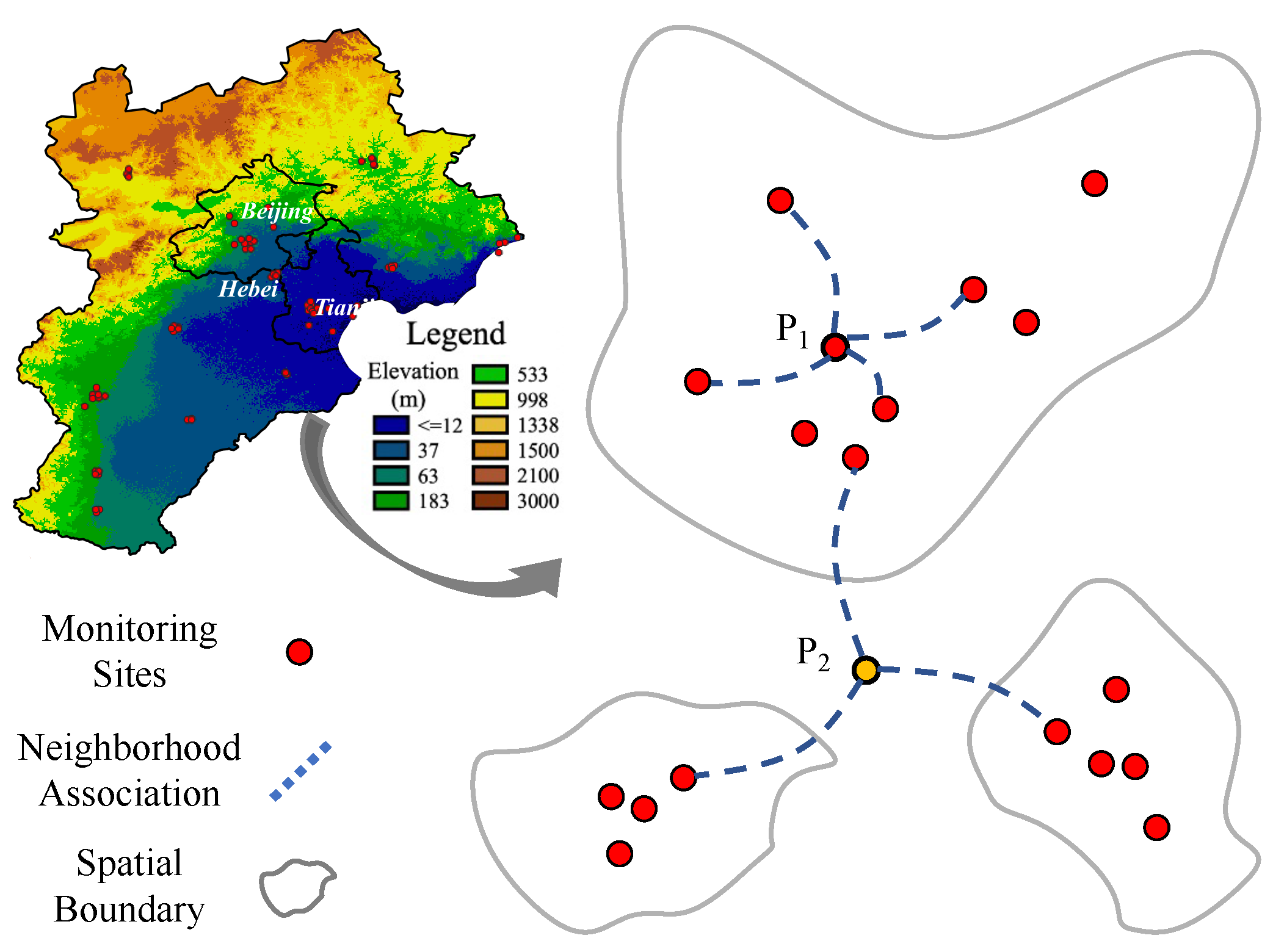
2.2.1. Spatial Features
2.2.2. Temporal Features
2.2.3. Random Forest
2.2.4. Model and Evaluation
| Algorithm 1 Attention Mechanism-Based Random Forest Algorithm for Estimation |
Input: Dataset , each contains F features (defined in Table 1). Training times is T. The random forest RF has M decision trees (DTree).
|
3. Results and Discussion
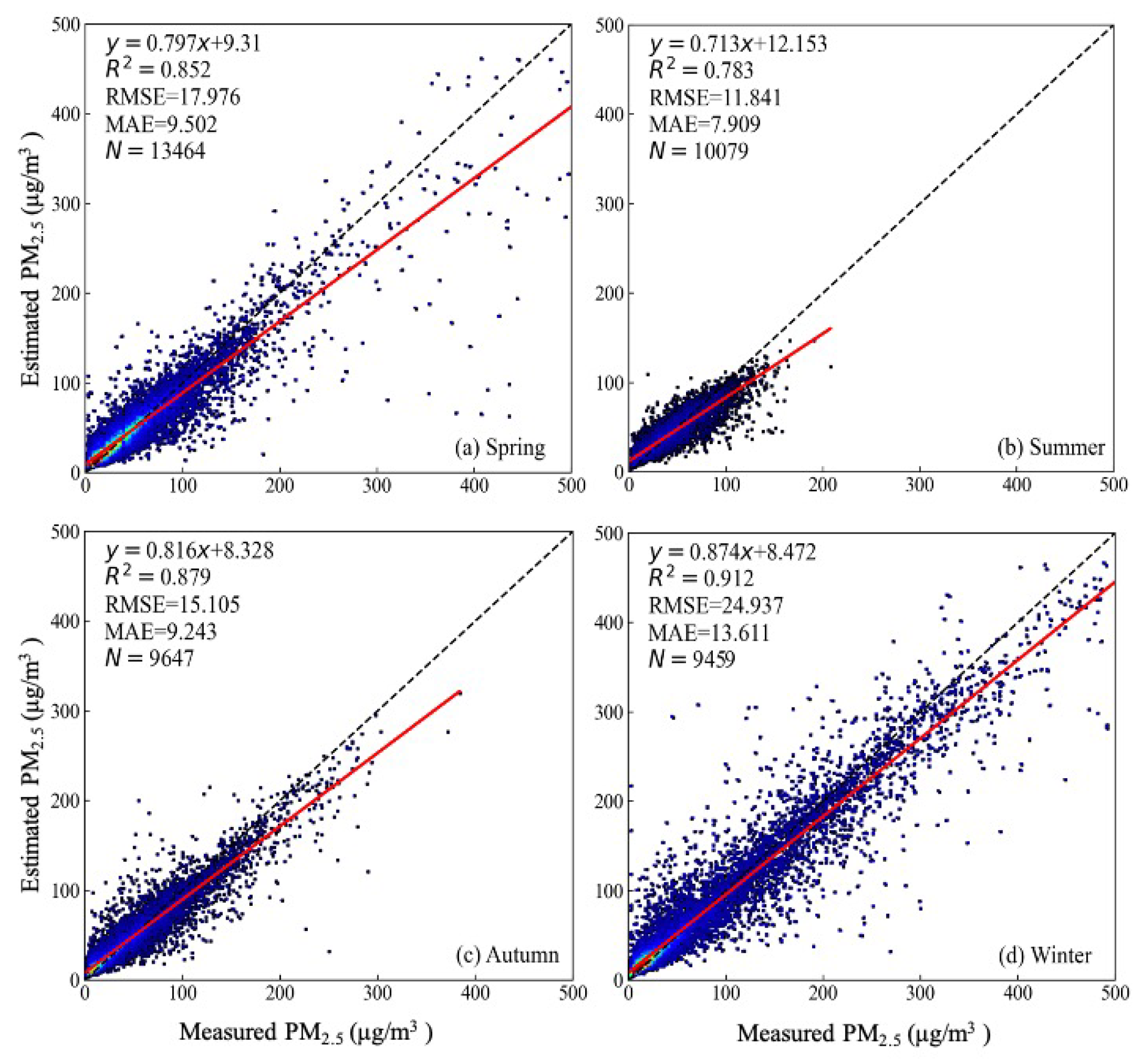
3.1. Model Performance
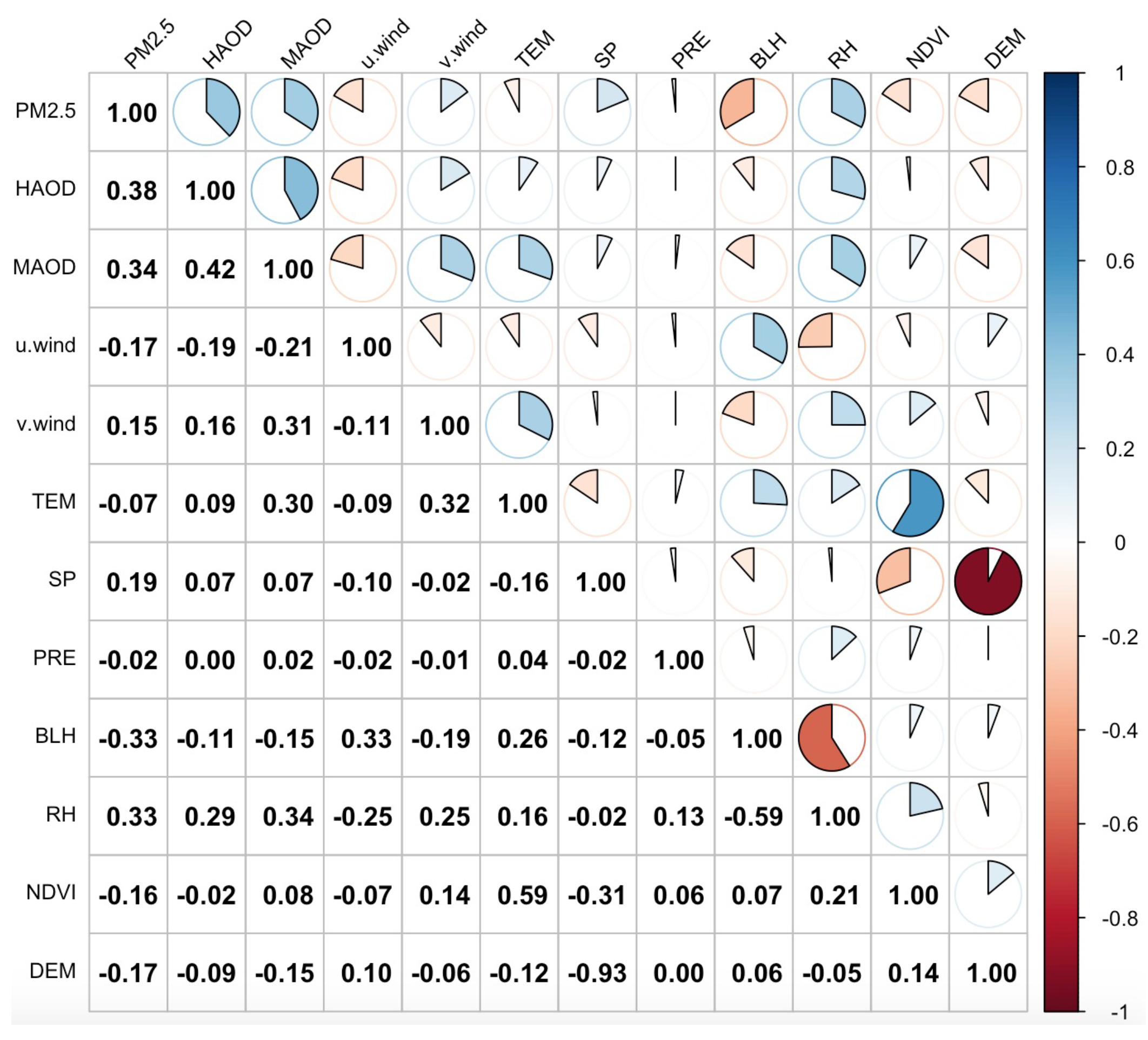
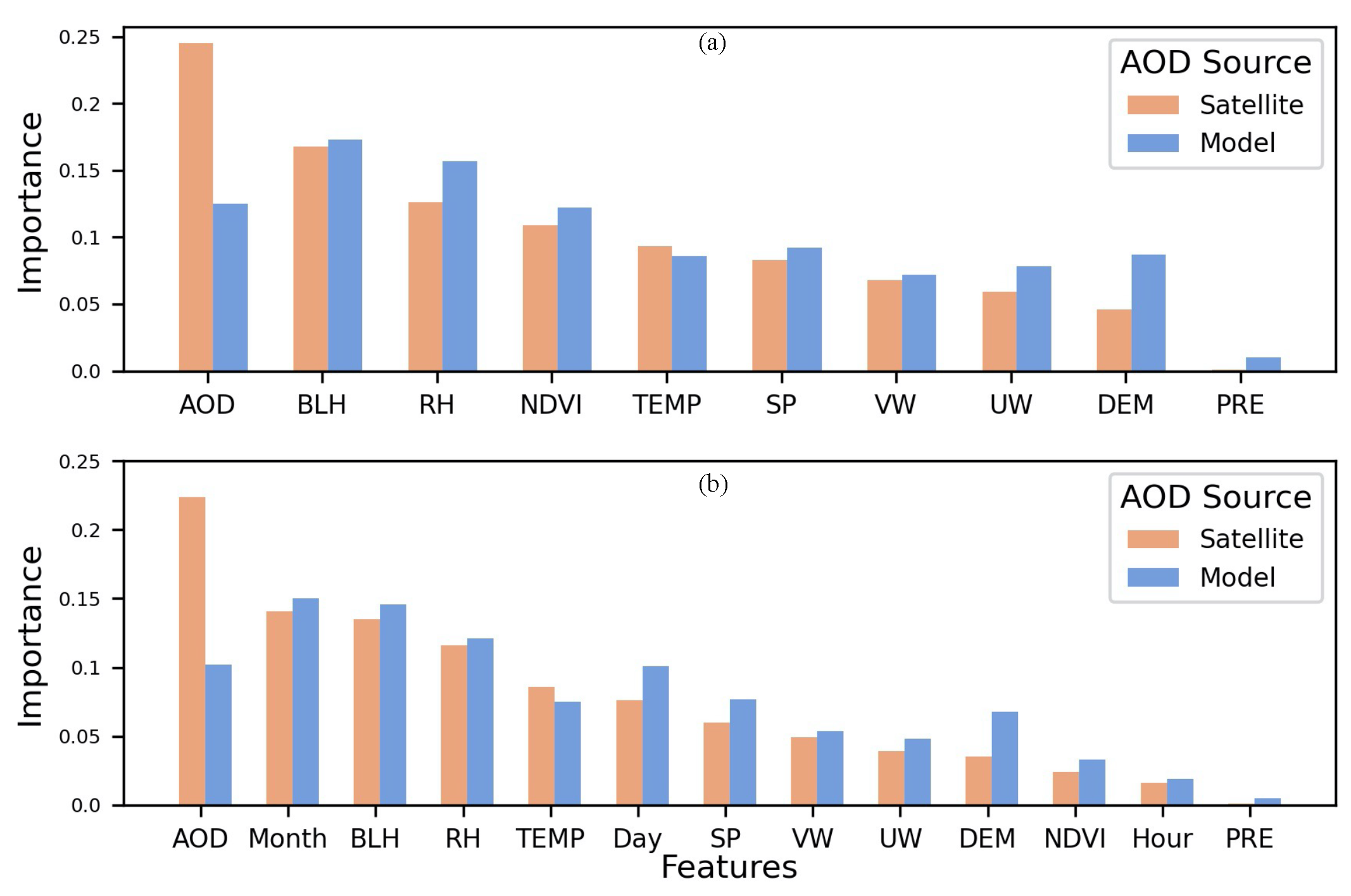
3.2. Feature Correlation and Importance Analysis
3.3. The Impact of AOD data Quality on Model Accuracy
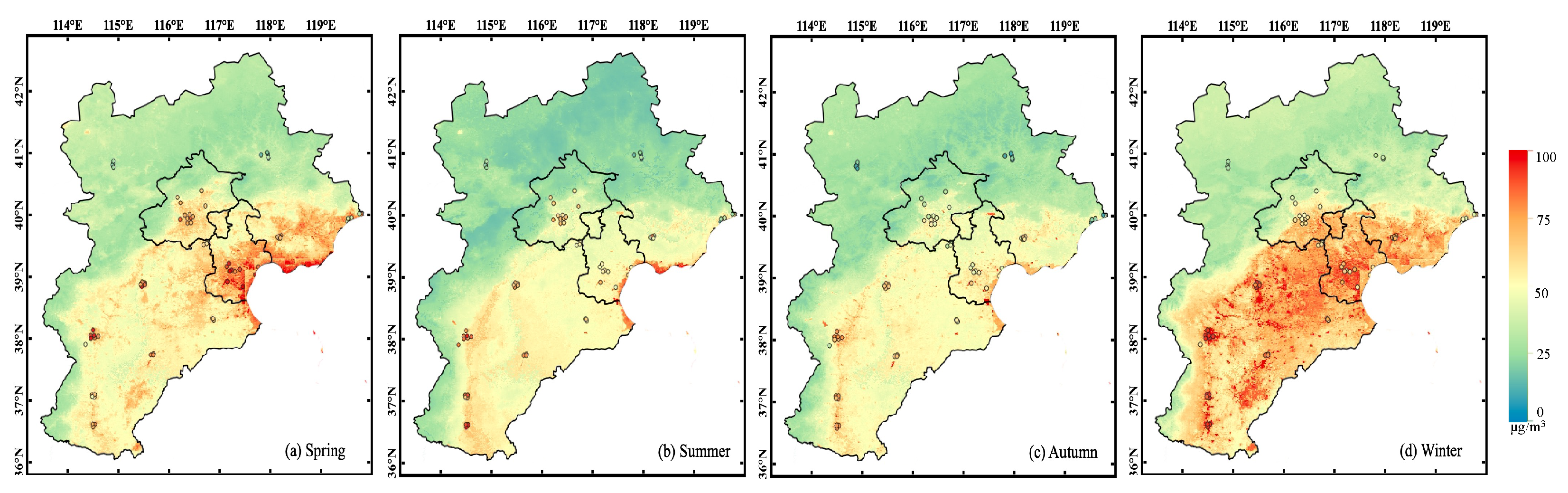
3.4. Spatio-temporal Validation and Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, Q.; Zheng, Y.; Tong, D.; Shao, M.; Hao, J. Drivers of improved PM2.5 air quality in China from 2013 to 2017. Proc. Natl. Acad. Sci. USA 2019, 116, 24463–24469. [Google Scholar] [CrossRef] [PubMed]
- Kim, K.H.; Kabir, E.; Kabir, S. A review on the human health impact of airborne particulate matter. Environ. Int. 2015, 74, 136–143. [Google Scholar] [CrossRef] [PubMed]
- Forouzanfar, M.H.; Afshin, A.; Alexander, L.T.; Anderson, H.R.; Bhutta, Z.A.; Biryukov, S.; Brauer, M.; Burnett, R.; Cercy, K.; Charlson, F.J. Global, regional, and national comparative risk assessment of 79 behavioural, environmental and occupational, and metabolic risks or clusters of risks, 1990–2015: A systematic analysis for the Global Burden of Disease Study 2015. Lancet 2016, 388, 1659–1724. [Google Scholar] [CrossRef]
- Grimm, N.B.; Faeth, S.H.; Golubiewski, N.E. Global change and the ecology of cities. Science 2008, 319, 756–760. [Google Scholar] [CrossRef]
- Giannadaki, D.; Giannakis, E.; Pozzer, A.; Lelieveld, J. Estimating health and economic benefits of reductions in air pollution from agriculture. Sci. Total Environ. 2018, 622–623, 1304–1316. [Google Scholar] [CrossRef]
- Xue, W.; Zhang, J.; Zhong, C.; Li, X.; Wei, J. Spatiotemporal PM2.5 variations and its response to the industrial structure from 2000 to 2018 in the Beijing-Tianjin-Hebei region. J. Clean. Prod. 2021, 279, 123742. [Google Scholar] [CrossRef]
- Shin, M.; Kang, Y.; Park, S.; Im, J.; Quackenbush, L.J. Estimating ground-level particulate matter concentrations using satellite-based data: A review. Giscience Remote Sens. 2019, 57, 174–189. [Google Scholar] [CrossRef]
- Ma, Z.; Dey, S.; Christopher, S.; Liu, R.; Bi, J.; Balyan, P.; Liu, Y. A review of statistical methods used for developing large-scale and long-term PM2.5 models from satellite data. Remote Sens. Environ. 2022, 269, 112827. [Google Scholar] [CrossRef]
- Bai, K.; Li, K.; Sun, Y.; Wu, L.; Zhang, Y.; Chang, N.B.; Li, Z. Global synthesis of two decades of research on improving PM2.5 estimation models from remote sensing and data science perspectives. Earth-Sci. Rev. 2023, 241, 104461. [Google Scholar] [CrossRef]
- Ma, Z.; Hu, X.; Sayer, A.M.; Levy, R.; Liu, Y. Satellite-Based Spatiotemporal Trends in PM2.5 Concentrations: China, 2004–2013. Environ. Health Perspect 2016, 124, 184–192. [Google Scholar] [CrossRef] [PubMed]
- Brokamp, C.; Jandarov, R.; Hossain, M.; Ryan, P. Predicting Daily Urban Fine Particulate Matter Concentrations Using a Random Forest Model. Environ. Sci. Technol. 2018, 52, 4173–4179. [Google Scholar] [CrossRef]
- Sorek-Hamer, M.; Chatfield, R.; Liu, Y. Review: Strategies for using satellite-based products in modeling PM2.5 and short-term pollution episodes. Environ. Int. 2020, 144, 106057. [Google Scholar] [CrossRef] [PubMed]
- van Donkelaar, A.; Martin, R.V.; Park, R.J. Estimating ground-level PM2.5 using aerosol optical depth determined from satellite remote sensing. J. Geophys. Res. Atmos. 2006, 111. [Google Scholar] [CrossRef]
- Ma, Z.; Hu, X.; Huang, L.; Bi, J.; Liu, Y. Estimating Ground-Level PM2.5 in China Using Satellite Remote Sensing. Environ. Sci. Technol. 2014, 48, 7436. [Google Scholar] [CrossRef] [PubMed]
- van Donkelaar, A.; Martin, R.V.; Brauer, M.; Hsu, N.C.; Kahn, R.A.; Levy, R.C.; Lyapustin, A.; Sayer, A.M.; Winker, D.M. Global Estimates of Fine Particulate Matter using a Combined Geophysical-Statistical Method with Information from Satellites, Models, and Monitors. Environ. Sci. Technol. 2016, 50, 3762–3772. [Google Scholar] [CrossRef] [PubMed]
- Gupta, P.; Levy, R.C.; Mattoo, S.; Remer, L.A.; Munchak, L.A. A surface reflectance scheme for retrieving aerosol optical depth over urban surfaces in MODIS dark target retrieval algorithm. Atmos. Meas. Tech. 2016, 9, 3293–3308. [Google Scholar] [CrossRef]
- Wang, X.; Sun, W.; Zheng, K.; Ren, X.; Han, P. Estimating hourly PM2.5 concentrations using MODIS 3km AOD and an improved spatiotemporal model over Beijing-Tianjin-Hebei, China. Atmos. Environ. 2020, 222, 117089. [Google Scholar] [CrossRef]
- Lyapustin, A.; Wang, Y.; Korkin, S.; Huang, D. MODIS Collection 6 MAIAC algorithm. Atmos. Meas. Tech. 2018, 11, 5741–5765. [Google Scholar] [CrossRef]
- Wei, J.; Huang, W.; Li, Z.; Xue, W.; Cribb, M. Estimating 1-km-resolution PM2.5 concentrations across China using the space-time random forest approach. Remote Sens. Environ. 2019, 231, 111221. [Google Scholar] [CrossRef]
- Yang, N.; Shi, H.; Tang, H.; Yang, X. Geographical and temporal encoding for improving the estimation of PM2.5 concentrations in China using end-to-end gradient boosting. Remote Sens. Environ. 2022, 269, 112828. [Google Scholar] [CrossRef]
- Liu, J.; Weng, F.; Li, Z. Satellite-based PM2.5 estimation directly from reflectance at the top of the atmosphere using a machine learning algorithm. Atmos. Environ. 2019, 208, 113–122. [Google Scholar] [CrossRef]
- Wei, J.; Li, Z.; Pinker, R.T.; Sun, L.; Li, R. Himawari-8-derived diurnal variations of ground-level PM2.5 pollution across China using a fast space-time Light Gradient Boosting Machine. Atmos. Chem. Phys. 2021, 21, 7863–7880. [Google Scholar] [CrossRef]
- Mao, F.; Hong, J.; Min, Q.; Gong, W.; Yin, J. Estimating hourly full-coverage PM2.5 over China based on TOA reflectance data from the Fengyun-4A satellite. Environ. Pollut. 2020, 270, 116119. [Google Scholar] [CrossRef] [PubMed]
- Hong, J.; Mao, F.; Gong, W.; Gan, Y.; Zang, L.; Quan, J.; Chen, J. Assimilating Fengyun-4A observations to improve WRF-Chem PM2.5 predictions in China. Atmos. Res. 2022, 265, 105878. [Google Scholar] [CrossRef]
- Borisov, V.; Leemann, T.; Seler, K.; Haug, J.; Pawelczyk, M.; Kasneci, G. Deep Neural Networks and Tabular Data: A Survey. arXiv 2021, arXiv:2110.01889. [Google Scholar] [CrossRef] [PubMed]
- Jeong, J.I.; Park, R.J.; Yeh, S.W.; Roh, J.W. Statistical predictability of wintertime PM2.5 concentrations over East Asia using simple linear regression. Sci. Total Environ. 2021, 776, 146059. [Google Scholar] [CrossRef]
- Ma, Z.; Liu, Y.; Zhao, Q.; Liu, M.; Zhou, Y.; Bi, J. Satellite-derived high resolution PM2.5 concentrations in Yangtze River Delta Region of China using improved linear mixed effects model. Atmos. Environ. 2016, 133, 156–164. [Google Scholar] [CrossRef]
- He, Q.; Huang, B. Satellite-based mapping of daily high-resolution ground PM2.5 in China via space-time regression modeling. Remote Sens. Environ. 2018, 206, 72–83. [Google Scholar] [CrossRef]
- Engel-Cox, J.A.; Holloman, C.H.; Coutant, B.W.; Hoff, R.M. Qualitative and quantitative evaluation of MODIS satellite sensor data for regional and urban scale air quality. Atmos. Environ. 2004, 38, 2495–2509. [Google Scholar] [CrossRef]
- Wu, J.; Yao, F.; Li, W.; Si, M. VIIRS-based remote sensing estimation of ground-level PM2.5 concentrations in Beijing–Tianjin–Hebei: A spatiotemporal statistical model. Remote Sens. Environ. 2016, 184, 316–328. [Google Scholar] [CrossRef]
- Jiang, T.; Chen, B.; Nie, Z.; Ren, Z.; Tang, S. Estimation of hourly full-coverage PM2.5 concentrations at 1-km resolution in China using a two-stage random forest model. Atmos. Res. 2020, 248, 105146. [Google Scholar] [CrossRef]
- Liu, P.; Li, J.; Wang, L.; He, G. Remote Sensing Data Fusion with Generative Adversarial Networks: State-of-the-Art Methods and Future Research Directions. IEEE Geosci. Remote Sens. Mag. 2022, 10, 295–328. [Google Scholar] [CrossRef]
- Zhang, L.; Liu, P.; Zhao, L.; Wang, G.; Zhang, W.; Liu, J. Air quality predictions with a semi-supervised bidirectional LSTM neural network. Atmos. Pollut. Res. 2021, 12, 328–339. [Google Scholar] [CrossRef]
- Liu, P.; Wang, L.; Ranjan, R.; He, G.; Zhao, L. A survey on active deep learning: From model-driven to data-driven. ACM Comput. Surv. (CSUR) 2021, 54, 1–34. [Google Scholar] [CrossRef]
- Lei, Z.; Zeng, Y.; Liu, P.; Su, X. Active Deep Learning for Hyperspectral Image Classification With Uncertainty Learning. IEEE Geosci. Remote Sens. Lett. 2021, 19, 5502405. [Google Scholar] [CrossRef]
- Ahmad, M.; Alam, K.; Tariq, S.; Anwar, S.; Mansha, M. Estimating fine particulate concentration using a combined approach of linear regression and artificial neural network. Atmos. Environ. 2019, 219, 117050. [Google Scholar] [CrossRef]
- Li, T.; Shen, H.; Yuan, Q.; Zhang, X.; Zhang, L. Estimating ground-level PM2.5 by fusing satellite and station observations: A geo-intelligent deep learning approach. Geophys. Res. Lett. 2017, 44, 11985–11993. [Google Scholar] [CrossRef]
- Chen, J.; Yin, J.; Zang, L.; Zhang, T.; Zhao, M. Stacking machine learning model for estimating hourly PM2.5 in China based on Himawari 8 aerosol optical depth data. Sci. Total Environ. 2019, 697, 134021.1–134021.8. [Google Scholar] [CrossRef] [PubMed]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Han, W.; Chen, J.; Wang, L.; Feng, R.; Li, F.; Wu, L.; Tian, T.; Yan, J. Methods for Small, Weak Object Detection in Optical High-Resolution Remote Sensing Images: A survey of advances and challenges. IEEE Geosci. Remote Sens. Mag. 2021, 9, 8–34. [Google Scholar] [CrossRef]
- Li, J.; Liu, Z.; Lei, X.; Wang, L. Distributed Fusion of Heterogeneous Remote Sensing and Social Media Data: A Review and New Developments. Proc. IEEE 2021, 109, 1350–1363. [Google Scholar] [CrossRef]
- Feng, R.; Li, H.; Wang, L.; Zhong, Y.; Zeng, T. Local Spatial Constraint and Total Variation for Hyperspectral Anomaly Detection. IEEE Trans. Geosci. Remote Sens. 2021, 60, 5512216. [Google Scholar] [CrossRef]
- Han, W.; Li, J.; Wang, S.; Zhang, X.; Dong, Y.; Fan, R.; Zhang, X.; Wang, L. Geological Remote Sensing Interpretation Using Deep Learning Feature and an Adaptive Multisource Data Fusion Network. IEEE Trans. Geosci. Remote Sens. 2022, 60, 4510314. [Google Scholar] [CrossRef]
- Gao, L.; Chen, L.; Li, C.; Li, J.; Che, Z.; Zhang, Y. Evaluation and possible uncertainty source analysis of JAXA Himawari-8 aerosol optical depth product over China. Atmos. Res. 2020, 248, 105248. [Google Scholar] [CrossRef]
- Kikuchi, M.; Murakami, H.; Suzuki, K.; Nagao, T.M.; Higurashi, A. Improved Hourly Estimates of Aerosol Optical Thickness Using Spatiotemporal Variability Derived From Himawari-8 Geostationary Satellite. IEEE Trans. Geosci. Remote Sens. 2018, 56, 3442–3455. [Google Scholar] [CrossRef]
- Zhang, L.; Liu, P.; Wang, L.; Liu, J.; Song, B.; Zhang, Y.; He, G.; Zhang, H. Improved 1-km-Resolution Hourly Estimates of Aerosol Optical Depth Using Conditional Generative Adversarial Networks. Remote Sens. 2021, 13, 3834. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention Is All You Need. arXiv 2017, arXiv:1706.03762. [Google Scholar]
- Guo, M.H.; Xu, T.X.; Liu, J.J.; Liu, Z.N.; Jiang, P.T.; Mu, T.J.; Zhang, S.H.; Martin, R.R.; Cheng, M.M.; Hu, S.M. Attention Mechanisms in Computer Vision: A Survey. Comput. Vis. Media 2022, 8, 331–368. [Google Scholar] [CrossRef]
- Tobler, W.R. A Computer Movie Simulating Urban Growth in the Detroit Region. Econ. Geogr. 1970, 46, 234–240. [Google Scholar] [CrossRef]
- Zhu, A.; Lu, G.; Liu, J.; Qin, C.; Zhou, C. Spatial prediction based on Third Law of Geography. Ann. Gis 2018, 24, 225–240. [Google Scholar] [CrossRef]
- Yao, F.; Si, M.; Li, W.; Wu, J. A multidimensional comparison between MODIS and VIIRS AOD in estimating ground-level PM2.5 concentrations over a heavily polluted region in China. Sci. Total Environ. 2018, 618, 819–828. [Google Scholar] [CrossRef]
- Ma, J.; Zhang, R.; Xu, J.; Yu, Z. MERRA-2 PM2.5 mass concentration reconstruction in China mainland based on LightGBM machine learning. Sci. Total Environ. 2022, 827, 154363. [Google Scholar] [CrossRef]
- Xu, Q.; Chen, X.; Yang, S.; Tang, L.; Dong, J. Spatiotemporal relationship between Himawari-8 hourly columnar aerosol optical depth (AOD) and ground-level PM2.5 mass concentration in mainland China. Sci. Total Environ. 2021, 765, 144241. [Google Scholar] [CrossRef]
- Rodríguez, J.; Pérez, A.; Lozano, J.A. Sensitivity Analysis of k-Fold Cross Validation in Prediction Error Estimation. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 569–575. [Google Scholar] [CrossRef]
- Just, A.C.; Arfer, K.B.; Rush, J.; Dorman, M.; Kloog, I. Advancing methodologies for applying machine learning and evaluating spatiotemporal models of fine particulate matter (PM2.5) using satellite data over large regions. Atmos. Environ. 2020, 239, 117649. [Google Scholar] [CrossRef] [PubMed]
- Ziyue, C.; Xiaoming, X.; Jun, C.; Danlu, C.; Bingbo, G.; Bin, H.; Nianliang, C.; Bing, X. Understanding meteorological influences on PM2.5 concentrations across China: A temporal and spatial perspective. Atmos. Chem. Phys. Discuss. 2018, 18, 5343–5358. [Google Scholar]
- Sun, J.; Gong, J.; Zhou, J. Estimating hourly PM2.5 concentrations in Beijing with satellite aerosol optical depth and a random forest approach. Sci. Total Environ. 2020, 762, 144502. [Google Scholar] [CrossRef] [PubMed]


| Type | Abbreviation | Content | Spatial Resolution | Temporal Resolution | Source |
|---|---|---|---|---|---|
| site | hourly | CNEMC | |||
| AOD | H-AOD | Himawari AOD | 5 km | hourly | JAXA |
| M-AOD | Himawari model AOD | 5 km | hourly | JAXA | |
| Meteorological | TEM | 2 m air temperature | 0.1° × 0.1° | hourly | ECMWF |
| UW | 10 m u-component of wind | 0.1° × 0.1° | hourly | ECMWF | |
| VW | 10 m v-component of wind | 0.1° × 0.1° | hourly | ECMWF | |
| PRE | Total precipitation | 0.1° × 0.1° | hourly | ECMWF | |
| SP | Surface pressure | 0.1° × 0.1° | hourly | ECMWF | |
| BLH | Boundary layer height | 0.25° × 0.25° | hourly | ECMWF | |
| RH | Relative humidity | 0.25° × 0.25° | hourly | ECMWF | |
| Land-related | NDVI | NDVI | 1 km | 16-day | MYD13A2 |
| DEM | DEM | 90 m | - | SRTM | |
| LULC | LULC | 500 m | annually | MCD12Q1 |
| Methods | Resolution | RMSE | MAE | Source AOD | Period | Region | Reference | |
|---|---|---|---|---|---|---|---|---|
| LME | 10 km, daily | 0.79 | 26.74 | - | MODIS | 2015 | China | Ma et al. (2016) [27] |
| GWR | 10 km, daily | 0.64 | 32.98 | 21.25 | MODIS | 2013 | China | Ma et al. (2014) [14] |
| GTWR | 3 km, daily | 0.80 | 18.00 | 12.03 | MODIS | 2015 | China | He et al. (2018) [28] |
| Geo-DBN | 10 km, daily | 0.88 | 13.03 | 8.54 | MODIS | 2015 | China | Li et al. (2017) [37] |
| DNN | 1 km, hourly | 0.84 | 19.90 | 11.89 | Himawari | 2017 | BTH | Sun et al. (2019) |
| Two-stage | 1 km, daily | 0.85 | 11.02 | - | MODIS, Himawari | 201804–201902 | China | Jiang et al. (2021) [26] |
| STRF | 1 km, daily | 0.85 | 15.57 | 9.77 | MODIS MAIAC | 2015–2016 | China | Wei et al. (2019) [19] |
| STET | 1 km, daily | 0.89 | 10.35 | 6.71 | MODIS MAIAC | 2017–2018 | China | Wei et al. (2020) |
| STLG | 5 km, hourly | 0.85 | 13.09 | 8.11 | Himawari | 2018 | China | Wei et al. (2021)[22] |
| XGBoost | 5 km, hourly | 0.84 | 18.10 | 11.40 | Himawari | 2016 | Central and Eastern China | Chen et al. (2019) [38] |
| RF | 1 km, hourly | 0.81 | 25.51 | 15.91 | Himawari | 2017 | BTH | This study |
| STAttenRF | 1 km, hourly | 0.89 | 18.31 | 11.17 | Himawari | 2017 | BTH | This study |
| Data | Method | Model Fitting | Model Validation | ||||
|---|---|---|---|---|---|---|---|
| RMSE | MAE | RMSE | MAE | ||||
| H-AOD | RF | 0.972 | 9.45 | 5.46 | 0.812 | 25.51 | 15.91 |
| STAttenRF | 0.983 | 7.56 | 4.51 | 0.887 | 18.31 | 11.17 | |
| M-AOD | RF | 0.973 | 9.94 | 5.66 | 0.805 | 27.86 | 15.35 |
| STAttenRF | 0.985 | 7.47 | 4.34 | 0.874 | 20.68 | 12.87 | |
| Mix-AOD | RF | 0.968 | 10.18 | 5.96 | 0.793 | 28.20 | 17.02 |
| STAttenRF | 0.981 | 7.63 | 4.54 | 0.861 | 22.43 | 13.66 | |
| Time | Samples | RMSE | MAE | Slope | Estimated | Measured | |
|---|---|---|---|---|---|---|---|
| 08:00 | 3099 | 0.817 | 16.32 | 10.52 | 0.72 | 50.2 ± 27.8 | 49.3 ± 34.7 |
| 09:00 | 4739 | 0.820 | 17.13 | 11.24 | 0.76 | 52.3 ± 32.9 | 49.8 ± 39.2 |
| 10:00 | 6931 | 0.855 | 22.19 | 12.11 | 0.78 | 57.4 ± 50.2 | 55.6 ± 59.4 |
| 11:00 | 7244 | 0.881 | 20.61 | 11.81 | 0.83 | 55.1 ± 51.7 | 53.2 ± 58.6 |
| 12:00 | 7188 | 0.884 | 19.46 | 10.82 | 0.85 | 51.3 ± 51.1 | 49.8 ± 56.6 |
| 13:00 | 6953 | 0.902 | 18.01 | 9.87 | 0.86 | 50.0 ± 51.7 | 49.7 ± 57.0 |
| 14:00 | 6848 | 0.891 | 19.02 | 10.54 | 0.85 | 49.4 ± 51.0 | 50.6 ± 56.9 |
| 15:00 | 6550 | 0.903 | 18.84 | 11.01 | 0.84 | 49.1 ± 52.2 | 52.2 ± 58.7 |
| 16:00 | 4500 | 0.878 | 18.76 | 10.83 | 0.80 | 44.6 ± 44.6 | 49.3 ± 51.2 |
| 17:00 | 2814 | 0.745 | 16.49 | 10.68 | 0.69 | 36.3 ± 22.3 | 41.9 ± 30.2 |
| ALL | 56,866 | 0.873 | 18.60 | 11.92 | 0.83 | 50.7 ± 48.1 | 50.9 ± 54.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Li, Z.; Guang, J.; Xie, Y.; Shi, Z.; Gu, H.; Zheng, Y. Improving the Estimation of PM2.5 Concentration in the North China Area by Introducing an Attention Mechanism into Random Forest. Atmosphere 2024, 15, 384. https://doi.org/10.3390/atmos15030384
Zhang L, Li Z, Guang J, Xie Y, Shi Z, Gu H, Zheng Y. Improving the Estimation of PM2.5 Concentration in the North China Area by Introducing an Attention Mechanism into Random Forest. Atmosphere. 2024; 15(3):384. https://doi.org/10.3390/atmos15030384
Chicago/Turabian StyleZhang, Luo, Zhengqiang Li, Jie Guang, Yisong Xie, Zheng Shi, Haoran Gu, and Yang Zheng. 2024. "Improving the Estimation of PM2.5 Concentration in the North China Area by Introducing an Attention Mechanism into Random Forest" Atmosphere 15, no. 3: 384. https://doi.org/10.3390/atmos15030384
APA StyleZhang, L., Li, Z., Guang, J., Xie, Y., Shi, Z., Gu, H., & Zheng, Y. (2024). Improving the Estimation of PM2.5 Concentration in the North China Area by Introducing an Attention Mechanism into Random Forest. Atmosphere, 15(3), 384. https://doi.org/10.3390/atmos15030384








