A Deep Learning-Based Downscaling Method Considering the Impact on Typhoons to Future Precipitation in Taiwan
Abstract
1. Introduction
2. Materials
2.1. Ground Observations
2.2. GCM Data
3. Methodology
3.1. Overview
- a.
- Application of KPCA to the identification of key input variables to the DNN model;
- b.
- DNN architecture design, which includes determining the number of hidden layers, the number of neurons in each hidden layer and the neuron activation function;
- c.
- Optimization of DNN model parameters.
3.2. Identification of Input Variables
3.2.1. Kernel Principal Component Analysis
3.2.2. KPCA for Identifying Key Input Features
3.3. Deep Neural Networks: Architecture Design
- (1)
- Choosing an optimizer (AdaGrad or Adam);
- (2)
- Determining the activation function (sigmoid or tanh);
- (3)
- Setting the learning rate (ranging from 0.01 to 0.0001);
- (4)
- Selecting the batch size (ranging from 16 to 64);
- (5)
- Determining the number of nodes (ranging from 10 to 100).
3.4. Optimization of Model Parameters
3.5. Model Assessment
4. Future Precipitation Assessment
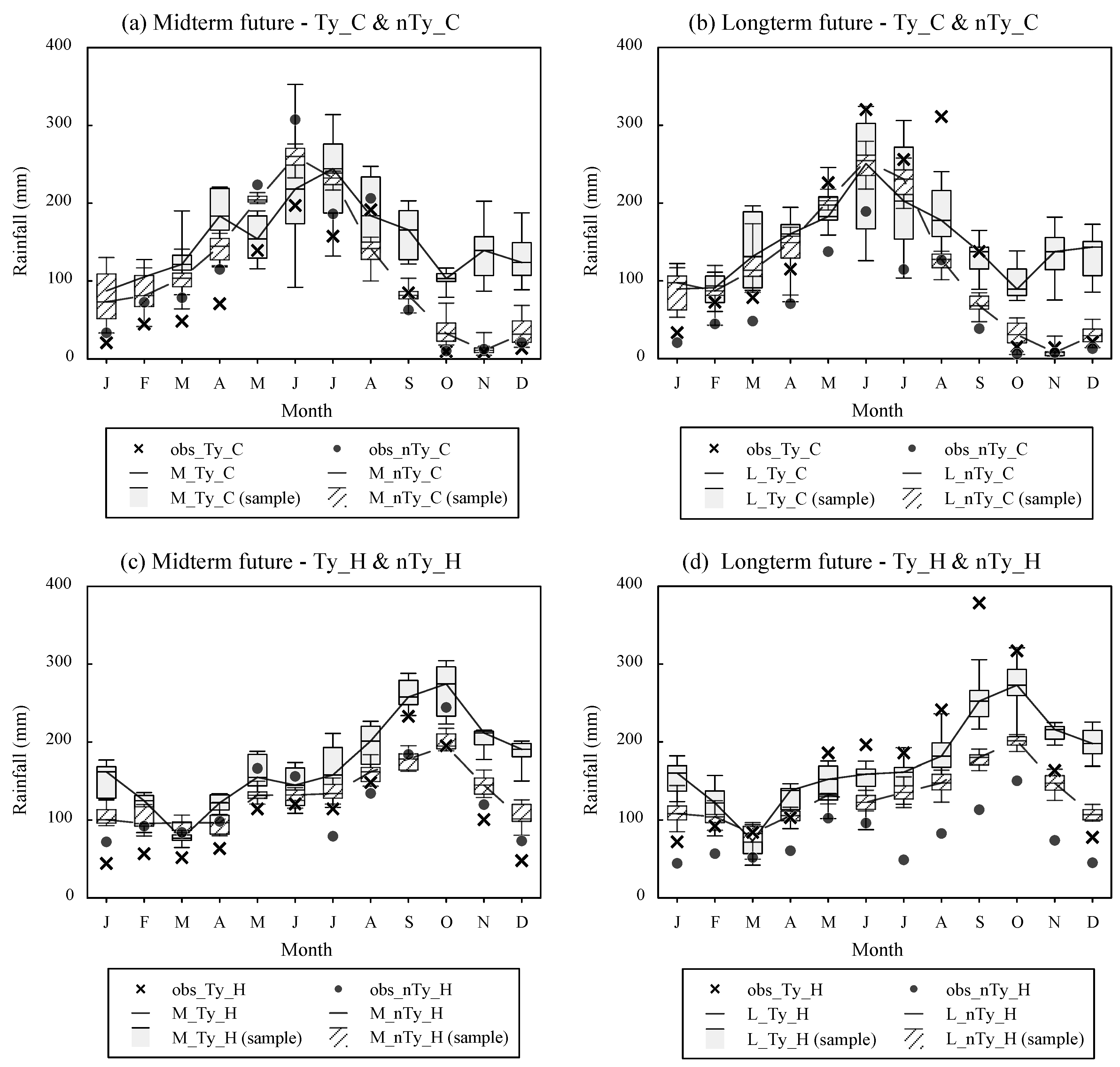
4.1. Three-Classification and Range Analysis of Future Scenario Precipitation
4.2. Future Scenario Precipitation Assessment
5. Conclusions
- For both Taichung and Hualien DNN downscaling models, the number of hidden layers is 1, the learning rate ranges from 0.001 to 0.0001, and the number of nodes is mostly 10;
- The DNN downscaling models were BCC and CAN models. Dimensionless RMSE shows opposite trends for Taichung and Hualien. Specifically, for the Hualien area, the performance of the BCC model is superior to that of the CAN model, and for the Taichung area, the performance of the CAN model is superior to that of the BCC model;
- According to the three-classification analysis of future scenario precipitation predictions, the summer precipitation for both Taichung and Hualien weather stations is mostly within the normal range, whereas the winter precipitation for Taichung is mostly too much, and the winter precipitation for Hualien is half normal and half too much;
- According to the analysis of future precipitation ranges, the mid-term precipitation for both Taichung and Hualien is mostly within 100 mm to 200 mm, while the long-term precipitation is mostly within 100 mm to 200 mm for Taichung and is generally within 0 mm to 100 mm and 100 mm to 200 mm for Hualien;
- According to the analysis of future monthly precipitation, the wet season precipitation is below the historical average and the dry season precipitation is above the historical average. For both Taichung and Hualien areas, the dry season precipitation variation is greater than the wet season precipitation variation and the long-term precipitation variation is greater than the mid-term precipitation variation. For the Taichung area, the long-term dry season precipitation is less significantly affected by typhoons and the long-term wet season precipitation is more significantly affected by typhoons. For Hualien mid-term precipitation, the model without the effect of typhoons shows a mid-term precipitation trend closer to the historical precipitation trend and the long-term wet season precipitation is more significantly affected by typhoons;
- According to the analysis of the probability of the future monthly precipitation exceeding the historical monthly average precipitation, for both the Taichung and Hualien areas, the mid-term/long-term dry season precipitation has a much higher probability of exceeding the historical average than the wet season precipitation, and the dry season precipitation for Taichung is more significantly affected by typhoons than that in Hualien.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Field, C.B.; Barros, V.R. (Eds.) Climate Change 2014—Impacts, Adaptation and Vulnerability: Regional Aspects; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Kitoh, A.; Endo, H.; Krishna Kumar, K.; Cavalcanti, I.F.; Goswami, P.; Zhou, T. Monsoons in a changing world: A regional perspective in a global context. J. Geophys. Res. Atmos. 2013, 118, 3053–3065. [Google Scholar] [CrossRef]
- Chou, C.; Liu, S.C. Observations of Global Climate Changes. Atmos. Sci. 2012, 40, 185–213. Available online: https://www.airitilibrary.com/Article/Detail?DocID=02540002-201209-201303010037-201303010037-185-213 (accessed on 11 March 2024).
- Huang, W.C.; Chiang, Y.; Wu, R.Y.; Lee, J.L.; Lin, S.H. The impact of climate change on rainfall frequency in Taiwan. Terr. Atmos. Ocean. Sci. 2012, 23, 553–564. [Google Scholar] [CrossRef]
- Giorgi, F.; Mearns, L.O. Approaches to the simulation of regional climate change: A review. Rev. Geophys. 1991, 29, 191–216. [Google Scholar] [CrossRef]
- Wilby, R.L.; Dawson, C.W.; Barrow, E.M. SDSM—A decision support tool for the assessment of regional climate change impacts. Environ. Model. Softw. 2002, 17, 145–157. [Google Scholar] [CrossRef]
- Lin, S.S.; Hu, Y.L.; Zhu, K.Y. Downscaling model for rainfall based on the influence of typhoon under climate change. J. Water Clim. Change 2022, 13, 2443–2458. [Google Scholar] [CrossRef]
- Li, C.Y.; Lin, S.S.; Chuang, C.M.; Hu, Y.L. Assessing future rainfall uncertainties of climate change in Taiwan with a bootstrapped neural network-based downscaling model. Water Environ. J. 2020, 34, 77–92. [Google Scholar] [CrossRef]
- Maraun, D. Bias correction, quantile mapping, and downscaling: Revisiting the inflation issue. J. Clim. 2013, 26, 2137–2143. [Google Scholar] [CrossRef]
- Li, C.Y.; Lin, S.S.; Lin, Y.F.; Kan, P.S. A bootstrap regional model for assessing the long-term impacts of climate change on river discharge. Int. J. Hydrol. Sci. Technol. 2019, 9, 84–108. [Google Scholar] [CrossRef]
- Aswin, S.; Geetha, P.; Vinayakumar, R. Deep learning models for the prediction of rainfall. In Proceedings of the 2018 International Conference on Communication and Signal Processing (ICCSP), Chennai, India, 3–5 April 2018; IEEE: Piscataway, NJ, USA; pp. 0657–0661. [Google Scholar] [CrossRef]
- Basha, C.Z.; Bhavana, N.; Bhavya, P.; Sowmya, V. Rainfall prediction using machine learning & deep learning techniques. In Proceedings of the 2020 International Conference on Electronics and Sustainable Communication Systems (ICESC), Coimbatore, India, 2–4 July 2020; IEEE: Piscataway, NJ, USA; pp. 92–97. [Google Scholar] [CrossRef]
- Bai, Y.; Chen, Z.; Xie, J.; Li, C. Daily reservoir inflow forecasting using multiscale deep feature learning with hybrid models. J. Hydrol. 2016, 532, 193–206. [Google Scholar] [CrossRef]
- Hinton, G.E.; Salakhutdinov, R.R. Reducing the dimensionality of data with neural networks. Science 2006, 313, 504–507. [Google Scholar] [CrossRef]
- Debruyne, M.; Hubert, M.; Van Horebeek, J. Detecting influential observations in Kernel PCA. Comput. Stat. Data Anal. 2010, 54, 3007–3019. [Google Scholar] [CrossRef]
- Jolliffe, I.T.; Cadima, J. Principal component analysis: A review and recent developments. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2016, 374, 20150202. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.C. The Analysis of Climatological Characteristics of Non-Typhoon Rainfall in Taiwan. Master’s Thesis, National Taiwan University, Taipei, Taiwan, 2006. [Google Scholar] [CrossRef]
- Schölkopf, B.; Smola, A.; Müller, K.R. Nonlinear component analysis as a kernel eigenvalue problem. Neural Comput. 1998, 10, 1299–1319. [Google Scholar] [CrossRef]
- Li, C.H.; Lin, C.T.; Kuo, B.C.; Chu, H.S. An automatic method for selecting the parameter of the RBF kernel function to support vector machines. In Proceedings of the 2010 IEEE International Geoscience and Remote Sensing Symposium, Honolulu, HI, USA, 25–30 July 2010; IEEE: Piscataway, NJ, USA; pp. 836–839. [Google Scholar] [CrossRef]
- Fix, E.; Hodges, J.L. Discriminatory analysis. Nonparametric discrimination: Consistency properties. Int. Stat. Rev. Rev. Int. Stat. 1989, 57, 238–247. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Schmidhuber, J. Deep learning. Scholarpedia 2015, 10, 32832. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Hawkins, D.M. The problem of overfitting. J. Chem. Inf. Comput. Sci. 2004, 44, 1–12. [Google Scholar] [CrossRef]
- Bai, Y.; Sun, Z.; Zeng, B.; Deng, J.; Li, C. A multi-pattern deep fusion model for short-term bus passenger flow forecasting. Appl. Soft Comput. 2017, 58, 669–680. [Google Scholar] [CrossRef]
- Bengio, Y. Practical recommendations for gradient-based training of deep architectures. In Neural Networks: Tricks of the Trade: Second Edition; Springer: Berlin/Heidelberg, Germany, 2012; pp. 437–478. [Google Scholar] [CrossRef]
- Liu, F.; Xu, F.; Yang, S. A flood forecasting model based on deep learning algorithm via integrating stacked autoencoders with BP neural network. In Proceedings of the 2017 IEEE third International Conference on Multimedia Big Data (BigMM), Laguna Hills, CA, USA, 19–21 April 2017; IEEE: Piscataway, NJ, USA; pp. 58–61. [Google Scholar] [CrossRef]
- Coppola, E.A., Jr.; Rana, A.J.; Poulton, M.M.; Szidarovszky, F.; Uhl, V.W. A neural network model for predicting aquifer water level elevations. Groundwater 2005, 43, 231–241. [Google Scholar] [CrossRef]








| Model | CanESM2 | BCC-CSM1.1 |
|---|---|---|
| Horizontal resolution | 128 × 64 | 128 × 64 |
| Output variable number | 30 | 30 |
| Length of historical data | January 1995–December 2005 | January 1995–December 2005 |
| Length of scenario data | January 2006–December 2099 | January 2006–December 2099 |
| Abbreviation | CAN | BCC |
| Long Name | Output Variable Name |
|---|---|
| Total Cloud Fraction | clt |
| Air Pressure at Convective Cloud Base | ccb |
| Air Pressure at Convective Cloud Top | cct |
| Cloud Area Fraction | cl |
| Mass Fraction of Cloud Liquid Water | clw |
| Condensed Water Path | clwvi |
| Evaporation | evspsbl |
| Relative Humidity | hur |
| Specific Humidity | hus |
| Surface Upward Latent Heat Flux | hfls |
| Near-Surface Specific Humidity | huss |
| Near-Surface Relative Humidity | hurs |
| Precipitation | pr |
| Convective Precipitation | pre |
| Water Vapor Path | prw |
| Surface Air Pressure | ps |
| Sea Level Pressure | psl |
| Surface Downward Longwave Radiation | rlds |
| Surface Upwelling Longwave Radiation | rlus |
| Surface Downwelling Clear-Sky Longwave Radiation | rldsc |
| Surface Upwelling Shortwave Radiation | rsus |
| Surface Upwelling Clear-Sky Shortwave Radiation | rsuscs |
| Air Temperature | ta |
| Near-Surface Air Temperature | tas |
| Surface Temperature | ts |
| Eastward Wind | ua |
| Eastward Near-Surface Wind | uas |
| Northward Wind | va |
| Northward Near-Surface Wind | vas |
| Daily-Mean Near Surface Wind Speed | sfcWind |
| Station | GCM Model | Source Of Rainfall Data | Accuracy (%) | KPC |
|---|---|---|---|---|
| Taichung | BCC | noTy | 0.11 | 23 |
| Total | 0.07 | 23 | ||
| CAN | noTy | 0.25 | 25 | |
| Total | 0.10 | 6 | ||
| Hualien | BCC | noTy | 0.10 | 12 |
| Total | 0.06 | 2 | ||
| CAN | noTy | 0.11 | 10 | |
| Total | 0.36 | 10 |
| n_Components = 4 = 0.0189 | Layer | Node | 10 | 50 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Ir | 0.01 | 0.001 | 0.0001 | 0.01 | 0.001 | 0.0001 | ||||
| C | Adagrad | sigmoid | 1 | RMSE | 1.07403 | 1.02925 | 1.16097 | 1.16673 | 1.03443 | 1.16714 |
| tanh | 1.32746 | 1.19892 | 0.99706 | 1.34455 | 1.02353 | 1.02408 | ||||
| Adam | sigmoid | 1 | RMSE | 1.34725 | 0.99238 | 1.03060 | 1.34434 | 1.16298 | 1.00758 | |
| tanh | 1.33056 | 1.33417 | 1.02146 | 1.32340 | 1.34432 | 1.21584 | ||||
| H | Adagrad | sigmoid | 1 | RMSE | 0.85935 | 0.84993 | 0.82558 | 0.85779 | 0.84836 | 0.86098 |
| tanh | 0.89153 | 0.84601 | 0.86170 | 0.89997 | 0.87658 | 0.86690 | ||||
| Adam | sigmoid | 1 | RMSE | 0.86541 | 0.86051 | 0.82198 | 0.92920 | 0.85073 | 0.81970 | |
| tanh | 0.88730 | 0.89611 | 0.85805 | 0.89033 | 0.89681 | 0.82764 | ||||
| GCM Model | Source of the Rainfall Data | Station | Output Variable Number | Optimizer | Activation Function | Learning Rate | Node | RMSE | |
|---|---|---|---|---|---|---|---|---|---|
| BCC | Total | C | 23 | 0.01931 | Adagrad | tanh | 0.0001 | 10 | 1.09106 |
| H | 4 | 0.03945 | Adagrad | tanh | 0.001 | 10 | 1.12866 | ||
| No_typhoon | C | 4 | 0.01894 | Adam | sigmoid | 0.001 | 10 | 0.99238 | |
| H | 12 | 0.05273 | Adam | sigmoid | 0.0001 | 50 | 0.81970 | ||
| CAN | Total | C | 6 | 0.01872 | Adam | sigmoid | 0.01 | 10 | 0.82479 |
| H | 10 | 0.03630 | Adam | tanh | 0.001 | 10 | 1.04221 | ||
| No_typhoon | C | 25 | 0.03339 | Adagrad | sigmoid | 0.01 | 10 | 0.82064 | |
| H | 10 | 0.06675 | Adam | tanh | 0.0001 | 10 | 0.80403 |
| Models | PU (%) | BR |
|---|---|---|
| Hualien_BCC_noTy | 33 | 6.31 |
| Hualien_BCC_Total | 36 | 12.33 |
| Hualien_CAN_noTy | 31 | 2.24 |
| Hualien_CAN_Total | 37 | 2.25 |
| Taichung_BCC_noTy | 48 | 5.10 |
| Taichung_BCC_Total | 37 | 7.47 |
| Taichung_CAN_noTy | 32 | 5.69 |
| Taichung_CAN_Total | 42 | 8.58 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, S.-S.; Zhu, K.-Y.; Wang, C.-Y. A Deep Learning-Based Downscaling Method Considering the Impact on Typhoons to Future Precipitation in Taiwan. Atmosphere 2024, 15, 371. https://doi.org/10.3390/atmos15030371
Lin S-S, Zhu K-Y, Wang C-Y. A Deep Learning-Based Downscaling Method Considering the Impact on Typhoons to Future Precipitation in Taiwan. Atmosphere. 2024; 15(3):371. https://doi.org/10.3390/atmos15030371
Chicago/Turabian StyleLin, Shiu-Shin, Kai-Yang Zhu, and Chen-Yu Wang. 2024. "A Deep Learning-Based Downscaling Method Considering the Impact on Typhoons to Future Precipitation in Taiwan" Atmosphere 15, no. 3: 371. https://doi.org/10.3390/atmos15030371
APA StyleLin, S.-S., Zhu, K.-Y., & Wang, C.-Y. (2024). A Deep Learning-Based Downscaling Method Considering the Impact on Typhoons to Future Precipitation in Taiwan. Atmosphere, 15(3), 371. https://doi.org/10.3390/atmos15030371







