Abstract
This work investigates the inter-model diversity of the Pacific Decadal Oscillation’s (PDO) impact on tropical cyclone frequency (TCF) over the Western North Pacific (WNP) from the historical simulation of twenty-two Coupled Model Intercomparison Project Phase 6 (CMIP6) models. The impact of the PDO is expressed as the TCF difference between the positive and negative PDO phases. The comparison between the models with high PDO skill and low PDO skill shows that the PDO-related sea surface temperature (SST) gradient between the western and central tropical Pacific plays an important role in changing the large-scale atmospheric dynamic fields for TC genesis and, thus, the TCF over the WNP. This SST gradient also significantly contributes to the inter-model spread of PDO’s impact on TCF across the 22 CMIP6 models. We, therefore, stress that the PDO-related eastward SST gradient between the western and central tropical Pacific triggers the lower troposphere westerly and eastward extending of the monsoon trough over the WNP. The moistening of the atmosphere and enhancing ascending motion in the mid-troposphere promote convection, leading to the easterly wind anomaly over the upper troposphere, which reduces the vertical wind shear. Those favorable dynamic conditions consistently promote the TC formation over the southeastern part of the Western North Pacific. Our results highlight that PDO could impact the WNP TCF through its associated tropical SST gradient.
1. Introduction
The Western North Pacific (WNP) is the most active ocean basin for tropical cyclone (TC) activity, with an increasing risk to the coastal areas of East Asia due to global warming [1,2,3,4]. Therefore, it is extremely valuable to comprehend the variations in tropical cyclone activity from both a scientific and social perspective. Recent studies have shown that the TC frequency (TCF) experiences significant decadal variability over the WNP. This decadal variation is mainly located over the southeastern part of the WNP (e.g., [5° N–20° N, 140° E–180° E]). It has been attributed to the Pacific Decadal Oscillation (PDO) [5,6,7,8], the Interdecadal Pacific Oscillation [9,10,11,12], the Atlantic Multidecadal Oscillation [13,14,15], and aerosol forcings [16,17,18,19]. The physical mechanisms were often verified in various climate models. Thus, it is essential to understand to what extent the current state-of-the-art CMIP6 models can reproduce the impact of those factors.
The PDO is the leading component of sea surface temperature (SST) anomaly fluctuation on the decadal timescale over the North Pacific [20]. During the positive phase of the PDO, sea surface temperatures (SST) are warmer along the west coast of the United States and extend to the tropics. Conversely, there are cold SST anomalies in the eastern region of Japan and the western Pacific Ocean. The reverse pattern is observed during the negative phase of PDO. Previous studies have extensively assessed the performances of the simulated PDO in CMIP3-6 models [21,22,23,24,25,26,27]. Considerable inter-model spread in reproducing the PDO-related SST anomaly is found in the CMIP3 models [21,23]. This inter-model diversity is relatively reduced in the CMIP5 models, mainly due to the significant improvements in the outlier models [23,28]. The evaluation of the PDO performance in historical experiments of CMIP5 models showed that the ensemble mean of the CMIP5 model can well reproduce the SST anomaly over the mid-latitude, while the skill is relatively low in simulating the low-latitude SST signal [29,30,31]. CMIP6 has greatly enhanced the simulation ability of the PDO compared to prior generations of CMIP [24,25,26]. Notably, the CMIP6 exhibits improved capability in accurately representing the impact of the PDO on SST in the equatorial region, and some CMIP6 models can accurately simulate tropical SST patterns associated with PDO that are similar to those observed [24]. This increases our confidence to assess the PDO’s impact on TC activities in CMIP6 models.
Several investigations have shown that the SST anomaly associated with the PDO has significant impacts on WNP TC activity [9,11,32,33,34,35,36,37]. The observed decrease in the WNP TCF over the period from the mid to late 1990s has been suggested to be associated with the transition of the PDO to its negative phase [10,11,12,38]. The SST cooling over the central Pacific could increase the vertical wind shear, which decreases the probability of tropical cloud clusters transiting to TCs over the southeastern part of WNP [12,39,40,41]. Moreover, this SST cooling can also weaken the low-level vorticity and ascending motion, inhibiting TC genesis [42,43,44,45,46,47]. Since the mid-1990s, there has been a prevailing tendency for TC in the WNP to move in a northwestward direction. This trend has resulted in a higher frequency of TC occurring in the South China Sea and the eastern side of the Philippines [10,48]. Studies found that during the negative phase of the PDO, there is an increase in the frequency of tropical cyclones making landfall on the eastern coast of China [49]. Moreover, the PDO significantly influences the occurrence of TC making landfall on the Korean Peninsula [50,51]. These TC track changes are mostly attributed to the anomalous cyclonic steering flow located in the WNP [49,51]. Changes in atmospheric circulation are attributed to the PDO-related SST anomaly [12].
Given the significance of PDO’s impact on WNP TCF and the increase in the fidelity of PDO simulation in CMIP6 models, it is an opportunity to investigate how the TCF changes in response to the PDO. In this study, we first explicitly detect the TCs in the daily output from the historical experiment of CMIP6 models. Then, we examine the TCF response to the PDO in the CMIP6 models, attempt to identify the key SST anomaly associated with the PDO in changing the large-scale environmental fields for TC genesis, and investigate the inter-model spread of the TCF response to the PDO. The subsequent sections of the paper are structured as follows: Section 2 provides a description of the data and the method used. The performance of PDO and explicitly detected TCs in the 22 CMIP6 models is evaluated in Section 3. Section 4 investigated the inter-model spread of the PDO-WNP TCF relationship on a decadal timescale. The final part provides a concise summary of the main findings.
2. Materials and Methods
2.1. Materials
The observed TC data for the period of 1950–2014 over the WNP are derived from the National Oceanic and Atmospheric Administration (NOAA) International Best Track Archive for Climate Stewardship version 4 (IBTrACS v4) [52]. This dataset includes an extensive amount of data relevant to the WNP TC, including the latitude, longitude, sustained wind speed, and minimum central pressure of the TC, with a time interval of 6 h. The location at which a TC’s maximum sustained wind initially increases to 34 knots is referred to as the genesis of the cyclone. TCs are most active in WNP during June–October (JJASO); therefore, we mainly focus on JJASO from 1950 to 2014.
The monthly average SST dataset, with a horizontal resolution of 2° × 2°, is obtained from the National Oceanic and Atmospheric Administration (NOAA) Extended Reconstructed SST, version 5 (ERSST.v5) [53]. Monthly mean atmospheric data, including meridional wind (V), zonal wind (U), and vertical velocity (Omega), with a resolution of 0.25° × 0.25° horizontal resolution, are obtained from the European Centre for Medium-Range Weather Forecasts Reanalysis v5 (ERA5) [54].
The simulated TCs during 1850–2014 are derived from the daily output of historical experiments in twenty-two CMIP6 models (Table 1). Since the observed TCF has been relatively reliable since the 1950s, we evaluated the detected TCF for the period of 1950–2014 as shown in Figure 1. In the rest of the paper, the TCF for the period 1850–2014 is used. The atmospheric circulation, atmospheric temperature, relative humidity, absolute humidity, sea level pressure, and surface wind speed are used in detecting TCs. The monthly mean SST and atmospheric circulation datasets from the 22 CMIP6 models are used to examine the impact of PDO on TC environmental fields.

Table 1.
The horizontal resolutions, detected TCFs during JJASO from 1950–2014, and simulated PDO TS2 skills in the 22 CMIP6 models. The five models with the highest (lowest) PDO TS2 skill are in bold (italic).
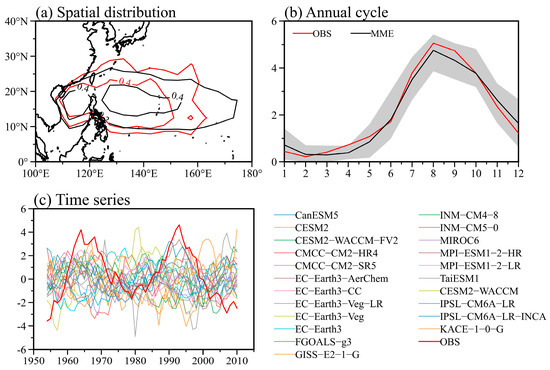
Figure 1.
Evaluation of the 22 CMIP6 historical experiment simulated TCF against the observation. (a) spatial distribution of observed (red) and simulated (black) TC genesis locations in JJASO over the box of 5° × 5° (events per year for one box). (b) TCF annual cycle from observation (red) and the ensemble mean of 22 CMIP6 models (black), with the shading indicating the uncertainty range of one standard deviation. (c) The decadal variation of TCF in observation (thick red line) and individual model (colored lines).
To obtain the decadal signal of TCF change, the detected TCs are detrended, and a 9-year running mean is applied. Correspondingly, the same procedure is applied to the monthly mean fields, including SST and atmospheric circulation, for both observation and simulation.
2.2. Methods
- a.
- PDO skill in CMIP6 models
The leading empirical orthogonal functions (EOFs) of the North Pacific (20°–70° N, 110° E–110° W) SST monthly anomalies represent the pattern of PDO; meanwhile, the PDO indices are regarded as the corresponding time expansion coefficients [55,56]. The model’s performance in simulating PDO-related SST patterns and magnitudes is evaluated using the Tayler skill score II (TS2) [57]. The TS2 is a commonly used evaluation method in the field of climatology that effectively assesses the accuracy of model predictions against observational data [57,58,59]. Therefore, it can be used as an important indicator for evaluating model skills [59]. Therefore, this work uses TS2 to measure the model’s performance in simulating PDO. The TS2 is defined as:
where indicates the pattern correlation coefficient (PCC) of SST between the simulated and the observed, is the greatest realizable correlation, which is 1.0 in this situation. represents the standard deviation of the simulated SST normalized by the corresponding observation. Table 1 provides the TS2 skill for PDO in the twenty-two CMIP6 models. In addition, the positive (negative) phase of PDO is when the PDO index is larger (smaller) than the plus (minus) half standard deviation from the mean.
- b.
- TC-detection algorithm
We used the Okubo-Weiss-Zeta (OWZ) parameter TC detector [60] to explicitly extract TC information from the historical experiment [61] of the 22 CMIP6 models (Table 1). This method is well described in [60] and widely used in detecting TCs in CMIP-type models with daily output variables [62,63,64]. In order to maintain consistency in the models, all daily output data are interpolated to a resolution of 1° × 1° prior to the detection of TCs. The extracted TCs meet the following criteria: (1) If the OWZ parameter at 850 hPa/500 hPa is greater than 6 × 10−5 s−1/5 × 10−5 s−1, it is considered that there is a TC. (2) The magnitude of the vertical wind shear should not exceed 12.5 m s−1. (3) The 950 hPa/700 hPa relative humidity is greater than 85%/70%. (4) The specific humidity at 950 hPa is greater than 14 g kg−1. (5) The latitude of the TC location should be south of 30° N. (b) The duration of the TC should have been a minimum of 48 h. Table 1 lists the detected TCF in JJASO during 1950–2014 in the 22 CMIP6 models. The simulated TCF in most of the models is close to the observed value of 19.2 events per year during the TC peak season. The ensemble mean of the 22 models is 18.2 events/year, with a standard deviation of 2.7 events/year.
- c.
- Dynamic TC genesis potential index
The genesis of TC depends on a large-scale environmental field. Thus, the correlation between the large-scale environmental and TC variables is referred to as the genesis potential index. Compared with the traditional view, the DGPI (dynamic genesis potential index) pays more attention to the influence of dynamic factors on TC [65]. Recently, studies have shown that DGPI can simulate the climate characteristics and interdecadal variation of TC, especially for WNP [15,65,66]. In this study, the DGPI is used to help understand the interaction between the large-scale environment and TC. The DGPI is expressed as:
In Equation (2), VOR is 850 hPa absolute vorticity (s−1), is the meridional gradient of zonal wind (s−1) at 500 hPa, is 500 hPa vertical pressure velocity (Pa s−1), and represents the difference in horizontal wind velocity between the 200 hPa and 850 hPa.
3. Results and Discussion
3.1. Evaluation of Model Performance in Simulating TCF Climatology and PDO
3.1.1. TCF Climatology
How well of a model in simulation the climatological distribution of TCF is the baseline for evaluating the decadal change of TCF. Figure 1 compares the observed and simulated TC genesis distribution, the TCF annual cycle, and the time evolution during 1950–2014. In the observation, TCs mainly form over the region of 5° N–30° N, 110° E–160° E, with the frequent genesis (over 0.4 events per year over a 5° × 5° box) region located over the South China Sea and Eastern Philippines (Figure 1a). The 22 models’ ensemble mean of simulated TC genesis location distribution resembles the observed one, while fewer TCs are simulated east of 160°E compared to the observation. The reasonable simulated TCF distribution increases our confidence to evaluate the PDO’s impact on TCF since PDO mainly modulates the decadal change of TCs over the southeastern part of WNP.
In terms of the annual cycle, the observation shows that TCs can form year-round over the WNP (Figure 1b). It has a unimodal feature, and the TCF maximum is in August. The TCs in the peak season (JJASO) account for about 75% (19.2 events in JJASO over 25.5 events annually) of the annual total. The MME can well capture the observed TCF annual cycle, exhibiting a correlation coefficient of 0.97. The simulated TCF is 25 events annually, and 18.2 events are in the peak season (JJASO). Thus, 73% of TCs are genesis over during the TC peak season, close to the observed one (75%). In the rest of the investigation, we will only focus on the TC peak season.
In observation, TCs over the WNP have apparent decadal variation, largely controlled by the earth system’s internal modes. TCs were relatively frequently formed in the 1960s and 1990s, while TCs were relatively inactive during the 1970s and mid-1990s. In the observation, the decadal change of TCF over the whole WNP basin is dominated by the southeastern part of WNP, as indicated by the correlation coefficient of 0.87 (p < 0.01). Figure 1c shows that the CMIP6 models can simulate the apparent decadal changes of TCFs over the southeastern part of WNP in the past several decades. The observed TCF decadal change is roughly in the spread of the detected TCs in the 22 CMIP6 models, although 22 CMIP6 simulations may be insufficient to sample the full range of decadal modes.
3.1.2. PDO Skills in CMIP6 Models
The Pacific Decadal Oscillation (PDO), an important form of decadal variability observed in the North Pacific, is characterized by its horseshoe-shaped SST. The SST-driven atmospheric circulation modulates the large-scale environmental conditions for TC genesis. Thus, evaluating the capability of the model to simulate the PDO-related SST pattern is of the utmost importance. Figure 2 compares the PDO-related SST pattern from the 22 models’ mean and individual models against the observation. In the observed positive PDO phase, the central and eastern tropical Pacific and the northeast and southeast subtropical Pacific experienced notable warming, and SST cooling occupied the central and western parts of the mid-latitude Pacific Ocean. The ensemble mean from the 22 CMIP6 models reproduced the observed large-scale SST feature well, with a PCC of 0.87 over [20°–70°N, 110°E–110°W]. However, the simulated SST anomalies over the tropical Pacific Ocean are weaker than the observed ones, and the SST warming center over the equatorial region is westward shifted compared to the observation (Figure 2a,b). It may cause a relatively weaker atmospheric circulation response in the simulation. The Taylor diagram demonstrates the performance of individual CMIP6 models in simulating the PDO-related SST pattern and magnitude (Figure 2c). Most of the models have the PCC skill close to or exceeding 0.8, while about half of the models underestimate the SST anomalies over the North Pacific (Figure 2c). According to the definition of the TS2 score, it synthesizes the PCC skill and the standard deviation of the SST anomaly. Five models with a high TS2 score (>0.72) are selected to represent the good model group. There are CESM2, CESM2-WACCM, CMCC-CM2-SR5, MIROC6, and IPSL-CM6A-LR. Correspondingly, five models with lower skills (<0.55), CMCC-CM2-HR4, INM-CM4-8, INM-CM5-0, CanESM5, and IPSL-CM6A-LR-INCA, are selected as the poor model group (Table 1). We also tested to decrease and increase the number of models for the good and poor models, and the analysis suggested our conclusion is robust. Therefore, in the next section, we will examine differences in TCF and large-scale environmental fields between the five good and poor models.
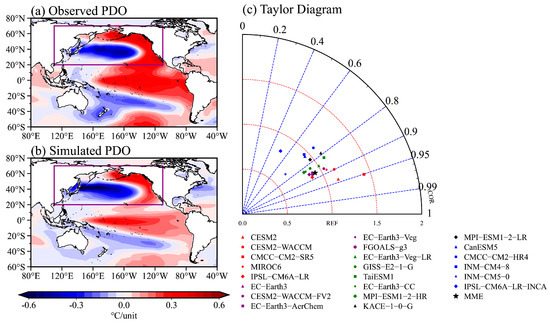
Figure 2.
Evaluation of PDO skill in CMIP6 models. Spatial distribution of (a) observed PDO−related SST and (b) ensemble mean of the 22 CMIP6 model simulated PDO−related SST. (c) Taylor diagram of the PDO performance of the 22 CMIP6 models. In (c), the red and blue dots show the selected five models with the highest Taylor skill scores and the five models with the lowest scores, respectively.
3.2. Inter-Model Spread of the PDO’s Impacts on WNP TCF
3.2.1. Impact of PDO on WNP TCF
Prior studies have demonstrated that the phase shift of the PDO significantly modulates WNP TCF on a decadal timescale, especially over the southeastern WNP [12,51,67,68]. Figure 3 illustrates the difference in TCF and TC-related large-scale environmental fields between the positive and negative phases of PDO in observation. The positive PDO period is when the observed PDO index exceeds 0.5 standard deviations, and the negative PDO period is when the observed PDO index is smaller than −0.5 standard deviations. As shown in Figure 3a, the PDO increases the TCF over the majority of the WNP, especially over the southeastern part of the WNP (5° N–20° N, 140° E–180° E), consistent with previous studies [12,67]. This study focuses on this region and defines it as the main development region (MDR). The decadal change in TCF over the MDR is largely attributed to the impact of large-scale atmospheric circulation fields. DGPI is a synthesized index from atmospheric dynamic fields. The changes in DGPI due to the PDO show an increase in DGPI over the southeastern part of the WNP, although it unrealistically simulates a reduction near the coast of China (Figure 3b).
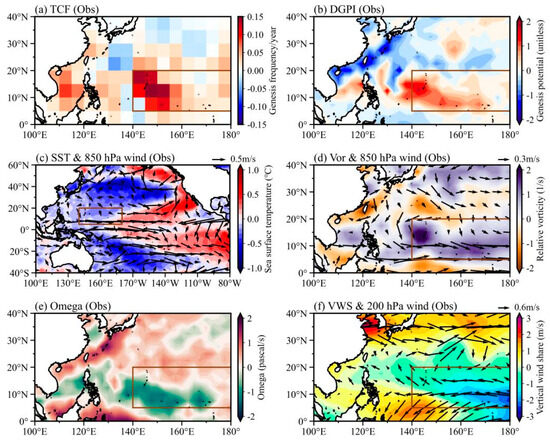
Figure 3.
Impacts of PDO on TCF and large−scale environmental fields. Differences in (a) TCF, (b) DGPI, (c) SST and 850 hPa circulation (m s−1), (d) relative vorticity (10−6 s−1) and circulation (m s−1) at 850 hPa, (e) omega (10−2 Pa s−1) at 500 hPa, and (f) vertical wind shear (m s−1) and 200 hPa circulation (m s−1) between the positive PDO and negative PDO phases. The brown boxes indicate the MDR (5° N–20° N, 140° E–180° E).
The TC-related environmental fields consistently show favorable conditions for the formation of TCs. Figure 3c shows the PDO-related SST anomaly and 850 hPa circulation. The SST exhibited a warming over the central and eastern tropical Pacific and an extensive horseshoe-shaped cooling over the western Pacific. The warmer central Pacific and its associated positive diabatic heating stimulate the ascending Rossby wave over its west and the Kevin wave response over its east [69]. Thus, the lower-troposphere circulation response is dominated by westerly wind anomalies over the tropical WNP (Figure 3b), indicating that the monsoon trough is extending eastward [70]. Thus, the positive vorticity anomalies and mid-troposphere ascending motion are dominated over the southeastern part of WNP (Figure 3d,e). The circulation change over the upper troposphere is highlighted by the easterly over the WNP (Figure 3f), suggesting the dominant role of the first baroclinic pattern response. The lower and upper troposphere circulations both decelerate the mean circulation over the southeastern WNP. It contributes to the weakened vertical wind shear over the southeastern WNP (Figure 3f). Therefore, the PDO-related SST drives the atmospheric circulation change mainly in a latitudinal manner, indicating the significant influence of tropical SSTs on atmospheric circulation. The zonal SST gradient results in an increase in westerly winds and vorticity in the lower troposphere, further enhancing vertical motion. The corresponding circulation changes in the upper troposphere contribute to a reduction in vertical wind shear. These favorable conditions may lead to the increased formation of TCs in the MDR.
3.2.2. Inter-Model Spread
Can the CMIP6 models reproduce the PDO’s impact on TC frequency as in the observation? Figure 4a,b compare the simulated and observed TCF changes due to the PDO phase change. The ensemble mean of the 22 CMIP6 models generally shows a similar pattern of TCF response to PDO as observed. More TCs form over the MDR in the ensemble mean, but the magnitude is remarkably underestimated. The 22 CMIP6 models have a considerable inter-model spread of TCF response to PDO over the MDR (Figure 4c). The magnitude of TCF change across the 22 CMIP6 models has a significant relationship with the performance of the PDO, as indicated by a correlation coefficient of 0.49 (p < 0.05). In other words, a model that has high PDO skill would suggest an increase in TCF over the MDR, and vice versa.
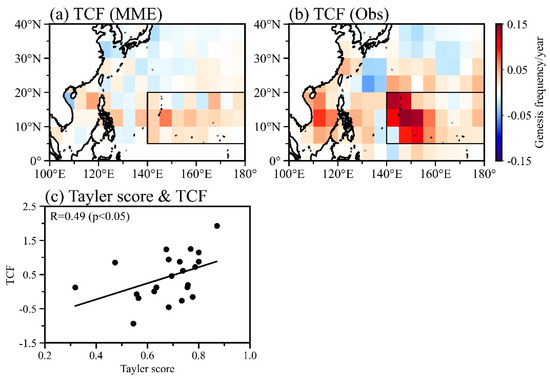
Figure 4.
Impacts of PDO on WNP TCF in CMIP6 models. Differences in (a) simulated TCF (MME), (b) observed TCF between the positive PDO and negative PDO phases. (c) is the inter-model relationship between PDO performances and TCF responses in the 22 CMIP6 model. The black boxes in a and b indicate the MDR (5° N–20° N, 140° E–180° E). The inter-model correlation coefficients (R) are displayed in the top left corner of the figure, with the p values in parentheses.
To identify the key physical processes responsible for the inter-model diversity of TCF, we first examine the TCF response in the five good models and the five poor models in terms of PDO performance (Figure 5). The ensemble mean of five good models demonstrates an apparent increase in TCF over the MDR during the PDO positive phase relative to the negative phase (Figure 5a). This is consistent with the results of the observation (Figure 4b) [5,6]. However, the ensemble mean of the five poor models shows a low consensus of TCF change over the MDR (Figure 5b). The area-averaged TCF change in the good models is 0.77 TCs, significantly larger than that from the poor models (−0.045 TCs). Thus, the weaker responses of TCF in the poor models may lead to the weak response of TCF in the 22 models’ ensemble mean result (Figure 4a). The difference in TCF change between the good models and poor models can arguably be explained by the dynamic large-scale environmental conditions since the DGPI also shows distinct changes between the good models and poor models (Figure 5c,d). The good models show an increase in DGPI in the MDR, while the DGPI in the poor models lacks this response (Figure 5e,f). The area-averaged DGPI anomaly is two times larger than that in the poor models.
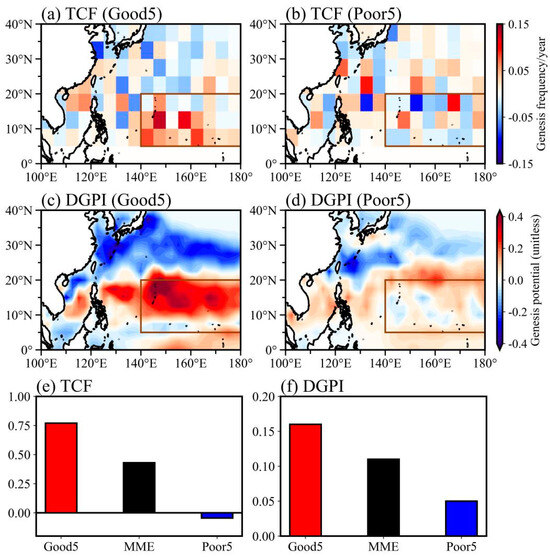
Figure 5.
Impacts of PDO on WNP TCF and DGPI in good models (Good5) and poor models (Poor5). Differences in (a) TCF from Good5, (b) TCF from Poor5, (c) DGPI from Good5, (d) DGPI from Poor5 between the positive PDO and negative PDO phases. (e,f) are the area-averaged TCF/DGPI changes; the brown boxes indicate the MDR (5° N–20° N, 140° E–180° E).
We further disentangle the detailed atmospheric and ocean conditions, which are related to the PDO, for the TC formation. The ensemble mean of good models well simulated the observed feature of the PDO-related SST pattern, especially the warm SST anomalies on the west coast of the United States and the tropical central Pacific (Figure 6a). This northeast-southwest elongated warm SST anomaly is missing in the poor models (Figure 6e). Thus, the good models have a clear eastward SST gradient between the western and central tropical Pacific, resulting in the apparent westerly wind anomaly. It could extend the climatological monsoon trough eastward, thus enhancing the lower troposphere’s cyclonic vorticity (Figure 6b). Meanwhile, the mid-level ascending motion is enhanced (Figure 6c). Over the upper troposphere, the circulation is dominated by the easterly wind over the MDR, leading to a reduction of vertical wind shear (Figure 6d). These large-scale environments consistently benefit TC formation. However, in the poor models, there is a lack of lower troposphere zonal wind change due to the nearly zonal uniform SST anomaly over the tropical Pacific Ocean. Thus, there are marginal changes in the lower troposphere, mid-level vertical motion, and vertical wind shear, consistent with the negligible change of TCF in the poor models (Figure 6e–h). The critical role of the zonal SST gradient over the western and central tropical Pacific in modulating the TCF is clearly illustrated in the right panel of Figure 6. The difference in SST anomaly between the good and poor models drives the distinct three denominational atmospheric circulations. Therefore, we underscore the significance of the zonal SST gradient between the western tropical Pacific (5° S–20° N, 170° E–130° W) and central tropical Pacific (5° S–20° N, 120° E–160° E).
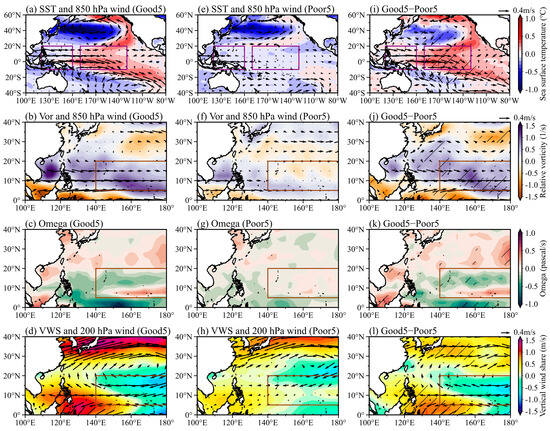
Figure 6.
Impacts of PDO on large−scale environment factors in good models (Good5, left panel) and poor models (Poor5, middle panel) and the difference between Good5 and Poor5 (right panel). (a) SST (K) and 850 hPa circulation (m s−1), (b) 850 hPa circulation (m s−1) and relative vorticity (10−6 s−1), (c) omega (10−2 Pa s−1) at 500 hPa, and (d) vertical wind shear (m s−1) and 200 hPa circulation (m s−1) from five good models. (e–h) as (a–d), but for Poor5. (i–l) show the differences between Good5 and Poor5. The “/” in (i–l) indicates that the difference is significant at a 99% confidence level.
We defined the PDO-related SST difference between the two boxes as the tropical Pacific SST gradient (TPG) index. The relationships among the TPG index, atmospheric dynamic fields over the MDR, and the resulting TCF are further used to confirm the aforementioned physical processes across the 22 CMIP6 models (Figure 7). Figure 7a exhibits a solid relationship between the TPG index and the TCF change in the MDR (R = 0.78, p < 0.01). Note that the relationship between the observed TPG index and TCF change (black star in Figure 7a) is close to the multimodel regression line, indicating the robust role of the tropical Pacific SST gradient. In the observation, this tropical SST gradient is a key nature of PDO in building up global teleconnection [71,72,73]. The underestimation of the SST gradient may lead to a weaker TCF response in the CMIP6 models. Fortunately, a recent evaluation study shows an increase in model capability in reproducing the tropical extended SST anomaly from CMIP3 models to CMIP6 models [25]. Figure 7b shows a close relationship between PDO performance and the TPG index. The correlation coefficient between TS2 and the TPG index is 0.68, significant at a 99% confidence level. It indicates that a model with good PDO performance is better skilled at reproducing its tropical impacts.
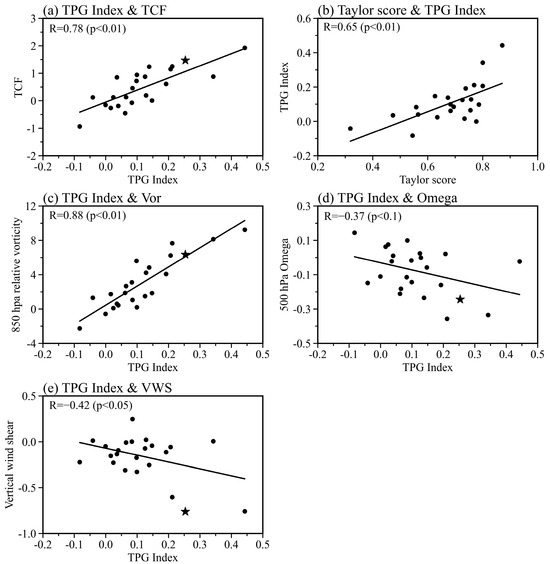
Figure 7.
Relationship chain of the atmospheric response from the simulated TPG index to TCF change. Scatterplots of the (a) TPG index and TCF, (b) TS2 of PDO and TPG index, (c) TPG index and 850 hPa vorticity (Vor), (d) TPG index and 500 hPa omega, and (e) TPG index and vertical wind shear (VWS). Black stars indicate observations. The inter-model correlation coefficients (R) are displayed in the top left corner of the figure, with the p values in parentheses.
Figure 7c–e proves the physical processes of how the SST gradient can drive atmospheric circulation to form favorable conditions for TC genesis. The TPG index is significantly correlated with the 850-hPa relative vorticity (r = 0.88, p < 0.01), vertical wind shear (r = −0.42, p < 0.05), and 500-hPa omega (r = −0.37, p < 0.1) across the models. The response of the atmospheric variables to the observed TPG index could further verify the important role of the zonal SST gradient since the observation is close to the multimodel regression lines, except for a stronger vertical wind shear (Figure 7e). It is suggested that a model with a strong zonal SST gradient can simulate strong lower troposphere relative vorticity and ascending motion and weak vertical wind shear, thus more TCs over the MDR.
This point of view is verifiable from the DGPI analysis (Figure 8). The combined effect of the dynamic fields, expressed by DGPI, is highly correlated with the TCF across the models and observations. The correlation coefficient between the DGPI and TCF is 0.75, suggesting the DGPI can well describe the PDO’s impact on TCF. The finding from a recent study is consistent with our result [74], suggesting the important role of the dynamic field in TCF decadal change. More importantly, there is a significant positive correlation between the TPG index and DGPI (r = 0.77, p < 0.01). Thus, the inter-model spread of the PDO-related tropical SST gradient, which drives distinct changes in the atmospheric circulation over the southeast part of the WNP across models, significantly modulates the TC genesis environment, resulting in the apparent difference in TCF changes.
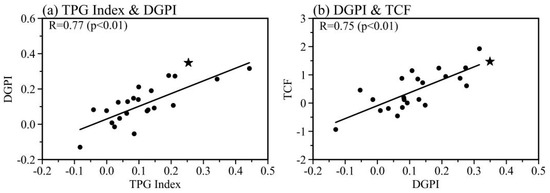
Figure 8.
Inter-model relation from TPG index to TCF via DGPI. Scatter plot of (a) TPG index and DGPI and (b) DGPI and TCF. Black stars indicate the observations. The inter-model correlation coefficients (R) are displayed in the top left corner of the figure, with the p values in parentheses.
4. Conclusions
The WNP is the most active TC basin in the world. Significant decadal changes in TCF have occurred in the past several decades. This TCF decadal change is dominated by the variation in the southeastern part of WNP, defined as MDR in this study. This study examined the PDO’s impacts on TCF in the MDR across the 22 CMIP6 models with explicitly detected TCs. Compared to the observation, the ensemble mean of the 22 CMIP6 models shows a weaker response of TCF to the PDO. It is due to the weaker TCF response of PDO, especially in the models with poor PDO skills. We compared the difference in large-scale environmental fields associated with the TC genesis between the five models with better PDO skills and the five models with poor PDO skills. The good models can well simulate the SST cooling over the western tropical Pacific and warming over the central tropical Pacific associated with the PDO, as well as the ensuring TCF increase over the MDR, consistent with the observation. However, the poor models failed to simulate this east–west SST gradient and TCF response. We stress the important role of the tropical SST gradient in driving atmospheric circulation changes, which provide the key dynamic conditions for TC genesis over the MDR. This tropical SST gradient is an essential part of the PDO’s impact on the Pacific SSTs, although the PDO index is derived from the North Pacific SST anomaly.
The inter-model diversity of the PDO-related tropical Pacific SST gradient (TPG) is an important factor leading to the TCF response diversity over the MDR. The physical mechanism responsible for the TCF response diversity is summarized as follows: The larger TPG index, indicating the westward SST gradient anomaly associated with PDO, triggers the westerly wind anomaly over the western tropical Pacific. It enhances and eastward shifts the climatological monsoon trough and, thus, increases the lower troposphere relative vorticity over the MDR. The humid monsoon flow enhances the convection and ascending motion in the mid-troposphere. In the upper troposphere, the easterly wind response would weaken the climatological westerly, yielding a weakened vertical wind shear over the MDR. Thus, the atmospheric dynamic responses to the TPG are all favorable for TC genesis, leading to an increase in TCF over the MDR.
The evaluations of PDO in previous studies mainly focus on the North Pacific region (e.g., poleward of 20°N), which indicates the increasing fidelity of PDO simulation in the coupled model. Fortunately, the current coupled models tend to better capture the tropical part of the SST anomaly, which is closely associated with PDO. Recent studies demonstrated that the tropical SST gradient has a significant role in modulating the TCF over the WNP in interannual and decadal timescales in the observation [75,76]. Thus, the improvement of the tropical expression of PDO in the coupled model may enhance the decadal predictability of TCF activity, especially over the southeastern part of WNP.
Author Contributions
Conceptualization, J.F. and J.C.; analysis, J.F. and J.C.; methodology, J.C., J.F., B.W. and K.Z.; writing, J.F. and J.C. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by the NSFC of Jiangsu Province (BK20220108) and the NSFC (42375034, 42005017). We acknowledge the computer resources at the NUIST High Performance Computer Center.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The CMIP6 model data is available from https://esgf-node.llnl.gov/projects/cmip6/ (accessed on 9 January 2024). We acknowledge the World Climate Research Programme’s Working Group on Coupled Modelling, which is responsible for CMIP.
Conflicts of Interest
The authors declare no conflicts of interests.
References
- Pielke, R.A., Jr.; Landsea, C.; Mayfield, M.; Layer, J.; Pasch, R. Hurricanes and global warming. Bull. Am. Meteorol. Soc. 2005, 86, 1571–1576. [Google Scholar] [CrossRef]
- Zhang, Q.; Wu, L.; Liu, Q. Tropical cyclone damages in China 1983–2006. Bull. Am. Meteorol. Soc. 2009, 90, 489–496. [Google Scholar] [CrossRef]
- Camargo, S.J.; Wing, A.A. Increased tropical cyclone risk to coasts. Science 2021, 371, 458–459. [Google Scholar] [CrossRef] [PubMed]
- Zhao, H.; Lu, Y.; Jiang, X.; Klotzbach, P.J.; Wu, L.; Cao, J. A statistical intraseasonal prediction model of extended boreal summer western North Pacific tropical cyclone genesis. J. Clim. 2022, 35, 2459–2478. [Google Scholar] [CrossRef]
- Lee, H.S.; Yamashita, T.; Mishima, T. Multi-decadal variations of ENSO, the Pacific Decadal Oscillation and tropical cyclones in the western North Pacific. Prog. Oceanogr. 2012, 105, 67–80. [Google Scholar] [CrossRef]
- Liu, C.; Zhang, W.; Geng, X.; Stuecker, M.F.; Jin, F.F. Modulation of tropical cyclones in the southeastern part of western North Pacific by tropical Pacific decadal variability. Clim. Dyn. 2019, 53, 4475–4488. [Google Scholar] [CrossRef]
- Hong, J.S.; Yeh, S.W.; Yang, Y.M. Interbasin interactions between the Pacific and Atlantic Oceans depending on the phase of Pacific decadal oscillation and Atlantic multidecadal oscillation. J. Clim. 2022, 35, 2883–2894. [Google Scholar] [CrossRef]
- Wang, H.; Wang, C. What caused the increase of tropical cyclones in the western North Pacific during the period of 2011–2020? Clim. Dyn. 2023, 60, 165–177. [Google Scholar] [CrossRef]
- Liu, K.S.; Chan, J.C. Inactive period of western North Pacific tropical cyclone activity in 1998–2011. J. Clim. 2013, 26, 2614–2630. [Google Scholar] [CrossRef]
- He, H.; Yang, J.; Gong, D.; Mao, R.; Wang, Y.; Gao, M. Decadal changes in tropical cyclone activity over the western North Pacific in the late 1990s. Clim. Dyn. 2015, 45, 3317–3329. [Google Scholar] [CrossRef]
- Hong, C.C.; Wu, Y.K.; Li, T. Influence of climate regime shift on the interdecadal change in tropical cyclone activity over the Pacific Basin during the middle to late 1990s. Clim. Dyn. 2016, 47, 2587–2600. [Google Scholar] [CrossRef]
- Zhao, J.; Zhan, R.; Wang, Y.; Xu, H. Contribution of the interdecadal Pacific oscillation to the recent abrupt decrease in tropical cyclone genesis frequency over the western North Pacific since 1998. J. Clim. 2018, 31, 8211–8224. [Google Scholar] [CrossRef]
- Yu, J.; Li, T.; Tan, Z.; Zhu, Z. Effects of tropical North Atlantic SST on tropical cyclone genesis in the western North Pacific. Clim. Dyn. 2016, 46, 865–877. [Google Scholar] [CrossRef]
- Zhang, W.; Vecchi, G.A.; Murakami, H.; Villarini, G.; Delworth, T.L.; Yang, X.; Jia, L. Dominant role of Atlantic multidecadal oscillation in the recent decadal changes in western North Pacific tropical cyclone activity. Geophys. Res. Lett. 2018, 45, 354–362. [Google Scholar] [CrossRef]
- Wang, C.; Wang, B.; Wu, L.; Luo, J.J. A Seesaw Variability in Tropical Cyclone Genesis between the Western North Pacific and the North Atlantic Shaped by Atlantic Multidecadal Variability. J. Clim. 2022, 35, 2479–2489. [Google Scholar] [CrossRef]
- Dunstone, N.J.; Smith, D.M.; Booth, B.B.B.; Hermanson, L.; Eade, R. Anthropogenic aerosol forcing of Atlantic tropical storms. Nat. Geosci. 2013, 6, 534–539. [Google Scholar] [CrossRef]
- Takahashi, C.; Watanabe, M.; Mori, M. Significant aerosol influence on the recent decadal decrease in tropical cyclone activity over the western North Pacific. Geophys. Res. Lett. 2017, 44, 9496–9504. [Google Scholar] [CrossRef]
- Cao, J.; Zhao, H.; Wang, B.; Wu, L. Hemisphere-asymmetric tropical cyclones response to anthropogenic aerosol forcing. Nat. Commun. 2021, 12, 6787. [Google Scholar] [CrossRef] [PubMed]
- Murakami, H. Substantial global influence of anthropogenic aerosols on tropical cyclones over the past 40 years. Sci. Adv. 2022, 8, eabn9493. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Wallace, J.M.; Battisti, D.S. ENSO-like Multidecadal Variability: 1900–93. J. Clim. 1997, 10, 1004–1020. [Google Scholar] [CrossRef]
- Oshima, K.; Tanimoto, Y. An evaluation of reproducibility of the Pacific decadal oscillation in the CMIP3 simulations. J. Meteor. Soc. Japan 2009, 87, 755–770. [Google Scholar] [CrossRef]
- Furtado, J.C.; Di Lorenzo, E.; Schneider, N.; Bond, N.A. North Pacific decadal variability and climate change in the IPCC AR4 models. J. Clim. 2011, 24, 3049–3067. [Google Scholar] [CrossRef]
- Newman, M.; Alexander, M.A.; Ault, T.R.; Cobb, K.M.; Deser, C.; Di Lorenzo, E.; Smith, C.A. The Pacific decadal oscillation, revisited. J. Clim. 2016, 29, 4399–4427. [Google Scholar] [CrossRef]
- Fasullo, J.T.; Phillips, A.; Deser, C. Evaluation of leading modes of climate variability in the CMIP archives. J. Clim. 2020, 33, 5527–5545. [Google Scholar] [CrossRef]
- Coburn, J.; Pryor, S.C. Differential credibility of climate modes in CMIP6. J. Clim. 2021, 34, 8145–8164. [Google Scholar] [CrossRef]
- Xia, S.; Liu, P.; Jiang, Z.; Cheng, J. Simulation evaluation of AMO and PDO with CMIP5 and CMIP6 models in historical experiment. Adv. Earth Sci. 2021, 36, 58. [Google Scholar]
- Xu, Y.; Li, T.; Xu, M.; Shen, S.; Hu, Z. Evaluation of the Pacific Decadal Oscillation from 1901 to 2014 in CMIP6 models. Clim. Res. 2023, 90, 1–15. [Google Scholar] [CrossRef]
- Polade, S.D.; Gershunov, A.; Cayan, D.R.; Dettinger, M.D.; Pierce, D.W. Natural climate variability and teleconnections to precipitation over the Pacific-North American region in CMIP3 and CMIP5 models. Geophys. Res. Lett. 2013, 40, 2296−2301. [Google Scholar] [CrossRef]
- Yim, B.Y.; Kwon, M.; Min, H.S.; Kug, J.S. Pacific decadal oscillation and its relation to the extratropical atmospheric variation in CMIP5. Clim. Dyn. 2015, 44, 1521–1540. [Google Scholar] [CrossRef]
- Zhao, Y.; Di Lorenzo, E.; Sun, D.; Stevenson, S. Tropical Pacific decadal variability and ENSO precursor in CMIP5 models. J. Clim. 2021, 34, 1023–1045. [Google Scholar] [CrossRef]
- Xia, S.; Liu, P.; Jiang, Z.; Tao, L.; Song, H. Evaluation and projection of the AMO and PDO variabilities in the CMIP5 models under different warming scenarios part1: Evaluation. Dyn. Atmos. Ocean. 2022, 97, 101260. [Google Scholar] [CrossRef]
- Zuki, Z.M.; Lupo, A.R. Interannual variability of tropical cyclone activity in the southern South China Sea. J. Geophys. Res. Atmos. 2008, 113. [Google Scholar] [CrossRef]
- Lee, M.H.; Ho, C.H.; Kim, J.H.; Song, H.J. Low-frequency variability of tropical cyclone-induced heavy rainfall over East Asia associated with tropical and North Pacific sea surface temperatures. J. Geophys. Res. Atmos. 2012, 117. [Google Scholar] [CrossRef]
- Wang, X.; Liu, H. PDO modulation of ENSO effect on tropical cyclone rapid intensification in the western North Pacific. Clim. Dyn. 2016, 46, 15–28. [Google Scholar] [CrossRef]
- Huangfu, J.; Huang, R.; Chen, W. Interdecadal variation of tropical cyclone genesis and its relationship to the convective activities over the central Pacific. Clim. Dyn. 2018, 50, 1439–1450. [Google Scholar] [CrossRef]
- Dai, Y.; Wang, B.; Wei, N.; Song, J.; Duan, Y. How has the North Pacific Gyre Oscillation affected peak season tropical cyclone genesis over the western North Pacific from 1965 to 2020? Environ. Res. Lett. 2022, 17, 104016. [Google Scholar] [CrossRef]
- Dai, Y.; Wang, B.; Sun, W. What drives the decadal variability of global tropical storm days from 1965 to 2019? Adv. Atmos. Sci. 2022, 39, 344–353. [Google Scholar] [CrossRef]
- Cao, X.; Liu, Y.; Wu, R.; Bi, M.; Dai, Y.; Cai, Z. Northwestwards shift of tropical cyclone genesis position during autumn over the western North Pacific after the late 1990s. Int. J. Climatol. 2020, 40, 1885–1899. [Google Scholar] [CrossRef]
- Cao, X.; Wu, R. Simulations of development of tropical disturbances associated with the monsoon trough over the western North Pacific. Atmos. Sci. Lett. 2018, 19, e801. [Google Scholar] [CrossRef]
- Zhao, H.; Chen, S.; Raga, G.B.; Klotzbach, P.J.; Wu, L. Recent decrease in genesis productivity of tropical cloud clusters over the Western North Pacific. Clim. Dyn. 2019, 52, 5819–5831. [Google Scholar] [CrossRef]
- Peng, X.; Wang, L.; Wu, M.; Gan, Q. A contrast of recent changing tendencies in genesis productivity of tropical cloud clusters over the western North Pacific in May and October. Atmosphere 2021, 12, 1177. [Google Scholar] [CrossRef]
- O’Neill, L.W.; Chelton, D.B.; Esbensen, S.K. The effects of SST-induced surface wind speed and direction gradients on midlatitude surface vorticity and divergence. J. Clim. 2010, 23, 255–281. [Google Scholar] [CrossRef]
- Dare, R.A.; McBride, J.L. The threshold sea surface temperature condition for tropical cyclogenesis. J. Clim. 2011, 24, 4570–4576. [Google Scholar] [CrossRef]
- Huangfu, J.; Chen, W.; Ma, T.; Huang, R. Influences of sea surface temperature in the tropical Pacific and Indian Oceans on tropical cyclone genesis over the western North Pacific in May. Clim. Dyn. 2018, 51, 1915–1926. [Google Scholar] [CrossRef]
- Wu, R.; Yang, Y.; Cao, X. Respective and combined impacts of regional SST anomalies on tropical cyclogenesis in different sectors of the western North Pacific. J. Geophys. Res. Atmos. 2019, 124, 8917–8934. [Google Scholar] [CrossRef]
- Wang, C.; Wang, B. Tropical cyclone predictability shaped by western Pacific subtropical high: Integration of trans-basin sea surface temperature effects. Clim. Dyn. 2019, 53, 2697–2714. [Google Scholar] [CrossRef]
- Wang, C.; Wang, B.; Cao, J. Unprecedented Northern Hemisphere tropical cyclone genesis in 2018 shaped by subtropical warming in the North Pacific and the North Atlantic. Geophys. Res. Lett. 2019, 46, 13327–13337. [Google Scholar] [CrossRef]
- Goh, A.Z.C.; Chan, J.C. Interannual and interdecadal variations of tropical cyclone activity in the South China Sea. Int. J. Climatol. A J. R. Meteorol. Soc. 2010, 30, 827–843. [Google Scholar] [CrossRef]
- Yang, L.; Chen, S.; Wang, C.; Wang, D.; Wang, X. Potential impact of the pacific decadal oscillation and sea surface temperature in the tropical Indian Ocean–Western Pacific on the variability of typhoon landfall on the China coast. Clim. Dyn. 2018, 51, 2695–2705. [Google Scholar] [CrossRef]
- Choi, J.-W.; Kim, H.-D. Negative relationship between Korea landfalling tropical cyclone activity and Pacific Decadal Oscillation. Dyn. Atmos. Ocean. 2019, 87, 101100. [Google Scholar] [CrossRef]
- Lee, M.; Kim, T.; Cha, D.H.; Min, S.K.; Park DS, R.; Yeh, S.W.; Chan, J.C. How does Pacific decadal oscillation affect tropical cyclone activity over far East Asia? Geophys. Res. Lett. 2021, 48, e2021GL096267. [Google Scholar] [CrossRef]
- Knapp, K.R.; Kruk, M.C.; Levinson, D.H.; Diamond, H.J.; Neumann, C.J. The international best track archive for climate stewardship (IBTrACS) unifying tropical cyclone data. Bull. Am. Meteorol. Soc. 2010, 91, 363–376. [Google Scholar] [CrossRef]
- Huang, B.; Peter, W.T.; Banzon, V.F.; Boyer, T.; Chepurin, G.; Lawrimore, J.H.; Menne, M.J.; Smith, T.M.; Vose, R.S.; Zhang, H.-M. Extended Reconstructed Sea Surface Temperature version 5 (ERSSTv5). Upgrades, validations, and intercomparisons. J. Clim. 2017, 30, 8179–8205. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Thépaut, J.N. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Trenberth, K.E.; Shea, D.J. Atlantic hurricanes and natural variability in 2005. Geophys. Res. Lett. 2006, 33, L12704. [Google Scholar] [CrossRef]
- Chen, X.; Wallace, J.M. ENSO-like variability: 1900–2013. J. Clim. 2015, 28, 9623–9641. [Google Scholar] [CrossRef]
- Taylor, K.E. Summarizing multiple aspects of model performance in a single diagram. J. Geophys. Res. Atmos. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]
- Du, Y.; Chen, H. Evaluation of CMIP6 model performance in simulating the PDO and its future change. Atmos. Ocean. Sci. Lett. 2023, 100449. [Google Scholar] [CrossRef]
- Luo, N.; Guo, Y.; Chou, J.; Gao, Z. Added value of CMIP6 models over CMIP5 models in simulating the climatological precipitation extremes in China. Int. J. Climatol. 2022, 42, 1148–1164. [Google Scholar] [CrossRef]
- Tory, K.J.; Chand, S.S.; McBride, J.L.; Ye, H.; Dare, R.A. Projected changes in late-twenty-first century tropical cyclone frequency in 13 coupled climate models from phase 5 of the Coupled Model Intercomparison Project. J. Clim. 2013, 26, 9946–9959. [Google Scholar] [CrossRef]
- Eyring, V.; Bony, S.; Meehl, G.A.; Senior, C.A.; Stevens, B.; Stouffer, R.J.; Taylor, K.E. Overview of the Coupled Model Intercomparison Project Phase 6 (CMIP6) experimental design and organization. Geosci. Model Dev. 2016, 9, 1937–1958. [Google Scholar] [CrossRef]
- Bell, S.S.; Chand, S.S.; Tory, K.J.; Turville, C. Statistical assessment of the OWZ tropical cyclone tracking scheme in ERA-Interim. J. Clim. 2018, 31, 2217–2232. [Google Scholar] [CrossRef]
- Tory, K.J.; Ye, H.; Brunet, G. Tropical cyclone formation regions in CMIP5 models: A global performance assessment and projected changes. Clim. Dyn. 2020, 55, 3213–3237. [Google Scholar] [CrossRef]
- Yamada, Y.; Kodama, C.; Satoh, M.; Sugi, M.; Roberts, M.J.; Mizuta, R.; Vidale, P.L. Evaluation of the contribution of tropical cyclone seeds to changes in tropical cyclone frequency due to global warming in high-resolution multi-model ensemble simulations. Prog. Earth Planet. Sci. 2021, 8, 11. [Google Scholar] [CrossRef]
- Wang, B.; Murakami, H. Dynamic genesis potential index for diagnosing present-day and future global tropical cyclone genesis. Environ. Res. Lett. 2020, 15, 114008. [Google Scholar] [CrossRef]
- Cao, J.; Wang, H.; Zhao, H.; Wang, B.; Wu, L.; Wang, C. Reversed and comparable climate impacts from historical anthropogenic aerosol and GHG on global-scale tropical cyclone genesis potential. Environ. Res. Lett. 2022, 17, 094027. [Google Scholar] [CrossRef]
- Cao, X.; Wu, R.; Bi, M.; Lan, X.; Dai, Y.; Zhao, J. Contribution of different timescale variations to the tropical cyclogenesis environment over the northern tropical Atlantic and comparison with the western North Pacific. J. Clim. 2019, 32, 6645–6661. [Google Scholar] [CrossRef]
- Basconcillo, J.; Moon, I.J. Increasing activity of tropical cyclones in East Asia during the mature boreal autumn linked to long-term climate variability. npj Clim. Atmos. Sci. 2022, 5, 4. [Google Scholar] [CrossRef]
- Gill, A.E. Some simple solutions for heat-induced tropical circulation. Q. J. R. Meteorol. Soc. 1980, 106, 447–462. [Google Scholar]
- Cao, X.; Chen, G.; Li, T.; Ren, F. Simulations of tropical cyclogenesis associated with different monsoon trough patterns over the western North Pacific. Meteorol. Atmos. Phys. 2016, 128, 491–511. [Google Scholar] [CrossRef]
- Delcroix, T.; Cravatte, S.; McPhaden, M.J. Decadal variations and trends in tropical Pacific sea surface salinity since 1970. J. Geophys. Res. Ocean. 2007, 112. [Google Scholar] [CrossRef]
- Grassi, B.; Redaelli, G.; Canziani, P.O.; Visconti, G. Effects of the PDO phase on the tropical belt width. J. Clim. 2012, 25, 3282–3290. [Google Scholar] [CrossRef]
- Wang, W.; Matthes, K.; Omrani, N.E.; Latif, M. Decadal variability of tropical tropopause temperature and its relationship to the Pacific Decadal Oscillation. Sci. Rep. 2016, 6, 29537. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Wang, Y.; Wang, B.; Wu, L.; Zhao, H.; Cao, J. Opposite skills of ENGPI and DGPI in depicting decadal variability of tropical cyclone genesis over the western North Pacific. J. Clim. 2023, 36, 8713–8721. [Google Scholar] [CrossRef]
- Liu, C.; Zhang, W.; Stuecker, M.F.; Jin, F.F. Pacific Meridional Mode-Western North Pacific tropical cyclone linkage explained by tropical Pacific quasi-decadal variability. Geophys. Res. Lett. 2019, 46, 13346–13354. [Google Scholar] [CrossRef]
- Zhou, Q.; Wei, L. Influence of the pace of El Niño decay on tropical cyclone frequency over the western north pacific during decaying El Niño summers. Atmos. Ocean. Sci. Lett. 2023, 16, 100328. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).