Topographic Elevation’s Impact on Local Climate and Extreme Rainfall: A Case Study of Zhengzhou, Henan

Abstract

The topography significantly influences local climate precipitation and the intensity of precipitation events, yet the specific differences in its elevational effects require further understanding. This study focuses on precipitation in Zhengzhou City, Henan Province, utilizing hourly data and a topographic elevation precipitation increment model to assess the impact of topography on local climate precipitation and extreme heavy rainfall events. The results indicate that the daily precipitation attributed to topographic elevation in Zhengzhou in July was 0.21 mm, accounting for 4.9% of the total precipitation. In the extreme heavy rainfall event on 20 July 2021 (“7.20” event), the precipitation due to topographic elevation reaches 48.7 mm, constituting 15.8% of the total precipitation. Additionally, numerical simulations using the Weather Research and Forecasting (WRF) model for the 20–21 July 2021 rainfall event in Zhengzhou show that the WRF model effectively reproduces the spatiotemporal characteristics of the precipitation process. The simulated topographic elevation precipitation intensity is 49.8 mm/day, accounting for 16.6% of daily precipitation, closely resembling observational data. Sensitivity experiments further reveal that reducing the heights of the Taihang Mountains and Funiu Mountains weakens the low-level easterly winds around Zhengzhou. Consequently, as the center of the heavy rainfall shifts northward or westward, the intensity of topographic elevation-induced precipitation decreases to 7.3 mm/day and 12.9 mm/day.

1. Introduction

China’s mountainous terrain, covering over 50% of the country’s land area, serves as a crucial water resource. Understanding the impact of topography on precipitation is essential [1,2,3,4,5]. Precipitation accumulation in mountains affects the availability of water resources, with intense precipitation contributing to runoff and triggering geological hazards. Despite advancements in numerical weather prediction, models still exhibit biases in China’s complex terrain [6,7]. Plateauader scale and topography, like the Qinghai-Tibet Plateau, influence global circulation and precipitation patterns [8,9]. Medium- to small-scale topography impacts local factors such as elevation, slope, and aspect [10]. Although these local topographic elements are nearly constant, their effects are non-linear due to the transient nature of airflow coupled with solar radiation-induced topography. Therefore, exploring the non-linear quantitative impact of topography on local precipitation across different time scales is crucial.

Built upon observational data, the multivariate regression statistical model, incorporating precipitation and topographic factors, stands as a fundamental approach for studying the impact of topography on precipitation. This method has been extensively utilized over the years [11,12,13]. Research on these models has provided a robust foundation for understanding the statistical relationships between local topographic factors and precipitation. The established regression statistical model, aside from being contingent on the number of introduced topographic factors, also depends on the study region, the spatiotemporal resolution of the data used to compute regression coefficients, and the prevailing season. These dependencies introduce certain limitations to the generalization and application of regression models. Another approach, grounded in the physical mechanisms of precipitation, focuses on atmospheric moisture conditions and the dynamic conditions leading to moisture condensation, cloud formation, and precipitation. This involves the development of simplified mathematical theoretical models or semi-empirical mathematical models for directly calculating precipitation [14,15,16]. While this method boasts a clear theoretical foundation, it necessitates specific assumptions and approximations, such as static equilibrium assumptions and the decay height of vertical velocity due to topographic uplift. The conclusions derived from this approach do not entirely represent the intricate influence of real topography on precipitation. The utilization of high-resolution data, encompassing hourly atmospheric data and topographic information, helps partially address these limitations by covering the interaction between land topography and the atmosphere.

With the advancement of numerical models, employing sensitivity experiments with models has become a crucial means to study the impact of topography on precipitation effects, especially with regional high-resolution mesoscale numerical models [17,18,19,20]. For instance, China’s independently developed GRAPES model, with a resolution of 3 km, demonstrates effective simulation capabilities for the distribution of 24 h cumulative precipitation averaged over seasons. This model exhibits a notable capacity to simulate the influence of topography on precipitation [21].

Zhengzhou, with an average elevation of 108 m, is situated in the transitional zone between the second and third-level topographical terraces on the eastern foothills of the Qinling Mountains. The terrain exhibits a higher elevation in the southwest and a lower elevation in the northeast. During west-to-southwest winds, Zhengzhou is positioned on the lee side of the Jishan and Songshan Mountains, while during northeast-to-east winds, it is on the windward side. On the afternoon of 20 July 2021, Zhengzhou experienced an extreme hourly precipitation of 201.9 mm, leading to severe flooding in metro stations and resulting in significant casualties and economic losses. Research attributes this extreme rainfall event to the crucial role played by topographic uplift [22,23,24]. Zhu et al. [25] indicate that both convective-scale ensemble forecasts effectively capture heavy precipitation near the Taihang Mountains through predictability studies. However, most ensemble members exhibit noticeable positional biases in forecasting extreme precipitation in Zhengzhou, and all ensemble members underestimate extreme hourly precipitation. This suggests that high-resolution models can highlight the impact of mountains but may not accurately simulate extreme heavy rainfall on the city edge, as observed in Zhengzhou in July 2021. The quantitative impact of topography on this extreme precipitation event in Zhengzhou and its differences from climatological scales require further investigation. This study utilizes hourly observations, reanalysis data, and fine-grained topographical factors influencing precipitation to estimate the topographic uplift-induced precipitation in Henan Province. It compares the differences in topographic impacts on the extreme rainfall event on 20 July 2021, and the monthly average precipitation, employing topographic sensitivity experiments to elucidate the quantitative influence of topography on precipitation in Zhengzhou across different time scales.

2. Data and Methods

2.1. Data

The precipitation observation data utilized in this study include CN05 daily precipitation data with a resolution of 0.5° × 0.5° for the years 1981–2019 and daily precipitation data from the Zhengzhou observation station for the years 1981–2021. Additionally, ground-level hourly precipitation data for 540 stations in Henan, Hebei, Shandong, Shanxi, Shaanxi, Hubei, Anhui, and Jiangsu provinces on 20–21 July 2021, were obtained from the database of the China Meteorological Administration Meteorological Information Center. These data were employed for precipitation intensity observation, analysis, and model verification. Reanalysis data, obtained from the European Centre for Medium-Range Weather Forecasts (ECMWF) in the form of fifth-generation data (ERA5) at 800 hPa, 850 hPa, 875 hPa, 900 hPa, 925 hPa, 950 hPa, 975 hPa and 1000 hPa levels on an hourly basis, including u, v and q, in July from 1981 to 2010 and 2021, were used for circulation analysis and the calculation of topographic uplift-induced precipitation. Moreover, we used the following formula to calculate the moisture flux:

$$q_s=\frac{qv}{g}$$

(1)

In the equation, $q_s$ represents moisture flux; $q$ represents specific humidity; $v$ represents wind vector; $g$ represents gravitational acceleration. The Weather Research and Forecasting (WRF) model was driven by 6-hourly reanalysis grid data (FNL) provided by the National Centers for Environmental Prediction (NCEP) with a resolution of 0.25° × 0.25°.High-resolution elevation data for Henan Province with a resolution of 30 m were obtained from the ASTER GDEM V2 global digital elevation data, downloaded from the Geospatial Data Cloud. Using ArcGIS, slope and aspect were computed based on this elevation data.

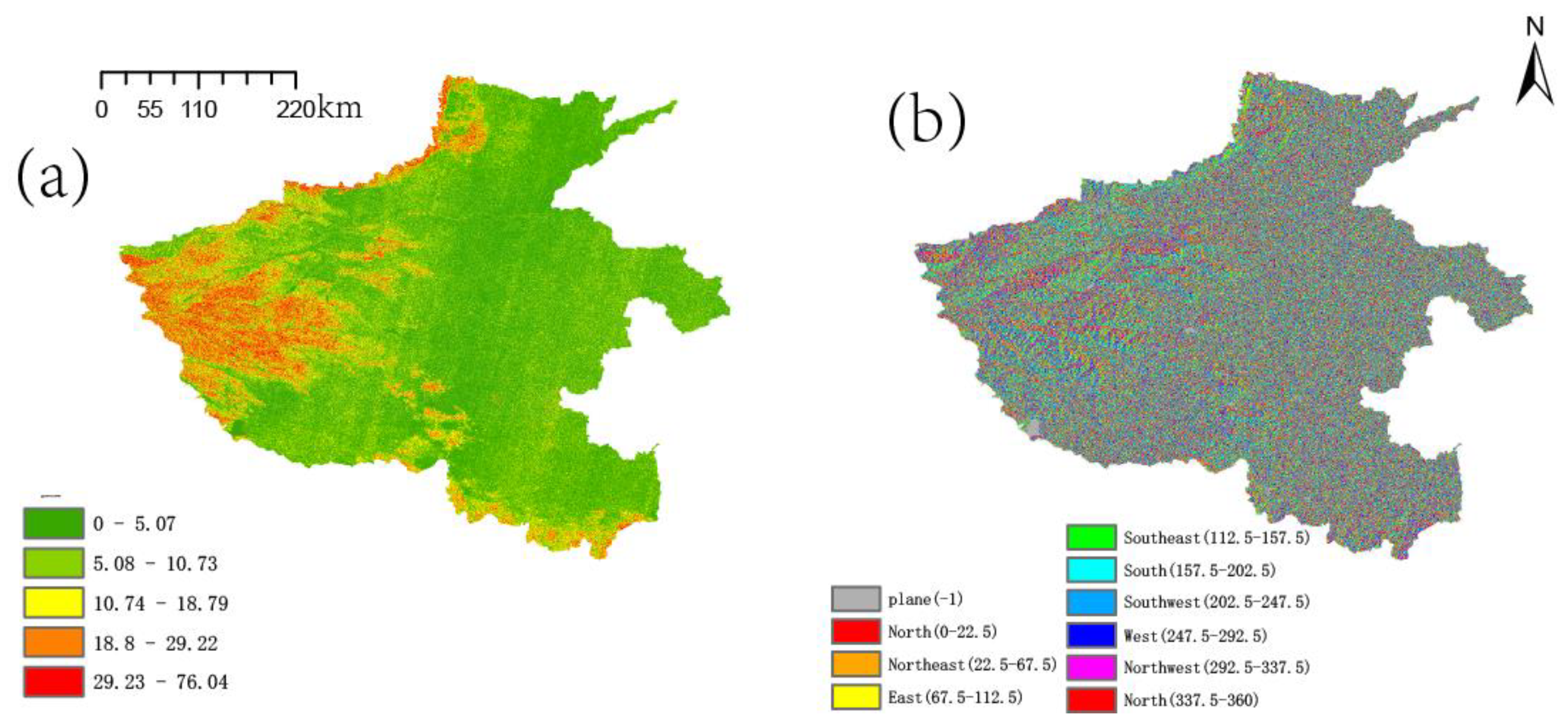
2.2. The Calculation of Topographic Elevation Precipitation

The formation of precipitation mainly depends on the two meteorological conditions of water vapor and vertical motion, so the water vapor equation is introduced to characterize the transport and variation of water vapor and simplify it appropriately as follows:

$$A=-\frac{1}{g}{\int }_0^{p_0}\frac{\partial q}{\partial t}dp-\frac{1}{g}{\int }_0^{p_0}▽•\overrightarrow{V}qdp-\frac{1}{g}\omega q{|}_0^{p_0}$$

(2)

The three items on the right are the local variation term of water vapor, the integral term of the divergence of water vapor flux and the variation term of vertical transport of water vapor with height. The third main consideration is that the vertical movement of water vapor caused by topography is essential for the formation of precipitation. This is used to introduce the precipitation correction generated by the terrain uplift, that is, the increase in the water raised by the terrain, and the incremental model of the water lift is constructed. Let $W_t$ be the topographic lift and water increment, and simplify it appropriately. The month with the highest precipitation in Henan Province is July. Emphasizing the influence of topographic uplift on precipitation in July, the estimation method proposed by Shi [14] was employed. The expression for this method is obtained as follows:

$$W_t=\rho w_{s}q \left(mm\right)$$

(3)

In the equation, ρ represents air density, taken as 1.293 kg/m³; $q$ denotes specific humidity. $w_s$ is the vertical velocity induced by topographic uplift, and its calculation method is as follows:

As shown in Figure 1a, OABC represents a windward slope where the horizontal projection of the normal line On is denoted as On’. OX points towards the true north direction. The slope angle (i.e., the angle between the slope surface normal direction and the horizontal plane) and the aspect angle are represented by α and β, respectively. $V_o$ is the horizontal wind vector, and $\delta$ is the angle between the wind vector and the slope aspect, i.e., the angle between wind direction and slope aspect. The wind direction angle is denoted by $\theta$, representing the angle between the wind vector $V_o$ and the true north direction. The wind vector $V_o$ can be decomposed into the component parallel to the mountain range, $V_s$, and the component perpendicular to the mountain range, $V_n$. Among these, $V_s$ is unaffected by the slope, while $V_n$ is influenced by the slope, leading to forced ascent of the airflow and generating vertical upward velocity, $w_s$.

Because both the wind direction angle and the slope aspect angle are defined with the true north direction as 0, $\delta$ can be expressed as:

$$\delta =\theta -\beta$$

(4)

From Figure 1a, it can be observed that the component of the wind vector, $V_n$, can be expressed as:

$$V_n=V_{o}cos\delta =V_{o}cos(\theta -\beta )$$

(5)

From Figure 1b, it can be observed that the ground vertical velocity, $w_s$, is the upward velocity generated by the lifting of $V_n$ at the ground:

$$w_s=V_{n}tan\alpha$$

(6)

Substituting Equation (5) into Equation (6) and expressing $V_0$ in terms of its meridional and zonal components, the formula for calculating the ground vertical velocity induced by topographic forcing is obtained. By substituting this into Equation (3), the theoretical estimation formula for topographic uplift-induced precipitation is given by:

$$W_t=\rho q\sqrt{u^2+v^2}tan\alpha cos(\theta -\beta )$$

(7)

In the equation, $W_t$ represents the topographic uplift-induced precipitation increment, u and v are the meridional and zonal wind speeds, respectively. The distribution of the slope angle α in Henan Province (Figure 2a) indicates that the eastern slope of Zhengzhou has a slope of around 4°, while the southwestern side reaches approximately 25°. β is the aspect angle (Figure 2b), i.e., the angle between the slope surface normal and the true north direction, measured clockwise. θ is the wind direction angle, i.e., the angle between the wind direction and the true north direction, also measured clockwise.

In the past, scholars have applied this model to calculate topographic uplift-induced precipitation at the climatic scale using monthly data [13,14]. This study, however, quantitatively compares the impact of topographic uplift on precipitation at both climatic and weather scales using hourly data, but there are some limitations: In the calculation of topographic lift precipitation, it is assumed that all condensed water vapor in the column descends, which is not practically feasible. Additionally, the conclusions are only applicable to the “7.20” extreme rainfall event, and the generalizability of the findings requires further validation through more case studies in the future. Additionally, due to the different resolutions of reanalysis data and topographic factor data, spatial scale integration is necessary. Firstly, ArcGIS is used to synthesize topographic factor data into a grid with a resolution of 0.0625° × 0.0625°, comprising 4130 grid points. Subsequently, the reanalysis data is interpolated using bilinear interpolation to match the resolution of 0.0625° × 0.0625° [26].

3. Results

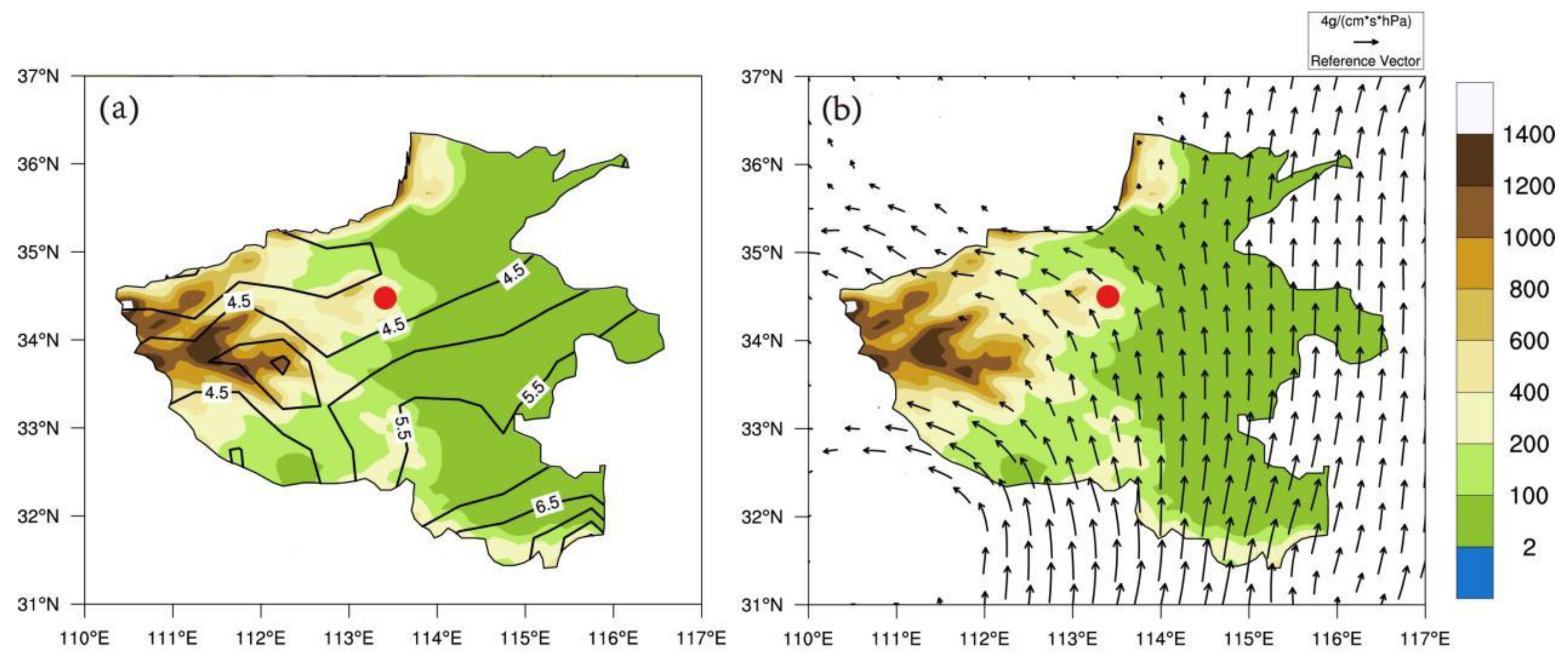
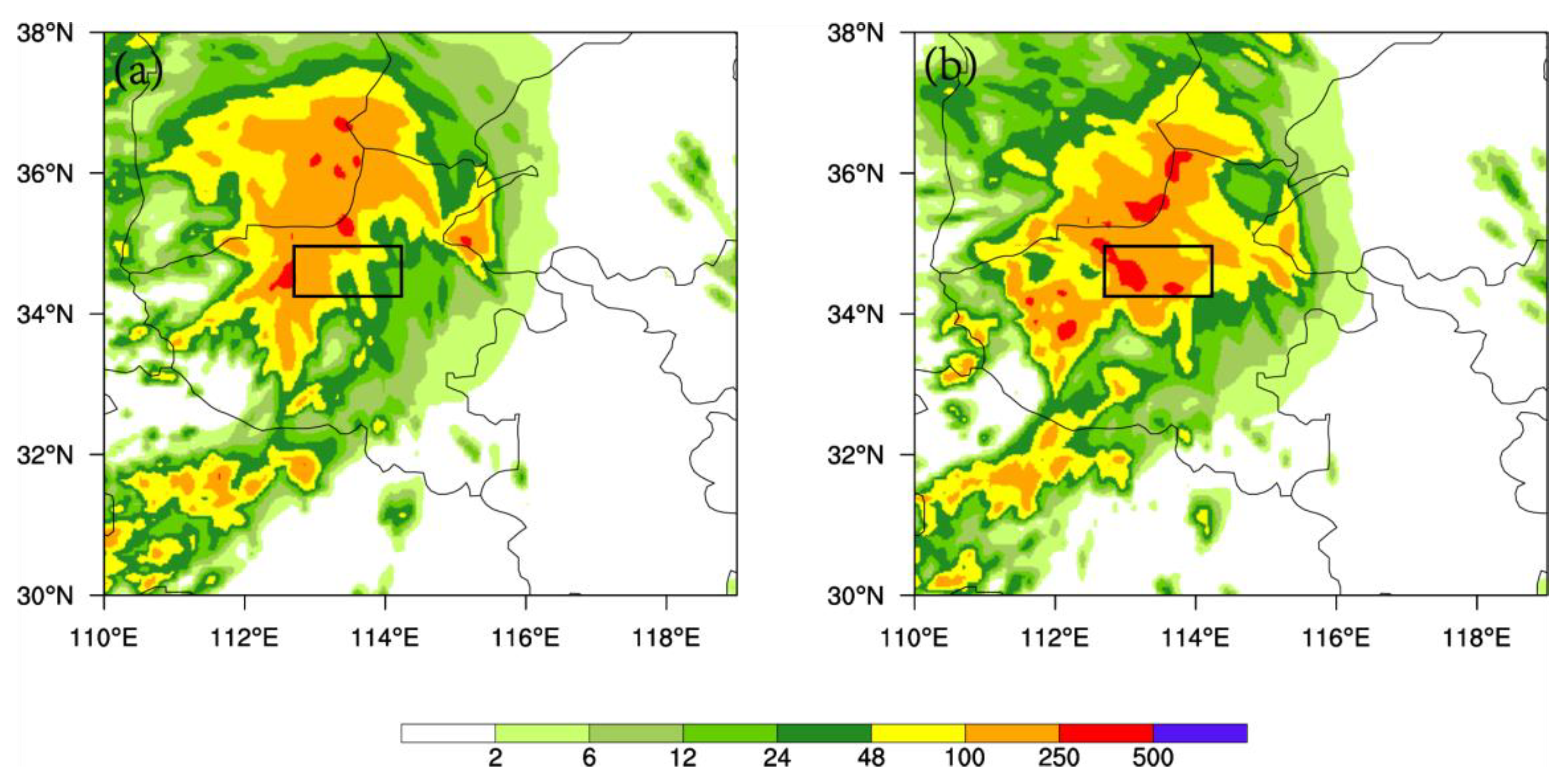
3.1. Spatial Distribution of July Precipitation in Henan and the Characteristics of Precipitation Anomalies in Zhengzhou

Figure 3 shows the spatial distribution of daily average precipitation and 925 hPa water vapor flux in Henan from 1981 to 2010. From the figure, it can be observed that the prevailing low-level atmospheric water vapor transport in July in Henan is mainly from south to north, creating an overall distribution characteristic of decreasing precipitation from south to north. The precipitation center is located on the southern slope of the Funiu Mountains, with a summit elevation of approximately 1300 m. The meridional gradient on the southern slope is approximately 3 × 10⁻² m/m (details in the figure are omitted). Under the background of prevailing southward water vapor transport, the uplifting effect of the terrain is evident. In July, the daily average precipitation in Zhengzhou is 4.74 mm, with an average elevation of 108 m. The meridional gradient of elevation was 0.2 × 10⁻² m/m. Under the prevailing southward water vapor transport, the uplifting effect of the terrain is noticeably weaker compared to mountainous areas like the Funiu Mountains. This precipitation distribution is related to the prevailing direction of low-level atmospheric water vapor transport flux and the coupling with the terrain structure.

To further investigate the impact of topography on precipitation in Zhengzhou, Figure 4 displays the precipitation series in Zhengzhou for July from 1981 to 2021. From the figure, it can be observed that the average monthly precipitation in July is 147 mm. However, in July 2021, the precipitation in Zhengzhou reached 685 mm, far exceeding its average monthly precipitation. This is closely related to the “7.20” heavy rainfall event in Zhengzhou.

From the above analysis, it is evident that the climatic distribution of July precipitation in Henan Province is closely related to the topographic structure. In July 2021, positive precipitation anomalies with values exceeding 200 mm occurred in the northern part of Henan Province, centered around Zhengzhou (Figure 5a). The anomalies in Zhengzhou and the northern part of Henan exceeded 600 mm. The anomalous distribution of low-level atmospheric water vapor flux (925 hPa) (Figure 5b) reveals anomalous eastward water vapor transport in the northern part of Henan. In the eastern part of Zhengzhou, with elevations of approximately 100–200 m, and the western part with elevations of 200–400 m, the meridional gradient of the terrain is about −0.7 × 10⁻² m/m. This indicates that Zhengzhou is located on the windward slope of the anomalous eastward moisture transport. The strong anomaly precipitation center is closely related to this, and the principle behind the formation of the precipitation anomaly center in the northern part of Henan is the same. This coupling relationship between water vapor transport flux and topographic structure lays the foundation for the formation of weather-scale heavy precipitation.

Simultaneously, it is observed that the precipitation in Zhengzhou in July 2008 was also exceptionally high, with anomalies exceeding 40 mm and anomalies in the southern part of Henan exceeding 120 mm (Figure 5c). The anomaly distribution of water vapor flux (Figure 5d) shows that Zhengzhou is located in anomalous north-to-south moisture transport. The meridional gradient of the terrain to the north of Zhengzhou is approximately −0.4 × 10⁻² m/m, indicating that Zhengzhou is situated on the windward slope of the anomalous northward moisture transport. The close relationship between anomalous precipitation and this factor is evident, and the same principle applies to the formation of precipitation anomalies in the southern part of Henan.

Comparing the two precipitation anomalies, we found that the central locations of the two anomalies were not the same, in Zhengzhou City and northern Henan Province in July 2021 and in southern Henan Province in July 2008, which in my opinion is related to the location of water vapor uplift. In July 2021, the anomalous water vapor transport from east to west was uplifted in Funiu Mountain and Taihang Mountain, forming two precipitation anomaly centers in Zhengzhou City and northern Henan Province, while in July 2008, the anomalous water vapor transport from north to south was uplifted in Dabie Mountain, forming the precipitation anomaly center in southern Henan Province.

3.2. The Impact of Terrain Uplift on Precipitation in Henan Province in July

Figure 6a shows the spatial distribution of terrain-induced precipitation in July from 1981 to 2010 in Henan Province. Positive values indicate an increase in precipitation due to terrain, observed on windward slopes, while negative values indicate a decrease, observed on leeward slopes. The regions with significant terrain-induced precipitation are concentrated in the western Funiu Mountains, the northern Taihang Mountains, and a smaller area in the southern Dabie Mountains. In the relatively flat central region, the terrain-induced precipitation is between ±0.4 mm, indicating minimal impact from terrain uplift. In July, southward prevailing winds over Henan (Figure 3b) resulted in significant terrain-induced precipitation exceeding 0.4 mm on the southern slopes of the Funiu Mountains, corresponding to the precipitation center (Figure 3a).

The latitude and longitude range for Zhengzhou city is 112.7° E–114.23° E, 34.27° N–34.97° N. Calculating the regional averages for July, the daily average precipitation and terrain elevation precipitation for Zhengzhou city are 4.27 mm and 0.21 mm, respectively. From the results, it appears that the influence of terrain on the July precipitation in Zhengzhou is not significant, accounting for only 4.9% of the total precipitation.

Figure 6b illustrates the cumulative terrain elevation precipitation in Henan Province from 00:00 on July 20 to 00:00 on 21 July 2021. It is evident that the terrain elevation precipitation on this day far exceeds the daily average values from 1981 to 2010 (Figure 6a). This situation is closely related to the extreme precipitation event on that day (Figure 7a).

On 20 July 2021, Zhengzhou city observed an average precipitation of 307.5 mm, with terrain-induced precipitation contributing 48.7 mm. The terrain’s impact on the precipitation during this period accounted for 15.8% of the actual precipitation. In comparison to the 4.9% at the climatic scale, the terrain’s influence on this weather-scale precipitation event is much more significant. The subsequent investigation will use numerical models to explore how terrain specifically affects this precipitation event.

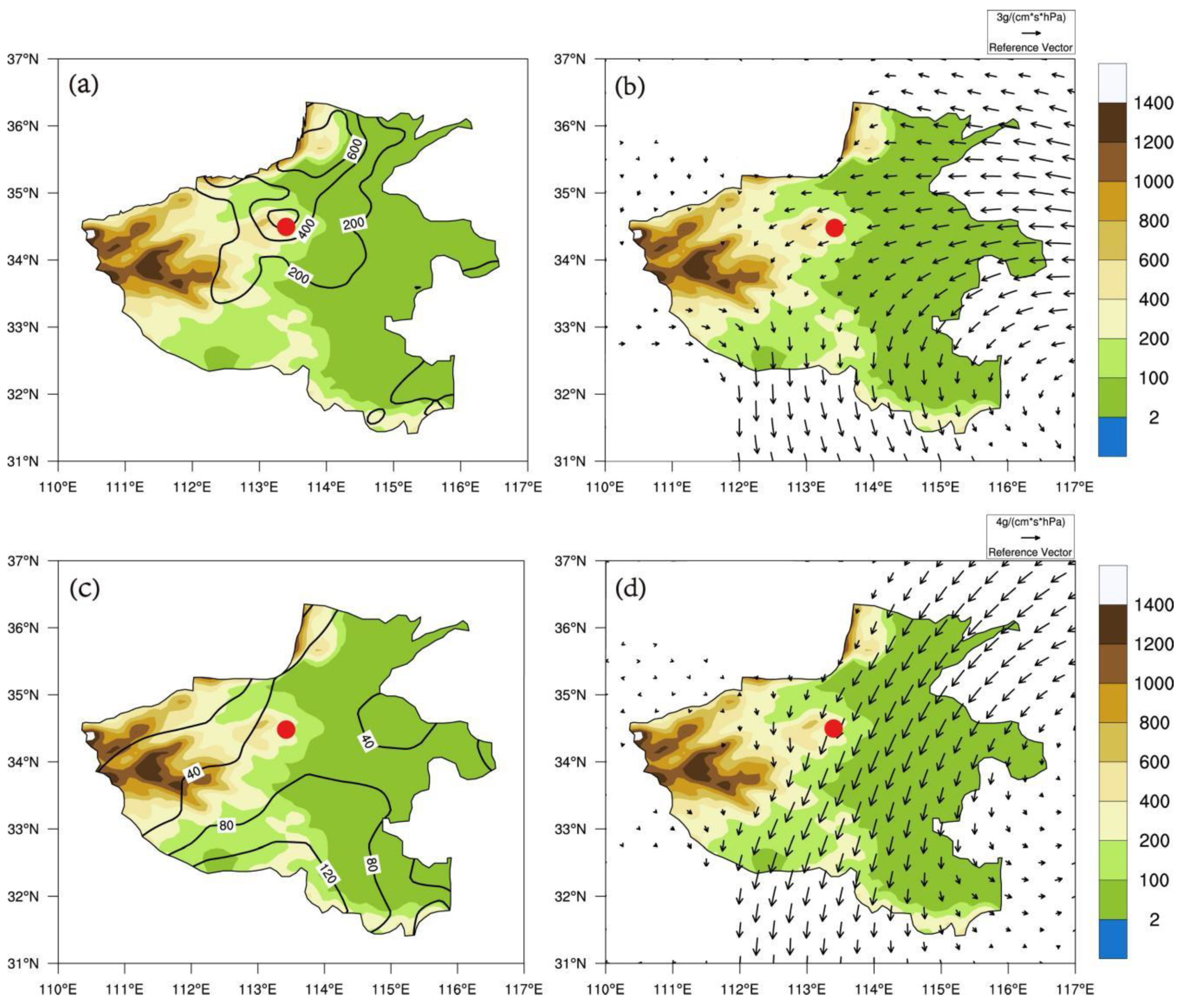
3.3. Experiments on the Sensitivity of Extreme Rainfall to Terrain Elevation

The WRF3.6 model was employed to simulate the extreme rainfall event as the control experiment. The initial and boundary fields for the model were derived from the NCEP reanalysis grid data (FNL). The integration period covered from 06:00 on 19 July 2021, to 06:00 on 21 July 2021, spanning 48 h with a time step of 30 s. The vertical structure consisted of 30 layers, and the model utilized a double-nested two-way configuration, producing output every 1 h, denoted as CTRL. Further details, including the physics parameterization schemes, are provided in

Table 1. Parameterization scheme of control test.

Units	Domain1	Domain2
Central point	(31.5° N, 115.0° E)	(30.0° N, 115.0° E)
Grid distance	27 km	9 km
Grid numbers	111 × 148	247 × 334
Micro Physics Schemes	Thompson
Longwave Schemes	RRTM
Shortwave Schemes	Goddard
Planetary Boundary Layer Schemes	YSU
Land Surface Schemes	5–layer Thermal Diffusion
Cumulus Parameterization Schemes	Tiedtke

.

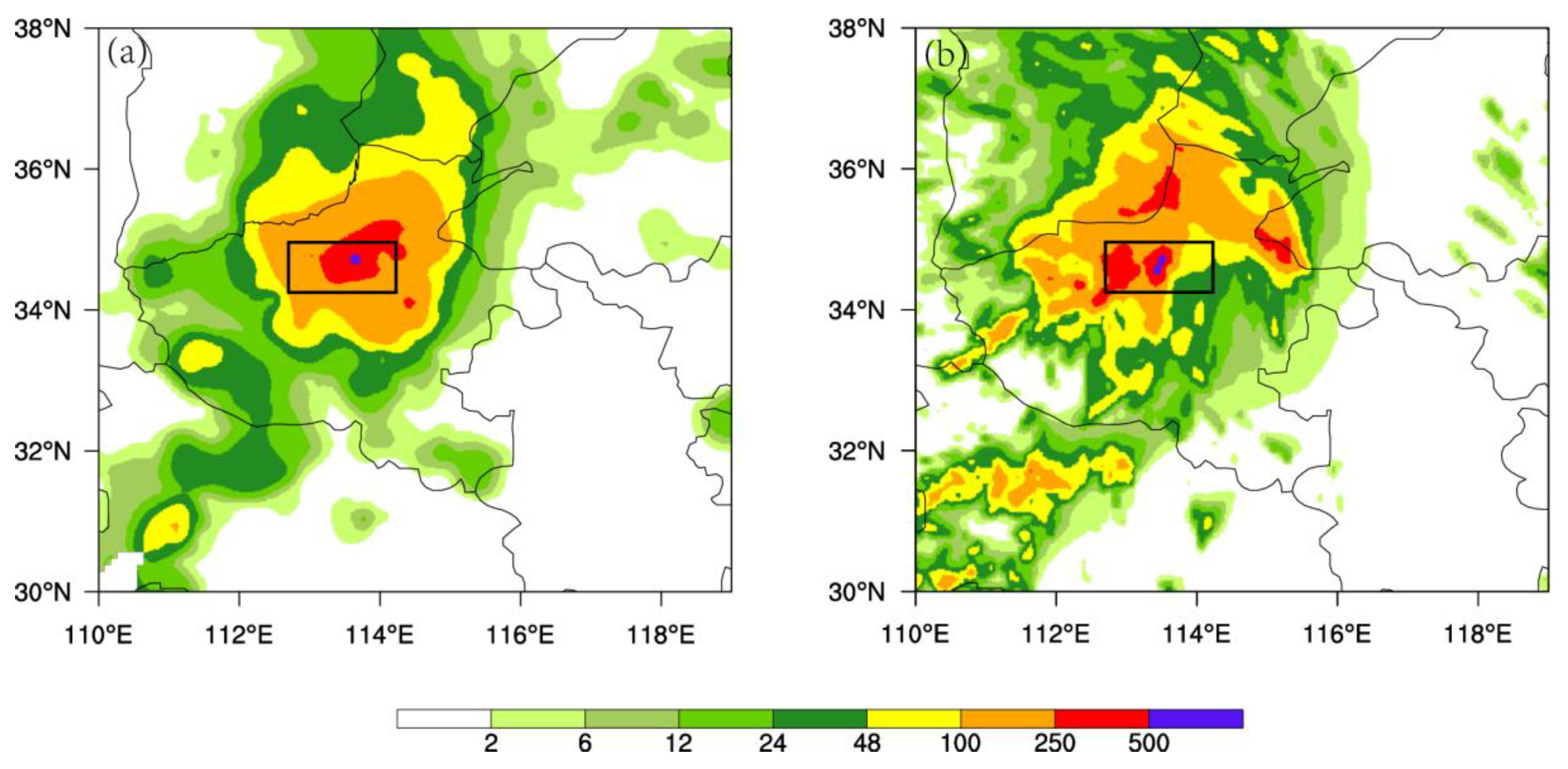
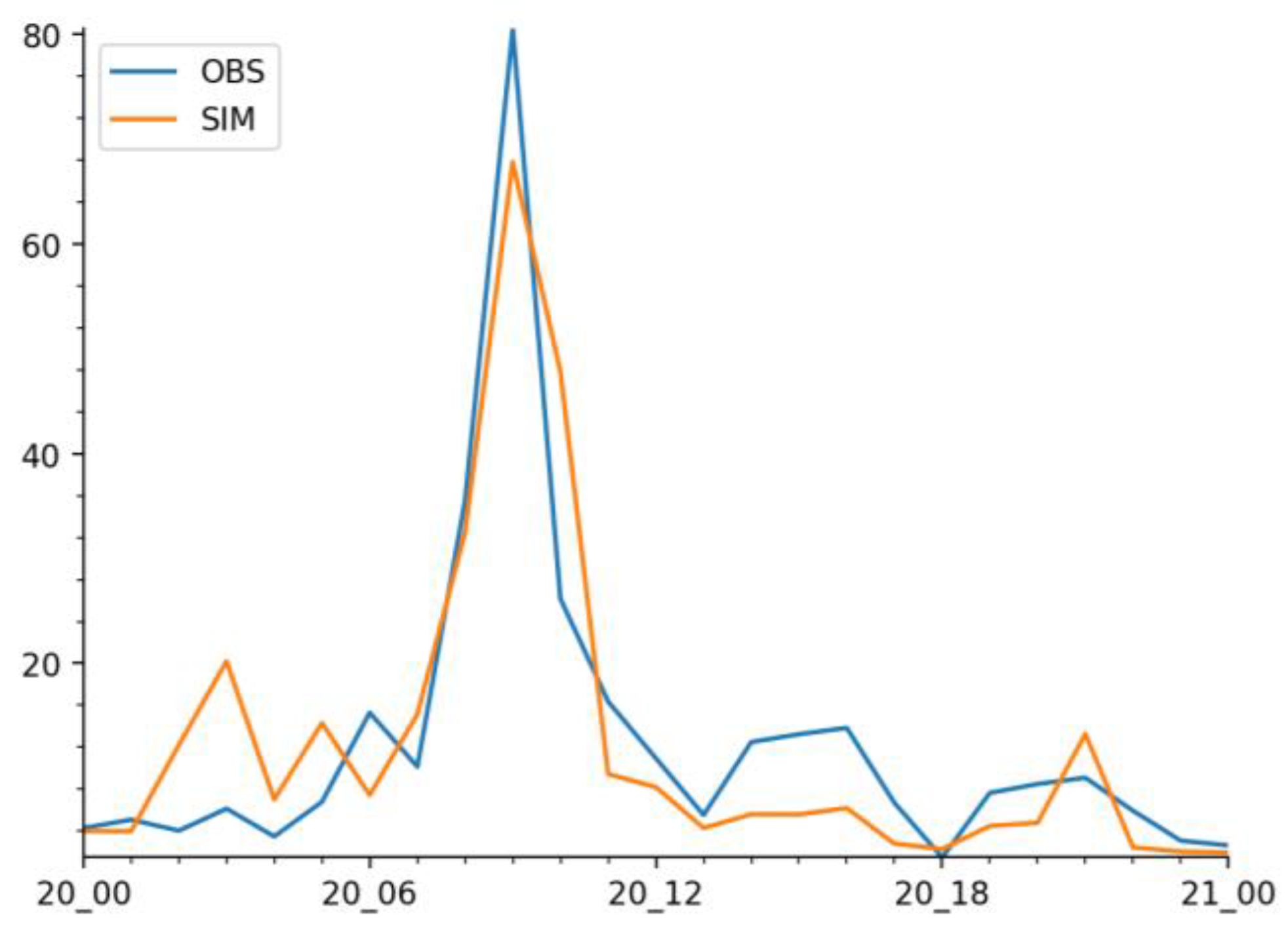
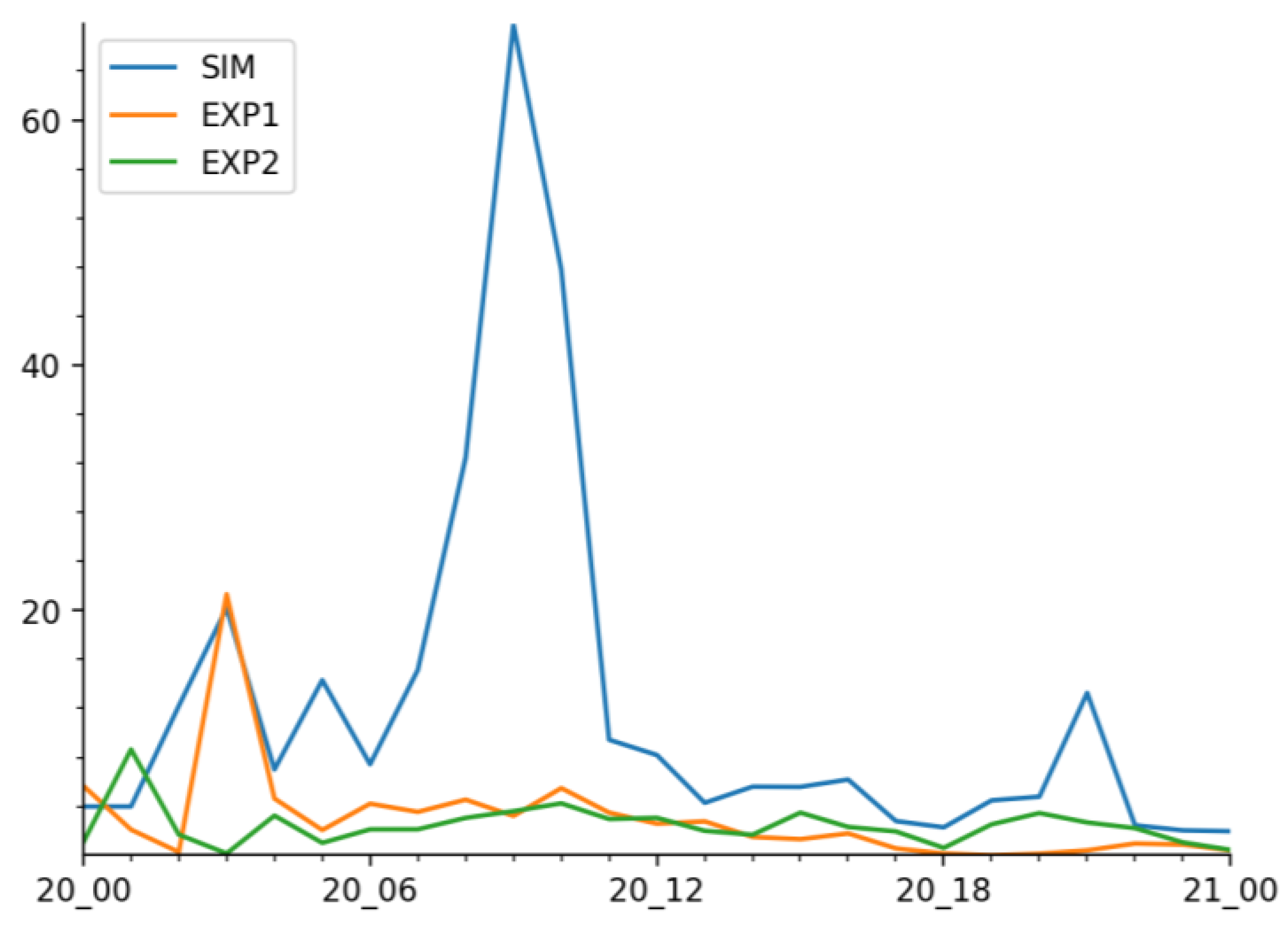
3.3.1. The Simulation of Precipitation and Circulation by the Model

Figure 7 shows the 24 h accumulated precipitation distribution on 20 July 2021. Analysis reveals that the simulated precipitation areas closely resemble the actual conditions. The simulated heavy rainfall area (50–100 mm) and intense rainfall area (100–250 mm) generally align with the observed distribution, with a slight northwestward shift. The extremely heavy rainfall area (250 mm and above), especially the region with over 500 mm of extreme precipitation, corresponds well with the observations, particularly around the (34.7° N, 113.7° E) coordinates near the Zhengzhou observation station. The model successfully captures the cumulative precipitation for this event.

Figure 8 shows the regional average hourly precipitation series for Zhengzhou on 20 July 2021, comparing the actual observations with the model simulations. Analysis reveals that the model roughly captures the diurnal variation of precipitation on that day, with a correlation coefficient of 0.763. The simulated daily precipitation is 298.5 mm, which is close to the observed 307.5 mm. The short-term extreme precipitation simulated by the model from 08:00 to 09:00 on the 20th is 67.8 mm; although it slightly differs from the observed 80.5 mm, it still demonstrates extremity, being the maximum precipitation moment of the day and significantly higher than other times. Moreover, the model’s result of 175.6 mm during the observed extreme precipitation of 201.9 mm at the Zhengzhou station from 08:00 to 09:00 on the 20th is also quite satisfactory.

Figure 9 shows the circulation distribution of ERA5 data and WRF at 09:00 on 20 July 2021. From Figure 9a, it can be observed that at this moment, the Zhengzhou region experiences an easterly wind with a speed of 12 m/s. Comparing with Figure 9b, the Zhengzhou region exhibits a similar easterly wind pattern with a speed of around 12 m/s. In the northeast part of Henan Province, there is a disparity between the simulation and the actual conditions, where the actual wind is from the southeast, while the simulated result indicates an easterly wind with relatively lower intensity. Considering that the circulation field in the northeast is not within the scope of this study and has a minor impact on this extreme rainfall event, it is considered that the model reasonably simulated the circulation pattern of this extreme rainfall event.

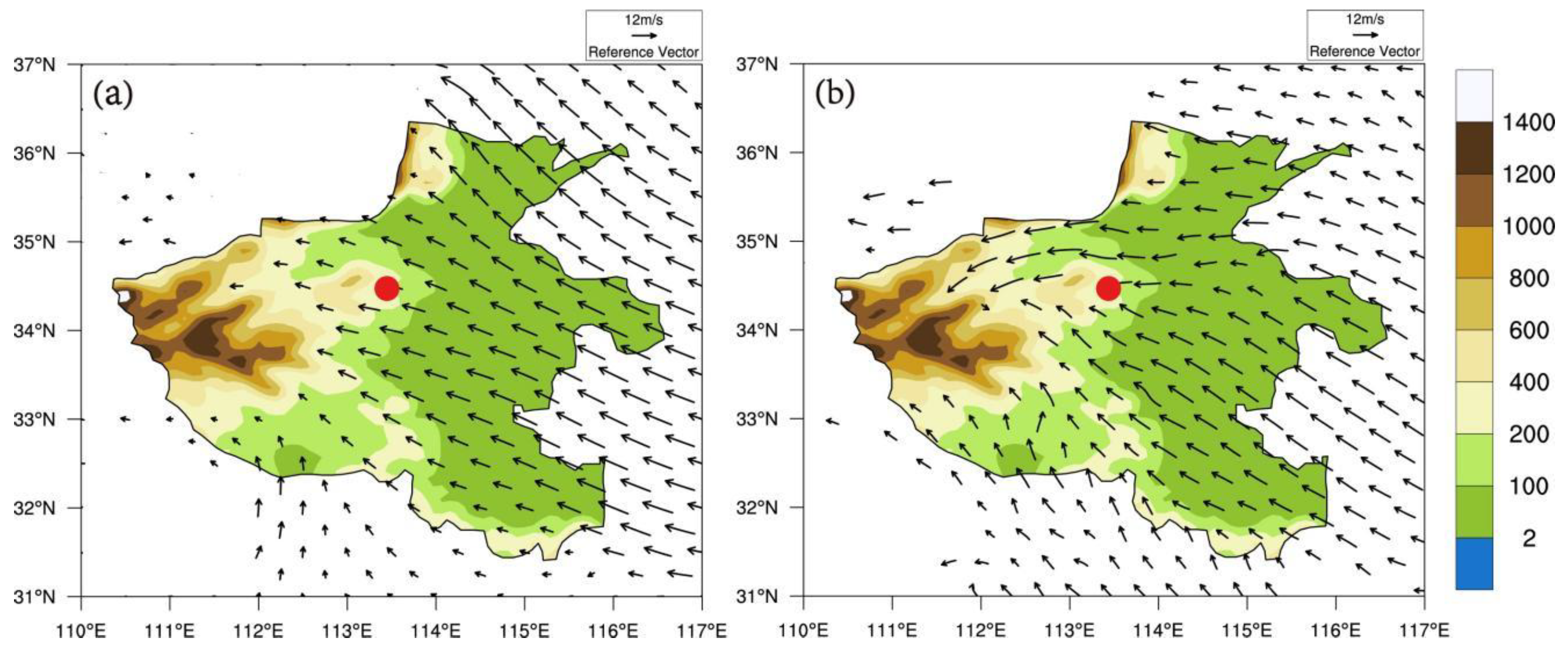
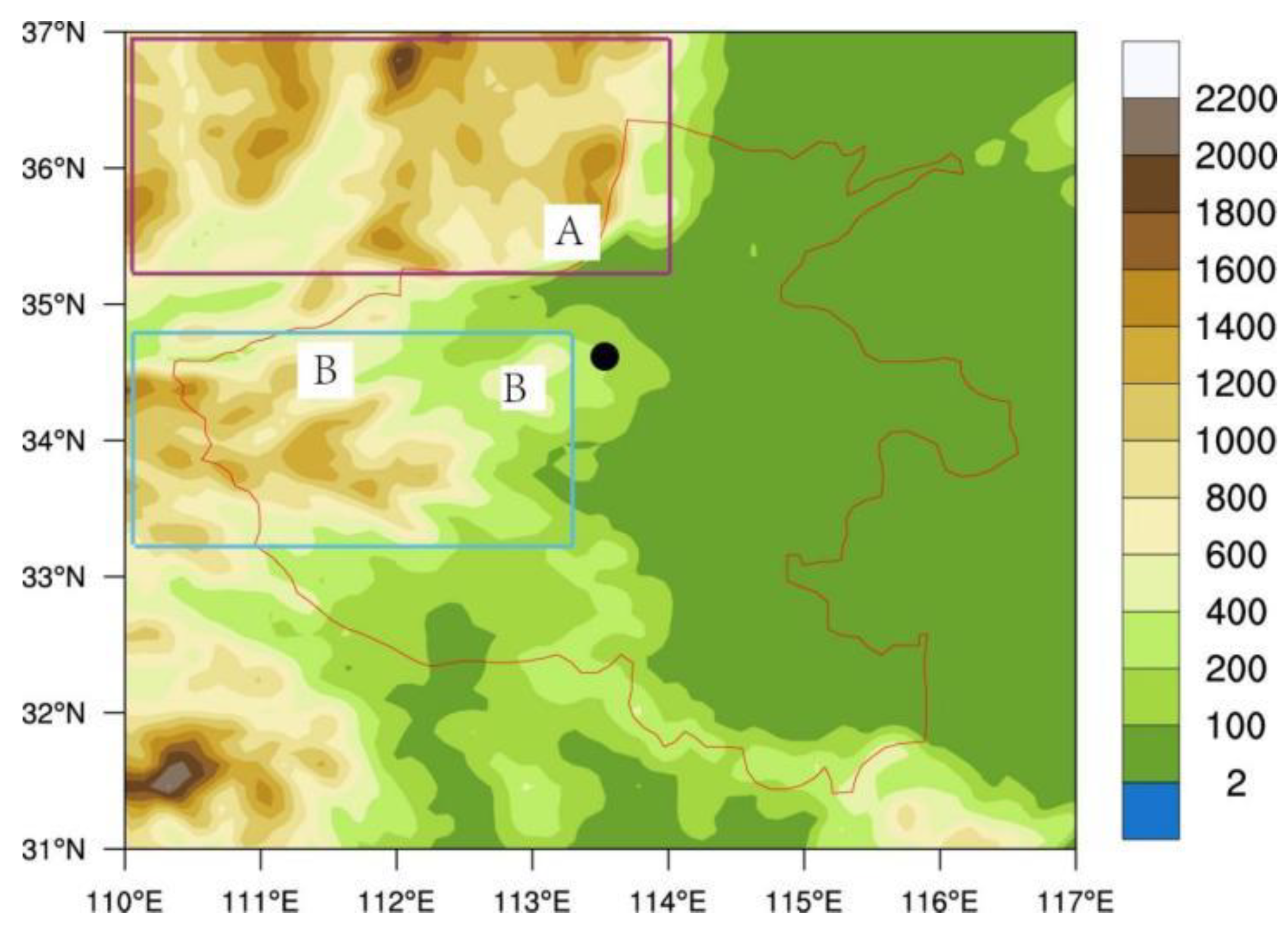
3.3.2. Terrain Sensitivity Experiment

The terrain conditions in the Zhengzhou area are extremely complex (Figure 10). In order to study the impact of the Taihang Mountains and Funiu Mountains on this heavy rainfall process, two sensitivity experiments were designed based on the control experiment. They are EXP1: reducing the height of the Taihang Mountains by 50%; and EXP2: reducing the height of the Funiu Mountains by 50%. After conducting multiple experiments with reduced terrain heights, it was found that neglecting the continuous changes in height around the terrain does not affect the qualitative results of the numerical experiments. After reducing the terrain height, the meteorological elements at the original mountain locations are provided by the model based on the initial and boundary conditions. Songshan belongs to the Funiu Mountains and is referred to as the Funiu Mountains in this study.

3.3.3. The Impact of Terrain Height on Precipitation

Figure 11 shows the distribution of 24 h precipitation intensity for the two terrain sensitivity experiments. Analysis reveals noticeable changes in both intensity and position of the precipitation center when lowering the height of the Taihang Mountains (Figure 11a) compared to the control experiment (Figure 7b). The precipitation center shifts approximately 70 km to the north, and the central precipitation intensity decreases to 210 mm, with a significant reduction in the area of values above 250 mm. This indicates that the high terrain of the Taihang Mountains impedes the movement of the precipitation system, causing the concentration of the precipitation maximum on the southern side of the mountains and an enhancement in precipitation intensity. When lowering the height of the Funiu Mountains (Figure 11b), the precipitation center shifts about 50 km to the southwest, and the central precipitation decreases to 180 mm. The area of values above 250 mm is similarly dispersed, but its size is not significantly different from the control experiment. Overall, these results demonstrate the sensitivity of the precipitation center’s intensity and position to changes in terrain height.

Figure 12 shows the regional averages hourly precipitation in Zhengzhou for the control experiment and two sensitivity experiments. The analysis reveals significant differences between EXP1, EXP2, and the control experiment, especially before 04:00 on the 20th. The disparities are most noticeable between 07:00 and 10:00 on the 20th, and during 00:00 to 04:00 on the 20th, both EXP1 and EXP2 exhibit peak daily precipitation earlier than the control experiment. This indicates that both the Taihang Mountains and the Funiu Mountains’ terrain have an impact on the timing and intensity of extreme precipitation around 08:00 to 09:00 on the 20th.

Figure 13 presents the spatial distribution of orographic lifting precipitation obtained from the control experiment and two sensitivity experiments. The regional average precipitation and orographic lifting precipitation for Zhengzhou, along with their respective proportions, were calculated. The results for the control experiment were 298.5 mm, 49.8 mm, and 16.6%, which closely resemble the observed values. In the sensitivity experiments, EXP1 yielded results of 68.6 mm, 7.3 mm, and 10.6%, while EXP2 produced results of 125.4 mm, 12.9 mm, and 10.3%. The orographic lifting precipitation amounts in both sensitivity experiments showed a significant decrease compared to the control experiment, with EXP1 being particularly pronounced. Additionally, the proportion of orographic lifting precipitation also experienced a certain degree of reduction. The results indicate that the orographic lifting precipitation and its proportion in the Zhengzhou region are highly sensitive to changes in the terrain heights at the two locations.

Figure 14 displays the difference fields of 925 hPa winds between the two sensitivity experiments (EXP1 and EXP2) and the control experiment for the period on 20 July 2021. It can be observed from the figure that, in both EXP1 and EXP2, the Zhengzhou region experiences an increment in southward and westward winds, respectively. This results in a noticeable weakening of orographic lifting effects; moreover, lowering the terrain leads in the case of EXP1 to downwind flows from the mountains (in EXP2 too, but not so intense), leading to a significant reduction in orographic lifting precipitation amounts.

4. Conclusions and Research Prospects

This study employs a terrain-induced precipitation increment model to quantitatively assess the influence of topography on local climate precipitation and extreme rainfall events in Zhengzhou during July. Additionally, it conducts a simulation and analysis of the extraordinary rainfall weather process in Zhengzhou on 20–21 July 2021. The research includes the design of two sets of terrain sensitivity experiments based on the topography of the Taihang Mountains and Funiu Mountains. The primary objective is to further investigate the impact of topography on weather-scale extreme heavy precipitation in Zhengzhou. The conclusions drawn from these investigations are outlined below:

(1)

In terms of the spatial distribution of precipitation climatology, the precipitation in Zhengzhou during July does not exhibit prominence. The daily precipitation generated by topographic lift is 0.18 mm, accounting for only 4.3% of the total precipitation. The impact of topography on local climate-scale precipitation increments is not significant.

(2)

However, in the “7.20” extreme rainfall event in Zhengzhou, the topographic lift precipitation reached 48.7 mm, accounting for 15.8% of the total precipitation. The topographic lift precipitation in this event is significantly higher than the topographic lift precipitation at the climatic scale, and the proportion of total precipitation is also noticeably higher at the weather scale.

(3)

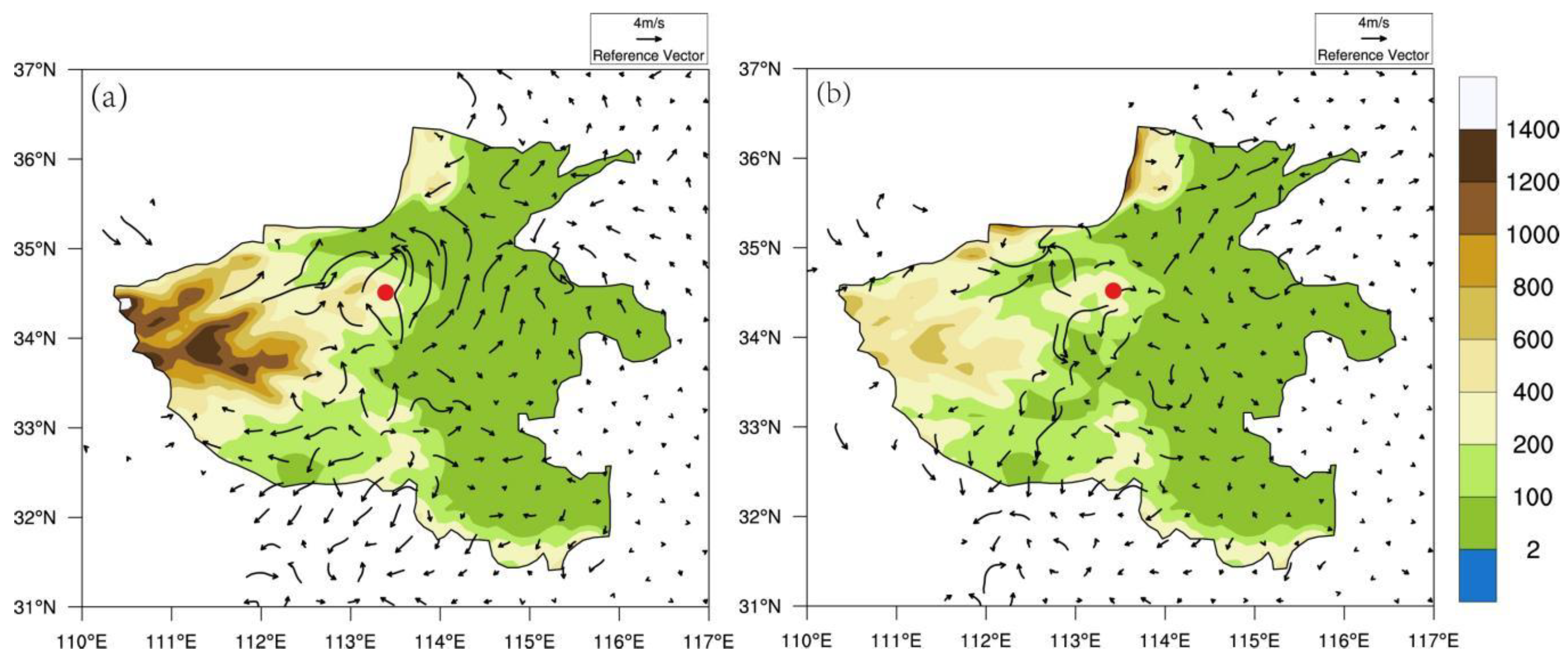
The WRF model effectively captures the spatiotemporal distribution characteristics of the precipitation process and the topographic lift precipitation. This precipitation event is highly sensitive to the surrounding topography. When reducing the heights of the Taihang and Funiu Mountains, the center of the heavy rainfall shifts northward and westward, and the intensity of the heavy rainfall decreases. The circulation around Zhengzhou weakens the east wind and strengthens the west and north winds, resulting in a reduction of topographic lift precipitation to 7.3 mm and 12.9 mm, respectively. The proportion of topographic lift precipitation to total precipitation also decreases to 10.6% and 10.3%, respectively.

This study quantitatively analyzes the impact of topography on local climatological precipitation and heavy precipitation in July in Zhengzhou based on the topographic lift precipitation increment model. The estimation results are satisfactory, and the future research prospects are broad, e.g., experiments on increasing topography height, changing angles, investigating sensitivity to different degrees of topography height changes, etc., as well as investigating in more detail the different large-scale conditions and their possible role in precipitation anomaly formation. In addition, this model mainly discusses dynamic processes, and the discussion of thermal processes can be added in the future to make the model more complete.