Implementation of an On-Line Reactive Source Apportionment (ORSA) Algorithm in the FARM Chemical-Transport Model and Application over Multiple Domains in Italy
Abstract
1. Introduction
2. Methodology
2.1. Tagged Species Source Apportion Algorithms
2.1.1. Advection–Diffusion
2.1.2. Gas-Phase Chemistry
2.1.3. Specific Algorithms for O3
- The row and column corresponding to O3 in the matrix are set to zero (except the diagonal element, which is set to one, i.e., the diagonal element of ), whereas the matrix remains the same, because (its O3 column) is needed in Equation (28).
- For each tag m, (the O3 component of ) is substituted with the sum .
- The solution for all species is then obtained by means of KPP subroutines.
- The O3 component of the solution is finally replaced with , previously obtained by means of the O3 specific algorithm.
2.1.4. Aerosol Processes
2.1.5. Cloud Processes
2.2. Modelling Setup
2.2.1. Emissions
- For LOMB, the regional inventory of ARPA (Regional Environmental and Protection Agency) Lombardy for the year 2012 [64], describing emission sources at the municipality level (EU NUTS 4 territorial units);
- For NI and IT, the ISPRA (Italian Institute for Environmental Protection and Research) Italian inventory for the year 2015 [65], disaggregated on provinces (EU NUTS3 territorial units) and, for the portions of the surrounding countries inside the domains, the European TNO-MACC_III inventory, the updated version of TNO-MACC_II [66].
- The speciation of organic compounds and particulate matter, based on typical profiles of each activity;
- The disaggregation on the calculation grid, with the aid of thematic spatial proxies;
- The temporal modulation with hourly resolution using annual, weekly, and daily profiles typical of each activity.
2.2.2. Boundary Conditions and Meteorological Input
2.2.3. Computing Architecture
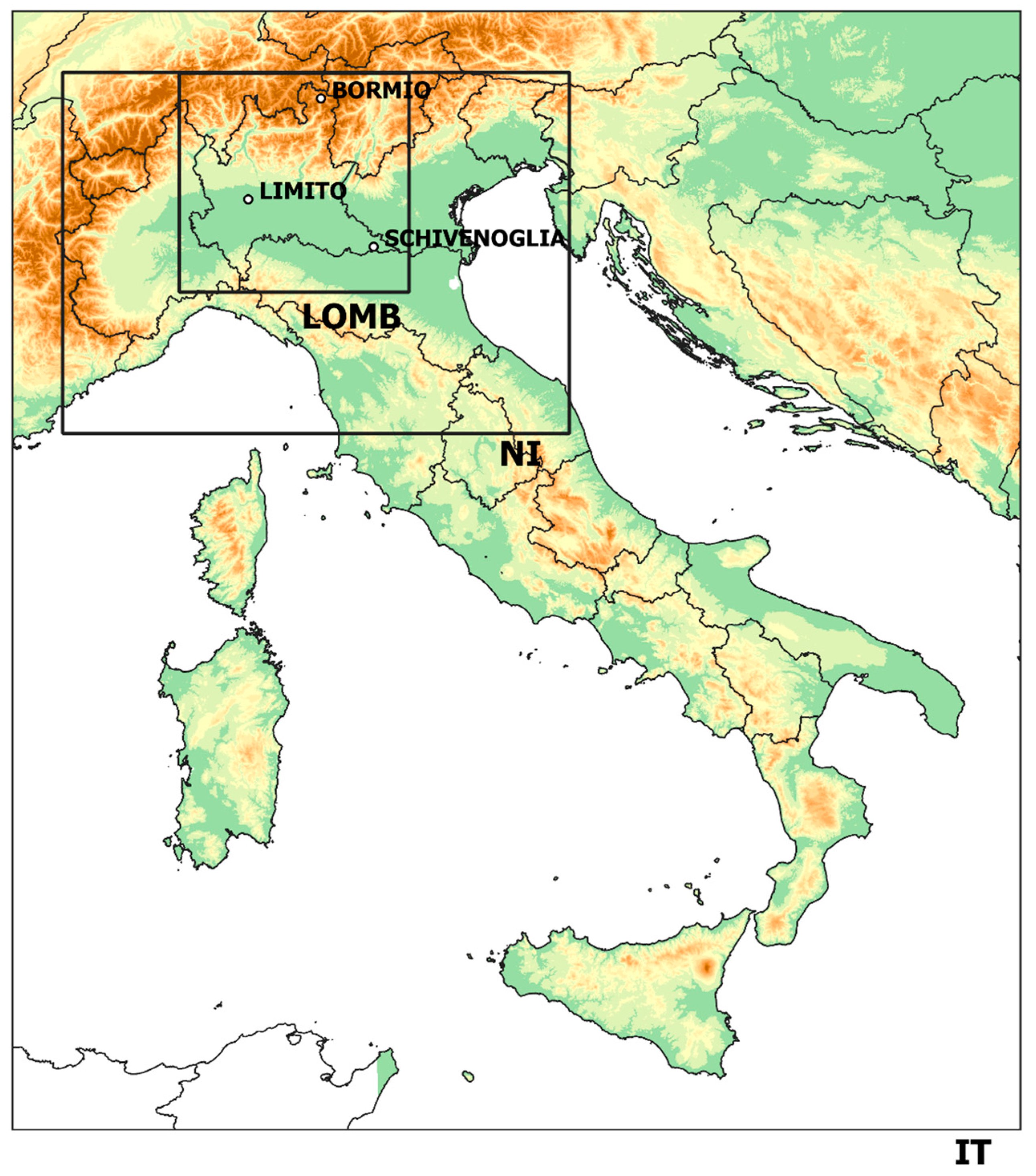
3. Application and Evaluation
3.1. Validation of Simulations
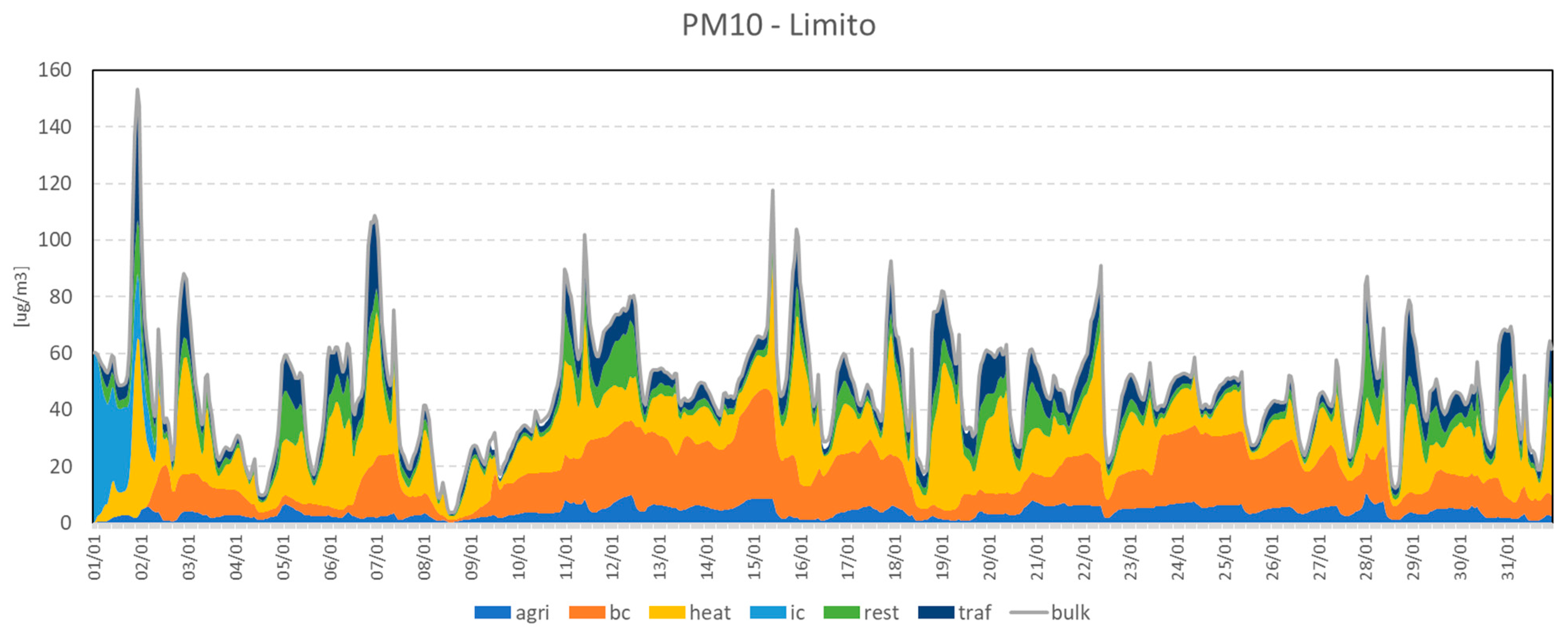
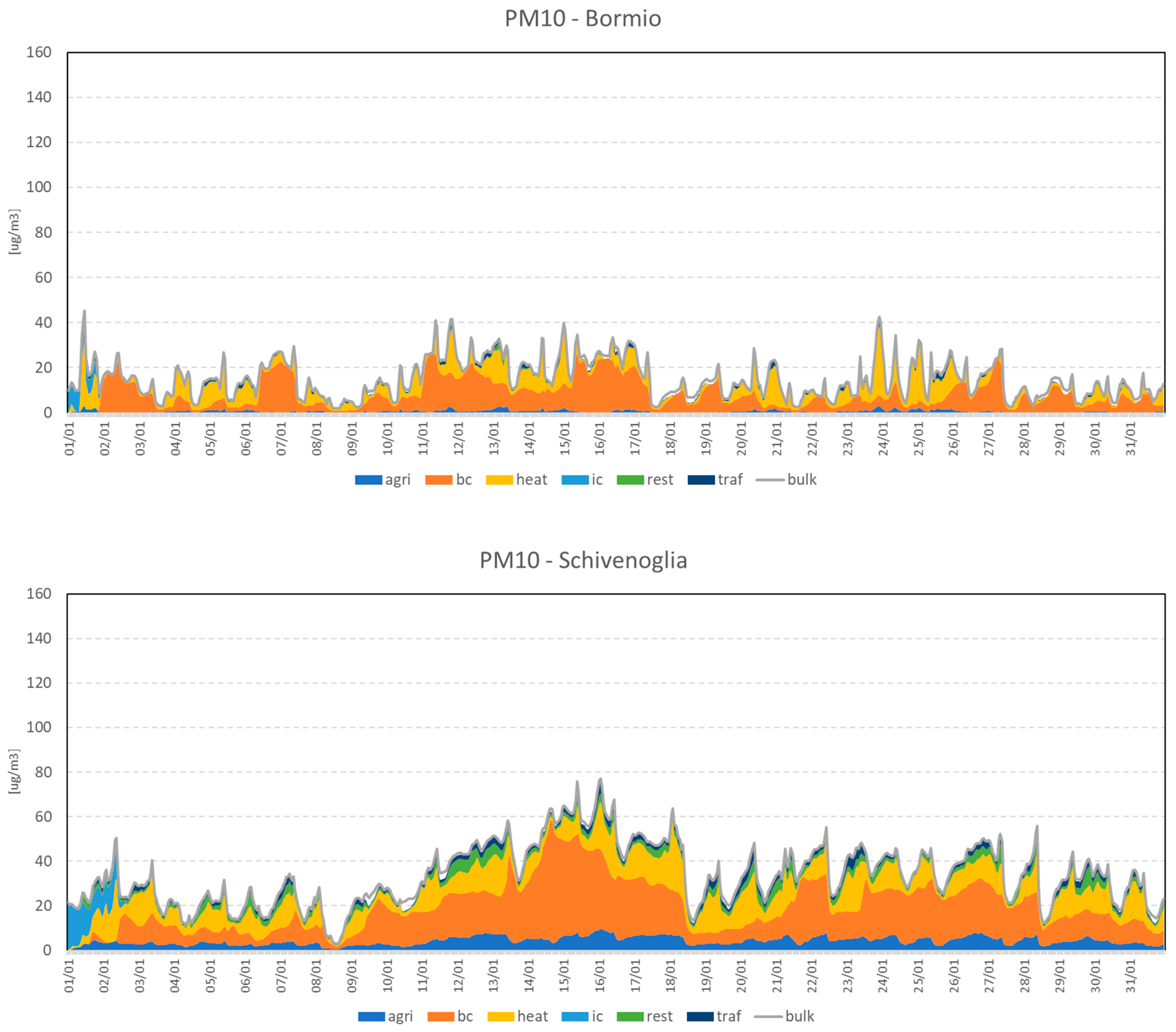
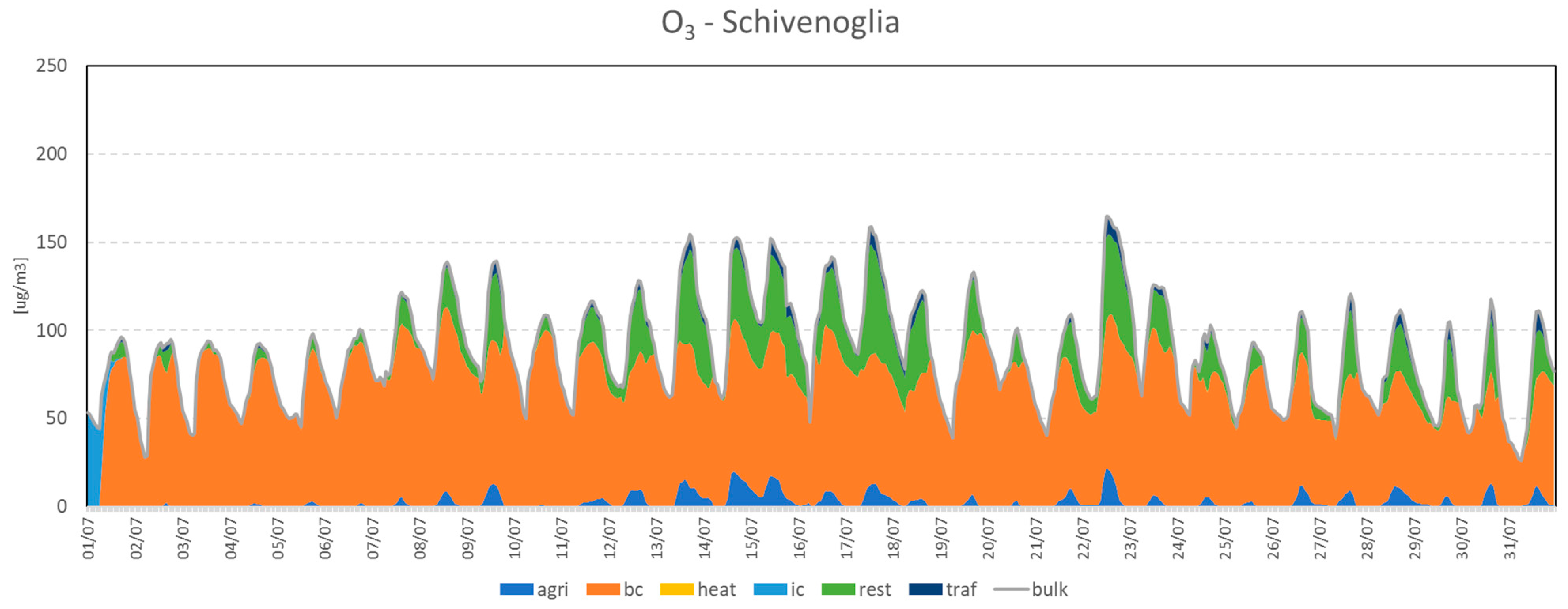
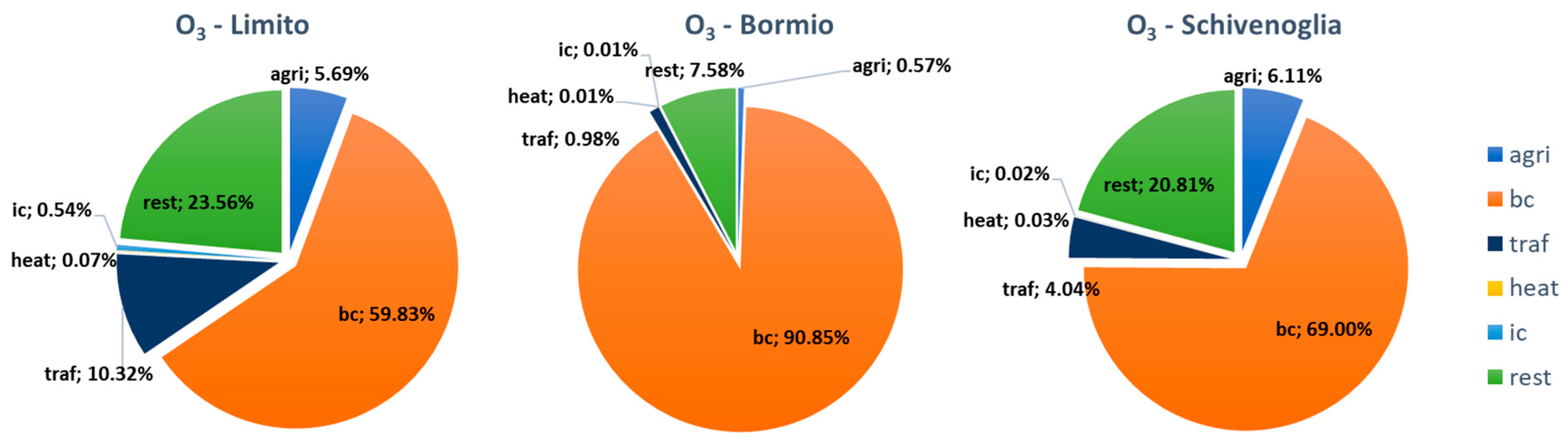
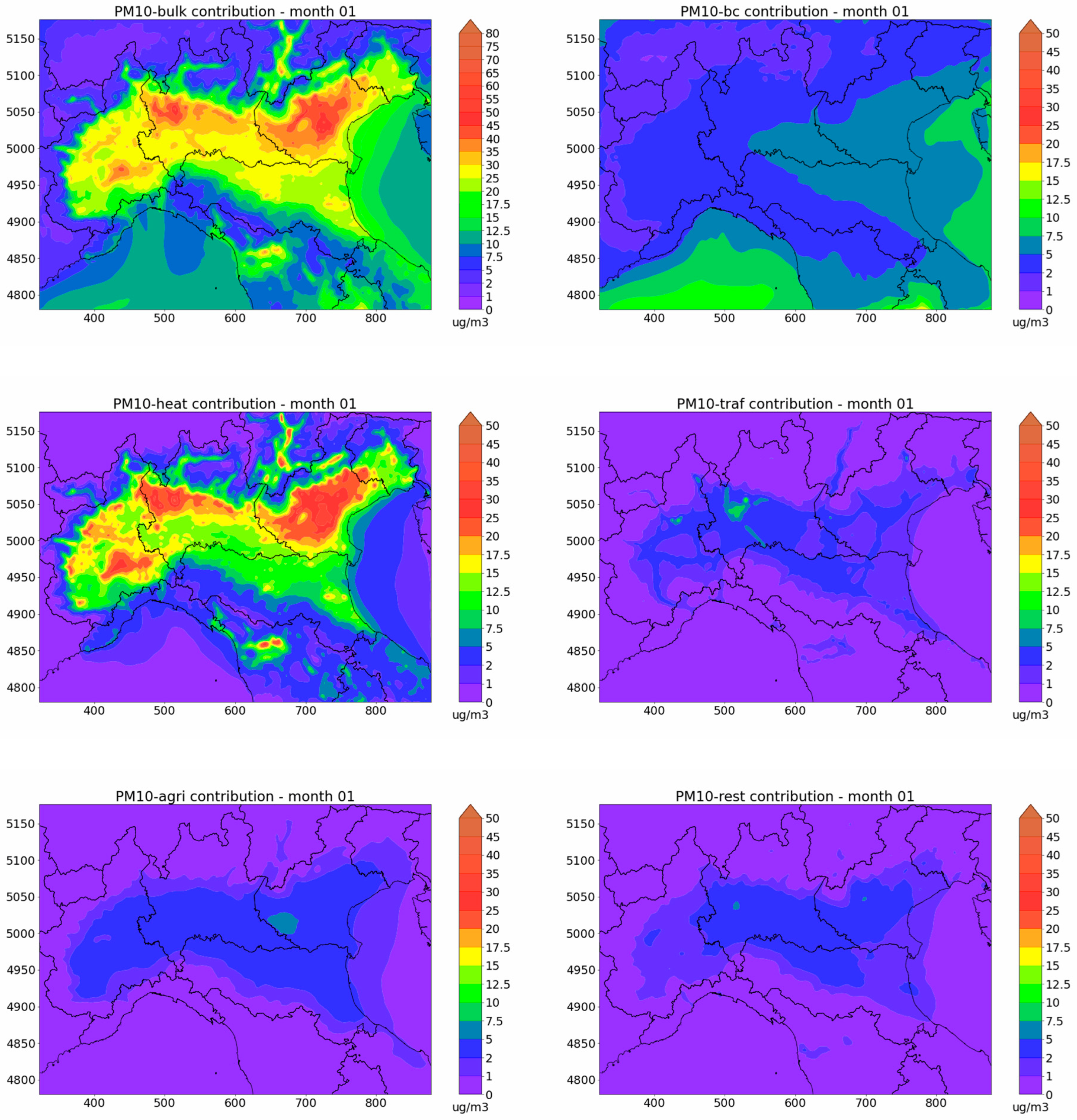
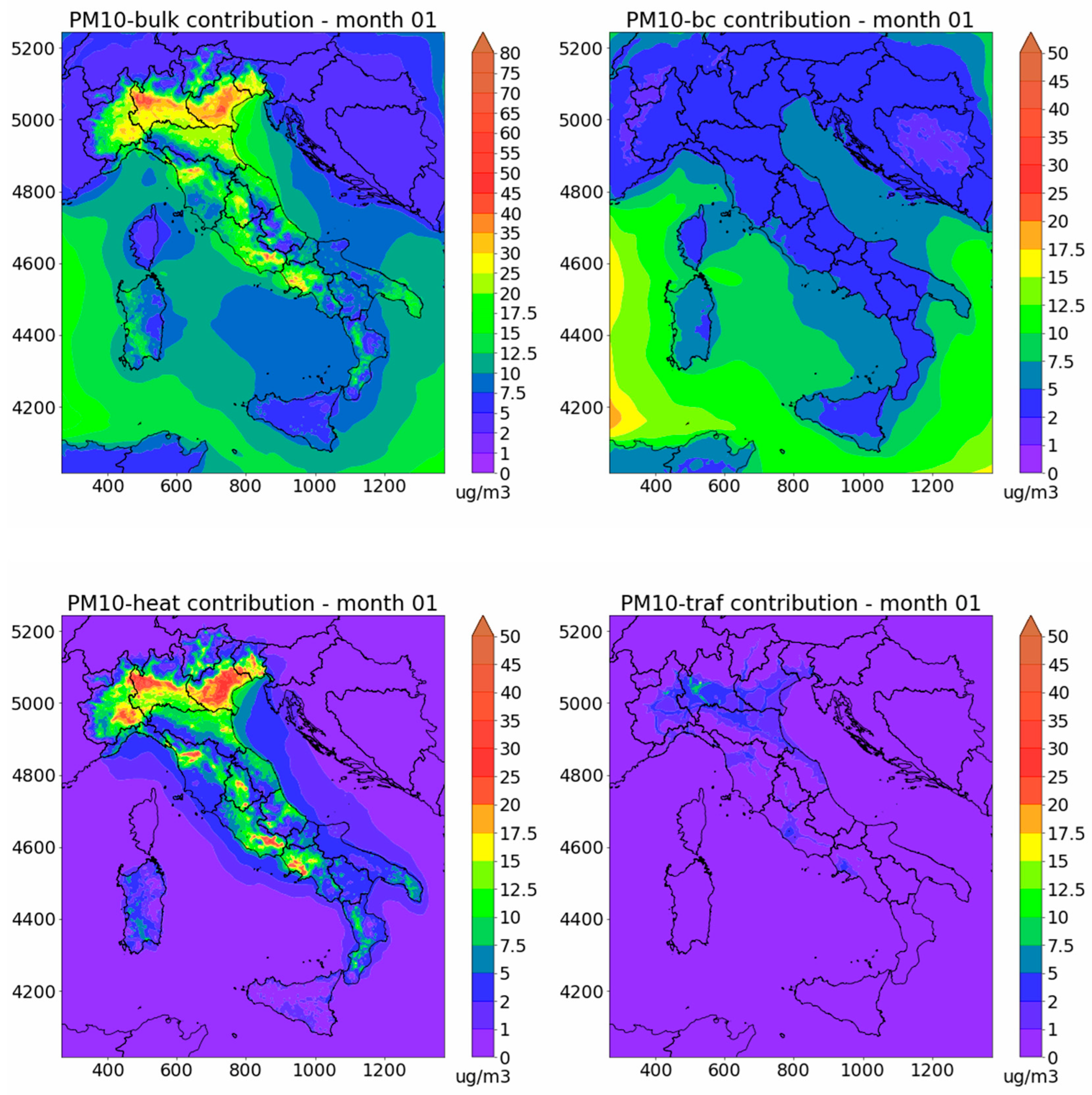
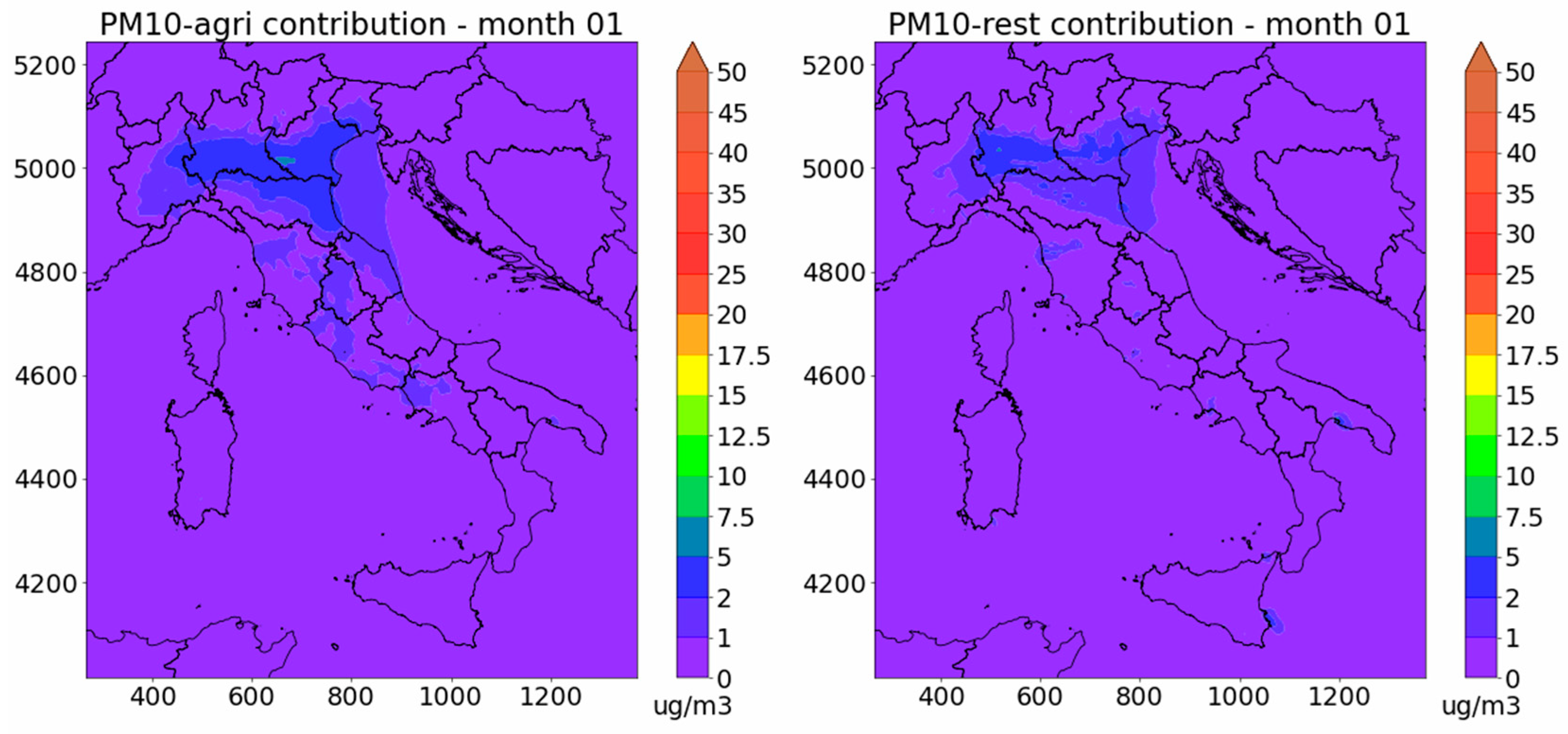
3.2. Sector Contributions
3.2.1. LOMB Domain
3.2.2. NI and IT Domains
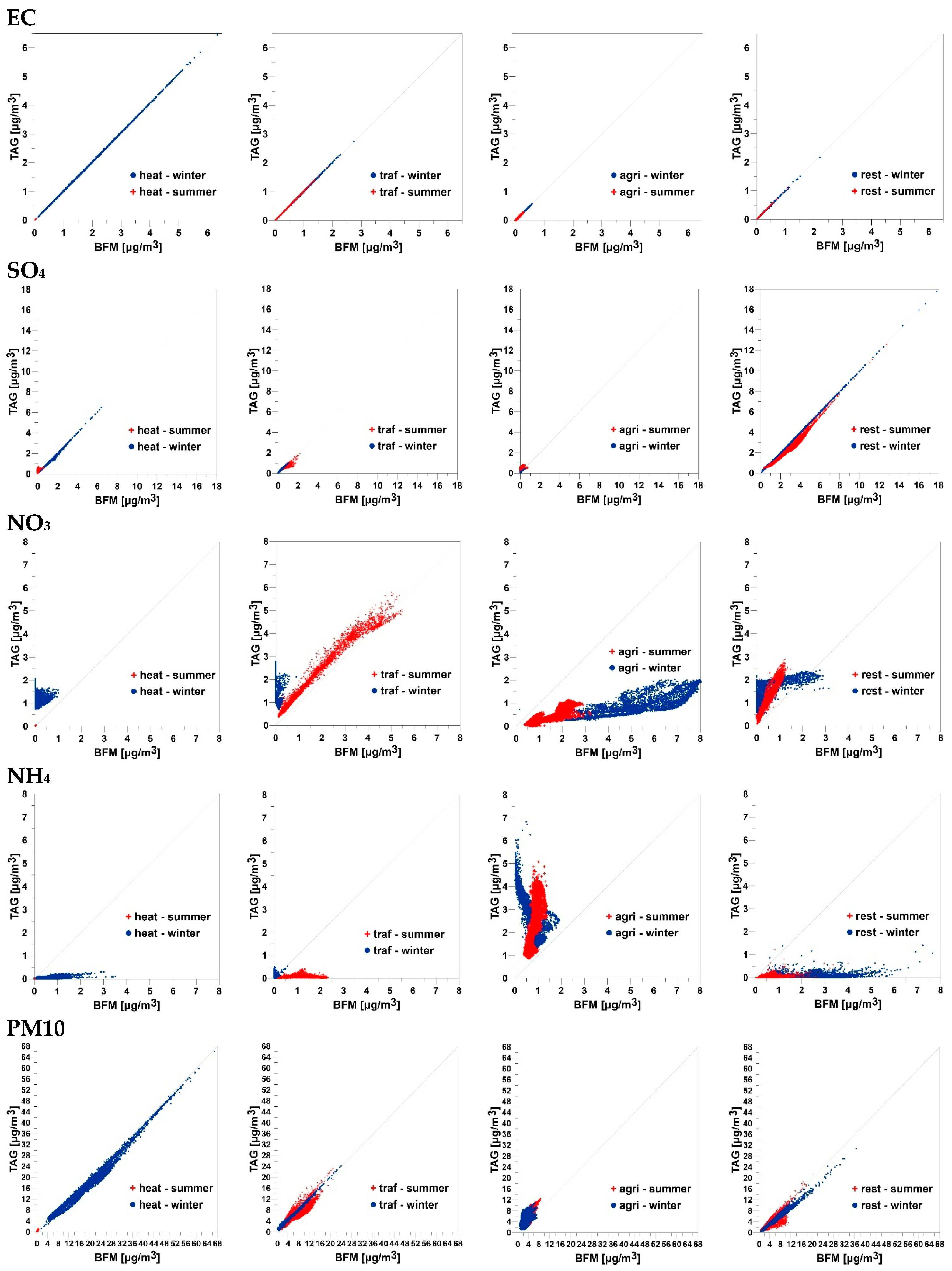
3.3. Comparison against Brute Force Method—LOMB
4. Discussion and Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- European Commission, Joint Research Centre; Belis, C.A.; Favez, O.; Mircea, M.; Diapouli, E.; Manousakas, M.-I.; Vratolis, S.; Gilardoni, S.; Paglione, M.; Decesari, S.; et al. European Guide on Air Pollution Source Apportionment with Receptor Models: Revised Version 2019; Publications Office: Luxembourg, 2019. [Google Scholar]
- Hopke, P.K. Review of Receptor Modeling Methods for Source Apportionment. J. Air Waste Manag. Assoc. 2016, 66, 237–259. [Google Scholar] [CrossRef] [PubMed]
- Viana, M.; Kuhlbusch, T.A.J.; Querol, X.; Alastuey, A.; Harrison, R.M.; Hopke, P.K.; Winiwarter, W.; Vallius, M.; Szidat, S.; Prévôt, A.S.H.; et al. Source Apportionment of Particulate Matter in Europe: A Review of Methods and Results. J. Aerosol Sci. 2008, 39, 827–849. [Google Scholar] [CrossRef]
- European Commission, Joint Research Centre; Belis, C.A.; Pirovano, G.; Mircea, M.; Calori, G. European Guide on Air Pollution Source Apportionment for Particulate Matter with Source Oriented Models and Their Combined Use with Receptor Models; Publications Office: Luxembourg, 2020. [Google Scholar]
- Belis, C.A.; Pernigotti, D.; Pirovano, G.; Favez, O.; Jaffrezo, J.L.; Kuenen, J.; Denier van Der Gon, H.; Reizer, M.; Riffault, V.; Alleman, L.Y.; et al. Evaluation of Receptor and Chemical Transport Models for PM10 Source Apportionment. Atmos. Environ. X 2020, 5, 100053. [Google Scholar] [CrossRef]
- European Commission, Joint Research Centre; Thunis, P.; Clappier, A.; Pirovano, G.; Riffault, V.; Gilardoni, S. Source Apportionment to Support Air Quality Management Practices: A Fitness for Purpose Guide (V 4.0); Publications Office: Luxembourg, 2022. [Google Scholar]
- Thunis, P.; Clappier, A.; Tarrason, L.; Cuvelier, C.; Monteiro, A.; Pisoni, E.; Wesseling, J.; Belis, C.A.; Pirovano, G.; Janssen, S.; et al. Source Apportionment to Support Air Quality Planning: Strengths and Weaknesses of Existing Approaches. Environ. Int. 2019, 130, 104825. [Google Scholar] [CrossRef] [PubMed]
- Burr, M.J.; Zhang, Y. Source Apportionment of Fine Particulate Matter over the Eastern U.S. Part I: Source Sensitivity Simulations Using CMAQ with the Brute Force Method. Atmos. Pollut. Res. 2011, 2, 300–317. [Google Scholar] [CrossRef]
- Marmur, A.; Unal, A.; Mulholland, J.A.; Russell, A.G. Optimization-Based Source Apportionment of PM2.5 Incorporating Gas-to-Particle Ratios. Environ. Sci. Technol. 2005, 39, 3245–3254. [Google Scholar] [CrossRef] [PubMed]
- EMEP. Transboundary Particulate Matter, Photo-Oxidants, Acidifying and Eutrophying Components; EMEP Satus Report 1/2015; EMEP: Ankara, Turkey, 2015. [Google Scholar]
- Koo, B.; Wilson, G.M.; Morris, R.E.; Yarwood, G.; Dunker, A.M. Evaluation of CAMx Probing Tools for Particulate Matter; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Thunis, P.; Degraeuwe, B.; Pisoni, E.; Trombetti, M.; Peduzzi, E.; Belis, C.A.; Wilson, J.; Clappier, A.; Vignati, E. PM2.5 Source Allocation in European Cities: A SHERPA Modelling Study. Atmos. Environ. 2018, 187, 93–106. [Google Scholar] [CrossRef]
- Dunker, A.M. Efficient Calculation of Sensitivity Coefficients for Complex Atmospheric Models. Atmos. Environ. 1967, 15, 1155–1161. [Google Scholar] [CrossRef]
- Dunker, A.M.; Yarwood, G.; Ortmann, J.P.; Wilson, G.M. The Decoupled Direct Method for Sensitivity Analysis in a Three-Dimensional Air Quality Model Implementation, Accuracy, and Efficiency. Environ. Sci. Technol. 2002, 36, 2965–2976. [Google Scholar] [CrossRef]
- Koo, B.; Dunker, A.M.; Yarwood, G. Implementing the Decoupled Direct Method for Sensitivity Analysis in a Particulate Matter Air Quality Model. Environ. Sci. Technol. 2007, 41, 2847–2854. [Google Scholar] [CrossRef]
- Napelenok, S.; Cohan, D.; Hu, Y.; Russell, A. Decoupled Direct 3D Sensitivity Analysis for Particulate Matter (DDM-3D/PM). Atmos. Environ. 2006, 40, 6112–6121. [Google Scholar] [CrossRef]
- Yang, Y.-J.; Wilkinson, J.G.; Russell, A.G. Fast, Direct Sensitivity Analysis of Multidimensional Photochemical Models. Environ. Sci. Technol. 1997, 31, 2859–2868. [Google Scholar] [CrossRef]
- Cohan, D.S.; Hakami, A.; Hu, Y.; Russell, A.G. Nonlinear Response of Ozone to Emissions: Source Apportionment and Sensitivity Analysis. Environ. Sci. Technol. 2005, 39, 6739–6748. [Google Scholar] [CrossRef] [PubMed]
- Hakami, A.; Odman, M.T.; Russell, A.G. High-Order, Direct Sensitivity Analysis of Multidimensional Air Quality Models. Environ. Sci. Technol. 2003, 37, 2442–2452. [Google Scholar] [CrossRef] [PubMed]
- Koo, B.; Yarwood, G.; Cohan, D.S. Higher-Order Decoupled Direct Method (HDDM) for Ozone Modeling Sensitivity Analyses and Code Refinements; ENVIRON International Corporation: Novato, CA, USA, 2008. [Google Scholar]
- Zhang, W.; Capps, S.L.; Hu, Y.; Nenes, A.; Napelenok, S.L.; Russell, A.G. Development of the High-Order Decoupled Direct Method in Three Dimensions for Particulate Matter: Enabling Advanced Sensitivity Analysis in Air Quality Models. Geosci. Model Dev. 2012, 5, 355–368. [Google Scholar] [CrossRef]
- Yarwood, G.; Morris, R.E.; Wilson, G.M. Particulate Matter Source Apportionment Technology (PSAT) in the CAMx Photochemical Grid Model. In Air Pollution Modeling and Its Application XVII; Borrego, C., Norman, A.-L., Eds.; Springer: Boston, MA, USA, 2007; pp. 478–492. [Google Scholar]
- Yarwood, G.; Morris, R.; Yocke, M.; Hogo, H.; Chico, T. Development of a Methodology for Source Apportionment of Ozone Concentration Estimates from a Photochemical Grid Model; Air & Waste Management Association: Pittsburgh, PA, USA, 1996. [Google Scholar]
- ENVIRON. CAMx—User’s Guide—Comprehensive Air Quality Model with Extensions—Version 6.1; Environ: Novato, CA, USA, 2014. [Google Scholar]
- Wagstrom, K.M.; Pandis, S.N.; Yarwood, G.; Wilson, G.M.; Morris, R.E. Development and Application of a Computationally Efficient Particulate Matter Apportionment Algorithm in a Three-Dimensional Chemical Transport Model. Atmos. Environ. 2008, 42, 5650–5659. [Google Scholar] [CrossRef]
- Bhave, P.V.; Pouliot, G.A.; Zheng, M. Diagnostic Model Evaluation for Carbonaceous PM2.5 Using Organic Markers Measured in the Southeastern U.S. Environ. Sci. Technol. 2007, 41, 1577–1583. [Google Scholar] [CrossRef]
- Wang, Z.S.; Chien, C.-J.; Tonnesen, G.S. Development of a Tagged Species Source Apportionment Algorithm to Characterize Three-Dimensional Transport and Transformation of Precursors and Secondary Pollutants. J. Geophys. Res. 2009, 114, D21206. [Google Scholar] [CrossRef]
- Kwok, R.H.F.; Napelenok, S.L.; Baker, K.R. Implementation and Evaluation of PM2.5 Source Contribution Analysis in a Photochemical Model. Atmos. Environ. 2013, 80, 398–407. [Google Scholar] [CrossRef]
- Gao, J.; Zhu, B.; Xiao, H.; Kang, H.; Hou, X.; Shao, P. A Case Study of Surface Ozone Source Apportionment during a High Concentration Episode, under Frequent Shifting Wind Conditions over the Yangtze River Delta, China. Sci. Total Environ. 2016, 544, 853–863. [Google Scholar] [CrossRef]
- Romero-Alvarez, J.; Lupaşcu, A.; Lowe, D.; Badia, A.; Acher-Nicholls, S.; Dorling, S.R.; Reeves, C.E.; Butler, T. Sources of Surface O3 in the UK: Tagging O3 within WRF-Chem; Gases/Atmospheric Modelling/Troposphere/Chemistry (chemical composition and reactions); EGU: Munich, Germany, 2022. [Google Scholar]
- Zhao, Y.; Li, Y.; Kumar, A.; Ying, Q.; Vandenberghe, F.; Kleeman, M.J. Separately Resolving NOx and VOC Contributions to Ozone Formation. Atmos. Environ. 2022, 285, 119224. [Google Scholar] [CrossRef]
- Brandt, J.; Silver, J.D.; Christensen, J.H.; Andersen, M.S.; Bønløkke, J.H.; Sigsgaard, T.; Geels, C.; Gross, A.; Hansen, A.B.; Hansen, K.M.; et al. Contribution from the Ten Major Emission Sectors in Europe and Denmark to the Health-Cost Externalities of Air Pollution Using the EVA Model System—An Integrated Modelling Approach. Atmos. Chem. Phys. 2013, 13, 7725–7746. [Google Scholar] [CrossRef]
- Kranenburg, R.; Segers, A.J.; Hendriks, C.; Schaap, M. Source Apportionment Using LOTOS-EUROS: Module Description and Evaluation. Geosci. Model Dev. 2013, 6, 721–733. [Google Scholar] [CrossRef]
- Pay, M.T.; Gangoiti, G.; Guevara, M.; Napelenok, S.; Querol, X.; Jorba, O.; Pérez García-Pando, C. Ozone Source Apportionment during Peak Summer Events Over Southwestern Europe. Atmos. Chem. Phys. 2019, 19, 5467–5494. [Google Scholar] [CrossRef] [PubMed]
- Pepe, N.; Pirovano, G.; Balzarini, A.; Toppetti, A.; Riva, G.M.; Amato, F.; Lonati, G. Enhanced CAMx Source Apportionment Analysis at an Urban Receptor in Milan Based on Source Categories and Emission Regions. Atmos. Environ. X 2019, 2, 100020. [Google Scholar] [CrossRef]
- Lupaşcu, A.; Butler, T. Source Attribution of European Surface O3 Using a Tagged O3 Mechanism. Atmos. Chem. Phys. 2019, 19, 14535–14558. [Google Scholar] [CrossRef]
- ARIANET. FARM (Flexible Air Quality Regional Model)—Model Formulation and User Manual—Version 5.1; ARIANET S.R.L.: Milan, Italy, 2020. [Google Scholar]
- Silibello, C.; Calori, G.; Brusasca, G.; Giudici, A.; Angelino, E.; Fossati, G.; Peroni, E.; Buganza, E. Modelling of PM10 Concentrations over Milano Urban Area Using Two Aerosol Modules. Environ. Model. Softw. 2008, 23, 333–343. [Google Scholar] [CrossRef]
- D’Elia, I.; Briganti, G.; Vitali, L.; Piersanti, A.; Righini, G.; D’Isidoro, M.; Cappelletti, A.; Mircea, M.; Adani, M.; Zanini, G.; et al. Measured and Modelled Air Quality Trends in Italy over the Period 2003–2010. Atmos. Chem. Phys. 2021, 21, 10825–10849. [Google Scholar] [CrossRef]
- Mircea, M.; Ciancarella, L.; Briganti, G.; Calori, G.; Cappelletti, A.; Cionni, I.; Costa, M.; Cremona, G.; D’Isidoro, M.; Finardi, S.; et al. Assessment of the AMS-MINNI System Capabilities to Simulate Air Quality over Italy for the Calendar Year 2005. Atmos. Environ. 2014, 84, 178–188. [Google Scholar] [CrossRef]
- Adani, M.; Piersanti, A.; Ciancarella, L.; D’Isidoro, M.; Villani, M.G.; Vitali, L. Preliminary Tests on the Sensitivity of the FORAIR_IT Air Quality Forecasting System to Different Meteorological Drivers. Atmosphere 2020, 11, 574. [Google Scholar] [CrossRef]
- Adani, M.; D’Isidoro, M.; Mircea, M.; Guarnieri, G.; Vitali, L.; D’Elia, I.; Ciancarella, L.; Gualtieri, M.; Briganti, G.; Cappelletti, A.; et al. Evaluation of Air Quality Forecasting System FORAIR-IT over Europe and Italy at High Resolution for Year 2017. Atmos. Pollut. Res. 2022, 13, 101456. [Google Scholar] [CrossRef]
- SNPA. Descrizione dei Modelli di Qualità Dell’aria Utilizzati Nell’ambito del Sistema Agenziale e Delle Relative Caratteristiche Tecniche e di Disponibilità; ISPRA (Italian Institute for Environmental Protection and Research): Lombardy, Italy; National Network for the Environmental Protection (SNPA): Santa Monica, CA, USA, 2016. [Google Scholar]
- Sandu, A.; Daescu, D.N.; Carmichael, G.R. Direct and Adjoint Sensitivity Analysis of Chemical Kinetic Systems with KPP: Part I—Theory and Software Tools. Atmos. Environ. 2003, 37, 5083–5096. [Google Scholar] [CrossRef]
- Carter, W.P.L. Documentation of the SAPRC-99 Chemical Mechanism for VOC Reactivity Assessment; University of California: Riverside, CA, USA, 2000. [Google Scholar]
- Binkowski, F.S.; Roselle, S.J. Models-3 Community Multiscale Air Quality (CMAQ) Model Aerosol Component 1. Model Description. J. Geophys. Res. 2003, 108, 2001JD001409. [Google Scholar] [CrossRef]
- Fountoukis, C.; Nenes, A. ISORROPIA II: A Computationally Efficient Aerosol Thermodynamic Equilibrium Model for K+, Ca2+, Mg2+, NH4+, Na+, SO42−, NO3−, Cl−, H2O Aerosols. Atmos. Chem. Phys. 2007, 7, 4639–4659. [Google Scholar] [CrossRef]
- Schell, B.; Ackermann, I.J.; Hass, H.; Binkowski, F.S.; Ebel, A. Modeling the Formation of Secondary Organic Aerosol within a Comprehensive Air Quality Model System. J. Geophys. Res. 2001, 106, 28275–28293. [Google Scholar] [CrossRef]
- EEA. Air Quality in Europe 2021; European Environment Agency Report No. 15/2021; European Environment Agency: Copenhagen, Denmark, 2021.
- Piersanti, A.; D’Elia, I.; Gualtieri, M.; Briganti, G.; Cappelletti, A.; Zanini, G.; Ciancarella, L. The Italian National Air Pollution Control Programme: Air Quality, Health Impact and Cost Assessment. Atmosphere 2021, 12, 196. [Google Scholar] [CrossRef]
- Jakovljević, T.; Lovreškov, L.; Jelić, G.; Anav, A.; Popa, I.; Fornasier, M.F.; Proietti, C.; Limić, I.; Butorac, L.; Vitale, M.; et al. Impact of Ground-Level Ozone on Mediterranean Forest Ecosystems Health. Sci. Total Environ. 2021, 783, 147063. [Google Scholar] [CrossRef] [PubMed]
- Michetti, M.; Gualtieri, M.; Anav, A.; Adani, M.; Benassi, B.; Dalmastri, C.; D’Elia, I.; Piersanti, A.; Sannino, G.; Zanini, G.; et al. Climate Change and Air Pollution: Translating Their Interplay into Present and Future Mortality Risk for Rome and Milan Municipalities. Sci. Total Environ. 2022, 830, 154680. [Google Scholar] [CrossRef] [PubMed]
- Belis, C.A.; Pirovano, G.; Villani, M.G.; Calori, G.; Pepe, N.; Putaud, J.P. Comparison of Source Apportionment Approaches and Analysis of Non-Linearity in a Real Case Model Application. Geosci. Model Dev. 2021, 14, 4731–4750. [Google Scholar] [CrossRef]
- Arunachalam, S. Peer Review of Source Apportionment Tools in CAMx and CMAQ; University of North Carolina Institute for the Environment: Chapel Hill, NC, USA, 2009. [Google Scholar]
- Burr, M.J.; Zhang, Y. Source Apportionment of Fine Particulate Matter over the Eastern U.S. Part II: Source Apportionment Simulations Using CAMx/PSAT and Comparisons with CMAQ Source Sensitivity Simulations. Atmos. Pollut. Res. 2011, 2, 318–336. [Google Scholar] [CrossRef]
- Koo, B.; Wilson, G.M.; Morris, R.E.; Dunker, A.M.; Yarwood, G. Comparison of Source Apportionment and Sensitivity Analysis in a Particulate Matter Air Quality Model. Environ. Sci. Technol. 2009, 43, 6669–6675. [Google Scholar] [CrossRef] [PubMed]
- Butler, T.; Lupascu, A.; Nalam, A. Attribution of Ground-Level Ozone to Anthropogenic and Natural Sources of Nitrogen Oxides and Reactive Carbon in a Global Chemical Transport Model. Atmos. Chem. Phys. 2020, 20, 10707–10731. [Google Scholar] [CrossRef]
- Clappier, A.; Belis, C.A.; Pernigotti, D.; Thunis, P. Source Apportionment and Sensitivity Analysis: Two Methodologies with Two Different Purposes. Geosci. Model Dev. 2017, 10, 4245–4256. [Google Scholar] [CrossRef]
- Grewe, V.; Tsati, E.; Hoor, P. On the Attribution of Contributions of Atmospheric Trace Gases to Emissions in Atmospheric Model Applications. Geosci. Model Dev. 2010, 3, 487–499. [Google Scholar] [CrossRef]
- Kwok, R.H.F.; Baker, K.R.; Napelenok, S.L.; Tonnesen, G.S. Photochemical Grid Model Implementation and Application of VOC, NOx, and O3 Source Apportionment. Geosci. Model Dev. 2015, 8, 99–114. [Google Scholar] [CrossRef]
- Kumar, N.; Lurmann, F.W. Peer Review of ENVIRON’s Ozone Source Apportionment Technology and CAMx Air Quality Model; Sonoma Technology, Inc.: Santa Rosa, CA, USA, 1997. [Google Scholar]
- Sillman, S. The Use of NOy, H2O2, and HNO3 as Indicators for Ozone-NOx-Hydrocarbon Sensitivity in Urban Locations. J. Geophys. Res. 1995, 100, 14175. [Google Scholar] [CrossRef]
- Seinfeld, J.H.; Pandis, S.N. Atmospheric Chemistry and Physics from Air Pollution to Climate Change; Wiley-Interscience—John Wiley & Sons: New York, NY, USA, 1998; ISBN 978-0-471-17816-3. [Google Scholar]
- ARPA. Lombardia. INEMAR—Inventario Emissioni Aria—ARPA Regione Lombardia; ARPA: Lombardy, Italy, 2014. [Google Scholar]
- ISPRA. Italian Emission Inventory 1990–2019. Informative Inventory Report 2021; ISPRA: Rome, Italy, 2021. [Google Scholar]
- Kuenen, J.J.P.; Visschedijk, A.J.H.; Jozwicka, M.; Denier van der Gon, H.A.C. TNO-MACC_II Emission Inventory; a Multi-Year (2003–2009) Consistent High-Resolution European Emission Inventory for Air Quality Modelling. Atmos. Chem. Phys. 2014, 14, 10963–10976. [Google Scholar] [CrossRef]
- ARIA Technologies. ARIANET Emission Manager—Processing System for Model-Ready Emission Input—User’s Guide; ARIA Technologies: Paris, France, 2013. [Google Scholar]
- Guenther, A.; Karl, T.; Harley, P.; Wiedinmyer, C.; Palmer, P.I.; Geron, C. Estimates of Global Terrestrial Isoprene Emissions Using MEGAN (Model of Emissions of Gases and Aerosols from Nature). Atmos. Chem. Phys. 2006, 6, 3181–3210. [Google Scholar] [CrossRef]
- EEA. EMEP/CORINAIR Atmospheric Emission Inventory Guidebook—Second Edition 1999. European Environment Agency; Technical Report No 30/2000; EEA: Copenhagen, Denmark, 2000. [Google Scholar]
- Veratti, G.; Stortini, M.; Amorati, R.; Bressan, L.; Giovannini, G.; Bande, S.; Bissardella, F.; Ghigo, S.; Angelino, E.; Colombo, L.; et al. Impact of NOx and NH3 Emission Reduction on Particulate Matter across Po Valley: A LIFE-IP-PREPAIR Study. Atmosphere 2023, 14, 762. [Google Scholar] [CrossRef]
- D’Isidoro, M.; D’Elia, I.; Vitali, L.; Briganti, G.; Cappelletti, A.; Piersanti, A.; Finardi, S.; Calori, G.; Pepe, N.; Di Giosa, A.; et al. Lessons Learnt for Air Pollution Mitigation Policies from the COVID-19 Pandemic: The Italian Perspective. Atmos. Pollut. Res. 2022, 13, 101620. [Google Scholar] [CrossRef]
- D’Allura, A.; Costa, M.P.; Silibello, C. QualeAria: European and National Scale Air Quality Forecast System Performance Evaluation. IJEP 2018, 64, 110. [Google Scholar] [CrossRef]
- Pielke, R.A.; Cotton, W.R.; Walko, R.L.; Tremback, C.J.; Lyons, W.A.; Grasso, L.D.; Nicholls, M.E.; Moran, M.D.; Wesley, D.A.; Lee, T.J.; et al. A Comprehensive Meteorological Modeling System—RAMS. Meteorl. Atmos. Phys. 1992, 49, 69–91. [Google Scholar] [CrossRef]
- ARIA. Technologies SWIFT Wind Field Model, General Design Manual; ARIA Technologies: Paris, France, 2010. [Google Scholar]
- Heymann, Y. (Ed.) CORINE Land Cover: Technical Guide; Office for Official Publications of the European Communities: Luxembourg, 1994; ISBN 978-92-826-2578-1. [Google Scholar]
- Vitali, L.; Adani, M.; Ciancarella, L.; Cremona, G.; D’Isidoro, M.; Mircea, M.; Piersanti, A.; Briganti, G.; Cappelletti, A.; D’Elia, I.; et al. AMS-MINNI National Air Quality Simulation on Italy for the Calendar Year 2015. Annual Air Quality Simulation of MINNI Atmospheric Modelling System: Results for the Calendar Year 2015 and Comparison with Observed Data; ENEA Technical Report, RT/2019/15/ENEA; ENEA: Stockholm, Sweden, 2019. [Google Scholar]
- Inness, A.; Ades, M.; Agustí-Panareda, A.; Barré, J.; Benedictow, A.; Blechschmidt, A.-M.; Dominguez, J.J.; Engelen, R.; Eskes, H.; Flemming, J.; et al. The CAMS Reanalysis of Atmospheric Composition. Atmos. Chem. Phys. 2019, 19, 3515–3556. [Google Scholar] [CrossRef]
- Skamarock, W.C.; Klemp, J.B.; Dudhia, J.; Gill, D.O.; Liu, Z.; Berner, J.; Wang, W.; Powers, J.G.; Duda, M.G.; Barker, D.M.; et al. A Description of the Advanced Research WRF Model Version 4; National Center for Atmospheric Research: Boulder, CO, USA, 2008. [Google Scholar]
- Marras, G.F.; Silibello, C.; Calori, G. A Hybrid Parallelization of Air Quality Model with MPI and OpenMP. In Recent Advances in the Message Passing Interface; Träff, J.L., Benkner, S., Dongarra, J.J., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2012; Volume 7490, pp. 235–245. ISBN 978-3-642-33517-4. [Google Scholar]
- Iannone, F.; Ambrosino, F.; Bracco, G.; De Rosa, M.; Funel, A.; Guarnieri, G.; Migliori, S.; Palombi, F.; Ponti, G.; Santomauro, G.; et al. CRESCO ENEA HPC Clusters: A Working Example of a Multifabric GPFS Spectrum Scale Layout. In Proceedings of the 2019 International Conference on High Performance Computing & Simulation (HPCS), Dublin, Ireland, 15–19 July 2019; IEEE: Dublin, Ireland, 2019; pp. 1051–1052. [Google Scholar]
- Chang, J.C.; Hanna, S.R. Air Quality Model Performance Evaluation. Meteorol. Atmos. Phys. 2004, 87, 167–196. [Google Scholar] [CrossRef]
- Bessagnet, B.; Pirovano, G.; Mircea, M.; Cuvelier, C.; Aulinger, A.; Calori, G.; Ciarelli, G.; Manders, A.; Stern, R.; Tsyro, S.; et al. Presentation of the EURODELTA III Intercomparison Exercise—Evaluation of the Chemistry Transport Models’ Performance on Criteria Pollutants and Jointanalysis with Meteorology. Atmos. Chem. Phys. 2016, 16, 12667–12701. [Google Scholar] [CrossRef]
- Schaap, M.; Cuvelier, C.; Hendriks, C.; Bessagnet, B.; Baldasano, J.M.; Colette, A.; Thunis, P.; Karam, D.; Fagerli, H.; Graff, A.; et al. Performance of European Chemistry Transport Models as Function of Horizontal Resolution. Atmos. Environ. 2015, 112, 90–105. [Google Scholar] [CrossRef]



| Source Set | Corresponding SNAP Categories |
|---|---|
| Heating | 2—Non-industrial combustion |
| Road traffic | 7—Road transport |
| Agriculture | 10—Agriculture 8.6—Other moving sources and machinery—Agriculture |
| Rest | 1—Energy production and fuel transformation 3—Combustion in industry 4—Production processes 5—Extraction and distribution of fuels 6—Use of solvents 8—Other moving sources and machinery (excluding agriculture) 9—Treatment and disposal of waste (other sources) 11—Natural sources |
| Fractional bias (FB) | |
| Correlation (R) | |
| Normalized mean square error (NMSE) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Calori, G.; Briganti, G.; Uboldi, F.; Pepe, N.; D’Elia, I.; Mircea, M.; Marras, G.F.; Piersanti, A. Implementation of an On-Line Reactive Source Apportionment (ORSA) Algorithm in the FARM Chemical-Transport Model and Application over Multiple Domains in Italy. Atmosphere 2024, 15, 191. https://doi.org/10.3390/atmos15020191
Calori G, Briganti G, Uboldi F, Pepe N, D’Elia I, Mircea M, Marras GF, Piersanti A. Implementation of an On-Line Reactive Source Apportionment (ORSA) Algorithm in the FARM Chemical-Transport Model and Application over Multiple Domains in Italy. Atmosphere. 2024; 15(2):191. https://doi.org/10.3390/atmos15020191
Chicago/Turabian StyleCalori, Giuseppe, Gino Briganti, Francesco Uboldi, Nicola Pepe, Ilaria D’Elia, Mihaela Mircea, Gian Franco Marras, and Antonio Piersanti. 2024. "Implementation of an On-Line Reactive Source Apportionment (ORSA) Algorithm in the FARM Chemical-Transport Model and Application over Multiple Domains in Italy" Atmosphere 15, no. 2: 191. https://doi.org/10.3390/atmos15020191
APA StyleCalori, G., Briganti, G., Uboldi, F., Pepe, N., D’Elia, I., Mircea, M., Marras, G. F., & Piersanti, A. (2024). Implementation of an On-Line Reactive Source Apportionment (ORSA) Algorithm in the FARM Chemical-Transport Model and Application over Multiple Domains in Italy. Atmosphere, 15(2), 191. https://doi.org/10.3390/atmos15020191








