Assessing Nowcast Models in the Central Mexico Region Using Radar and GOES-16 Satellite Data
Abstract
1. Introduction
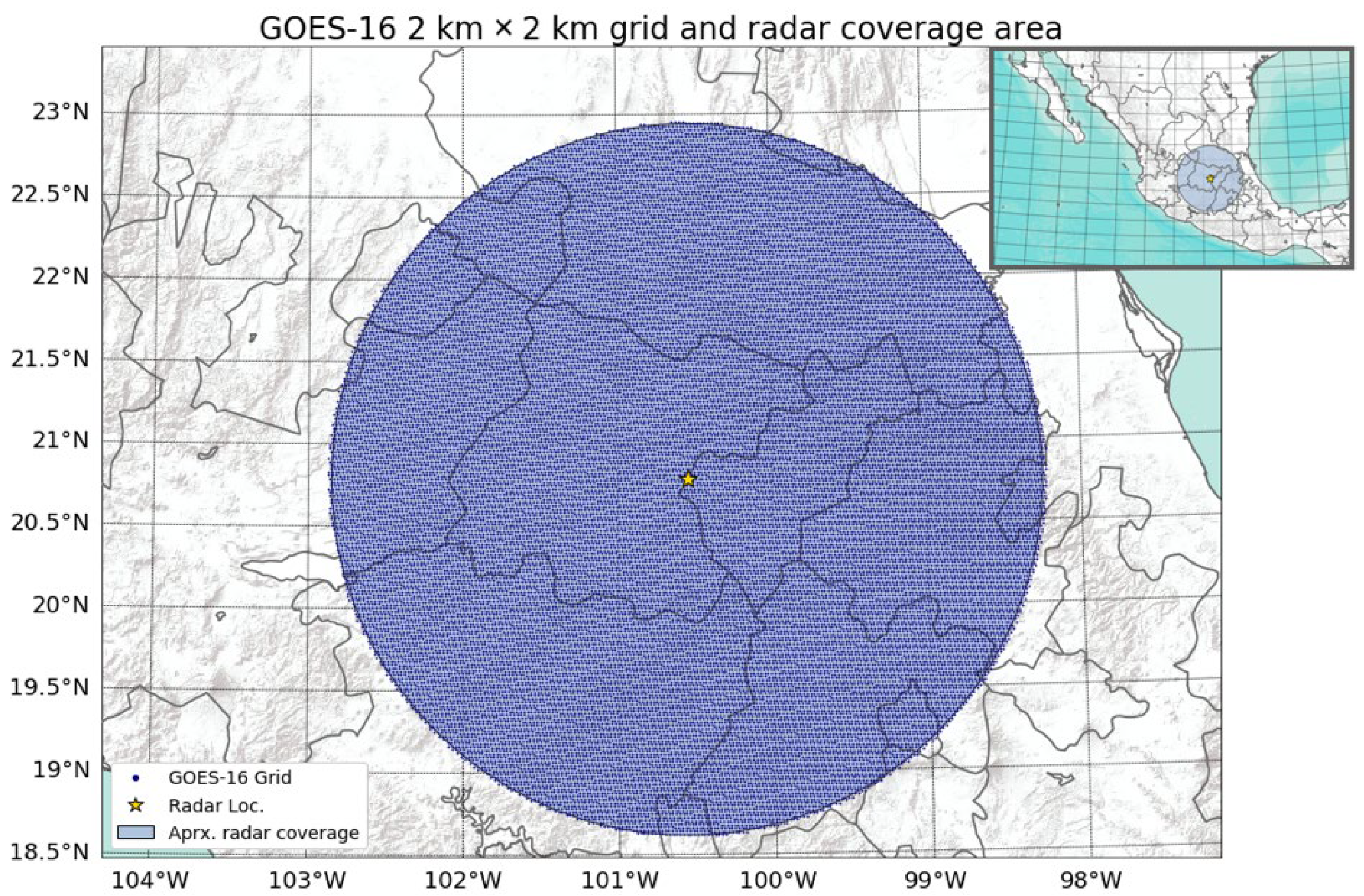
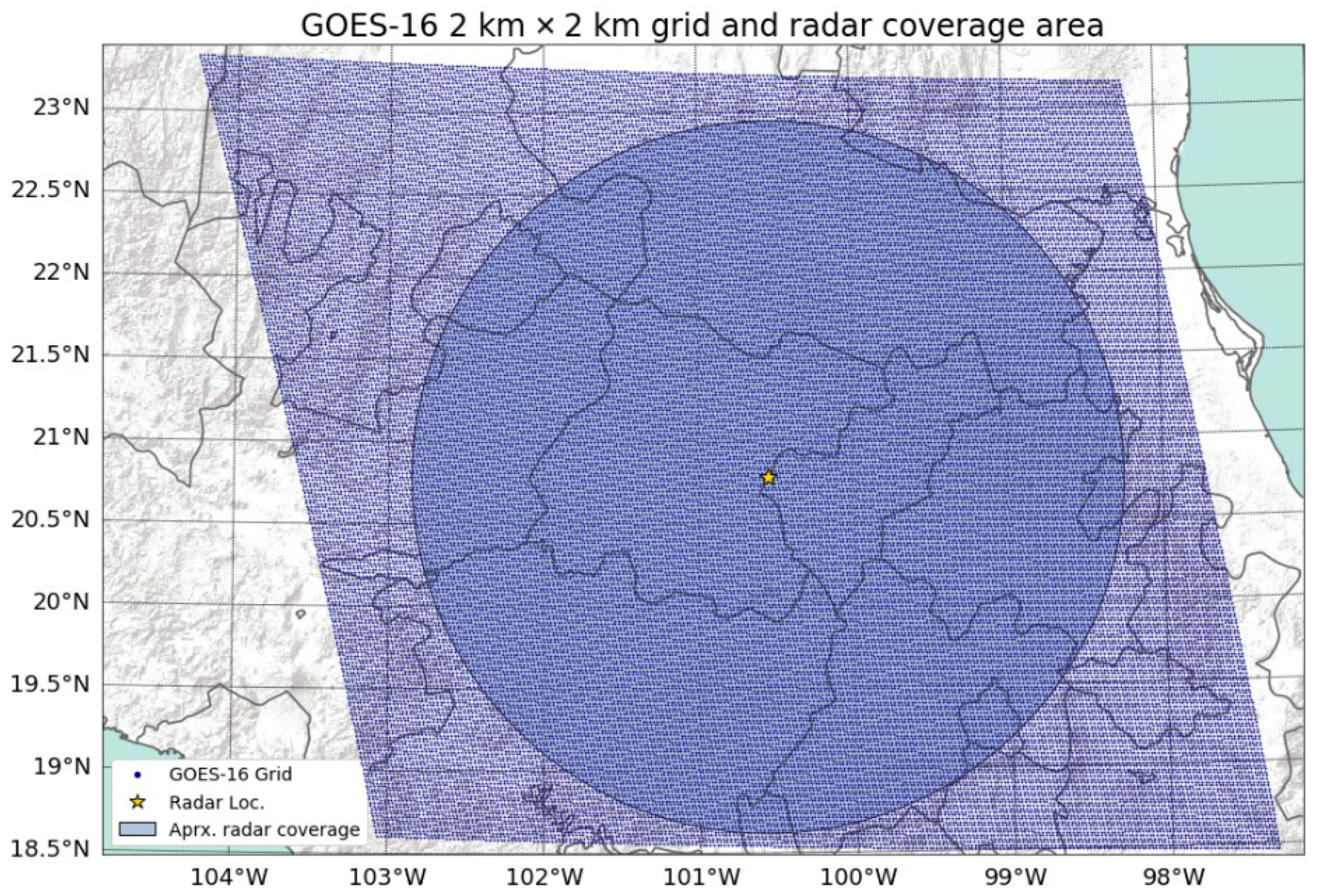
2. Materials and Methods
3. Results
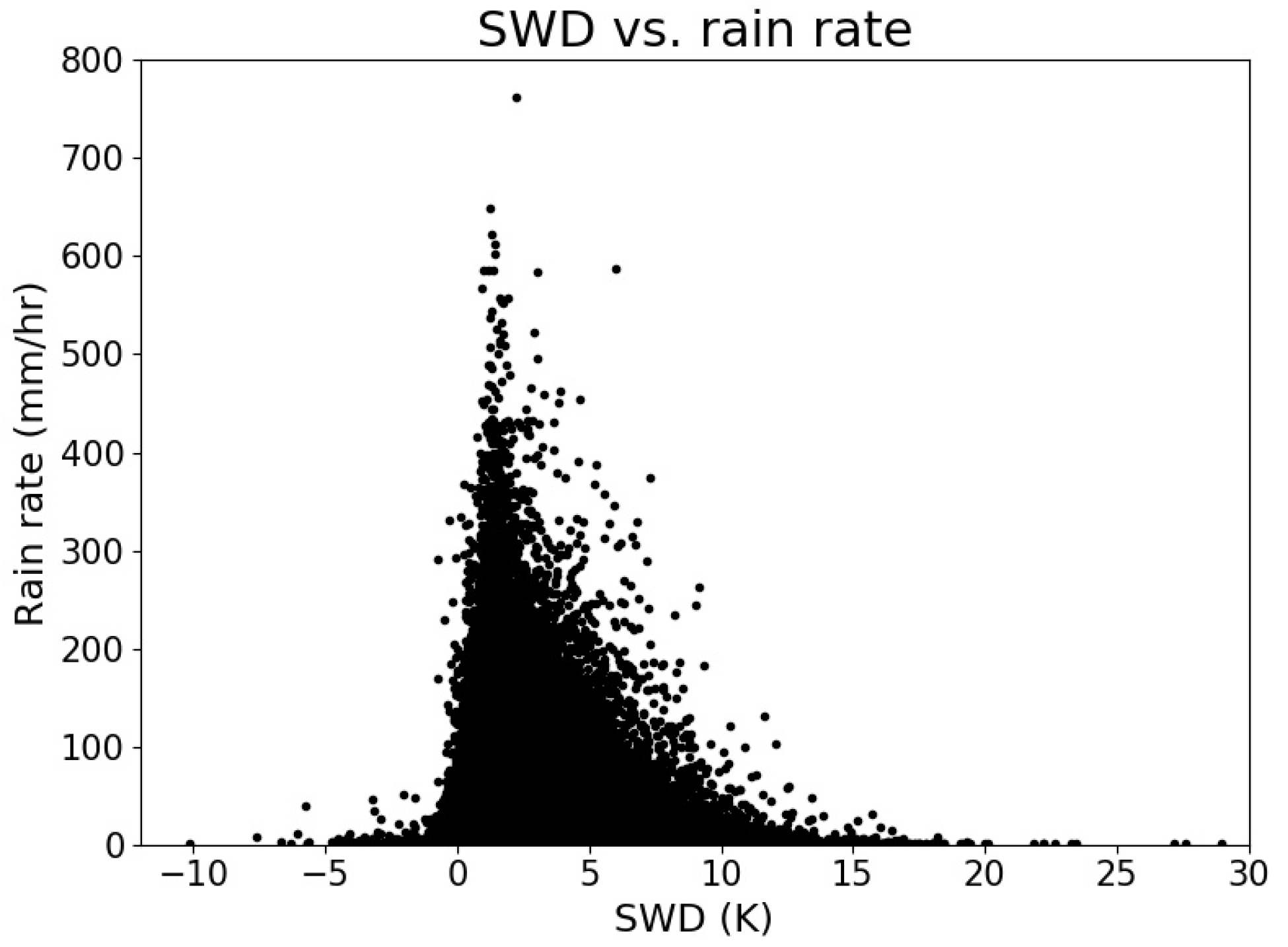
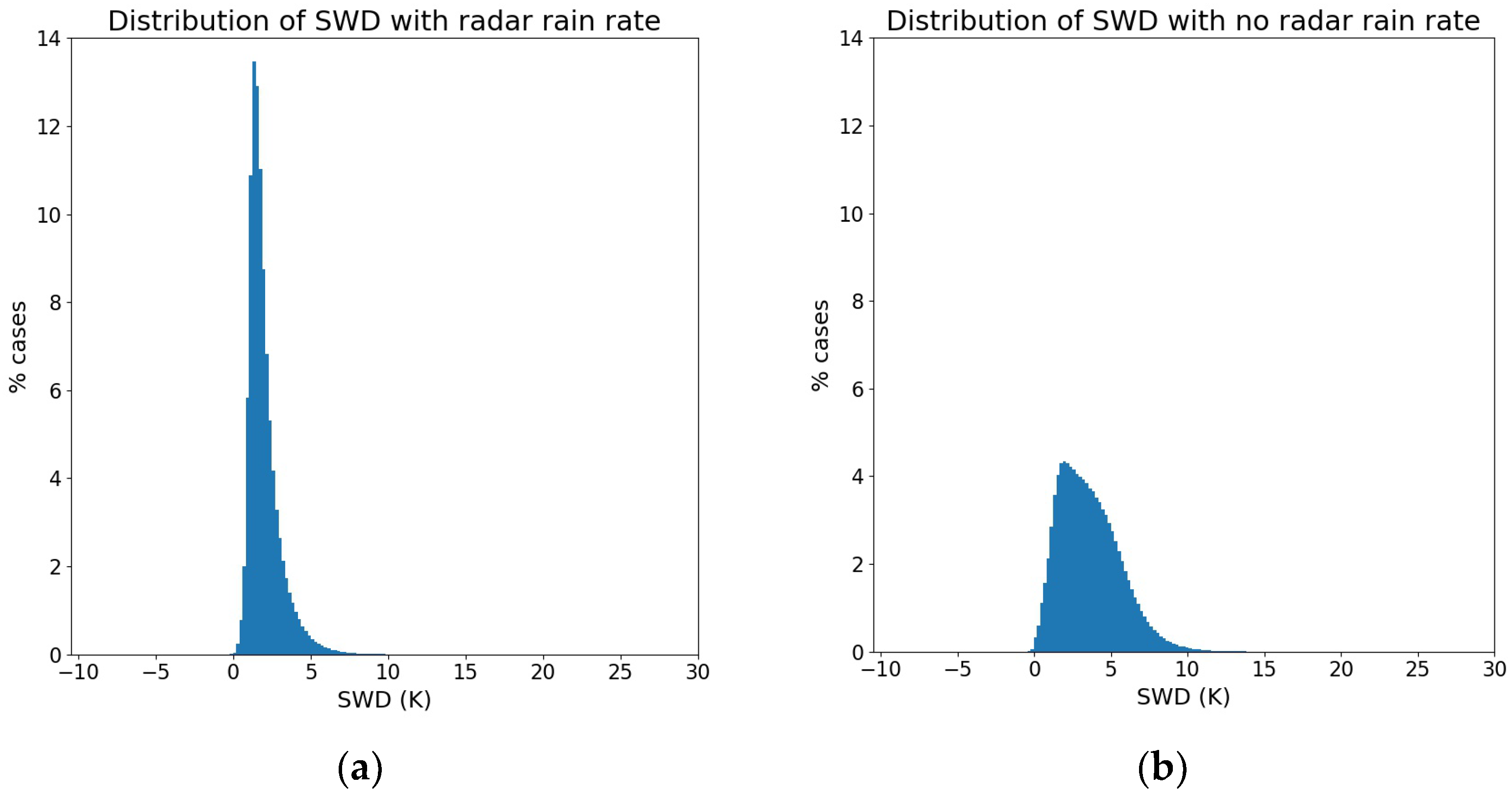
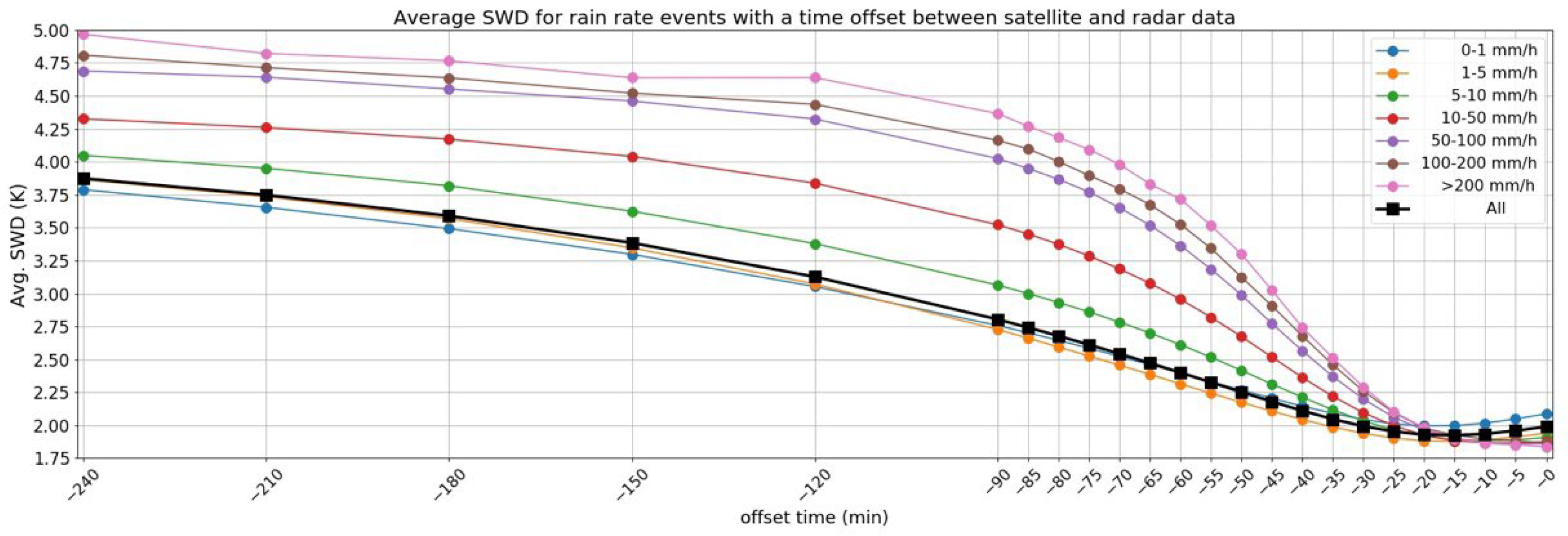
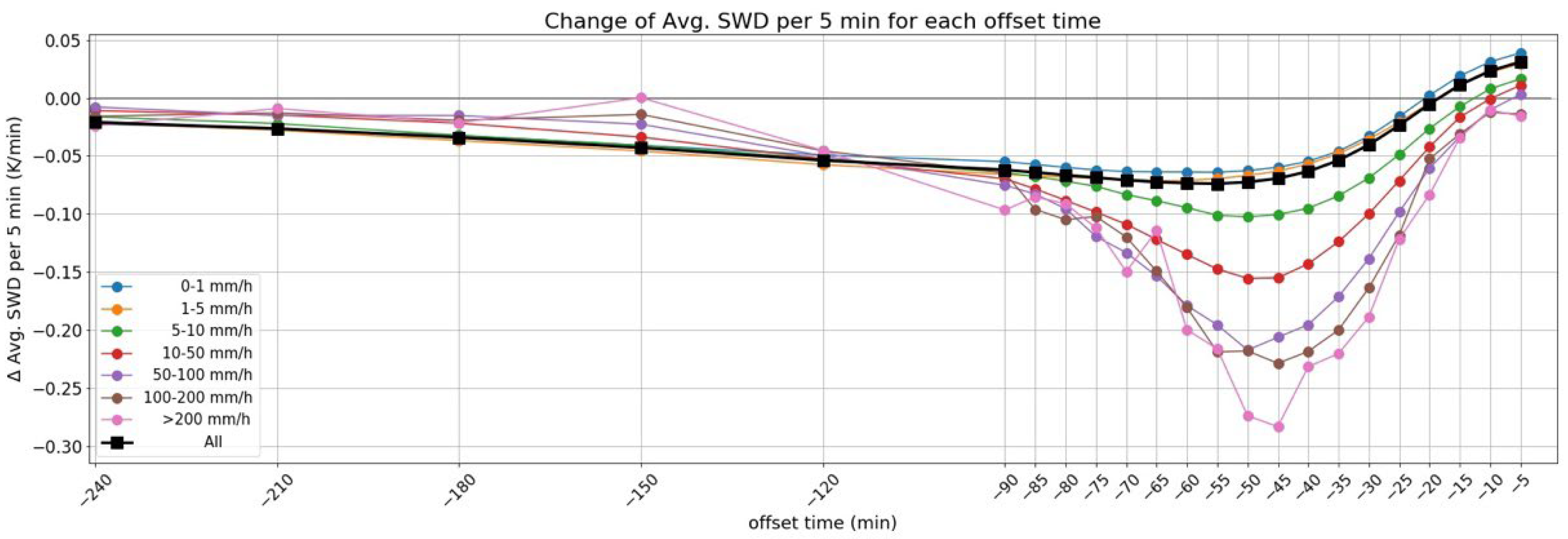
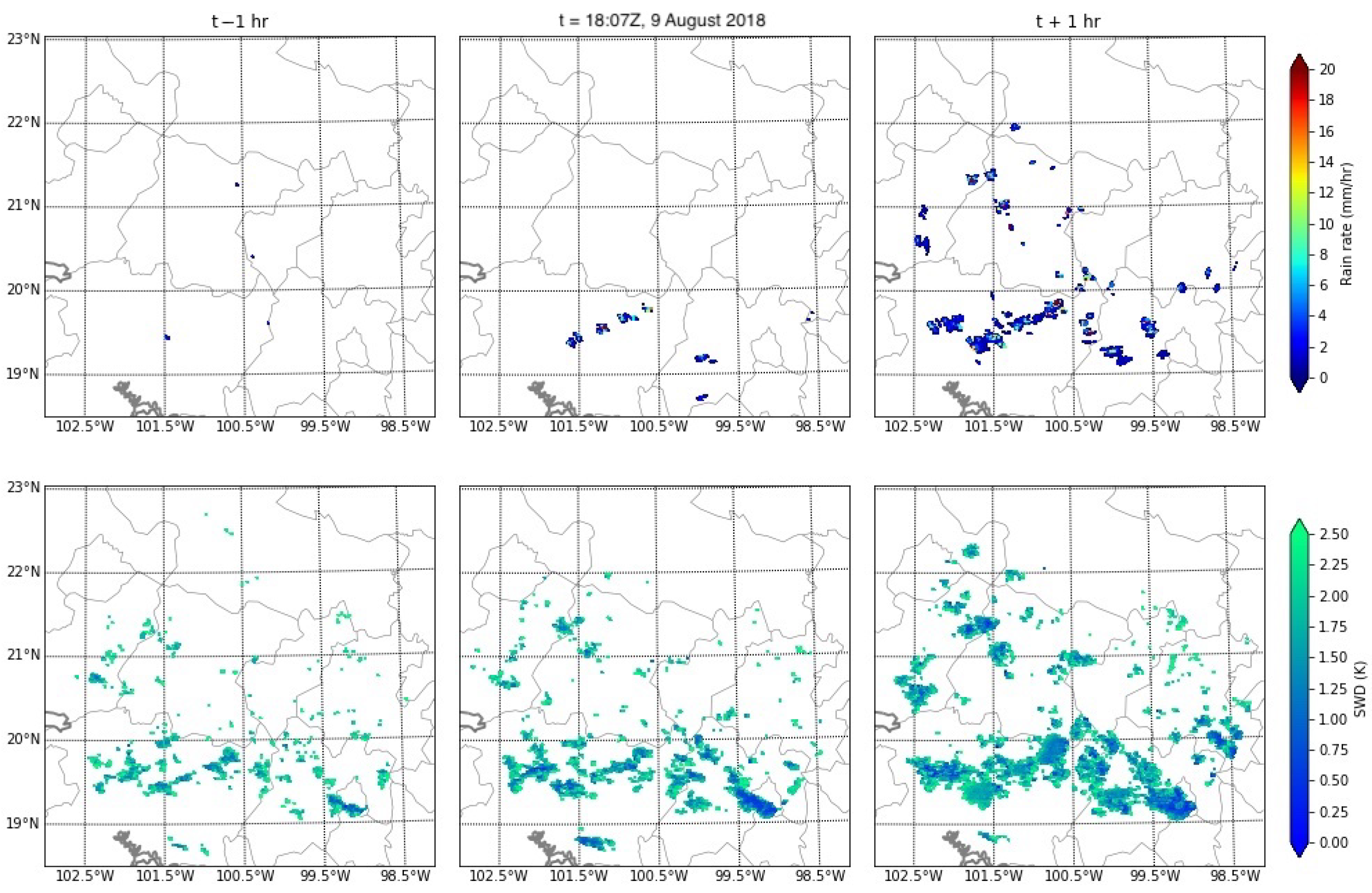
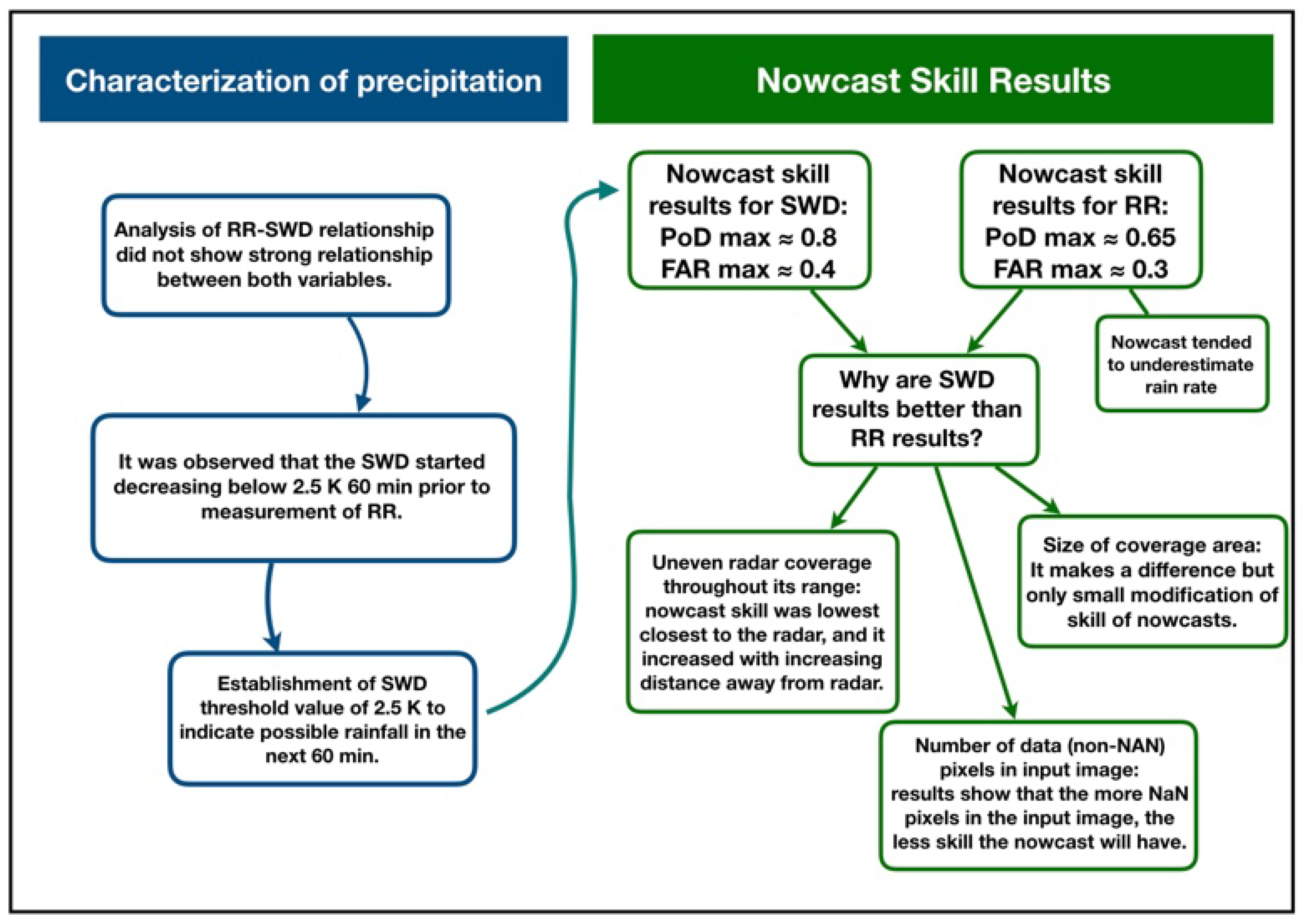
3.1. SWD Relationship with Radar Rain Rate
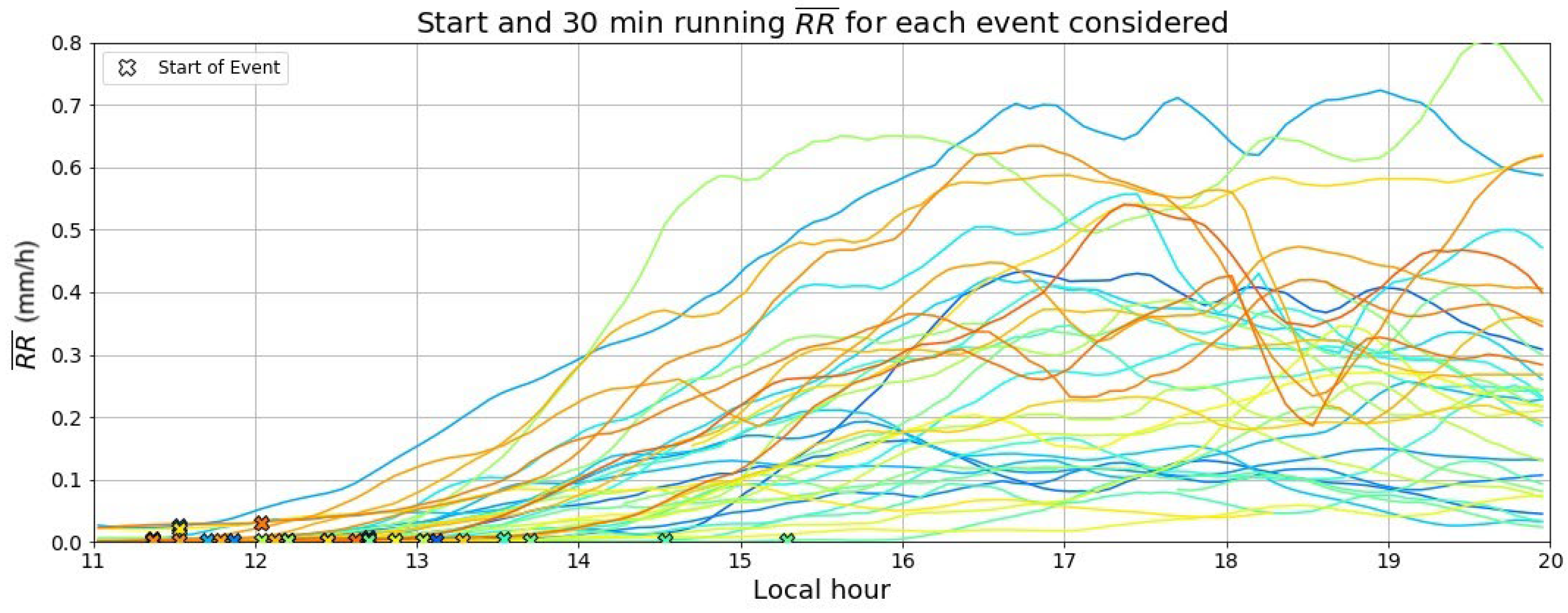
Diurnal Cycle
3.2. Results of the Nowcast Model Evaluation
3.2.1. Why SWD?
3.2.2. Setup SWD and Event Selection
3.2.3. Evaluation of Nowcast Models Using SWD Data
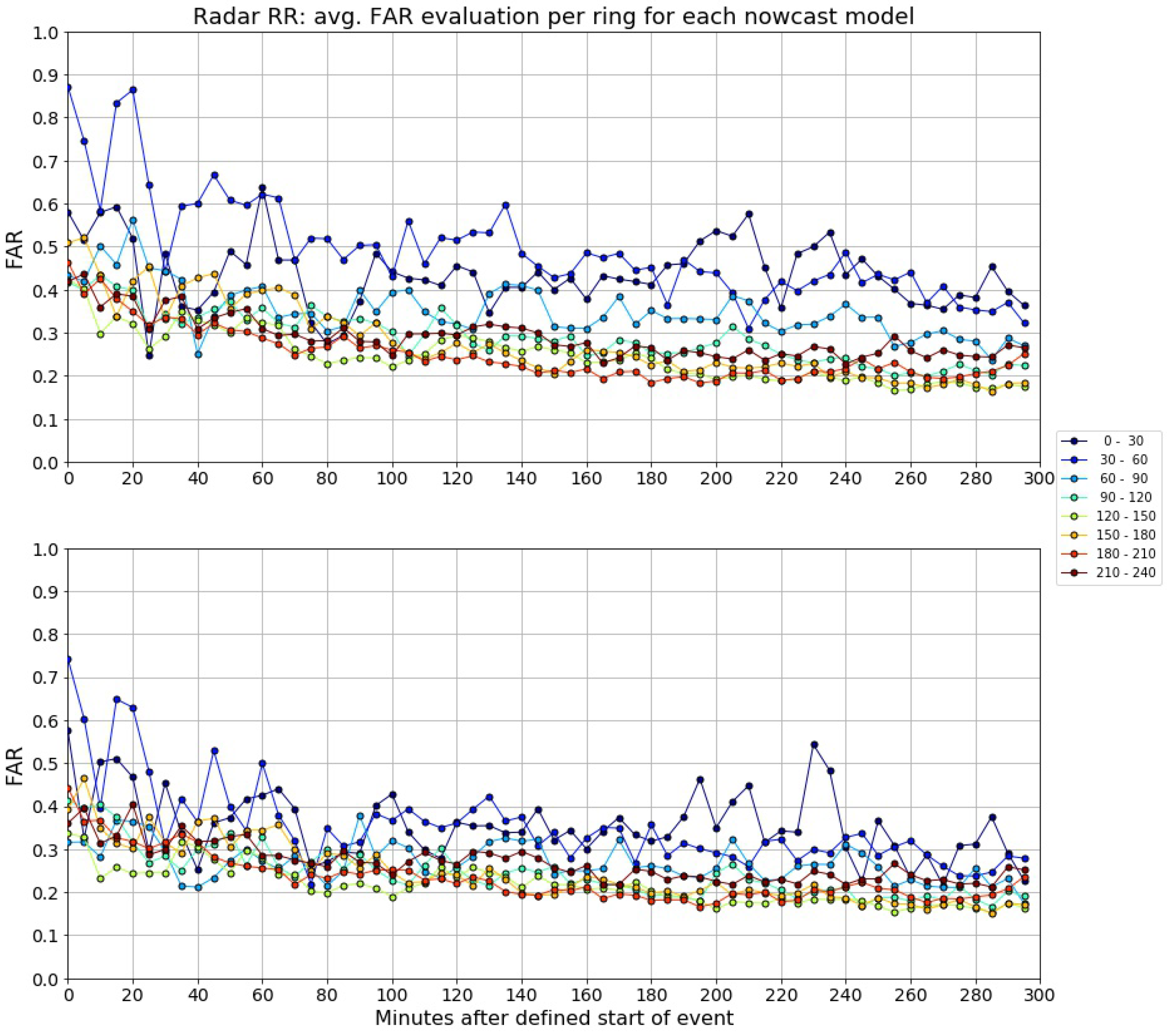
3.2.4. Evaluation of Nowcast Models Using Radar Data
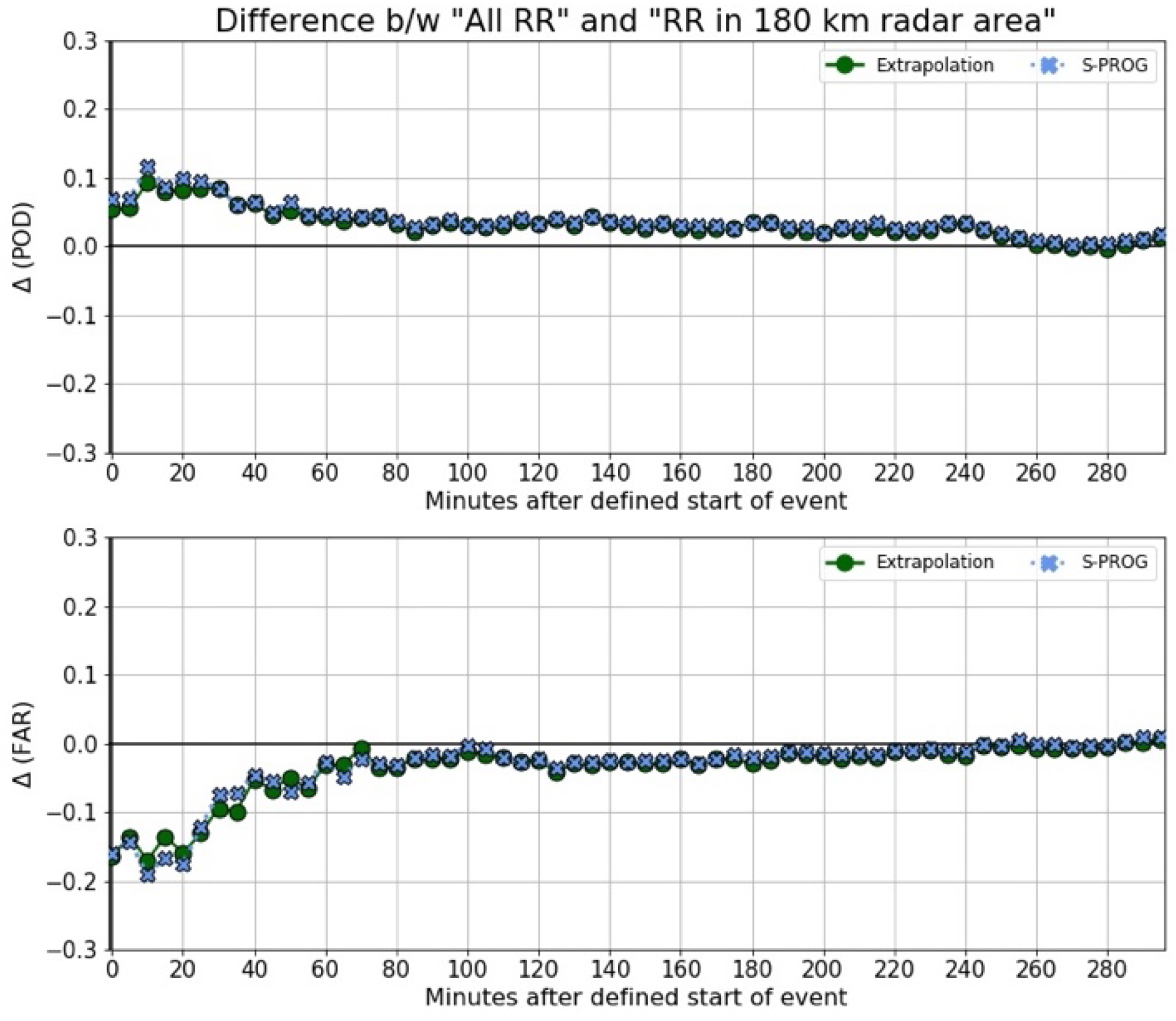
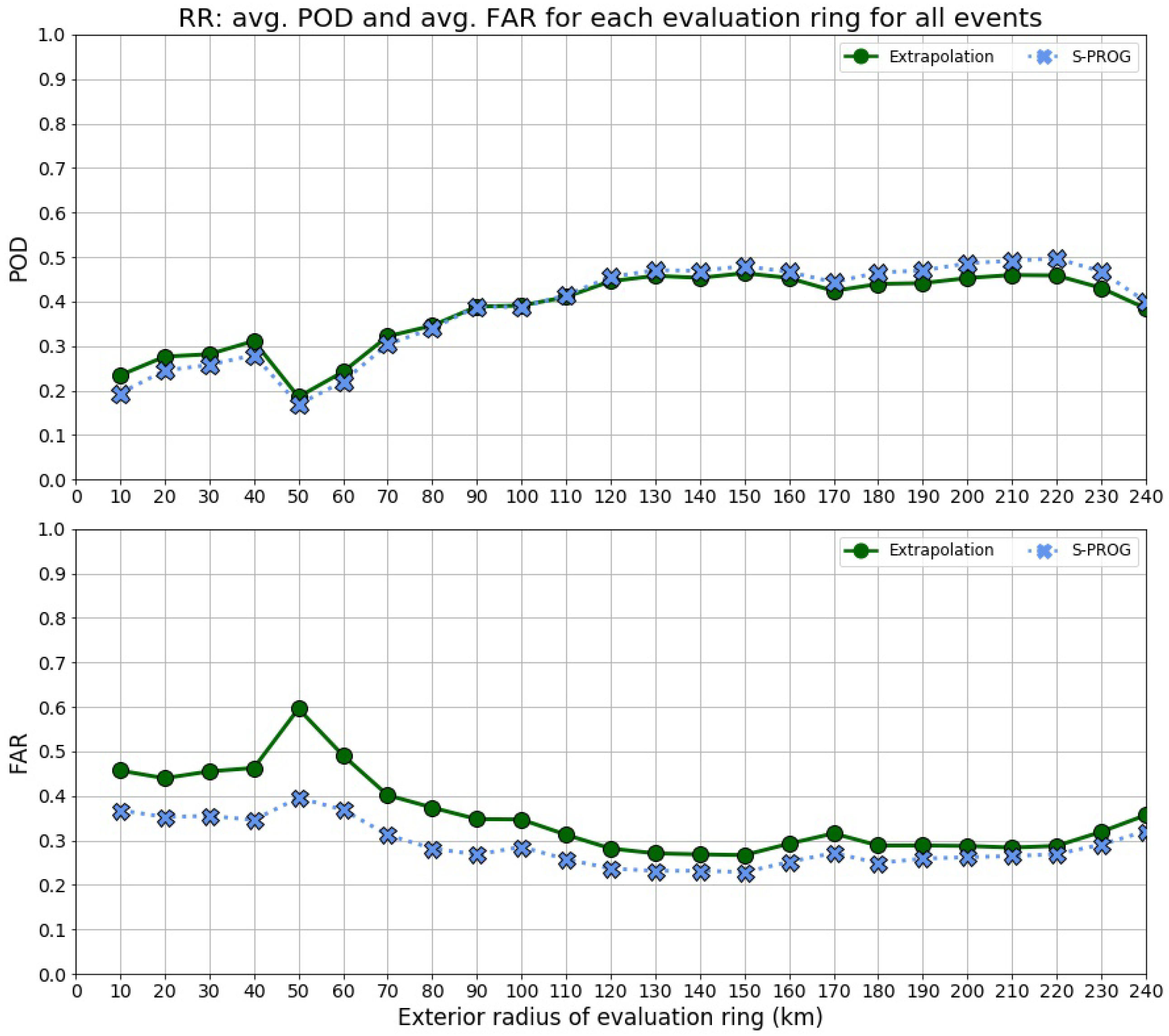
3.2.5. Evaluation of Nowcast Models with Variation in Coverage Area
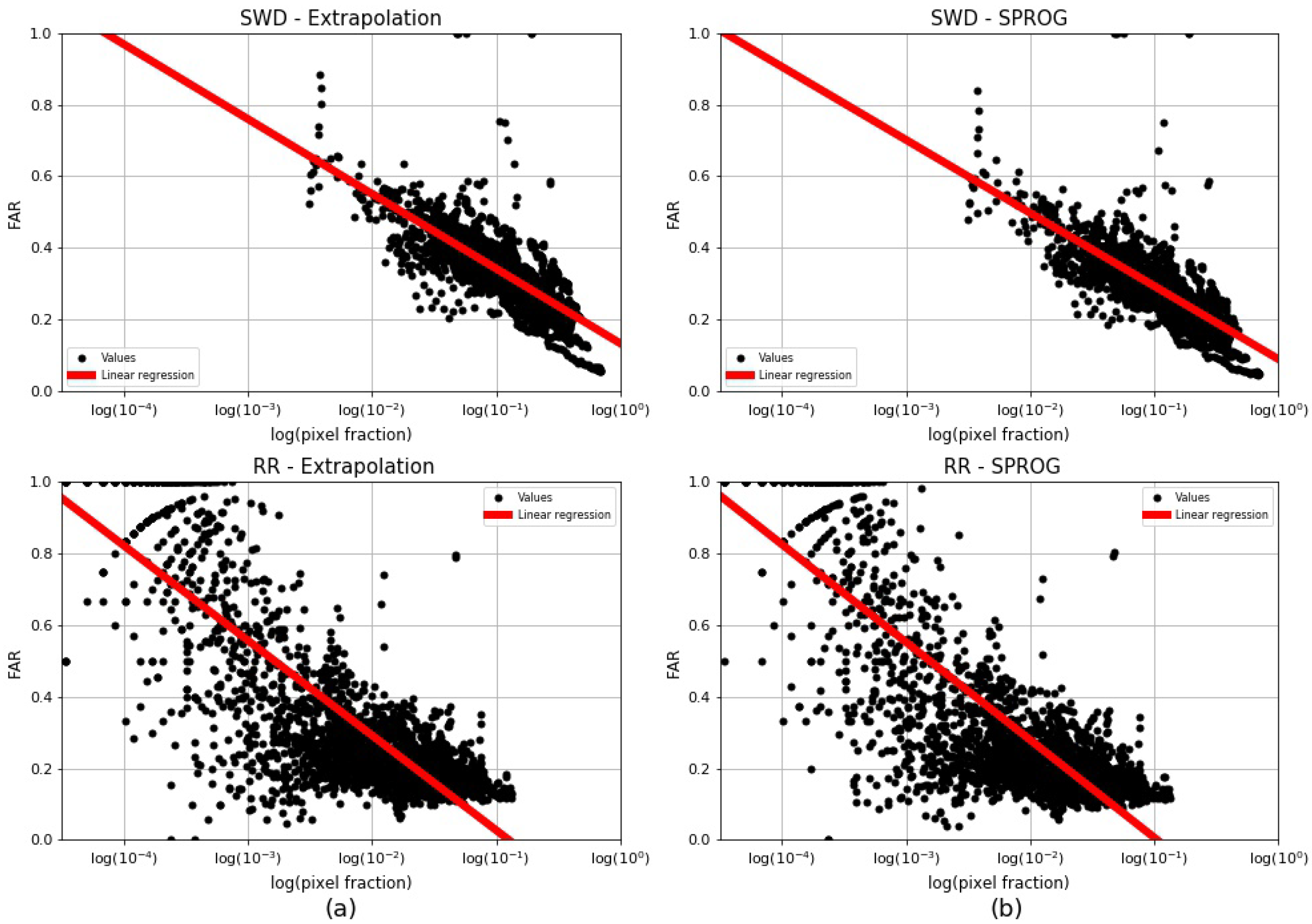
3.2.6. Real-Data Pixels and Statistics Results Relationship
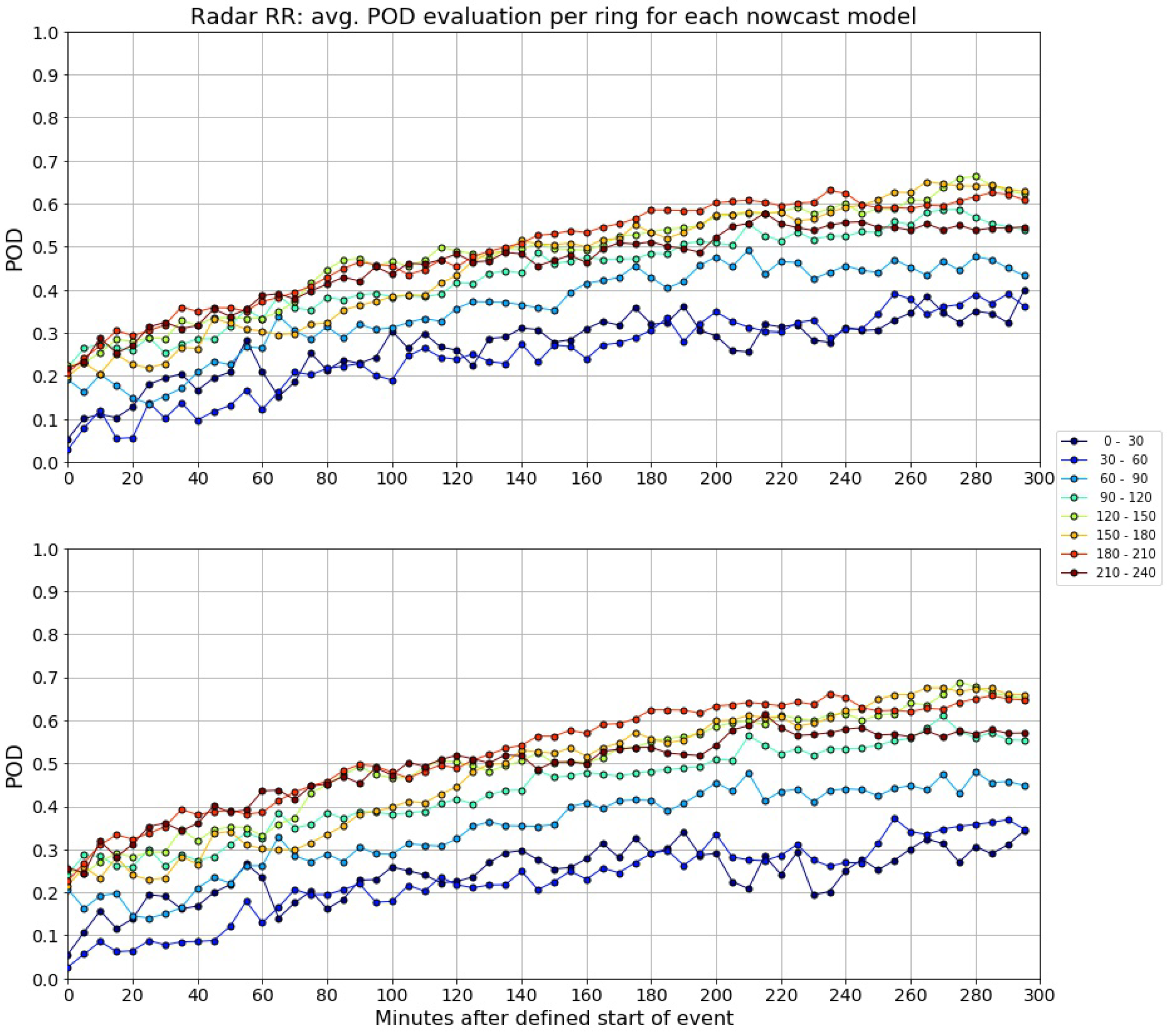
3.2.7. Deeper Evaluation of Nowcast Models with Radar Data
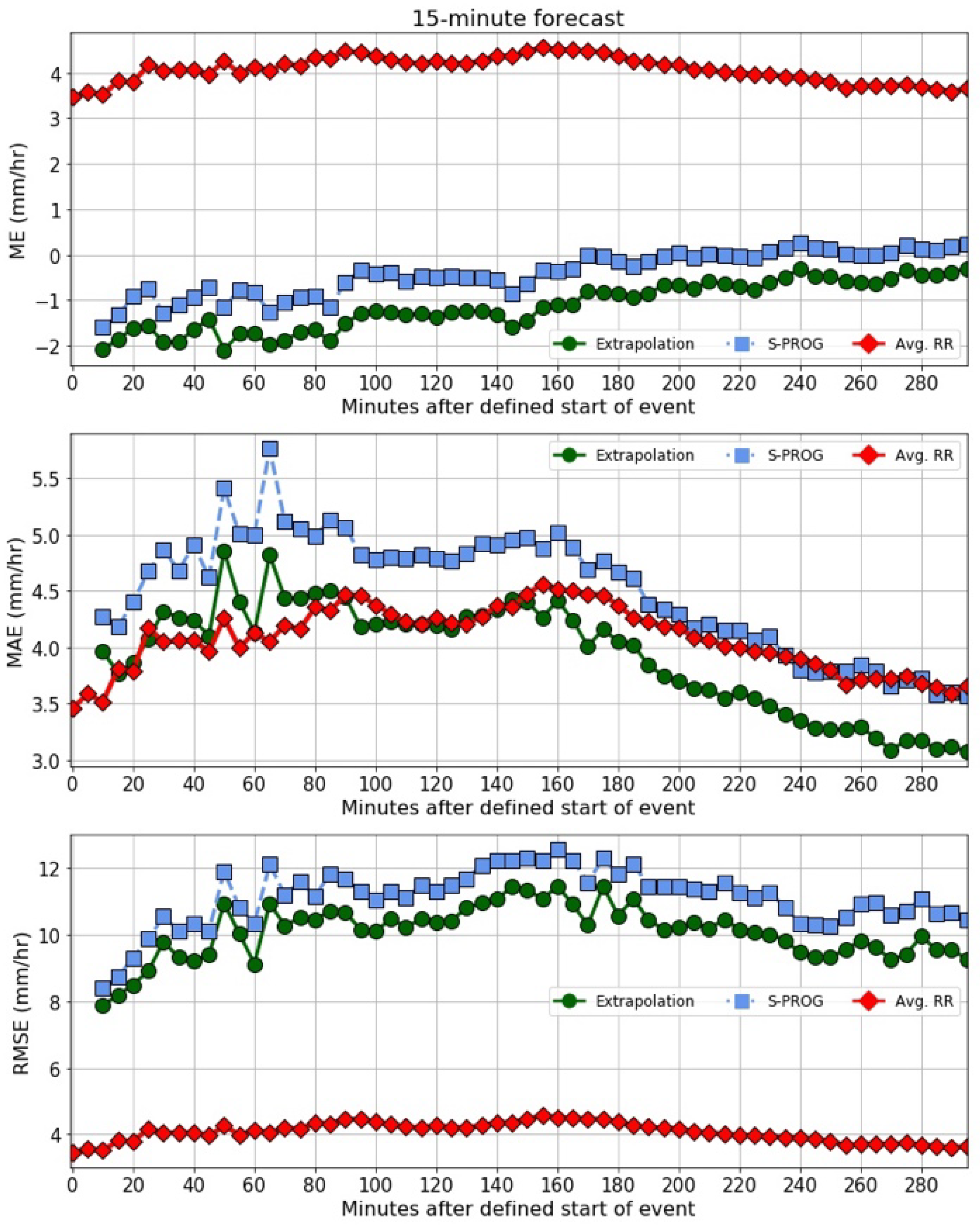
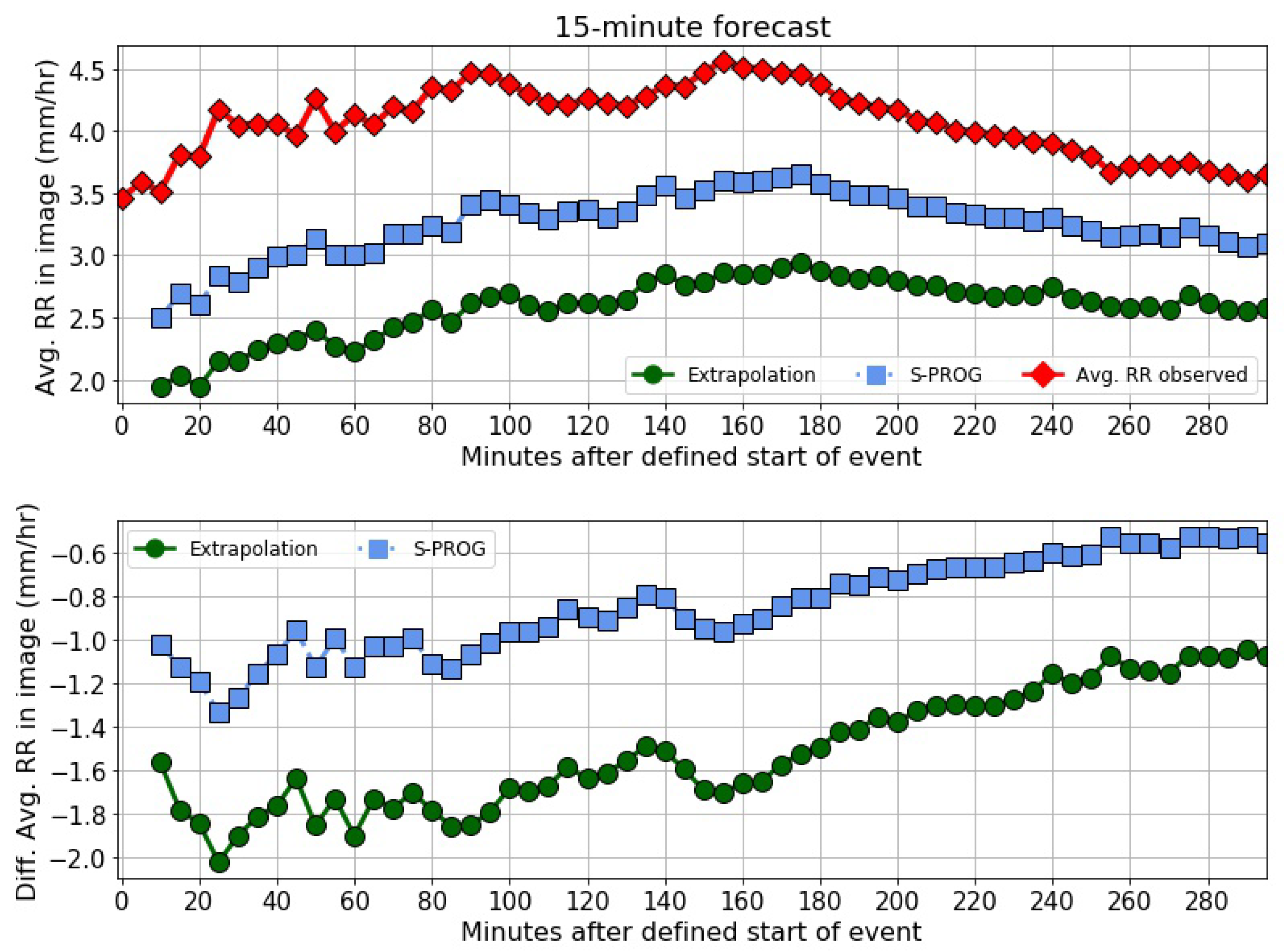
3.2.8. Evaluation of the Intensity of Rain Rate Forecast by the Nowcast Models
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Seed, A.W. A dynamic and spatial scaling approach to advection forecasting. J. Appl. Meteorol 2003, 42, 381–388. [Google Scholar] [CrossRef]
- Hering, A.M.; Morel, C.; Galli, G.; Ambrosetti, P.; Boscacci, M. Nowcasting thunderstorms in the alpine region using a radar based adaptive thresholding scheme. In Proceedings of the Third ERAD together with the COST 717 Final Seminar, Visby, Island of Gotland, Sweden, 6–10 September 2004; pp. 206–211. [Google Scholar]
- Bowler, N.E.; Pierce, C.E.; Seed, A.W. STEPS: A probabilistic precipitation forecasting scheme which merges an extrapolation nowcast with downscaled NWP. Q. J. R. Meteorol. Soc. 2006, 132, 2127–2155. [Google Scholar] [CrossRef]
- Ruzanski, E.; Chandrasekar, V.; Wang, Y. The CASA nowcasting system. J. Atmos. Ocean. Technol. 2011, 28, 640–655. [Google Scholar] [CrossRef]
- Mandapaka, P.V.; Germann, U.; Panziera, L.; Hering, A. Can Lagrangian extrapolation of radar fields be used for precipitation nowcasting over complex alpine orography? Weather Forecast. 2012, 27, 28–49. [Google Scholar] [CrossRef]
- James, P.M.; Reichert, B.K.; Heizenreder, D. NowCastMIX: Automatic integrated warnings for severe convection on Nowcasting time scales at the German Weather Service. Weather Forecast. 2018, 33, 1413–1433. [Google Scholar] [CrossRef]
- Foresti, L.; Sideris, I.V.; Nerini, D.; Beusch, L.; Germann, U. Using a 10-year radar archive for nowcasting precipitation growth and decay: A probabilistic machine learning approach. Weather Forecast. 2019, 34, 1547–1569. [Google Scholar] [CrossRef]
- Pulkkinen, S.; Chandrasekar, V.; von Lerber, A.; Harri, A.-M. Nowcasting of convective rainfall using volumetric radar observations. IEEE Trans. Geosci. Remote Sens. 2020, 58, 7845–7859. [Google Scholar] [CrossRef]
- Pulkkinen, S.; Nerini, D.; Perez Hortal, A.; Velasco-Forero, C.; Germann, U.; Seed, A.; Foresti, L. pySTEPS: An open-source Python library for probabilistic precipitation nowcasting (v1.0). Geosci. Model Dev. 2019, 12, 4185–4219. [Google Scholar] [CrossRef]
- Pysteps Developers. Pysteps References, Release 1.4.1. 2021. Available online: https://pysteps.readthedocs.io/_/downloads/en/latest/pdf/ (accessed on 28 January 2021).
- Cuomo, J.; Chandrasekar, V. Use of Deep Learning for Weather Radar Nowcasting. J. Atmos. Ocean. Technol. 2021, 38, 1641–1656. [Google Scholar] [CrossRef]
- Niu, D.; Huang, J.; Zang, Z.; Xu, L.; Che, H.; Tang, Y. Two-Stage Spatiotemporal Context Refinement Network for Precipitation Nowcasting. Remote Sens. 2021, 13, 4285. [Google Scholar] [CrossRef]
- Saadi, M.; Furusho-Percot, C.; Belleflamme, A.; Trömel, S.; Kollet, S.; Reinoso-Rondinel, R. Comparison of Three Radar-Based Precipitation Nowcasts for the Extreme July 2021 Flooding Event in Germany. J. Hydrometeor. 2021, 24, 1241–1261. [Google Scholar] [CrossRef]
- Van der Kooij, E.; Schleiss, M.; Taormina, R.; Fiorenelli, F.; Lugt, D.; van Hoek, M.; Leijnse, H.; Overeem, A. Nowcasting heavy precipitation over the Netherlands using a 13-year radar archive: A machine learning approach. In Proceedings of the EGU Gen. Assem. Conf. 2021, online, 19–30 April 2021. [Google Scholar] [CrossRef]
- Han, L.; Zhang, J.; Chen, H.; Zhang, W.; Yao, S. Toward the Predictability of a Radar-Based Nowcasting System for Different Precipitation Systems. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1005705. [Google Scholar] [CrossRef]
- Cambier van Nooten, C.; Schreurs, K.; Wijnands, J.S.; Leijnse, H.; Schmeits, M.; Whan, K.; Shapovalova, Y. Improving precipitation nowcasting for high-intensity events using deep generative models with balanced loss and temperature data: A case study in the Netherlands. Artif. Intell. Earth Syst. 2023, in press. [Google Scholar] [CrossRef]
- Ritvanen, J.; Harnist, B.; Aldana, M.; Mäkinen, T.; Pulkkinen, S. Advection-Free Convolutional Neural Network for Convective Rainfall Nowcasting. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 1654–1667. [Google Scholar] [CrossRef]
- Imhoff, R.O.; Overeem, A.; Brauer, C.C.; Leijnse, H.; Weerts, A.H.; Uijlenhoet, R. Rainfall nowcasting using commercial microwave links. Geophys. Res. Lett. 2020, 47, e2020GL089365. [Google Scholar] [CrossRef]
- Imhoff, R.O.; De Cruz, L.; Dewettinck, W.; Brauer, C.C.; Uijlenhoet, R.; van Heeringen, K.-J.; Valesco-Forero, C.; Nerini, D.; Ginderachter, M.; Weerts, A.H. Scale-dependent blending of ensemble rainfall nowcasts and numerical weather prediction in the open-source pysteps library. Q. J. R. Meteorol. Soc. 2023, 149, 1335–1364. [Google Scholar] [CrossRef]
- Kober, K.; Tafferner, A. Tracking and nowcasting of convective cells using remote sensing data from radar and satellite. Meteorol. Z. 2009, 18, 75–84. [Google Scholar] [CrossRef]
- Siewert, C.W.; Koenig, M.; Mecikalski, J.R. Application of Meteosat second generation data towards improving the nowcasting of convective initiation. Meteorol. Appl. 2010, 17, 442–451. [Google Scholar] [CrossRef]
- Mecikalski, J.R.; Sandmael, T.H.; Murillo, E.M.; Homeyer, C.R.; Bedka, K.M.; Apke, J.M.; Jewett, C.R. A Random-Forest model to assess predictor importance and nowcast severe storms using high-resolution radar-GOES satellite-lightning observations. Mon. Weather Rev. 2021, 149, 1725–1746. [Google Scholar] [CrossRef]
- Zinner, T.; Mannstein, H.; Tafferner, A. Cb-TRAM: Tracking and monitoring severe convection from onset over rapid development to mature phase using multi-channel Meteosat-8 SEVIRI data. Meteorol. Atmos. Phys. 2008, 101, 191–210. [Google Scholar] [CrossRef]
- Mecikalski, J.R.; MacKenzie, W.M.; König, M.; Muller, S. Cloud-Top Properties of Growing Cumulus prior to Convective Initiation as Measured by Meteosat Second Generation. Part I: Infrared Fields. J. Appl. Meteorol. Climatol. 2010, 49, 521–534. [Google Scholar] [CrossRef]
- Mecikalski, J.R.; MacKenzie, W.M.; König, M.; Muller, S. Cloud-Top Properties of Growing Cumulus prior to Convective Initiation as Measured by Meteosat Second Generation. Part II: Use of Visible Reflectance. J. Appl. Meteorol. Climatol. 2010, 49, 2544–2558. [Google Scholar] [CrossRef]
- Sieglaff, J.M.; Cronce, L.M.; Feltz, W.F.; Bedka, K.M.; Pavolonis, M.J.; Heidinger, A.K. Nowcasting Convective Storm Initiation Using Satellite-Based Box Averaged Cloud-Top and Cloud-Type Trends. J. Appl. Meteorol. Climatol. 2011, 50, 110–126. [Google Scholar] [CrossRef]
- Lebedev, V.; Ivashkin, V.; Rudenko, I.; Ganshin, A.; Molchanov, A.; Ovcharenko, S.; Grokhovetskiy, R.; Bushmarinov, I.; Solomentsev, D. Precipitation Nowcasting with Satellite Imagery. In Proceedings of the 25th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, Anchorage, AK, USA, 4–8 August 2019. [Google Scholar] [CrossRef]
- Ribeiro, B.Z.; Machado, L.A.T.; Huamán, C.J.H.; Biscaro, T.S.; Freitas, E.D.; Mozer, K.W.; Goodman, S.J. An Evaluation of the GOES-16 Rapid Scan for Nowcasting in Southeastern Brazil: Analysis of a Severe Hailstorm Case. Weather Forecast. 2019, 34, 1829–1848. [Google Scholar] [CrossRef]
- Rivolta, G.; Marzano, F.S.; Coppola, E.; Verdecchia, M. Artificial neural-network technique for precipitation nowcasting from satellite imagery. Adv. Geosci. 2006, 7, 97–103. [Google Scholar] [CrossRef]
- Hill, P.G.; Stein, T.H.M.; Roberts, A.J.; Fletcher, J.K.; Marsham, J.H.; Groves, J. How skilful are Nowcasting Satellite Applications Facility products for tropical Africa? Meteorol. Appl. 2020, 27, e1966. [Google Scholar] [CrossRef]
- Kumar, A.; Islam, T.; Sekimoto, Y.; Mattmann, C.; Wilson, B. Convcast: An embedded convolutional LSTM based architecture for precipitation nowcasting using satellite data. PLoS ONE 2020, 15, e0230114. [Google Scholar] [CrossRef]
- Ehsani, M.R.; Zarei, A.; Gupta, H.V.; Barnard, K.; Lyons, E.; Behrangi, A. NowCasting-Nets: Representation Learning to Mitigate Latency Gap of Satellite Precipitation Products Using Convolutional and Recurrent Neural Networks. IEEE Trans. Geosci. Remote Sens. 2022, 60, 4706021. [Google Scholar] [CrossRef]
- Grasso, L.; Bikos, D.; Dostalek, J.; Wu, T.-C.; Hilburn, K.; Szoke, E.; Torres, J. Application of the GOES-16 Advance Baseline Imager: Morfology of a Preconvective Environment on 17 April 2019. Electron. J. Sev. Storms Meteor. 2020, 15, 1–24. [Google Scholar] [CrossRef]
- Lindsey, D.T.; Grasso, L.; Dostalek, J.F.; Kerkmann, J. Use of the GOES-R Split-Window Difference to Diagnose Deepening Low-Level Water Vapor. J. Appl. Meteorol. 2014, 53, 2005–2016. [Google Scholar] [CrossRef][Green Version]
- Lindsey, D.T.; Bikos, D.; Grasso, L. Using GOES-16 Split Window Difference to Detect a boundary prior to cloud formation. Bull. Am. Meteorol. Soc. 2018, 99, 1541–1544. [Google Scholar] [CrossRef]
- Chesters, D.; Ucellini, L.W.; Robinson, W.D. Low-level water vapor fields from VISSR Atmospheric Sounder (VAS) ‘Split-Window’ channels. J. Appl. Meteorol. Climatol. 1983, 22, 725–743. [Google Scholar] [CrossRef]
- CIMSS, 2018 ABI Band 13 (10.3 μm)—Quick Guide. Online Leaflet. Available online: https://cimss.ssec.wisc.edu/goes/OCLOFactSheetPDFs/ABIQuickGuide_Band13.pdf (accessed on 1 April 2020).
- CIMSS, 2018 ABI Band 15 (12.3 μm)—Quick Guide. Online Leaflet. Available online: https://www.star.nesdis.noaa.gov/goes/documents/ABIQuickGuide_Band15.pdf (accessed on 1 April 2020).
- O’Hora, F.; Bech, J. Operational use of pulse compression in weather radar. In Proceedings of the 32nd Conference on Radar Meteorology of the American Meteorological Society, Alburquerque, NM, USA, 22–29 October 2005. [Google Scholar]
- Gabella, M.; Notarpietro, R. Ground clutter characterization and elimination in mountainous terrain. In Proceedings of the ERAD, Delft, The Netherlands, 19 November 2002; pp. 305–311. [Google Scholar]
- Heistermann, M.; Jacobi, M.; Pfaff, T. Technical Note: An open-source library for processing weather radar data (wradlib). Hydrol. Earth Syst. Sci. 2013, 17, 863–871. [Google Scholar] [CrossRef]
- Esri. “World_Terrain_Base” [basemap]. Scale: 1:1m. “World Terrain Base”. 2020. Available online: https://www.arcgis.com/home/item.html?id=c61ad8ab017d49e1a82f580ee1298931 (accessed on 30 May 2022).
- Jauregui, E.; Romales, E. Urban Effects on convective precipitation in Mexico City. Atmos. Environ. 1996, 30, 3383–3389. [Google Scholar] [CrossRef]
- Magaña, V.; Perez, J.; Mendez, M. Diagnosis and prognosis of extreme precipitation events in the Mexico City Basin. Geofis. Int. 2003, 41, 247–259. [Google Scholar] [CrossRef]
- Ochoa, A.C.; Quintanar, A.I.; Raga, G.B.; Baumgardner, D. Changes in intense precipitation events in Mexico City. J. Hydrometeorol. 2015, 16, 1804–1820. [Google Scholar] [CrossRef]
- Burton, R.R.; Blyth, A.M.; Cui, Z.; Groves, J.; Lamptey, B.L.; Fletcher, J.K.; Marsham, J.H.; Parker, D.J.; Roberts, A. Satellite-Based Nowcasting of West African Mesoscale Storms Has Skill at up to 4-h Lead Time. Weather Forecast. 2022, 37, 445–455. [Google Scholar] [CrossRef]

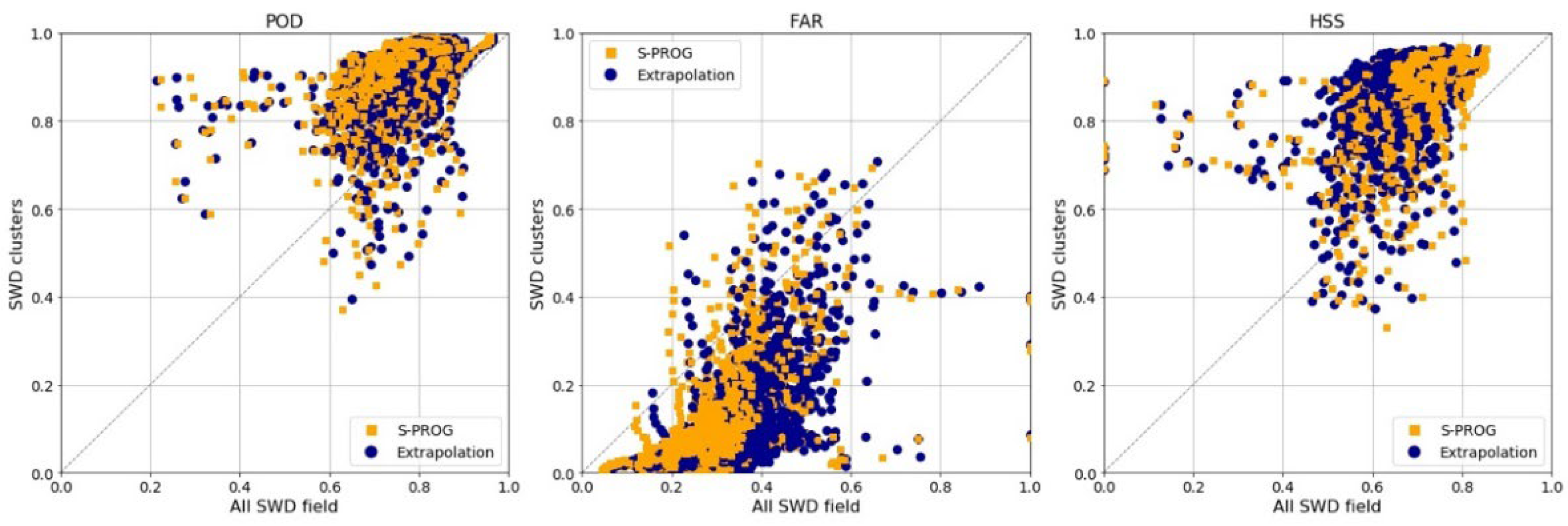


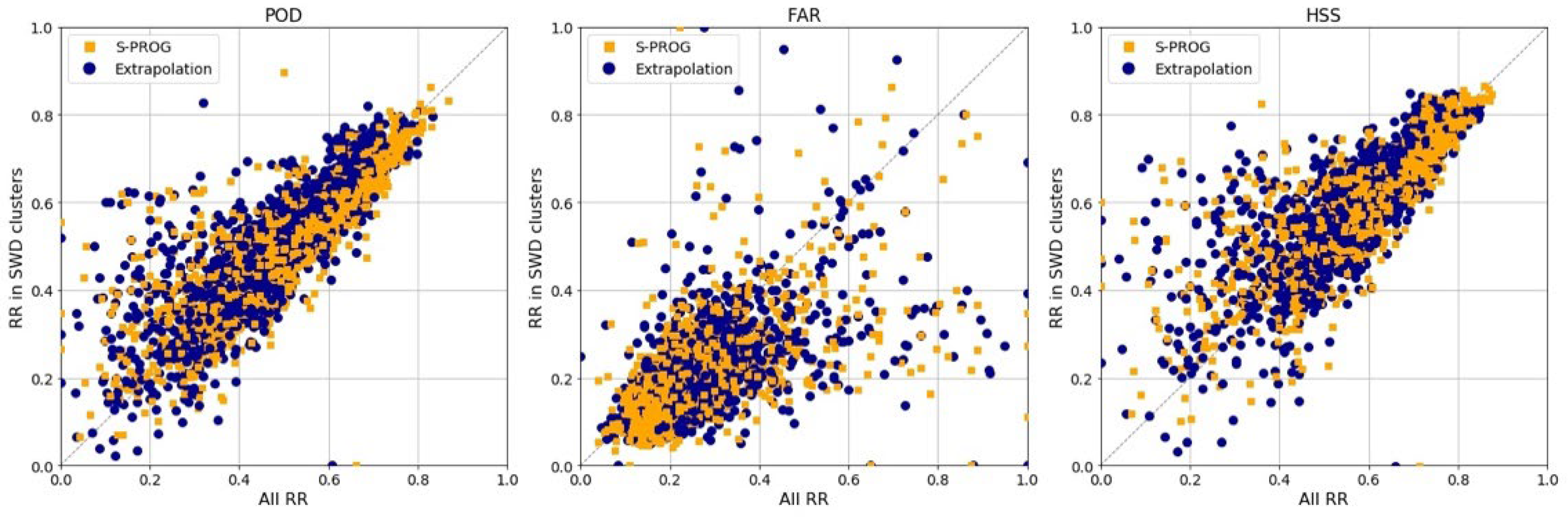
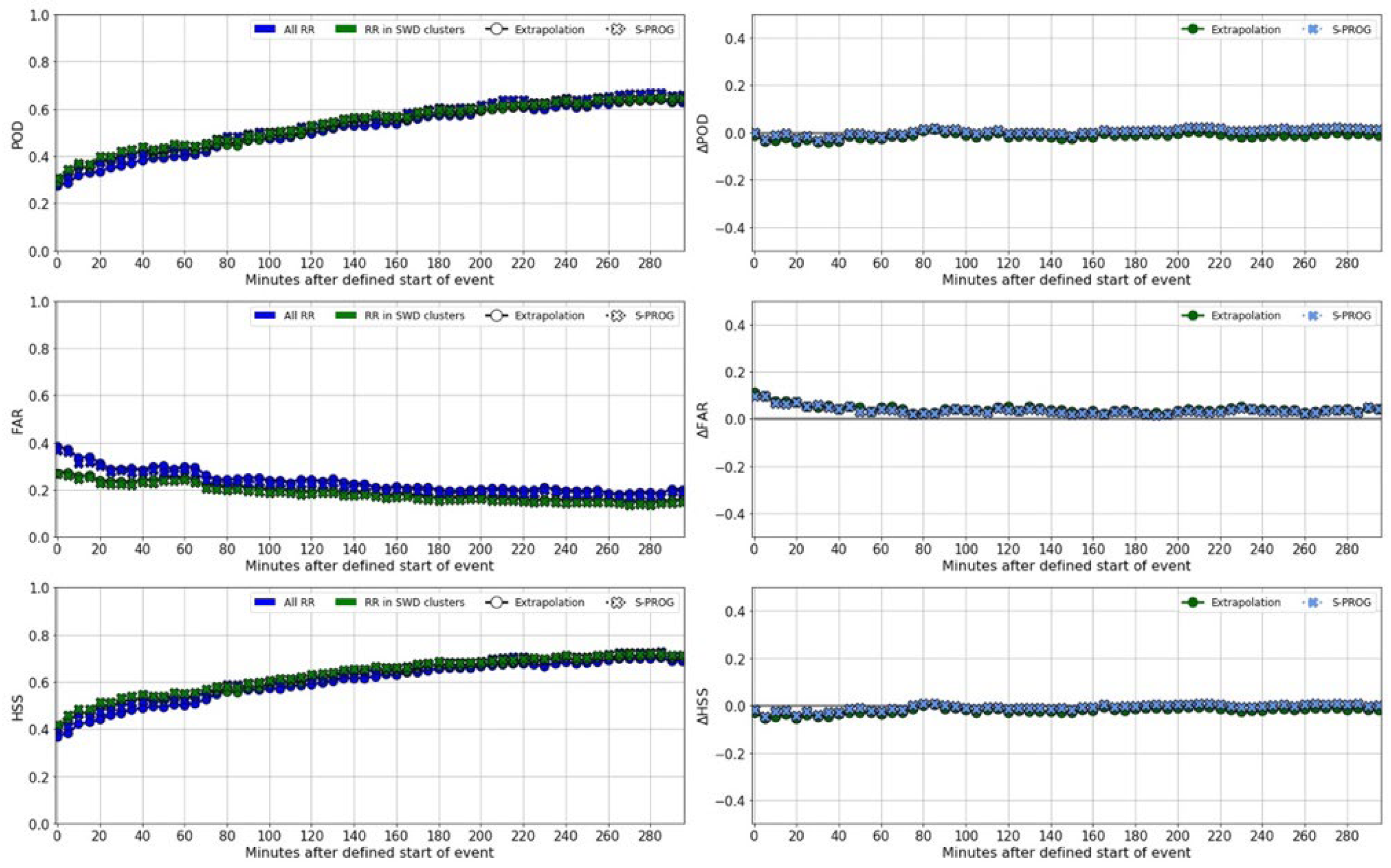
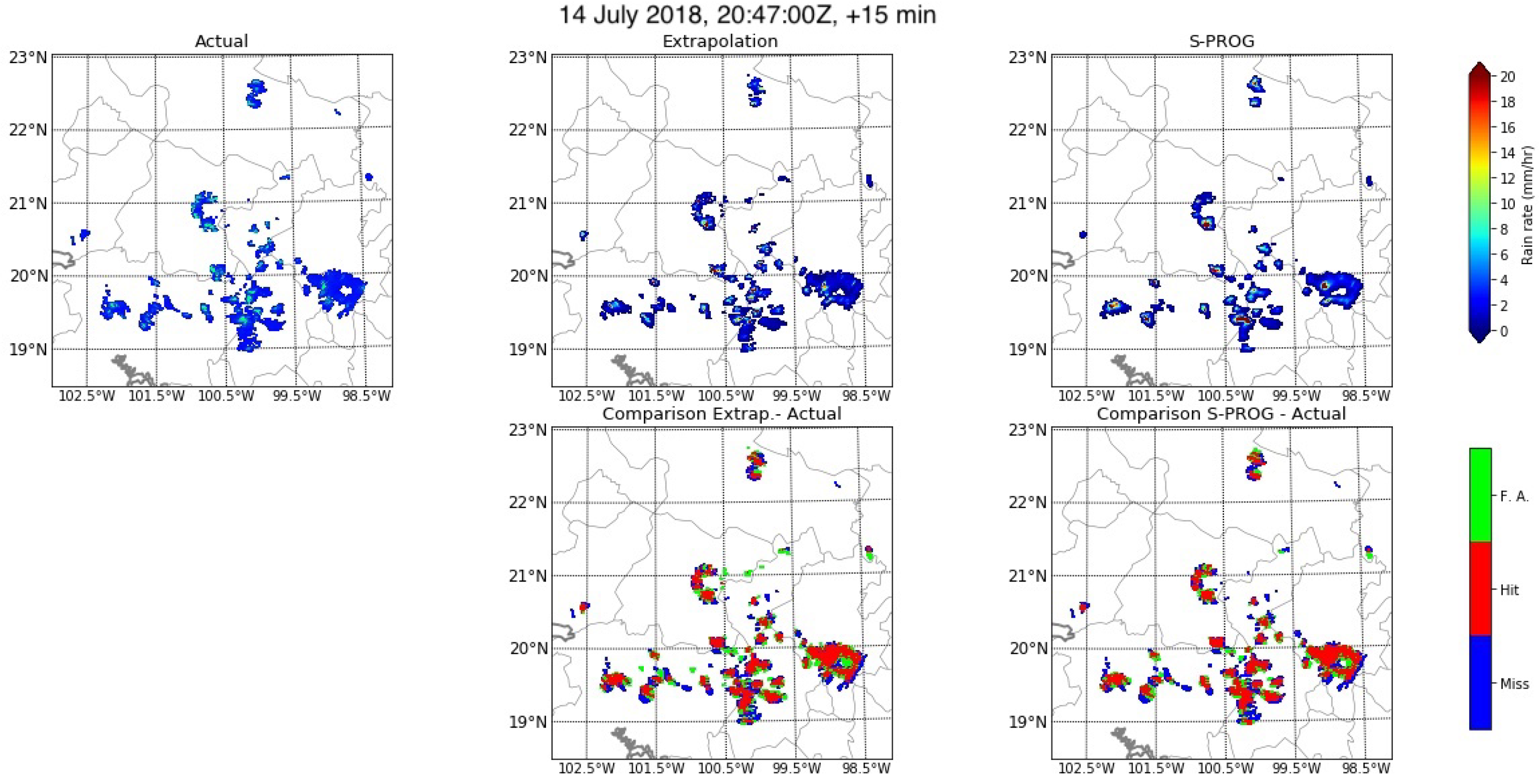

| Statistic | Model | Pearson’s R | Spearman’s Rank | ||
|---|---|---|---|---|---|
| SWD | RR | SWD | RR | ||
| PoD * | Extrap | 0.77 | 0.91 | 0.83 | 0.88 |
| S-PROG | 0.78 | 0.91 | 0.84 | 0.87 | |
| FAR * | Extrap | −0.79 | −0.84 | −0.83 | −0.73 |
| S-PROG | −0.79 | −0.84 | −0.84 | −0.73 | |
| HSS * | Extrap | 0.55 | 0.91 | 0.60 | 0.87 |
| S-PROG | 0.60 | 0.91 | 0.66 | 0.87 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Islas-Flores, D.; Magaldi, A. Assessing Nowcast Models in the Central Mexico Region Using Radar and GOES-16 Satellite Data. Atmosphere 2024, 15, 152. https://doi.org/10.3390/atmos15020152
Islas-Flores D, Magaldi A. Assessing Nowcast Models in the Central Mexico Region Using Radar and GOES-16 Satellite Data. Atmosphere. 2024; 15(2):152. https://doi.org/10.3390/atmos15020152
Chicago/Turabian StyleIslas-Flores, Diana, and Adolfo Magaldi. 2024. "Assessing Nowcast Models in the Central Mexico Region Using Radar and GOES-16 Satellite Data" Atmosphere 15, no. 2: 152. https://doi.org/10.3390/atmos15020152
APA StyleIslas-Flores, D., & Magaldi, A. (2024). Assessing Nowcast Models in the Central Mexico Region Using Radar and GOES-16 Satellite Data. Atmosphere, 15(2), 152. https://doi.org/10.3390/atmos15020152








