Abstract
Numerical modeling of primary cosmic ray protons’ transport through the Earth’s atmosphere was performed for the energy spectra of solar energetic particle events (SEPs). Several events in the last three solar cycles were considered. A comparative analysis of the characteristics of coronal mass ejections and primary proton fluxes was carried out. The main results were quantitative estimates of the calculated atmospheric ionization count rate for a wide range of altitudes (from sea level up to 98 km). The difference in the influence of solar protons on the Earth’s atmosphere is considered for seven SEPs divided into three groups with similar solar sources (X-flare magnitude and coordinates) but with different characteristics of accelerated particle fluxes. The data obtained in this work are very important for future studies of radio wave propagation, atmospheric chemistry and climate change.
1. Introduction
Cosmic rays (CRs) are charged particles with a wide range of energies (up to 1021 eV). Basically, cosmic rays include protons that compose at least 90% of the total number of particles reaching the Earth. Electrons, helium nuclei and the nuclei of heavy elements with Z > 2 account for the remaining parts. Galactic cosmic rays (GCRs) have a fairly extended energy spectrum and include protons of high and very high energies, which can give rise to cascades of secondary particles of various types and play a significant role in the ionization of the middle and lower atmosphere (0–100 km). The process of ionization induced by CRs is quite well studied and has been investigated by various research groups using both experimental and numerical methods [1,2,3,4].
The differential energy spectrum of GCRs has a pronounced 11-year cycle. Its high-energy part (0.5–100 GeV) that is considered in this work practically does not change, while its low-energy part (10–500 MeV) can vary within certain limits. In this case, the maximum fluxes for the low-energy part of the spectrum are observed precisely during the solar activity minima. However, along with the impact of GCR protons on the Earth’s atmosphere, it is possible to distinguish relatively short-term solar activity phenomena—SEP (solar energetic particle) and GLE (ground level enhancement) events, which can also have a significant influence on the state of the atmosphere, e.g., [5,6,7,8].
SEPs are characterized by a fairly soft differential energy spectrum, which means that protons during such events cannot generate cascades and greatly influence the lower atmosphere (from sea level up to ~30 km). However, such phenomena are often characterized by a significant increase in particle fluxes in the energy range of 10–100 MeV, which can be expected to increase the ionization of the upper layers of the Earth’s atmosphere (from 30 km up to 100 km) and potentially affect its chemical properties at high latitudes and in polar regions. Currently, the high-latitude region is attracting a lot of attention because of alternative trade tracks. Hence, applications demonstrating the influence of SEPs on the upper atmosphere have become particularly important for navigation and radio communication in this region, e.g., [9].
GLE events occur less frequently than SEPs because many conditions must be met for them to occur (first of all, particles must accelerate to higher energies with a fairly hard energy spectrum; see [10]). However, during such events, the differential energy spectrum includes protons with energies up to 10 GeV and fluxes exceeding the GCR level by several orders of magnitude. Then, as in the case of GCRs, solar cosmic ray (SCR) protons can interact in dense layers of the Earth’s atmosphere (~30 km) with air nuclei (mainly nitrogen and oxygen), giving rise to cascades of secondary particles. Some of these particles (such as neutrons, photons and muons) have sufficient energy, as well as a long mean free path, to allow them to reach sea level. On ground-based detectors, this is observed as an increase in the count rate, which leads to the name of this phenomenon—ground-level enhancement. It can be assumed that during such events, the ionization rate increases significantly, especially at altitudes of about 10 km, which can lead to an effect on the general properties of the atmosphere, especially in the region of low geomagnetic cutoff rigidities [10].
Despite the large number of studies mentioned above, the issue of CR particles’ influence on the Earth’s atmosphere remains very important. In this work, we consider seven SEP and GLE events divided into three groups with similar solar sources (X-flare magnitude and coordinates) for the last three cycles of solar activity, but our work is not a statistical study due to its small sample. The characteristics and features of events are described in detail; a comparative analysis of the characteristics of parent X-flares and coronal mass ejections (CMEs) is carried out along with a discussion of primary proton fluxes. Then the passage of primary cosmic ray protons through the Earth’s atmosphere is modelled with our own software package—the RUSCOSMICS (Eugene Maurchev, Russia), implemented using the GEANT4 version 11.2.0 (GEometry ANd Tracking) software development kit (CERN, Meyrin, Switzerland). The influence of SCR particles on the ionization rate of the Earth’s atmosphere is assessed for different cases. Altitude profiles are provided for a wide range from 0 to 98 km. The results obtained may be useful for research in the field of the influence of cosmic radiation on the Earth’s atmosphere, radio wave propagation, atmospheric chemistry and climate change. In this work calculations are made for two points of geomagnetic cutoff rigidity (0.17 GV and 0.64 GV) corresponding to polar and high-latitude regions (e.g., Apatity and Oulu).
2. Data and Methods
For this research paper, the X-ray flare and proton enhancement database [11] was used. SCR enhancements were selected on the basis of measurements of protons with energy >10 (P10) and >100 MeV (P100) and X-ray flares were selected using GOES (Geostationary Operational Environmental Satellites) data. The data of the world network of neutron monitors (NMDB—neutron monitor database https://www.nmdb.eu/, accessed on 19 January 2024) were also analyzed. The data on CMEs were taken from CME catalog, which is generated and maintained at the CDAW Data Center by NASA and the Catholic University of America in cooperation with the Naval Research Laboratory.
The RUSCOSMICS software toolkit (https://ruscosmics.ru, accessed on 19 January 2024) was used in this work to calculate the ionization rate values [12]. Its implementation is based on the use of the GEANT4 software development toolkit, which utilizes the Monte Carlo method and provides classes for developing models to calculate the interaction of elementary particles and matter [13,14].
2.1. Geometry Implementation
The parameterization of the values for density, temperature and percentage composition of elements (nitrogen, oxygen, argon and helium) is the principal point in the model of the particles’ transport through the Earth’s atmosphere. The NRLMSISE-00 model [15] (NRLMSISE—Naval Research Laboratory Mass Spectrometer and Incoherent Scatter Radar Exosphere) is integrated into RUSCOSMICS, for the purpose of obtaining the indicated values with interannual and seasonal variability. The atmospheric model configuration was implemented as a so-called flat approximation (http://astro.vaporia.com/start/planeparallelatmosphere.html, accessed on 19 January 2024). In this case, a column of the air divided into layers is modeled, while the edge length is extremely large (1000 km) in order to exclude the particles that escape. Moreover, it allows us to approximate the conditions as close as possible to the case in which the model configuration is spherical (since the atmosphere height is 10 times less than the edge length, so particle tracks can be considered as if they were passing through a local section of spherical geometry). Additionally, optimization based on the fact that each layer should contain some fixed percentage of the mass substance from the total atmospheric mass column is performed, in order to increase the computing speed. Thus, the number of layers is reduced, while maintaining the model validity. The most efficient value of the total mass was found (5%) via experiments, e.g., [12]. In this case, the atmospheric model consists of 20 layers (i.e., instead of 1000 layers from the original NRLMSISE data, only 20 layers are formed, each of which contains 5% of the matter mass from the total mass of the atmospheric column). The program logic that performs such a calculation is based on tabular data presented in Figure 1. It is repeated N − 1 times, where N is the number of atmospheric layers. The calculation is performed by simply averaging the remaining values in the table at the N-stage. Note that the percentage composition of elements (hydrogen, helium, oxygen, nitrogen and argon) is calculated as well as density according to data that are already known. It can be described as follows: at the initial stage, the number of layers (N) is determined (under conditions of 5% of the column total mass in one layer):
N = 100/5 = 20
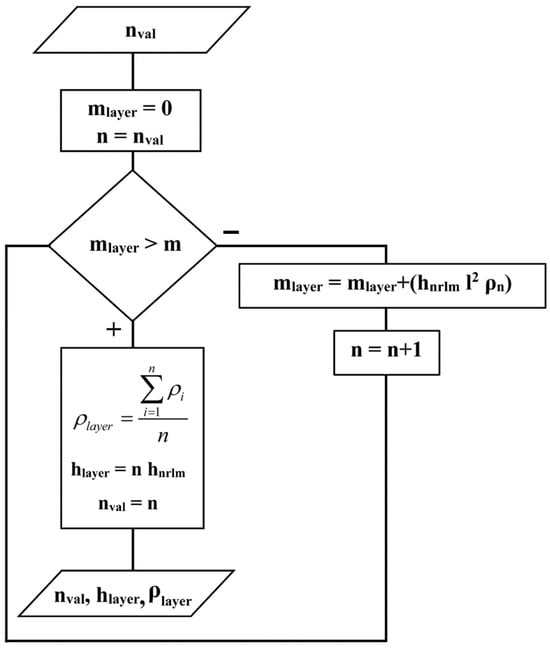
Figure 1.
A control flow chart of height and density value calculations for one atmospheric layer in the model of CR protons’ transport. This process is repeated the required number of times (corresponding to number of layers—for this work, n = 20), and the calculations are performed by simply averaging the remaining values in the NRLMSISE-00 data table on the last layer.
The air mass of the entire column (M) is defined as follows:
where hi is the layer height in the output data of the NRLMSISE-00 model, ρi is the substance density in this layer, l is the plain length, and k is the number of layers in the data file. Then the estimated mass of the substance in each layer (m) of the forming model is as follows:
m = M/N
Since the density value is particularly small, these values from the NRLMSISE-00 dataset are divided into an equal number without remainder, and the resulting datasets are also averaged at the final layer. Thus, the final layer is divided into a given number of uniform layers with averaged density values (for example, if there are 42 layers left from the NRLMSISE-00 model, and 21 division factor is selected, then 21 datasets of 2 density values will be obtained and each layer will be averaged over these two values). The dividing factor is chosen solely based on how much time can be spent on modeling, and it is a variable value. As a result, the necessary sets for configuration parameter setting are obtained (Figure 2). It should be noted that the above-described algorithm is not implemented as a separate program but integrated into a listing in order to ensure the compactness of final executing files.
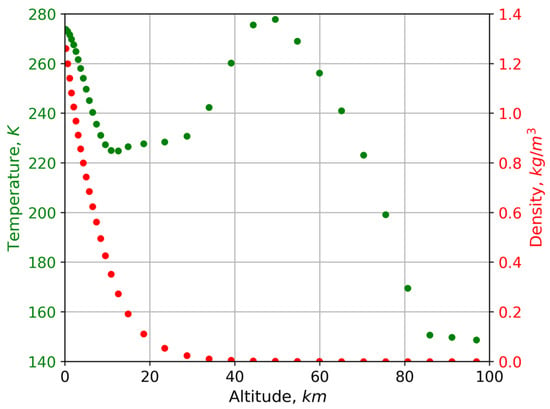
Figure 2.
Graphical representation of the Earth’s atmosphere model parameters (density and temperature) used to calculate the CR protons’ transport and the ionization rate. It should be noted that this approach significantly reduces the number of layers and leads to an increase in calculation speed.
2.2. Physics Implementation and Ionization Rate Detector Features
As discussed, primary protons passing through the Earth’s atmosphere can deposit their energy both during ionization and during the production of cascades. Therefore, a standard set of GEANT4 interaction models, which includes electromagnetic interactions models, Bertini cascades (BERT) [16], the quark-gluon string model (QGSP) [17,18] and a precision model of neutrons transport (HP) for energies below 20 MeV [19], was used in this work. Electrons, positrons, photons, hadrons and muons leave their energy both in the detecting layer when passing through it and in the main atmospheric model layers. Thereby, the number of ion pairs for the detector at h altitude is determined in the same way as the ionization yield function as follows [4]:
where ∆E/∆x is the mean energy loss in the sensitive detector layer at the altitude h, Ei = 35 eV is the standard ionization potential, and is normalization factor including zenith angle θ in range from 0 to 90 degrees. Such detector layers are located at altitudes from 0 to 98 km with 1 km spatial step. Detector layers that allow us to extract information about the secondary particles’ flux value (protons, electrons, positrons, photons, muons, pions and neutrons), their angular distributions and energy spectra are also implemented. This information is used to verify the RUSCOSMICS model through experimental data obtained during the balloon experiment, as well as during civil aircraft flight with compact Geiger–Müller counters [20].
2.3. Primary Particle Source
The source of primary protons is modeled as a point-source with specified angular distribution and a standard probability density function corresponding to the form of the primary protons’ energy spectrum. It is located at the atmospheric model’s upper boundary (100 km), while particles are emitted into the entire lower hemisphere. Discrete sample is used to calculate the spectrum in a standard probability density function, while Fi should be denoted as its weight along the ordinate axis for each xi value (corresponding to the energy value, i.e., Fi = F(E) and xi = E):
Here . After the Pi and xi values are determined, the sampling algorithm is as follows:
- A random number is generated with a uniform probability distribution density.
- The comparison of and for is conducted until the condition occurs. In the case of negative comparison result, the following operations are carried out next: and .
- The corresponding value for is selected.
The positive aspect of this method is its unlimited possibility for implementing a sample from a given probability density function, even in the absence of an analytical representation. A typical illustration of the model geometry, the primary proton source and the particle tracking is shown in Figure 3.
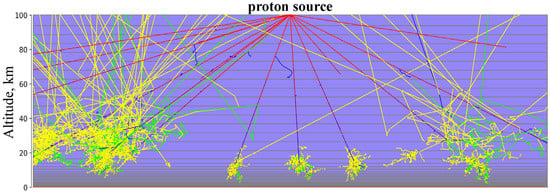
Figure 3.
Example of the CR particles’ transport through the Earth’s atmosphere using the RUSCOSMICS model geometry (only part of the projection is shown). The picture shows a flat geometry approximation; a primary particle gun is defined as a point source with an isotropic angle distribution and secondary particle tracking. The Earth’s atmosphere is divided into the layers and parametrized with the NRLMSISE-00 model. Red represents positively charged particles, blue represents negatively charged particles, green represents neutrons and yellow represents photons.
2.4. Primary CR Protons’ Spectra
The differential energy spectrum of GCR primary protons is defined according to the following formula [21]:
where E is the proton kinetic energy in MeV, and values of E0, D, B, C and α depend on the phase of the 11-year cycle parameters, which are presented in Table 1.

Table 1.
Coefficients of the GCR proton spectra depending on the solar activity cycle.
It should be noted that the data obtained using this formula are in very good agreement with the spectra data obtained using the PAMELA (Payload for Antimatter Matter Exploration and Light-nuclei Astrophysics) spacecraft and averaged over the period of 6 December 2009–1 January 2010 [22,23]. Therefore, it follows that the above-mentioned methodology for determining differential energy spectra is an efficient approximation, and it can be used as an input parameter when modeling CR transport through the Earth’s atmosphere.
Differential energy spectra for SEPs were obtained from experimental data provided by the GOES satellites. In our methodology, several values are obtained from the differential channels of the satellite. Then the spectrum is approximated using a simple power law dependence F(E) = a E−γ. In this case, a and γ parameters are fitted in a way that the standard deviation of the obtained values from the experimental data is minimal. A more detailed description of this technique is given in our previous work [24].
GLE events (GLE 60, GLE 71 and GLE 72) are also considered in this work apart from SEPs. GLE 60 (15 April 2001) was registered with an increase in the counting rate from 100% to 225% at 7 neutron monitor stations (https://gle.oulu.fi/, accessed on 19 January 2024). GLE 71 (17 May 2012) was relatively low and was accompanied by a 18% counting rate increase for the Oulu and Apatity neutron monitors and an 8% increase for the South Pole. GLE 72 (10 September 2017) was accompanied by a slight increase (not exceeding 6%). However, it was simultaneously noted at several stations of the worldwide neutron monitor network [25]. The spectra parameters of the primary protons for these events were obtained from the works of [10], in which the method of inverse problem solution is used. In these circumstances, the data from the network of neutron monitor stations is utilized. Note that the dependence describing the differential energy spectrum of protons for all GLE events is exponential. Figure 4 shows all above-described spectra that were used in calculating CR protons’ transport through the Earth’s atmosphere and the ionization rate assessments for a large altitude range. This plot allows us to evaluate quantitatively, qualitatively and comparatively the difference in the particles’ spectral characteristics during different events.
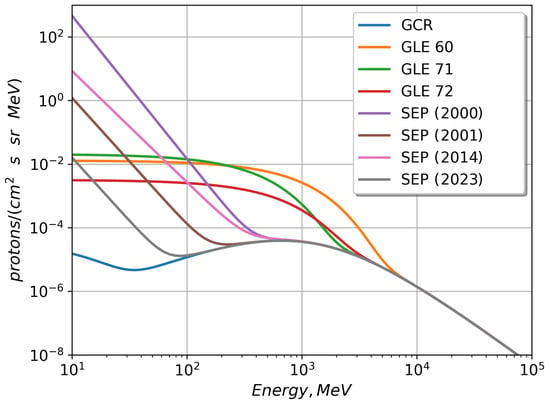
Figure 4.
The derived differential proton energy spectra for SEP and GLE events used in modeling of the CR transport through the Earth’s atmosphere and the ionization rate estimation.
3. Results and Discussion
3.1. Description of Events
For this study, SEPs with sufficiently large primary proton fluxes (P10 > 100 pfu—particle flux unit, 1 particle per cm2 per s per sr) were selected, since it is precisely such events that are of the greatest interest when estimating the rate of atmospheric ionization. Note that in the 23d solar cycle (SC 23), only 48 such SEPs were recorded; in SC 24, there were 12 events, and in the current SC 25, so far there has been only 1 event (as of 1 December 2023). To compare the last three SCs, the solar sources of these SEPs were analyzed, and the events belonging to the different SCs with similar heliocoordinates and X-ray flare magnitudes were selected. That is, in SC 23 and 24, we found a pair of similar flares (group I) with coordinates that were far west (W85 and W88) and that had large magnitudes (X14.4 and X8.2, respectively). Also, in these cycles, there was a pair of flares (group II) with similar central coordinates (W09 and W11) and magnitudes (X2.3 and X1.2, respectively). And to compare three cycles (23–25) to the only event of SC 25 (W87, M5.7), flares with similar coordinates (W77 and W76) and magnitudes (M7.4 and M5.1, respectively) were selected, thus obtaining group III (out of the three events). Additionally, the characteristics of CMEs associated with selected solar flares were also analyzed. All the main characteristics of the described SEP events and their solar sources are given in Table 2.

Table 2.
Main characteristics of the described SEP events and their solar sources.
Various authors have previously noted the existence of a relationship between the class of X-flares, the velocities of associated CMEs and subsequent proton flux enhancements; however, it has always been noted that this relationship is not entirely linear, and the correlation coefficients between these parameters, even for fairly large samples (several tens of events), do not exceed 0.6 [11,26,27,28,29,30,31,32,33]. In addition, the conditions for the propagation of particles in interplanetary space are no less important—in particular, the existence of magnetic barriers that have different effects on the registration of particles near Earth [11,33].
In our case, the most obvious conclusion due to the small number of events seems to involve certain threshold values of the X-flare magnitude and CME speed, for which we should expect a fairly large increase in proton fluxes of different energies. The sample under study included only flares > the M5 class and corresponding CME velocities >1100 km/s, provided they were registered in the western part of the solar disk.
Figure 5, Figure 6 and Figure 7 show the behavior of proton fluxes (particles with energies >10 MeV are indicated by red curve; those with energies >50 MeV are indicated in blue; those with energies >100 MeV are indicated in green; and the horizontal dashed red line defines the chosen threshold of 100 pfu) for selected events according to GOES satellite data. The maximum values of particle fluxes are given in Table 2. It is clearly seen that, despite the similar characteristics of solar sources within the discussed groups of events, the profiles and maximum fluxes of these SEPs differ.
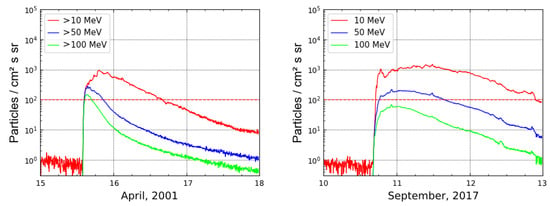
Figure 5.
Fluxes of protons of different energies for group I: 15 April 2001 (left) and 10 September 2017 (right).
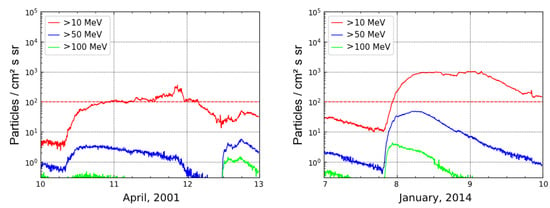
Figure 6.
Fluxes of protons of different energies for group II: 10 April 2001 (left) and 7 January 2014 (right).
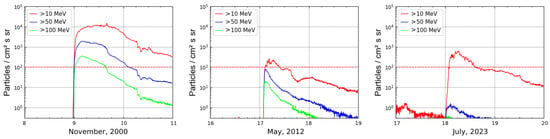
Figure 7.
Fluxes of protons of different energies for group III: 08 November 2000 (left), 17 May 2012 (middle) and 17 July 2023 (right).
Events 1 and 2 (see Table 2 and Figure 5), having similar heliocoordinates and solar flare classes, differ in the profiles of the resulting SEPs: despite the close maximum values of the proton fluxes, the fluence in event 2 is much higher. This can be explained by differences in the velocities of associated CMEs and in the conditions for particle propagation in the interplanetary medium. For both events, during the registration of SEP in the Earth’s orbit, high-speed streams from coronal holes had an influence. But in the first one, this was already ending, and in the second, the Earth was just entering the corotating interaction region, which, apparently, led to the existence of some magnetic barrier between the solar source of particle acceleration and the Earth. As a result, one can see a slower decline in the particle flux. We also note that these two events are associated with ground-level enhancements (GLE60 and GLE72, respectively), whose characteristics are discussed in detail in the works of [34,35,36,37,38,39].
Events with central solar sources (Figure 6) are distinguished by a longer duration and a smoother increase in particle fluxes. The registration of the proton flux maximum most often occurs not at the beginning of the event, but much later. Events that are far to the west (Figure 5 and Figure 7), on the contrary, are characterized by a sharper increase and rapid decline, as previously noted by other authors (for example, [31,32,33]). Both events shown in Figure 6 did not start at the background level. Moreover, event 3 is one of a series of proton flux enhancements recorded after large flares in the same active region, AR 9415 [40,41,42]. The same AR subsequently became the source of the event discussed above (event 1). In event 4, the proton fluxes were also initially elevated due to the previous SEP, but in this case, they were associated with a distant flare and CME beyond the western limb.
Figure 7 clearly demonstrates the differences in the spectra of events 5–7. The characteristics of their solar sources are similar but event 5, belonging to the 23rd cycle of solar activity, has maximum particle fluxes that are several times higher than the events of subsequent SCs. This indirectly confirms the assumptions previously made by various authors about a decrease in the geoeffectiveness of solar events in SCs 24 and 25 [43]. In addition, event 5 is different because, despite the hard spectrum of particles, GLE registration did not follow (see [5,44,45]), and event 6, despite its lower maximum particle fluxes, is associated with GLE 71 described in the works of [38,46]. The profiles of the discussed SEPs in this group are further complicated by conditions in the interplanetary medium: in event 5, the decline in proton fluxes slowed in the first half of 10 November 2000, because the interplanetary CME associated with this event was detected in the Earth’s orbit at that time and contained some trapped particles. In events 6 and 7, at the time of SEP registration, the Earth was experiencing interplanetary disturbances caused by the impact of a CME that had occurred several days earlier, which also affected the observed SEP profile.
The diagram in Figure 8 shows the relationship between the CME velocity and the corresponding particle fluxes of different energies during the discussed SEPs (on a logarithmic scale). The analysis shows that high CME velocities are not the only sufficient conditions for registering SEPs with a hard spectrum; on the contrary, in the sample under discussion, rather large fluxes of particles with energies >100 MeV were recorded in the event with the lowest velocity (event 1). Moreover, event 5, in which the CME velocity is not the highest, its particle fluxes exceed the others by one to two orders of magnitude. Apparently, the source of its event was located in a favorable longitudinal zone, which led to the registration of a significantly larger SEP. We also note that in event 7, which is related to 25 SC, a sufficient CME speed was observed, but it had a rather soft spectrum: only an increase in the fluxes of particles with energies >10 MeV was recorded, and higher-energy particles were not detected in near-Earth space.
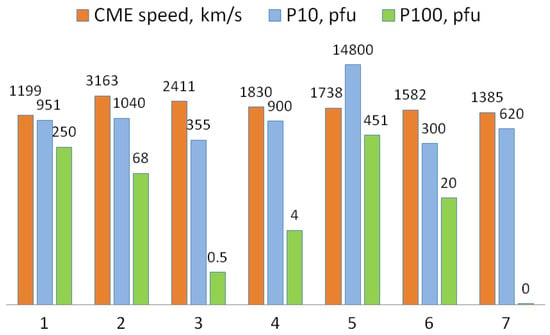
Figure 8.
Relationship between the CME velocity and the corresponding particle fluxes of different energies during the discussed SEPs. All values are given on a logarithmic scale.
3.2. Calculated Ionization Rate
From our calculation of the GCR and SCR protons’ transport through the Earth’s atmosphere, the ionization rates depending on the altitude were obtained (Figure 9). The data are presented for two geomagnetic cutoff rigidity values (0.17 GV and 0.64 GV) and at a wide range of altitudes (0–98 km). It can be clearly seen that the maximum of ion-pair formation is at the altitudes of 10–15 km for GCR protons. This maximum is shifted higher during GLE and SEP events and reaches altitudes of 30 km and 50 km, respectively. Both the absolute values and the profiles’ shape are in very good agreement with those from previous works [2,3]. The left panel of Figure 9 also presents the experimental data described in [47]. There is a good agreement up to 20 km. Some discrepancies at altitudes >20 km can be explained by a different spectrum for the primary protons, since for these altitudes, the part of the spectrum with E < 500 MeV is important and can vary depending on solar activity.
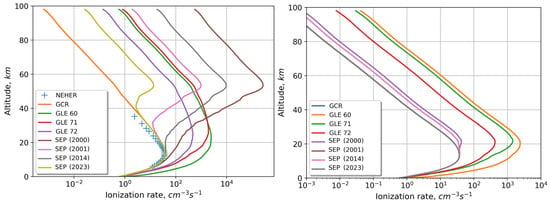
Figure 9.
The calculated ionization rate obtained by modeling CR protons’ transport through the Earth’s atmosphere during SEP and GLE events, as well as for GCR. Data are presented for relatively low (0.17 GV, left panel) and higher (0.64 GV, right panel) geomagnetic cutoff rigidity values.
The influence of the geomagnetic cutoff rigidity should be pointed out. Protons of relatively low energies in regions with a low cutoff rigidity value during SEPs have a substantial effect on the formation of ion pairs at altitudes from 50 to 100 km. This is due to a significant increase in fluxes with the energy range from 10 to 100 MeV. At the same time, the influence of low-energy protons becomes insignificant for the geomagnetic cutoff rigidity values ≥ 0.64 GV (Figure 9, right panel), and the greatest contribution is observed only during GLE events. Note that the ionization rate curves for events 3 and 7 almost coincide with the GCR curve.
Table 3 presents the calculated ionization count rates for all considered events for a geomagnetic cutoff rigidity of 0.17 GV at various altitudes (10–45 km). As one can see, the largest contribution to the ionization rate at altitudes of 0–20 km is made by protons with an energy spectrum corresponding to GLE events. At the same time, at altitudes >20 km, an increase in the ionization count rate occurs due to protons with an energy spectrum corresponding to SEPs. The presented data make it possible to quantify the influence of primary CR protons on the Earth’s atmosphere and can be used for studies related to atmospheric chemistry.

Table 3.
Calculated ionization count rates (in cm−3s−1) for different events and altitudes (for rigidity of 0.17 GV).
4. Conclusions
Seven SEP and GLE events with similar solar sources but belonging to three different SCs were considered in this work. Their detailed characteristics and features, as well as a comparative analysis of the characteristics of parent X-flares and coronal mass ejections (CMEs), are presented. The SCR proton spectra of all the analyzed events were obtained with our own method for data approximation using the differential energy spectra obtained from GOES data. Estimates of the ionization rate were carried out by applying these data and numerical methods (based on the Monte-Carlo method). It is important to note that, in contrast to [2,3,4], for our purpose, we used our own RUSCOSMICS model that was designed for calculations of CR particles’ transport through the Earth’s atmosphere. Ionization count rate profiles were obtained for all the SEP and GLE events considered. The differences in primary CR protons’ impact on the Earth’s atmosphere in the altitude range of 0–98 km between SEP and GLE events were described. Additionally, two geomagnetic cutoff rigidity values (0.17 and 0.64 GV, corresponding to polar and high-latitude regions) were considered. All the above mentioned results made it possible to quantify the effect of SCR protons on the Earth’s atmosphere. The results obtained are very important for understanding the influence of cosmic radiation on radio wave propagation, the thermodynamical regime and chemistry of the Earth’s atmosphere and applications for the urbanization of high-latitude regions, especially in the context of solar climate change.
Author Contributions
Methodology, E.A.M., N.S.S. and M.A.A.; software, E.A.M. and K.A.D.; validation, E.A.M.; formal analysis, N.S.S. and M.A.A.; writing—original draft preparation E.A.M., N.S.S. and M.A.A.; writing—review and editing, A.V.B., N.S.S., M.A.A., K.A.D., A.A.A. and A.V.D. All authors have read and agreed to the published version of the manuscript.
Funding
No additional grants to carry out or direct this particular research were obtained. The work of A.V.D. was conducted under the scientific research topic “Research of the Sun, monitoring and modeling of the radiation environment and plasma processes in the heliosphere and near-Earth space”.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The RUSCOSMICS software toolkit is available at https://ruscosmics.ru/ (accessed on 19 January 2024). GOES data on protons with energy >10 and >100 MeV and GOES data on X-ray flares are obtained from Space Weather Prediction Center of National Oceanic and Atmospheric Administration (https://www.swpc.noaa.gov/products/goes-proton-flux (accessed on 19 January 2024), https://www.ncei.noaa.gov/data/goes-space-environment-monitor/access/full/ (accessed on 19 January 2024), https://www.swpc.noaa.gov/products/goes-x-ray-flux (accessed on 19 January 2024), https://services.swpc.noaa.gov/json/goes/ (accessed on 19 January 2024)). The NMDB data are available at http://www.nmdb.eu/ (accessed on 19 January 2024). The CME catalog is available at https://cdaw.gsfc.nasa.gov/CME_list/ (accessed on 19 January 2024). A plane-parallel atmosphere model description is available at http://astro.vaporia.com/start/planeparallelatmosphere.html (accessed on 19 January 2024). GLE data are available at https://gle.oulu.fi/ (accessed on 19 January 2024).
Acknowledgments
We would like to thank the CDAW Data Center of NASA and the Catholic University of America in cooperation with the Naval Research Laboratory, as well as the SOHO project of international cooperation between ESA and NASA for generating and maintaining the CME catalog. We are also grateful to the Space Weather Prediction Center of the National Oceanic and Atmospheric Administration for providing the data from their GOES satellites. We acknowledge the NMDB database www.nmdb.eu, founded under the European Union’s FP7 programme (contract no. 213007) for providing data.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Dorman, L. Cosmic Ray Interactions, Propagation, and Acceleration in Space Plasmas; Springer: Dordrecht, The Netherlands, 2006; 847p. [Google Scholar]
- Bazilevskaya, G.A.; Usoskin, I.G.; Flückiger, E.O.; Harrison, R.G.; Desorgher, L.; Bütikofer, R.; Krainev, M.B.; Makhmutov, V.S.; Stozhkov, Y.I.; Svirzhevskaya, A.K.; et al. Cosmic Ray Induced Ion Production in the Atmosphere. Space Sci. Rev. 2008, 137, 149–173. [Google Scholar] [CrossRef]
- Mironova, I.A.; Aplin, K.L.; Arnold, F.; Bazilevskaya, G.A.; Harrison, R.G.; Krivolutsky, A.A.; Nicoll, K.A.; Rozanov, E.V.; Turunen, E.; Usoskin, I.G. Energetic Particle Influence on the Earth’s Atmosphere. Space Sci. Rev. 2015, 194, 1–96. [Google Scholar] [CrossRef]
- Usoskin, I.G.; Kovaltsov, G.A. Cosmic Ray Induced Ionization in the Atmosphere: Full Modeling and Practical Applications. J. Geophys. Res. 2006, 111, D21206. [Google Scholar] [CrossRef]
- Jackman, C.H.; Deland, M.T.; Labow, G.J.; Fleming, E.L.; Weisenstein, D.K.; Ko, M.K.W.; Sinnhuber, M.; Anderson, J.; Russell, J.M. The influence of the several very large solar proton events in years 2000–2003 on the neutral middle atmosphere. Adv. Space Res. 2005, 35, 445–450. [Google Scholar] [CrossRef][Green Version]
- Kirillov, A.S.; Belakhovsky, V.B.; Maurchev, E.A.; Balabin, Y.V.; Germanenko, A.V.; Gvozdevsky, B.B. Vibrational Kinetics of NO and N2 in the Earth’s Middle Atmosphere During GLE69 on 20 January 2005. J. Geophys. Res. Atmos. 2003, 128, e2023JD038600. [Google Scholar] [CrossRef]
- Funke, B.; Baumgaertner, A.; Calisto, M.; Egorova, T.; Jackman, C.H.; Kieser, J.; Krivolutsky, A.; López-Puertas, M.; Marsh, D.R.; Reddmann, T.; et al. Composition changes after the ‘‘Halloween” solar proton event: The High Energy Particle Precipitation in the Atmosphere (HEPPA) model versus MIPAS data intercomparison study. Atmos. Chem. Phys. 2011, 11, 9089–9139. [Google Scholar] [CrossRef]
- Calisto, M.; Usoskin, I.; Rozanov, E. Influence of a Carrington-like event on the atmospheric chemistry, temperature and dynamics: Revised. Environ. Res. Lett. 2013, 8, 045010. [Google Scholar] [CrossRef]
- Dmitriev, A.V.; Jayachandran, P.T.; Tsai, L.-C. Elliptical model of cutoff boundaries for the solar energetic particles measured by POES satellites in December 2006. J. Geophys. Res. 2010, 115, A12244. [Google Scholar] [CrossRef]
- Vashenyuk, E.V.; Balabin, Y.V.; Gvozdevsky, B.B. Features of relativistic solar proton spectra derived from ground level enhancement events (GLE) modeling. Astrophys. Space Sci. Trans. 2011, 7, 459–463. [Google Scholar] [CrossRef]
- Belov, A.V. Flares, ejections, proton events. Geomagn. Aeron. 2017, 57, 727–737. [Google Scholar] [CrossRef]
- Maurchev, E.A.; Balabin, Y.V. RUSCOSMICS—The new software toolbox for detailed analysis of cosmic ray interactions with matter. Solar–Terr. Phys. 2016, 2, 3–10. [Google Scholar]
- Agostinelli, S.; Allison, J.; Amako, K.; Apostolakis, J.; Araujo, H.; Arce, P.; Asai, M.; Axen, D.; Banerjee, S.; Barrand, G.J.N.I.; et al. GEANT4—A simulation toolkit. Nucl. Instrum. Methods Phys. Res. Sec. A Terr. Accel. Spectrometers Detect. Assoc. Equip. 2003, 506, 250–303. [Google Scholar] [CrossRef]
- Allison, J.; Amak, K.; Apostolakis, J.; Arce, P.; Asai, M.; Aso, T.; Bagli, E.; Bagulya, A.; Banerjee, S.; Barrand, G.J.N.I.; et al. Recent developments in Geant4. Nucl. Instrum. Methods Phys. Res. Sec. A Terr. Accel. Spectrometers Detect. Assoc. Equip. 2016, 835, 186–225. [Google Scholar] [CrossRef]
- Picone, J.M.; Hedin, A.E.; Drob, D.P.; Aikin, A.C. NRLMSISE-00 empirical model of the atmosphere: Statistical comparison and scientific issues. J. Geophys. Res. 2002, 107, 1468. [Google Scholar] [CrossRef]
- Heikkinen, A.; Stepanov, N.; Wellish, J.P. Bertini intra–nuclear cascade implementation in Geant4. In Proceedings of the 13th International Conference on Computing in High-Enery and Nuclear Physics (CHEP 2003), La Jolla, CA, USA, 24–28 March 2003. [Google Scholar]
- Amelin, N.S.; Armesto, N. Monte Carlo model for nuclear collisions from SPS to LHC energies. Eur. Phys. J. C—Part. Fields 2001, 22, 149–163. [Google Scholar] [CrossRef]
- Amelin, N.S.; Gudima, K.K.; Toneev, V.D. Quark—Gluon String Model and Ultrarelativistic Heavy Ion Interactions. Sov. J. Nucl. Phys. 1990, 51, 327–333. [Google Scholar]
- Garny, S.; Leuthold, G.; Mares, V.; Paretzke, H.G.; Ruhm, W. GEANT4 Transport Calculations for Neutrons and Photons below 15 MeV. IEEE Trans. Nuclear Sci. 2009, 56, 2392–2396. [Google Scholar] [CrossRef]
- Maurchev, E.A.; Balabin, Y.V.; Germanenko, A.V. Compact Geiger Counters as Additional Tools for Verifying Models of Cosmic Ray Transport through the Earth’s Atmosphere. Bull. Russ. Acad. Sci. Phys. 2021, 85, 1294–1296. [Google Scholar] [CrossRef]
- GOST 25645.122-85; Protons of Galactic Cosmic Rays. USSR State Committee for Standards: Moscow, Russia, 1985; 11p. (In Russian)
- Adriani, O.; Barbarino, G.C.; Bazilevskaya, G.A. PAMELA Measurements of Cosmic–Ray Proton and Helium Spectra. Science 2011, 332, 69–72. [Google Scholar] [CrossRef]
- Adriani, O.; Barbarino, G.C.; Bazilevskaya, G.A. Time dependence of the proton flux measured by PAMELA during 2006 July–2009 December solar minimum. Astrophys. J. 2013, 765, 1–8. [Google Scholar] [CrossRef]
- Maurchev, E.; Shlyk, N.; Abunina, M.; Abunin, A.; Belov, A.; Didenko, K. A Method for the Ambient Equivalent Dose Estimation in a Wide Range of Altitudes during SEP and GLE Events. Atmosphere 2024, 15, 92. [Google Scholar] [CrossRef]
- Balabin, Y.V.; Gvozdevsky, B.B.; Germanenko, A.V.; Maurchev, E.A. GLE events in 24th solar cycle. E3S Web Conf. 2018, 62, 01006. [Google Scholar] [CrossRef]
- Kahler, S.W. The correlation between solar energetic particle peak intensities and speeds of coronal mass ejections: Effects of ambient particle intensities and energy spectra. J. Geophys. Res. Space Phys. 2001, 106, 20947–20956. [Google Scholar] [CrossRef]
- Kurt, V.; Belov, A.; Mavromichalaki, H.; Gerontidou, M. Statistical analysis of solar proton events. Ann. Geophys. 2004, 22, 2255–2271. [Google Scholar] [CrossRef]
- Belov, A.; Garcia, H.; Kurt, V.; Mavromichalaki, H.; Gerontidou, M. Proton Enhancements and Their Relation to the X-ray Flares During the Three Last Solar Cycles. Solar Phys. 2005, 229, 135–159. [Google Scholar] [CrossRef]
- Wang, R.G. Statistical characteristics of solar energetic proton events from January 1997 to June 2005. Astropart. Phys. 2006, 26, 202–208. [Google Scholar] [CrossRef]
- Cliver, E.W.; Ling, A.G.; Belov, A.; Yashiro, S. Size distributions of solar flares and solar energetic particle events. Astrophys. J. Lett. 2012, 756, L29. [Google Scholar] [CrossRef]
- Lario, D.; Aran, A.; Gómez-Herrero, R.; Dresing, N.; Heber, B.; Ho, G.C.; Decker, R.B.; Roelof, E.C. Longitudinal and Radial Dependence of Solar Energetic Particle Peak Intensities: STEREO, ACE, SOHO, GOES, and MESSENGER Observations. Astrophys. J. 2013, 767, 41. [Google Scholar] [CrossRef]
- Dierckxsens, M.; Tziotziou, K.; Dalla, S.; Patsou, I.; Marsh, M.S.; Crosby, N.B.; Malandraki, O.; Tsiropoula, G. Relationship between Solar Energetic Particles and Properties of Flares and CMEs: Statistical Analysis of Solar Cycle 23 Events. Solar Phys. 2015, 290, 841–874. [Google Scholar] [CrossRef]
- Zhang, J.; Temmer, M.; Gopalswamy, N.; Malandraki, O.; Nitta, N.V.; Patsourakos, S.; Shen, F.; Vršnak, B.; Wang, Y.; Webb, D.; et al. Earth-affecting solar transients: A review of progresses in solar cycle 24. Prog. Earth Planet. Sci. 2021, 8, 56. [Google Scholar] [CrossRef]
- Johnson, A.S.; Golightly, M.J.; Lin, T.; Semones, E.J.; Shelfer, T.; Weyland, M.D.; Zapp, E.N. A comparison of measurements and predictions for the April 15 and April 18, 2001 solar proton events. Adv. Space Res. 2006, 37, 1678–1684. [Google Scholar] [CrossRef]
- Plainaki, C.; Mavromichalaki, H.; Belov, A.; Eroshenko, E.; Andriopoulou, M.; Yanke, V. A New Version of the Neutron Monitor Based Anisotropic GLE Model: Application to GLE60. Solar Phys. 2010, 264, 239–254. [Google Scholar] [CrossRef][Green Version]
- Kocharov, L.; Mishev, A.; Riihonen, E.; Vainio, R.; Usoskin, I. A Comparative Study of Ground-level Enhancement Events of Solar Energetic Particles. Astrophys. J. 2023, 958, 122. [Google Scholar] [CrossRef]
- Kurt, V.; Belov, A.; Kudela, K.; Yushkov, B. Some characteristics of GLE on 2017 September 10. Contrib. Astron. Obs. Skalnate Pleso 2018, 48, 329–338. [Google Scholar]
- Cohen, C.M.S.; Mewaldt, R.A. Energetic Particle Events of Cycle 24. Space Weather 2018, 16, 1616–1623. [Google Scholar] [CrossRef]
- de Koning, C.A.; Pizzo, V.J.; Seaton, D.B. The Solar Eruption of 2017 September 10: Wavy with a Chance of Protons. Astrophys. J. 2022, 924, 106. [Google Scholar] [CrossRef]
- Asai, A.; Ishii, T.T.; Kurokawa, H.; Yokoyama, T.; Shimojo, M. Evolution of Conjugate Footpoints inside Flare Ribbons during a Great Two-Ribbon Flare on 2001 April 10. Astrophys. J. 2003, 586, 624–629. [Google Scholar] [CrossRef]
- Wang, H.-M.; Song, H.; Jing, J.; Yurchyshyn, V.; Deng, Y.-Y.; Zhang, H.-Q.; Falconer, D.; Li, J. The Relationship between Magnetic Gradient and Magnetic Shear in Five Super Active Regions Producing Great Flares. Chin. J. Astron. Astrophys. 2006, 6, 477–488. [Google Scholar] [CrossRef]
- Pohjolainen, S.; Al-Hamadani, F.; Valtonen, E. Propagation of Solar Energetic Particles During Multiple Coronal Mass Ejection Events. Solar Phys. 2016, 291, 487–511. [Google Scholar] [CrossRef][Green Version]
- Belov, A.V.; Belova, E.A.; Shlyk, N.S.; Abunina, M.A.; Abunin, A.A. Geoefficiency of Sporadic Phenomena in Solar Cycle 24. Geomagn. Aeron. 2023, 63, 486–496. [Google Scholar] [CrossRef]
- Thakur, N.; Gopalswamy, N.; Mäkelä, P.; Akiyama, S.; Yashiro, S.; Xie, H. Two Exceptions in the Large SEP Events of Solar Cycles 23 and 24. Solar Phys. 2016, 291, 513–530. [Google Scholar] [CrossRef]
- Wang, Y.; Lyu, D.; Qin, G.; Xiao, B. The Effects of Magnetic Boundary on the Uniform Distribution of Energetic Particle Intensities Observed by Multiple Spacecraft. Astrophys. J. 2021, 913, 66. [Google Scholar] [CrossRef]
- Firoz, K.A.; Gan, W.Q.; Li, Y.P.; Rodriguez-Pacheco, J. On the possible mechanism of the first ground level enhancement in cosmic ray intensity of solar cycle 24. Astrophys. Space Sci. 2014, 350, 21–32. [Google Scholar] [CrossRef]
- Neher, H.V. Cosmic rays at high latitudes and altitudes covering four solar maxima. J. Geophys. Res. 1971, 76, 1637–1651. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).