Geo-Statistical Characterization of Annual Maximum Daily Rainfall Variability in Semi-Arid Regions
Abstract
1. Introduction
2. Materials and Methods
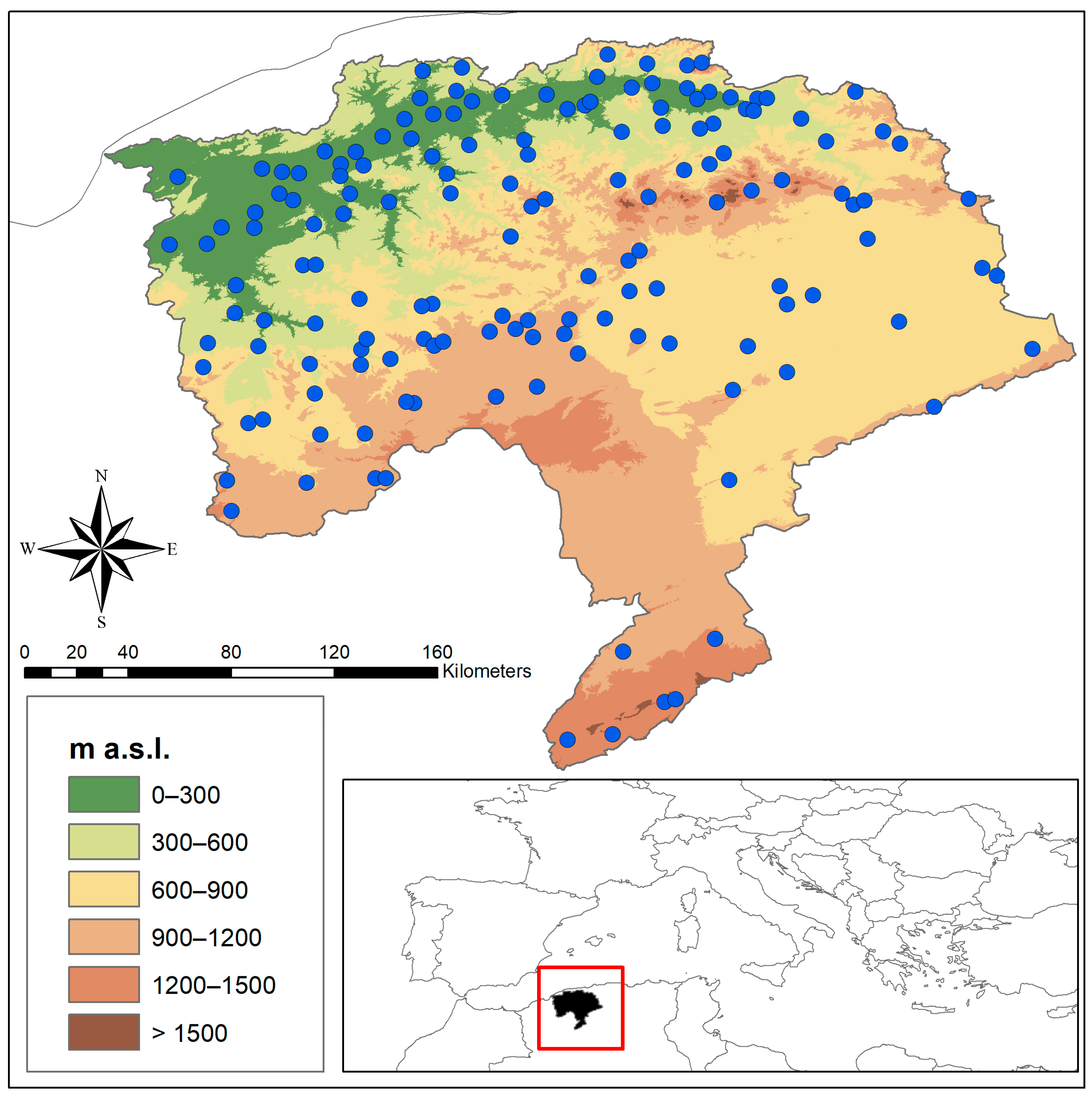
2.1. Study Area and Data
2.2. Methodology
2.2.1. Temporal Variability
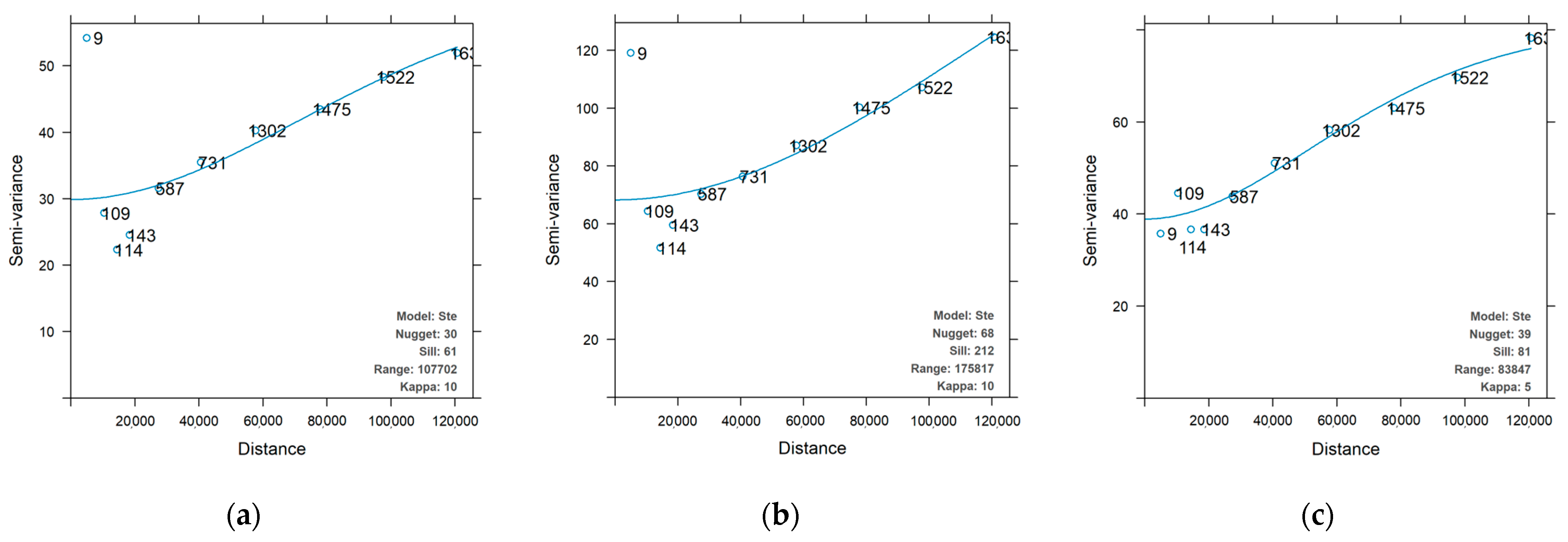
2.2.2. Spatial Variability
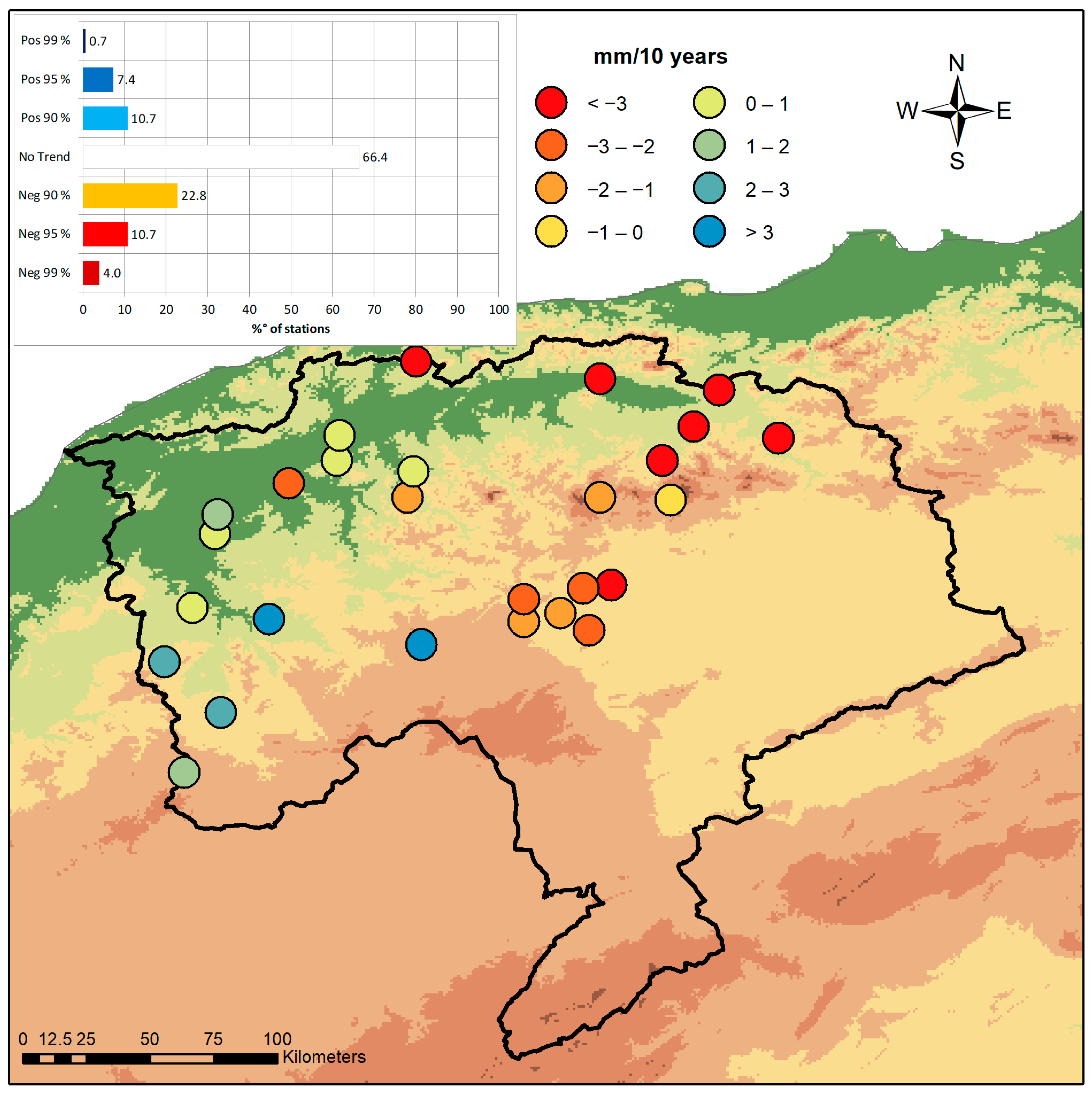
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Javari, M. Geostatistical modeling to simulate daily rainfall variability in Iran. Cogent Geosci. 2017, 3, 1416877. [Google Scholar] [CrossRef]
- Volkert, H. Heavy Precipitation in the Alpine Region (HERA): Areal Rainfall Determination for Flood Warnings Through in-situ Measureme nts, Remote Sensing and Atmospheric Modelling. Meteorol. Atmos. Phys. 2000, 72, 73–85. [Google Scholar] [CrossRef][Green Version]
- Cristiano, E.; ten Veldhuis, M.C.; van de Giesen, N. Spatial and temporal variability of rainfall and their effects on hydrological response in urban areas—A review. Hydrol. Earth Syst. Sci. 2017, 21, 3859–3878. [Google Scholar] [CrossRef]
- Gupta, A.; Kamble, T.; Machiwal, D. Comparison of ordinary and Bayesian kriging techniques in depicting rainfall variability in arid and semi-arid regions of north-west India. Environ. Earth Sci. 2017, 76, 512. [Google Scholar] [CrossRef]
- Kisaka, M.O.; Mucheru-Muna, M.; Ngetich, F.K.; Mugwe, J.N.; Mugedi, D.; Maurura, F. Rainfall Variability, Drought Characterization, and Efficacy of Rainfall Data Reconstruction: Case of Eastern Kenya. Adv. Meteorol. 2015, 2015, 380404. [Google Scholar] [CrossRef]
- Bachir, H.; Semar, A.; Mazari, A. Statistical and geostatistical analysis related to geographical parameters for spatial and temporal representation of rainfall in semi-arid environments: The case of Algeria. Arab. J. Geosci. 2016, 9, 486. [Google Scholar] [CrossRef]
- Tabari, H.; Somee, B.S.; Zadeh, M.R. Testing for long-term trends in climatic variables in Iran. Atmos. Res. 2011, 100, 132–140. [Google Scholar] [CrossRef]
- Ghorbani, M.A.; Mahmoud Alilou, S.; Javidan, S.; Naganna, S.R. Assessment of spatio-temporal variability of rainfall and mean air temperature over Ardabil province, Iran. SN Appl. Sci. 2021, 3, 728. [Google Scholar] [CrossRef]
- Otto, T.; Russchenberg, H.W.J. Estimation of Specific Differential Phase and Differential Backscatter Phase from Polarimetric Weather Radar Measurements of Rain. IEEE Geosci. Remote Sens. Lett. 2011, 8, 988–992. [Google Scholar] [CrossRef]
- Di Piazza, A.; Conti, F.L.; Noto, L.V.; Viola, F.; La Loggia, G. Comparative analysis of different techniques for spatial interpolation of rainfall data to create a serially complete monthly time series of precipitation for Sicily, Italy. Int. J. Appl. Earth Obs. Geoinf. 2011, 13, 396–408. [Google Scholar] [CrossRef]
- Moccia, B.; Papalexiou, S.M.; Russo, F.; Napolitano, F. Spatial variability of precipitation extremes over Italy using a fine-resolution gridded product. J. Hydrol. Reg. Stud. 2021, 37, 100906. [Google Scholar] [CrossRef]
- Modarres, R.; Sarhadi, A. Rainfall trends analysis of Iran in the last half of the twentieth century. J. Geophys. Res. Atmos. 2009, 114, D03101. [Google Scholar] [CrossRef]
- Pechlivanidis, I.G.; McIntyre, N.; Wheater, H.S. The significance of spatial variability of rainfall on simulated runoff: An evaluation based on the Upper Lee catchment, UK. Hydrol. Res. 2016, 48, 1118–1130. [Google Scholar] [CrossRef]
- Syed, K.H.; Goodrich, D.C.; Myers, D.E.; Sorooshian, S. Spatial characteristics of thunderstorm rainfall fields and their relation to runoff. J. Hydrol. 2003, 271, 1–21. [Google Scholar] [CrossRef]
- Vischel, T.; Lebel, T. Assessing the water balance in the Sahel: Impact of small scale rainfall variability on runoff. Part 2: Idealized modeling of runoff sensitivity. J. Hydrol. 2007, 333, 340–355. [Google Scholar] [CrossRef]
- Fortesa, J.; Latron, J.; García-Comendador, J.; Tomàs-Burguera, M.; Company, J.; Calsamiglia, A.; Estrany, J. Multiple Temporal Scales Assessment in the Hydrological Response of Small Mediterranean-Climate Catchments. Water 2020, 12, 299. [Google Scholar] [CrossRef]
- Achite, M.; Ceribasi, G.; Ceyhunlu, A.I.; Wałęga, A.; Caloiero, T. The Innovative Polygon Trend Analysis (IPTA) as a Simple Qualitative Method to Detect Changes in Environment—Example Detecting Trends of the Total Monthly Precipitation in Semi-arid Area. Sustainability 2021, 13, 12674. [Google Scholar] [CrossRef]
- Ali, R.; Kuriqi, A.; Abubaker, S.; Kisi, O. Long-Term Trends and Seasonality Detection of the Observed Flow in Yangtze River Using Mann-Kendall and Sen’s Innovative Trend Method. Water 2019, 11, 1855. [Google Scholar] [CrossRef]
- Harka, A.E.; Jilo, N.B.; Behulu, F. Spatial-temporal rainfall trend and variability assessment in the Upper Wabe Shebelle River Basin, Ethiopia: Application of innovative trend analysis method. J. Hydrol. Reg. Stud. 2021, 37, 100915. [Google Scholar] [CrossRef]
- Kuriqi, A.; Ali, R.; Pham, Q.B.; Gambini, J.M.; Gupta, V.; Malik, A.; Lith, N.T.T. Seasonality shift and streamflow flow variability trends in central India. Acta Geophys. 2020, 68, 1461–1475. [Google Scholar] [CrossRef]
- Achite, M.; Krakauer, N.Y.; Wałęga, A.; Caloiero, T. Spatial and Temporal Analysis of Dry and Wet Spells in the Wadi Cheliff Basin, Algeria. Atmosphere 2021, 12, 798. [Google Scholar] [CrossRef]
- Sen, P.K. Estimates of the Regression Coefficient Based on Kendall’s Tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Mann, H.B. Non-parametric tests against trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods; Oxford University Press: New York, NY, USA, 1975. [Google Scholar]
- Bouklikha, A.; Habi, M.; Elouissi, A.; Hamoudi, S. Annual, Seasonal and Monthly Rainfall Trend Analysis in the Tafna Watershed, Algeria. Appl. Water Sci. 2021, 11, 77. [Google Scholar] [CrossRef]
- Kessabi, R.; Hanchane, M.; Brahim, Y.A.; El Khazzan, B.; Addou, R.; Belmahi, M. Characterization of Annual and Seasonal Rainfall Trend Using Innovative Trend Analysis (ITA) and Classical Methods: The Case of Wadi Sebou Basin (WSB) Morocco. Euro-Mediterr. J. Environ. Integr. 2024, ahead of print. [CrossRef]
- Merabti, A.; Darouich, H.; Paredes, P.; Meddi, M.; Pereira, L.S. Assessing Spatial Variability and Trends of Droughts in Eastern Algeria Using SPI, RDI, PDSI, and MedPDSI-A Novel Drought Index Using the FAO56 Evapotranspiration Method. Water 2023, 15, 626. [Google Scholar] [CrossRef]
- Hassini, N.; Bouchama, M.; Dobbi, A. Trend of Precipitation in Algeria: Between Severe Drought and Torrential Rain. In Proceedings of the 8th International Conference on Water Resources and Arid Environments (ICWRAE 8), Riyadh, Saudi Arabia, 22–24 January 2019; pp. 104–108. [Google Scholar]
- Benali, K.M.; Metouchi, A.; Djoudar Hallal, D.; el Amine Khelfi, M.; Önsoy, H.; Toumi, S. Spatiotemporal characterization of the annual rainfall variability in the Isser Watershed (Algeria). Arab. J. Geosci. 2022, 15, 190. [Google Scholar] [CrossRef]
- Berhail, S.; Tourki, M.; Merrouche, I.; Bendekiche, H. Geo-Statistical Assessment of Meteorological Drought in the Context of Climate Change: Case of the Macta Basin (Northwest of Algeria). Model. Earth Syst. Environ. 2022, 8, 81–101. [Google Scholar] [CrossRef]
- Mrad, D.; Dairi, S.; Boukhari, S.; Djebbar, Y. Applied Multivariate Analysis on Annual Rainfall in the Northeast of Algeria. J. Water Clim. Chang. 2020, 11, 1165–1176. [Google Scholar] [CrossRef]
- Diatta, S.; Diedhiou, C.W.; Dione, D.M.; Sambou, S. Spatial Variation and Trend of Extreme Precipitation in West Africa and Teleconnections with Remote Indices. Atmosphere 2020, 11, 999. [Google Scholar] [CrossRef]
- Lorente Castelló, J.; Casas Castillo, M.C.; Rodríguez Solà, R.; Redaño Xipell, A. Extreme Rainfall Rates and Probable Maximum Precipitation; Adverse Weather in Spain; World Climate Research Programme: Geneva, Switzerland, 2013; pp. 135–148. [Google Scholar]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Achite, M.; Caloiero, T.; Jehanzaib, M.; Wałęga, A.; Kuriqi, A.; Pellicone, G. Geo-Statistical Characterization of Annual Maximum Daily Rainfall Variability in Semi-Arid Regions. Atmosphere 2024, 15, 1519. https://doi.org/10.3390/atmos15121519
Achite M, Caloiero T, Jehanzaib M, Wałęga A, Kuriqi A, Pellicone G. Geo-Statistical Characterization of Annual Maximum Daily Rainfall Variability in Semi-Arid Regions. Atmosphere. 2024; 15(12):1519. https://doi.org/10.3390/atmos15121519
Chicago/Turabian StyleAchite, Mohammed, Tommaso Caloiero, Muhammad Jehanzaib, Andrzej Wałęga, Alban Kuriqi, and Gaetano Pellicone. 2024. "Geo-Statistical Characterization of Annual Maximum Daily Rainfall Variability in Semi-Arid Regions" Atmosphere 15, no. 12: 1519. https://doi.org/10.3390/atmos15121519
APA StyleAchite, M., Caloiero, T., Jehanzaib, M., Wałęga, A., Kuriqi, A., & Pellicone, G. (2024). Geo-Statistical Characterization of Annual Maximum Daily Rainfall Variability in Semi-Arid Regions. Atmosphere, 15(12), 1519. https://doi.org/10.3390/atmos15121519










