Abstract
Tropical cyclone prediction is often described as chaotic and unpredictable on time scales that cross into stochastic regimes. Predictions are bounded by the depth of understanding and the limitations of the physical dynamics that govern them. Slight changes in global atmospheric and oceanic conditions may significantly alter tropical cyclone genesis regions and intensity. The purpose of this paper is to characterize the predictability of seasonal storm characteristics in the North Atlantic basin by utilizing the Largest Lyapunov Exponent and Takens’ Theorem, which is rarely used in weather or climatological analysis. This is conducted for a post-weather satellite era (1960–2022). Based on the accumulated cyclone energy (ACE) time series in the North Atlantic basin, cyclone activity can be described as predictable at certain timescales. Insight and understanding into this coupled non-linear system through an analysis of time delay, embedded dimension, and Lyapunov exponent-reconstructed phase space have provided critical information for the system’s predictability.
1. Introduction
Chaos is the term used to describe the nonperiodic behavior of a system. Mathematician and meteorologist Edward Lorenz [1] shaped the understanding of chaotic systems by describing variable evolution through sensitive dependence on initial conditions [2]. In atmospheric science, predictability is defined as the longest time interval to which the accuracy and preciseness of a forecast become no better than the climatological mean [3,4,5]. According to Lorenz [6], predictability is bounded by a non-deterministic atmosphere, observational limitations, and inadequate characterizations of the atmospheric system. From these limitations, forecasts of systems without clear periodicity will inevitably degrade over time. The Accumulated Cyclone Energy (ACE) dataset, a singular time series used to characterize tropical cyclone basin activity (e.g., [7]), is a likely non-deterministic candidate for further analysis using methods that are akin to the chaotic nature that Lorenz describes. It is through the utilization of ACE that we can infer the behavior of the Atlantic basin cyclone energy by invoking Takens’ theorem to recover phase space behavior and determine the predictability of the system. Though there is no single method for determining the predictability of weather phenomena and their variables, this quantification is important when dealing with real-time forecasts [5].
Lupo et al. [8] and Lupo [9] describe significant interannual and interdecadal variability in Atlantic tropical cyclones. Higher frequency El Niño-Southern Oscillation (ENSO) variability is consistent with tropical cyclone activity from a 3 to 7-year period, while lower frequency variations are represented at the interdecadal period by the Pacific Decadal Oscillation (PDO). Other positively correlated teleconnections include the easterly phase of the Quasi-biennial Oscillation (QBO) and the Madden–Julian Oscillation (MJO) (e.g., [8,10]); however, during La-Nina years, the QBO teleconnection was not an effective driver of activity in recent years as of the publication of [8]. The Atlantic Multidecadal Oscillation (AMO) index also illustrates patterns of SST variability in the North Atlantic. There exists a significant link between the AMO and the North Atlantic Oscillation (NAO) and the development of tropical storms and hurricanes in the basin [10,11,12,13].
Additionally, during 2020, there was an explosion in tropical activity in the basin, surpassing the most ever recorded named storms, occurring in 2005 with 28, by two. There has also been concern that the recent rise in global temperatures is linked to the rise in tropical cyclone activity in the Atlantic Ocean Basin, which has been significant (e.g., [14,15,16]). Lastly, ACE, as a metric of basin behavior, provides a time series through which the contributions of teleconnections on many time scales can be linked to tropical cyclone occurrence [7]. According to [17] and others, ACE is a metric that synthesizes tropical cyclone occurrence, lifespan, and intensity.
Often, seasonal tropical cyclone prediction is executed through various statistical methods, including regression, curve fitting, and cross-correlation, which can give rise to the oversimplification of deep coupled systems. Takens’ theorem lets us describe state variables from the intrinsic nature of the information encoded from the time series to the Takens’ manifold. The manifold would then serve as a representative statistical correlation definition of ACE to include embedded signals [18] that arise from teleconnections modulating the ACE signal. These teleconnections are the linkage between the changes in the atmospheric circulation occurring in widely separated parts of the globe, both in the atmosphere and ocean [19].
The goal of this paper is to investigate the use of the Takens’ Method and apply it to the time series for ACE and tropical cyclone activity in the North Atlantic Basin as well as determine the post-satellite era predictability of ACE using the Largest Lyapunov Exponent (LLE) technique. The chaotic time series, not displaying truly stochastic variations, will have limited predictability based on the LLE. Thus, it is expected that the model forecast should deviate from the observations with time [5]. Per our literature review, this study was not conducted previously.
2. Data and Methods
2.1. Study Region
The North Atlantic Basin was chosen as the study region using ACE as the diagnostic variable from a post-satellite era of 1960–2022. This region captures the primary thoroughfare for hurricane and tropical storm development, shown in Figure 1. From the West African coast, cutting across through the Caribbean and Southwest Atlantic, tropical cyclones propagate along with easterly wave trains stemming from convection generated as far east as the Ethiopian highlands.
Figure 1.
The study region. The Atlantic Region as provided by the National Hurricane Center, 2022 [20].
2.2. Data
Colorado State University created a dataset that provides ACE time series values from 1851 to 2022 for the North Atlantic basin. Figure 2 shows that the overall behavior of ACE values in the basin has nearly doubled in the most recent decades compared to the first few. In Figure 2, it can also be observed that as ACE increases, there exists a proportional increase in the number of named storms. This very close trend in behavior between ACE and named storms validates the intuitive source of energy modulating the magnitude of ACE values in the basin. Statistics from the Colorado States tropical project were calculated from the International Best Track Archive for Climate Stewardship [21,22]. The correlation between these two time series is robust at 0.73 for the whole dataset but 0.75 for the time period 1960–2022. Tropical cyclone days [21] correlate to ACE at 0.93 for the whole and 0.92 for the shorter time period, respectively. Correlations are similar or even higher for hurricanes, major hurricanes, and the respective cumulative days.
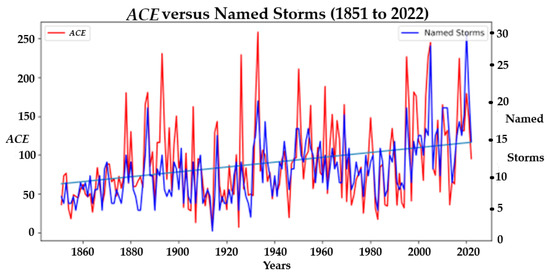
Figure 2.
A time series graph of yearly ACE (red—× 104 kt2), the linear regression trend of ACE (blue line), and named storms (blue) from 1851 to 2022. The correlation between ACE and named storms = 0.73, p = 0.01.
2.3. Time Series
A time series is a collection of observations of well-defined data that has been obtained throughout a duration, with repeated measurements [23]. A time series is typically used to determine the underlying causes and/or trends over a period. The notation used to typically represent the time series of a dataset is shown in Equation 1.
Here, stands for the collection of observations indexed by time, where t is a member of T, the set of allowed times.
Previous research from this group demonstrated interdecadal variability in tropical cyclone numbers as correlated with the PDO [8,9,16]. Figure 3 shows that the variability of ACE during warm and cool phases aligns in the last two cycles. Despite the lack of satellite imagery before the 1960s, it was noted as early as the mid-1920s that the cool phases of the PDO could be marked by higher basin activity.
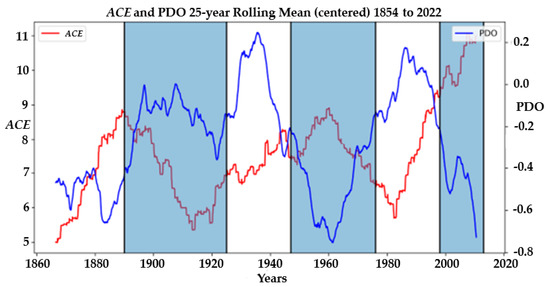
Figure 3.
A line graph showing the accumulated cyclone energy ACE (red) in comparison to the year and PDO Index (blue) for the North Atlantic Ocean.
To consider the behavior over the time series, we used ACE to assess the system’s state variables. ACE is an index used by the National Oceanic and Atmospheric Administration (NOAA) that depicts tropical basin activity; for this study, specifically, the North Atlantic Hurricane Basin [23,24,25,26]. ACE was chosen over other parameters, such as named storms, tropical storms, and major/minor hurricanes, as a proxy for the basin activity since ACE captured a portion of state variables summed over the entire basin, as shown in Figure 3. This study addresses the degree to which ACE may then be used as a predictive measure for Atlantic Basin storm activity [23,24,25,26]. The time series was analyzed using RStudio, version 4.2.1 [27], Python, version 2.7.16 (via Spyder [28]), and Julia programming, version 1.17.9.0 [29] to compute and visually distinguish the characteristics of the time series. The correlation between ACE and the raw PDO Index is −0.19 for the whole time series and −0.18 from 1960–2022, respectively, and these are significant at p = 0.10. The correlation between tropical cyclones and the raw PDO index was −0.35, p = 0.01.
Hurricane/tropical cyclone data that was provided by Colorado State University—Department of Atmospheric Science|Tropical Meteorology Project [21] provides the following tropical activity information: year, number of named storms, the days that had a named storm, the number of hurricanes, number of hurricane days, the number of major hurricanes, the number of major hurricane days, and the accumulated cyclone energy, which is also known as ACE. The equation used to calculate ACE is shown below in Equation (2), where is the estimated sustained maximum wind speed measured in knots.
3. Results
As shown in Figure 4, there are trends and embedded stochastic behavior from 1851–2022 in ACE that agree with previously published results of tropical cyclone activity (e.g., [14,15,16]). To discuss the data shown in Figure 4, we observe that the typical range of the ACE index is from 2.5 to 245.3. In the 1930s, the ACE index reached its peak of around 258. From the years 1950 to 1995, the ACE Index averaged close to 100 and ranged between 17 and 250. Recently, from 2005 to the present, we have observed a spike in the ACE index values that are below 250 but are higher than in years past. Overall, the time series demonstrates broad trends with embedded complexity.
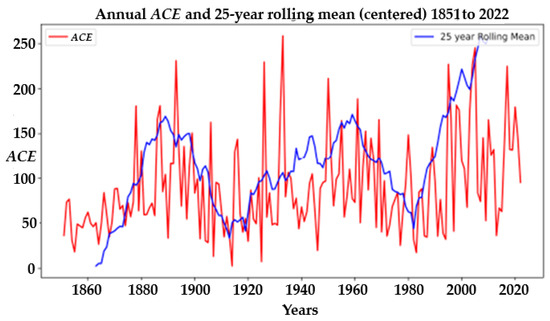
Figure 4.
Time series based on accumulated cyclone energy (red × 104 kt2) computed via Python for the years 1851–2022. The blue line is the ‘centered’ running mean.
Various techniques were used throughout this study. The techniques used were time delay with automutual information, embedded dimensions based on Cao’s algorithm, Takens’ theorem, and the Lyapunov exponent. These techniques were conducted for an ACE time series, post-weather satellite era of 1960–2022.
3.1. Time Delay with Auto Mutual Information (AMI)
An estimation of time delay was calculated via mutual information, which has been shown to produce a preferable phase portrait representation over choosing a zero from the autocorrelation function [30]. With this mutual information technique from Fraser and Swinney [31], the dependence of the information in the dataset from the values of X(t + τ) is compared to the values of X(t). The equation used to calculate the time delay is shown as Equation (3). From this equation, if [s,q] = [X(t), X(t + τ)], then the information in the coupled system (s,q) can be measured. The estimated joint distribution, Psq, given by the delayed image of Q from S, builds on specifying the accuracy of the measurements from a comparison of information similarity [30].
To calculate the specific time delay for the phase portrait, we chose the first local minima of the automutual information (I in Equation (3) and AMI in the text) as the time delay heuristic.
Examining Figure 5, we see that the time delay is determined to be one. The heuristic was to choose an optimal time delay by inspecting the delay that corresponded with the first local minimum value of I or when the AMI monotonically decreased to a ratio of I(τ)/I(0) = 0.2 or 1/e [32].
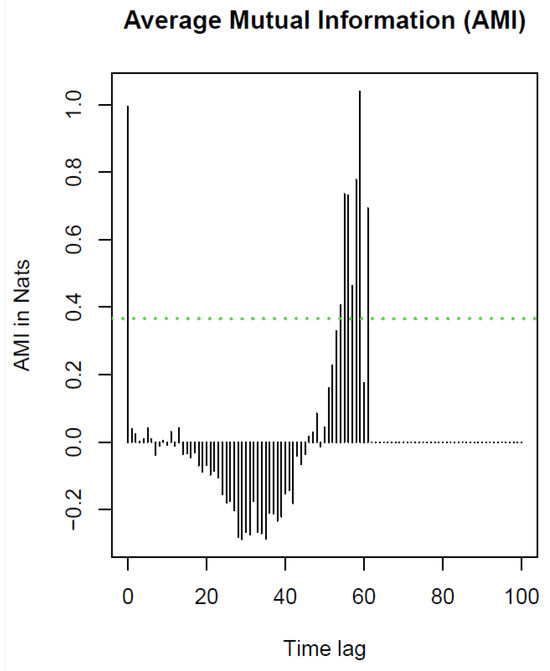
Figure 5.
A graph of the time delay against mutual information for the annual values of ACE (1960–2022) showing the first local minimum. The time delay was determined to be one. The green dased line represents the threshold of e−1.
3.2. Embedded Dimensions Based on Cao’s Algorithm
Embedding is a method where information in low-dimensional space can translate to high-dimensional vectors [33]. Embedding in a reconstructed phase space allows for the identification of order and hidden structures within the stochastic behavior. For instance, our one-dimensional time series was found to need six embedded dimensions to properly gain appropriate information for a diagnostic evaluation. This lent itself to constructing a reconstructed phase space in a three-dimensional phase plane with an x, y, and z-axis [34].
The embedding dimension can be determined using the false nearest neighbor embedding method (FNN) [18] or Cao’s algorithm. Though we describe both methods briefly, we have utilized Cao’s methodology in our analysis because it has the advantage of being less sensitive to the number of points in the dataset and not including any subjective parameters. This method also can differentiate between deterministic and stochastic signals in the series [32].
For the FNN method, the parameter of m was determined by evaluating the change in neighboring points’ distance in phase space as the original time series is embedded in higher dimensions [35]. The general idea of FNN is for each point, say, in the time series, using its nearest neighbor, in an m-dimensional space, to compute their distance given by . We can determine the change in distance by adding a dimension to evaluate the closeness of the points.
If exceeds a threshold, say, then this point is deemed as having a false nearest neighbor. The criterion is the embedding dimension and is relatively large enough such that the fraction of points for which is zero or sufficiently small. This criterion can be used to test the sequence of points as the dimensions increase and find where the fraction of false neighbors goes to zero [36].
For the Cao’s method, we consider a time series, say, , and for an embedding of m and m + 1, let and be Takens’ reconstructed time series where i = 1, 2, …, N and N = n − (m − 1)τ. Also, let the nearest neighbor to be denoted as . Similarly, we define n(i, m + 1). We then consider Equation (5) as [32]:
where is the max norm. Let E(m), the average of this variable over all i, be defined as Equation (6) [32].
It is given that two points in m-dimensional reconstructed space will be close to (m + 1) reconstructed space for them to be termed true neighbors. This is measured by the parameter E1(m) given by Equation (7) [32].
The minimum embedding dimension can be identified when E1(m) is a constant.
Also, to determine whether the data are stochastic or deterministic, we analyze a second function, E2(m), defined in Equation (8) [32].
where .
If the dataset is deterministic, then E2(m) is dependent on m; as such, there will exist at least one m such that E2(m) ≠ 1 (or any). If the data are random, then for all m, E2(m) = 1 [32]. We found that the appropriate embedded dimension associated with the dataset was six, as seen in Figure 6. This is where E1(m) plateaus. This signifies that the time series is sufficient in capturing the chaotic dynamics, as its numerical value for the embedding dimension is not significantly large. This is so because high-dimensional deterministic chaos, although non-existent for all random noise, translates to stochastic variability [5]. Also, this dataset was determined to be deterministic rather than stochastic because there exist embedding dimensions, m (in Figure 6, m = d), for which E2(m) is not equal to 1.
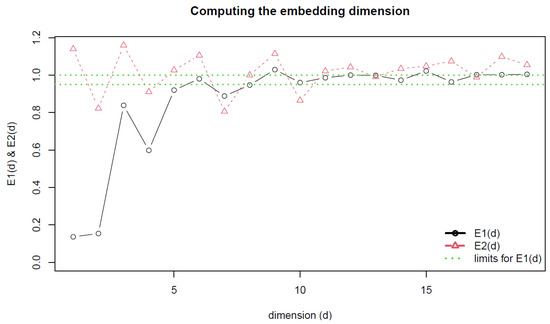
Figure 6.
A graph of E1(d) and E2(d) against dimensions (d) for the ACE (1960 to 2022). The embedding dimension was determined to be six.
3.3. Takens’ Theorem
Takens’ theorem was created by Floris Takens in 1981 [34]. In this paper, we used this theorem to reconstruct our one-dimensional time series dataset in reconstructed phase space. This method offered insights into the nature of the ACE series.
Tigurius [37] explained that using the Takens’ Embedded Theorem, for time series with indices, i = 1, 2, …, N and N = n − (m − 1)τ [32], sampled from a higher-dimensional attractor via the multivariate time series, is the delay and m is the embedding dimension [37]. The following is a formal definition given by Takens in [34]. Let M be a compact manifold of dimension m. For pairs (φ,y), where φ: M→M is a smooth diffeomorphism (an invertible function that maps one differentiable manifold to another such that both the function and its inverse are smooth) and y: M→R a smooth function, it is a generic property that the map : M→ defined by
is an embedding.
Figure 7 depicts the non-linear variations of Takens’ vectors with an embedding dimension of six and a lag of one. Based on the results, the exterior circular trajectories around the divergent cone indicate feedback within the system around several multiple stable regions. These stable regions, or clumping of vectors, indicate local continuities and regional stability around these discrete limit orbits. These stable regions are translated around the cone’s central stable axis. The increasing diameter of the cone can be related to the increasing instability in the system represented by the time series. With this information, the ACE time series’ displays both chaotic and regionally deterministic characteristics [32,33]. However, the results shown in Figure 7 for this analysis and similar techniques do not correspond to particular phenomena, only that there are periods of time when the ACE (or any) time series demonstrates stability (e.g., behaving like a damped oscillator) and there are periods of time when the time series is unstable (see [38,39]). Additional testing would be needed to demonstrate for which timescales there may be predictability and the related phenomenon.
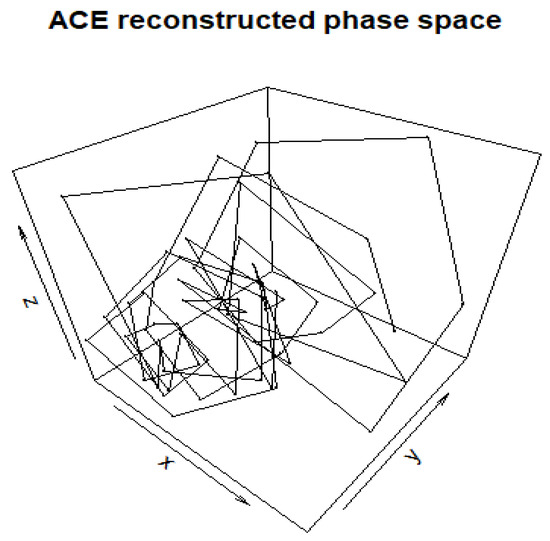
Figure 7.
Takens’ reconstructed phase space for accumulated cyclone energy from 1960 to 2022. The abscissa is the unfiltered time series, the ordinate is the time series with a lag of one year, and the applicate is the time series with a lag of two years.
3.4. Lyapunov Exponent
The Lyapunov exponent is defined as the average rate of the exponential divergence or convergence of nearby trajectories [40]. We calculated the Lyapunov exponent for the ACE time series. Equation (11) provides a method to calculate the Lyapunov exponent.
To be considered in a steady state, the Lyapunov exponent would have to be zero or negative for the duration of the dataset. With a Lyapunov exponent value being positive and ranging between two and four, this indicates a stochastic regime.
The process is as described in [33] and given briefly here. Within the chaotic trajectory, there would be points with distance d0(t0) at some time t0, and after some time t1, the distance can be described by d1(t1). The time evolution can be represented by t1–t0, and then after renormalizing, a new starting point is found.
The method used in this paper considers that a delayed coordinate embedding of a time series dataset that shows the exponential divergence of nearby states adheres to Equation (12) [29].
In Equation (12), E(k) is the average logarithmic distance between states of a neighborhood evolved in k time steps; is the time interval between samples of the time series. The slope of E(k) against k gives an estimate of the maximum Lyapunov exponent, . The LLE was determined from Figure 8 to be 0.084.
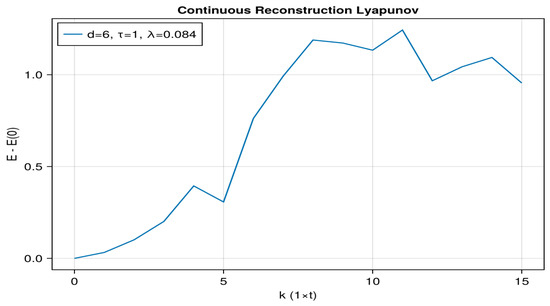
Figure 8.
The maximum Lyapunov exponent of accumulated cyclone energy is 0.084.
Since the system is chaotic, , and the series can be predicted with a forecast horizon of:
where is the maximum number of observations that can be predicted with an uncertainty of 1.96ε, which represents a 95% confidence band [32]. From this relation, it is determined that the prediction horizon is approximately eight time steps.
4. Discussion
Observing the ACE time series using a reconstructed phase space diagnostic approach, it is clear from both the attractor and Lyapunov exponent that the system is primarily chaotic. Despite the chaotic nature, it is evident that stable embedded characteristics exist. The time series showed that the data were not only chaotic, but there were also regions of stability in phase space. These may correspond to intrinsic teleconnection signals (e.g., ENSO, PDO) found within the system, such as those found in many studies [8,9,10,11,12,13,14] using different techniques such as Fourier decomposition or contingency analysis. Coupling the results from the Lyapunov evaluation, reconstructed phase space, mutual information, and the embedded dimension, the activity of the tropical cyclones was found to have traits of deterministic chaos.
This procedure to determine the chaotic nature of the ACE series, as well as the predictability in terms of climatic variations, was undertaken. However, due to an insufficient number of data points for the two separate 30-year periods, 1960–1989 and 1990–2019, the construction of the attractor and the subsequent determination of the Lyapunov exponent was not feasible. If there are too few data points, these methods may incur errors due to noise or the inability to capture convergence on a solution. As such, the changes in the predictability horizon of the system within a 30-year period could not be established.
It could be argued that ACE is not a suitable diagnostic to use here for tropical cyclone activity as the intensity of these storms is partly controlled by internal dynamics. While that is true, the high correlation between ACE and tropical cyclone numbers suggests the ACE time series is an appropriate surrogate as used elsewhere (e.g., [7,41]) since ACE captures aggregate seasonal tropical cyclone occurrence, duration, and intensity [17].
Additionally, the time series of monthly sea surface temperatures (SST) in the Niño 3.4 region, as provided by [42] for 1960–2019, were tested in order to determine whether similar behavior to that of Figure 7 could be derived. These SSTs were averaged over July through October annually to capture the more active part of the tropical cyclone season in the Atlantic (see [9]). This also provides a measure of the SST time series that is consistent with that of seasonal ACE. Additionally, ACE correlates with the Nino 3.4 SSTs at −0.24 annually and −0.27 for the bulk of the tropical season, as described above, and these are significant at p = 0.05. For comparison, Atlantic tropical cyclone occurrence and days for all named storms, hurricanes, and major hurricanes correlated similarly to Niño 3.4 region SSTs, from −0.19 to −0.28 for occurrence and −0.21 to −0.30 for days, respectively. All these correlations are significant at p = 0.10 at the lower end of the range and −0.05 at the higher end.
Figure 9 shows that Taken’s algorithm produced similar results to those found in Figure 7 in that there were periods of time where the series was more stable and other periods where the series was unstable. In Figure 9, the Takens method produced an embedding dimension of nine and a lag of one. Thus, we can have confidence that the behavior of ACE and the SSTs for the region typically used in seasonal tropical cyclone prediction exhibit similar behavior.
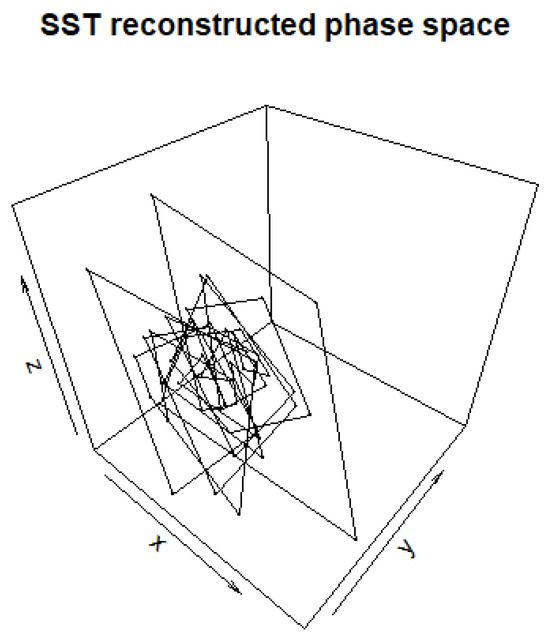
Figure 9.
Takens’ reconstructed phase space for SSTs from 1960 to 2019. The abscissa is the unfiltered time series, the ordinate is the time series with a lag of one year, and the applicate is the time series with a lag of two years.
The result in section two indicates there is variability in the ACE time series, which correlated highly with the tropical cyclone occurrences at the time scale of the PDO, confirming the results of several previous researchers. The ENSO variability in tropical cyclone numbers and, thus, ACE is well-known. This result would have implications for forecasting seasonal tropical cyclone variability and beyond using the Lyapunov exponent and using a method in chaos theory called empirical dynamical modeling [32]. The results here suggest that predictability of tropical cyclone frequency out to the time scale of ENSO (eight years as found using Equation (13)) and even beyond would be possible since predictability is possible out to the timescale of the development and lifecycle of a particular phenomenon [43]. ENSO dominates the signal on the interannual timescale. Using simpler time series analysis (e.g., contingency tables) [44] projected more active tropical cyclone activity for the early 21st century. Additionally, this analysis could be performed for other tropical cyclone activity in ocean basins.
5. Conclusions
Using the time series for accumulated cyclone energy (ACE) for the Atlantic Ocean Basin from 1960 to 2022, the Takens’ Algorithm and the Lyapunov Exponent were applied to characterize the chaotic behavior of the time series. The time series for ACE was analyzed here in order to demonstrate that the trend and interdecadal variability in ACE is consistent with the behavior of the time series for named tropical cyclones. There is a statistically significant correlation between these two time series and the PDO index, making the ACE diagnostic useful for analysis here.
The Taken’s Algorithm has not been used frequently in meteorological analysis in the past, but it is becoming more common only very recently [45]. This work demonstrates the utility of the method in time series analysis. It was found that the time series displayed deterministic chaos. This work also compared the results from the ACE analysis with those of the tropical season sea surface temperatures (SSTs) for the Nino 3.4 region, and the results were similar. Additionally, there was a statistically significant correlation between these SST and ACE. The Lyapunov Exponent technique confirmed that ACE data can be characterized as possessing chaos and having a predictability horizon of eight years.
This work has implications for forecasting both short-term seasonal and longer-term interannual tropical cyclone activity in the North Atlantic, depending on the time step used. Tropical cyclone forecasts for the near future (interannual and interdecadal) can be made with some confidence based on this work and similar to that of earlier studies. Our group will perform additional analysis in future research in other ocean basins.
Author Contributions
Conceptualization, S.M.W., C.A.S., J.J.S., and A.R.L.; methodology, all; validation, all; formal analysis, all; investigation, all; resources, all; data curation, C.A.S., J.J.S., and S.S.B.; writing—original draft preparation, S.M.W., C.A.S., and J.J.S.; writing—review and editing, all; visualization, all; supervision, S.S.B. and A.R.L.; project administration, A.R.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Most of the results in this paper are analyzed from products available online. Information regarding accumulated cyclone energy can be found at https://tropical.atmos.colostate.edu/Realtime/ accessed on 31 October 2024.
Acknowledgments
The authors would like to acknowledge the three anonymous reviewers for their time and effort in making suggestions that strengthened this work.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
| ACE | Accumulated Cyclone Energy |
| NHC | National Hurricane Center |
| ENSO | El Niño Southern Oscillation |
| PDO | Pacific Decadal Oscillation |
| AMO | Atlantic Multidecadal Oscillation |
| NOAA | National Oceanic and Atmospheric Administration |
| Vmax | Estimated Sustained Maximum Wind Speed |
| MI | Mutual Information |
References
- Lorenz, E.N. Deterministic Nonperiodic Flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef]
- Lorenz, E.N.; Martin, P. The Essence of Chaos; AIP Publishing: Melville, NY, USA, 1993; Volume 48. [Google Scholar]
- Shukla, J. Predictability. Adv. Geop. 1985, 28, 87–122. [Google Scholar]
- DelSole, T. Predictability and Information Theory. Part I: Measures of Predictability. J. Atmos. Sci. 2004, 61, 2425–2440. [Google Scholar] [CrossRef]
- Kieu, C.; Cai, W.; Fan, W.T. On the Existence of Low-Dimensional Chaos of the Tropical Cyclone Intensity in an Idealized Axisymmetric Simulation. J. Atmos. Sci. 2023, 80, 797–811. [Google Scholar] [CrossRef]
- Lorenz, E.N. A Study of the Predictability of a 28-variable Atmospheric Model. Tellus A Dyn. Meteorol. Oceanogr. 1965, 17, 321–333. [Google Scholar] [CrossRef]
- Wang, C.; Lee, S.K. Co-variability of tropical cyclones in the North Atlantic and the eastern North Pacific. Geophy. Res. Lett. 2009, 36, 24. [Google Scholar] [CrossRef]
- Lupo, A.R.; Latham, T.K.; Magill, T.H.; Clark, J.; Melick, C.J.; Market, P.S. The Interannual variability of hurricane activity in the Atlantic and east pacific regions. Natl. Weather Dig. 2008, 32, 119–135. [Google Scholar]
- Lupo, A.R. Interannual and Interdecadal variability in hurricane activity. In Recent Hurricane Research: Climate, Dynamics, and Societal Impacts; Hurricane Research; Lupo, A.R., Ed.; Intech Publishers: Vienna, Austria, 2011; 616p, ISBN 978-953-307-238-8. [Google Scholar]
- Camargo, S.J.; Sobel, A.H.; Barnston, A.G.; Klotzbach, P.J. The influence of natural climate variability on tropical cyclones, and seasonal forecasts of tropical cyclone activity. Global Perspectives on Tropical Cyclones. World Sci. Ser. Asian Pac. Weather. Clim. 2010, 4, 325–360. [Google Scholar]
- Molinari, R.L.; Mestas-Nuñez, A.M. North Atlantic decadal variability and the formation of tropical storms and hurricanes. Geophys. Res. Lett. 2003, 30, 1541. [Google Scholar] [CrossRef]
- Trenberth, K.E.; Shea, D.J. Atlantic hurricanes and natural variability in 2005. Geophys. Res. Lett. 2006, 33, 2006. [Google Scholar] [CrossRef]
- Klotzbach, P.J.; Gray, W.M. Multidecadal variability in North Atlantic tropical cyclone activity. J. Clim. 2008, 21, 3929–3935. [Google Scholar] [CrossRef]
- Walsh, K.J.E.; McBride, J.L.; Klotzbach, P.J.; Balachandran, S.; Camargo, S.J.; Holland, G.; Knutson, T.R.; Kossin, J.P.; Lee, T.C.; Sobel, A.; et al. Tropical cyclones and climate change. Wiley Interdiscip. Rev. Clim. Change 2015, 7, 65–89. [Google Scholar] [CrossRef]
- Intergovernmental Panel on Climate Change (IPCC). Climate Change 2021: The Physical Scientific Basis. 2021. Available online: http://www.ipcc.ch (accessed on 12 December 2023).
- Lupo, A.R.; Heaven, B.; Matzen, J.; Rabinowitz, J.L. The interannual and interdecadal variability in tropical cyclone activity: A decade of changes in the climatological character. In Current Topics in Tropical Cyclone Research; Lupo, A.R., Ed.; Intech Publishers: London, UK, 2020; 146p, ISBN 978-1-83880-361-2. [Google Scholar]
- Murakami, H.; Li, T.; Hsu, P.-C. Contributing Factors to the Recent High Level of Accumulated Cyclone Energy (ACE) and Power Dissipation Index (PDI) in the North Atlantic. J. Clim. 2014, 27, 3023–3034. [Google Scholar] [CrossRef]
- Google. 2022: Foundational Courses: Embeddings. Available online: https://developers.google.com/machine-learning/crash-course/embeddings/video-lecture (accessed on 2 December 2022).
- National Weather Service. Glossary—Teleconnection. Available online: https://forecast.weather.gov/glossary.php?letter=t (accessed on 23 November 2022).
- National Hurricane Center and Central Pacific Hurricane Center. NHC Marine Forecasts & Analyses. Available online: https://www.nhc.noaa.gov/marine/ (accessed on 2 December 2022).
- Colorado State University Statistics. North Atlantic Ocean Historical Tropical Cyclone Statistics 1851–2022. Available online: http://tropical.atmos.colostate.edu/Realtime/index.php?arch&loc=northatlantic (accessed on 10 October 2022).
- Vaughan, T. Accumulated Cyclone Energy and Tropical Cyclone Tracks: An In-Depth Analysis of the Anomalously Inactive 2013 Atlantic Hurricane Season. 2015. Available online: https://thescholarship.ecu.edu/handle/10342/4804 (accessed on 2 December 2022).
- Australian Bureau of Statistics, Time Series Analysis. The Basics. Available online: https://www.abs.gov.au/websitedbs/D3310114.nsf/home/Time+Series+Analysis:+The+Basics (accessed on 2 December 2022).
- Sneiderman, R. A Quick Introduction to Time Series Analysis. Available online: https://towardsdatascience.com/a-quick-introduction-to-time-series-analysis-d86e4ff5fdd (accessed on 5 December 2022).
- Drews, C. Separating the ACE Hurricane Index into Number, Intensity, and Duration. 2007. Available online: https://acomstaff.acom.ucar.edu/drews/hurricane/SeparatingTheACE.html (accessed on 22 November 2022).
- National Weather Service. 2022: Background Information: North Atlantic Hurricane Season. Available online: https://www.cpc.ncep.noaa.gov/products/outlooks/Background.html (accessed on 2 December 2022).
- Posit, RStudio IDE. The Most Trusted IDE for Open-Source Data Science. Available online: https://posit.co/products/open-source/rstudio/ (accessed on 1 December 2022).
- Spyder. Overview. Available online: https://www.spyder-ide.org/ (accessed on 6 December 2022).
- Chaos Tools. ChaosTools. Available online: https://juliadynamics.github.io/ChaosTools.jl/dev/ (accessed on 8 July 2024).
- Hunt, N.H. Autocorrelation Function, Mutual Information, and Correlation Dimension. In Nonlinear Analyses of Human Movement Variability; Stergiou, N., Ed.; Routledge, Taylor and Francis Group: Abingdon, UK, 2016; pp. 301–341. Available online: https://www.routledge.com/NonlinearAnalysis-for-Human-Movement-Variability/Stergiou/p/book/9781498703321 (accessed on 2 December 2022).
- Fraser, A.M.; Swinney, H.L. Independent coordinates for strange attractors from mutual information. Phys. Rev. A 1986, 33, 1134. [Google Scholar] [CrossRef]
- Balkissoon, S.; Fox, N.I.; Lupo, A.R. Determining chaotic characteristics and forecasting tall tower wind speeds in Missouri using Empirical dynamical modeling (EDM). Renew. Energy 2021, 170, 1292–1307. [Google Scholar] [CrossRef]
- Liu, Z. Chaotic Time Series Analysis. Math. Probl. Eng. 2010, 2010, 720190. [Google Scholar] [CrossRef]
- Takens, F. Detecting Strange Attractors in Turbulence. In Dynamical Systems and Turbulence, Warwick 1980; Rand, D., Young, L.S., Eds.; Lecture Notes in Mathematics; Springer: Berlin/Heidelberg, Germany, 1981; Volume 898. [Google Scholar] [CrossRef]
- Wallot, S.; Mønster, D. Calculation of average mutual information (AMI) and false-nearest neighbors (FNN) for the estimation of embedding parameters of multidimensional time series in matlab. Front. Psychol. 2018, 9, 365315. [Google Scholar] [CrossRef]
- Marín Carrión, I.; Arias Antúnez, E.; Artigao Castillo, M.M.; Miralles Canals, J.J. Parallel implementations of the False Nearest Neighbors method for distributed memory architectures. Concurr. Comput. Pract. Exp. 2011, 23, 1–16. [Google Scholar] [CrossRef]
- Tigurius. Introduction to Taken’s Embedding. 2018. Available online: https://www.kaggle.com/code/tigurius/introduction-to-taken-s-embedding (accessed on 15 November 2023).
- Zdunkowski, W.; Bott, A. Dynamics of the Atmosphere: A Course in Theoretical Meteorology; Cambridge University Press: Cambridge, UK, 2003; 719p. [Google Scholar]
- Lupo, A.R.; Kelsey, E.P.; Weitlich, D.K.; Woolard, J.E.; Mokhov, I.I.; Guinan, P.E.; Akyuz, F.A. Interannual and interdecadal variability in the predominant Pacific region SST anomaly patterns and their impact on climate in the mid-Mississippi valley region. Atmosfera 2007, 20, 171–196. [Google Scholar]
- Sayama, H. Lyapunov Exponent. 2022. Available online: https://math.libretexts.org/Bookshelves/Scientific_Computing_Simulations_and_Modeling/Book%3A_Introduction_to_the_Modeling_and_Analysis_of_Complex_Systems_(Sayama)/09%3A_Chaos/9.03%3A_Lyapunov_Exponent (accessed on 27 November 2022).
- Maue, R.N. Recent historically low global tropical cyclone activity. Geophys. Res. Lett. 2011, 38, L14803. [Google Scholar] [CrossRef]
- Center for Ocean-Atmospheric Prediction Studies (COAPS). 2024. Available online: https://www.coaps.fsu.edu (accessed on 14 October 2024).
- Jensen, A.; Lupo, A.R.; Mokhov, I.I.; Akperov, M.G.; Sun, F. The dynamic character of Northern Hemisphere flow regimes in a near term climate change projection. Atmosphere 2018, 9, 27. [Google Scholar] [CrossRef]
- Lupo, A.R.; Johnston, G. The interannual variability of Atlantic Ocean basin hurricane occurrence and intensity. Natl. Weather Dig. 2000, 24, 1–11. [Google Scholar]
- Wang, Z.; Sun, S.; Xu, W.; Chen, R.; Ma, X.; Liu, G. Research on multiscale atmospheric chaos based on infrared remote sensing and reanalysis data. Remote Sens. 2024, 16, 3376. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).