Impact Assessment of Coupling Mode of Hydrological Model and Machine Learning Model on Runoff Simulation: A Case of Washington
Abstract
1. Introduction
2. Materials and Methods
2.1. Research Area and Data
2.2. Models and Methods
2.2.1. Introduction to Hydrological Models
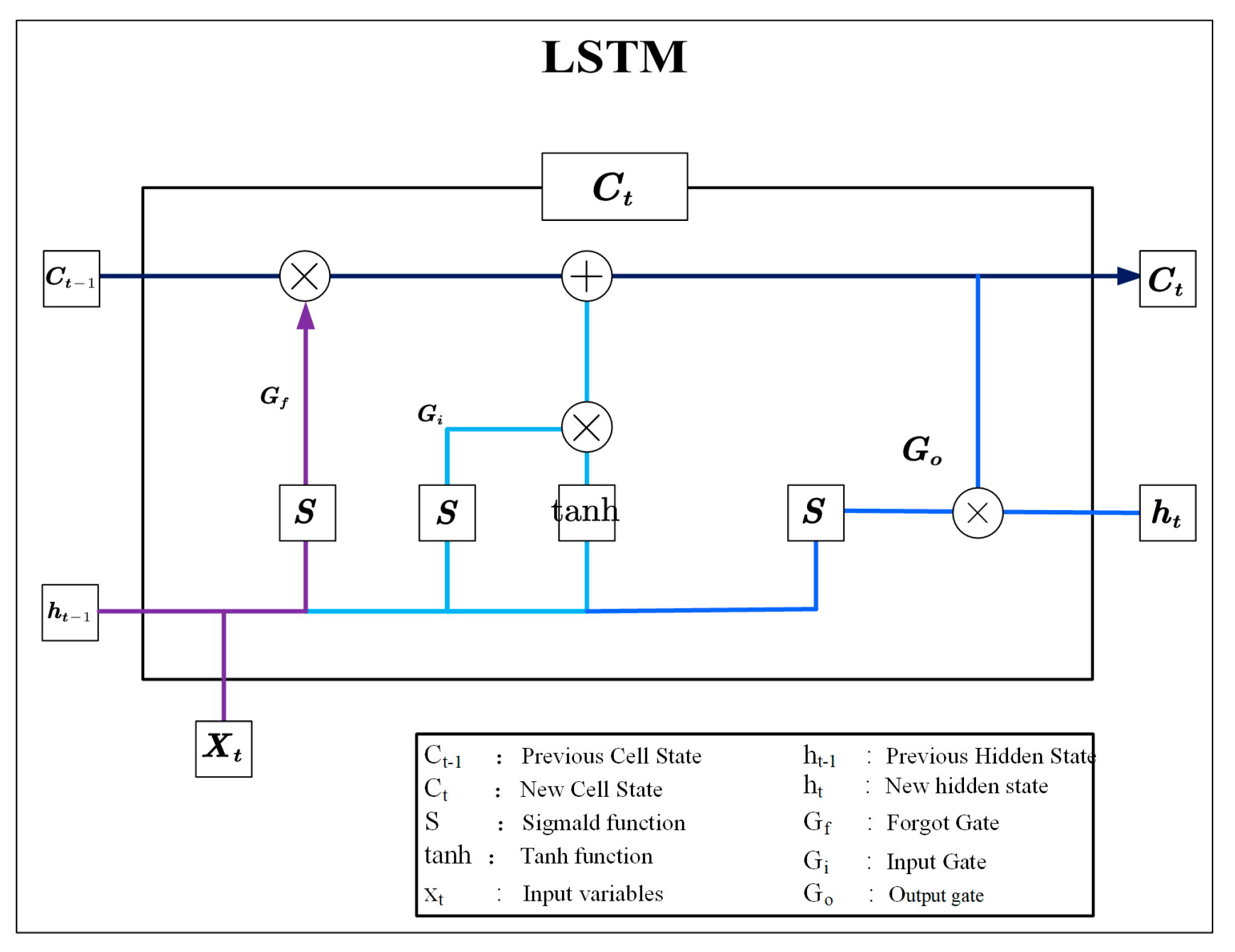
2.2.2. Introduction to LSTM Model
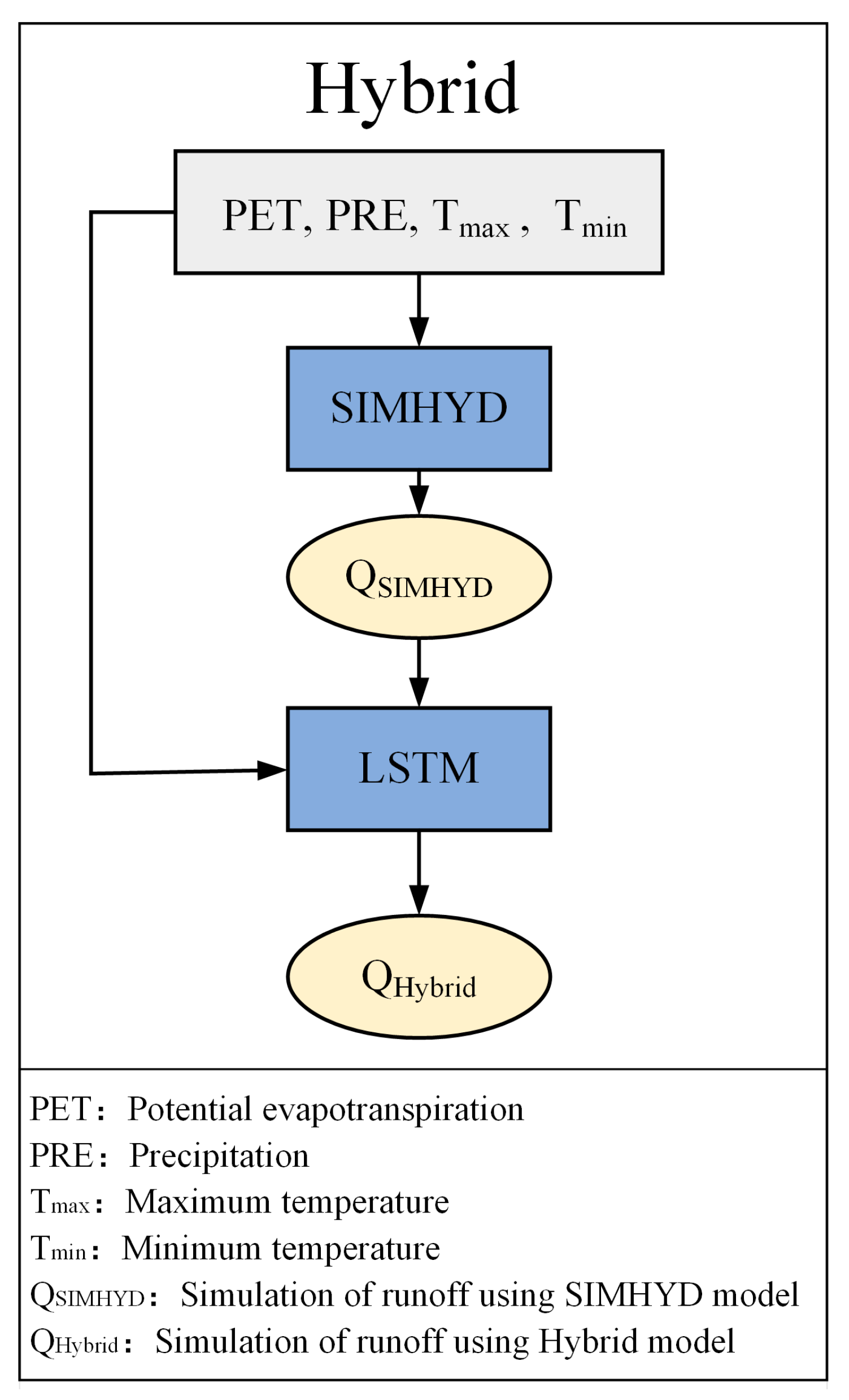
2.2.3. Combined Model Hybrid
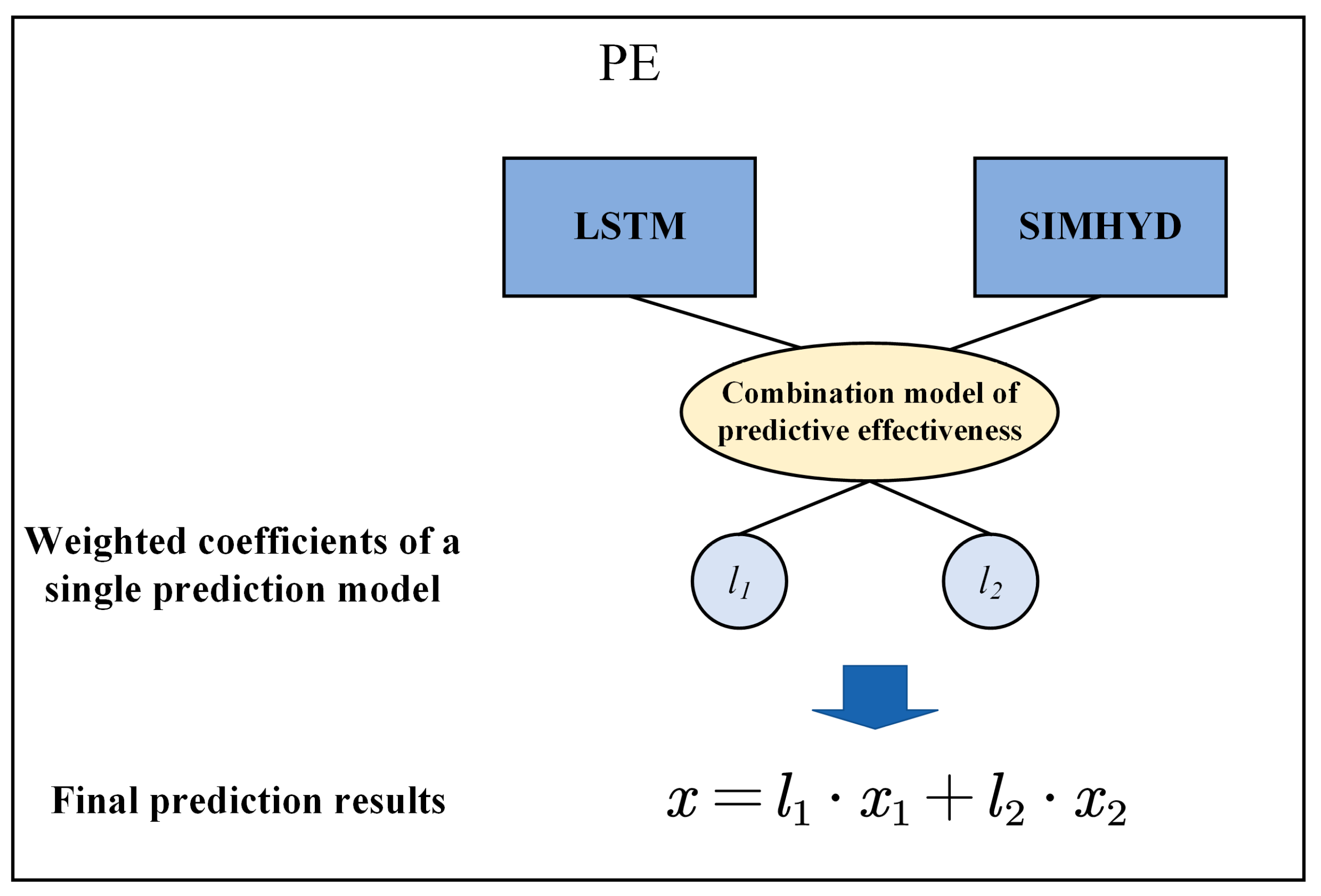
2.2.4. Combined Forecasting Model for Dynamic Prediction Effectiveness
The Combination Prediction Model for Prediction Effectiveness
A Combined Forecasting Model for Dynamic Prediction Effectiveness
2.2.5. Model Evaluation Indicators
3. Results
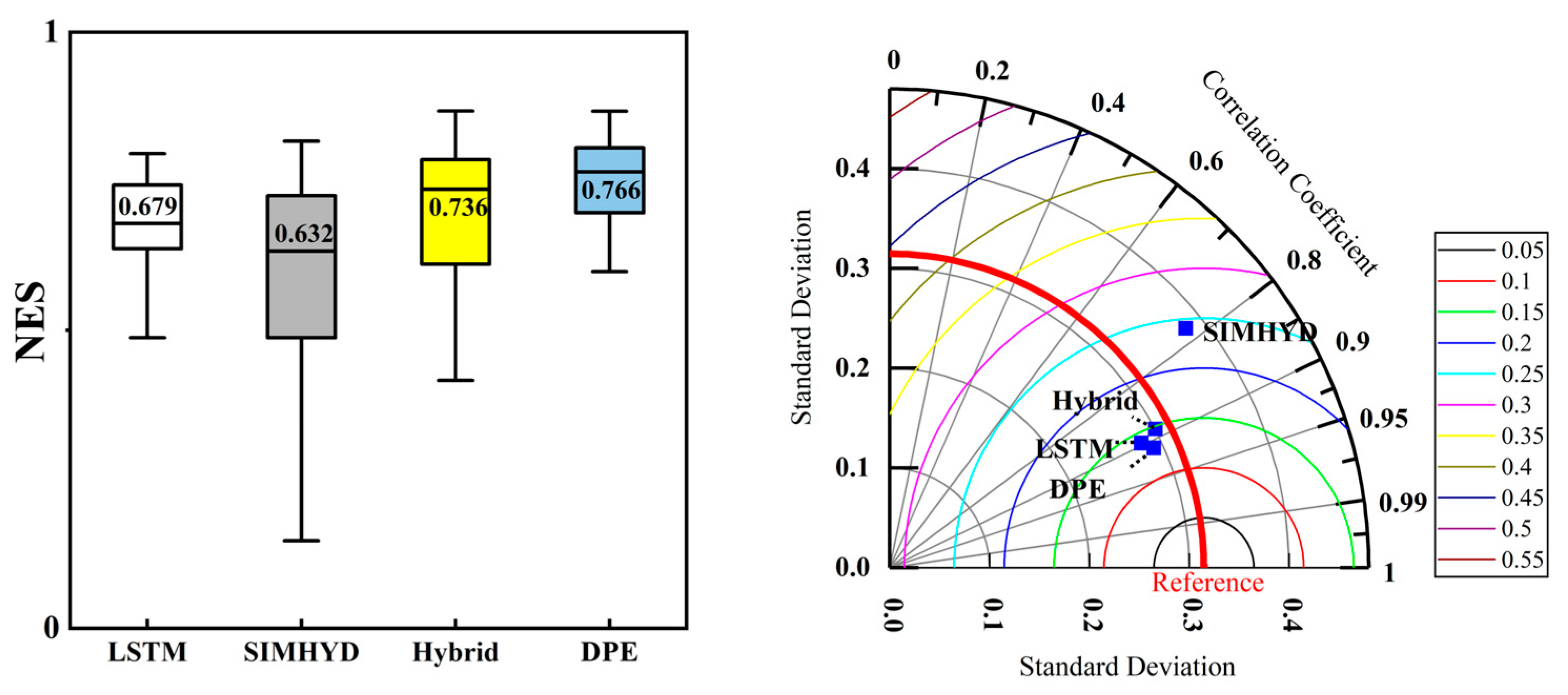
3.1. Model Runoff Simulation Capability
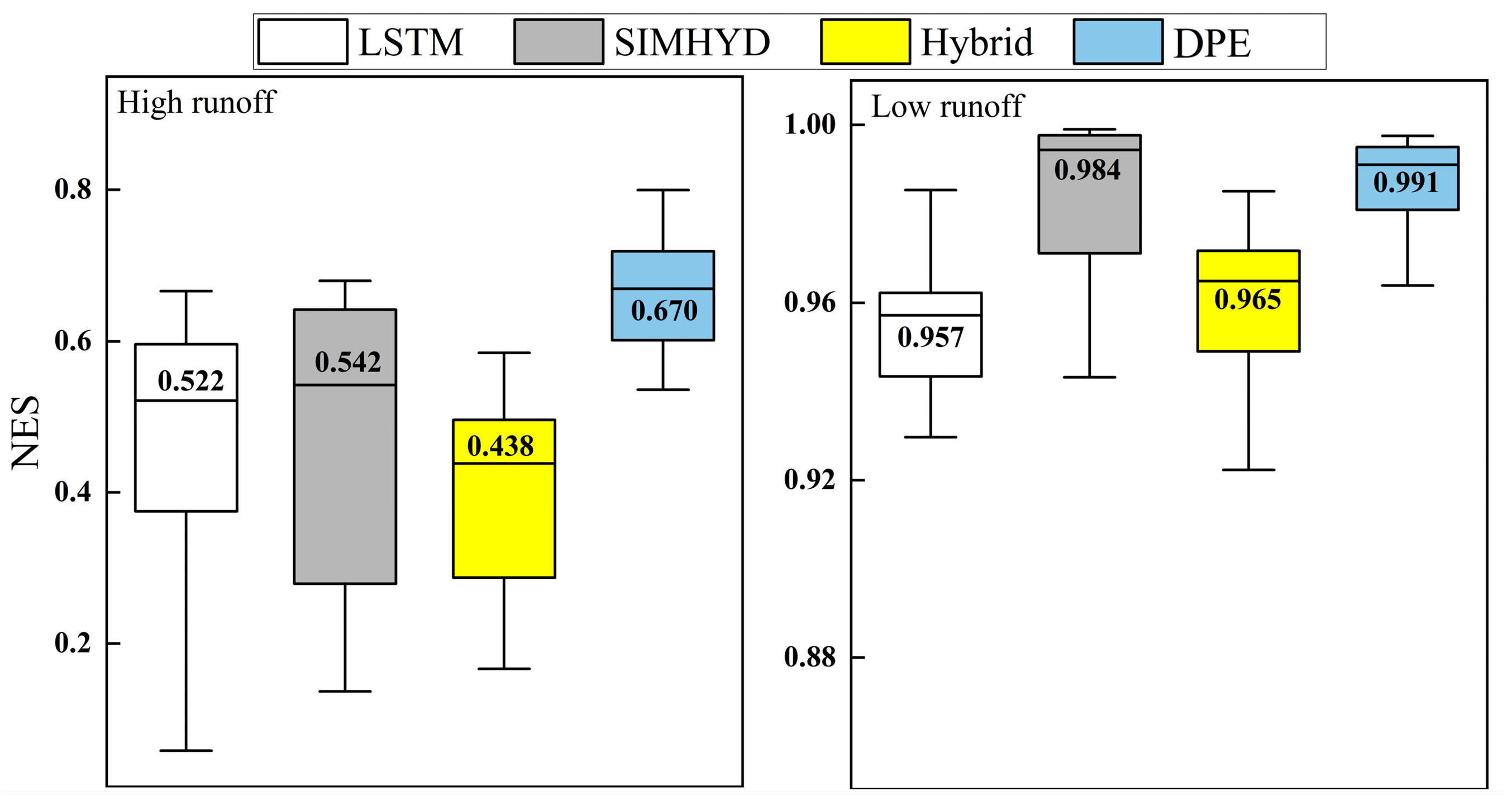
3.2. The Ability of the Model to Simulate Extreme Traffic
4. Discussion
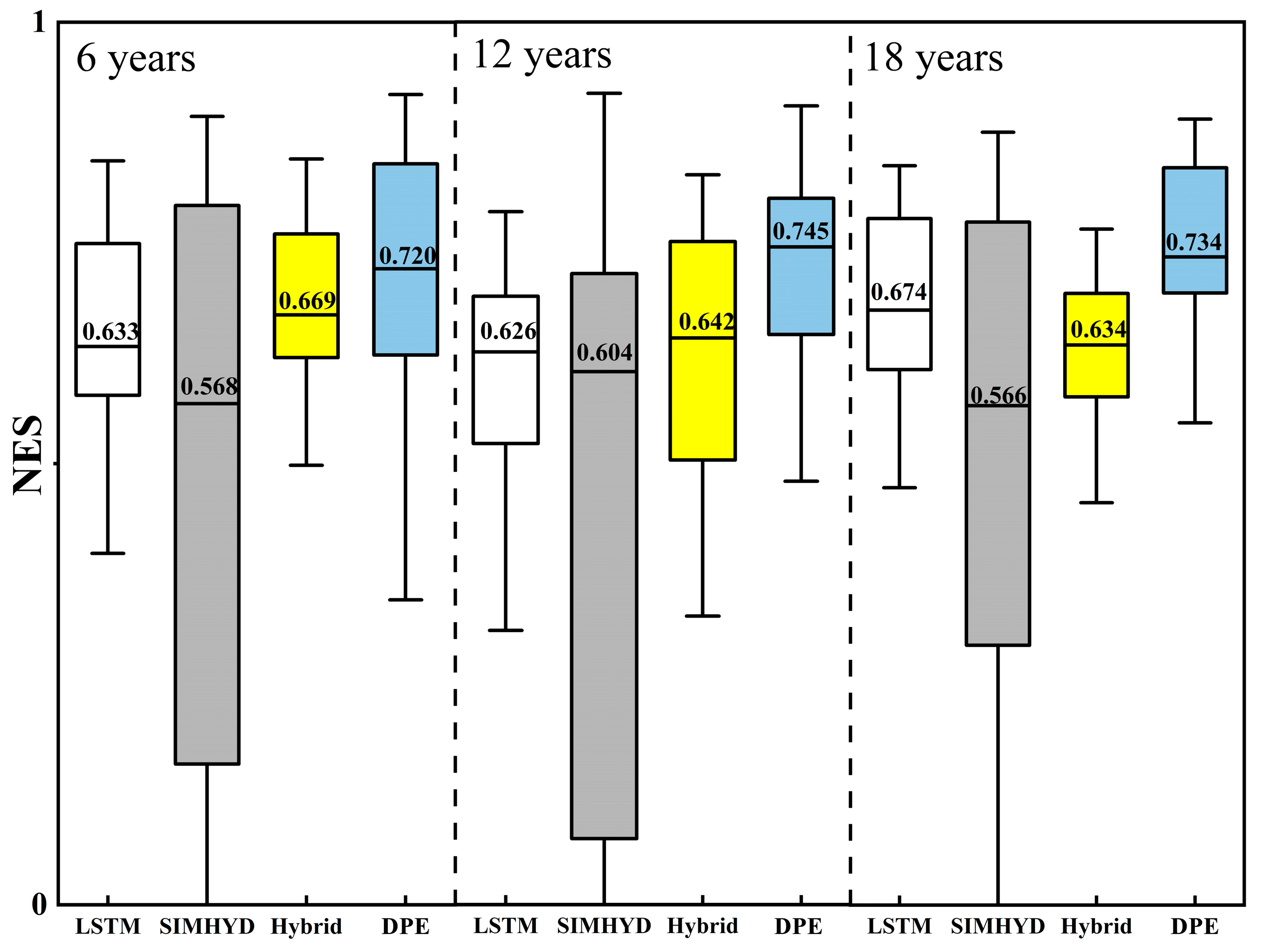
4.1. The Predictive Performance of the Model Under Different Training Periods of Length
4.2. The Runoff Simulation Ability of Individual and Combined Models
4.3. Limitations and Future Challenges
5. Conclusions
- The hybrid model has better runoff simulation capability than traditional hydrological models, significantly improving the median NSE during the validation period.
- The hybrid model DPE performs better in simulating extreme flow conditions than the individual model, contributing to better early warning of floods and droughts.
- The overall improvement in the hybrid model’s performance demonstrates the hybrid model’s ability to improve runoff simulation accuracy. Although this study only selected river basins in Washington State, and the results may not be generalized to other basins, the excellent hybrid approach provided can be used as a reference for other regions. However, there are still some issues that need to be addressed in our future research:
- (1)
- Further optimize the model combination method of the hybrid model to improve its learning ability.
- (2)
- Explore the runoff simulation capability of hybrid models in different climatic regions.
- (3)
- Enhance the model’s ability to simulate high flows and improve its capability to forecast flood disasters.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Doycheva, K.; Horn, G.; Koch, C.; Schumann, A.; König, M. Assessment and weighting of meteorological ensemble forecast members based on supervised machine learning with application to runoff simulations and flood warning. Adv. Eng. Inform. 2017, 33, 427–439. [Google Scholar] [CrossRef]
- Kreibich, H.; Thieken, A.H.; Petrow, T.; Müller, M.; Merz, B. Flood loss reduction of private households due to building precautionary measures—lessons learned from the Elbe flood in August 2002. Nat. Hazards Earth Syst. Sci. 2005, 5, 117–126. [Google Scholar] [CrossRef]
- Blöschl, G.; Sivapalan, M. Scale issues in hydrological modelling: A review. Hydrol. Process. 1995, 9, 251–290. [Google Scholar] [CrossRef]
- Wang, X.; Liu, T.; Yang, W. Development of a robust runoff-prediction model by fusing the rational equation and a modified SCS-CN method. Hydrol. Sci. J. 2012, 57, 1118–1140. [Google Scholar] [CrossRef]
- Gebregiorgis, A.S.; Hossain, F. Understanding the dependence of satellite rainfall uncertainty on topography and climate for hydrologic model simulation. IEEE Trans. Geosci. Remote Sens. 2012, 51, 704–718. [Google Scholar] [CrossRef]
- Burges, S.J. Streamflow prediction: Capabilities, opportunities, and challenges. Hydrol. Sci. Tak. Stock. Look. Ahead 1998, 5, 101–134. [Google Scholar]
- Talei, A.; Chua LH, C. Influence of lag time on event based rainfall–runoff modeling using the data driven approach. J. Hydrol. 2012, 438, 223–233. [Google Scholar] [CrossRef]
- Xiao, W.; Zhou, J.; Yang, J.; Mo, L.; Xu, Z.X.; Yang, Y.Q. Long-term runoff forecast in the middle and lower reaches of the Yangtze River based on machine learning. Water Resour. Power 2022, 40, 31–34+26. [Google Scholar] [CrossRef]
- Nayak, P.; Venkatesh, B.; Krishna, B.; Jain, S.K. Rainfall-runoff modeling using conceptual, data driven, and wavelet based computing approach. J. Hydrol. 2013, 493, 57–67. [Google Scholar] [CrossRef]
- Chang, C.W.; Dinh, N.T. Classification of machine learning frameworks for data-driven thermal fluid models. Int. J. Therm. Sci. 2019, 135, 559–579. [Google Scholar] [CrossRef]
- Gharari, S.; Razavi, S. A review and synthesis of hysteresis in hydrology and hydrological modeling: Memory, path-dependency, or missing physics? J. Hydrol. 2018, 566, 500–519. [Google Scholar] [CrossRef]
- Noble, W.S. What is a support vector machine? Nat. Biotechnol. 2006, 24, 1565–1567. [Google Scholar] [CrossRef]
- Rigatti, S.J. Random forest. J. Insur. Med. 2017, 47, 31–39. [Google Scholar] [CrossRef]
- Yin, C.; Zhu, Y.; Fei, J.; He, X. A deep learning approach for intrusion detection using recurrent neural networks. IEEE Access 2017, 5, 21954–21961. [Google Scholar] [CrossRef]
- Yang, Y.; McVicar, T.R.; Donohue, R.J.; Zhang, Y.; Roderick, M.L.; Chiew, F.H.; Zhang, L.; Zhang, J. Lags in hydrologic recovery following an extreme drought: Assessing the roles of climate and catchment characteristics. Water Resour. Res. 2017, 53, 4821–4837. [Google Scholar] [CrossRef]
- Siami Namini, S.; Namin, A.S. Forecasting economics and financial time series: ARIMA vs. LSTM. arXiv 2018, arXiv:1803.06386. [Google Scholar]
- Amalou, I.; Mouhni, N.; Abdali, A. Multivariate time series prediction by RNN architectures for energy consumption forecasting. Energy Rep. 2022, 8, 1084–1091. [Google Scholar] [CrossRef]
- Man, Y.; Yang, Q.; Shao, J.; Wang, G.; Bai, L.; Xue, Y. Enhanced LSTM model for daily runoff prediction in the upper Huai river basin, China. Engineering 2022, 24, 229–238. [Google Scholar] [CrossRef]
- Kanai, S.; Fujiwara, Y.; Iwamura, S. Preventing gradient explosions in gated recurrent units. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Kim, C.; Kim, C.S. Comparison of the performance of a hydrologic model and a deep learning technique for rainfall-runoff analysis. Trop. Cyclone Res. Rev. 2021, 10, 215–222. [Google Scholar] [CrossRef]
- Yuan, X.; Chen, C.; Lei, X.; Yuan, Y. Monthly runoff forecasting based on LSTM–ALO model. Stoch. Environ. Res. Risk Assess. 2018, 32, 2199–2212. [Google Scholar] [CrossRef]
- Adnan, R.M.; Dai, H.-L.; Mostafa, R.R.; Parmar, K.S.; Heddam, S.; Kisi, O. Modeling multistep ahead dissolved oxygen concentration using improved support vector machines by a hybrid metaheuristic algorithm. Sustainability 2022, 14, 3470. [Google Scholar] [CrossRef]
- Adnan, R.M.; Mostafa, R.R.; Dai, H.-L.; Heddam, S.; Kuriqi, A.; Kisi, O. Pan evaporation estimation by relevance vector machine tuned with new metaheuristic algorithms using limited climatic data. Eng. Appl. Comput. Fluid Mech. 2023, 17, 2192258. [Google Scholar] [CrossRef]
- Okkan, U.; Ersoy, Z.B.; Kumanlioglu, A.A.; Fistikoglu, O. Embedding machine learning techniques into a conceptual model to improve monthly runoff simulation: A nested hybrid rainfall-runoff modeling. J. Hydrol. 2021, 598, 126433. [Google Scholar] [CrossRef]
- Liu, J.; Yuan, X.; Zeng, J.; Jiao, Y.; Li, Y.; Zhong, L.; Yao, L. Ensemble streamflow forecasting over a cascade reservoir catchment with integrated hydrometeorological modeling and machine learning. Hydrol. Earth Syst. Sci. 2022, 26, 265–278. [Google Scholar] [CrossRef]
- Yang, S.; Yang, D.; Chen, J.; Santisirisomboon, J.; Lu, W.; Zhao, B. A physical process and machine learning combined hydrological model for daily streamflow simulations of large watersheds with limited observation data. J. Hydrol. 2020, 590, 125206. [Google Scholar] [CrossRef]
- Liu, Q.; Ma, X.; Yan, S.; Liang, L.; Pan, J.; Zhang, J. Lag in hydrologic recovery following extreme meteorological drought events: Implications for ecological water requirements. Water 2020, 12, 837. [Google Scholar] [CrossRef]
- Yu, Q.; Jiang, L.; Wang, Y.; Liu, J. Enhancing streamflow simulation using hybridized machine learning models in a semi-arid basin of the Chinese loess Plateau. J. Hydrol. 2023, 617, 129115. [Google Scholar] [CrossRef]
- Ackerman, E.A. The Köppen classification of climates in North America. Geogr. Rev. 1941, 31, 105–111. [Google Scholar] [CrossRef]
- Bai, P.; Liu, X.; Yang, T.; Li, F.; Liang, K.; Hu, S.; Liu, C. Assessment of the influences of different potential evapotranspiration inputs on the performance of monthly hydrological models under different climatic conditions. J. Hydrometeorol. 2016, 17, 2259–2274. [Google Scholar] [CrossRef]
- Liu, J.; Du, J.; Wang, F.; Liu, D.L.; Tang, J.; Lin, D.; Tang, Y.; Shi, L.; Yu, Q. Optimal Methods for Estimating Shortwave and Longwave Radiation to Accurately Calculate Reference Crop Evapotranspiration in the High-Altitude of Central Tibet. Agronomy 2024, 14, 2401. [Google Scholar] [CrossRef]
- Proutsos, N.D.; Fotelli, M.N.; Stefanidis, S.P.; Tigkas, D. Assessing the Accuracy of 50 Temperature-Based Models for Estimating Potential Evapotranspiration (PET) in a Mediterranean Mountainous Forest Environment. Atmosphere 2024, 15, 662. [Google Scholar] [CrossRef]
- Chiew FH, S.; Peel, M.C.; Western, A.W. Application and testing of the simple rainfall-runoff model SIMHYD. Math. Models Small Watershed Hydrol. Appl. 2002, 335–367. [Google Scholar]
- Bai, P.; Liu, X.; Xie, J. Simulating runoff under changing climatic conditions: A comparison of the long short-term memory network with two conceptual hydrologic models. J. Hydrol. 2020, 592, 125779. [Google Scholar] [CrossRef]
- Lin, F.; Chen, X.; Yao, H. Evaluating the use of nash-sutcliffe efficiency coefficient in goodness-of-fit measures for daily runoff simulation with SWAT. J. Hydrol. Eng. 2017, 22, 05017023. [Google Scholar] [CrossRef]
- Michaud, J.; Sorooshian, S. Comparison of simple versus complex distributed runoff models on a midsized semiarid watershed. Water Resour. Res. 1994, 30, 593–605. [Google Scholar] [CrossRef]
- Elshorbagy, A.; Simonovic, S.P.; Panu, U.S. Performance evaluation of artificial neural networks for runoff prediction. J. Hydrol. Eng. 2000, 5, 424–427. [Google Scholar] [CrossRef]
- Piotrowski, A.P.; Napiorkowski, J.J. A comparison of methods to avoid overfitting in neural networks training in the case of catchment runoff modelling. J. Hydrol. 2013, 476, 97–111. [Google Scholar] [CrossRef]
- Hong, J.; Wang, Z.; Yao, Y. Fault prognosis of battery system based on accurate voltage abnormity prognosis using long short-term memory neural networks. Appl. Energy 2019, 251, 113381. [Google Scholar] [CrossRef]
- Gu, J.; Zheng, Z.; Lan, Z.; White, J.; Hocks, E.; Park, B.H. Dynamic meta learning for failure prediction in large scale systems: A case study. In Proceedings of the 2008 37th International Conference on Parallel Processing, Portland, OR, USA, 9–12 September 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 157–164. [Google Scholar]
- Zheng, Q.; Yang, M.; Yang, J.; Zhang, Q.; Zhang, X. Improvement of generalization ability of deep CNN via implicit regularization in two-stage training process. IEEE Access 2018, 6, 15844–15869. [Google Scholar] [CrossRef]
- Zhang, G.P.; Qi, M. Neural network forecasting for seasonal and trend time series. Eur. J. Oper. Res. 2005, 160, 501–514. [Google Scholar] [CrossRef]
- Mohammadi, B.; Safari, M.J.S.; Vazifehkhah, S. IHACRES, GR4J and MISD based multi conceptual machine learning approach for rainfall runoff modeling. Sci. Rep. 2022, 12, 12096. [Google Scholar] [CrossRef] [PubMed]
- Zarei, E.; Saleh, F.N.; Dalir, A.N. Comparing the hybrid-lumped-LSTM model with a semi-distributed model for improved hydrological modeling. J. Water Clim. Chang. 2024, 15, 4099–4113. [Google Scholar] [CrossRef]
- Sezen, C.; Šraj, M. Improving the simulations of the hydrological model in the karst catchment by integrating the conceptual model with machine learning models. Sci. Total Environ. 2024, 926, 171684. [Google Scholar] [CrossRef] [PubMed]
- Sharma, S.; Kumari, S. Comparison of machine learning models for flood forecasting in the Mahanadi River Basin, India. J. Water Clim. Chang. 2024, 15, 1629–1652. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, T.; Kang, A.; Li, J.; Lei, X. Research on runoff simulations using deep-learning methods. Sustainability 2021, 13, 1336. [Google Scholar] [CrossRef]
- Lee, M.H.; Im, E.S.; Bae, D.H. Impact of the spatial variability of daily precipitation on hydrological projections: A comparison of GCM-and RCM-driven cases in the Han River basin, Korea. Hydrol. Process. 2019, 33, 2240–2257. [Google Scholar] [CrossRef]
- Kavetski, D.; Fenicia, F.; Clark, M.P. Impact of temporal data resolution on parameter inference and model identification in conceptual hydrological modeling: Insights from an experimental catchment. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Swagatika, S.; Paul, J.C.; Sahoo, B.B.; Gupta, S.K.; Singh, P.K. Improving the forecasting accuracy of monthly runoff time series of the Brahmani River in India using a hybrid deep learning model. J. Water Clim. Chang. 2024, 15, 139–156. [Google Scholar] [CrossRef]
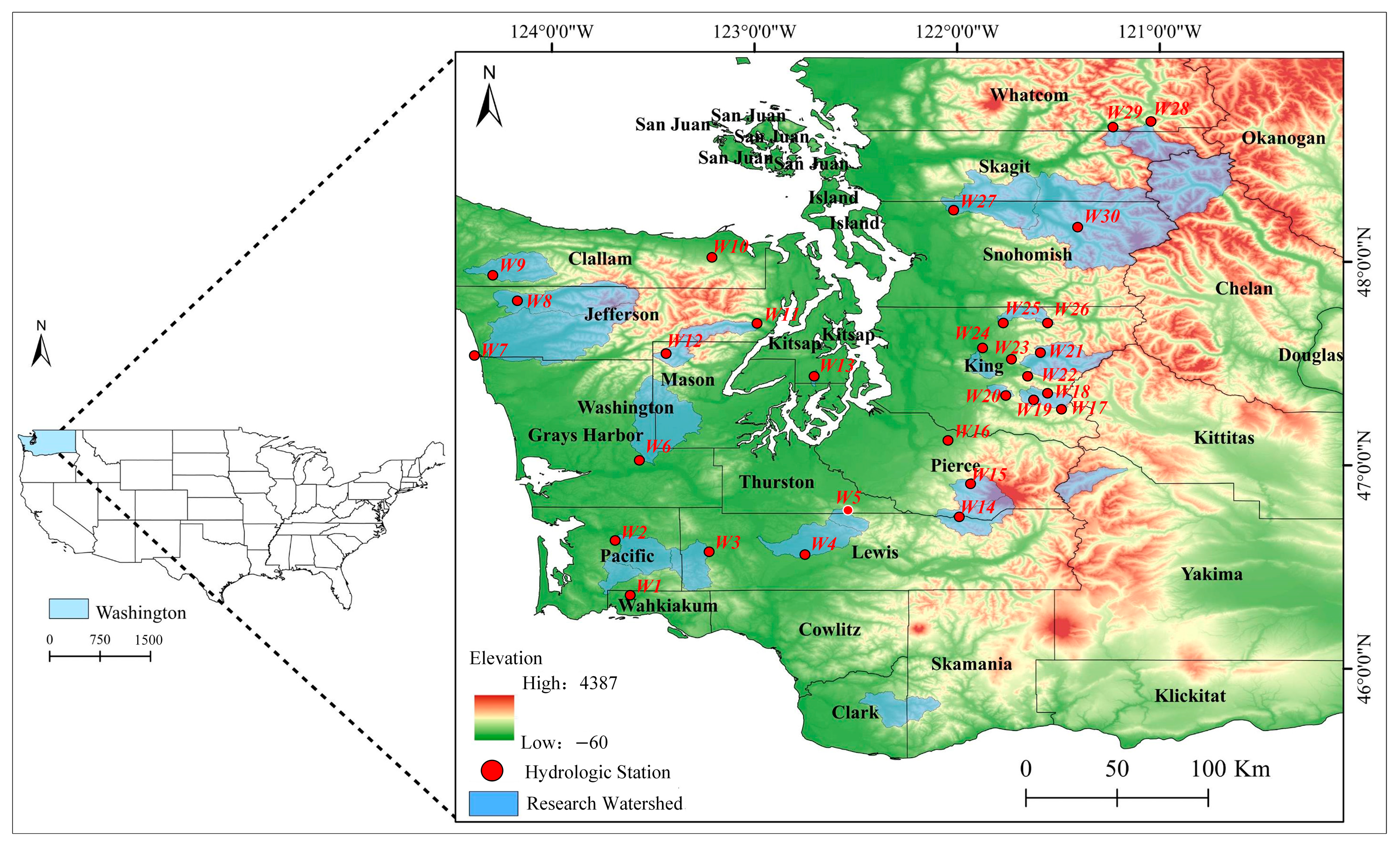


| Site | Hydrological Station Name | Latitude | Longitude |
|---|---|---|---|
| W1 | Naselle River Near Naselle | 46.37 | −123.74 |
| W2 | Willapa River Near Willapa | 46.65 | −123.65 |
| W3 | Chehalis River Near Doty | 46.62 | −123.28 |
| W4 | Newaukum River Near Chehalis | 46.62 | −122.95 |
| W5 | Skookumchuck River Near Vail | 46.77 | −122.59 |
| W6 | Satsop River Near Satsop | 47.00 | −123.49 |
| W7 | Queets River Near Clearwater | 47.54 | −124.32 |
| W8 | Hoh River At Us Highway 101 Near Forks | 47.81 | −124.25 |
| W9 | Calawah River Near Forks | 47.96 | −124.39 |
| W10 | Dungeness River Near Sequim | 48.01 | −123.13 |
| W11 | Duckabush River Near Brinnon | 47.68 | −123.01 |
| W12 | Nf Skokomish R Bl Staircase Rpds Nr Hoodsport | 47.51 | −123.33 |
| W13 | Huge Creek Near Wauna | 47.39 | −122.70 |
| W14 | Nisqually River Near National | 46.75 | −122.08 |
| W15 | Puyallup River Near Electron | 46.90 | −122.04 |
| W16 | South Prairie Creek At South Prairie | 47.14 | −122.09 |
| W17 | Cedar River Below Bear Creek Near Cedar Falls | 47.34 | −121.55 |
| W18 | Cedar River Near Cedar Falls | 47.37 | −121.63 |
| W19 | Rex River Near Cedar Falls | 47.35 | −121.66 |
| W20 | Taylor Creek Near Selleck | 47.39 | −121.85 |
| W21 | Middle Fork Snoqualmie River Near Tanner | 47.49 | −121.65 |
| W22 | Sf Snoqualmie River At Edgewick | 47.45 | −121.72 |
| W23 | Sf Snoqualmie River At North Bend | 47.49 | −121.79 |
| W24 | Raging River Near Fall City | 47.54 | −121.91 |
| W25 | North Fork Tolt River Near Carnation | 47.71 | −121.79 |
| W26 | South Fork Tolt River Near Index | 47.71 | −121.60 |
| W27 | Nf Stillaguamish River Near Arlington | 48.26 | −122.05 |
| W28 | Thunder Creek Near Newhalem | 48.67 | −121.07 |
| W29 | Newhalem Creek Near Newhalem | 48.66 | −121.24 |
| W30 | Sauk River Ab Whitechuck River Near Darrington | 48.17 | −121.47 |
| Parameter | Setting Values | Parameter | Setting Values |
|---|---|---|---|
| Number of hidden units | 32 | Abandonment rate | 0.4 |
| Maximum Number of Iterations | 300 | Gradient truncation threshold | 1 |
| optimizer | Adam | Learning rate reduction cycle | 200 |
| Batch size | 32 | Learning rate reduction factor | 0.1 |
| Initial learning rate | 0.005 |
| Model | Input | Output | Target |
|---|---|---|---|
| SIMHYD | PRE, Tmax, Tmin, PET | Qsimhyd | Qobs |
| LSTM | PRE, Tmax, Tmin, PET | Qlstm | Qobs |
| Hybrid | PRE, Tmax, Tmin, PET, Qsimhyd | Qhybrid1 | Qobs |
| NES | R2 | |||||||
|---|---|---|---|---|---|---|---|---|
| LSTM | SIMHYD | Hybrid | DPE | LSTM | SIMHYD | Hybrid | DPE | |
| W1 | 0.751 | 0.783 | 0.752 | 0.853 | 0.897 | 0.788 | 0.921 | 0.928 |
| W2 | 0.764 | 0.819 | 0.738 | 0.850 | 0.901 | 0.830 | 0.912 | 0.922 |
| W3 | 0.680 | 0.719 | 0.688 | 0.779 | 0.779 | 0.727 | 0.817 | 0.821 |
| W4 | 0.774 | 0.801 | 0.595 | 0.840 | 0.894 | 0.836 | 0.793 | 0.931 |
| W5 | 0.742 | 0.756 | 0.715 | 0.821 | 0.853 | 0.802 | 0.873 | 0.881 |
| W6 | 0.795 | 0.793 | 0.752 | 0.889 | 0.891 | 0.805 | 0.914 | 0.919 |
| W7 | 0.778 | 0.820 | 0.755 | 0.858 | 0.869 | 0.855 | 0.872 | 0.900 |
| W8 | 0.772 | 0.747 | 0.673 | 0.789 | 0.853 | 0.798 | 0.850 | 0.854 |
| W9 | 0.777 | 0.545 | 0.688 | 0.817 | 0.851 | 0.664 | 0.853 | 0.857 |
| W10 | 0.542 | 0.274 | 0.505 | 0.697 | 0.558 | 0.352 | 0.538 | 0.719 |
| W11 | 0.535 | 0.696 | 0.473 | 0.767 | 0.549 | 0.735 | 0.536 | 0.804 |
| W12 | 0.618 | 0.671 | 0.542 | 0.786 | 0.656 | 0.678 | 0.644 | 0.816 |
| W13 | 0.717 | 0.546 | 0.674 | 0.788 | 0.792 | 0.553 | 0.790 | 0.838 |
| W14 | 0.667 | 0.635 | 0.610 | 0.766 | 0.715 | 0.648 | 0.727 | 0.816 |
| W15 | 0.757 | 0.727 | 0.752 | 0.854 | 0.906 | 0.750 | 0.910 | 0.931 |
| W16 | 0.729 | 0.708 | 0.677 | 0.815 | 0.810 | 0.720 | 0.837 | 0.851 |
| W17 | 0.771 | 0.779 | 0.759 | 0.883 | 0.898 | 0.797 | 0.911 | 0.909 |
| W18 | 0.751 | 0.700 | 0.692 | 0.856 | 0.823 | 0.761 | 0.829 | 0.869 |
| W19 | 0.677 | 0.063 | 0.593 | 0.698 | 0.719 | 0.613 | 0.804 | 0.812 |
| W20 | 0.734 | 0.766 | 0.708 | 0.870 | 0.841 | 0.828 | 0.827 | 0.878 |
| W21 | 0.697 | 0.339 | 0.732 | 0.813 | 0.751 | 0.469 | 0.821 | 0.855 |
| W22 | 0.643 | 0.527 | 0.697 | 0.813 | 0.676 | 0.549 | 0.803 | 0.854 |
| W23 | 0.554 | 0.501 | 0.488 | 0.606 | 0.571 | 0.503 | 0.604 | 0.624 |
| W24 | 0.700 | 0.774 | 0.670 | 0.858 | 0.752 | 0.782 | 0.822 | 0.870 |
| W25 | 0.517 | 0.513 | 0.570 | 0.612 | 0.539 | 0.001 | 0.573 | 0.632 |
| W26 | 0.665 | 0.705 | 0.741 | 0.802 | 0.740 | 0.730 | 0.860 | 0.893 |
| W27 | 0.678 | 0.720 | 0.676 | 0.828 | 0.745 | 0.729 | 0.773 | 0.860 |
| W28 | 0.082 | 0.208 | 0.132 | 0.288 | 0.115 | 0.218 | 0.133 | 0.297 |
| W29 | 0.713 | 0.788 | 0.783 | 0.855 | 0.894 | 0.795 | 0.911 | 0.923 |
| W30 | 0.704 | 0.788 | 0.736 | 0.844 | 0.856 | 0.788 | 0.899 | 0.906 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Li, J.; Zhao, H.; Wang, W.; Lv, N.; Zhang, B.; Liu, Y.; Yang, X.; Guo, M.; Dong, Y. Impact Assessment of Coupling Mode of Hydrological Model and Machine Learning Model on Runoff Simulation: A Case of Washington. Atmosphere 2024, 15, 1461. https://doi.org/10.3390/atmos15121461
Zhang J, Li J, Zhao H, Wang W, Lv N, Zhang B, Liu Y, Yang X, Guo M, Dong Y. Impact Assessment of Coupling Mode of Hydrological Model and Machine Learning Model on Runoff Simulation: A Case of Washington. Atmosphere. 2024; 15(12):1461. https://doi.org/10.3390/atmos15121461
Chicago/Turabian StyleZhang, Junqi, Jing Li, Huiyizhe Zhao, Wen Wang, Na Lv, Bowen Zhang, Yue Liu, Xinyu Yang, Mengjing Guo, and Yuhao Dong. 2024. "Impact Assessment of Coupling Mode of Hydrological Model and Machine Learning Model on Runoff Simulation: A Case of Washington" Atmosphere 15, no. 12: 1461. https://doi.org/10.3390/atmos15121461
APA StyleZhang, J., Li, J., Zhao, H., Wang, W., Lv, N., Zhang, B., Liu, Y., Yang, X., Guo, M., & Dong, Y. (2024). Impact Assessment of Coupling Mode of Hydrological Model and Machine Learning Model on Runoff Simulation: A Case of Washington. Atmosphere, 15(12), 1461. https://doi.org/10.3390/atmos15121461





