1. Introduction
A variety of granular materials (raw materials, semi- and final products, waste, etc.) are typically stacked in the open yards of mineral and metallurgical industrial sites, and thus exposed to the wind erosive action (i.e., industrial wind erosion). The emission of Particulate Matter (PM) from those exposed erodible surfaces may represent an important impact factor for human health and the environment as a whole.
To design and implement effective measures of emission reduction and control, it is essential to assess the emission potential of the bulk materials under consideration. The evaluation of a source emission potential by means of on-site measurements is subjected to several complexities, as the emission depends on the specific meteorological conditions (mainly wind speed and direction), the physical and chemical properties of the granular material under investigation (moisture content, specific weight, particle size distribution, aggregation state, presence of crusts) and the specific geometry of the open storage (stockpile type, shape and dimension), which can also vary over time and space within the same industrial yard. As a consequence, several studies have been carried out over the last few decades, using Environmental Wind Tunnels (EWTs) to allow for the simulation of the exposure conditions and isolate the influence of the many influencing variables [
1,
2,
3,
4,
5,
6,
7,
8]. The EWTs are designed to reproduce the Atmospheric Boundary Layer (ABL) observed on-site and analyze the effect of the wind action on samples of the erodible materials under investigation. The correct reproduction of the ABL is the basis for the reliability and significance of the PM concentration measurements, which are subsequently carried out as part of the experimental research to determine the site-specific Emission Factor (EFs) of the investigated erodible materials. Depending on the characteristics of the ABL to be reproduced, various EWT layouts are proposed by the technical literature, based on different combinations of turbulence generators and surface roughness elements [
9,
10,
11,
12]. Whatever the chosen layout, once built-up the EWT needs to be validated by measuring the wind velocity inside the tunnel and comparing the simulated wind profiles with the ABL assumed to be the design target.
Previous studies have been carried out in Cagliari University (
Department of Civil and Environmental Engineering and Architecture (DICAAR)) using a first EWT design to estimate the PM emission potential of granular raw materials (typically used in the industrial plants that operates in southern Sardinia, Italy) and muds disposed in tailing basins (i.e., landfill of mineralogical processing residue) [
5,
6,
13]. The research on red mud basins [
5], in particular, led to the definition of a site-specific EF that describes the relationship between the PM emission and the main influencing parameters (wind friction speed and mud water content).
Recently, an updated EWT has been designed and built up in Cagliari University. The new tunnel was set-up using specific turbulence generators (spires) and surface roughness elements with the aim of simulating the wind velocity profiles that develop over the surfaces of coarse and heterogeneous granular materials. The EWT’s ability to generate the desired wind profiles was verified through wind velocity tests.
In addition, a Computational Fluid Dynamics (CFD) 3D model of the EWT has been developed. The tunnel CFD model is conceived as a complementary tool to the experimental apparatus, which is necessary to analyze the erosive and emissive processes within the entire tunnel volume. The data derived from the CFD simulation complete the results of the experimental measurements (e.g., wind speed or PM concentration measurements), which are typically carried out in a discrete number of points within selected tunnel cross-sections. Furthermore, the CFD model will enable a preliminary observation of the wind field generated in the tunnel deriving from changes in its configuration [
14,
15,
16,
17]. The accuracy of the CFD model has been verified by comparing the simulation data with the results of the experimental measurements.
This article discusses the main characteristic of the updated DICAAR EWT, the results of the validation procedure and the potential offered by the integrated use of the CFD model and the experimental apparatus.
2. The Updated Environmental Wind Tunnel
2.1. Design and Construction
The updated DICAAR EWT in
Figure 1 (top and side view) consists of three main sections: a 1.9 m long Convergence Section, an 8.1 m long Working Section (0.93 m high and 0.75 m wide), including a 5.1 m long Flow Development Section and a 3 m long Test Section, and a final 1.4 m long Drive Section.
The Convergence Section (CS) promotes the acceleration and the alignment of the airflow and simultaneously reduces the air turbulence [
18,
19,
20,
21]. The ambient air enters the tunnel through a 1.60 m high and 1.10 m wide honeycomb flow straightener (i.e., a grid of small hexagonal cells). The honeycomb cells have a length-to-diameter ratio of 8, which effectively aligns the airflow parallel with the longitudinal axis of the tunnel [
19,
20].
The CS is followed by the Flow Development Section (FDS) that allows for the full development of the required Atmospheric Boundary Layer (ABL) before the Test Section (TS). In the TS floor, a 1 m long, 0.02 m deep and 0.2 m wide niche is provided to insert the aluminum tray that contains the sample of granular material to be tested, so that the sample surface and the wind tunnel floor define a continuous horizontal plane. Two collecting devices are installed at the TS entrance and 2.3 m downstream, to allow for the interception of the airflow and the connection with the measurement instruments placed outside the tunnel. The position of those devices can be adjusted to any distance from the floor and the lateral walls, to cover all measurement points within two designed reference cross-sections. Specifically, wind velocity measurements are taken at the first reference cross-section (device U in
Figure 1) by means of a Pitot tube anemometer, whereas PM concentration measurements are taken upwind and downwind of the sample tray (device U and D in
Figure 1) with two dust analyzers (DustTrak DRX 8533). The Drive Section (DS) is designed to provide a regular transition from the rectangular to the circular cross-section and enable the installation of the 5.5 kW axial suction fan at the end of the tunnel. In
Figure 2, two photographs of the new EWT are presented: (a) view from the tunnel entrance (CS, with the honeycomb flow straightener); (b) view from the tunnel exit (DS, with the fan).
2.2. Advancements in Design and Construction
Compared to the original design [
5], the new EWT has larger dimensions: the height and width of the cross-section are increased by 50% in order to minimize the edge effects of the walls, especially downstream of the Test Section (TS), where the PM concentration measurements are to be performed. The walls are made of transparent material in order to improve the operational management of the experimental phase (for example, the correct positioning of the measurement probes and the subsequent control/adjustment during experimental tests), and also to enable a visual observation of the erosion and emission processes under investigation. The transparency of the walls, in particular, will allow for the video-recording of those processes with high-speed cameras and the reconstruction of the particle motion in the emission phase (Particle Image Velocimetry (PIV) methods): the acquired visual data will constitute the experimental basis for the development of the emission physical models.
2.3. Setup
The tunnel setup is based on the specific material to be tested and requires the correct sizing of the spires (i.e., passive turbulence generators at the tunnel entrance) and the reproduction of the appropriate roughness on the pavement along the FDS (the same roughness of the material to be tested).
The tunnel is, in fact, designed to simulate the ABL that takes form over erodible surfaces of assigned roughness (friction coefficient).
Equation (1) is the power law that represents the wind profile to be simulated within the test section:
where
α is the friction coefficient (i.e., Hellman exponent),
δ is the ABL thickness to be simulated,
u(
z) is the wind velocity at a given distance
z from the tunnel floor, and
uδ is the wind velocity at
z =
δ.
Once the target parameters
α and
δ are defined, the dimensions of the spires can be calculated, according to Irwin [
12], with Equations (2) and (3):
where
h and
b are the height and the base of the spires,
α and
δ are the project parameters,
H is the wind tunnel height in the working section, and
ψ is a function of
α and
δ [
12]. According to Irwin, the designed spires generate the target ABL at a distance that is 6 times
h (length that ensures the lateral uniformity of the flow when the spires are spaced at intervals of
h/2).
The project value δ was set at 0.45 m, about half the FDS height, according to Al Nehari [
21]. The Hellman exponent (α) was set at 0.16, referring to the recommendation of the technical literature for
open terrain [
22,
23]. The spires were designed according to Equations (2) and (3): 57 cm high and 6.5 cm wide spires were spaced at 25 cm (
Figure 3). Downstream of the spires, the tunnel floor was covered with coarse-grit sandpaper (P20) to simulate the surface roughness of the erodible surfaces under study.
2.4. Experimental Validation
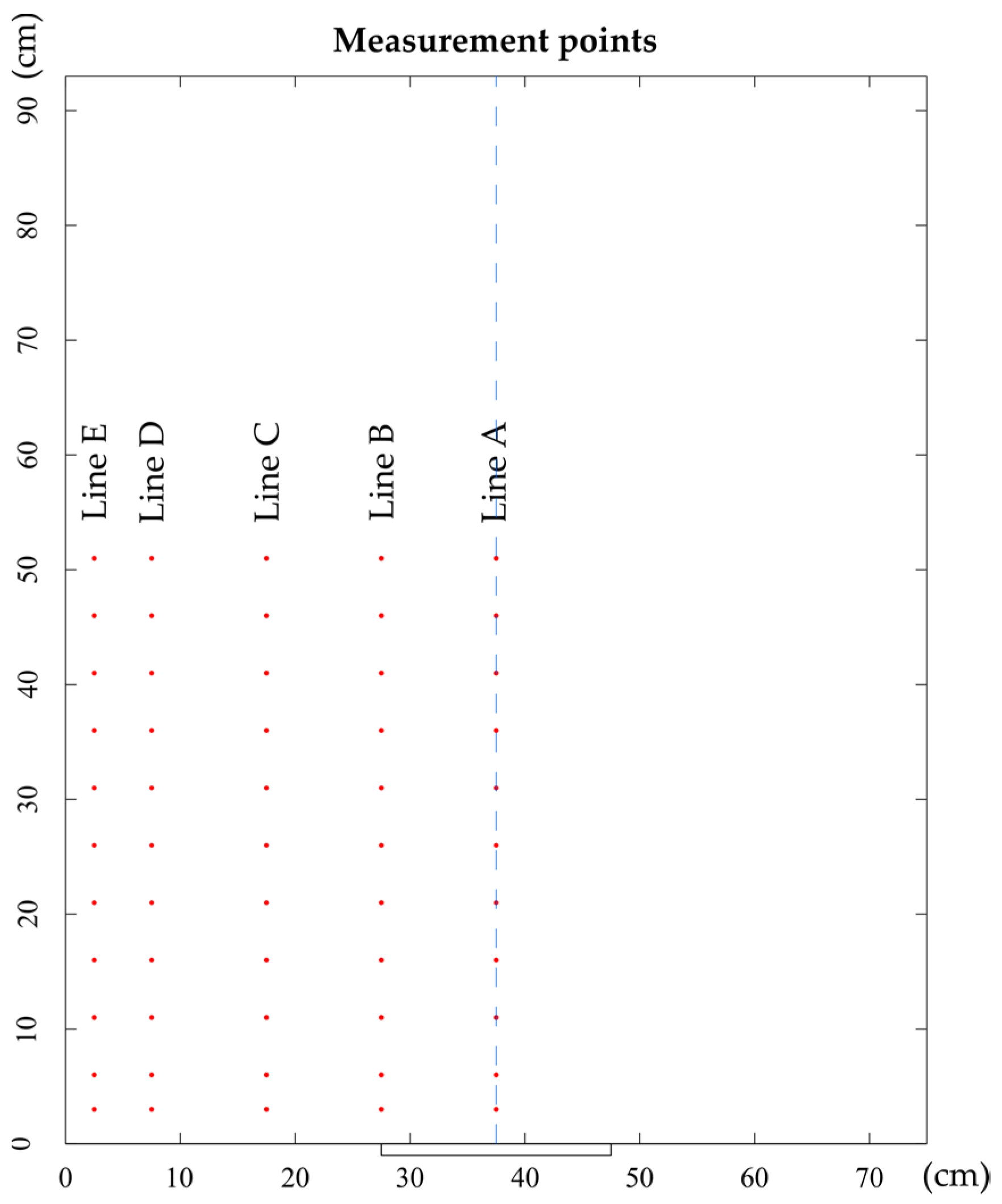
A series of wind velocity measurements were performed at the reference cross-section located at the entrance of the test section, aiming to verify the tunnel’s ability to replicate the required ABL. The wind velocity was measured at 55 points along five different vertical lines lying on the reference cross-section (
Figure 4): line A (the symmetry vertical axis of the tunnel cross-section, 37.5 cm from the side walls), lines B, C, D and E (27.5 cm, 17.5 cm, 7.5 cm and 2.5 cm from the wind tunnel wall, respectively). The measurements covered only half of the cross-section, assuming the lateral flow symmetry.
Along each line, 11 measurement points were located between 3 and 51 cm above the tunnel floor; at each point, the measurement was extended to 300 s, to reach a steady value of the integrated mean speed. The Turbulence Intensity (TI) was calculated at each point as the ratio between the standard deviation and the mean value of the wind velocity. The measurements were carried out at two different operating velocities of the fan: 1500 and 2700 RPM.
The experimental data measured at the red points indicated in
Figure 4 were interpolated using the MATLAB software (MATLAB R2022a) to create plots of the wind velocity and the TI field (
Figure 5 and
Figure 6, respectively). In both figures, the dashed white vertical lines define the lateral limits of the sample tray.
Figure 5 illustrates the increase in wind speed as the measurement points get farther from the tunnel walls, both laterally and vertically.
Figure 6 shows a decrease in the turbulence intensity with increasing distance from the walls, with values dropping below 1% within undisturbed regions. Both figures emphasize the lateral uniformity of the air flow within the test area (i.e., the absence of effects induced by the side walls at distances greater than 15–20 cm). Hence, the location of the insertion niche, which is meant to contain the tray with the sample of the material to be tested, with longitudinal boundaries located at 27.5 cm from the tunnel vertical walls, is appropriately designed.
Table 1 reports the wind velocity values measured along line A (centerline of the wind tunnel cross-section): the data show that the air velocity is no longer influenced by the tunnel floor for distances above 0.41 m. The values of the ABL thickness (δ) and the friction coefficient (α) were determined by fitting the power-law wind profile (Equation (1)) to the wind velocity data taken along line A.
The fitting is illustrated in
Figure 7 and
Figure 8, which refer to fan operating speeds of 1500 and 2700 RPM, respectively. In both figures, the
x-axis represents the distance from the measurement point from the wind tunnel floor, while the
y-axis represents the ratio of the velocity u to the velocity at z = δ. The red points represent the experimental values and the blue curve represents the power-law fit. The fitting results are summarized in
Table 2, showing that the curve’s adaptation to the experimental data is very accurate (R
2 equal to 0.98 for both fan-operating velocities). The values obtained for the parameters α (arithmetic mean = 0.17) and δ (arithmetic mean = 0.46 m) were consistent with the values set as project parameters (0.16 and 0.45 m, respectively).
3. CFD Modelling
3.1. Methodology
The CFD model of the EWT was developed using the ANSYS Fluent 2022 R2 software. The tunnel’s geometry and the mesh were created using the Ansys Design Modeler and the Ansys Meshing applications, respectively.
Only half of the geometry was modelled to enhance the computational efficiency, taking into account the symmetry of the tunnel with respect to its vertical mid-longitudinal plane. This approach allowed for a reduction in the number of mesh elements, and thus the simulation time. An unstructured mesh was employed, comprising approximately 4.7 million tetrahedral cells, as illustrated in
Figure 9. An optimal control volume discretization strategy was adopted to locally refine the mesh (lower image in
Figure 9). Mesh face sizing was implemented for the spires, while an inflation layer was added to the bottom wall of the working section to achieve an acceptable value for y+.
The model was set to replicate the wind conditions generated in the tunnel during the velocity tests (operating speeds of 1500 and 2700 RPM). To achieve this purpose, a three-dimensional steady-state approach was implemented, using the Reynolds-averaged Navier–Stokes (RANS) method, with the k-w SST turbulence model.
Inlet and outlet velocity boundary conditions were set on the basis of the velocity data measured during the tests. Symmetric boundary conditions were applied at the midplane, while the tunnel’s top, lateral, and bottom walls were set as no-slip walls. The roughness of the bottom wall (i.e., pavement) was set at 1 × 10−4 m.
The Coupled solution approach was employed in the pressure–velocity algorithm and a second-order upwind scheme was applied to the momentum, turbulent kinetic energy, and specific dissipation rate equations. Convergence was considered to be achieved when the outlet mass flow rate remained stable.
Mesh Independence Study
The adequacy of the mesh used for the CFD model was assessed using the Grid Convergence Index Method (GCI), which is widely adopted to estimate the discretization error associated with CFD studies. The GCI is derived from Roache’s generalized Richardson extrapolation method, which quantifies numerical uncertainty regarding spatial and temporal discretization errors [
24]. Specifically, the relative error of the grid independence test necessitates solutions from three grids with varying resolutions. The GCI can be computed using Equation (4) [
25]:
where
is 1.25, as recommended by Roache for three or more grids [
24],
is the approximate relative error,
is the grid refinement ratio, and
is the order of accuracy.
Three grids were tested with fine, medium, and coarse dimensions having 4,771,224, 3,537,397, and 2,688,657 cells, respectively. The grid independence test and the wind speed predictions were evaluated at three different positions along the vertical mid-longitudinal plane (y = 0 m): 0.50 m from the inlet of the FDS (position a), 2.5 m from the inlet of the FDS (position b), and test section inlet (position c). A total of 60 points were taken for each grid.
The average GCI values were 0.12%, 0.51%, and 0.26%, respectively, for the three positions (a, b, and c). These results indicate that the discretization error remains within the acceptable limits (<1%) so that the numerical solutions produced by the three grids were almost equivalent. The outcome is confirmed by
Figure 10, which indicates that the wind profiles obtained with the three grids exhibit good relative agreement. Even though, when using the coarser grids, the results were quite satisfactory, the computational cost involved in adopting the fine grid was judged to be acceptable. Therefore, it was decided to adopt the fine grid in order to ensure that the best possible results were produced.
3.2. Results
The results of the CFD simulations were used to analyze the wind velocity field development within the EWT. To this purpose, the wind velocity magnitude contours were plotted at the control sections positioned at 0.5, 1, 1.5, 2.5, 5, 6, and 7 m from the inlet of the FDS. The first four control sections are within the FDS, the fifth is located at the transition between the FDS and the TS, while the last two are placed within the TS, at the ends of the sample section.
Figure 11 and
Figure 12 illustrate the influence of the spires on the wind velocity field generation. The spires induce turbulence on the wind tunnel floor, which is crucial for creating wind velocity profiles that are representative of the real scale environmental conditions. The turbulence generates non-uniform wind velocity fields on the horizontal plane of the FDS for approximately three meters. However,
Figure 11 highlights that, within the three control sections in the TS, at 5, 6, and 7 m from the spires (last three plots in
Figure 11), the velocity fields exhibit good lateral uniformity.
Figure 12 shows that the wind field is fully stabilized before entering the FDS. The simulated velocity fields at the inlet of the Test Section are presented in
Figure 13 for the two operating regimes (1500 and 2700 RPM).
Table 3 presents the simulated velocity values at the measuring points along line A, which were investigated as part of the experimental validation (
Section 2.4). The comparison between the data in
Table 3 (simulation) and
Table 2 (measurement) reveals that in the CFD simulation the wind velocity values were overestimated by about 5%. The power law fitting was applied to the dataset reported in
Table 3, as shown in
Figure 14 and
Figure 15, where the simulated wind velocity data are the red dots and the adaptation of the power law is the blue curve. The results of the fitting to the simulated data are reported in
Table 4.
The results in
Table 4 lead to the following main observations:
- -
The wind power law was adapted with great accuracy to the simulated velocity data (R2 = 0.97).
- -
The value of the ABL thickness (δ), determined by fitting the power law to the simulated data (δ = 0.45 m), was found to be in close agreement with that determined from the experimental data (δ = 0.46 m).
- -
The value of the friction coefficient (α = 20) was found to be of the same order of magnitude but not perfectly aligned with the value derived from the measurements (α = 0.17).
4. Discussion
An EWT was designed and set up using specific turbulence generators and roughness elements to reproduce the ABL (i.e., target ABL) that develops over the wide and flat surfaces of coarse and heterogeneous granular materials. Wind speed measurements were performed inside the tunnel test section and a CFD model was developed to study the wind speed field within the entire tunnel volume. Therefore, a first verification concerned the comparison between the measured velocity values (experimental data) and those simulated with the CFD model, with the aim of validating the CFD model to be used in the subsequent analysis of the wind field within the entire tunnel volume.
To achieve this purpose, a comparison of the simulated and measured wind profiles is illustrated in
Figure 16 (for the fan-operating velocity of 2700 RPM), which leads to the following considerations:
- -
The simulated and measured wind velocities progressively decrease as the points approach the tunnel floor due to the combined effect of the spires and the roughness of the floor surface.
- -
The simulated wind velocity fields, as well as those experimentally measured, exhibit good lateral uniformity in the area designated for the sample tray placement (located at a distance greater than 25 cm from the tunnel side walls).
- -
The simulated wind velocity values were found to be slightly higher compared to the measured values across the entire measurement cross-section. This fact becomes apparent near the lateral walls, where the assumed surface roughness value was probably slightly underestimated.
As mentioned before, the value of the friction coefficient derived from the CFD simulation (α = 20) was found to be higher than that deriving from the experimental test (α = 17). That difference in α is highlighted in
Figure 17, which shows that the curve representing the fit of the simulated data (in blue) has a higher gradient than that representing the experimental data (in red).
A second verification was performed to assess the correctness of the tunnel design and set-up. This involved a comparison between the wind field reproduced in the tunnel, which can be known on the basis of both the velocity measurements and the results of the model simulations, with the target ABL.
Table 5 shows the values of the parameters of the ABL equation (α and δ), which were originally set as project objectives (i.e., target parameters), those that were obtained experimentally and those derived through numerical simulation. A comparison between the data reported in
Table 5 highlights that the tunnel accurately reproduces the target ABL, and is therefore correctly designed and calibrated for the analysis of the wind erosion over the surfaces of granular materials.
It is worth noting that, while the simulated boundary layer thickness (δ) closely matched that obtained through experimental measurements, there is an 18% disparity between the value derived from experimental tests and that obtained through CFD simulations for the parameter α. In its current state, in fact, the CFD model of the DICAAR EWT does not perfectly reproduce the experimental value of α, potentially due to minor inaccuracies in the boundary input conditions. Nevertheless, this difficulty is highlighted in similar studies published in the technical and scientific literature, which report significant differences between experimental and simulated α values [
26], while the evaluation of that coefficient is challenging even with in situ measurements [
22]. Furthermore, the availability of the CFD model allows for an analysis of the wind field downstream the spires along the working section of the EWT, confirming that the length of the Flow Development Section (FDS) was correctly designed and the wind field is well-developed and uniform in the section designated for the emission tests. In addition, the CFD model allows for an investigation of the wind field near the roof, which was not characterized in the experimental test.
5. Conclusions
This research aimed to develop tools and methodologies for the reliable and repeatable reproduction of the emission of Particulate Matter (PM) generated by the erosion of granular materials exposed to wind (i.e., industrial wind erosion). In that context, the design, development and verification phases of the new DICAAR Environmental Wind Tunnel (EWT) are detailed and critically analyzed, as well as the procedures for creating and validating the tunnel’s CFD model.
The new wind tunnel was built with larger dimensions compared to the one previously used in Cagliari University, and with transparent walls, mainly to enable the video recording of the erosion and emission processes with high-speed cameras, and thus the reconstruction of the particles’ motion during the emission phase.
In the calibration phase, the turbulence generators (spires) and the roughness of the tunnel floor were chosen to reproduce the wind velocity profiles that develop over the wide and flat surfaces of coarse and heterogeneous granular materials.
The validation, which was carried out via a comparison between the data measured in the tunnel and the target wind profiles, highlighted that the new wind tunnel accurately reproduces the desired ABL. It can therefore be used to produce a database that will allow for the development or integration of physical–mathematical models of the emission phenomenon. Those models will be validated thanks to the possibility of video-recording the particles’ motion by mean of high-speed cameras set outside the tunnel walls (Particle Image Velocimetry methods).
Once validated through comparison with the experimental data, the CFD model was used to obtain complete information on the wind flow at each point of the wind tunnel’s volume. In particular, the CFD simulations allowed for an investigation of the wind field near the roof and along the FDS, providing additional information to that provided by the experimental apparatus.
The integrated use of the CFD model and the experimental equipment represents an advance compared to the state of the art of the research on PM emissions determined by means of environmental wind tunnels. In a continuation of this research, the CFD model will be further developed in order to include a simulation of the PM transport phenomenon in the air and validated through a comparison of the simulated PM concentrations and those measured experimentally in the tunnel. Once the integration and validation stages will be accomplished, the model will allow for a three-dimensional reconstruction of the PM plume and a more reliable evaluation of the PM mass emitted per unit of time.
Author Contributions
Conceptualization, B.G. and V.D.; methodology, B.G., V.D. and F.P.; software, A.L. and O.B.; validation, F.P., A.L. and O.B.; formal analysis, F.P. and A.L.; investigation, F.P. and A.L.; resources, C.A. and M.S.; data curation, F.P., A.L. and O.B.; writing—original draft preparation, F.P. and A.L.; writing—review and editing, B.G. and V.D.; supervision, B.G. and V.D.; project administration, B.G. and V.D.; funding acquisition, B.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by PON “Ricerca e innovazione” 2014–2020–Azione IV.4 CUP F25F21002190003.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to the complexity of historical data processing.
Acknowledgments
Investigation carried out in the framework of projects conducted by CINIGeo (National Inter-university Consortium for Georesources Engineering Rome, Italy) and CESA (Center of excellence of environmental sustainability).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Aimar, S.B.; Mendez, M.J.; Funk, R.; Buschiazzo, D.E. Soil Properties Related to Potential Particulate Matter Emissions (PM10) of Sandy Soils. Aeolian Res. 2012, 3, 437–443. [Google Scholar] [CrossRef]
- Wu, W.; Yan, P.; Wang, Y.; Dong, M.; Meng, X.; Ji, X. Wind Tunnel Experiments on Dust Emissions from Different Landform Types. J. Arid. Land. 2018, 10, 548–560. [Google Scholar] [CrossRef]
- Roney, J.A.; White, B.R. Estimating Fugitive Dust Emission Rates Using an Environmental Boundary Layer Wind Tunnel. Atmos. Environ. 2006, 40, 7668–7685. [Google Scholar] [CrossRef]
- Avecilla, F.; Panebianco, J.E.; Buschiazzo, D.E. A Wind-Tunnel Study on Saltation and PM10 Emission from Agricultural Soils. Aeolian Res. 2016, 22, 73–83. [Google Scholar] [CrossRef]
- Dentoni, V.; Grosso, B.; Pinna, F. Experimental Evaluation of Pm Emission from Red Mud Basins Exposed to Wind Erosion. Minerals 2021, 11, 405. [Google Scholar] [CrossRef]
- Dentoni, V.; Grosso, B.; Pinna, F.; Lai, A.; Bouarour, O. Emission of Fine Dust from Open Storage of Industrial Materials Exposed to Wind Erosion. Atmosphere 2022, 13, 320. [Google Scholar] [CrossRef]
- Preston, C.A.; McKenna Neuman, C.; Boulton, J.W. A Wind Tunnel and Field Evaluation of Various Dust Suppressants. J. Air Waste Manage Assoc. 2020, 70, 915–931. [Google Scholar] [CrossRef]
- McKenna Neuman, C.; Boulton, J.W.; Sanderson, S. Wind Tunnel Simulation of Environmental Controls on Fugitive Dust Emissions from Mine Tailings. Atmos. Environ. 2009, 43, 520–529. [Google Scholar] [CrossRef]
- Counihan, J. Simulation of an Adiabatic Urban Boundary Layer in a Wind Tunnel. Atmos. Environ. 1973, 7, 673–689. [Google Scholar] [CrossRef]
- Wooding, R.A.; Bradley, E.F.; Marshall, J.K. Drag Due to Regular Arrays of Roughness Elements of Varying Geometry. Boundary Layer Meteorol. 1973, 5, 285–308. [Google Scholar] [CrossRef]
- Counihan, J. An Improved Method of Simulating an Atmospheric Boundary Layer in a Wind Tunnel. Atmos. Environ. 1969, 3, 197–214. [Google Scholar] [CrossRef]
- Irwin, H.P.A.H. The Design of Spires for Wind Simulation. J. Wind Eng. Ind. Aerodyn. 1981, 7, 361–366. [Google Scholar] [CrossRef]
- Dentoni, V.; Grosso, B.; Massacci, G.; Pinna, F. Validation of a Wind Erosion Model for Tailings Basins: Wind Tunnel Design and Atmospheric Boundary Layer Simulation. Int. J. Min. Reclam. Environ. 2019, 34, 562–572. [Google Scholar] [CrossRef]
- Yeo, D.; Shi, L. Computational versus Wind Tunnel Simulation of Atmospheric Boundary Layer Flow for Structural Engineering Applications. In Ind Engineering for Natural Hazards: Modeling, Simulation and Mitigation of Windstorm Impact on Critical Infrastructure; American Society of Civil Engineers (ASCE): Reston, VA, USA, 2018; pp. 169–191. [Google Scholar]
- Hlevca, D.; Degeratu, M. Atmospheric Boundary Layer Modeling in a Short Wind Tunnel. Eur. J. Mech. B/Fluids 2020, 79, 367–375. [Google Scholar] [CrossRef]
- Chen, Z.; Wei, C.; Chen, Z.; Wang, S.; Tang, L. Numerical Simulation of Atmospheric Boundary Layer Turbulence in a Wind Tunnel Based on a Hybrid Method. Atmosphere 2022, 13, 2044. [Google Scholar] [CrossRef]
- Abubaker, A.; Kostić, I.; Kostić, O.; Stefanović, Z. CFD Modeling of Atmospheric Boundary Layer Simulations in Wind Tunnels. Tehnički Vjesnik 2018, 25, 1595–1602. [Google Scholar] [CrossRef]
- Mehta, R.D. The Aerodynamic Design of Blower Tunnels with Wide-Angle Diffusers. Progress. Aerosp. Sci. 1979, 18, 59–120. [Google Scholar] [CrossRef]
- Mehta, R.D.; Bradshaw, P. Design Rules for Small Low Speed Wind Tunnels. Aeronaut. J. 1979, 83, 443–453. [Google Scholar] [CrossRef]
- Mathew, J. Design, Fabrication and Characterization of an Anechoic Wind Tunnel Facility. In Proceedings of the 11th AIAA/CEAS Aeroacoustics Conference, Monterey, CA, USA, 23–25 May 2005. [Google Scholar]
- Al-Nehari, H.A.; Abdel-Rahman, A.K.; Nassib, A.E.-M.; Shafey, H.M. Design and construction of a wind tunnel for environmental flow studies. J. Eng. Sci. 2010, 38, 177–193. [Google Scholar] [CrossRef]
- Kaltschmitt, M.; Streicher, W.; Wiese, A. Renewable Energy Technology, Economics and Environment; Springer: Berlin/Heidelberg, Germany, 2007; ISBN 978-3-540-70947-3. [Google Scholar]
- Davenport, A.G. The Relationship of Wind Structure to Wind Loading. In Proceedings of the Symposium No. 16—Wind Effects on Buildings and Structures; Her Majesty’s Stationery Office: London, UK; Teddington, UK, 1963. [Google Scholar]
- Roache, P.J. Perspective: A Method for Uniform Reporting of Grid Refinement Studies. J. Fluids Eng. 1994, 116, 405–413. [Google Scholar] [CrossRef]
- Celik, I.B.; Ghia, U.; Roache, P.J.; Freitas, C.J.; Coleman, H.; Raad, P.E. Procedure for Estimation and Reporting of Uncertainty Due to Discretization in CFD Application. J. Fluids Eng. 2008, 130, 078001. [Google Scholar] [CrossRef]
- Abdulrahim, A.; Elfarra, M.; Uzol, O. A Numerical Assessment of Atmospheric Boundary Layer Simulation Inside Two Different Boundary Layer Wind Tunnels. In Proceedings of the 10th Ankara International Aerospace Conference, Ankara, Turkey, 10–12 September 2019. [Google Scholar]
Figure 1.
Schematic representation of the DICAAR Environmental Wind Tunnel.
Figure 1.
Schematic representation of the DICAAR Environmental Wind Tunnel.
Figure 2.
(a) View of the EWT from the Convergent Section (flow entrance); (b) view of the EWT from the Drive Section (flow exit).
Figure 2.
(a) View of the EWT from the Convergent Section (flow entrance); (b) view of the EWT from the Drive Section (flow exit).
Figure 3.
Frontal view of the spires installed at the entrance of the FDS.
Figure 3.
Frontal view of the spires installed at the entrance of the FDS.
Figure 4.
Wind velocities data collection points in the reference cross section.
Figure 4.
Wind velocities data collection points in the reference cross section.
Figure 5.
Wind velocity fields measured at fan operating speeds of 1500 and 2700 RPM.
Figure 5.
Wind velocity fields measured at fan operating speeds of 1500 and 2700 RPM.
Figure 6.
Turbulence intensity fields measured at fan operating speeds of 1500 and 2700 RPM.
Figure 6.
Turbulence intensity fields measured at fan operating speeds of 1500 and 2700 RPM.
Figure 7.
Fitting of the Power Law wind profile to the experimental data at fan-operating velocity of 1500 RPM.
Figure 7.
Fitting of the Power Law wind profile to the experimental data at fan-operating velocity of 1500 RPM.
Figure 8.
Fitting of the Power Law wind profile to the experimental data at fan-operating velocity of 2700 RPM.
Figure 8.
Fitting of the Power Law wind profile to the experimental data at fan-operating velocity of 2700 RPM.
Figure 9.
Unstructured mesh geometry.
Figure 9.
Unstructured mesh geometry.
Figure 10.
Velocity profiles and error bars for grid independence study for the EWT conducted at: (a) 50 cm from the inlet of the FDS, (b) 2.5 m from the inlet of the FDS, and (c) test section inlet.
Figure 10.
Velocity profiles and error bars for grid independence study for the EWT conducted at: (a) 50 cm from the inlet of the FDS, (b) 2.5 m from the inlet of the FDS, and (c) test section inlet.
Figure 11.
Contours of the velocity magnitude at various cross-sections along the tunnel (fan operating velocity of 2700 RPM).
Figure 11.
Contours of the velocity magnitude at various cross-sections along the tunnel (fan operating velocity of 2700 RPM).
Figure 12.
Velocity magnitude contours along the midplane of the tunnel at a fan operating velocity of 2700 RPM.
Figure 12.
Velocity magnitude contours along the midplane of the tunnel at a fan operating velocity of 2700 RPM.
Figure 13.
Simulated wind velocity fields in the TS at fan operating velocities of 1500 and 2700 RPM.
Figure 13.
Simulated wind velocity fields in the TS at fan operating velocities of 1500 and 2700 RPM.
Figure 14.
Fitting of the Power Law wind profile to the results of CFD simulations corresponding to fan operating velocity of 1500 RPM.
Figure 14.
Fitting of the Power Law wind profile to the results of CFD simulations corresponding to fan operating velocity of 1500 RPM.
Figure 15.
Fitting of the Power Law wind profile to the results of CFD simulations corresponding to a fan operating velocity of 2700 RPM.
Figure 15.
Fitting of the Power Law wind profile to the results of CFD simulations corresponding to a fan operating velocity of 2700 RPM.
Figure 16.
Comparison of experimentally measured and simulated wind fields—2700 RPM.
Figure 16.
Comparison of experimentally measured and simulated wind fields—2700 RPM.
Figure 17.
Fitting of the power law wind profile to the experimental data (red dots) and the CFD data (blue dots)—2700 RPM.
Figure 17.
Fitting of the power law wind profile to the experimental data (red dots) and the CFD data (blue dots)—2700 RPM.
Table 1.
Experimental values of the wind velocity measured along the symmetry vertical axis of the reference cross-section.
Table 1.
Experimental values of the wind velocity measured along the symmetry vertical axis of the reference cross-section.
| z | 1500 RPM | 2700 RPM |
|---|
| (m) | (m/s) | (m/s) |
|---|
| 0.51 | 5.92 | 10.60 |
| 0.46 | 5.91 | 10.59 |
| 0.41 | 5.89 | 10.60 |
| 0.36 | 5.78 | 10.46 |
| 0.31 | 5.61 | 10.15 |
| 0.26 | 5.38 | 9.72 |
| 0.21 | 5.11 | 9.20 |
| 0.16 | 4.80 | 8.71 |
| 0.11 | 4.51 | 8.15 |
| 0.06 | 4.19 | 7.55 |
| 0.03 | 3.93 | 6.92 |
Table 2.
Results of the wind power law fitting to the experimental data.
Table 2.
Results of the wind power law fitting to the experimental data.
| | α (-) | δ (m) | R2 |
|---|
| 1500 | 0.17 | 0.47 | 0.98 |
| 2700 | 0.17 | 0.45 | 0.98 |
| Mean | 0.17 | 0.46 | |
Table 3.
Simulated values of the wind velocity along the symmetry vertical axis of the reference cross-section.
Table 3.
Simulated values of the wind velocity along the symmetry vertical axis of the reference cross-section.
| z | 1500 RPM | 2700 RPM |
|---|
| (m) | (m/s) | (m/s) |
|---|
| 0.51 | 6.02 | 11.11 |
| 0.46 | 6.02 | 11.12 |
| 0.41 | 6.04 | 11.14 |
| 0.36 | 5.99 | 11.02 |
| 0.31 | 5.81 | 10.68 |
| 0.26 | 5.51 | 10.10 |
| 0.21 | 5.19 | 9.50 |
| 0.16 | 4.80 | 8.78 |
| 0.11 | 4.44 | 8.13 |
| 0.06 | 4.05 | 7.44 |
| 0.03 | 3.69 | 6.92 |
Table 4.
Results of the Power Law fitting to the CFD results.
Table 4.
Results of the Power Law fitting to the CFD results.
| | α (-) | δ (m) | R2 |
|---|
| 1500 | 0.20 | 0.44 | 0.98 |
| 2700 | 0.20 | 0.45 | 0.97 |
| Mean | 0.20 | 0.45 | |
Table 5.
Project parameters (target values, experimental results and simulation results).
Table 5.
Project parameters (target values, experimental results and simulation results).
| | α (-) | δ (m) |
|---|
| Target parameters | 0.16 | 0.45 |
| Experimental results | 0.17 | 0.46 |
| CFD simulation | 0.20 | 0.45 |
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).