Industrial Heat Source-Related PM2.5 Concentration Estimates and Analysis Using New Three-Stage Model in the Beijing–Tianjin–Hebei Region
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data Source
2.2.1. PM2.5 Concentration Data
2.2.2. Natural Geographic Data
2.2.3. Socio-Economic Data
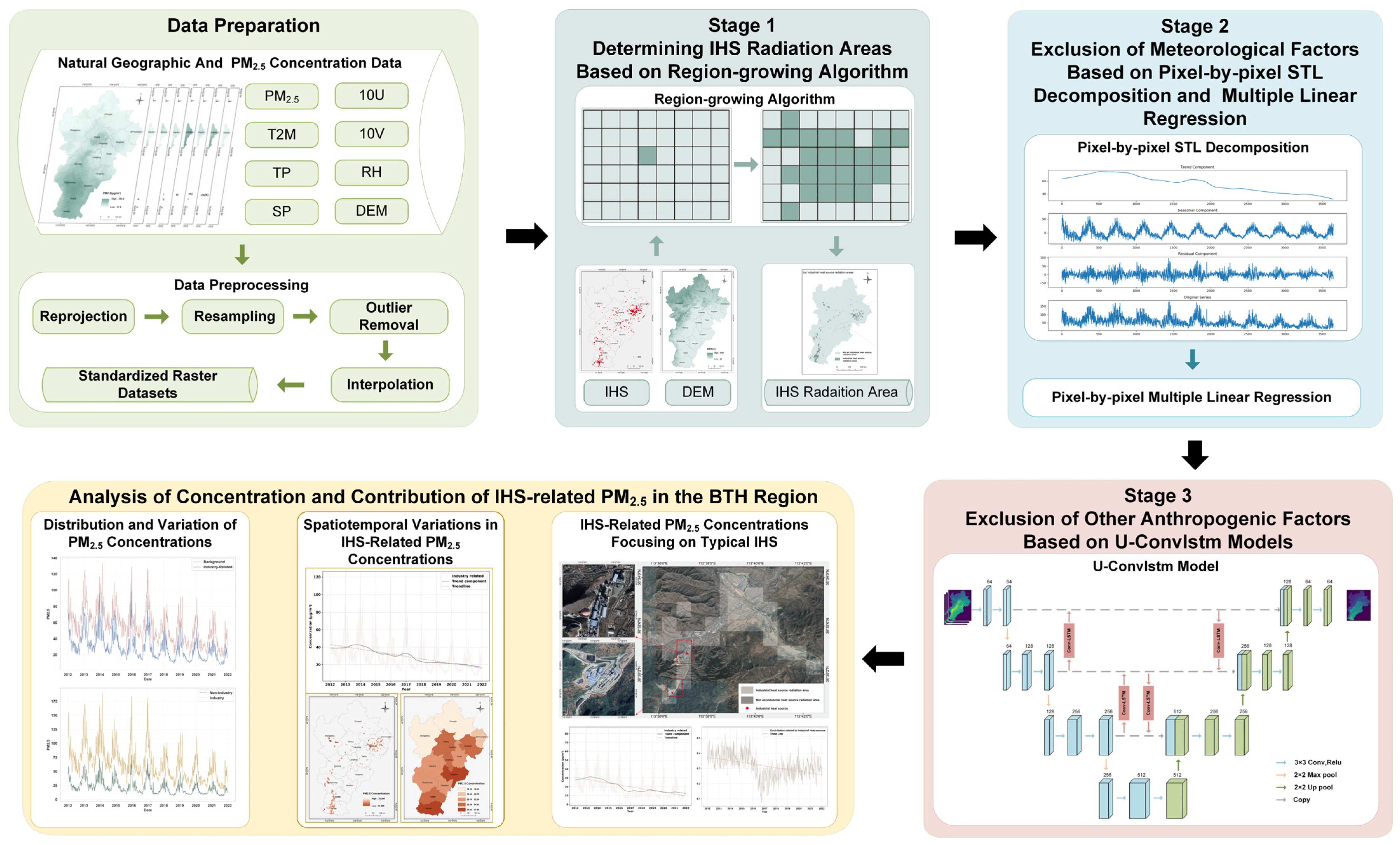
2.3. Method
2.3.1. Data Preparation
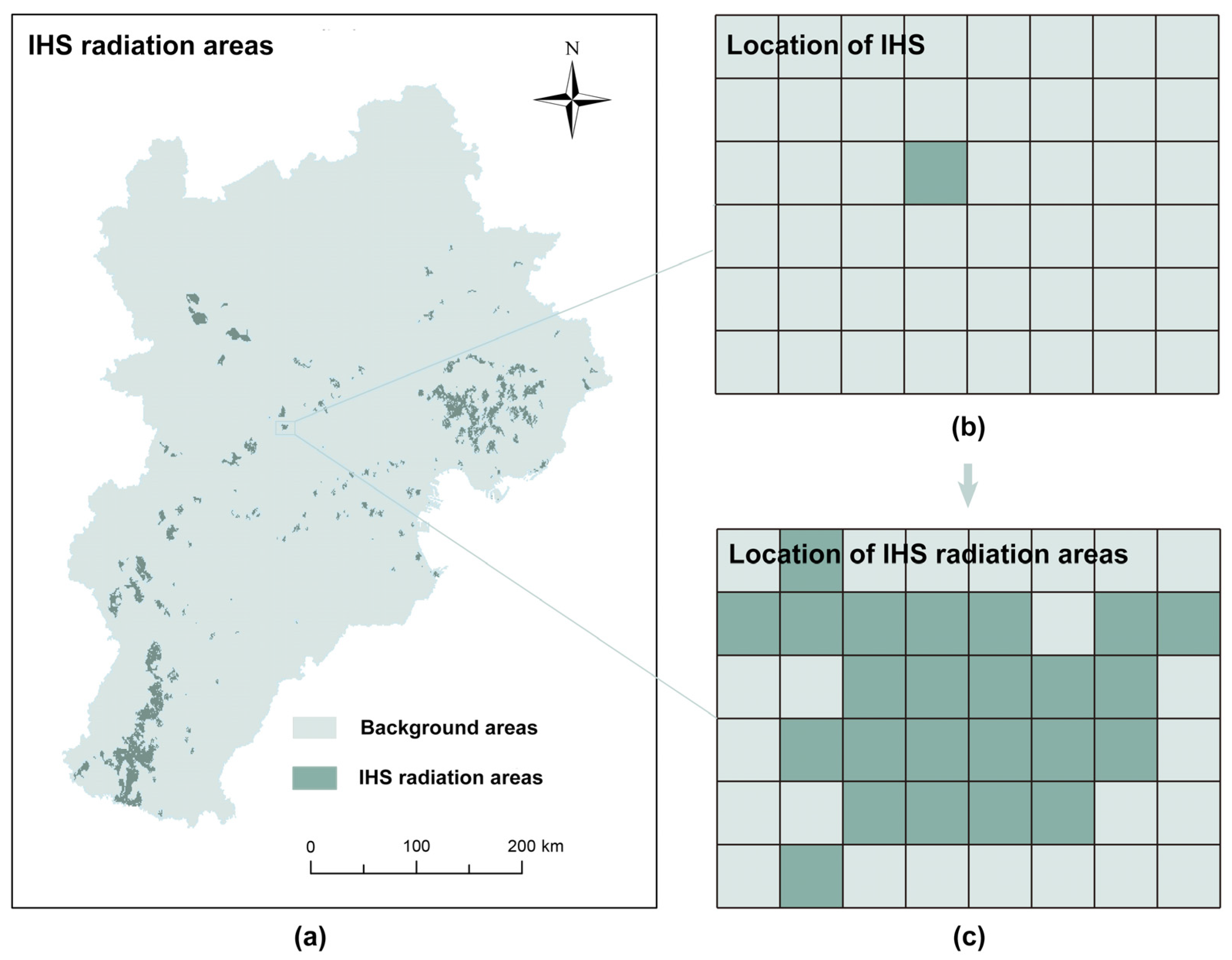
2.3.2. Stage 1: Determining IHS Radiation Areas Based on Region-Growing Algorithm Using IHS and DEM Data
- (1)
- The IHS data were transformed from vector to raster format. The DEM and IHS data were resampled to align with the PM2.5 concentration grid as a reference layer.
- (2)
- The region-growing algorithm was initiated from the central grid representing the IHSs, identified in Figure 3b. This grid’s elevation was compared with the surrounding eight pixels. If the adjacent pixels displayed lower elevations, they were amalgamated into the IHS grid.
- (3)
- Repeat step (2) with all newly added grids serving as new growth points. The process persisted until either no lower elevation grids were identified or the predefined maximum impact distance was reached; at this point, the expansion ceased. Consequently, all incorporated grids were classified as the IHS radiation areas. The maximum distance for each IHS pollution impact was set to 10 km, according to the recommended method for the risk assessment of environmental emergencies in administrative regions (Figure 3c) [52].
- (4)
- Replicating steps 2 and 3 was repeated to delineate all IHS radiation areas of each IHSs, as shown in Figure 3a.
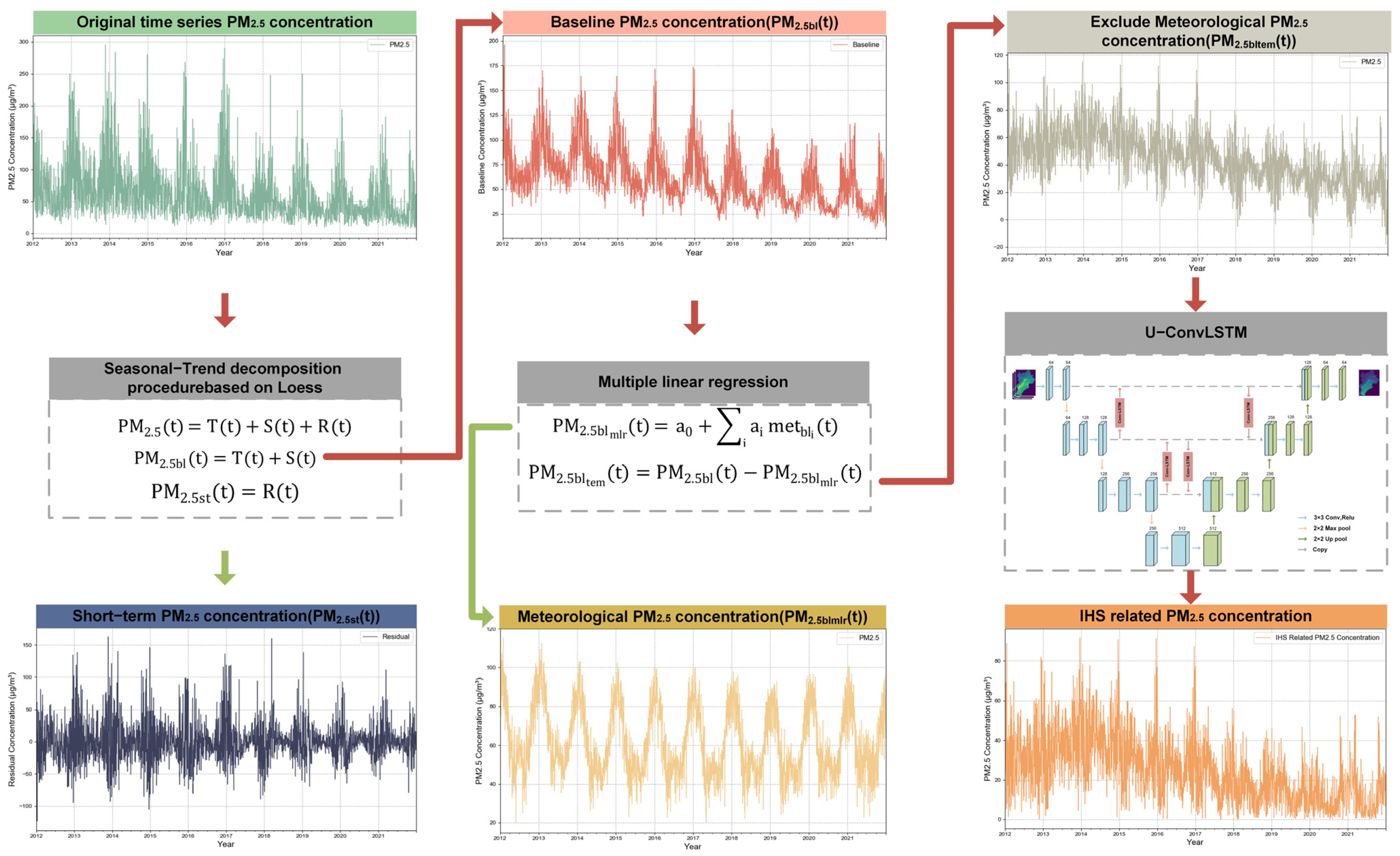
2.3.3. Stage 2: Exclusion of Meteorological Factors Based on Pixel-by-Pixel STL Decomposition and Multiple Linear Regression
- Exclusion of Short-term Meteorological Factors Based on STL Decomposition
- 2.
- Exclusion of Long-term Meteorological Factors Based on Multiple linear regression
2.3.4. Stage 3: Exclusion of Other Anthropogenic Factors Based on U-ConvLSTM Model
2.3.5. Statistical Analysis of IHS-Related PM2.5 Concentrations
3. Results
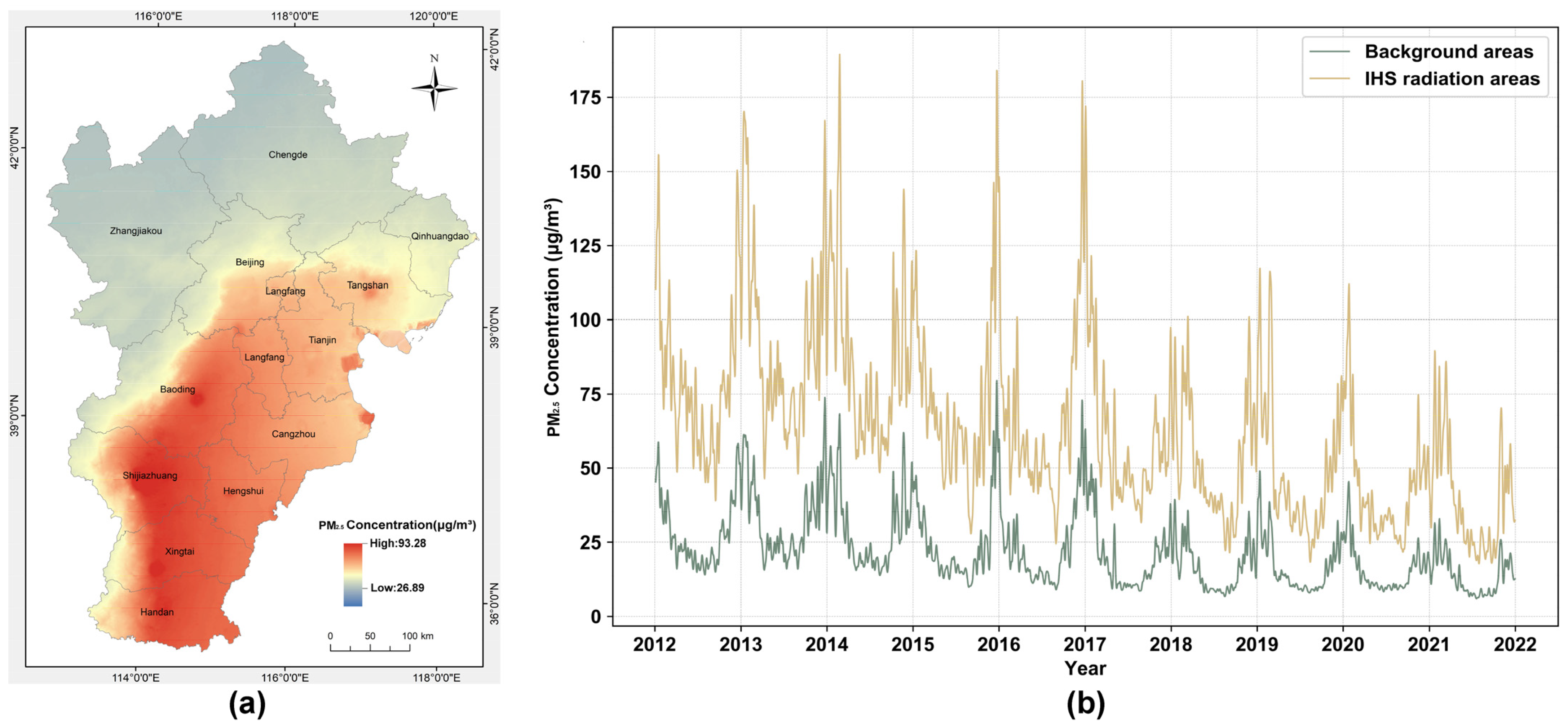
3.1. Overall Spatial and Temporal Trends of PM2.5 in the BTH Region
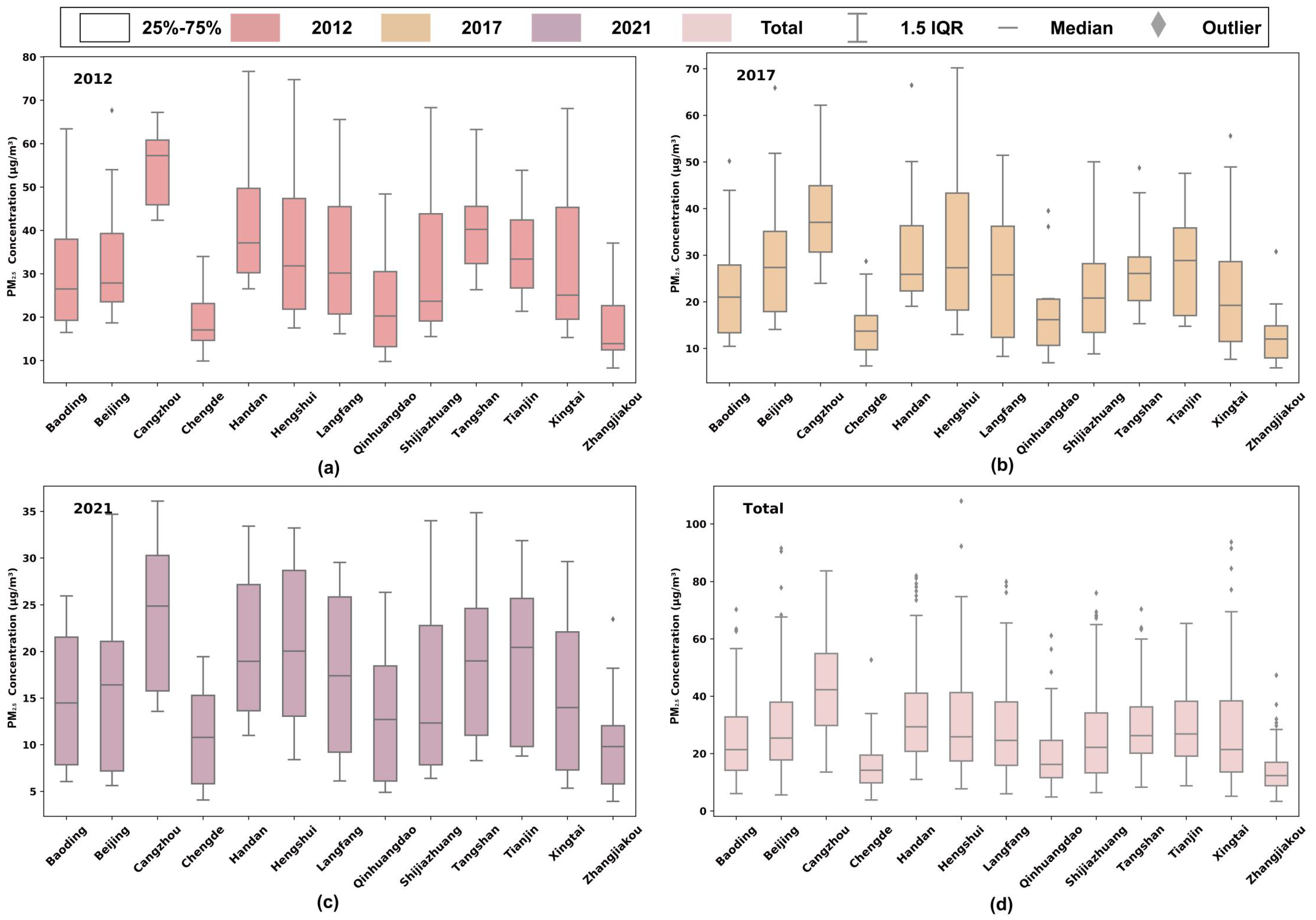
3.1.1. Distribution and Variation of PM2.5 Concentrations in the BTH Region
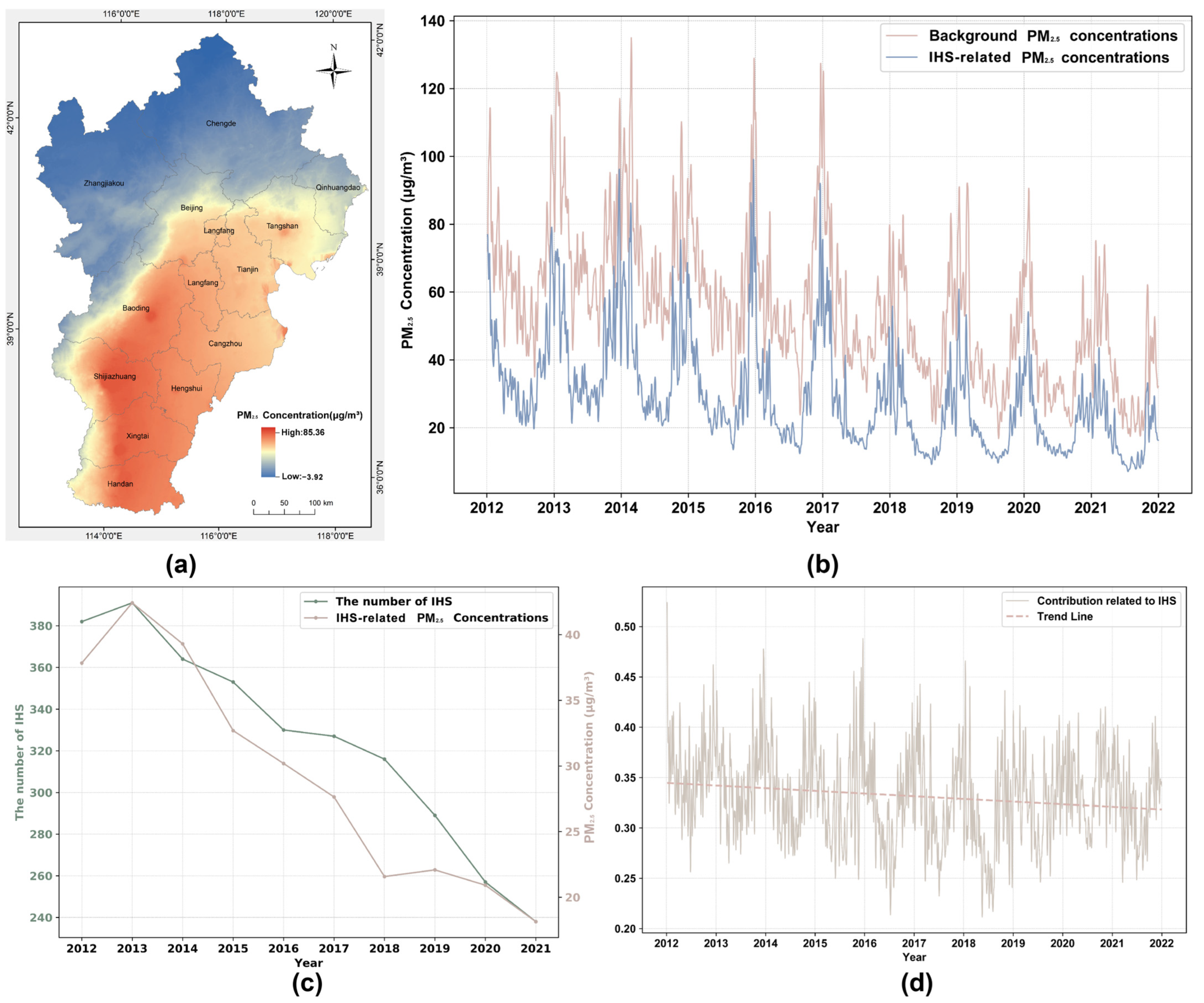
3.1.2. Analysis of IHS-Related PM2.5 Concentrations and Influencing Factors in the BTH Region
3.2. Analysis of the Spatial and Temporal Variations on IHS-Related PM2.5 Concentrations in the BTH Region
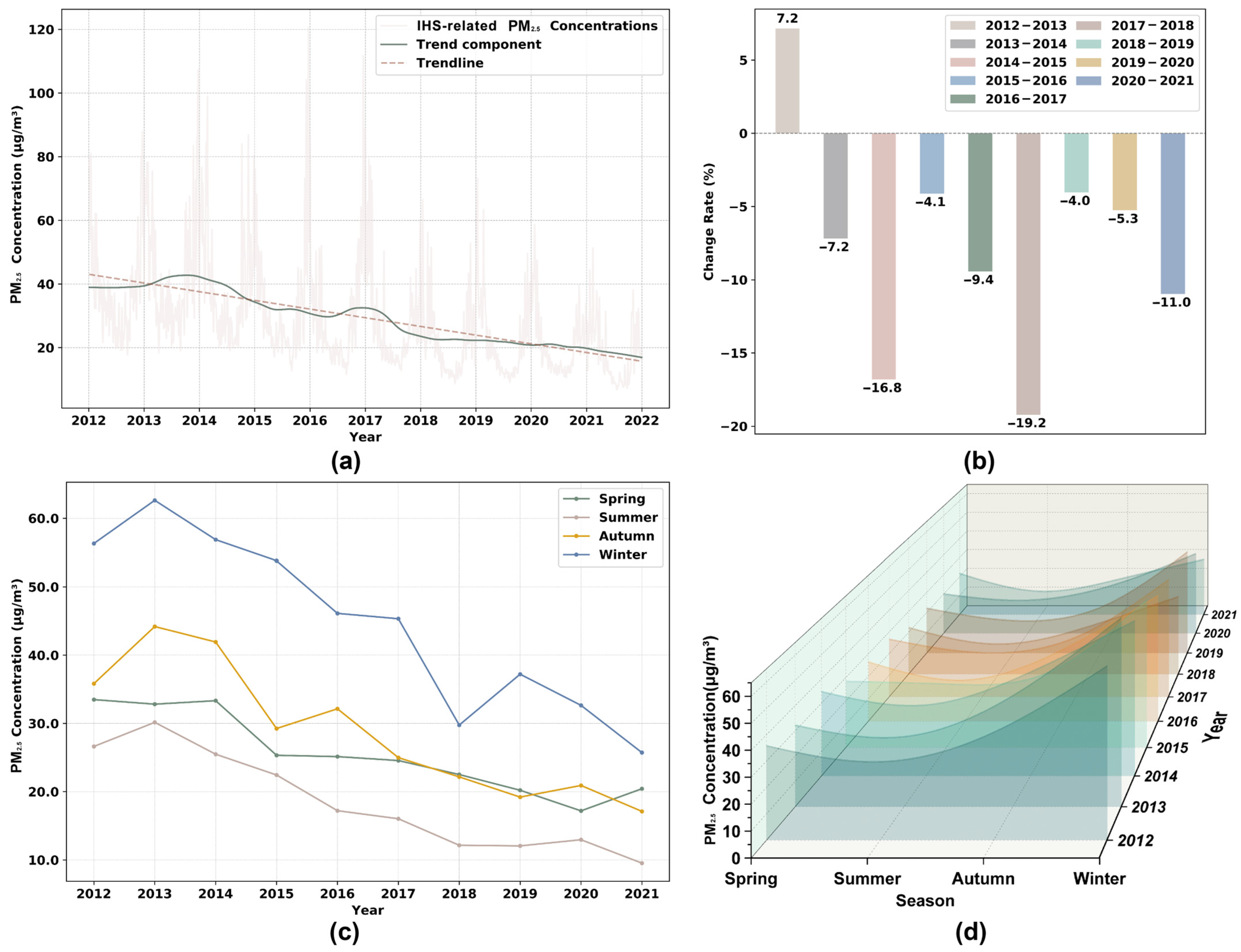
3.2.1. Temporal Trends and Seasonal Fluctuations on IHS-Related PM2.5 Concentrations
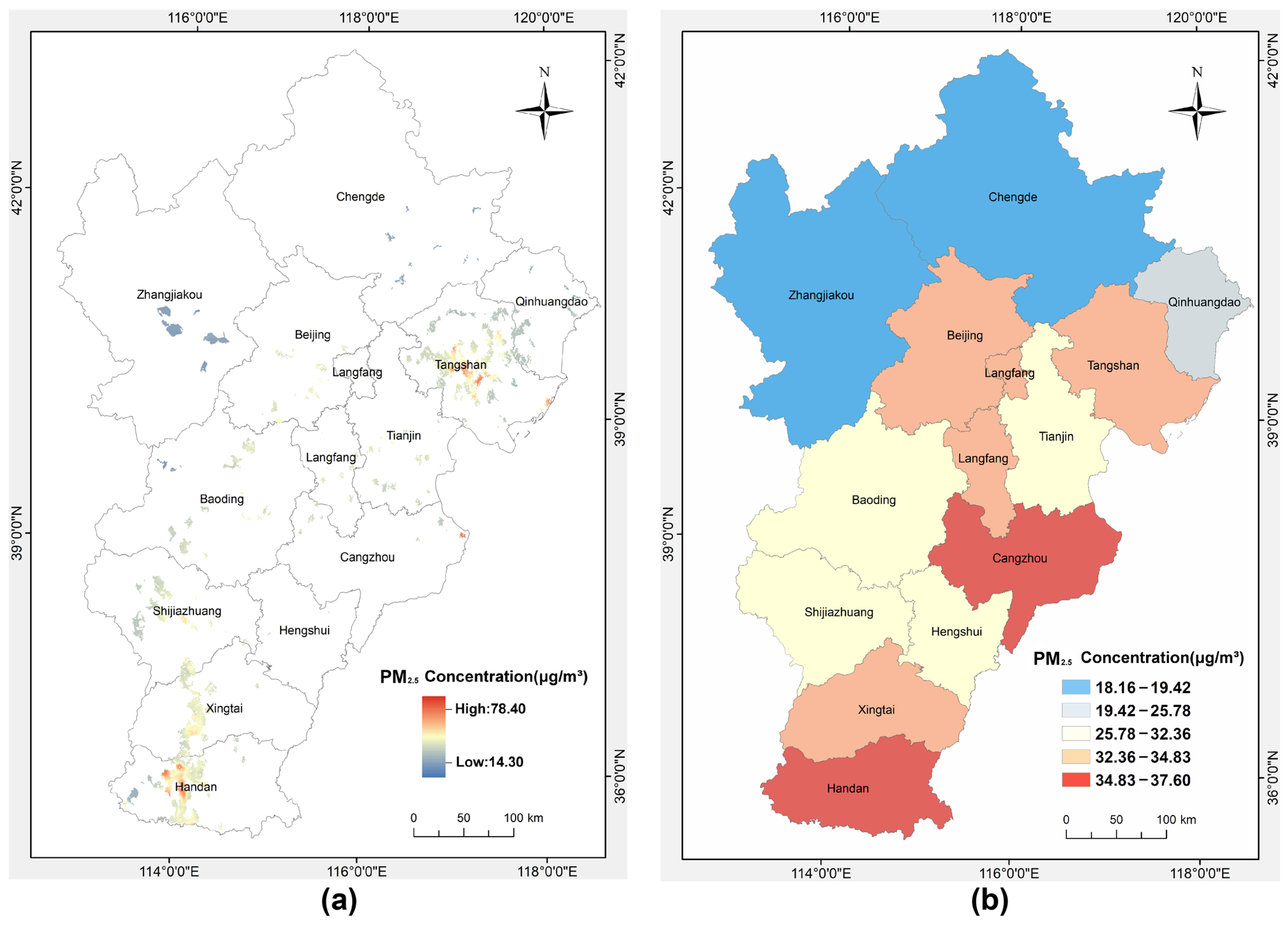
3.2.2. Spatial Distribution and Analysis of IHS-Related PM2.5 Concentrations
3.2.3. Heterogeneity and Evolution of IHS-Related PM2.5 Concentrations in the BTH
3.3. Analysis of IHS-Related PM2.5 Concentrations Focusing on Typical IHS
4. Discussion
4.1. Interrelations of Factors Affecting IHS-Related PM2.5 Concentrations
- (1)
- The quantity of operational IHSs across the three provinces exhibited a potent positive correlation with IHS-related PM2.5 concentrations. Considering the direct emission of particulates from these IHSs during production processes, the number and active status of these IHSs have been identified as significant factors influencing ambient PM2.5 concentrations.
- (2)
- Metrics like energy consumption level, industry scale, and secondary sector gross domestic product (GDP) were highly correlated with IHS-related PM2.5 concentrations, especially in Hebei (0.93, 0.88, and 0.95, respectively). This implied that the existence of IHSs and their operational magnitudes substantially impact air quality. Significantly, regional differences were evident in the correlations between IHS-related PM2.5 concentrations and industrial indices. Industry scale in Tianjin and secondary sector GDP in Beijing with IHS-related PM2.5 concentrations were relatively modest. This pattern indicated that higher economic output was not necessarily synonymous with increased pollution levels, potentially signifying a shift in the economic composition of these regions towards cleaner technologies and services.
- (3)
- The correlations between raw material production and IHS-related PM2.5 concentrations exhibited notable variations. These differences suggested that distinct production processes, varying degrees of technological adoption, and the effectiveness of pollution control measures significantly impact PM2.5 emissions. Steel and cement production in Beijing and Tianjin moderately correlated with IHS-related PM2.5 concentrations, indicating contributions to particulate levels, yet subject to policy-induced production moderation and response adjustments. The exceedingly high correlation with raw coal production (0.98) in Hebei signaled the region’s historical dependence on coal and high-polluting industrial processes. Also, it highlighted the province’s pace of coal industry reform, directly affecting PM2.5 levels. Conversely, the negative correlation with steel production (−0.86) reflected a transition to modernized steel production technologies, ensuring environmental cleanliness while boosting production efficiency.
- (4)
- SO2 and NOx emissions across all three provinces were strongly correlated with IHS-related PM2.5 concentrations, notably at 0.94 for SO2 and 0.93 for NOx in Hebei. These correlations highlight the need for improved combustion efficiency and better desulfurization and denitrification processes. Additionally, transitioning to cleaner energy sources is essential for substantially reducing PM2.5 levels. The high correlation between industrial wastewater discharges and carbon emissions reflects broader environmental management practices within industries. Adequate wastewater treatment and low-carbon energy sources reduce IHS-related PM2.5 concentrations.
4.2. Comparison with Other Previous Studies
- (1)
- Long Time Series with High Temporal Resolution: Unlike past studies that have mainly analyzed PM2.5 compositions over shorter monthly periods, our study provided a long-term daily time series of IHS-related PM2.5 concentrations. This supported the identification of daily anomalies and long-term trends in industrial production.
- (2)
- Focus on individual IHS targets: In advancing past the methodologies of the previous research that have predominantly utilized regional emission inventories, this study uniquely pinpointed the exact locations of each IHS. This precision facilitated a more granular analysis of the specific impact exerted by individual IHS units on PM2.5 concentrations. Constructing a 1 km x 1 km resolution radiation area around each IHS accurately extracted IHS-related PM2.5 concentrations for the impacted areas, providing a scientific basis for assessing the specific impact of factories on air quality.
- (3)
- Model Portability and Computational Efficiency: The model employed in this study not only demonstrated computational efficiency but also offered adaptability across different industrial and geographical contexts. This versatility enhanced the model’s applicability in varied environmental research scenarios.
4.3. Significance and Uncertainties of the Study
5. Conclusions
- (1)
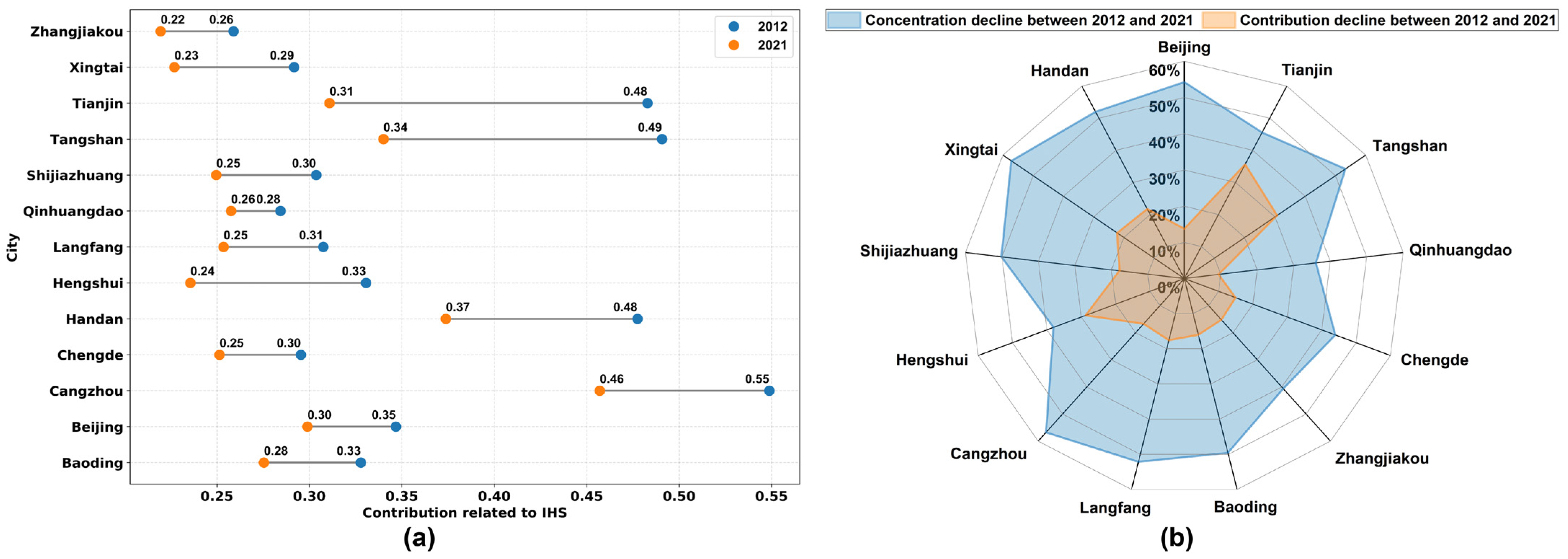
- Within the study area, the average PM2.5 concentrations in IHS radiation areas were significantly higher than in background areas, with approximately 33.16% of PM2.5 concentration attributable to IHS activities. Furthermore, a year-over-year decline in the contribution of IHS-related PM2.5 was observed, indicating the effectiveness of industrial reform measures.
- (2)
- The annual mean IHS-related PM2.5 concentration in the BTH region exhibited a general downward trend with a 5.78% average annual reduction. Seasonal analysis revealed a pronounced “low in spring-summer, high in autumn-winter” pattern, with the highest concentrations in winter. Spatial distribution analysis showed that IHS-related PM2.5 concentrations in the southern, industrially dense areas were significantly higher than in the north, and the 13 cities within the region displayed varied temporal and spatial trends in IHS-related PM2.5 concentrations. These findings underscore the importance of industrial activities and regional environmental policies in air pollution control.
- (3)
- In the specific industrial area of She County, Handan, two IHSs contributed an average of 19.20 µg/m3 to the IHS-related PM2.5 concentration. From 2012 to 2021, these concentrations fluctuated dynamically, peaking in 2013 and notably decreasing during partial shutdowns of IHS operations. This highlights the significant impact of the operational status of IHSs on local air quality.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pozo-Luyo, C.A.; Cruz-Duarte, J.M.; Amaya, I.; Ortiz-Bayliss, J.C. Forecasting PM2.5 Concentration Levels Using Shallow Machine Learning Models on the Monterrey Metropolitan Area in Mexico. Atmos. Pollut. Res. 2023, 14, 101898. [Google Scholar] [CrossRef]
- Xiang, X.; Shi, G.; Wu, X.; Yang, F. The Extraordinary Trend of the Spatial Distribution of PM2.5 Concentration and Its Meteorological Causes in Sichuan Basin. Atmosphere 2022, 13, 853. [Google Scholar] [CrossRef]
- Silva, R.A.; Adelman, Z.; Fry, M.M.; West, J.J. The Impact of Individual Anthropogenic Emissions Sectors on the Global Burden of Human Mortality Due to Ambient Air Pollution. Environ. Health Perspect. 2016, 124, 1776–1784. [Google Scholar] [CrossRef] [PubMed]
- Rai, P.; Furger, M.; Slowik, J.G.; Zhong, H.; Tong, Y.; Wang, L.; Duan, J.; Gu, Y.; Qi, L.; Huang, R.-J.; et al. Characteristics and Sources of Hourly Elements in PM10 and PM2.5 during Wintertime in Beijing. Environ. Pollut. 2021, 278, 116865. [Google Scholar] [CrossRef]
- Sharma, K.; Kumar, P.; Sharma, J.; Thapa, S.D.; Gupta, A.; Rajak, R.; Baruah, B.; Prakash, A.; Ranjan, R.K. Characterization of Polycyclic Aromatic Hydrocarbons (PAHs) Associated with Fine Aerosols in Ambient Atmosphere of High-Altitude Urban Environment in Sikkim Himalaya. Sci. Total Environ. 2023, 870, 161987. [Google Scholar] [CrossRef] [PubMed]
- Nawaz, M.O.; Henze, D.K.; Anenberg, S.C.; Braun, C.; Miller, J.; Pronk, E. A Source Apportionment and Emission Scenario Assessment of PM2.5- and O3-Related Health Impacts in G20 Countries. GeoHealth 2023, 7, e2022GH000713. [Google Scholar] [CrossRef]
- Xie, Z.; Li, Y.; Qin, Y. Allocation of Control Targets for PM2.5 Concentration: An Empirical Study from Cities of Atmospheric Pollution Transmission Channel in the Beijing-Tianjin-Hebei District. J. Clean. Prod. 2020, 270, 122545. [Google Scholar] [CrossRef]
- Zhu, Z.; Liao, H. Evaluation on the Effects of Joint Prevention and Control of Air Pollution in Beijing-Tianjin-Hebei Region and Its Surrounding Areas—An Empirical Study Based on Multi-period Difference-in-Difference Model. J. China Univ. Geosci. 2022, 22, 142–156. [Google Scholar] [CrossRef]
- Lestari, P.; Arrohman, M.K.; Damayanti, S.; Klimont, Z. Emissions and Spatial Distribution of Air Pollutants from Anthropogenic Sources in Jakarta. Atmos. Pollut. Res. 2022, 13, 101521. [Google Scholar] [CrossRef]
- Artíñano, B.; Salvador, P.; Alonso, D.G.; Querol, X.; Alastuey, A. Anthropogenic and Natural Influence on the PM10 and PM2.5 Aerosol in Madrid (Spain). Analysis of High Concentration Episodes. Environ. Pollut. 2003, 125, 453–465. [Google Scholar] [CrossRef]
- Tessum, M.W.; Anenberg, S.C.; Chafe, Z.A.; Henze, D.K.; Kleiman, G.; Kheirbek, I.; Marshall, J.D.; Tessum, C.W. Sources of Ambient PM2.5 Exposure in 96 Global Cities. Atmos. Environ. 2022, 286, 119234. [Google Scholar] [CrossRef] [PubMed]
- Pan, C.M.; Zhu, X.; Wang, J.; Xiang, F.; Qiu, F.; Wan, P.J. Research Progress on Emission Inventory of Air Pollution Sources. Environ. Sci. Surv. 2020, 39, 72–78. [Google Scholar] [CrossRef]
- Gupta, L.; Bansal, M.; Nandi, P.; Habib, G.; Sunder Raman, R. Source Apportionment and Potential Source Regions of Size-Resolved Particulate Matter at a Heavily Polluted Industrial City in the Indo-Gangetic Plain. Atmos. Environ. 2023, 298, 119614. [Google Scholar] [CrossRef]
- Oh, S.-H.; Park, K.; Park, M.; Song, M.; Jang, K.-S.; Schauer, J.J.; Bae, G.-N.; Bae, M.-S. Comparison of the Sources and Oxidative Potential of PM2.5 during Winter Time in Large Cities in China and South Korea. Sci. Total Environ. 2023, 859, 160369. [Google Scholar] [CrossRef]
- Zhang, Q.; Xue, D.; Liu, X.; Gong, X.; Gao, H. Process Analysis of PM2.5 Pollution Events in a Coastal City of China Using CMAQ. J. Environ. Sci. 2019, 79, 225–238. [Google Scholar] [CrossRef] [PubMed]
- Mebust, M.R.; Eder, B.K.; Binkowski, F.S.; Roselle, S.J. Models-3 Community Multiscale Air Quality (CMAQ) Model Aerosol Component 2. Model Evaluation. J. Geophys. Res. Atmos 2003, 108, 2001JD001410. [Google Scholar] [CrossRef]
- Liu, D.R.; Lee, S.J.; Huang, Y.; Chiu, C.J. Air Pollution Forecasting Based on Attention-Based LSTM Neural Network and Ensemble Learning. Expert Syst. 2020, 37, e12511. [Google Scholar] [CrossRef]
- Danesh, Y.M.; Kuang, Z.; Dimakopoulou, K.; Barratt, B.; Suel, E.; Amini, H.; Lyapustin, A.; Katsouyanni, K.; Schwartz, J. Predicting Fine Particulate Matter (PM2.5) in the Greater London Area: An Ensemble Approach using Machine Learning Methods. Remote Sens. 2020, 12, 914. [Google Scholar] [CrossRef]
- López-Aparicio, S.; Guevara, M.; Thunis, P.; Cuvelier, K.; Tarrasón, L. Assessment of Discrepancies between Bottom-up and Regional Emission Inventories in Norwegian Urban Areas. Atmos. Environ. 2017, 154, 285–296. [Google Scholar] [CrossRef]
- Zhou, J.B.; Wang, X.; Xiu, R.L.; Li, L.N. Comparative Analysis of Atmospheric Pollutant Inventory and Environmental Statistics. Environ. Monit. China 2021, 37, 83–88. [Google Scholar] [CrossRef]
- Duan, W.J.; Lang, J.L.; Cheng, S.Y.; Jia, J.; Wang, X.Q. Air Pollutant Emission Inventory from Iron and Steel Industry in the Beljing-Tianjin-Hebei Region and lts Impact on PM2.5. Environ. Sci. 2018, 39, 1445–1454. [Google Scholar] [CrossRef]
- An, J.; Huang, Y.; Huang, C.; Wang, X.; Yan, R.; Wang, Q.; Wang, H.; Jing, S.; Zhang, Y.; Liu, Y.; et al. Emission Inventory of Air Pollutants and Chemical Speciation for Specific Anthropogenic Sources Based on Local Measurements in the Yangtze River Delta Region, China. Atmos. Chem. Phys. 2021, 21, 2003–2025. [Google Scholar] [CrossRef]
- Wang, L. Research on the Source Apportionment and Regional Transport of Fine Particulate Matter in the Atmosphere of Changchun City; Jilin University: Changchun, China, 2023. [Google Scholar]
- Pino-Cortés, E.; Carrasco, S.; Acosta, J.; de Almeida Albuquerque, T.T.; Pedruzzi, R.; Díaz-Robles, L.A. An Evaluation of the Photochemical Air Quality Modeling Using CMAQ in the Industrial Area of Quintero-Puchuncavi-Concon, Chile. Atmos. Pollut. Res. 2022, 13, 101336. [Google Scholar] [CrossRef]
- Mazzeo, A.; Zhong, J.; Hood, C.; Smith, S.; Stocker, J.; Cai, X.; Bloss, W.J. Modelling the Impact of National vs. Local Emission Reduction on PM2.5 in the West Midlands, UK Using WRF-CMAQ. Atmosphere 2022, 13, 377. [Google Scholar] [CrossRef]
- Dong, D.M.; Du, S.S.; Huang, Y.S.; Man, R.Q.; Yao, M.Y.; Du, R.H.; Liang, D.P.; Ning, Y. Pollution Characteristics and Source Apportionment of PM2.5 in Winter and Spring in Changchun City. J. Jilin Univ. 2020, 58, 1278–1286. [Google Scholar] [CrossRef]
- Liu, X.; Bai, X.; Tian, H.; Wang, K.; Hua, S.; Liu, H.; Liu, S.; Wu, B.; Wu, Y.; Liu, W.; et al. Fine Particulate Matter Pollution in North China: Seasonal-Spatial Variations, Source Apportionment, Sector and Regional Transport Contributions. Environ. Res. 2020, 184, 109368. [Google Scholar] [CrossRef]
- Wang, S.; Ren, Y.; Xia, B. PM2.5 and O3 Concentration Estimation Based on Interpretable Machine Learning. Atmos. Pollut. Res. 2023, 14, 101866. [Google Scholar] [CrossRef]
- Murray, N.L.; Holmes, H.A.; Liu, Y.; Chang, H.H. A Bayesian Ensemble Approach to Combine PM2.5 Estimates from Statistical Models Using Satellite Imagery and Numerical Model Simulation. Environ. Res. 2019, 178, 108601. [Google Scholar] [CrossRef]
- Yuen, K.K.F. Towards Multiple Regression Analyses for Relationships of Air Quality and Weather. J. Adv. Inf. Technol. 2017, 8, 135–140. [Google Scholar] [CrossRef]
- Ding, J.; Dai, Q.; Fan, W.; Lu, M.; Zhang, Y.; Han, S.; Feng, Y. Impacts of Meteorology and Precursor Emission Change on O3 Variation in Tianjin, China from 2015 to 2021. J. Environ. Sci. 2023, 126, 506–516. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Lin, S.; Shi, K.; Ye, Z.; Fang, Y. Seasonal Prediction of Daily PM2.5 Concentrations with Interpretable Machine Learning: A Case Study of Beijing, China. Environ. Sci. Pollut. Res. 2022, 29, 45821–45836. [Google Scholar] [CrossRef]
- Xu, W.; Fu, F.; Zhang, Q.; Wang, L. A Deep Learning-Based Multi-Objective Optimization Model for PM2.5 Prediction. Int. J. Comput. Intell. Syst. 2023, 16, 141. [Google Scholar] [CrossRef]
- Li, X.; Peng, L.; Yao, X.; Cui, S.; Hu, Y.; You, C.; Chi, T. Long Short-Term Memory Neural Network for Air Pollutant Concentration Predictions: Method Development and Evaluation. Environ. Pollut. 2017, 231, 997–1004. [Google Scholar] [CrossRef]
- Rawat, W.; Wang, Z. Deep Convolutional Neural Networks for Image Classification: A Comprehensive Review. Neural Comput. 2017, 29, 2352–2449. [Google Scholar] [CrossRef] [PubMed]
- Huang, C.J.; Kuo, P.H. A Deep CNN-LSTM Model for Particulate Matter (PM2.5) Forecasting in Smart Cities. Sensors 2018, 18, 2220. [Google Scholar] [CrossRef] [PubMed]
- Chattopadhyay, A.; Mustafa, M.; Hassanzadeh, P.; Bach, E.; Kashinath, K. Towards Physics-Inspired Data-Driven Weather Forecasting: Integrating Data Assimilation with a Deep Spatial-Transformer-Based U-NET in a Case Study with ERA5. Geosci. Model Dev. 2022, 15, 2221–2237. [Google Scholar] [CrossRef]
- Ma, Y.; Wang, L.; Zhao, F. Study on PM2.5 Concentration Prediction Method Based on CONVLSTM and U-Net. Environ. Eng. 2023, 41, 1300–1304. [Google Scholar]
- Wei, J.; Li, Z.; Lyapustin, A.; Sun, L.; Peng, Y.; Xue, W.; Su, T.; Cribb, M. Reconstructing 1-Km-Resolution High-Quality PM2.5 Data Records from 2000 to 2018 in China: Spatiotemporal Variations and Policy Implications. Remote Sens. Environ. 2021, 252, 112136. [Google Scholar] [CrossRef]
- Wei, J.; Li, Z.; Cribb, M.; Huang, W.; Xue, W.; Sun, L.; Guo, J.; Peng, Y.; Li, J.; Lyapustin, A.; et al. Improved 1Km Resolution PM2.5 Estimates across China Using Enhanced Space–Time Extremely Randomized Trees. Atmos. Chem. Phys. 2020, 20, 3273–3289. [Google Scholar] [CrossRef]
- Wei, J.; Li, Z. ChinaHighPM2.5: Big Data Seamless 1 km Ground-level PM2.5 Dataset for China (2000–2021); National Tibetan Plateau/Third Pole Environment Data Center: Beijing, China, 2023. [Google Scholar] [CrossRef]
- Liang, X.; Liu, Z.; Zhai, L.; Ji, L.; Feng, Y.; Sang, H. Spatial Terrestrial Carbon Emissions/Sequestrations Evolution Based on Ecological Network Analysis in Beijing-Tianjin-Hebei Urban Agglomeration. Ecol. Eng. 2023, 189, 106914. [Google Scholar] [CrossRef]
- Xue, W.; Zhang, J.; Hu, X.; Yang, Z.; Wei, J. Hourly Seamless Surface O3 Estimates by Integrating the Chemical Transport and Machine Learning Models in the Beijing-Tianjin-Hebei Region. Int. J. Environ. Res. Public Health 2022, 19, 8511. [Google Scholar] [CrossRef] [PubMed]
- Liu, N.; Li, S.; Zhang, F. Multi-Scale Spatiotemporal Variations and Drivers of PM2.5 in Beijing-Tianjin-Hebei from 2015 to 2020. Atmosphere 2022, 13, 1993. [Google Scholar] [CrossRef]
- Qiao, Y.; Ji, D.; Shang, H.; Xu, J.; Xu, R.; Shi, C. The Fusion of ERA5 and MERRA-2 Atmospheric Temperature Profiles with Enhanced Spatial Resolution and Accuracy. Remote Sens. 2023, 15, 3592. [Google Scholar] [CrossRef]
- Sun, X.; Zhao, T.; Bai, Y.; Kong, S.; Zheng, H.; Hu, W.; Ma, X.; Xiong, J. Meteorology Impact on PM2.5 Change over a Receptor Region in the Regional Transport of Air Pollutants: Observational Study of Recent Emission Reductions in Central China. Atmos. Chem. Phys. 2022, 22, 3579–3593. [Google Scholar] [CrossRef]
- Sinergise. Copernicus Global Digital Elevation Model; Open Topography: San Diego, CA, USA, 2021. [Google Scholar] [CrossRef]
- Ma, C.; Yang, J.; Chen, F.; Ma, Y.; Liu, J.; Li, X.; Duan, J.; Guo, R. Assessing Heavy Industrial Heat Source Distribution in China Using Real-Time VIIRS Active Fire/Hotspot Data. Sustainability 2018, 10, 4419. [Google Scholar] [CrossRef]
- Ma, C.; Sui, X.; Zeng, Y.; Yang, J.; Xie, Y.; Li, T.; Zhang, P. Classification of Industrial Heat Source Objects Based on Active Fire Point Density Segmentation and Spatial Topological Correlation Analysis in the Beijing–Tianjin–Hebei Region. Sustainability 2022, 14, 11228. [Google Scholar] [CrossRef]
- Wang, M.; Chen, H.; Lei, M. Identifying Potentially Contaminated Areas with MaxEnt Model for Petrochemical Industry in China. Environ. Sci. Pollut. Res. 2022, 29, 54421–54431. [Google Scholar] [CrossRef]
- Jiang, Y.; Guo, X.; Ye, Y.; Xu, Z.; Zhou, Y.; Xia, F.; Shi, Z. Spatiotemporal Assessment and Scenario Simulation of the Risk Potential of Industrial Sites at the Regional Scale. Sci. Total Environ. 2024, 906, 167537. [Google Scholar] [CrossRef]
- The Recommended Method for Risk Assessment of Environmental Emergencies in Administrative Regions. Available online: https://www.mee.gov.cn/gkml/hbb/bgt/201802/t20180206_430931.htm (accessed on 30 June 2023).
- Wang, G.; Li, X.; Zhao, K.; Li, Y.; Sun, X. Quantifying the Spatio-Temporal Variations and Impacts of Factors on Vegetation Water Use Efficiency Using STL Decomposition and Geodetector Method. Remote Sens. 2022, 14, 5926. [Google Scholar] [CrossRef]
- Trull, O.; García-Díaz, J.C.; Peiró-Signes, A. Multiple Seasonal STL Decomposition with Discrete-Interval Moving Seasonalities. Appl. Math. Comput. 2022, 433, 127398. [Google Scholar] [CrossRef]
- Wang, S.; Gao, J.; Guo, L.; Nie, X.; Xiao, X. Meteorological Influences on Spatiotemporal Variation of PM2.5 Concentrations in Atmospheric Pollution Transmission Channel Cities of the Beijing–Tianjin–Hebei Region, China. Int. J. Environ. Res. Public Health 2022, 19, 1607. [Google Scholar] [CrossRef] [PubMed]
- Gong, S.; Zhang, L.; Liu, C.; Lu, S.; Pan, W.; Zhang, Y. Multi-Scale Analysis of the Impacts of Meteorology and Emissions on PM2.5 and O3 Trends at Various Regions in China from 2013 to 2020 2. Key Weather Elements and Emissions. Sci. Total Environ. 2022, 824, 153847. [Google Scholar] [CrossRef] [PubMed]
- Jia, F.; Tan, J.; Lu, X.; Qian, J. Radar Timing Range–Doppler Spectral Target Detection Based on Attention ConvLSTM in Traffic Scenes. Remote Sens. 2023, 15, 4150. [Google Scholar] [CrossRef]
- Hu, H.C.; Chen, L. Parametric Hypothesis Test of P-Norm Distribution. J. Wuhan Univ. 2021, 67, 173–178. [Google Scholar] [CrossRef]
- Li, Y.Y.; Hu, C.R. Experimental Design and Data Processing; Chemical Industry Press: Beijing, China, 2017; pp. 104–107. [Google Scholar]
- Gocic, M.; Trajkovic, S. Analysis of Changes in Meteorological Variables Using Mann-Kendall and Sen’s Slope Estimator Statistical Tests in Serbia. Glob. Planet. Chang. 2013, 100, 172–182. [Google Scholar] [CrossRef]
- Song, C.; Yu, Q.; Jin, K. Forest Resource Quality and Human Activity Intensity Change and Spatial Autocorrelation Analysis in Yulin City, China. Forests 2023, 14, 1929. [Google Scholar] [CrossRef]
- Wang, L.T.; Wei, Z.; Yang, J.; Zhang, Y.; Zhang, F.F.; Su, J.; Meng, C.C.; Zhang, Q. The 2013 Severe Haze over Southern Hebei, China: Model Evaluation, Source Apportionment, and Policy Implications. Atmos. Chem. Phys. 2014, 14, 3151–3173. [Google Scholar] [CrossRef]
- Li, X.; Zhang, Q.; Zhang, Y.; Zheng, B.; Wang, K.; Chen, Y.; Wallington, T.J.; Han, W.; Shen, W.; Zhang, X.; et al. Source Contributions of Urban PM2.5 in the Beijing–Tianjin–Hebei Region: Changes between 2006 and 2013 and Relative Impacts of Emissions and Meteorology. Atmos. Environ. 2015, 123, 229–239. [Google Scholar] [CrossRef]
- Wang, S.E. Study on Source Apportionment of Air Complex Pollution in “2+26” Cities Around Beijing–Tianjin–Hebei Region; Nanjing University: Nanjing, China, 2020. [Google Scholar] [CrossRef]

| No. | Factors | Code | Datasets | Period | Space Resolution | Time Resolution | Data Source |
|---|---|---|---|---|---|---|---|
| 1 | ChinaHighPM2.5 concentration | PM2.5 | Comprehensive High-Resolution Air Pollution | 2012–2021 | 1 km | 1-day | National Tibetan Plateau/Third Pole Environment Data Center (https://doi.org/10.5281/zenodo.3539349, accessed on 30 June 2023.) |
| 2 | 2 m Air Temperature | T2M | ERA5 | 2012–2021 | 0.1° × 0.1° | 1-day | Google Earth Engine (https://earthengine.google.com/, accessed on 30 June 2023.) |
| 3 | Total Precipitation | TP | ERA5 | 2012–2021 | 0.1° × 0.1° | 1-day | Google Earth Engine (https://earthengine.google.com/, accessed on 30 June 2023.) |
| 4 | Surface Pressure | SP | ERA5 | 2012–2021 | 0.1° × 0.1° | 1-day | Google Earth Engine (https://earthengine.google.com/, accessed on 30 June 2023.) |
| 5 | 10 m U Wind Component | 10U | ERA5 | 2012–2021 | 0.1° × 0.1° | 1-day | Google Earth Engine (https://earthengine.google.com/, accessed on 30 June 2023.) |
| 6 | 10 m V Wind Component | 10V | ERA5 | 2012–2021 | 0.1° × 0.1° | 1-day | Google Earth Engine (https://earthengine.google.com/, accessed on 30 June 2023.) |
| 7 | Relative Humidity | RH | ERA5 | 2012–2021 | 0.1° × 0.1° | 1-day | Google Earth Engine (https://earthengine.google.com/, accessed on 30 June 2023.) |
| 8 | Copernicus DEM | DEM | ESA | 2015 | 30 m × 30 m | 1-year | ESA (https://panda.copernicus.eu/panda, accessed on 30 June 2023.) |
| 9 | Industrial Heat Sources | IHS | A dataset of in-operation industrial heat source objects in BTH | 2012–2021 | 375 m | 1-year | Science Data Bank (https://doi.org/10.57760/sciencedb.j00001.00430, accessed on 30 June 2023.) |
| 10 | Carbon Emissions | CE | CCG | 2015, 2020 | City | 1-year | China City Greenhouse Gas Working Group (http://www.cityghg.com/toCauses?id=4, accessed on 30 June 2023.) |
| 11 | Industrial Indices | II | Statistical yearbooks of Beijing, Tianjin and Hebei provinces | 2012–2021 | Province | 1-year | City Data Query Platform (https://www.gotohui.com/, accessed on 30 June 2023.) |
| 12 | Environmental Emissions | EE | Statistical yearbooks of Beijing, Tianjin and Hebei provinces | 2012–2021 | Province | 1-year | City Data Query Platform (https://www.gotohui.com/, accessed on 30 June 2023.) |
| 13 | Raw Material Production | RP | Statistical yearbooks of Beijing, Tianjin and Hebei provinces | 2012–2021 | Province | 1-year | City Data Query Platform (https://www.gotohui.com/, accessed on 30 June 2023.) |
| 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | 2021 | Decline between 2012 and 2021 (%) | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Baoding Beijing | 24.19 24.93 | 29.93 29.86 | 30.90 30.10 | 23.99 26.86 | 23.65 24.54 | 19.12 20.09 | 15.78 15.62 | 14.03 13.47 | 13.15 12.07 | 12.19 11.41 | 49.59% 54.24% |
| Cangzhou | 55.14 | 60.87 | 57.93 | 51.72 | 48.55 | 39.13 | 31.34 | 30.57 | 29.39 | 23.83 | 56.79% |
| Chengde | 14.33 | 15.17 | 16.32 | 12.28 | 11.31 | 10.45 | 8.66 | 8.30 | 7.67 | 8.03 | 43.97% |
| Handan | 42.86 | 44.59 | 42.61 | 37.63 | 33.12 | 32.13 | 24.12 | 27.59 | 25.50 | 20.57 | 52.00% |
| Hengshui | 22.69 | 28.41 | 23.83 | 21.81 | 19.58 | 23.24 | 18.19 | 18.60 | 11.99 | 14.05 | 38.09% |
| Langfang | 25.38 | 30.17 | 28.17 | 24.49 | 22.94 | 18.05 | 14.24 | 14.52 | 13.17 | 12.15 | 52.13% |
| Qinhuangdao | 16.95 | 19.93 | 18.86 | 15.83 | 15.52 | 13.90 | 11.52 | 12.10 | 10.41 | 10.83 | 36.09% |
| Shijiazhuang | 24.46 | 34.09 | 31.25 | 23.47 | 24.50 | 19.53 | 15.74 | 14.88 | 13.21 | 12.19 | 50.17% |
| Tangshan | 41.08 | 44.52 | 38.24 | 31.34 | 28.54 | 27.30 | 20.88 | 21.94 | 20.68 | 19.19 | 53.29% |
| Tianjin | 34.66 | 40.93 | 38.43 | 34.09 | 22.33 | 28.63 | 25.44 | 24.14 | 22.80 | 18.88 | 45.54% |
| Xingtai | 26.91 | 37.40 | 33.30 | 24.76 | 22.53 | 18.34 | 15.01 | 14.77 | 12.15 | 11.51 | 57.23% |
| Zhangjiakou | 12.44 | 12.76 | 12.93 | 10.95 | 9.98 | 9.82 | 8.68 | 7.21 | 6.98 | 7.39 | 40.61% |
| Associated Indicators | Beijing | Tianjin | Hebei | |
|---|---|---|---|---|
| IHS | Operational IHSs | 0.94 | 0.82 | 0.92 |
| Industrial indices | Energy consumption level | 0.82 | 0.79 | 0.93 |
| Industry scale | 0.89 | 0.69 | 0.88 | |
| Secondary sector GDP | 0.80 | 0.92 | 0.95 | |
| Raw material production | Raw coal production | NAN 1 | NAN | 0.98 |
| Steel production | 0.21 | 0.35 | −0.86 | |
| Gas production | −0.24 | −0.83 | 0.95 | |
| Cement production | 0.82 | 0.75 | 0.29 | |
| Environmental emissions | SO2 emissions | 0.72 | 0.50 | 0.94 |
| NOx emissions | 0.89 | 0.91 | 0.93 | |
| Industrial wastewater discharges | 0.86 | 0.83 | NAN | |
| Industrial energy carbon emissions | 0.86 | |||
| Date | Region | This Study | Similar Studies | Reference |
|---|---|---|---|---|
| 2013.1–2013.2 | Shijiazhuang | 35.79% | 37.00% | Li (2015) [63] |
| 36.20% | Wang (2014) [62] | |||
| 29.20% | Wang (2020) [64] | |||
| Xingtai | 36.26% | 30.00% | Li (2015) [63] | |
| 34% | Wang (2014) [62] | |||
| 32% | Wang (2020) [64] | |||
| 2012.7 | Beijing | 22.55% | 24% | Liu (2020) [27] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, Y.; Sui, X.; Ma, C.; Liao, R.; Yang, J.; Wang, D.; Zhang, P. Industrial Heat Source-Related PM2.5 Concentration Estimates and Analysis Using New Three-Stage Model in the Beijing–Tianjin–Hebei Region. Atmosphere 2024, 15, 131. https://doi.org/10.3390/atmos15010131
Zeng Y, Sui X, Ma C, Liao R, Yang J, Wang D, Zhang P. Industrial Heat Source-Related PM2.5 Concentration Estimates and Analysis Using New Three-Stage Model in the Beijing–Tianjin–Hebei Region. Atmosphere. 2024; 15(1):131. https://doi.org/10.3390/atmos15010131
Chicago/Turabian StyleZeng, Yi, Xin Sui, Caihong Ma, Ruilin Liao, Jin Yang, Dacheng Wang, and Pengyu Zhang. 2024. "Industrial Heat Source-Related PM2.5 Concentration Estimates and Analysis Using New Three-Stage Model in the Beijing–Tianjin–Hebei Region" Atmosphere 15, no. 1: 131. https://doi.org/10.3390/atmos15010131
APA StyleZeng, Y., Sui, X., Ma, C., Liao, R., Yang, J., Wang, D., & Zhang, P. (2024). Industrial Heat Source-Related PM2.5 Concentration Estimates and Analysis Using New Three-Stage Model in the Beijing–Tianjin–Hebei Region. Atmosphere, 15(1), 131. https://doi.org/10.3390/atmos15010131





