Study on Dynamic Characteristics of Magnetic Coagulation of Fe-Based Fine Particles in Iron and Steel Industry
Abstract
:1. Introduction
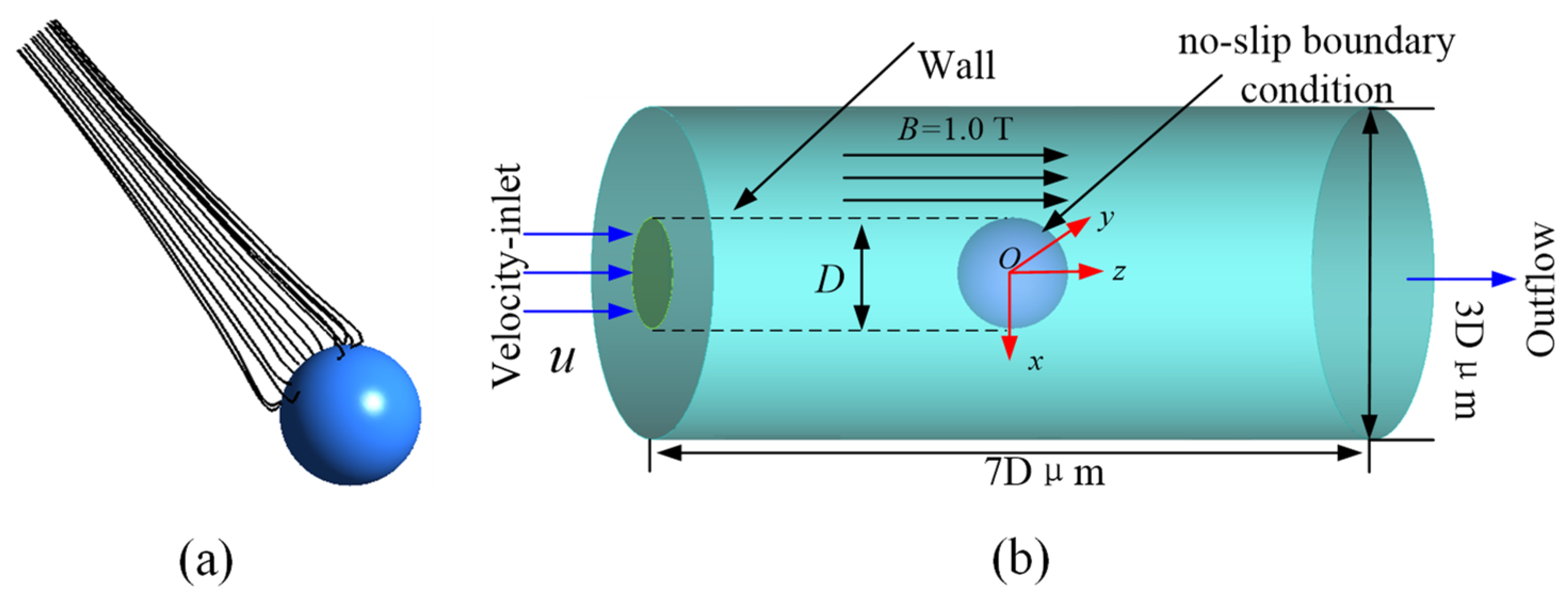
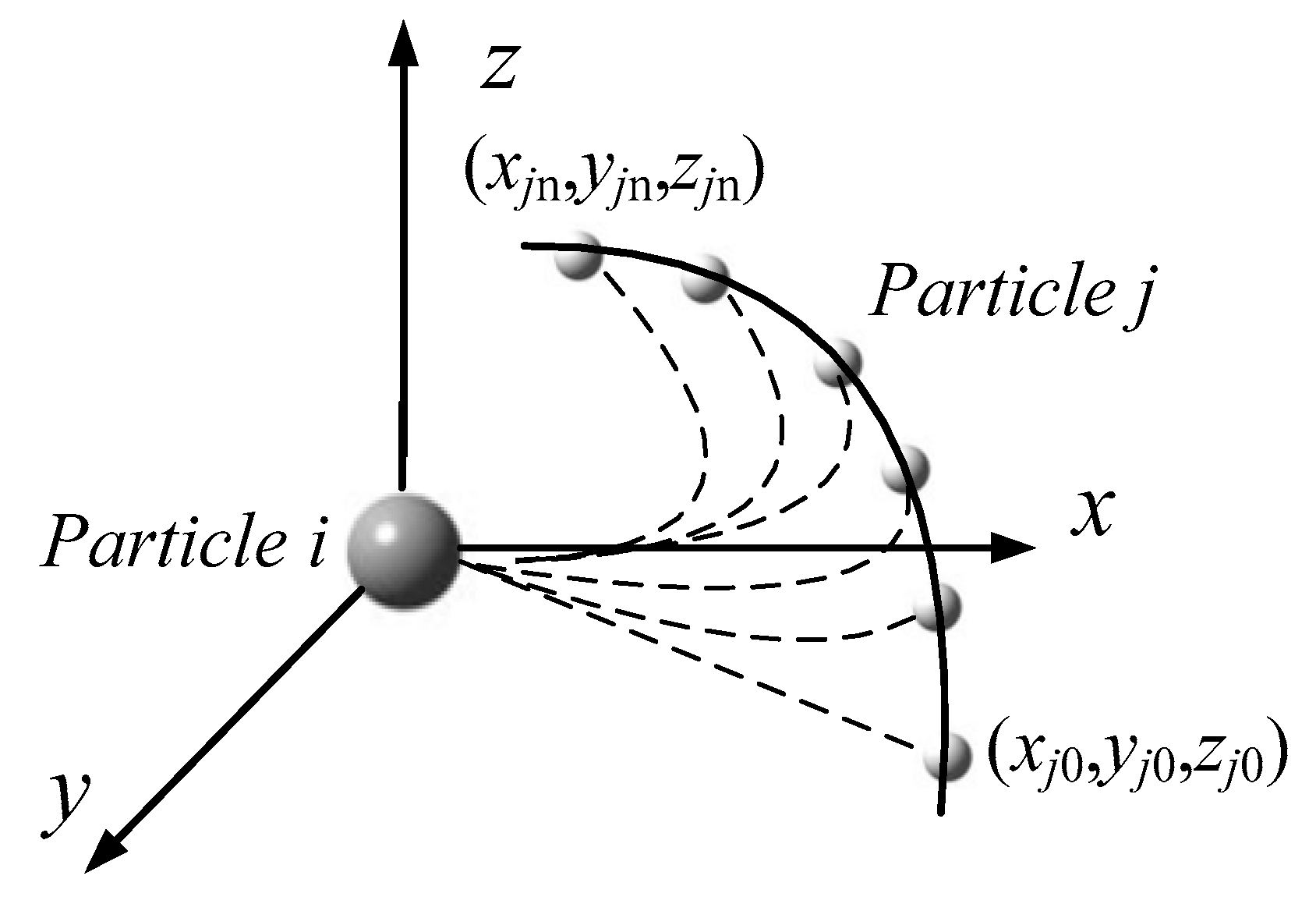
2. Physical Model and Boundary Conditions
3. Numerical Calculation Equations
3.1. Governing Equations for the Fluid Phase
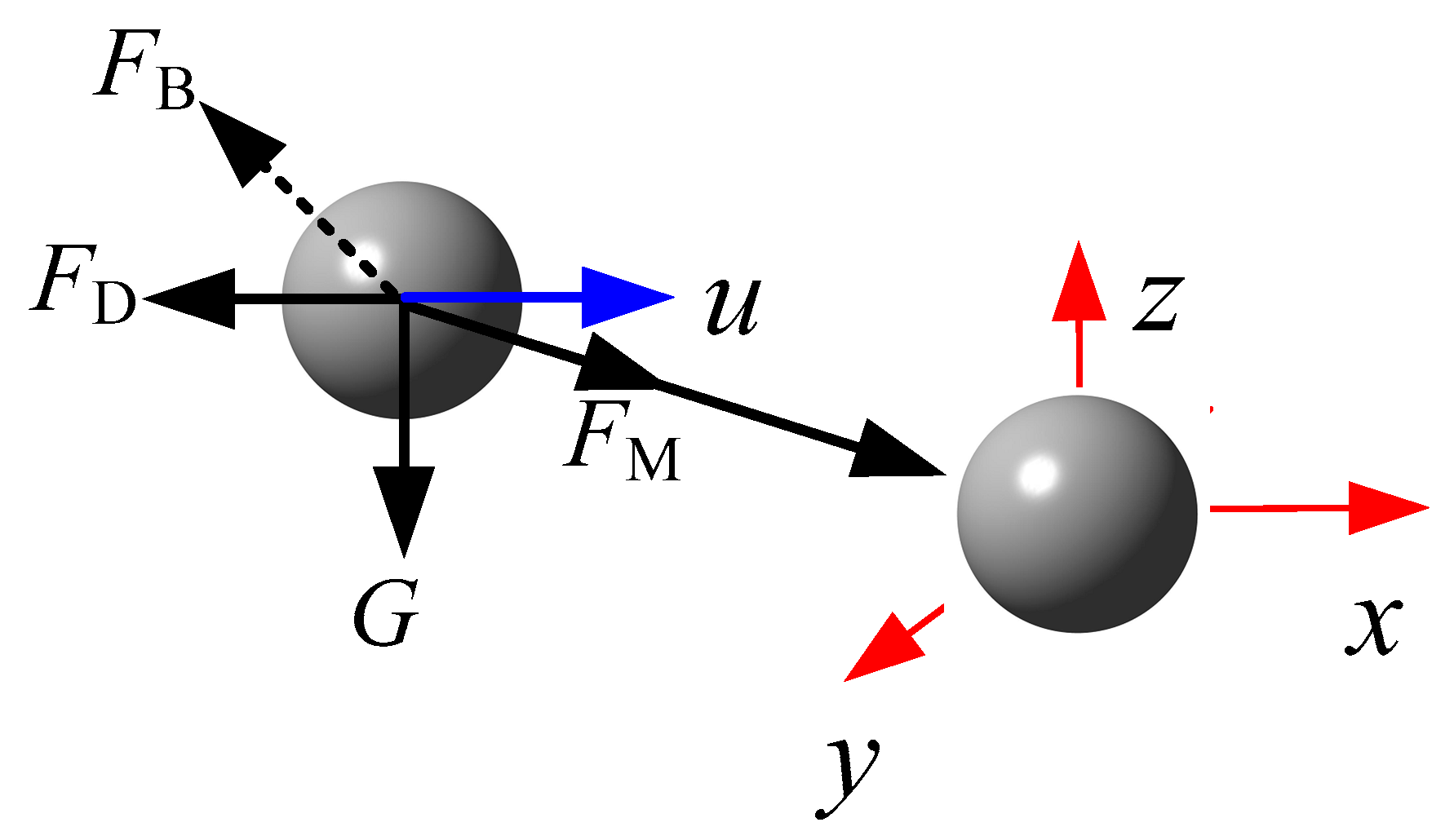
3.2. Governing Equations for the Particles
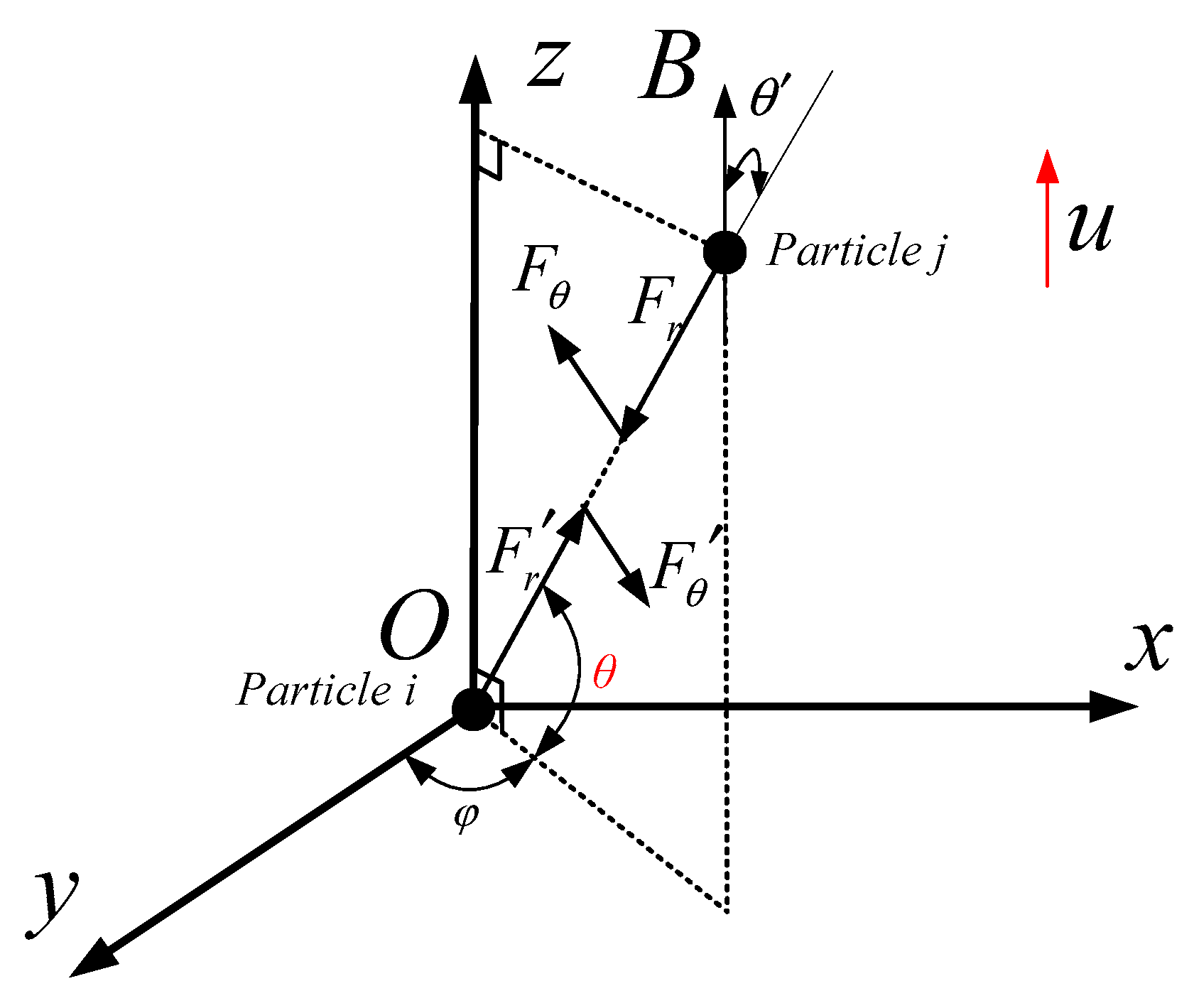
3.3. Calculation of the Magnetic Coagulation of Fe-Based Fine Particles Based on CFD-PBM
4. Simulation Correctness Verification
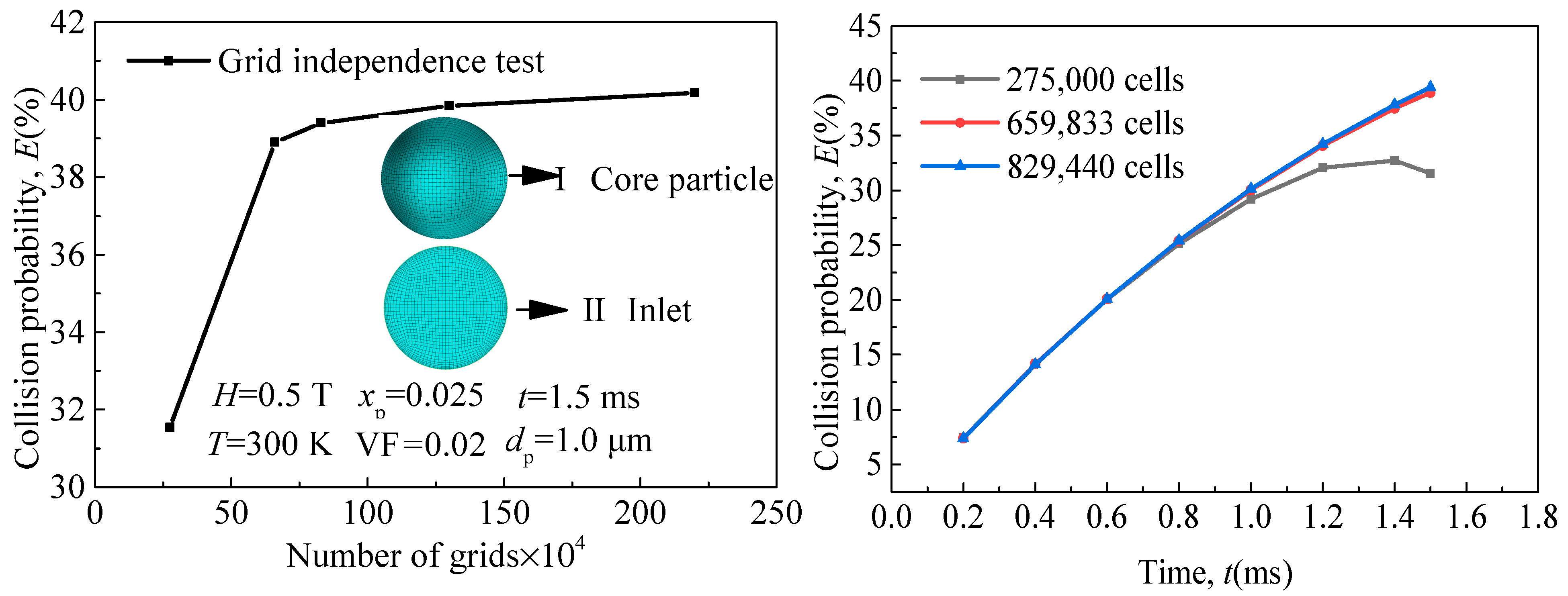
4.1. Grid Independence Test
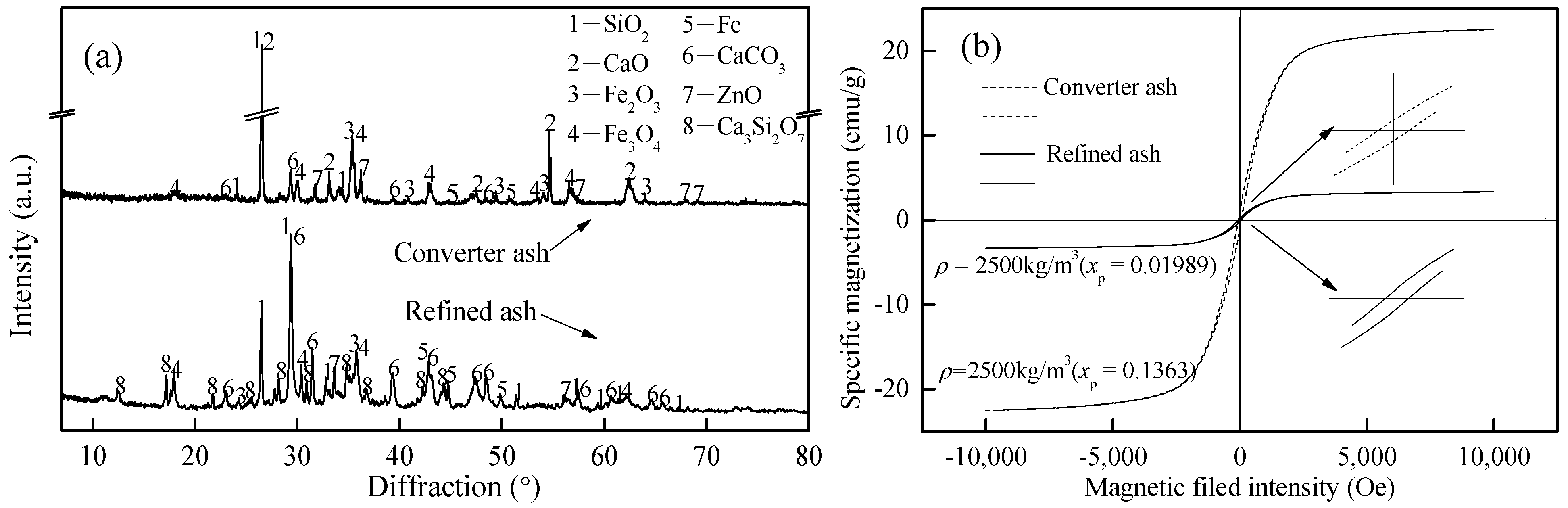
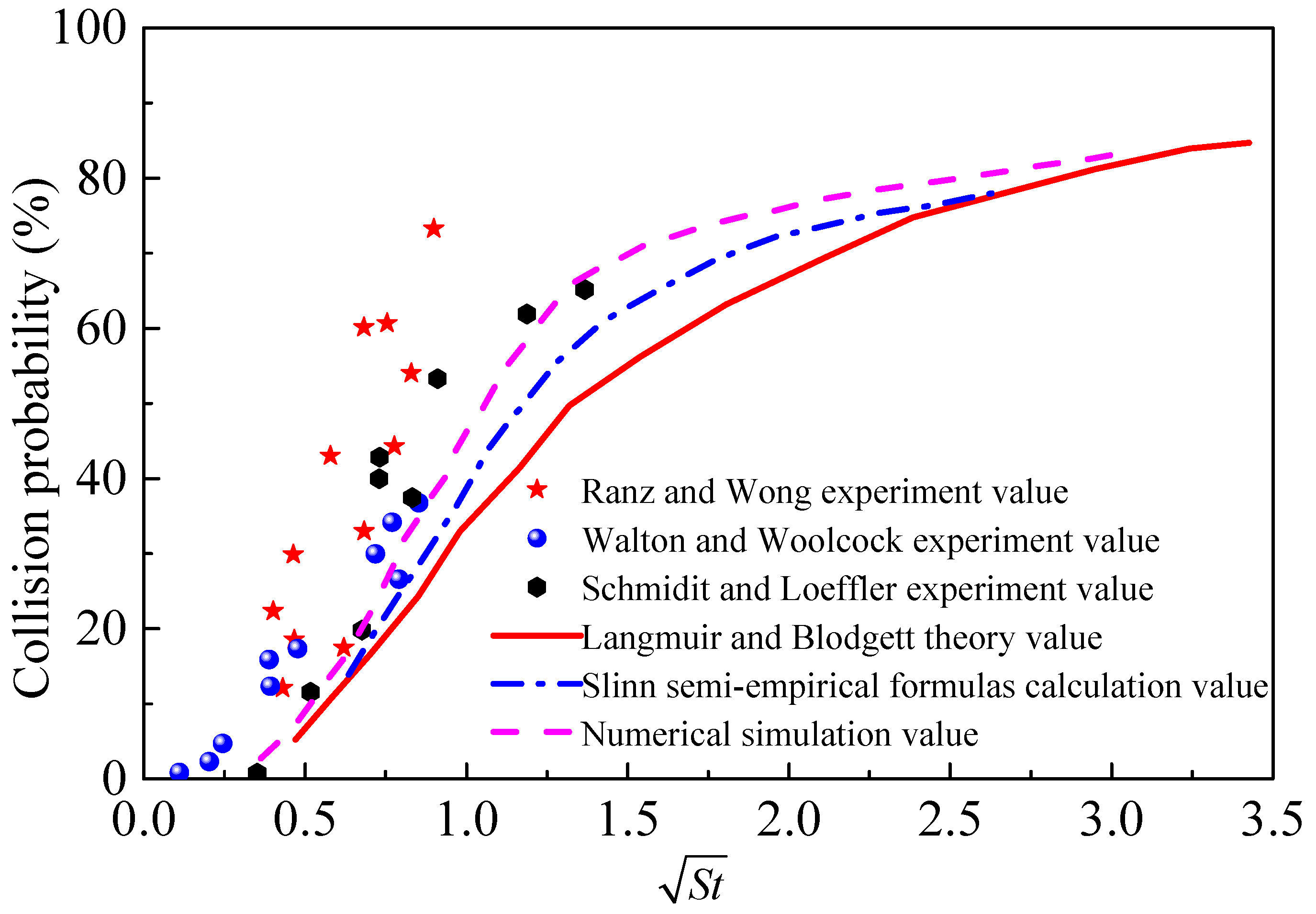
4.2. Experiment Verification of the Simulation Method
5. Numerical Simulation Calculation Results
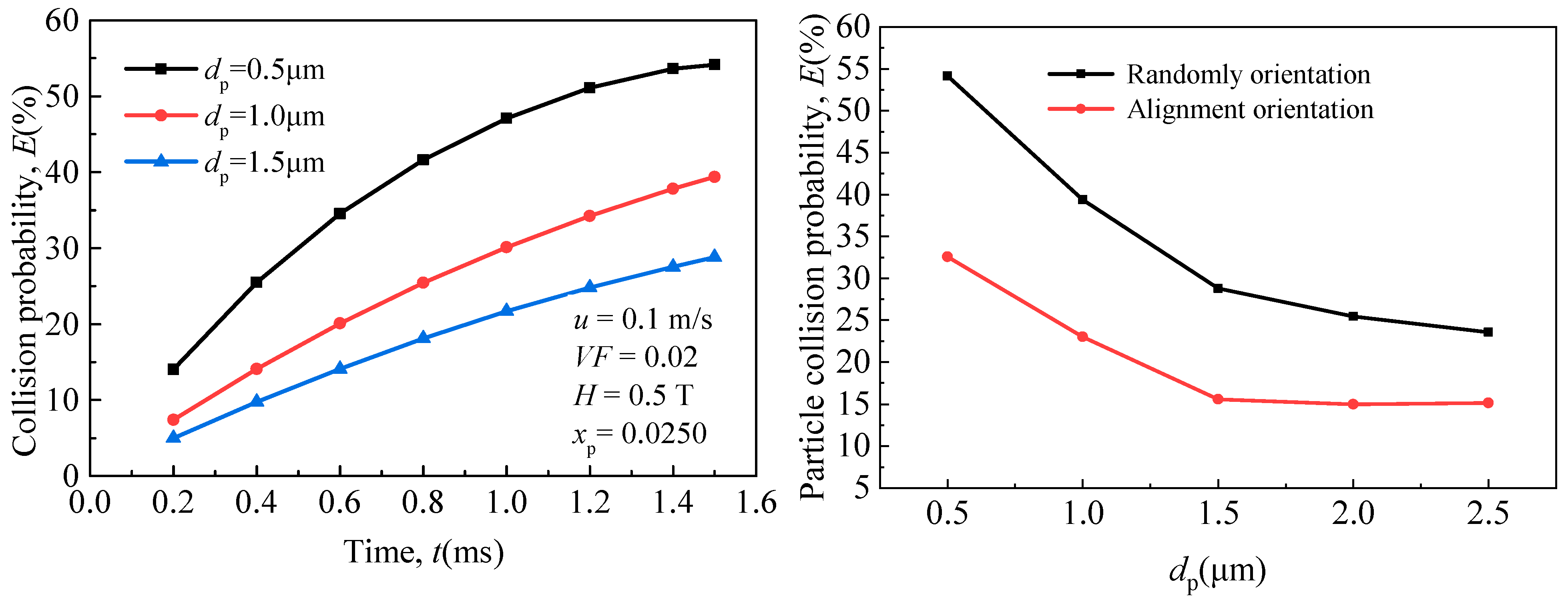
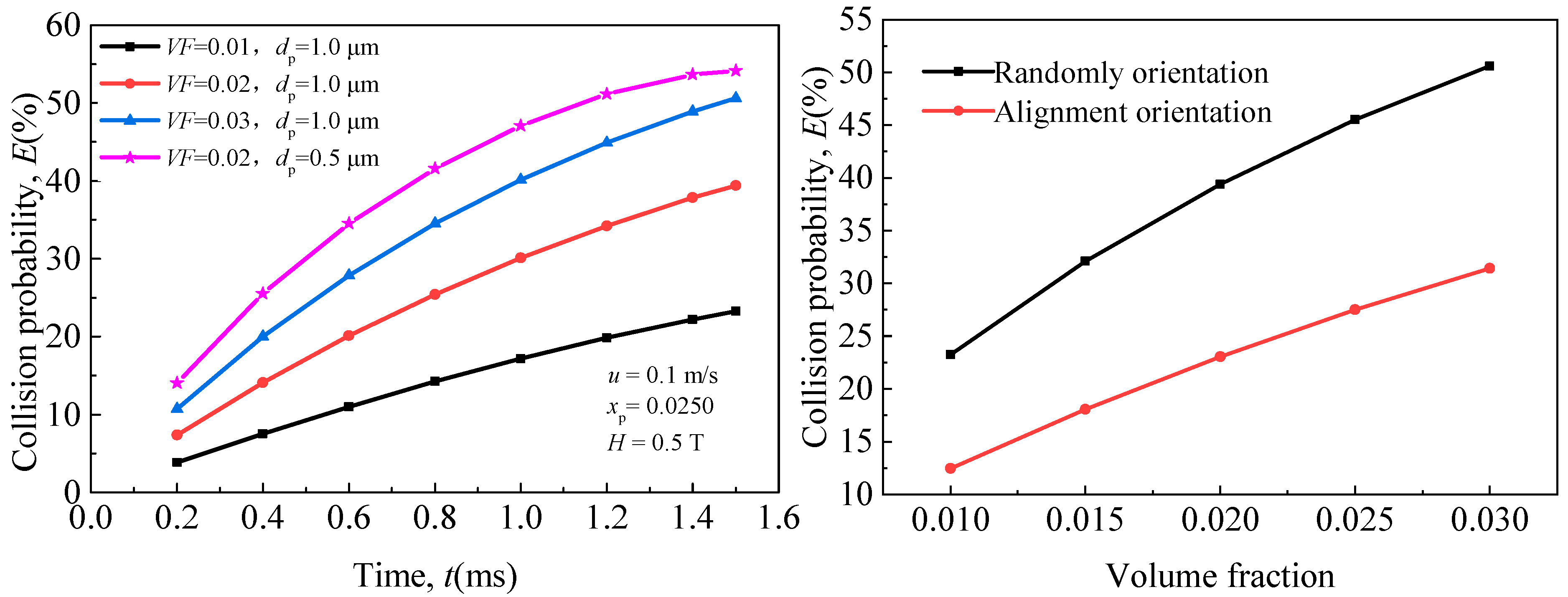
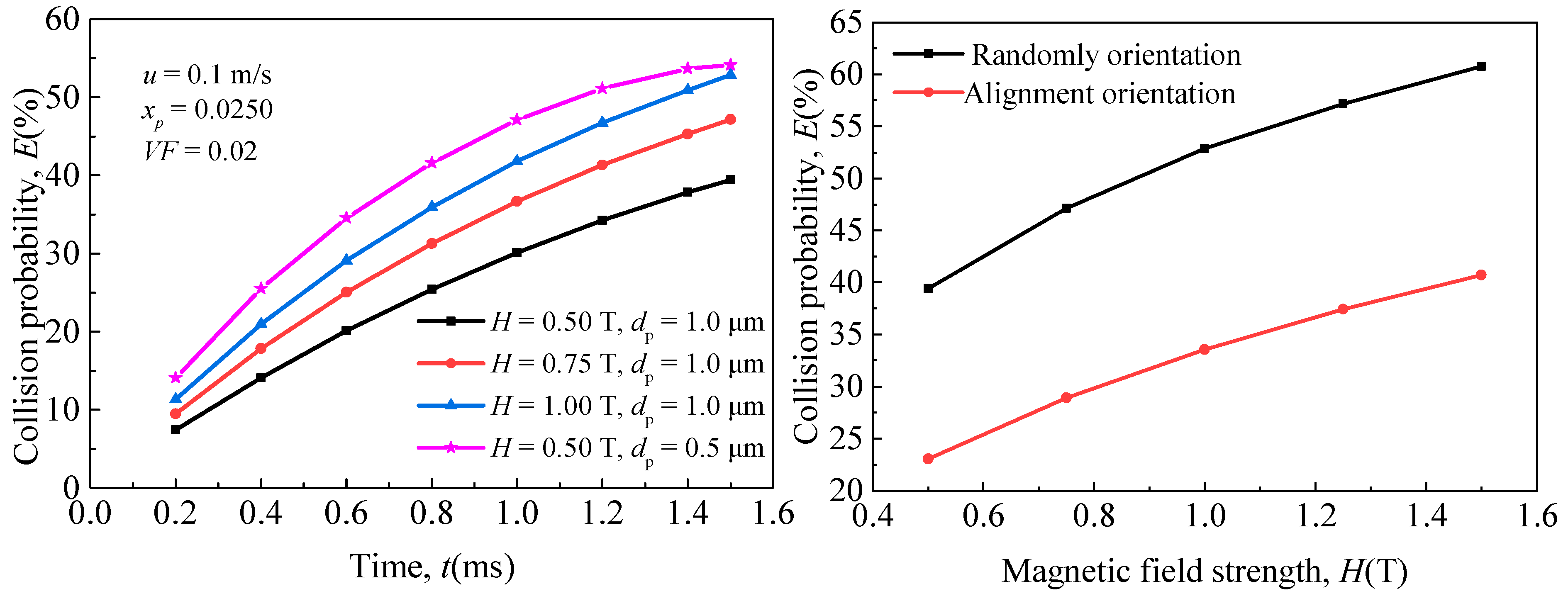
5.1. Effect of Particle Size on Magnetic Coagulation Removal Efficiency of Fe-Based Fine Particles
5.2. Effect of Particle Volume Fraction on Magnetic Coagulation Removal Efficiency of Fe-Based Fine Particles
5.3. Effect of External Magnetic Field Strength on Magnetic Coagulation Removal Efficiency of Fe-Based Fine Particles
5.4. Effect of Particle Magnetic Susceptibility on Magnetic Coagulation Removal Efficiency of Fe-Based Fine Particles
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Cc | Cunningham correction factor |
| dp | particle diameter, μm |
| FB | Brownian force, N |
| FD | drag force, N |
| Fg | gravity, N |
| fs | interval particle volume, m3 |
| g | gravitational acceleration, m/s2 |
| Kn | particle Knudsen number |
| kb | Boltzmann constant, 1.38 × 10−23 J/K |
| Mp | particle saturated magnetization, A/m |
| mi | particle i magnetic dipole moment, A·m2 |
| mj | particle j magnetic dipole moment, A·m2 |
| mp | particle mass, kg |
| ρp | particle density, kg/m3 |
| Re | Reynolds number |
| S0 | noise spectral intensity, m2/s3 |
| T | absolute temperature, K |
| t | time, s |
| u | fluid velocity, m/s |
| up | particle velocity, m/s |
| Vk | interval particle volume growth factor |
| μ0 | vacuum permeability, 1.256 × 10−6 N/A2 |
| Greek symbols | |
| α | volume fraction |
| θ | polar angle, rad |
| λ | air molecules average free path, nm |
| ν | fluid dynamic viscosity, Pa·s |
| ρ | fluid density, kg/m3 |
| Subscripts | |
| i | particle i |
| j | particle j |
| mag | magnetic field |
| sat | saturation magnetization |
References
- Lin, B.; Wu, R. Designing Energy Policy Based on Dynamic Change in Energy and Carbon Dioxide Emission Performance of China’s Iron and Steel Industry. J. Clean. Prod. 2020, 256, 120412. [Google Scholar] [CrossRef]
- Li, Q.; Wen, B.; Wang, G.; Cheng, J.; Zhong, W.; Dai, T.; Liang, L.; Han, Z. Study on Calculation of Carbon Emission Factors and Embodied Carbon Emissions of Iron-containing Commodities in International Trade of China. J. Clean. Prod. 2018, 191, 119–126. [Google Scholar] [CrossRef]
- Feng, C.; Huang, J.; Wang, M. Analysis of Green Total-factor Productivity in China’s Regional Metal Industry: A Meta-frontier Approach. Resour. Policy 2018, 58, 219–229. [Google Scholar] [CrossRef]
- He, Z.; Guo, Q.; Wang, Z.; Li, X. Prediction of Monthly PM2.5 Concentration in Liaocheng in China Employing Artificial Neural Network. Atmosphere 2022, 13, 1221. [Google Scholar] [CrossRef]
- Zhao, C.; Pu, W.; Niu, M.; Wazir, J.; Song, S.; Wei, L.; Li, L.; Su, Z.; Wang, H. Respiratory Exposure to PM2.5 Soluble Extract Induced Chronic Lung Injury by Disturbing the Phagocytosis Function of Macrophage. Environ. Sci. Pollut. R. 2022, 29, 13983–13997. [Google Scholar] [CrossRef]
- Zhou, G.; Low, Z.; Feng, S.; Zhang, F.; Zhong, Z.; Xing, W. Effect of Relative Humidity and Dust Moisture Content on Filtration Performance of Bag Filter. Sep. Purif. Technol. 2023, 308, 122952. [Google Scholar] [CrossRef]
- Hosseini, S.A.; Tafreshi, H.V. On the Importance of Fibers’ Cross-sectional Shape for Air Filters Operating in the Slip Flow Regime. Powder. Technol. 2011, 212, 425–431. [Google Scholar] [CrossRef]
- Bao, L.; Musadiq, M.; Kijima, T.; Kenmochi, K. Influence of Fibers on the Dust Dislodgement Efficiency of Bag Filters. Text. Res. J. 2014, 84, 764–771. [Google Scholar] [CrossRef]
- Huang, H.; Wang, K.; Zhao, H. Numerical Study of Pressure Drop and Diffusional Collection Efficiency of Several Typical Noncircular Fibers in Filtration. Powder Technol. 2016, 292, 232–241. [Google Scholar] [CrossRef]
- Kasper, G.; Schollmeier, S.; Meyer, J. Structure and Density of Deposits Formed on Filter Fibers by Inertial Particle Deposition and Bounce. J. Aerosol. Sci. 2010, 41, 1167–1182. [Google Scholar] [CrossRef]
- Zhou, J.; Zhang, L.; Zhang, B.; Gong, W. Study on Filtration Performance of Elliptical Fiber with Different Arrangements. J. Eng. Fiber. Fabr. 2020, 15, 1–11. [Google Scholar] [CrossRef]
- Fakron, O.M.; Field, D.P. 3D Image Reconstruction of Fiber Systems Using Electron Tomography. Ultramicroscopy 2015, 149, 21–25. [Google Scholar] [CrossRef] [PubMed]
- Qian, F.; Huang, N.; Zhu, X.; Lu, J. Numerical Study of the Gas–solid Flow Characteristic of Fibrous Media Based on SEM Using CFD-DEM. Powder Technol. 2013, 249, 63–70. [Google Scholar] [CrossRef]
- Li, W.; Shen, S.; Li, H. Study and Optimization of the Filtration Performance of Multi-fiber Filter. Adv. Powder Technol. 2016, 27, 638–645. [Google Scholar] [CrossRef]
- Yue, C.; Zhang, Q.; Zhai, Z. Numerical Simulation of the Filtration Process in Fibrous Filters Using CFD-DEM Method. J. Aerosol. Sci. 2016, 101, 174–187. [Google Scholar] [CrossRef]
- Shu, Z.; Qian, F.; Fang, C.; Zhu, J. Numerical Simulation of Particle Spatial Distribution and Filtration Characteristic in the Pleated Filter Media Using OpenFOAM. Indoor Built Environ. 2020, 30, 1159–1172. [Google Scholar] [CrossRef]
- Cao, B.; Wang, S.; Dong, W.; Zhu, J.; Qian, F.; Lu, J.; Han, Y. Investigation of the Filtration Performance for Fibrous Media: Coupling of a Semi-analytical Model with CFD on Voronoi-based Microstructure. Sep. Purif. Technol. 2020, 251, 117364. [Google Scholar] [CrossRef]
- Bucher, T.M.; Tafreshi, H.V.; Tepper, G.C. Modeling Performance of Thin Fibrous Coatings with Orthogonally Layered Nanofibers for Improved Aerosol Filtration. Powder Technol. 2013, 249, 43–53. [Google Scholar] [CrossRef]
- Subrenat, A.; Bellettre, J.; Cloirec, P.L. 3-D Numerical Simulations of Flows in a Cylindrical Pleated Filter Packed with Activated Carbon Cloth. Chem. Eng. Sci. 2003, 58, 4965–4973. [Google Scholar] [CrossRef]
- Dong, M.; Li, J.; Shang, Y. Numerical Investigation on Deposition Process of Submicron Particles in Collision with A Single Cylindrical Fiber. J. Aerosol. Sci. 2019, 129, 1–15. [Google Scholar] [CrossRef]
- Huang, H.; Zheng, C.; Zhao, H. Numerical Investigation on Non-steady-state Filtration of Elliptical Fibers for Submicron Particles in the “Greenfield gap” Range. J. Aerosol. Sci. 2017, 114, 263–275. [Google Scholar] [CrossRef]
- Nazaroff, W. Indoor Particle Dynamics. Indoor Air 2004, 14, 175–183. [Google Scholar] [CrossRef] [PubMed]
- Guo, Y.; Gao, X.; Zhu, T.; Luo, L.; Zheng, Y. Chemical Profiles of PM Emitted from the Iron and Steel Industry in Northern China. Atmos. Environ. 2017, 150, 187–197. [Google Scholar] [CrossRef]
- Jia, J.; Cheng, S.; Yao, S.; Xu, T.; Zhang, T.; Ma, Y.; Wang, H.; Duan, W. Emission Characteristics and Chemical Components of Size-segregated Particulate Matter in Iron and Steel Industry. Atmos. Environ. 2018, 182, 115–127. [Google Scholar] [CrossRef]
- Hleis, D.; Fernández-Olmo, I.; Ledoux, F.; Kfoury, A.; Courcot, L.; Desmonts, T.; Courcot, D. Chemical Profile Identification of Fugitive and Confined Particle Emissions from an Integrated Iron and Steelmaking Plant. J. Hazard. Mater. 2013, 250–251, 246–255. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Diao, Y.; Jiang, J.; Chu, M.; Han, K.; Shen, H. Study on Turbulent Aggregation Dynamics in the Process of Fine Particles Capture by Single Fibers. Particul. Sci. Technol. 2023, 41, 222–230. [Google Scholar] [CrossRef]
- Zhang, W.; Qi, H.; You, C.; Xu, X. Mechanical analysis of agglomeration and fragmentation of particles during collisions. J. Tsinghua Univ. Sci. Technol. 2002, 42, 1639–1643. [Google Scholar]
- Ku, J.; Chen, H.; He, K.; Yan, Q. Simulation and Observation of Magnetic Mineral Particles Aggregating into Chains in a Uniform Magnetic Field. Miner. Eng. 2015, 79, 10–16. [Google Scholar] [CrossRef]
- Ku, J.; Chen, H.; He, K.; Xu, L.; Yan, Q. Numerical Simulation of Agglomeration Process Dynamics of Ferromagnetic Mineral Particles in a Weak Magnetic Field. Int. J. Miner. Process. 2014, 133, 46–51. [Google Scholar] [CrossRef]
- Ke, C.; Shu, S.; Zhang, H.; Yuan, H. LBM-IBM-DEM Modelling of Magnetic Particles in a Fluid. Powder Technol. 2017, 314, 264–280. [Google Scholar] [CrossRef]
- Senkawa, K.; Nakai, Y.; Mishima, F.; Akiyama, Y.; Nishijima, S. Measurement of the Adhesion Force Between Particles for High Gradient Magnetic Separation of Pneumatic Conveyed Powder Products. Physica C 2011, 471, 1525–1529. [Google Scholar] [CrossRef]
- Karvelas, E.G.; Lampropoulos, N.K.; Benos, L.T.; Karakasidis, T.; Sarris, I.E. On the Magnetic Aggregation of Fe3O4 Nanoparticles. Comput. Meth. Prog. Bio. 2021, 198, 105778. [Google Scholar] [CrossRef] [PubMed]
- Hua, F.; Kang, Y.; Zhong, K. Influent of Turbulent Effect on the Collection Process of Aerosols by Raindrops. China Environ. Sci. 2017, 37, 13–20. [Google Scholar]
- Dastoori, K.; Kolhe, M.; Mallard, C.; Makin, B. Electrostatic precipitation in a small scale wood combustion furnace. J. Electrostat. 2011, 69, 466–472. [Google Scholar] [CrossRef]
- Fuchs, N.A.; Daisley, R.E.; Fuchs, M.; Davies, C.N.; Straumanis, M.E. The Mechanics of Aerosols. Phys. Today 1965, 18, 73. [Google Scholar] [CrossRef]
- Li, Y.; Zhao, C.; Wu, X.; Lu, D.; Han, S. Aggregation Mechanism of PM10 from Coal Combustion in Uniform Magnetic Field. CIESC. J. 2007, 58, 987–993. [Google Scholar]
- Kumar, P.; Biswas, P. Analytical Expressions of the Collision Frequency Function for Aggregation of Magnetic Particles. J. Aerosol. Sci. 2005, 36, 455–469. [Google Scholar] [CrossRef]
- Allen, M.D.; Raabe, O.G. Slip Correction Measurements of Spherical Solid Aerosol Particles in an Improved Millikan Apparatus. Aerosol. Sci. Technol. 1985, 4, 269–286. [Google Scholar] [CrossRef]
- Zhao, H.; Zheng, C.; Xu, M. Multi-Monte Carlo Method for General Dynamic Equation Considering Particle Coagulation. Appl. Math. Mech. 2005, 26, 875–882. [Google Scholar]
- Poon, J.M.H.; Immanuel, C.D.; Doyle, F.J.; Litster, J.D. A Three-dimensional Population Balance Model of Granulation with a Mechanistic Representation of the Nucleation and Aggregation Phenomena. Chem. Eng. Sci. 2008, 63, 1315–1329. [Google Scholar] [CrossRef]
- Ranz, W.; Wong, J. Impaction of Dust and Smoke Particles on Surface and Body Collectors. Ind. Eng. Chem. 1952, 44, 1371–1381. [Google Scholar] [CrossRef]
- Walton, W.; Woolcoke, A. The Suppression of Airborne Dust by Water Spray. Int. J. Air Pollut. 1960, 3, 129–153. [Google Scholar] [PubMed]
- Schmidt, M.; Loffler, F. Experimental Investigations on Two-phase Flow Past a Sphere Using Digital Particle-image-velocimetry. Exp. Fluids 1993, 14, 296–304. [Google Scholar] [CrossRef]
- Langmuir, I.; Blodgett, K.B. A mathematical investigations of water droplet trajectories. AAF Techmical. Rep. 1946, 29, 8–20. [Google Scholar]
- Slinn, W.G.N. Some approximations for the wet and dry removal of particles and gases from the atmosphere. Water Air Soil Pollut. 1977, 7, 513–543. [Google Scholar] [CrossRef]

| dp (μm) | λ (nm) | Kn | Cc |
|---|---|---|---|
| 0.5 | 68.41 | 0.2736 | 2.010 |
| 1.0 | 68.41 | 0.1368 | 1.933 |
| 1.5 | 68.41 | 0.09121 | 1.597 |
| 2.0 | 68.41 | 0.06841 | 1.438 |
| 2.5 | 68.41 | 0.05473 | 1.346 |
| dp (μm) | 0.01 | 0.1 | 1 | 10 |
|---|---|---|---|---|
| Kn | 10~100 | 1~10 | 0.1~1 | 0.01~0.1 |
| Zone | Free molecular zone | Transition zone | Near-continuous zone/Slip zone | Continuous zone |
| Interval Number | Average Particle Diameter (m) | Proportion (%) | Particle Volume Fraction (VF) |
|---|---|---|---|
| Bin-0 | 5.040 × 10−6 | 0 | 0 |
| Bin-1 | 4.000 × 10−6 | 0 | 0 |
| Bin-2 | 3.175 × 10−6 | 0 | 0 |
| Bin-3 | 2.520 × 10−6 | 0 | 0 |
| Bin-4 | 2.000 × 10−6 | 0 | 0 |
| Bin-5 | 1.587 × 10−6 | 0 | 0 |
| Bin-6 | 1.260 × 10−6 | 0 | 0 |
| Bin-7 | 1.000 × 10−6 | 100 | 0.01420 |
| Average Particle Diameter (μm) | Bin-7 | Bin-6 | Bin-5 | Bin-4 | Bin-3 | Bin-2 | Bin-1 | Bin-0 | |
|---|---|---|---|---|---|---|---|---|---|
| Particle Diameter (μm) | d7 | d6 | d5 | d4 | d3 | d2 | d1 | d0 | |
| 0.5000 | 0.500 | 0.630 | 0.793 | 1.000 | 1.260 | 1.587 | 2.000 | 2.520 | |
| 1.000 | 1.000 | 1.260 | 1.587 | 2.000 | 2.520 | 3.175 | 4.000 | 5.040 | |
| 1.500 | 1.500 | 1.890 | 2.381 | 3.000 | 3.780 | 4.762 | 6.000 | 7.560 | |
| 2.000 | 2.000 | 2.520 | 3.175 | 4.000 | 5.040 | 6.350 | 8.000 | 10.08 | |
| 2.500 | 2.500 | 3.150 | 3.969 | 5.000 | 6.300 | 7.937 | 10.00 | 12.60 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, D.; Hu, Z.; Zhang, L.; Zhang, W. Study on Dynamic Characteristics of Magnetic Coagulation of Fe-Based Fine Particles in Iron and Steel Industry. Atmosphere 2023, 14, 1434. https://doi.org/10.3390/atmos14091434
Xu D, Hu Z, Zhang L, Zhang W. Study on Dynamic Characteristics of Magnetic Coagulation of Fe-Based Fine Particles in Iron and Steel Industry. Atmosphere. 2023; 14(9):1434. https://doi.org/10.3390/atmos14091434
Chicago/Turabian StyleXu, Dengke, Zuxiang Hu, Li’an Zhang, and Wenqing Zhang. 2023. "Study on Dynamic Characteristics of Magnetic Coagulation of Fe-Based Fine Particles in Iron and Steel Industry" Atmosphere 14, no. 9: 1434. https://doi.org/10.3390/atmos14091434
APA StyleXu, D., Hu, Z., Zhang, L., & Zhang, W. (2023). Study on Dynamic Characteristics of Magnetic Coagulation of Fe-Based Fine Particles in Iron and Steel Industry. Atmosphere, 14(9), 1434. https://doi.org/10.3390/atmos14091434









