Abstract
Based on the basic nonlinear parameter system of the solid oxide electrolysis cell, the data-driven method was used for system identification. The basic model of the solid oxide electrolysis cell was accomplished in Simulink and experiments were performed under a diversified input/output operating environment. The experimental results of the solid oxide electrolysis cell basic parameter system generated 15 datasets. The system identification process involved the utilization of these datasets with the application of nonlinear autoregressive-exogenous models. Initially, data identification came from the Matlab mechanism model. Then, the nonlinear autoregressive-exogenous structures were estimated and selected exploratively through an individual operating condition. In terms of fitness, we conclude that the solid oxide electrolysis cell parameter system cannot be satisfied by a solitary autoregressive-exogenous model for all datasets. Nevertheless, the nonlinear autoregressive-exogenous model utilized S-type nonlinearities to fit a total of 2 validation datasets and 15 estimated datasets. The obtained results were compared with the basic parameter system of a solid oxide electrolysis cell, and the nonlinear autoregressive-exogenous projected output demonstrated an accuracy of over 93% across diverse operational circumstances—regardless of whether there was noise interference. This result has positive significance for the future use of the solid oxide electrolysis cell to achieve the dual carbon goal in China.
1. Introduction
The utilization of hydrogen energy is a sustainable approach to significantly enhance energy-saving control technology [1] and optimize operational effectiveness, with the potential to substitute traditional fossil fuels [2,3,4]. Nevertheless, the existing techniques for generating hydrogen still possess certain drawbacks, such as ecological contamination and the limited effectiveness of photovoltaic hydrogen production under elevated temperatures [5]. Hence, the solid oxide electrolysis cell (SOEC) has emerged as a secure, eco-friendly, and effective technique for generating hydrogen [6] while pursuing the objective of discovering an environmentally friendly and efficient method for hydrogen production. However, it is difficult to achieve its working process accurately, which involves electrochemical reactions, modeling, and control tasks [7,8]. Model identification has become one of the effective and high-precision modeling methods for it.
In the past decades, the SOEC has received attention for its advantages of being a green and clean energy source. After an SOEC produces hydrogen, it can be used to generate electricity, which is conducive to changing the traditional forms of power generation that produce large amounts of CO2 emissions, such as thermal power and coal power. Engineering problems are present in nearly all types of SOECs [9]. The hydrogen production mission of an SOEC can be seen as the reverse operation of a solid oxide fuel cell (SOFC), with two pathways for fuel supply. One is for the circuit and the other is for the hydrolysis of SOEC hydrogen production and power supply. Therefore, the SOEC has the advantages of quietness and high efficiency but also has potential stability problems due to the complexity of the internal operation mechanism. To tackle this issue, various control methods have been utilized, such as state feedback [10,11] for the establishment of hydrogen-production-based power plants [10]. Subsequently, the use of an SOEC for a solar free-standing building energy system was reported [12], which uses electrical power and fuel utilization as the primary dynamic controls to drive solid oxide cells. Various control methods, including PID control [13], robust control [14,15,16], and optimal control [17], have been employed for the development of trajectory SOFC tracking control systems. Extensive research has been conducted on the simulation of SOEC parametric systems on the flat plane [18,19,20,21]. Moreover, the twenty-first century is the century of data. Ref. [22] used a symbolic regression machine learning approach based on genetic programming to process data. Ref. [23] combined sparsity facilitation techniques and machine learning with nonlinear dynamical systems for coefficient identification of nonlinear dynamics by discovering governing equations from noisy measurement data.
Based on the analysis of existing studies, it is evident that the current uncertainty of various parameters is a result of the intricate assumptions and mathematical modeling involved in nonlinear parameter systems. Therefore, there is a need for a method that can estimate system parameters based on experimental observations. In reference [19], the comparison was made between the findings of various linear and nonlinear SOFC models. Refs. [20,21] introduced the use of neural networks to identify SOEC parameter systems. One issue with this technology is its failure to offer training datasets and transients that only consider an individual operating condition. In Matlab, the system identification toolbox is introduced in reference [24] for optimal control design through system identification. In reference [25], a novel SOEC model was introduced, featuring a distinct gas property of the oxygen electrode/electrolyte interface oxygen pressure associated with oxygen electrode stratification. Ref. [26] proposed a data-driven link function degradation model and used a cyclic recognition program based on the maximum likelihood method to identify SOEC parameters online. Ref. [27] introduced an adaptive polynomial approximation (APA) method for modeling an SOEC. Ref. [28] proposed an innovative multi-physics coupled model of different configurations of an integrated coal gasification fuel cell combined cycle (IGFC) system employing an SOEC for CO2 capture. A three-dimensional multiscale IT-SOEC unit model was developed in reference [29]. The model comprehensively considers the detailed mass transfer, electrochemical reaction, and heat transfer processes. Ref. [30] combined segmented SOEC experiments, multiphysics field simulations, and neural networks to jointly optimize inhomogeneity and efficiency to develop a three-dimensional (3D) cell model. Previous studies using data-driven methods were unable to determine the parameters of systems such as the SOEC and SOFC under different operating conditions. Therefore, this paper proposes the use of a nonlinear autoregressive-exogenous (NLARX) model to conduct system identification for the SOEC parameter system under 15 different operating conditions, and has a good effect.
The contributions of this paper are as follows:
- Model identification was performed using SOEC data, which facilitates the development of the controller.
- The data-driven SOEC-based model achieved a 93% accuracy and 98% mean value.
The rest of this document consists of the following elements. Section 2 provides a brief overview of the system parameters and the structure of the autoregressive-exogenous (ARX) model. The methodology is explained in Section 3, followed by the presentation of simulations and results in Section 4. Section 5 encompasses the analysis and discussion, while Section 6 presents the conclusions.
2. SOEC on the Plane of the Parameter System and ARX Model Structure
The parameters designed in the SOEC system are shown in Table 1.

Table 1.
The parameters designed in the SOEC system.
The SOEC operating schematic is shown in Figure 1.
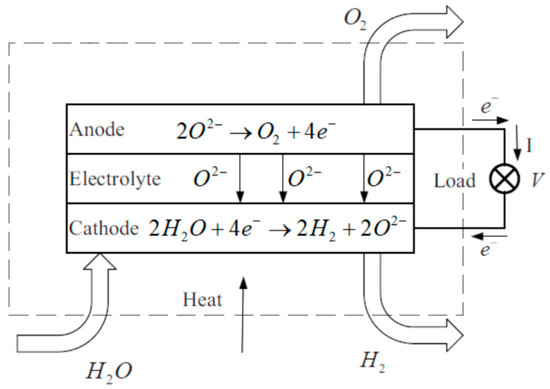
Figure 1.
SOEC operating schematic.
Since the water supply and power supply differ with time, the quantities of hydrogen and oxygen produced per unit time also vary. The state equation of the system is represented by Equations (1)–(9):
Equation (1) represents that the time-varying state (generated hydrogen and oxygen, supplied water, and electricity) caused by the motion of the SOEC.Electrochemical equations and cell-level definitions of heat transfer:
Nernst voltage :
where g is the energy of the molar Gibbs free radical reaction, Tcell is the operating temperature of the cell, R is the universal gas constant, F is Faraday’s constant, Pref is the operating pressure of the cell, and pi is the partial pressure of each species:
where ASR0 is the initial temperature-dependent value of the resistance at a particular constant-area temperature T0, T0 is the reference temperature for ASR0, and Ea is the activation energy:
where N is the number of discrete volumes, and Acell is the working surface area of a cell segment:
where hconv is the convective heat transfer coefficient:
where h is the molar enthalpy of a reaction.
The energy balance and temperature regime defined at the cell plate level is
where m is the cell mass, is the heat exchanged through each thermal interface of the cell, and is the enthalpy flow:
where Qwall is 0, because the solid structure (PEN) and the interconnect (wall) are assumed to be at the same temperature; and cp is the specific heat capacity at constant pressure.
The specified SOEC requires the utilization of reagents and the maintenance of the air ratio.
where is the molar flow rate of each substance. We use the above model to obtain data in MATLAB/Simulink.
2.1. Structure of ARX Model
One of the most useful and common types of mathematical models for parameter estimation is the ARX model. According to this model, the current output of the system depends on the last “m” system inputs and the last “n” system outputs. The analytical presentation of this method has been demonstrated to be the most useful approach for solving linear regression equations. Furthermore, as the system’s order increases, so does the technology’s performance and accuracy. Equation (10) provides the general format of this method [26].
where is the disturbance, is the input, and is the output.
2.2. Structure of NLARX Model
An NLARX model, comprising conventional and personalized predictors along with a nonlinear estimator, is employed as the initial approach to analyze the functioning of an SOEC system. By utilizing flexible nonlinear functions like sigmodins and wavelet networks, this framework enables the representation of intricate nonlinear systems. According to [31], the model typically represents the actual output y(t) in a general manner:
This is the location at which the function f (.) relies on a limited set of preceding inputs u and outputs y. Moreover, the number of preceding output terms and the number of preceding input terms, both of which are utilized for forecasting the current output, are represented by and , respectively, while denotes the time delay between the input and output.
Especially in this work, the SOEC system is identified as a black box model. The NLARX model’s input data are determined by the signals related to the power of SOEC operation, quantity of feedwater, temperature, and hydrogen production, while the output signals include hydrogen production quantity and efficiency. Furthermore, every input undergoes two delays while each output experiences a single delay. The structure of the NLARX model and the input data vectors used to identify the SOEC run under consideration are depicted in the block diagram of Figure 2.
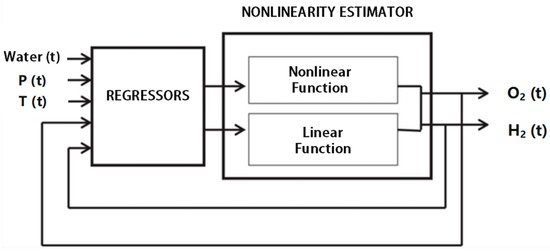
Figure 2.
Nonlinear autoregressive identifier structure.
Furthermore, further examinations are conducted to enhance the degree of modification achieved. To achieve this objective, the structure and quantity of delays in the input data vectors for both the input and output are altered. The next section presents the findings for each assessment case.
Equation (12) demonstrates that the cost function represents the average squared difference between the predicted output of a nonlinear parameter system and the simulated outcome of the model.
where and represent the output of the Simulink model and the estimation results of the identification model, respectively.
3. Methodology
The first step is to simulate and emulate the given equations in Matlab/Simulink. By changing the parameter values of temperature, water supply, and power, 15 different datasets are generated under different possible conditions. In total, 3600 samples are collected and subsequently exported using the System Identification Toolbox.
To choose the order of the model before rebuilding the dataset and estimating parameters, the format [na, nb, nk] determines the order of the system based on the desired delays, inputs, and outputs. Here, “nb” and “nk” represent ny-by-nu matrices, while “na” represents an ny-by-ny matrix. The order of the parameter system is automatically adjusted to make the system perform better. Two kinds of datasets are subjected to the application of ARX and NLARX models, one for each single dataset and another for the merged dataset, following a specified order.
4. Simulation Process and Experiment Results
4.1. Generating Datasets
Table 2 displays the specifics of various operating conditions.

Table 2.
SOEC dynamic operating conditions.
All datasets are taken at different time points, as shown in Table 1. The nonlinear parametric system of the SOEC, described earlier in Equations (1)–(9), yields these datasets. S-functions are used to implement the parameter system of the SOEC in the Simulink environment. The input and output of the SOEC are considered to be composed of multiple physical parameters, reflecting the relationship between temperature, power, water supply, and hydrogen production, as shown in Equation (13).
where N is the quantity of gas in L, P is the input power value reflecting the quantity of electricity in W or kW, and T is the SOEC operating temperature in °C.
4.2. Projected Outcomes from the NLARX Model
The NLARX model derived from the experiment was utilized to estimate the 15 operational states (Table 2) and then compared to the nonlinear parameter systems gained from the 15 estimated datasets. Except for two datasets, all the other datasets exhibited a mean precision of 98% (Table 3).

Table 3.
Identification accuracy and MSE result.
For convenience, Figure 3 displays only the outcomes of the first operating condition. In order to validate the NLARX model, the validation dataset employed estimated the responses (Figure 4 and Figure 5).
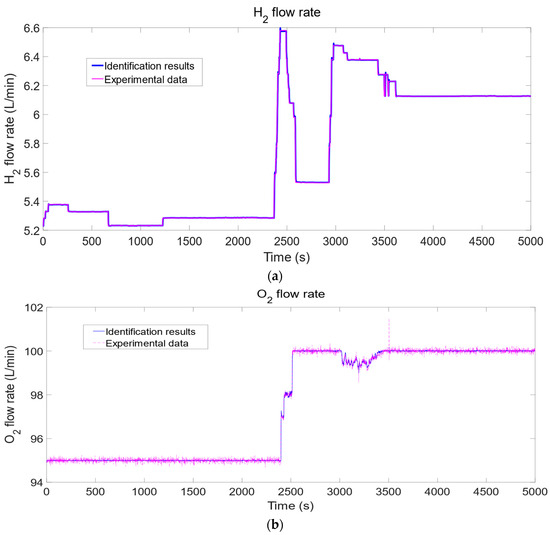
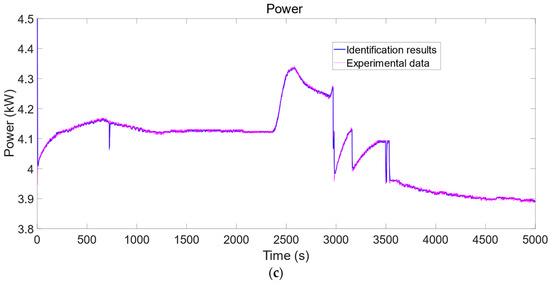
Figure 3.
The identification effect diagram of (a) H2 flow rate, (b) O2 flow rate, and (c) power of the first dataset.
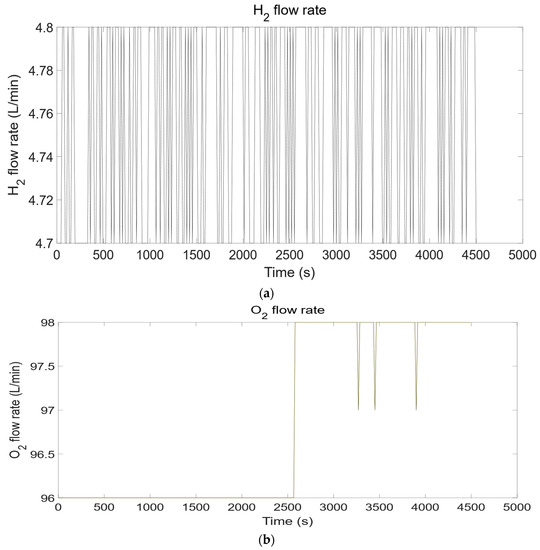
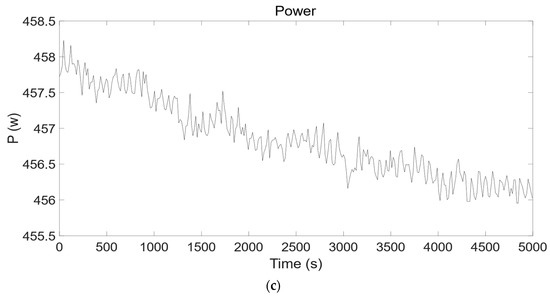
Figure 4.
The identification effect diagram of (a) H2 flow rate, (b) O2 flow rate, and (c) power of the second dataset.
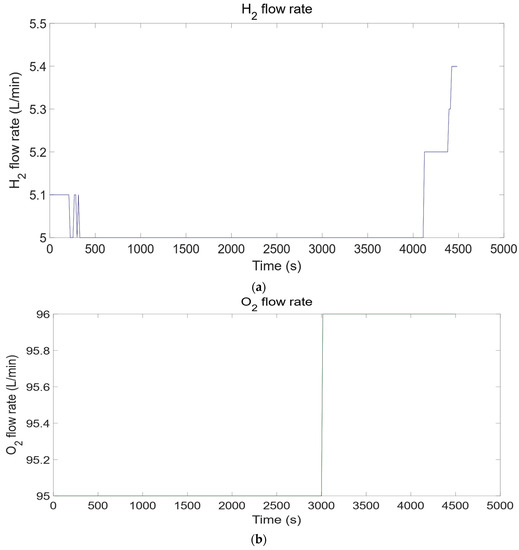
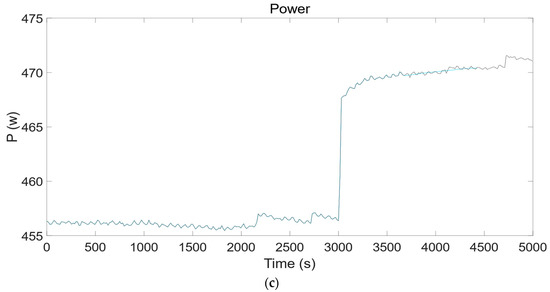
Figure 5.
The identification effect diagram of (a) H2 flow rate, (b) O2 flow rate, and (c) power of the third dataset.
5. Discussion and Analysis
This paper utilized the data-driven approach to identify the nonlinear SOEC system with unidentified parameters in various operating conditions. Simulink was used to implement the fundamental SOEC model and conduct experiments under different input/output operating conditions (Table 2). For the identification of the SOEC model, 15 estimated datasets were generated from the simulation results of the SOEC fundamental parameter system. The development of these datasets was based on the analysis of the nonlinear parameters system of the SOEC. The analysis shows that when the SOEC water supply or external power supply is equal to 0, the SOEC hydrogen production will be 0; otherwise, the SOEC will produce the corresponding hydrogen according to the working temperature, water supply, and power supply (Figure 3, Figure 4 and Figure 5). These observations led to the identification of 15 different operating environments. Estimating the parameter system of the SOEC was performed through the utilization of the NLARX model. Originally, the ARX structures were selected and estimated heuristically under an individual operating condition. In terms of fitness, our conclusion is that a solitary ARX model does not meet the requirements of the SOEC parameter system for every dataset. However, the NLARX model was used to fit 2 validation datasets and 15 estimated datasets, incorporating S-type nonlinearity. The experimental results suggest that the NLARX model is the best match for the validation dataset when comparing the simulated responses of the NLARX estimation model with the SOEC basic parameter system under validated operating conditions (Figure 4 and Figure 5). The experimental results show that the controller developed based on the high-precision model facilitates the precise control of the SOEC system. Consequently, the NLARX structure exhibited satisfactory performance in system identification for the SOEC. Furthermore, the results presented in this paper exceed in accuracy the work already presented [11], which used a neural network approach to similar but less complex noise-free systems. The neural network cited requires extensive training and the model recognition accuracy is only 86%, while the model proposed in this paper achieves a mean value of 98%, which is not as accurate as the work presented in this paper. Table 3 presents the outcomes in terms of fitting accuracy and Mean Square Error (MSE). And the accuracy of the NLARX model remains high in the presence of noise. The experimental results show that the error does not exceed 0.5% in the presence of noise (Table 4).

Table 4.
Identification accuracy and MSE result under noisy conditions.
The uncertainty formula of the system is represented by Equation (14):
where u is the uncertainty, xi is each measurement, x is the average of all measurements, and n is the number of measurements.
The relative uncertainty formula of the system is represented by Equation (15):
where v is the relative uncertainty, u is the uncertainty, xi is each measurement, and n is the number of measurements.
From Equations (14) and (15), the uncertainty of this experiment was calculated from the uncertainty formula to be 0.15214 and the relative uncertainty was 0.15517.
6. Conclusions
In this paper, using a data-driven approach, the NLARX model is used for the first time for system identification of basic nonlinear parameterized systems in an SOEC. The predicted reaction of the NLARX model is contrasted with the fundamental parameter structure of the SOEC. According to the results, the NLARX model demonstrates the highest level of accuracy for the validation dataset. As a result, the system identification of the SOEC using the NLARX structure performs well, and the predictive output of the model shows more than 93% of accuracy with a mean value of 98% under various operating conditions. It could potentially be appropriate for future application in analog feedback control systems. And, in contrast to methods using neural networks even in the presence of interference, this article uses the NLARX model to estimate and validate the complex model of the SOEC basic parameter system with maximum accuracy. Therefore, the article provides a higher-accuracy model for model identification of the SOEC. This result has positive significance for the future use of a solid oxide electrolysis cell to achieve the dual carbon goal in China.
Author Contributions
Conceptualization, X.W. (Xiaolong Wu) and Y.H.; methodology, L.H.; validation, D.H.; formal analysis, Y.Y. and X.W. (Xiaofeng Wan); investigation, Y.Y.; resources, X.L.; writing—original draft preparation, D.H.; writing—review and editing, W.M.; supervision, X.L.; project administration, X.L.; funding acquisition, X.W. (Xiaolong Wu), L.H. and X.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (Grant no. 62203204, U2066202, 81960327), Jiangxi Provincial Natural Science Foundation (Grant no. 20232BAB202028, 20212BAB212013) and National Key Research and Development Program (Grant no. 2022YFB4002200).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data will be made available on request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Xiao, F.; Wu, X.; Xia, Y. Development of energy saving and rapid temperature control technology for intelligent greenhouses. IEEE Access 2021, 9, 29677–29685. [Google Scholar]
- Xie, H.; Zhao, Z.; Liu, T.; Wu, Y.; Lan, C.; Jiang, W.; Zhu, L.; Wang, Y.; Yang, D.; Shao, Z. A membrane-based seawater electrolyser for hydrogen generation. Nature 2022, 612, 673–678. [Google Scholar] [CrossRef] [PubMed]
- Shi, J.; Zhu, Y.; Feng, Y.; Yang, J.; Xia, C. A prompt decarbonization pathway for shipping: Green hydrogen, ammonia, and methanol production and utilization in marine engines. Atmosphere 2023, 14, 584. [Google Scholar] [CrossRef]
- Zekenova, A.; Nazhipkyzy, M.; Li, W.; Kalybayeva, A.; Zhumanova, G.; Zubova, O. Advances of Biowaste-Derived Porous Carbon and Carbon–Manganese Dioxide Composite in Supercapacitors: A Review. Inorganics 2022, 10, 160. [Google Scholar] [CrossRef]
- Gong, M.; Zhang, X.; Chen, M.; Ren, Y. Proton Exchange Membrane Fuel Cell as an Alternative to the Internal Combustion Engine for Emission Reduction: A Review on the Effect of Gas Flow Channel Structures. Atmosphere 2023, 14, 439. [Google Scholar] [CrossRef]
- Javed, H.; Sabato, A.G.; Mansourkiaei, M.; Ferrero, D.; Santarelli, M.; Herbrig, K.; Walter, C.; Smeacetto, F. Glass-ceramic sealants for SOEC: Thermal characterization and electrical resistivity in dual atmosphere. Energies 2020, 13, 3682. [Google Scholar] [CrossRef]
- Ma, R.; Gao, F.; Breaz, E.; Huangfu, Y.; Briois, P. Multidimensional reversible solid oxide fuel cell modeling for embedded applications. IEEE Trans. Energy Convers. 2017, 33, 692–701. [Google Scholar] [CrossRef]
- Wu, X.; Li, Y.; Gao, Z.; Xu, Y.; Peng, J.; Xia, Z.; Hu, L.; Hu, J.; Wang, Z.; Li, X. Robust Control of RSOC/Li-ion Battery Hybrid System Based on Modeling and Active Disturbance Rejection Technology. Atmosphere 2023, 14, 947. [Google Scholar] [CrossRef]
- Zhao, J.; Lin, Z.; Zhou, M. Three-Dimensional Modeling and Performance Study of High Temperature Solid Oxide Electrolysis Cell with Metal Foam. Sustainability 2022, 14, 7064. [Google Scholar] [CrossRef]
- Koiwa, K.; Cui, L.; Zanma, T.; Liu, K.-Z.; Tamura, J. A coordinated control method for integrated system of wind farm and hydrogen production: Kinetic energy and virtual discharge controls. IEEE Access 2022, 10, 28283–28294. [Google Scholar] [CrossRef]
- Wu, X.-L.; Xu, Y.-W.; Zhao, D.-Q.; Zhong, X.-B.; Li, D.; Jiang, J.; Deng, Z.; Fu, X.; Li, X. Extended-range electric vehicle-oriented thermoelectric surge control of a solid oxide fuel cell system. Appl. Energy 2020, 263, 114628. [Google Scholar] [CrossRef]
- Pawar, P.; Kumar, A.; Ballav, R. A Review on Experimental Studies in Electrochemical Discharge Machining. In Hybrid Micromachining and Microfabrication Technologies: Principles, Varieties and Applications; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2023; pp. 17–100. [Google Scholar]
- Qin, Y.; Sun, L.; Hua, Q.; Liu, P. A fuzzy adaptive PID controller design for fuel cell power plant. Sustainability 2018, 10, 2438. [Google Scholar] [CrossRef]
- Liu, H.; Clausen, L.R.; Wang, L.; Chen, M. A robust design of heat exchanger network for high temperature electrolysis systems. In Computer Aided Chemical Engineering; Elsevier: Amsterdam, The Netherlands, 2022; Volume 49, pp. 739–744. [Google Scholar]
- Choi, J.; Shin, Y.; Choi, M.; Park, W.-K.; Lee, I.-W. Robust control of a microgrid energy storage system using various approaches. IEEE Trans. Smart Grid 2018, 10, 2702–2712. [Google Scholar] [CrossRef]
- Wu, X.; Gao, D. Optimal robust control strategy of a solid oxide fuel cell system. J. Power Sources 2018, 374, 225–236. [Google Scholar] [CrossRef]
- Cai, Q.; Adjiman, C.S.; Brandon, N.P. Optimal control strategies for hydrogen production when coupling solid oxide electrolysers with intermittent renewable energies. J. Power Sources 2014, 268, 212–224. [Google Scholar] [CrossRef]
- Bianchi, F.R.; Baldinelli, A.; Barelli, L.; Cinti, G.; Audasso, E.; Bosio, B. Multiscale modeling for reversible solid oxide cell operation. Energies 2020, 13, 5058. [Google Scholar] [CrossRef]
- Ba, S.; Xia, D.; Gibbons, E.M. Model identification and strategy application for Solid Oxide Fuel Cell using Rotor Hopfield Neural Network based on a novel optimization method. Int. J. Hydrogen Energy 2020, 45, 27694–27704. [Google Scholar] [CrossRef]
- Grondin, D.; Deseure, J.; Ozil, P.; Chabriat, J.-P.; Grondin-Perez, B.; Brisse, A. Solid oxide electrolysis cell 3D simulation using artificial neural network for cathodic process description. Chem. Eng. Res. Des. 2013, 91, 134–140. [Google Scholar] [CrossRef]
- Han, J.; Wang, X.; Yan, L.; Dahlak, A. Modelling the performance of an SOEC by optimization of neural network with MPSO algorithm. Int. J. Hydrogen Energy 2019, 44, 27947–27957. [Google Scholar] [CrossRef]
- El Hasadi, Y.M.F.; Padding, J.T. Solving fluid flow problems using semi-supervised symbolic regression on sparse data. AIP Adv. 2019, 9, 115218. [Google Scholar] [CrossRef]
- Brunton, S.L.; Proctor, J.L.; Kutz, J.N. Discovering governing equations from data by sparse identification of nonlinear dynamical systems. Proc. Natl. Acad. Sci. USA 2016, 113, 3932–3937. [Google Scholar] [CrossRef] [PubMed]
- Anitha, M.; Prusty, S.B. System Identification and Analysis of Temperature Control System. In Proceedings of the 2023 International Conference on Advances in Electronics, Communication, Computing and Intelligent Information Systems (ICAECIS), Bangalore, India, 19–21 April 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 622–626. [Google Scholar]
- Xia, Z.; Zhao, D.; Li, Y.; Deng, Z.; Kupecki, J.; Fu, X.; Li, X. Control-oriented dynamic process optimization of solid oxide electrolysis cell system with the gas characteristic regarding oxygen electrode delamination. Appl. Energy 2023, 332, 120490. [Google Scholar] [CrossRef]
- Chi, Y.; Qiu, Y.; Lin, J.; Song, Y.; Hu, Q.; Li, W.; Mu, S. Online identification of a link function degradation model for solid oxide fuel cells under varying-load operation. Int. J. Hydrogen Energy 2022, 47, 2622–2646. [Google Scholar] [CrossRef]
- Chi, Y.; Qiu, Y.; Lin, J.; Song, Y.; Li, W.; Hu, Q.; Mu, S.; Liu, M. A robust surrogate model of a solid oxide cell based on an adaptive polynomial approximation method. Int. J. Hydrogen Energy 2020, 45, 32949–32971. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, C.R.; Wang, Y.; Yang, Z.; Du, Q.; Jiao, K. Assessment of CO2 enrichment mechanism in integrated coal gasification fuel cell combined cycle system with carbon capture. Front. Energy Res. 2023, 10, 1017829. [Google Scholar] [CrossRef]
- Shao, Y.; Li, Y.; Fu, Z.; Li, J.; Zhu, Q. Numerical Investigation on the Performance of IT-SOEC with Double-Layer Composite Electrode. Energies 2023, 16, 2525. [Google Scholar] [CrossRef]
- Chi, Y.; Yokoo, K.; Nakajima, H.; Ito, K.; Lin, J.; Song, Y. Optimizing the homogeneity and efficiency of a solid oxide electrolysis cell based on multiphysics simulation and data-driven surrogate model. J. Power Sources 2023, 562, 232760. [Google Scholar] [CrossRef]
- Khan, M.A.; Baig, D.Z.; Ashraf, B.; Ali, H.; Rashid, J.; Kim, J. Dynamic modeling of a nonlinear two-wheeled robot using data-driven approach. Processes 2022, 10, 524. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).