1. Introduction
Nowadays, lasers have been widely applied in various fields such as national defense, military, information communication, industrial processing, healthcare, and scientific research [
1,
2,
3]. Since the appearance of lasers, the beam qualities of various laser beams have been studied. In practical laser technologies such as laser manufacturing, both laser power and laser beam quality need to be considered. The energy of a laser represents the processing capability of a laser manufacturing system, while the laser beam quality directly determines the processing methods, propagation distance, obtained spot size, and ultimately, the processing quality. Due to the widespread application of laser beams, whenever a new type of laser device is introduced, it is necessary to specify the beam quality of the laser beam emitted by the laser device [
4,
5,
6,
7,
8,
9,
10,
11,
12,
13]. The quality of the laser beam can be said to be the core of modern laser technology, especially laser manufacturing technology, and plays a crucial role throughout the laser manufacturing process. Various methods have been used historically to measure the beam quality of lasers. Scientists first proposed using the M-mode factor to measure the order of higher-order Gaussian beams. Soon after, evaluation methods such as the bucket brigade method and the product of beam parameters were also proposed [
14]. In addition, the Strehl ratio was also one of the primary methods used to evaluate laser beam quality in the early days, initially used to describe stellar imaging [
15]. In the 1990s, A.E. Siegman and others introduced the concepts of spatial frequency and intensity moments, and established a relatively complete theoretical model for the M
2 factor concept that was used to evaluate laser beam quality [
16,
17]. The International Organization for Standardization (ISO) published draft standards and revisions related to laser beam quality from 1991 to 1993, proposing the use of the M
2 factor to describe the quality of laser beams, and standardizing its measurement. In 2005, ISO published the latest version of the M
2 factor measurement standard, ISO11146 [
18]. Since then, the method of evaluating laser beam quality using the M
2 factor has become the most widely used and accepted parameter for laser beam quality. The M
2 factor takes into account the actual waist diameter and far-field divergence angle of the laser beam, and is an invariant in free space [
19]. Unlike free space propagation, the quality of a laser beam will degrade as the distance increases when passed through turbulent atmosphere, meaning that the laser beam quality will be affected by atmospheric turbulence.
Atmospheric turbulence is a random air motion and a fundamental characteristic of atmospheric movement [
20,
21]. People have always maintained a strong interest in the impact of atmospheric turbulence on laser beams, primarily due to the practical needs of long-distance free-space optical communication. In atmospheric optics, the power spectral density of atmospheric turbulence refractive index fluctuations is an important basis for establishing various theoretical models. Among them, the most commonly used in the literature is the locally isotropic Kolmogorov spectrum. However, recent experiments have revealed deviations from isotropic statistical behavior. On the other hand, airborne laser systems have attracted great interest due to their high precision, high resolution, flexibility, maneuverability, and efficiency. Typically, aircraft platforms face challenges because jet engines induce anisotropic atmospheric turbulence. Using an aircraft to carry cloud particle detectors and using laser beams to probe the atmosphere, one can obtain real-time information about the subtle physical changes within cloud particles. Recently, the power spectral density function of atmospheric turbulence induced by jet exhaust has been proposed, providing a convenient way to analyze and discuss the transmission characteristics of laser beams in atmospheric turbulence induced by jet exhaust [
22]. In 2020, Ding et al. discussed in detail the propagation characteristics of low-coherence Gaussian beams in atmospheric turbulence induced by jet engines, suggesting that reducing the coherence of laser beams can effectively reduce the impact of the turbulence [
23]. Subsequently, the propagation characteristics of partially coherent Gaussian–Schell model beam arrays in atmospheric turbulence induced by jet engines were studied [
24,
25]. Meanwhile, the propagation characteristics of hollow higher-order cosh-Gaussian beams [
26] and hyperbolic sinusoidal Gaussian beam [
27] in turbulence induced by jet engines were also investigated. Recently, it was found that regulating the correlation structure of laser beams can effectively reduce the impact of atmospheric turbulence [
28]. Under this motivation, the propagation characteristics in atmospheric turbulence induced by jet engines were studied for different coherence structures, such as multi-Gaussian correlation [
29], Bessel–Gaussian correlation [
30], and Laguerre–Gaussian correlation [
31,
32] of low-coherence light. It should be pointed out that all these laser beams are assumed to propagate along a straight line in free space. One of the innovative points of this article is to discuss the propagation beam quality of a self-bending Airy laser beam in the jet-engine-exhaust-induced turbulence.
Under normal circumstances without encountering obstacles, laser beams typically propagate in straight lines [
33]. However, theoretical predictions by American scientists proposed the possibility of laser beams propagating along curved paths in free space [
34]. These laser beams, which differ from the bending of beams around massive celestial bodies, were experimentally generated by the research team in 2007 [
35]. The main lobe of the laser beam was observed to propagate along a curved path within the laboratory range of approximately 25 cm. Due to the transverse mode of this beam being described by Airy functions, it is known as a self-accelerating Airy beam [
36]. The term “self-accelerating” refers to the beam’s propagation trajectory resembling the parabolic path of an accelerated particle [
37]. This beam not only exhibits self-acceleration but also possesses properties such as non-diffraction [
38] and self-healing [
39,
40], which have sparked widespread research interest. The self-accelerating Airy beam has found applications in various fields, including plasma channel generation [
41], optical sweeping [
42], particle manipulation [
43], electron acceleration [
44], and imaging [
45]. Additionally, the bending nature of these beams allows for enhanced security in optical communication and the propagation characteristics of an Airy beam through turbulent atmospheres has been extensively studied. However, most of the existing research focuses on the propagation properties of an Airy beam in isotropic turbulent media [
46,
47], while the transmission properties in anisotropic turbulent media remain less explored. Furthermore, the interaction mechanism between the Airy beam and the jet-engine-exhaust-induced turbulence has not been reported.
The goal of this paper is to investigate the laser beam quality of a low-coherence Airy beam in the jet-engine-exhaust-induced turbulence. We will discuss in detail various factors that affect the beam quality of the Airy beam, aiming to provide theoretical guidance for the practical application of the Airy beam, such as utilizing a curved Airy beam in airborne laser systems. The paper is organized as follows: in
Section 1, the research progress of laser beam quality factors, the research progress of the propagation characteristics of various laser beam in the jet-engine-exhaust-induced turbulence, and the research progress of the Airy beam are introduced. In
Section 2, the analytical expression for the quality factor of the Airy beam in the jet-engine-exhaust-induced turbulence is derived. A detailed numerical analysis is conducted in
Section 3, and a brief summary is included in
Section 4.
2. Formulation
Due to the irregular fluctuations in amplitude and phase in the wave field generated by actual light sources, the field often undergoes random changes over time, resulting in partially coherent laser beams [
48]. This article specifically discusses a partially coherent Airy (PCA) beam and treats a completely coherent Airy beam as a special case when the coherence length tends to infinity. Compared to completely coherent beams, partially coherent beams cannot be described directly by the optical field E, but require statistical parameters of the optical field for description [
49]. In the spatial-frequency domain of scalar optical fields, the cross-spectral density function is commonly used to describe the second-order statistical properties of the optical field [
50]. At the incident plane of the PCA beam, its cross-spectral density function can be expressed as:
where
represents the Airy function,
x,
y are the positions of two points in the optical field,
and
describe the correlation of the optical field, and
is the transverse characteristic width of the Airy beam, which can be analogized to the waist of a Gaussian beam. It determines the range of the Airy beam spot, with a larger
corresponding to a larger spot size. At the same time,
is also related to the total power of the Airy beam. Under the same conditions for other parameters, the larger the value of
, the greater the total power. The parameter
is the truncation parameter, and a smaller value of a results in more sidelobes in the Airy beam. Therefore, “
a” is also related to the total power of the Airy beam. In other words, the smaller the value of “
a”, the greater the total power of the Airy beam.
is the coherence length of the PCA beam, and a longer coherence length indicates a closer approximation to complete coherence. Conversely, a shorter coherence length indicates closer proximity to complete incoherence. In practice, laser beams are always partially coherent.
In 1971, R. Lutomirski and H. Yura proposed a relatively simple method for characterizing the propagation properties of laser beams in turbulent media, called the generalized Huygens–Fresnel diffraction integral method [
51]. This method can effectively handle the propagation of laser beams with different modes in turbulent media and has been widely used by researchers. In the paraxial case, the generalized Huygens–Fresnel diffraction integral can be used to obtain the cross-spectral density function of the PCA beam after propagating a distance z in turbulent media. The Wigner distribution function can be obtained by integrating the cross-spectral density function. The quality factor involves the second moment of the laser beam, and all moments can be given by the Wigner distribution function. For the PCA beam, the Wigner distribution function is [
52]:
where
represents the position vector,
represents the divergence angle along the propagation direction, and
represents the position vector in the spatial frequency domain.
The following substitutions are used here:
The moments of the PCA beam can be obtained by integrating the Wigner distribution function. The result is as follows [
53,
54]:
where
P is the total power, which is also known as the zeroth moment, and its value is:
The total power is directly proportional to the square of the characteristic width and is also related to the truncation parameter , as mentioned earlier. Smaller values of truncation parameter correspond to larger total powers. For example, for an Airy beam with m, when a = 0.63 (approximately the Gaussian beam shape), the total power P is 0.2 milliwatts; when a = 0.11, P is 0.9 milliwatts; when a = 0.08, P is 1.3 milliwatts; and when a = 0.05, P is 2.0 milliwatts.
By substituting Equations (2) and (5) into Equation (4), we can obtain the following:
where Equation (6) represents the second moment of the PCA beam in the spatial domain, which is related to the beam width. Equation (8) represents the second moment of the PCA beam in the space-frequency domain, which is related to the far-field divergence angle of the beam. Equation (7) is the cross term that takes into account both factors and can be referred to as the cross-moment. All of these equations describe the second moments of the PCA beam obtained by integrating the Wigner function.
Based on the above second moments, we can obtain the quality factor of the PCA beam in turbulent media. The formula is [
53,
54]:
The analytical expression of the quality factor can be obtained by substituting Equations (6)–(8) into Equation (9) and the result is:
It is evident that the quality factor of the PCA beam can be divided into four parts. The first term is 1, representing the quality factor of Gaussian beams. The second term represents the influence of truncation parameter on the quality factor. The third term represents the influence of coherence on the quality factor. The fourth term, related to T, represents the influence of turbulent medium on the quality factor of the PCA beam. As the value of T increases and the propagation distance becomes longer, the quality of the beam degrades.
If there is no influence from turbulent media (
), the result of the Equation (10) degenerates to:
The quality factor here is the quality factor propagated in vacuum, which is independent of the propagation distance z and is a transmission invariant. Furthermore, if the coherence length tends to infinity, the quality factor can be simplified as Obviously, as the value of decreases, the quality factor increases, indicating poorer laser beam quality. The reason for this is that as the value of decreases, the propagation trajectory of an Airy beam becomes more curved, resulting in poorer quality, and therefore, a larger quality factor.
The term
T in Equation (10) refers to the turbulent effects in the equation and the expression is:
where
represents the power spectral density of the jet exhaust region. Here, we directly provide the result of the
T induced by the atmospheric turbulence of the jet engine exhaust [
23]:
with:
In Equations (13)–(15), is the Gamma function. The is the generalized exponent parameter with the range is 3–4 generally. is the inner scales and is the outer scales of the jet-engine-exhaust-induced turbulence. and are the anisotropic factors. is the structure constant of the jet-engine-exhaust-induced turbulence. Q and are fixed parameters determined by experimental results. Substituting Equations (13)–(15) into Equation (10), we can get the final formula of -factor of the PCA beam in atmospheric turbulence in atmospheric turbulence induced by jet engine exhaust.
Finally, we obtained the quality factor (M2 factor) of the PCA beam in the turbulent induced by jet exhaust. Thus, we have derived the analytical expression for the quality factor. From the obtained results, it can be seen that the quality factor of the PCA beam is influenced by both the parameters of the light source, such as the characteristic width, truncation parameter, coherence length, and wavelength of the Airy beam, and the turbulent parameters induced by jet engine exhaust, such as internal and external scales, structure constant, anisotropic factors, as well as the influence of Q and Ls determined by experiments.
3. Numerical Results and Analysis
First, we discuss the quality factor of the PCA beam in the absence of turbulence. As mentioned earlier, in this case, the quality factor is a propagation invariant. From Equation (11), it can be seen that the quality factor is a function of the truncation parameter, characteristic width, and coherence length of the Airy beam. Therefore, here, we discuss the variation of the quality factor with respect to the truncation parameter for different coherence lengths and characteristic widths.
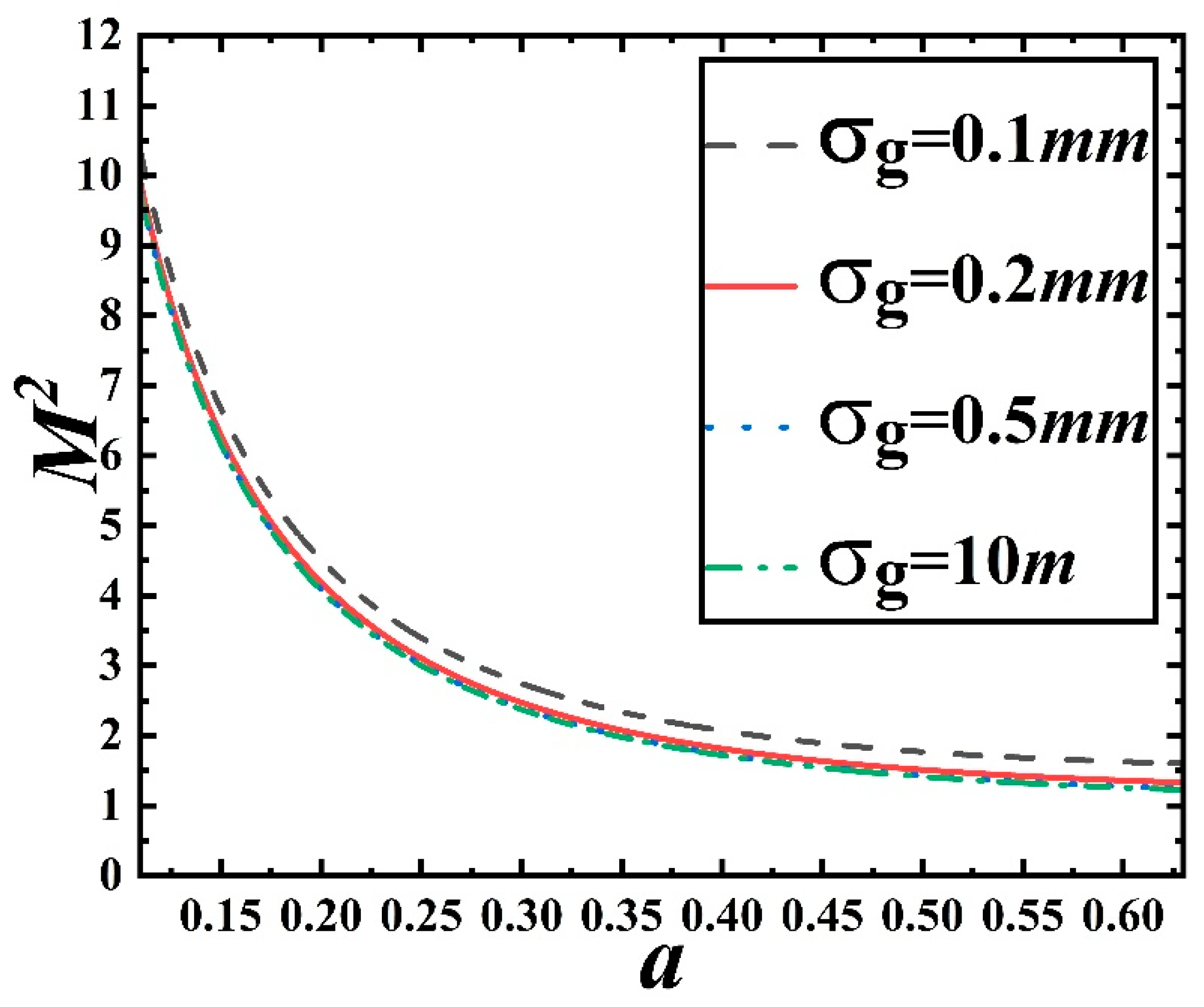
Figure 1 shows the variation of the quality factor of the PCA beam in vacuum with respect to the truncation parameter for four different coherence lengths. The range of truncation parameter
in the figure is from 0.11 to 0.63, where 0.11 represents the value of
in the earliest experiments generating an Airy beam [
35] and 0.63 indicates that the transverse spatial structure of the Airy beam at this point is similar to that of a Gaussian beam distribution [
55]. From the graph, it can be observed that as the value of
decreases, the quality factor of the laser beam increases, indicating poorer laser beam quality. This is because a smaller “
a” value implies a more curved propagation trajectory of the Airy beam in vacuum, leading to lower quality. It should be noted that the quality factor is a measure of beam collimation, with smaller values indicating a closer resemblance to the quality factor of a Gaussian beam, which has a minimum value of 1. The quality factors of other laser beams are greater than 1, indicating poorer quality as the factor increases. The graph also reveals that as the coherence length increases, the quality factor of the Airy beam decreases. This is different from the case in turbulent atmosphere [
47]. However, this behavior is similar to other laser beams, as reducing the coherence of the laser beam in vacuum leads to degradation in quality. From the numerical results, it can be concluded that the coherence length has minimal impact on the quality factor of the PCA beam.
Figure 2 shows the variation of the quality factor of the PCA beam in vacuum with respect to the truncation parameter for four different characteristic widths. Similarly, it can be observed that smaller values of “
a” result in higher quality factors for the Airy beam. From
Figure 2, it is also evident that as the characteristic width decreases, the quality factor decreases as well.
Next, we will discuss the numerical analysis of the propagation quality factor of the PCA beam in turbulent atmospheres caused by jet engine exhaust. In order to emphasize the comparison between the presence of turbulence and vacuum, we will use the relative quality factor to discuss numerical values.
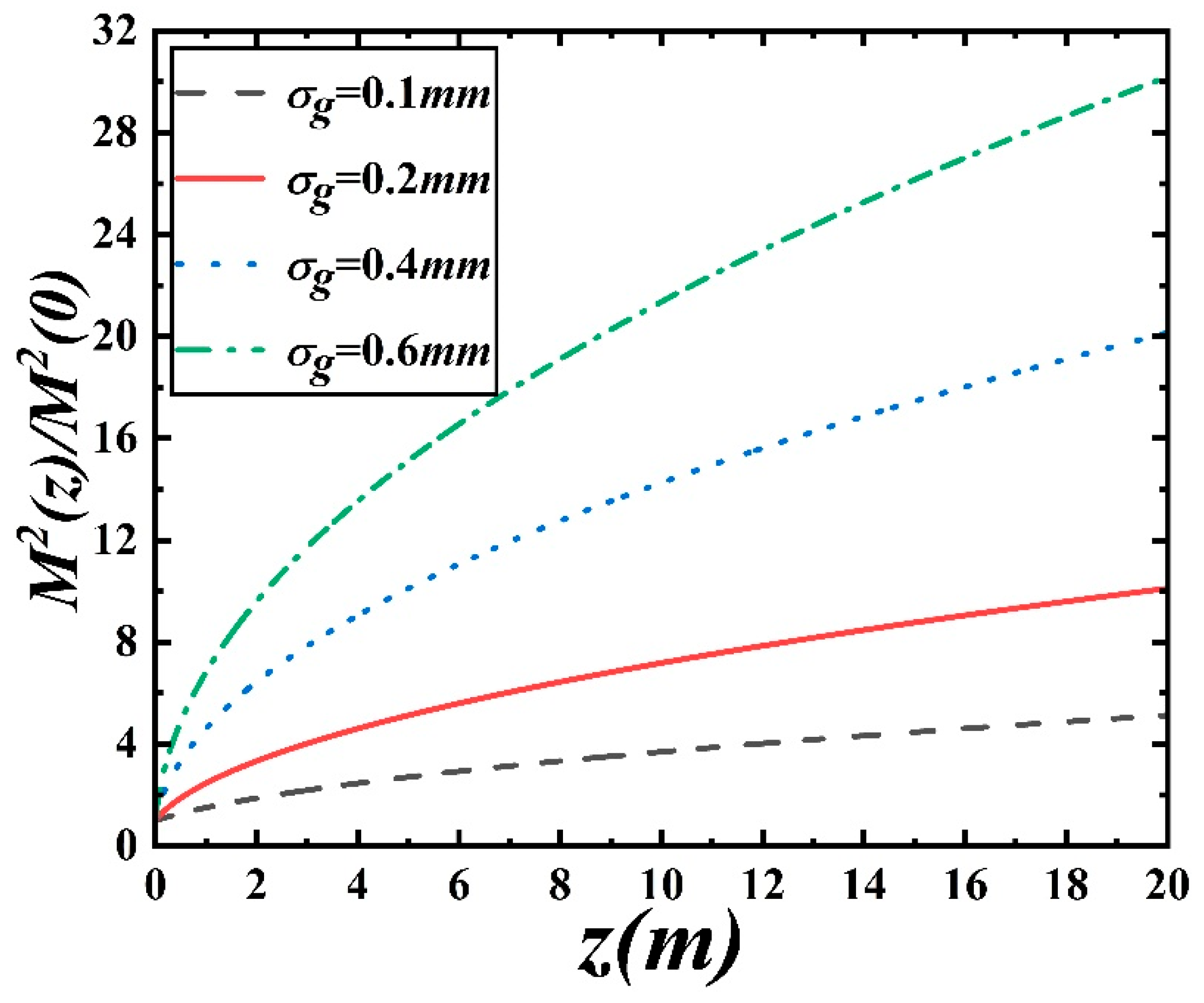
Figure 3 shows the variation of the
of the PCA beam in turbulent atmospheres induced by jet exhaust as a function of the propagation distance for different turbulence structure constants. Here, the maximum value of the propagation distance is set to 20 m [
23]. The other calculation parameters are
,
,
,
,
,
,
,
,
,
, and
. From
Figure 3, we can observe that the relative quality of the Airy beam increases with the increase in the propagation distance. Clearly, the effect of turbulence accumulates and continuously degrades the quality of the laser beam as the propagation distance increases. Furthermore, from
Figure 3, we can also see that a larger turbulence structure constant corresponds to a larger relative quality factor of the beam, indicating a greater degradation in quality. This is because the turbulence structure constant represents the strength of turbulence, and stronger turbulence exerts a greater destructive effect on the laser beam, resulting in poorer laser beam quality. When the turbulence structure constant is
, the relative quality factor of the Airy beam reaches 2.71 at a transmission distance of 20 m, indicating that the turbulence induced by jet exhaust has a significant impact on the propagation of the laser beam. When the turbulence structure constant is large, such as
, the relative quality factor even reaches 13.81 for a propagation distance of 20 m.
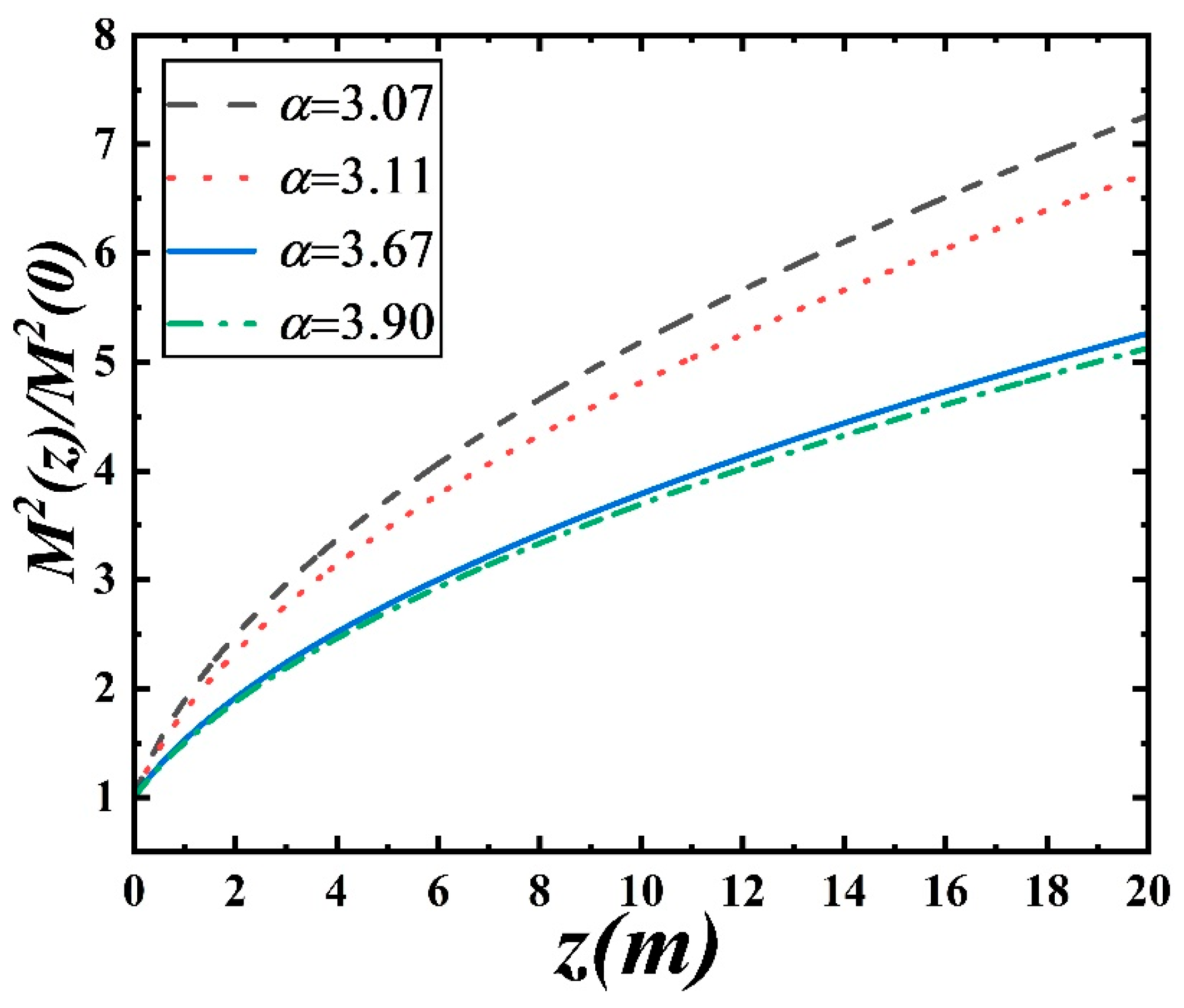
Figure 4 shows the variation of the relative quality factor of the PCA beam with different generalized exponent parameter
as a function of the propagation distance. Similarly, the quality of the Airy beam degrades with increasing propagation distance. In this case, the values of parameter “
“ are 3.07, 3.11, 3.67, and 3.90 and the value of structure constant is
, while other calculation parameters are the same as in
Figure 3. From the figure, it can be observed that the relative quality factor of the PCA beam decreases with increasing “
”. This is different from the case of non-Kolmogorov turbulence, where the quality factor is maximum at
. This also indicates that the intensity of turbulence induced by jet exhaust decreases with increasing “
”.
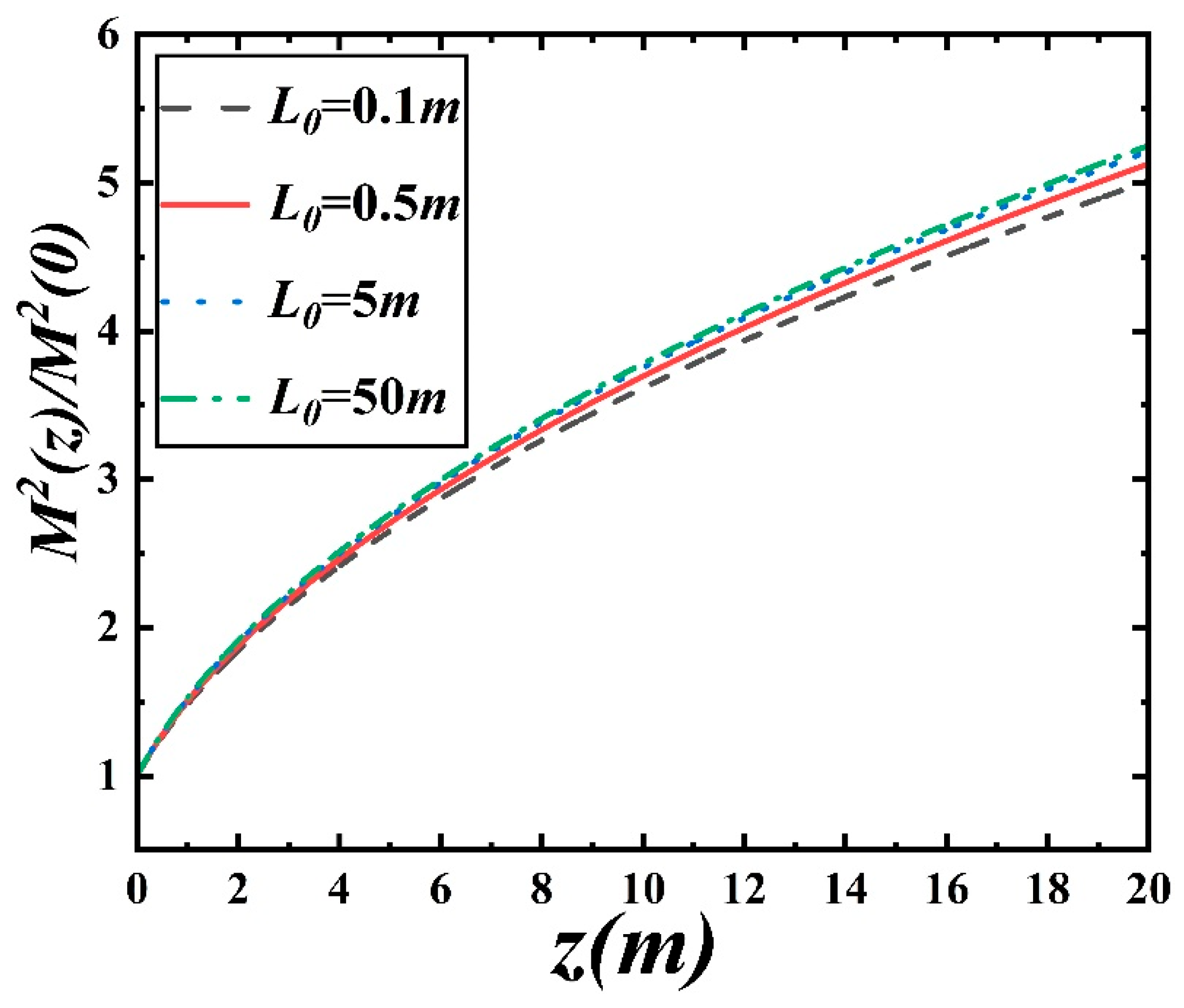
Figure 5 shows the variation of the relative quality factor of the PCA beam with different outer scales as a function of the propagation distance. From the figure, it can be seen that the smaller the outer scale of turbulence, the smaller the relative quality factor of the Airy beam. This is different from ordinary isotropic turbulence. Additionally, it can be observed from
Figure 5 that the outer scale has little impact on the quality of the Airy beam.
Figure 6 shows the variation of the relative quality factor of the Airy beam with different inner scales as a function of the propagation distance. From the figure, it can be seen that the smaller the inner scale of turbulence, the larger the relative quality factor of the Airy beam, indicating poorer laser beam quality. This is similar to ordinary isotropic turbulence. The reason for this is that the smaller the inner scale, the stronger the interaction between the laser beam and turbulence, resulting in a greater impact on the propagation quality of the laser beam.
Figure 7 illustrates the influence of coherence length on the relative quality factor of the Airy beam. From the figure, it can be observed that as the coherence length decreases, the relative quality factor of the PCA beam also decreases. Therefore, reducing the coherence of the Airy beam is beneficial for improving its propagation quality, which is why low-coherence lasers are often used in communication. It is worth noting that the coherence length mentioned here is very small, indicating that for a self-bending Airy beam, effective control of their coherence within a small range is required to improve their propagation quality in the jet-engine-exhaust-induced turbulence. In fact, it is now possible to control the coherence of laser beams within such a small range.
Figure 8 shows the variation of the relative quality factor of the PCA beam with respect to the propagation distance for different characteristic widths. The characteristic widths used here are different from the parameters in vacuum. This is because when
and
, the corresponding initial powers are
milliwatts. Such powers are required to form stable light beams in atmospheric turbulence. From the figure, it can be observed that as the characteristic width increases, the quality factor of the Airy beam decreases, indicating better laser beam quality. This is due to two reasons. Firstly, a larger characteristic width corresponds to a higher power, which effectively counteracts the influence of turbulence on the PCA beam. Secondly, in a physical sense, the larger characteristic scales mean the larger spot sizes for the Airy beam, indicating better collimation performance. Therefore, the PCA beam with larger scale factor can better suppress the influence of the jet-engine-exhaust-induced turbulence.
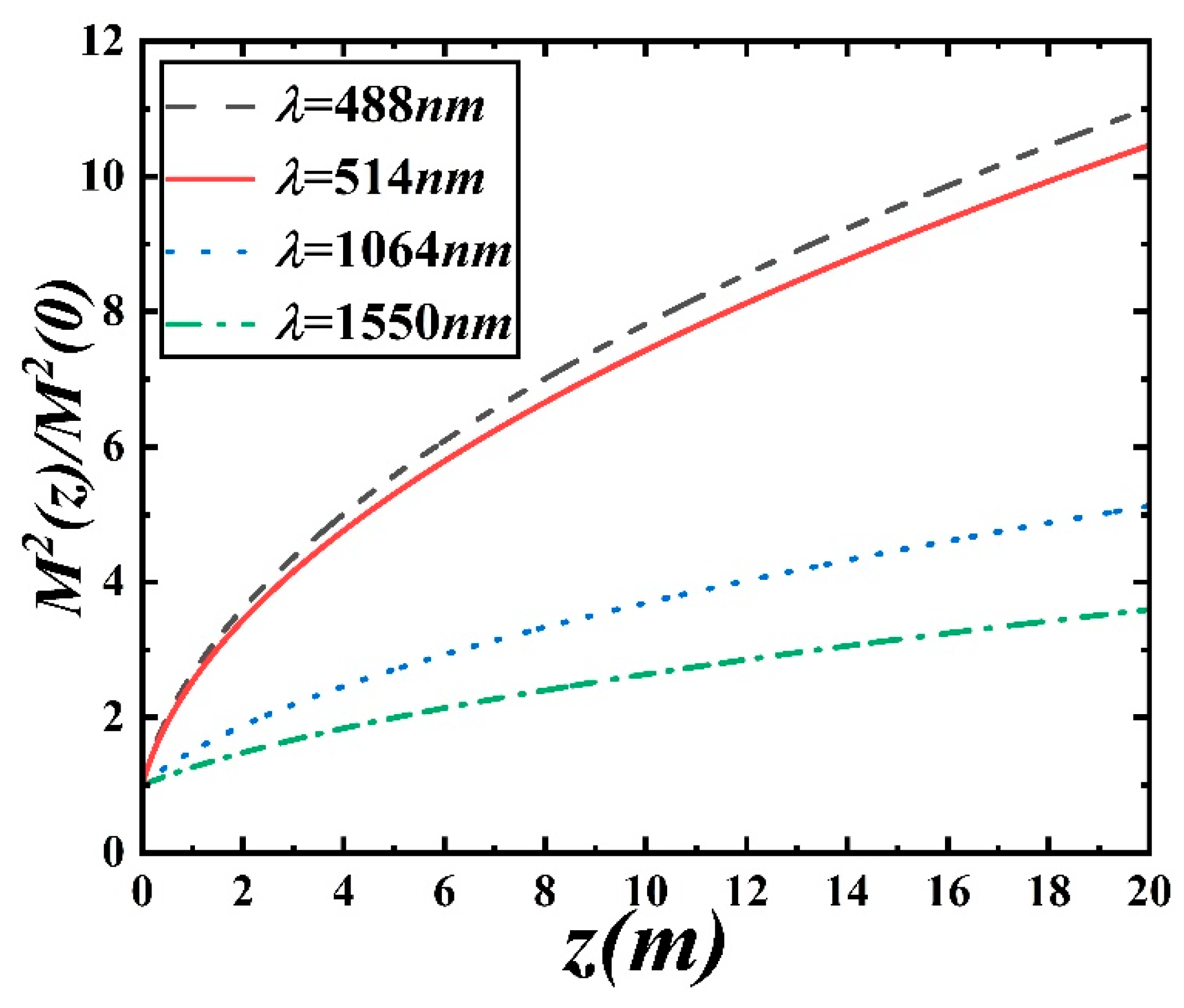
Figure 9 shows the variation of the relative quality factor of the PCA beam with respect to the propagation distance for different wavelengths. From the figure, it can be observed that as the wavelength of the Airy beam increases, the corresponding relative quality factor decreases, indicating better propagation quality. Therefore, when utilizing an Airy beam, it is preferable to choose an Airy beam with longer wavelengths.
There are two points that need to be clarified. Firstly, the truncation factor of the Airy beam has almost no influence on its quality factor in the atmospheric turbulence induced by jet exhaust, so the variation of the quality factor under different truncation factors is not shown here. Secondly, the curves depicting the variation of the Airy beam’s quality factor with propagation distance are all upward convex curves, indicating that there will be saturation of the quality factor when the propagation distance is large. However, at this point, the corresponding quality factor will be high, and the region affected by the atmospheric turbulence induced by the jet exhaust will not be very extensive, so no data are shown for this case.