Thermospheric Density Response to the QBO Signal
Abstract
:1. Introduction
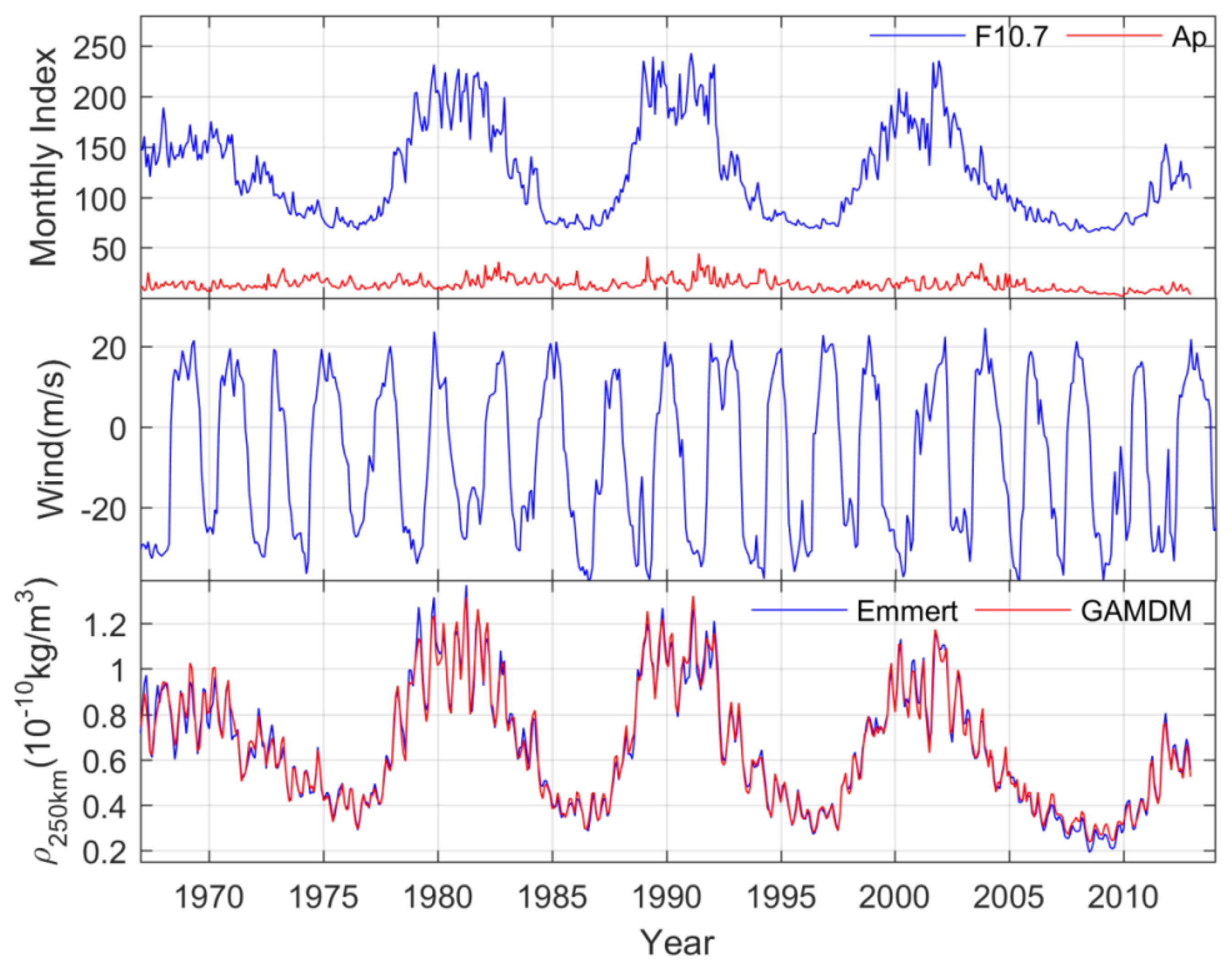
2. Datasets
3. Results and Discussion
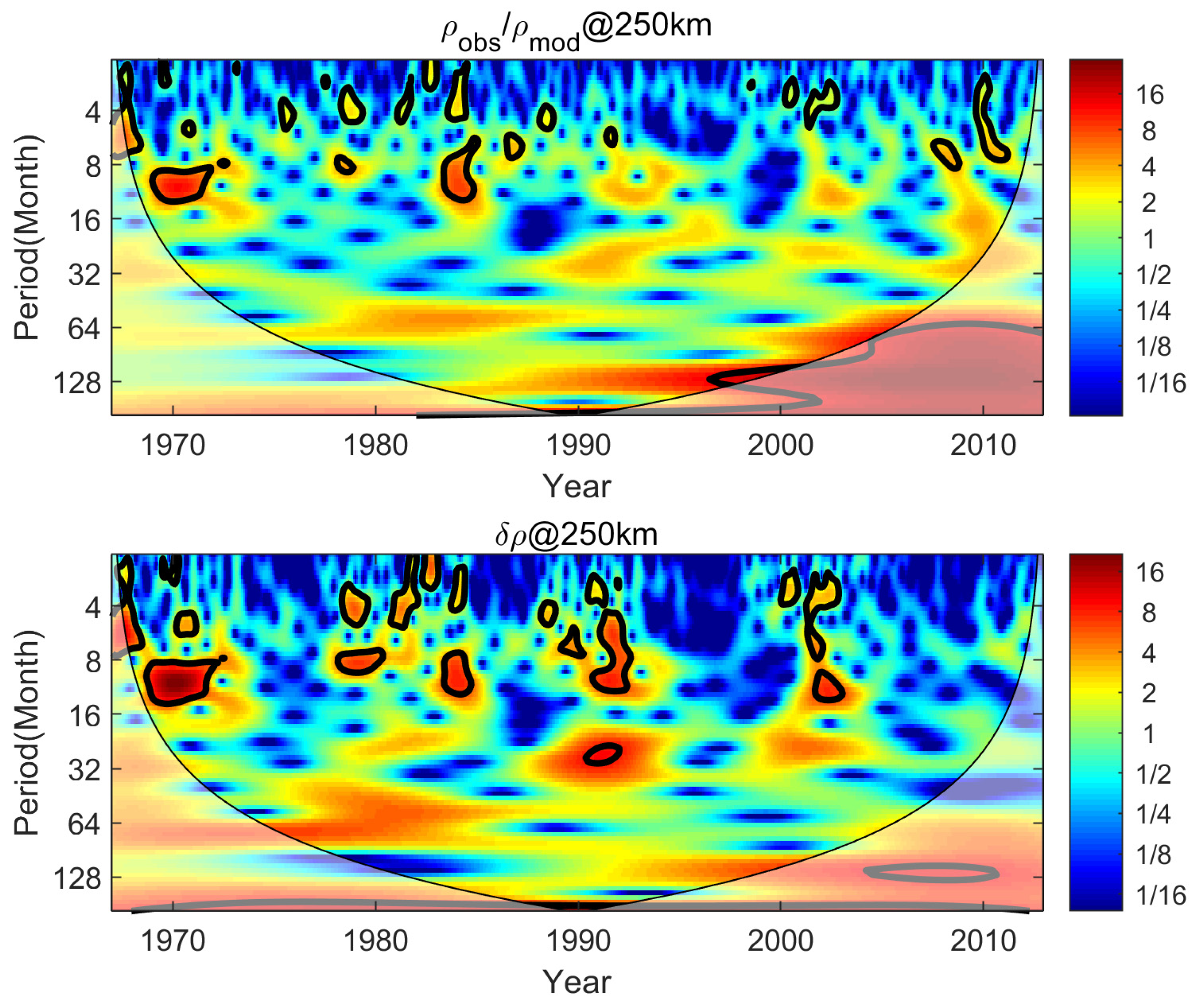
3.1. Period Analysis
3.2. QBO Signal Diagnosis
4. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Qian, L.; Solomon, S.C. Thermospheric density: An overview of temporal and spatial variations. Space Sci. Rev. 2012, 168, 147–173. [Google Scholar] [CrossRef]
- Emmert, J. Thermospheric mass density: A review. Adv. Space Res. 2015, 56, 773–824. [Google Scholar] [CrossRef]
- Weng, L. Characterization and Modeling of Thermospheric Density Variations; University of Science and Technology of China: Hefei, China, 2019. [Google Scholar]
- Emmert, J.T. Altitude and solar activity dependence of 1967–2005 thermospheric density trends derived from orbital drag. J. Geophys. Res. Space Phys. 2015, 120, 2940–2950. [Google Scholar] [CrossRef]
- Weng, L.; Lei, J.; Zhong, J.; Dou, X.; Fang, H. A machine-learning approach to derive long-term trends of thermospheric density. Geophys. Res. Lett. 2020, 47, e2020GL087140. [Google Scholar] [CrossRef]
- Calabia, A.; Jin, S. New modes and mechanisms of thermospheric mass density variations from GRACE accelerometers. J. Geophys. Res. Space Phys. 2016, 121, 11.191–11.212. [Google Scholar] [CrossRef]
- Calabia, A.; Jin, S. Solar cycle, seasonal, and asymmetric dependencies of thermospheric mass density disturbances due to magnetospheric forcing. Ann. Geophys. 2019, 37, 989–1003. [Google Scholar] [CrossRef]
- Dunkerton, T.J.; Baldwin, M.P. Quasi-biennial Modulation of Plantary-wave Fluxes in the Northern Hemisphere Winter. J. Atmos. Sci. 1991, 48, 1043–1061. [Google Scholar] [CrossRef]
- Labitzke, K.G.; Loon, H.V. The Quasi-Biennial Oscillation (QBO). The Stratosphere; Springer: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- Matthes, K.; Marsh, D.R.; Garcia, R.R.; Kinnison, D.E.; Sassi, F.; Walters, S. Role of the QBO in modulating the influence of the 11 year solar cycle on the atmosphere using constant forcings. J. Geophys. Res. Atmos. 2010, 115, D18110. [Google Scholar] [CrossRef]
- Sağır, S.; Atıcı, R. Comparison of the QBO and F10.7 Solar Flux Effects on Total Mass Density. Geomagn. Aeron. 2018, 58, 841–845. [Google Scholar] [CrossRef]
- Yu, C. Simulation of the Stratospheric Wind Quasi-Biennial Oscillation in the Whole Atmosphere Community Climate Model; University of Science and Technology of China: Hefei, China, 2019. [Google Scholar]
- Koval, A.V.; Gavrilov, N.M.; Kandieva, K.K.; Ermakova, T.S.; Didenko, K.A. Numerical simulation of stratospheric QBO impact on the planetary waves up to the thermosphere. Sci. Rep. 2022, 12, 21701. [Google Scholar] [CrossRef]
- Koval, A.V.; Gavrilov, N.M.; Pogoreltsev, A.I.; Kandieva, K.K. Dynamical Impacts of Stratospheric QBO on the Global Circulation up to the Lower Thermosphere. J. Geophys. Res. Atmos. 2022, 127, e2021JD036095. [Google Scholar] [CrossRef]
- Yue, J.; Yu, W.; Pedatella, N.; Bruinsma, S.; Wang, N.; Liu, H. Contribution of the lower atmosphere to the day-to-day variation of thermospheric density. Adv. Space Res. 2022, in press. [CrossRef]
- Kane, R.P. Quasi-biennial oscillation in ionospheric parameters measured at Juliusruh (55°N, 13°E). J. Atmos. Sol.-Terr. Phys. 1995, 75, 415–419. [Google Scholar] [CrossRef]
- Tang, W.; Xue, X.-H.; Lei, J.; Dou, X.-K. Ionospheric quasi-biennial oscillation in global TEC observations. J. Atmos. Sol.-Terr. Phys. 2013, 107, 36–41. [Google Scholar] [CrossRef]
- Liu, H. Thermospheric inter-annual variability and its potential connection to ENSO and stratospheric QBO. Earth Planets Space 2016, 68, 77. [Google Scholar] [CrossRef]
- Oindrila, N.; Kuttippurath, J.; Sridharan, S.; Feng, W. Seasonal, interannual and long-term changes in the middle atmospheric carbon monoxide in the tropics. Atmos. Environ. 2023, 310, 119958. [Google Scholar] [CrossRef]
- Emmert, J.T.; McDonald, S.E.; Drob, D.P.; Meier, R.R.; Lean, J.L.; Picone, J.M. Attribution of interminima changes in the global thermosphere and ionosphere. J. Geophys. Res. Space Phys. 2014, 119, 6657–6688. [Google Scholar] [CrossRef]
- Picone, J.M.; Hedin, A.E.; Drob, D.P.; Aikin, A.C. NRLMSISE-00 empirical model of the atmosphere: Statistical comparisons and scientific issues. J. Geophys. Res. 2002, 107, 1468. [Google Scholar] [CrossRef]
- Torrence, C.; Compo, G.P. A Practical Guide to Wavelet Analysis. Bull. Am. Meteorol. Soc. 1998, 79, 61–78. [Google Scholar] [CrossRef]
- Qian, L.; Solomon, S.C.; Kane, T.J. Seasonal variation of thermospheric density and composition. J. Geophys. Res. Atmos. 2009, 114, A01312. [Google Scholar] [CrossRef]
- He, C.; Yang, Y.; Carter, B.; Kerr, E.; Wu, S.; Deleflie, F.; Cai, H.; Zhang, K.; Sagnières, L.; Norman, R. Review and comparison of empirical thermospheric mass density models. Prog. Aerosp. Sci. 2018, 103, 31–51. [Google Scholar] [CrossRef]
- Calabia, A.; Tang, G.; Jin, S. Assessment of new thermospheric mass density model using NRLMSISE-00 model, GRACE, Swarm-C, and APOD observations. J. Atmos. Sol.-Terr. Phys. 2020, 199, 105207. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, B.; Cui, R.; Weng, L. Thermospheric Density Response to the QBO Signal. Atmosphere 2023, 14, 1317. https://doi.org/10.3390/atmos14081317
Li B, Cui R, Weng L. Thermospheric Density Response to the QBO Signal. Atmosphere. 2023; 14(8):1317. https://doi.org/10.3390/atmos14081317
Chicago/Turabian StyleLi, Bo, Ruifei Cui, and Libin Weng. 2023. "Thermospheric Density Response to the QBO Signal" Atmosphere 14, no. 8: 1317. https://doi.org/10.3390/atmos14081317
APA StyleLi, B., Cui, R., & Weng, L. (2023). Thermospheric Density Response to the QBO Signal. Atmosphere, 14(8), 1317. https://doi.org/10.3390/atmos14081317





