1. Introduction
Constructing simple models that reproduce the phenomenologically complex behaviour of fluid flows has always been a driving force in turbulence research and is a direction in which Jack Herring’s work excelled. There are numerous works in his career explaining complex phenomena in fluid dynamics with simplified models [
1,
2,
3,
4,
5,
6,
7,
8,
9,
10,
11,
12,
13]. In particular, the energy cascade in scale space is a phenomenon that has met various modeling approaches in the literature, such as direct interaction approximation [
1,
5,
14,
15,
16], eddy damping quasi-normal Markovian models [
17,
18,
19,
20] energy diffusion models [
21,
22], and shell models [
23,
24,
25,
26]. Such models have led to predictions about the direction of cascade, the power-law exponents of the energy spectra, and intermittency. Intermittency that still escapes a firm quantitative understanding manifests itself as a deviation from self-similarity and from the prediction obtained on purely dimensional grounds. In particular, shell models have been used to study intermittency for many years now. Their simplicity has enabled examining asymptotically large Reynolds numbers and merits various rigorous analytical studies [
27,
28,
29,
30,
31,
32]. Recent reviews can be found in [
33,
34,
35]. Typically, shell models quantify all structures of a given scale
ℓ by a single real or complex amplitude
. As such, spatial intermittency that is linked to the appearance of rare but extremely intense structures cannot be captured this way. Nonetheless, the temporal variation of the modes
does display intermittency, as has been demonstrated by many models [
24,
25,
26,
36]. This type of intermittency has been recently linked to the fluctuation dissipation theorem [
37]. Furthermore, a solvable (but not energy-conserving) model was also derived and studied in [
38].
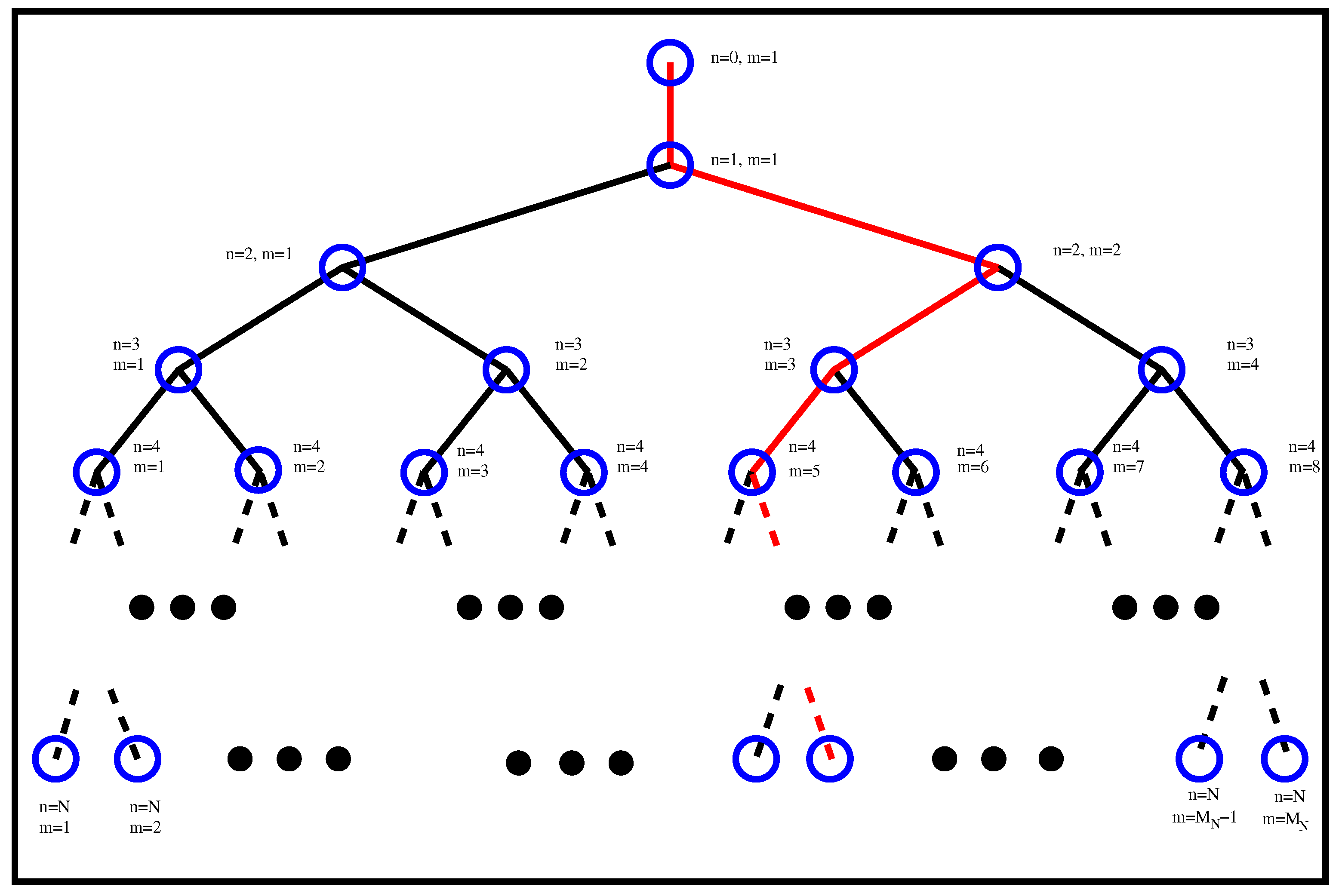
In the spirit discussed in the first paragraph, we here construct and study a binary tree shell model for turbulence that displays intermittency. In this model, energy at each scale is split between multiple different structures. Each structure transfers its energy into two smaller-scale structures, building a binary tree structure as shown in
Figure 1. In this way, the number of structures increases exponentially as smaller scales are reached. Such models with binary structure were introduced in the 1990s but have not been investigated extensively [
39,
40,
41]. Here, we follow a similar analysis as in [
42], where stationary solutions of non-binary shell models were investigated. We demonstrate that such analysis allows the construction of exact stationary solutions that display intermittency.
2. Multi-Branch Shell Models
We consider the evolution of a turbulent flow modeled by the real amplitudes
of structures of scale
where
and
. At scale
, there is one structure whose amplitude is given by
; this structure will transfer its energy to
structures of scale
, each one of which will transfer its energy to
structures of scale
and so on, as shown in
Figure 1 for
. The volume of each structure is given by
, where
D is the spatial dimension. If the cascade process is space-filling, the number of substructures
is related to
and
D by
Accordingly, at energy scale
, we have
(with
) structures so that if we consider
N such scales we have a total of
structures. The energy of every structure is given by
so the total energy is given by
where
is from now on taken to be unity.
In the Desnianskii and Novikov model [
23], structures of scale
interact with only structures of scale
and
, and there is no branching
. The amplitudes
then follow the following dynamical equation:
For
and
, this system conserves the energy (
5) (with
) for any value of
. The flux of energy across a scale
is given by:
The Desnianskii and Novikov model [
23] is the simplest energy-conserving model one can consider. Since its construction, more complex models have been designed that include more distant mode couplings and complex amplitude modes. The newer models display chaotic dynamics and also conserve more invariants than just the energy. The most popular ones are the SABRA and the GUY model [
24,
25,
26,
36]. A comparison of the two can be found in [
34]. Although these models are more realistic, here, we are going to keep the structure of the Desnianskii and Novikov model [
23] because its simplicity allows for analytical treatment.
Expanding on the Desnianskii and Novikov model, allowing each structure to branch out to two (
) smaller-scale structures
results in the following dynamical equation:
where
is the viscosity,
is the forcing, and
are again free parameters. The branching diagram for the model given in (
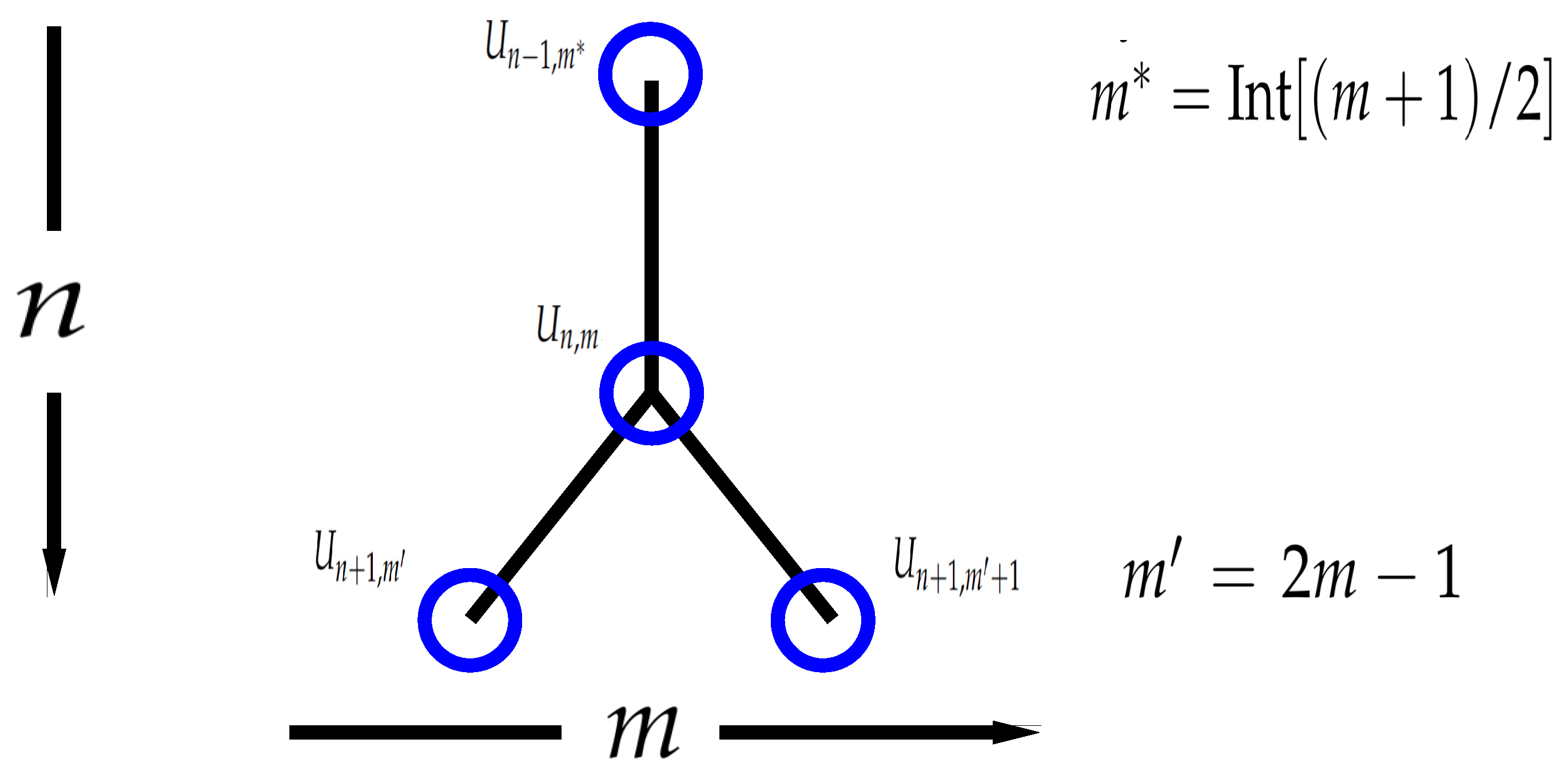
9) is provided in
Figure 1. The integers
and
correspond to the index of scales
, with which the mode
is linked where
is explicitly given by
and
corresponds to the index of scale
linked to
given by
, as illustrated in the left panel of
Figure 2. For
,
, and, for any value of
, the system conserves the energy (
5), where now
. The energy flux
through a scale
and structure (
) expressing the rate energy from the large scales (
) is lost to the smaller scales (
) through the structure
m due to the non-linearity, which is given by
The total flux through scale
is then given by
Conservation of energy by the non-linear terms implies that, at scales smaller than the forcing scale and larger than the dissipation scale (
), the flux
is constant and equal to the energy injection/dissipation
where
and
The range , where forcing and viscous effects can be neglected, is called the inertial range.
In
Figure 3, we plot the energy spectra
as a function of
n with blue dots, while the red dots indicate the averaged value
from a realisation of a simulation of Equation (
9) performed with
forced at
, while the amplitude of the mode
was kept fixed at
. The forcing for this simulation was constant in time and random initial conditions were used. The spectra were calculated a few turnover times after the initialization. At that time, the amplitudes
appear to be very dispersed even for the same value of
n. The averaged value follows power law close to the Kolmogorov scaling
, although individual
can vary orders of magnitude from this mean value. This indicates that higher-order statistics can deviate from the dimensional analysis spectrum. If the simulation is carried over to longer times, there is a slow synchronisation between same
n modes for large
n such that
attain similar values for all
m. This effect is due to viscosity and has been noted in previous works [
40,
41] and is referred to as phase synchronisation. It can be avoided if additional interaction terms between same
n modes are added. Here, we do not add this further complexity and consider only interactions as depicted in
Figure 2 and focus only on the inertial properties.
The present model is computationally expensive as its complexity increases as . As a result, it is not easy to obtain a long inertial range (large N) to investigate the resulting power-law behaviours numerically. On the other hand, its simplicity allows for analytical treatment, which is what we are examining in the next section by constructing exact inertial range solutions of arbitrary large n.
3. Inertial Range Intermittent Solutions
We look for stationary solutions of Equation (
9) in the inertial range where forcing and dissipation can be ignored. Stationarity implies that, for any
:
The way we proceed to find such a solution is the following: given
and
, we look for
and
such that the equation above is satisfied; then, we proceed to the next scale and search for
and
and so on, finding a recursive relation that provides all
. The solutions only depend on the relative amplitude of
, so we define their normalised ratio as
To simplify the notation, we denote
and then stationary solutions of (
12) satisfy
which simplifies to
which has real solutions only if
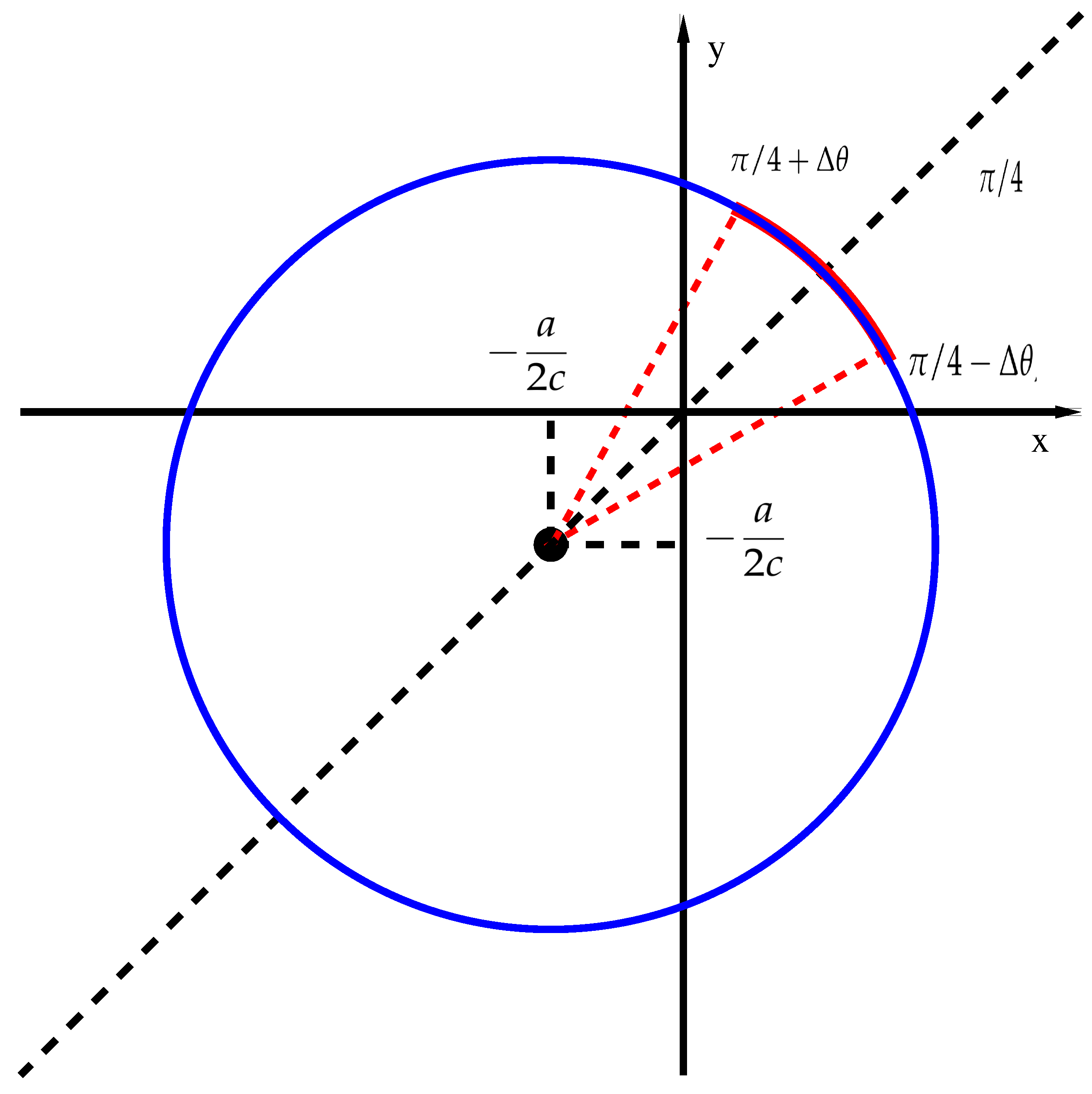
The solutions
form a circle in the
plane centered at
and with radius
R depicted in the right panel of
Figure 4. It is important to note that any point
in this circle is a solution of (
16), and thus we have multiple possible solutions. The condition (
17) is satisfied for positive
, which will be the focus of the present investigation. Returning to the
notation, the values of
and
that satisfy the stationarity condition can be written in full generality as
where
is arbitrary. Equations (
18) and (
19) form a recurrence relation out of which, given
and a choice of
, one can construct all
. Then, given
, one can obtain
based on (
14) as
where
are the
m one crosses along the path from (1,1) to (
) as shown by the red line in
Figure 1. This recurrence relation, however, does not always lead to bounded solutions of
. For some values of
, the resulting
can be negative or zero. Negative values can lead to un-physical solutions with negative flux from the small to the large scales. If the flux
is negative for some (n,m), then the sum of the flux of the “daughter” nodes
has to be negative and equal to
and so on for their “daughter” nodes. There would then exist at least one descendant at each scale with negative flux, and this can only be realised if there is a source of energy at the very small scales, which is un-physical. Negative flux stationary solutions are thus not accepted. Furthermore, if
x or
y is zero, it means that the particular branch is zero for all subsequent values (i.e., all descendants). We need thus to limit the choice of
so that positive and finite
are obtained.
The simplest case is obtained by choosing . It corresponds to an equal part of energy being distributed to the left and the right branch and leads to the Kolmogorov solution or in terms of the velocity ) (where is assumed). It corresponds to a finite flux non-intermittent (self-similar) solution.
Intermittency, however, can manifest itself if we chose
so that energy is not equally distributed in the left and right branch. Here, we will chose
randomly with uniform distribution in the range
for a given
, as shown in red in
Figure 4. Then, it can be shown that, for
, there exists
such that, for all
, both
and
. For
, the recurrence relation converges either to
or
and we are going to limit ourselves only to the
case here. To obtain
, one needs to note that, from the recurrence relation (
19), the largest value of
is obtained when
and
, while the smallest value of
is obtained when
and
. This leads to the following relations
We arrive at exactly the same relations if we examine Equation (
19).
We solved Equations (
21) and (
22) numerically and the results are shown in the left panel of
Figure 5 for three different values of
. For
, only the Kolmogorov solution is allowed with
. As
increases,
cover a wider range of values up until a critical value of
for which
becomes zero and
diverges. The value of this critical angle as a function
is shown in the right panel of the same figure.
is zero for
and grows for larger values approaching
as
(not demonstrated here).
For any given choice of
, we can construct an ensemble of exact solutions of the present model by following the recurrence relations (
18) and (
19), picking each time randomnly
and reconstructing
by Equation (
20). We note that, other than
, the only other parameter that controls the ensemble of solutions considered is
, which provides a measure of how much our ensemble deviates from the Kolmogorov solution
. This process has direct links with the random cascade models studied in the past [
43,
44,
45]; however, we need to note that, unlike the random cascade models, the solutions found here are energy-conserving.
4. Statistical Behaviour and Intermittency
In this section, we examine a large ensemble of the exact solutions shown in the previous section and investigate their properties. For our investigation, we have set
and we consider only a single path (as the one shown in red in
Figure 1) and not the full tree. The differences in the statistics between the two choices (single path and full tree) lie in the cross correlations between different modes that are not captured in the single path. As an example, we mention that the flux
in Equation (
10) is identically equal to
for every realisation, while the flux
given in Equation (
9) fluctuates and only its mean value is equal to
Along such path, we consider three different ensembles for , each one composed of different solutions. The solutions were constructed by picking randomly for each node examined, from a uniform distribution between and . The value of n varied from to . We note that, if the full tree was investigated instead of a single path for such large value n, it would require to solve for degrees of freedom, which is computationally unattainable.
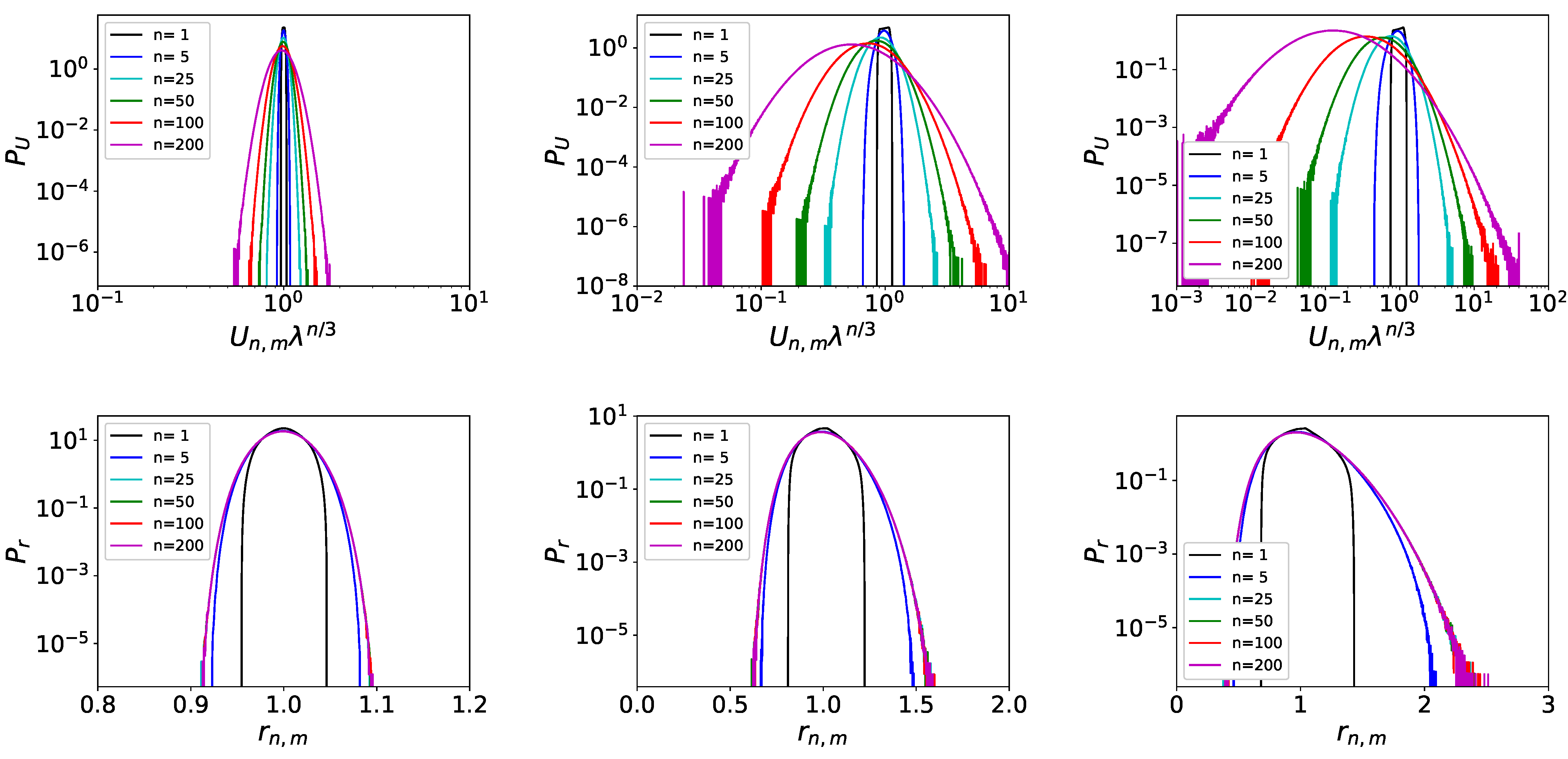
In the top panels of
Figure 6, we plot the probability distribution function (PDF)
of the variable
for the three values of
(from left to right) and different values of
n. The PDFs of different values of
n do not seem to overlap, although the
x-axis has been normalised by the Kolmogorov prediction
. Instead, as large values of
n are reached, the PDFs display larger tails, reaching values of
much larger and much smaller than their mean values. The closer
is to the critical value
, the larger this deviation is. On the other hand, the PDFs
of the ratios
that are displayed in the lower panels of
Figure 6 do not display such widening. For sufficiently large
n, all PDFs collapse to the same functional form that depends only on the choice of
. This implies that, while
are not self-similar under scale transformations, their ratios
are!
The same behaviour can be observed for the energy fluxes
. In the top panels of
Figure 7, we plot the PDFs
of
for the same values of
and
n as in
Figure 6. As with the velocity amplitudes
, as
n is increased, the PDFs of
widen without collapsing to an
n-independent form. In the lower panel of the same figure, we plot the the PDFs
of the flux ratio
. It is defined as
after a little algebra and using (
9) and (
18) leads to
where
. The flux ratio, much like the velocity ratio
, does converge to an
n-independent PDF as large values of
n are reached. Furthermore, the functional form of this PDF appears to be flat, limited by a minimum and a maximum value of
. This appears to be so because
in (
24) varies little with
r for small variations in
r and the variations in
are mostly controlled by the variations in
.
Given that the PDFs of
and
arrive at an
n-independent form, a large
n has some implications for the evolution in
n of the PDFs
. Both
and
can be written as a product of all
and
with
. As a result, the logarithms of
and
can be written as
where
and
stand for the mean value of the logarithms of
and
, respectively:
The properties of
and
remind of the random cascades studied in the past [
43,
44,
45]. However, while the random cascade models were not conserving energy, in the present model, energy is conserved exactly. Another important difference here is that
and
are not independent but each one depends on the value of the previous one. Nonetheless, we can proceed assuming such independence, although not entirely correct. In that case,
and
can be reconstructed using large deviation theory [
46]. In this framework,
and
follow for large
n a distribution of the form
where
and
are called the rate functions that can in principle be obtained from
and
using the Legendre–Fenchel transform [
46]. Here, we limit ourselves in noting that, if
and
follow the form of Equation (
27), then the distributions of
and
that are linked to
and
by (
25) should take the form
where only the largest terms in
n are kept. To test this prediction, we plot in
Figure 8 as a function
(top panels) and
as a function
, where
and
correspond to the value at which the probability obtains its maximum
. With this normalization, the PDFs both for
and for
collapse, indicating that the large deviation principle works well for this model.
As a final look at the intermittency problem, we display in the top panels of
Figure 9 the first ten structure functions
defined as
where the angular brackets stand for ensemble average. The structure functions have been normalised by the Kolmogorov scaling to emphasise the differences. The structure functions are fitted to power laws
and the measured exponents
are plotted in the lower panels of
Figure 9. The exponents show similar behaviour, with real turbulence displaying larger values for
and smaller values for
, while the exact result
is satisfied. It is worth noting that the deviations from the Kolmogorov scaling are not universal but depend on our choice of ensemble, which is controlled by
.
5. Discussion and Conclusions
One can argue that the exact stationary solutions obtained in this work have little to do with real turbulence that displays chaotic spatio-temporal dynamics. This may be true and multi-branch models with two neighbour interactions as in [
39,
40,
41] that display chaotic dynamics should be investigated instead. The present results, however, do point to a clear instructive demonstration of how intermittency can appear in realistic flows and how it can be modeled. Furthermore, it leads to a series of clear messages that are described below that are of great use in future turbulence research and can guide measurements in numerical simulations and experiments.
First, we note that intermittency appearing in stationary fields found here comes in contrast with the typical shell model studies in single-branch models for which intermittency comes from the temporal dynamics alone as only a single structure exists for each scale
. In the latter case, intermittency has been linked to the temporal dynamics through the fluctuation dissipation theorem [
37]. In reality, both temporal and spatial dynamics contribute to the presence of intermittency and their role needs to be clarified.
In the present model, randomness comes from our choice of
and the resulting intermittency depends on that choice. In reality (or in more complex shell models), such randomness comes from local chaotic dynamics that need to studied in order to clarify which processes lead to enhanced cascade and with what probability. Multi-branch models based on the more complex GOY or SABRA as proposed in [
39,
40,
41] can help in this direction. The additional coupling terms introduced in these works avoid phase synchronization and lead to chaotic dynamics. Chaos can remove the arbitrariness of the choice of
that should ideally be self-imposed by the dynamics.
Perhaps the most interesting implication of this work is that it suggests new ways to plot data from experimental and numerical simulations. One way suggested by this work is, instead of focusing on the PDFs of velocity differences, experimental or numerical data could focus on the PDFs of ratios of velocity differences. The latter are shown in this work to become scale-independent and could lead to more precise measurements. An alternative way is to re-scale the PDFs of velocity differences using the large deviation prediction (
27), as was conducted in
Figure 8. Of course, realistic data
are not precisely defined and an optimal choice should be searched for.
A good model of a complex phenomenon, in the authors’ opinion, is not one that quantitatively reproduces experimental measurements through parameter fitting but rather one that unravels the processes involved. In that respect, we believe that the present model and results are very fruitful. We only hope that this work comes close to the standards set by Jack Herring. A.A. met Jack Herring during his ASP post doc in 2004–2006. Jack is fondly remembered stopping by the offices of post docs just to see if they are OK. He will be greatly missed.