Long Memory Cointegration in the Analysis of Maximum, Minimum and Range Temperatures in Africa: Implications for Climate Change

Abstract

This paper deals with the analysis of the temperatures in a group of 36 African countries. By looking at the maximum, minimum and the range (the difference between the maximum and the minimum) and using a long memory model based on fractional integration and cointegration, we first show that all series display a long memory pattern, with a significant positive time trend in 29 countries for the maximum temperatures and in 33 for the minimum ones. Looking at the range, the estimated value for the order of integration is smaller than the one based on maximum or minimum temperatures in 17 countries. Performing fractional cointegration tests between the maximum and minimum temperatures, our results indicate that the two series cointegrate in the classical sense (i.e., with a short memory equilibrium relationship) in a group of 11 countries, and there is another group of eight countries displaying cointegration in the fractional sense. The remaining 17 countries with no evidence of cointegration are therefore at a very high risk of climate change due to the absence of long-term co-movement in their maximum and minimum temperatures. Findings in this paper are of tremendous interpretations and relevance for the analysis and climate projections in Africa.

1. Introduction

Temperature is a key indicator of climate change, and monitoring changes in temperature over time can help identify potential impacts on ecosystems, agriculture, and human health [1]. In a report by the Intergovernmental Panel on Climate Change [2], it is mentioned that global warming induced by human activity will produce temperatures around 1.0 °C higher than in times of the pre-industrial period, and that if current trends continue, global warming is expected to rise by 1.5 °C between 2030 and 2052. The report also noted that some regions of the globe are experiencing more warming than others due to vegetation cover and other factors [3,4,5,6,7,8,9]. There are also clear evidences to show the dependency of global warming on the diurnal temperature range (DTR), that is, the difference between the maximum and minimum temperatures [10]. The National Oceanic and Atmospheric Administration (NOAA) and National Aeronautics and Space Administration (NASA) have measured and determined the year 2010 to be the warmest year on record when compared to the average baseline of the 20th century and of the period 1951–1980, respectively. Hansen et al. [11] and Cahill et al. [12] have proven that the temperature increase in trend would likely continue due to the continuous increases in the greenhouse gas (GHG) concentration, while in the sub-Saharan African region, the warming is likely to be higher compared to the global average, and the speed of temperature rise will be more than the rise in the global mean temperature (see, e.g., [13,14]). Africa is particularly vulnerable to the effects of climate change due to its dependence on rain-fed agriculture and limited infrastructure to cope with extreme weather events [15,16]. Furthermore, the large-scale climate patterns such as El Niño–Southern Oscillation (ENSO), Indian Ocean Dipole (IOD), and Atlantic Multidecadal Oscillation (AMO) often influence Africa’s climate, causing heatwaves, droughts, and floodings in different regions of the continent [16].

In the very arid regions of Africa, the temperature is expected to rise faster compared to other parts of the world in the 21st century [17]. Thus, the African continent is very prone to climate variability changes due to its geographical location on the globe. Figure 1 shows the map of Africa, showing all African countries, and how the equator divides the continent into two parts, that is, the continent lies within the intertropical zone between the Tropic of Cancer and the Tropic of Capricorn, where the tropics are regions of the globe surrounding the equator. As it is observed in the map, the continent lies between 37° N and 35° S and in this position, the continent lies almost perfectly on the equator, and this latitudinal position of Africa between the equator and around the tropics causes rainfall, temperature, and humidity in Africa to be higher compared to other continents (https://en.wikipedia.org/wiki/Tropics, accessed on 15 April 2023).

There are also different climate types experienced annually. These are the equatorial climate, tropical wet and dry climate, tropical monsoon climate, semi-arid climate, desert climate, and subtropical highland climate (https://en.wikipedia.org/wiki/Climate_of_Africa, accessed on 18 July 2023). It is very rare to experience a temperate climate in any part of Africa except at very high elevations and along the fringes. African deserts are the hottest and driest worldwide due to subtropical ridges with hot, dry air masses. As predicted by IPCC AR6 (2021), temperatures in African countries are expected to have increased by 1.5–3 °C in 2050. Putting temperature on one side, the total annual greenhouse gasses are also rising fast at the rate of about 1.6% per annum with carbon dioxide emissions alone increasing by about 2% per year. This, together with the fast-rising temperature, could change the African climate in such a way that urgent intervention would be required, coupled with energy issues and poor amenities that most countries are experiencing. We acknowledge and thank the IPCC for their efforts in monitoring the African climate [15].

In terms of land area compared to other continents, Africa covers a total land area of about 30.2 million square kilometers, which is about one-fifth of the land area of the entire globe (https://www.mapsofworld.com/lat_long/africa.html#:~:text=Africa’s%20latitude%20and%20longitude%20lies,of%20the%20world’s%20land%20area, accessed on 18 July 2023).

Focusing on Africa, various studies have investigated the temperature dynamics and their maximum and minimum ranges on the continent. The mean annual DTR for Ethiopia, Sudan, South Africa, and Zimbabwe have been considered by Nicholls et al. [3], where the authors observed a decrease of 0.5 °C to 1.0 °C in the mean annual DTR for Sudan and Ethiopia. For countries in the southern part of the continent such as Zimbabwe and South Africa, the DTR reduced during the period 1950–1960. Kruger and Sekele [18] and Kruger and Nxumalo [19] find evidence of increasing warming trends in South Africa. Extending the analysis to other countries, New [20] investigated trends in daily climate extremes over Southern and Western Africa, and found a repeating pattern of temperature extremes associated with rising temperatures. Neumann et al. [21] found that temperature in the Volta basin, West Africa, exhibited highly significant positive trends. In a similar vein, Muthoni [22] studied temperatures in West Africa and also found a strong warming trend.

Meanwhile, there have been controversies in relation to the speed of temperature increase on the appropriate estimation method to model temperature across time. The most standard approach still recommends incorporating a linear trend in the modeling framework. Using the linear model with fractional integration methods, Gil-Alana et al. [23] examined issues such as linear trends, seasonality, and persistence in western, eastern, and southern regions of Africa and found that time trends are required in most of the countries to explain the climate features in the areas. They also found evidence of structural breaks in some of the countries. Other papers that have applied fractional integration in a linear framework to analyze temperature and rainfall data include [24,25,26,27,28].

A closely related research work to the present paper is the one conducted in three African countries, namely South Africa, Kenya, and Côte d’Ivoire by [29]. They checked for warming trends, and using fractional integration, they showed that only Kenya has experienced a significant temperature increase in the last 30 years at the time of the research.

In the current paper, we investigate persistence and linear trends in the maximum and minimum annual average temperatures in 36 African countries chosen by data availability from the Climate Change Knowledge Portal (CCKP). Due to the statistical distribution of maximum and minimum temperatures, we also examine the difference between the two series, which leads to the diurnal range, as this informs climate differences in the study area. High maximum temperatures and low minimum temperatures are experienced in desert or arid climate with scanty vegetation cover, while moderate maximum temperatures and low minimum temperatures are often recorded in temperature climate regions. The latter is unlikely to be experienced in the sub-Saharan region of Africa. Thus, changes in the distribution of maximum and minimum temperatures over time can indicate climatic changes as the frequency or intensity of extreme temperatures, and events such as heat waves or cold snaps can be indicative of climate change.

Having obtained the fractional integration estimates based on a linear trend specification, we conducted the homogeneity of paired Local Whittle (LW) estimates of fractional orders based on the Hausman-type test of [30], since the statistical equality of the fractional orders is a pre-requisite for cointegration—at least in the bivariate representation, as it is the case in this paper. We extended the analysis to fractional cointegration using narrow-band frequency domain least square (NBFDLS) estimates of [31] in the fractional cointegration framework of [32]. The NBFDLS estimates for the cointegrating vector were obtained and used to compute the model residuals in models linking each country’s maximum and minimum temperatures. Then, fractional integration estimates were obtained on the residuals based on the LW estimator. Note that cointegration is relevant in the present context since it will inform us if there is a long-run equilibrium relationship between maximum and minimum temperatures. On the other hand, a lack of this property will suggest that the two series move apart, supporting potential extreme changes in temperatures.

In conclusion, the hypotheses to be tested in this paper are the following: we first consider the possibility of long memory or long-range dependence in the variables under examination, since this is a property widely observed in climatological data. Then, based on this observation, we claim that the estimation of the linear trends in the data is clearly affected by the long memory property, and to not take into account this issue will clearly produce biased estimates of the time trend coefficient to explain climate change. As a final issue, the possibility of cointegration is also examined by looking at the difference between maximum and minimum temperatures, claiming that under normal circumstances, both variables should be linked in a long-run equilibrium relationship.

2. Data

Maximum and minimum average annual temperature (°C) datasets for 36 African countries were analyzed to provide insights into climate change on the continent. The countries are Angola, Benin, Botswana, Burkina Faso, Cameroon, Central African Republic, Chad, Congo, Cote d’Ívoire, Egypt, Gabon, Ghana, Guinea, Guinea-Bissau, Kenya, Lesotho, Liberia, Libya, Madagascar, Malawi, Mali, Mauritania, Morocco, Namibia, Niger, Nigeria, Rwanda, Sierra Leone, Senegal, South Africa, Sudan, Tanzania, Tunisia, Uganda, Zambia, and Zimbabwe. The datasets were retrieved from the World Bank Climate Change Knowledge Portal at https://climateknowledgeportal.worldbank.org/, accessed on 18 July 2023 (see World Bank, 2021). This portal has been collecting historical monthly and annual climate data of countries throughout the world since 1901 till date, and the nature of the analysis to be carried out here required only annual data since monthly datasets could bias our results due to the interference of seasonality. In each of the five geographical zones of Africa, Figure 2 displays graphs showing the time series of maximum and minimum temperatures, whereas, in the case of the West African zone, we have temperature plots for Guinea and Nigeria; others are Chad (Central Africa), Egypt (North Africa), Kenya (East Africa) and South Africa (Southern Africa).

In all the plots, it is obvious to notice shifts in temperature trend, signaling global warming over time. In the case of Chad, the temperature increased consistently from 1950 to reach astronomic thermometric readings in 2010, similarly to Kenya, Nigeria, and South Africa. The temperature shift in temperature trends is noticed around 1970 in the case of Egyptian temperature plots, and between 1970 and 1980 in the case of Nigeria.

Table 1. Data summary.

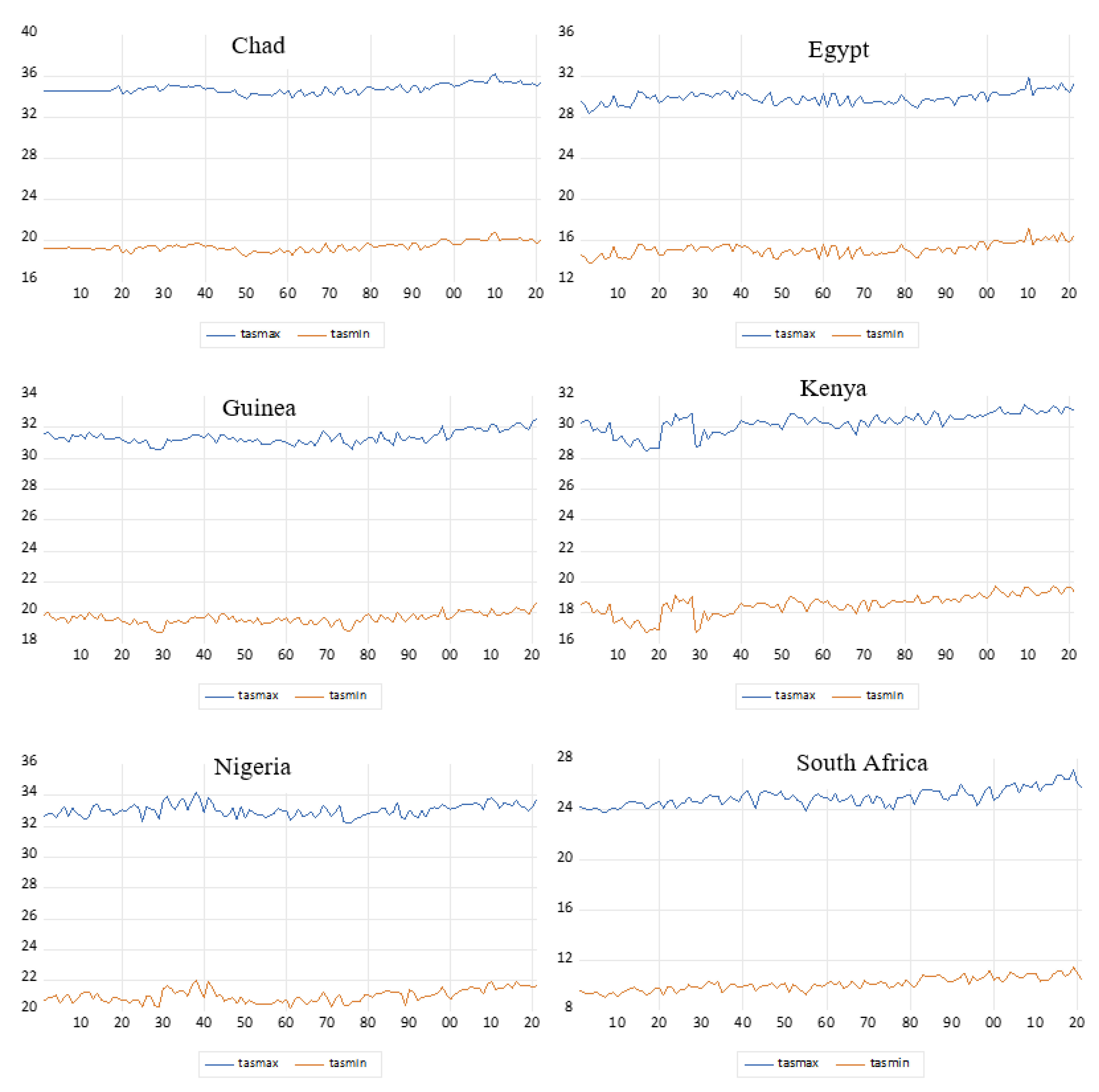
Country	Max. Temp (°C)		Min. Temp (°C)		Range (°C)
	1901	2021	1901	2021	1901	2021
Angola	28.18	28.60	14.51	14.93	13.67	13.67
Benin	33.23	34.47	21.58	22.98	11.65	11.49
Botswana	29.08	29.81	13.16	13.72	15.92	16.09
Burkina Faso	34.46	36.27	21.78	23.81	12.68	12.46
Cameroon	29.51	30.59	18.84	19.87	10.67	10.72
Central Afr. Rep.	31.34	32.16	18.60	19.45	12.74	12.71
Chad	34.58	35.42	19.32	20.06	15.26	15.36
Congo	28.77	29.77	19.72	20.73	9.05	9.04
Cote d’Ivoire	31.67	32.54	21.42	22.26	10.25	10.28
Egypt	29.64	31.27	14.69	16.53	14.95	14.74
Gabon	28.69	29.84	20.36	21.51	8.33	8.33
Ghana	32.17	33.4	21.97	23.25	10.2	10.15
Guinea	31.57	32.53	19.86	20.69	11.71	11.84
Guinea-Bissau	33.74	34.99	21.4	22.59	12.34	12.40
Kenya	30.28	31.11	18.51	19.39	11.77	11.72
Lesotho	17.24	19.45	4.35	5.11	12.89	14.34
Liberia	30.38	30.50	21.17	21.30	9.21	9.20
Libya	28.77	29.87	15.21	16.28	13.56	13.59
Madagascar	27.39	27.63	17.92	18.16	9.47	9.47
Malawi	27.23	28.10	16.41	17.54	10.82	10.56
Mali	35.28	36.93	20.99	22.68	14.29	14.25
Mauritania	34.65	36.02	21.27	22.62	13.38	13.40
Morocco	23.26	24.52	11.39	12.49	11.87	12.03
Namibia	27.34	27.62	12.28	12.66	15.06	14.96
Niger	34.77	35.70	19.99	20.52	14.78	15.18
Nigeria	32.63	33.74	20.69	21.65	11.94	12.09
Rwanda	24.88	25.29	12.78	13.19	12.10	12.10
Sierra Leone	31.69	32.25	21.70	22.18	9.99	10.07
Senegal	35.51	36.91	21.09	22.39	14.42	14.52
South Africa	24.25	25.73	9.55	10.44	14.70	15.29
Sudan	35.61	35.89	19.92	20.51	15.69	15.38
Tanzania	27.90	28.50	16.53	17.55	11.37	10.95
Tunisia	25.20	27.07	12.97	15.65	12.23	11.42
Uganda	28.67	29.34	16.55	17.14	12.12	12.20
Zambia	28.50	29.06	14.60	15.22	13.90	13.84
Zimbabwe	27.80	28.64	14.25	15.14	13.55	13.50

displays a data summary, showing the starting maximum and starting minimum temperatures in 1901 and corresponding ending maximum and minimum temperatures in 2021 for the 36 countries. It is found that ending temperatures in 2021 are quite higher than the starting temperatures in 1901, resulting in a positive shift in temperature due to global warming. The annual range—the difference between the annual maximum and annual minimum temperatures—which is used to proxy the diurnal temperature range (DTR), is also presented in the table for 1901 and 2021 data.

3. Econometric Methods

3.1. Testing for a Linear Trend

The analysis of climatological time series datasets takes its root from the seminal work of [33], where a linear model was employed to fit climate datasets. Hamilton [34] used a model of the form

$${\mathrm{y}}_{\mathrm{t}}=\alpha +\beta \mathrm{t}+{\mathrm{x}}_{\mathrm{t}},\hspace{1em}\mathrm{t}=1,2,\dots ,$$

(1)

where $y_t$ is the climatic time series under investigation and t is the time trend t = 1, 2, … Then, $x_t$ is the deviation term, derived from the original series $y_t$. The model’s parameters are α and β, which represent the intercept and slope, respectively. The slope, β, measures the average change in $y_t$ over time, when $t=t_0$. Thus, in the context of climatic research, there is long-run warming if the slope, β, is positive and statistically significant, implying that the temperature is rising. The estimation of the deviation term is critical in carrying out this assessment. This is determined by the distribution from which $x_t$ is created, and hence by the overall estimation of the process.

In most early studies, the error term x_t in (1) was assumed to be well behaved, i.e., displaying a short-memory (SM) structure, and also denominated an integration of order 0 or I(0) processes. In this context, the simplest structure was the white noise case where no time dependence is permitted. If that dependence is allowed, the ordinary Autoregressive Moving Average (ARMA) models were employed. However, the time dependence between the observations may display a higher range. Thus, it may exhibit long-term dependence (LTD) or long memory (LM), as observed in various climatological data by researchers such as [4,34,35,36,37], and others. Gil-Alana [38] then adapted the linear model of [33] to the fractional integration or I(d) framework where the dependency of historical temperature observations of Alaska over long past time periods is investigated. This phenomenon is known as the long-range dependency (LRD) or LTD. Climatic variables often exhibit this property due to the natural variability from year to year, and to the next. Climatic variables can also vary on much longer time scales such as from decades to centuries, and due to human interference, there may be a shift in the mean state of a particular climatic variable, such as temperature or rainfall. In this study, we shall rely on the properties of LRD or shift in a mean state of climatic variables based on the framework of fractional integration and cointegration. Note, LRD is an aspect of fractional integration; thus, LRD is often explained based on this broader perspective.

3.2. Testing for Fractional Integration

The following is the standard non-seasonal fractional integration model, i.e., an integration of order d or I(d) model:

$${(1-\mathrm{L})}^{\mathrm{d}}{\mathrm{x}}_{\mathrm{t}}={\mathrm{u}}_{\mathrm{t}},\hspace{1em}\mathrm{t}=1,2,\dots .$$

(2)

where d is any real number (such as integer or fractional values), L is the lag-operator $L{x}_t=x_{t-1}$, and $u_t$ denotes the white noise process, which is an I(0) process in the context of fractional integration I(d) processes (an I(0) process is defined as a covariance stationary process where the infinite sum of its autocovariances is finite; it includes the white noise model but also the stationary ARMA class of models). The polynomial (1 − L)^d in (2) in a binomial representation can be expanded as follows:

$${(1-\mathrm{L})}^{\mathrm{d}}={\displaystyle \sum _{\mathrm{j}=0}^{\infty }\left(\begin{array}{l}\mathrm{d}\\ \mathrm{j}\end{array}\right){(-1)}^{\mathrm{j}}}{\mathrm{L}}^{\mathrm{j}}=1-\mathrm{d}\mathrm{L}+\frac{\mathrm{d}(\mathrm{d}-1)}{2}{\mathrm{L}}^2-\dots$$

and therefore

$${(1-\mathrm{L})}^{\mathrm{d}}{\mathrm{x}}_{\mathrm{t}}={\mathrm{x}}_{\mathrm{t}}-\mathrm{d}{\mathrm{x}}_{\mathrm{t}-1}+\frac{\mathrm{d}(\mathrm{d}-1)}{2}{\mathrm{x}}_{\mathrm{t}-2}-\dots$$

depicts that Equation (2) can be written as

$${\mathrm{x}}_{\mathrm{t}}=\mathrm{d}{\mathrm{x}}_{\mathrm{t}-1}-\frac{\mathrm{d}(\mathrm{d}-1)}{2}{\mathrm{x}}_{\mathrm{t}-2}+\dots +{\mathrm{u}}_{\mathrm{t}}.$$

(3)

Intuitively, the role of $d$ in Equation (3) is clear as it is a slope coefficient between $x_t$ and its lagged values such as $x_{t-1}, x_{t-2},\dots$. Thus, it determines the degree of correlation between $x_t$ and its lagged values. Therefore, regression, or herein, correlation, in explaining fractional integration or LRD processes leads to a time series dependency or persistency as they are often used interchangeably. The model in (2) is a non-seasonal model type since the dataset at hand is of annual temperature series, and testing seasonality, in addition, is not of interest in this paper.

Many methods have been used to estimate the fractional dependence parameter d. Some of these methods are semi-parametric, while others are parametric methods. Semiparametric techniques are typically implemented in the frequency domain. In this study, we use a parametric frequency domain Whittle estimation approach (see [39]) in conjunction with a testing procedure by [40] that depends on the Lagrange Multiplier (LM) principle. Robinson [40] uses the null hypothesis test:

$${\mathrm{H}}_{\mathrm{o}}:\mathrm{d}={\mathrm{d}}_{\mathrm{o}},$$

(4)

for any real value d₀ in a model given by Equations (1) and (2), that is,

$$y_t=\alpha +\beta t+x_t, {(1-L)}^d{x}_t=u_t, t=1,2,\dots ,$$

(5)

where $u_t$ is a white noise process. The fundamental advantage of this approach is that, because it depends on the LM principle, all of it is evaluated under the null, and because d_o can be any actual number, it is valid even in nonstationary situations (i.e., d_o ≥ 0.5), with a regular normal limit distribution. In addition, this standard normal distribution holds independently of the inclusion or not of deterministic terms in the model like an intercept and/or a linear time trend, being this method the most efficient one in the Pitman sense against local departures from the null (See [41]).

In complement to the aforesaid parametric methodology, we also use a semiparametric method to conduct the analysis. It is named semiparametric because no functional form is imposed on the error term, making only the assumption that it is integrated of order zero, i.e., I(0). In other words, it might be a simple white noise process or an ARMA process with a weak dependency autocorrelation. We employ in the paper a “local” Whittle (LW) estimate in the frequency domain, which is based on a frequency band that degenerates to zero. This approach [42] is defined implicitly by:

$$\widehat{\mathrm{d}}=\arg \min { }_{\mathrm{d}}\left(\log {\mathrm{C}}^{*}(\mathrm{d})-2\mathrm{d}\frac{\mathrm{1}}{\mathrm{m}}{\displaystyle \sum _{\mathrm{j}=1}^{\mathrm{m}}\log {\lambda }_{\mathrm{j}}}\right)$$

(6)

$$\mathrm{for} \mathrm{d}\in (-1/2, 1/2);\hspace{1em}\overline{\mathrm{C}(\mathrm{d})}=\frac{1}{\mathrm{m}}{\displaystyle \sum _{\mathrm{j}=1}^{\mathrm{m}}\mathrm{I}({\lambda }_{\mathrm{j}}){\lambda }_{\mathrm{j}}^{2\mathrm{d}}},\hspace{1em}{\lambda }_{\mathrm{j}}=\frac{2\pi \mathrm{j}}{\mathrm{T}},\hspace{1em}\frac{1}{\mathrm{m}}+\frac{\mathrm{m}}{\mathrm{T}}\to 0,$$

where m represents the bandwidth parameter, and I(λ_j) represents the periodogram of the time series, x_t, which is given by:

$$\mathrm{I}({\lambda }_{\mathrm{j}})=\frac{1}{2\pi \mathrm{T}}{\left|{\displaystyle \sum _{\mathrm{t}=1}^{\mathrm{n}}{\mathrm{x}}_{\mathrm{t}}{\mathrm{e}}^{\mathrm{i}{\lambda }_{\mathrm{j}}\mathrm{t}}}\right|}^2.$$

Robinson [42] demonstrated under a finiteness of the fourth moment and other very mild conditions:

$$\sqrt{\mathrm{m}}(\widehat{\mathrm{d}}-{\mathrm{d}}_{\mathrm{o}}){\to }_{\mathrm{d}}\mathrm{N}(0, 1/4)\hspace{1em}\mathrm{as}\mathrm{T}\to \infty ,$$

where d_o is the actual value of d and in addition to the requirement that m→∞ is slower than T.

3.3. Homogeneity of Paired Fractional Integration Parameters

Following from the local Whittle estimate, it is important to perform the test of homogeneity of paired integration orders. As earlier argued, this is a necessary condition for testing cointegration in a bivariate system. The following null hypothesis is used to assess the homogeneity of the orders of integration:

$$H_0:d_{y1}=d_{y2}$$

(7)

where the orders of integration of the individual series are represented by $d_{y1}$ and $d_{y2}$ (see [30,43]). The test statistic is defined as

$${\widehat{T}}_{xy}=\frac{m^{1/2}\left({\widehat{d}}_{y1}-{\widehat{d}}_{y2}\right)}{{\left\{\frac{1}{2}\left[1-{\widehat{G}}_{y1.y2}^2/\left({\widehat{G}}_{y1}{\widehat{G}}_{y1.y2}\right)\right]\right\}}^{1/2}+h\left(T\right)}$$

(8)

where $h\left(T\right)>0$ and ${\widehat{G}}_{y1.y2}$ denote the (y1.y2)^th element of $\widehat{\mathrm{\Lambda }}{\left({\lambda }_j\right)}^{-1}I\left({\lambda }_j\right)\widehat{\mathrm{\Lambda }}\left({\lambda }_j\right)$ with $\widehat{\mathrm{\Lambda }}\left({\lambda }_j\right)=diag\left\{e^{i\pi {\widehat{d}}_{y1}/2}{\lambda }^{-{\widehat{d}}_{y1}}, e^{i\pi {\widehat{d}}_{y2}/2}{\lambda }^{-{\widehat{d}}_{y2}}\right\}$.

3.4. Narrow-Band Frequency Domain Least Square Approach

At this juncture, we considered the narrow-band frequency domain least square (NBFDLS) estimates in obtaining the cointegrating vector linking the maximum and minimum temperatures. This approach is applied when the cointegrating pairs are deemed to possess long memory, having weakly dependent regressors. Since the regressors and the residuals are of long memory, thus, they are deemed to be correlated even at a very long time span. In that case, both the least squares and generalized least square estimates will be inconsistent (see [44]). Robinson [41] earlier proposed a semi-parametric NBFDLS estimator, which uses OLS on a degenerated band of frequencies around the origin. An improved version of the test for the stationary time series is given in [31].

In the two-variable case, where $y_{1t}$ is for maximum temperature and $y_{2t}$ is for minimum temperature series, both of fractional integration order $d<0.5$ and residuals of order $d_e<d$, the NBFDLS estimator is given by

$$\widehat{\beta }={\left\{\frac{1}{m}{\displaystyle \sum _{j=1}^m\mathrm{Re}\left[I_{y_1{y}_1}\left({\lambda }_j\right)\right]}\right\}}^{-1}\times \frac{1}{m}{\displaystyle \sum _{j=1}^m\mathrm{Re}\left[I_{y_1{y}_1}\left({\lambda }_j\right)\right]}$$

(9)

which is asymptotically distributed as

$$\sqrt{m}{\lambda }_m^{d_e-d}\left(\widehat{\beta }-{\beta }_0\right)\stackrel{D}{\to }N\left[0,\frac{g_e{\left(1-2d\right)}^2}{2g_{y1}\left(1-2d-2d_e\right)}\right]$$

(10)

where $g_{y1}$ and $g_e$ are the elements of a $G$ diagonal $2\times 2$ matrix. From (10), the normality is ensured as long as $d+d_e<0.5$ [31].

4. Main Results

Having presented the dataset used in Section 2, we therefore present the main results obtained based on the econometric methods presented in Section 3. In

Table 2. Results of ADF unit root test.

Country	Max. Temp (°C)			Min. Temp (°C)			Range (°C)
	None	Intercept	Intercept + Trend	None	Intercept	Intercept + Trend	None	Intercept	Intercept + Trend
Angola	0.3171[2]	−3.1469[1]	−4.5576[1]	0.3355[2]	−3.1752[1]	−5.5564[0]	0.0020[4]	−5.6877[1]	−5.7386[1]
Benin	0.3490[2]	−3.9137[1]	−3.9400[1]	0.4778[3]	−2.6479[1]	−5.0183[0]	−0.1613[1]	−3.3023[1]	−5.7028[0]
Botswana	0.3105[2]	−2.5926[2]	−7.6741[0]	0.2941[2]	−4.6700[0]	−7.1066[0]	0.1823[4]	−8.9667[0]	−9.3857[0]
Burkina Faso	0.3541[1]	−5.7067[0]	−6.3192[0]	0.5060[3]	−3.4801[0]	−5.3749[0]	−0.2151[2]	−2.8794[1]	−4.1499[1]
Cameroon	0.5978[3]	−6.8662[0]	−7.5844[0]	0.6235[2]	−2.2884[2]	−2.7278[2]	−0.1049[3]	−8.0343[0]	−8.0094[0]
Central Afr. Rep.	0.5203[2]	−2.4402[2]	−3.2942[2]	0.5388[2]	−2.1126[2]	−3.0607[2]	−0.4083[4]	−2.7591[2]	−3.2665[2]
Chad	0.4917[2]	−1.5969[2]	−2.1705[2]	0.4425[2]	−1.5745[2]	−2.4938[2]	0.0663[2]	−3.2194[2]	−6.7898[0]
Congo	0.7671[2]	−1.5726[2]	−2.5181[2]	0.7625[2]	−1.5746[2]	−2.5178[2]	−0.3702[7]	−10.4267[0]	−10.3999[0]
Cote d’Ivoire	0.6385[3]	−2.2845[2]	−2.9577[2]	0.4687[3]	−4.2075[0]	−5.5144[0]	0.0725[1]	−3.8767[1]	−4.3940[1]
Egypt	1.3401[5]	−2.4317[2]	−2.8386[2]	0.8076[2]	−2.2244[2]	−2.9386[2]	−0.1216[3]	−2.2496[3]	−7.6871[0]
Gabon	0.8330[2]	−1.4901[2]	−2.3948[2]	0.8256[2]	−1.4763[2]	−2.3920[2]	0.1416[3]	−10.1007[0]	−10.1330[0]
Ghana	0.5132[2]	−3.4754[1]	−3.7306[1]	0.4655[3]	−3.8136[0]	−5.1423[0]	−0.0556[2]	−3.4082[1]	−4.4562[1]
Guinea	0.6804[3]	−1.4924[2]	−2.5401[2]	0.3832[2]	−1.9008[2]	−5.5536[0]	0.1458[1]	−3.4493[1]	−3.6109[1]
Guinea-Bissau	0.7792[3]	−0.6981[3]	−1.9087[3]	0.6523[3]	−1.6596[2]	−2.8914[2]	0.0566[1]	−5.5719[0]	−5.7066[0]
Kenya	0.2804[2]	−1.7647[2]	−5.8075[0]	0.3017[2]	−1.6298[2]	−6.2287[0]	−0.1759[2]	−9.8508[0]	−10.3136[0]
Lesotho	1.2995[4]	−1.9224[2]	−6.8761[0]	0.6396[3]	−1.7927[3]	−8.3858[0]	0.9444[4]	−3.4123[1]	−3.8653[1]
Liberia	0.1592[2]	−2.4895[2]	−2.88994[2]	0.1373[2]	−2.5105[2]	−2.9140[2]	0.0055[1]	−3.4392[1]	−3.43039[1]
Libya	0.8349[3]	−1.6497[2]	−2.8180[2]	1.0739[4]	−1.5606[2]	−2.7181[2]	0.0138[3]	−3.2888[2]	−3.2934[2]
Madagascar	0.0635[2]	−2.1187[2]	−1.9551[2]	0.0487[2]	−2.1117[2]	−1.9450[2]	0.3742[4]	−11.5073[0]	−11.5446[0]
Malawi	0.2509[2]	−2.7236[2]	−7.6837[0]	0.8124[5]	−5.4000[0]	−6.7249[0]	−0.2075[3]	−8.4672[0]	−8.4866[0]
Mali	0.3529[1]	−3.5324[1]	−6.9707[0]	0.3714[1]	−2.7152[1]	−5.9485[0]	−0.0972[2]	−3.1696[1]	−3.6366[1]
Mauritania	0.5921[3]	−1.5369[3]	−8.0244[0]	0.5942[3]	−1.3504[3]	−6.4320[0]	−0.0422[1]	−5.4342[0]	−5.4130[0]
Morocco	0.7185[2]	−1.3661[2]	−2.9879[2]	0.4502[2]	−2.8884[1]	−4.5408[1]	0.1326[1]	−5.8760[0]	−7.1333[0]
Namibia	0.2682[2]	−4.3714[0]	−5.8074[0]	0.4270[3]	−3.8688[0]	−5.4211[0]	−0.1240[1]	−5.3411[1]	−5.4117[1]
Niger	0.2721[2]	−2.5021[2]	−2.6363[2]	0.2250[3]	−1.9597[3]	−3.1829[2]	0.0795[2]	−3.0056[2]	−3.1562[2]
Nigeria	0.4313[3]	−3.0302[2]	−3.1060[2]	0.4166[2]	−2.1146[2]	−2.6235[2]	−0.3924[5]	−5.3338[1]	−8.1575[0]
Rwanda	0.1542[2]	−1.5675[2]	−5.2979[0]	0.1774[2]	−1.9275[2]	−6.3444[0]	−0.1543[2]	−3.4441[1]	−3.5358[1]
Sierra Leone	0.3976[2]	−1.5657[2]	−2.3501[2]	0.3002[2]	−1.9091[2]	−2.6355[2]	0.2008[2]	−3.2376[1]	−3.3123[1]
Senegal	0.7078[3]	−1.0306[3]	−6.1205[0]	0.4334[2]	−2.0313[2]	−6.1411[0]	0.0830[1]	−5.3179[0]	−5.5103[0]
South Africa	0.9217[3]	−2.1540[2]	−6.4079[0]	0.9368[3]	−1.5133[3]	−8.3558[0]	0.5516[4]	−4.0968[1]	−4.2192[1]
Sudan	0.2813[2]	−2.0396[2]	−2.3404[2]	0.5028[2]	−1.2508[2]	−2.3882[2]	−0.5557[3]	−0.9761[3]	−6.9848[0]
Tanzania	0.2266[2]	−1.7813[2]	−6.7236[0]	0.4748[2]	−1.4784[2]	−6.4684[0]	−0.2570[1]	−4.5037[1]	−4.4851[1]
Tunisia	1.1141[3]	−0.6051[3]	−4.5628[1]	1.0992[3]	−0.9542[3]	−3.9033[1]	−0.3608[1]	−6.2147[0]	−6.3774[0]
Uganda	0.2406[2]	−1.6153[2]	−5.3460[0]	0.2176[2]	−1.5610[2]	−6.0091[0]	−0.0973[2]	−8.7951[0]	−8.8230[0]
Zambia	0.1086[2]	−3.6010[1]	−4.7715[1]	0.2810[4]	−5.5308[0]	−6.4403[0]	−0.0471[3]	−4.3075[1]	−4.5314[1]
Zimbabwe	0.1805[2]	−2.5659[2]	−8.0439[0]	0.6485[5]	−5.6556[0]	−7.2592[0]	−0.0185[4]	−9.1363[0]	−9.4686[0]

Note: Significant unit root test t-statistics at 5% level are in bold. In squared brackets are the optimal lag lengths of the augmentation components, selected based on minimum information criteria.

, the results of temperature data stationarity are presented by employing the augmented Dickey–Fuller (ADF, [45]) unit root test for the cases of no deterministic term, an intercept only, and an intercept with a linear trend. The choice of the unit root test is motivated by its design in a linear framework, which mimics the assumed linear specification of climatological time series as in [33] (see Equation (1)). The results in Table 2 show a non-rejection of the unit root null hypothesis when no deterministic term (none) is assumed for maximum, minimum, and range temperature series. By testing with only intercept, very few countries out of the 36 countries showed a rejection of unit root null hypotheses in the case of both maximum and minimum temperatures, while in the case of the temperature range series, the null hypotheses of unit root were rejected in almost all the 36 cases. For the case of an intercept with a time trend specification, the results for the range temperature are similar to those from the intercept only. For intercept with trend, as in maximum and minimum temperatures, more rejections of unit root null were observed compared to that of an intercept-only specification of the test. This mixed decision of the results of the unit root tests for the temperature series may be due to the fact that the unit root test lacks power against trend stationarity and fractional alternatives [46,47,48]. Also, when the persistence is likely to fall in long-range dependence (i.e., $0<d<1$) or long memory range ($0<d<0.5$), ADF-like unit root tests may find it difficult to detect correctly the stationarity/non-stationarity of the series.

This weakness of the unit root test makes fractional integration (fractional unit root) attractive, since the differencing parameter may be a fractional value. Robinson’s [40] test can be seen as an ADF test in a fractional sense, since it allows for testing fractional integration based on no deterministic terms, intercept only, and intercept with the trend. This test is described earlier in Equations (4)–(6). Here, in

Table 3. Results of fractional integration based on linear trend.

Country	Max. Temp (°C)			Min. Temp (°C)			Range (°C)
	$\mathit{d}$	Intercept	Trend	$\mathit{d}$	Intercept	Trend	$\mathit{d}$	Intercept	Trend
Angola	0.31 (0.17, 0.45)	−0.2675 (−2.68)	0.0045 (3.45)	0.37 (0.22, 0.52)	−0.2532 (−2.39)	0.0043 (3.10)	0.11 (−0.03, 0.26)	−0.0131 (−0.61)	0.0002 (0.75)
Benin	0.43 (0.29, 0.58)	−0.1435 (−0.47)	0.0034 (0.84)	0.52 (0.37, 0.67)	−0.4087 (−1.11)	0.0094 (1.97)	0.49 (0.32, 0.66)	0.2755 (0.97)	−0.0057 (−1.54)
Botswana	0.26 (0.11, 0.41)	−0.6811 (−3.61)	0.0115 (4.61)	0.30 (0.15, 0.45)	−0.5774 (−3.66)	0.0096 (4.64)	0.13 (−0.02, 0.28)	−0.1067 (−1.57)	0.0018 (1.90)
Burkina Faso	0.41 (0.25, 0.57)	−0.2738 (−0.88)	0.0059 (1.47)	0.50 (0.34, 0.67)	−0.5762 (−1.41)	0.0125 (2.40)	0.49 (0.34, 0.64)	0.3700 (1.37)	−0.0066 (−1.88)
Cameroon	0.26 (0.11, 0.42)	−0.1617 (−1.48)	0.0030 (2.11)	0.35 (0.23, 0.48)	−0.1904 (−1.36)	0.0039 (2.16)	0.24 (0.09, 0.39)	0.0350 (0.34)	−0.0007 (−0.52)
Central Afr. Rep.	0.40 (0.25, 0.55)	−0.2546 (−1.64)	0.0047 (2.34)	0.41 (0.27, 0.55)	−0.2927 (−1.76)	0.0056 (2.57)	0.25 (0.13, 0.37)	0.0459 (1.54)	−0.0008 (−2.14)
Chad	0.47 (0.34, 0.59)	−0.3542 (−1.43)	0.0069 (2.14)	0.47 (0.34, 0.60)	−0.3864 (−1.61)	0.0075 (2.42)	0.36 (0.22, 0.51)	0.0398 (0.61)	−0.0007 (−0.88)
Congo	0.38 (0.24, 0.52)	−0.2349 (−1.71)	0.0047 (2.64)	0.38 (0.24, 0.53)	−0.2347 (−1.69)	0.0047 (2.62)	0.03 (−0.14, 0.19)	−0.0003 (−1.11)	5.02 × 10−6 (0.47)
Cote d’Ivoire	0.38 (0.24, 0.52)	−0.2606 (−1.49)	0.0050 (2.17)	0.46 (0.31, 0.62)	−0.2986 (−1.32)	0.0063 (2.13)	0.41 (0.26, 0.56)	0.0449 (0.36)	−0.0011 (−0.67)
Egypt	0.36 (0.23, 0.49)	−0.7025 (−2.48)	0.0110 (3.07)	0.33 (0.21, 0.46)	−0.7595 (−2.97)	0.0126 (3.78)	0.28 (0.14, 0.43)	0.0964 (1.57)	−0.0018 (−2.29)
Gabon	0.35 (0.22, 0.48)	−0.2371 (−1.87)	0.0047 (2.86)	0.35 (0.22, 0.48)	−0.2368 (−1.86)	0.0047 (2.89)	0.01 (−0.16, 0.17)	0.0010 (1.24)	−1.61 × 10−5 (−0.89)
Ghana	0.43 (0.28, 0.57)	−0.2533 (−0.10)	0.0051 (1.53)	0.52 (0.36, 0.69)	−0.3394 (−1.00)	0.0082 (1.87)	0.44 (0.29, 0.59)	0.1312 (0.64)	−0.0031 (−1.17)
Guinea	0.48 (0.34, 0.61)	−0.2960 (−1.20)	0.0069 (2.14)	0.43 (0.29, 0.58)	−0.2351 (−1.15)	0.0052 (1.96)	0.50 (0.35, 0.65)	−0.0652 (−0.49)	0.0015 (0.88)
Guinea-Bissau	0.43 (0.29, 0.56)	−0.3678 (−1.56)	0.0080 (2.62)	0.40 (0.27, 0.54)	−0.3134 (−1.48)	0.0068 (2.47)	0.49 (0.32, 0.65)	−0.0597 (−0.44)	0.0012 (0.70)
Kenya	0.51 (0.34, 0.69)	−0.8421 (−2.04)	0.0138 (2.57)	0.46 (0.29, 0.63)	−0.8897 (−2.60)	0.0148 (3.32)	0.01 (−0.15, 0.16)	0.0590 (2.18)	−0.0010 (−2.51)
Lesotho	0.33 (0.18, 0.48)	−1.2242 (−4.65)	0.0204 (5.91)	0.17 (0.01, 0.34)	−0.8300 (−7.89)	0.0133 (9.46)	0.39 (0.26, 0.52)	−0.3765 (−1.35)	0.0076 (2.07)
Liberia	0.46 (0.33, 0.60)	−0.1529 (−0.79)	0.0033 (1.31)	0.47 (0.33, 0.61)	−0.1567 (−0.77)	0.0034 (1.26)	0.52 (0.37, 0.67)	0.0009 (0.02)	−1.9 × 10−6 (−3.4 × 10−3)
Libya	0.30 (0.18, 0.41)	−0.5191 (−3.56)	0.0088 (4.62)	0.31 (0.19, 0.43)	−0.5245 (−3.58)	0.0089 (4.66)	0.29 (0.16, 0.41)	0.0056 (0.18)	−0.0001 (−0.27)
Madagascar	0.50 (0.37, 0.63)	0.2853 (1.04)	−0.0014 (−0.41)	0.50 (0.37, 0.63)	0.2848 (1.04)	−0.0014 (−0.41)	0.09 (−0.05, 0.24)	−0.0007 (−2.13)	1.17 × 10−5 (1.02)
Malawi	0.27 (0.14, 0.40)	−0.3624 (−2.27)	0.0065 (3.10)	0.34 (0.19, 0.49)	−0.3209 (−1.85)	0.0061 (2.74)	0.21 (0.05, 0.36)	−0.0315 (−0.34)	0.0005 (0.37)
Mali	0.34 (0.17, 0.50)	−0.4459 (−2.03)	0.0082 (2.91)	0.44 (0.28, 0.60)	−0.5188 (−1.81)	0.1002 (2.81)	0.47 (0.33, 0.60)	0.1233 (0.84)	−0.0022 (−1.14)
Mauritania	0.24 (0.11, 0.38)	−0.5051 (−3.45)	0.0089 (4.62)	0.37 (0.23, 0.51)	−0.4718 (−2.30)	0.0088 (3.33)	0.54 (0.37, 0.72)	0.0044 (0.02)	0.0001 (0.04)
Morocco	0.31 (0.19, 0.43)	−0.7799 (−3.99)	0.0131 (5.12)	0.33 (0.19, 0.47)	−0.6570 (−3.10)	0.0110 (3.95)	0.32 (0.16, 0.48)	−0.1260 (−1.88)	0.0022 (2.54)
Namibia	0.43 (0.27, 0.59)	−0.3729 (−2.03)	0.0063 (2.62)	0.46 (0.30, 0.62)	−0.3898 (−2.06)	0.0067 (2.72)	0.16 (0.01, 0.31)	0.0302 (0.63)	−0.0005 (−0.82)
Niger	0.38 (0.25, 0.51)	−0.2735 (−0.97)	0.0051 (1.37)	0.40 (0.26, 0.54)	−0.3080 (−1.20)	0.0059 (1.78)	0.47 (0.32, 0.62)	0.0149 (0.06)	−0.0006 (−0.20)
Nigeria	0.34 (0.20, 0.47)	−0.1288 (−0.64)	0.0028 (1.05)	0.44 (0.30, 0.58)	−0.2389 (−0.93)	0.0055 (1.65)	0.23 (0.08, 0.38)	0.1611 (1.47)	−0.0028 (−1.94)
Rwanda	0.56 (0.40, 0.72)	−0.7239 (−2.07)	0.0112 (2.45)	0.43 (0.27, 0.60)	−0.5405 (−2.36)	0.0092 (3.11)	0.49 (0.35, 0.63)	−0.1847 (−0.67)	0.0022 (0.62)
Sierra Leone	0.49 (0.36, 0.63)	−0.2284 (−0.98)	0.0054 (1.76)	0.47 (0.33, 0.60)	−0.1962 (−0.92)	0.0045 (1.61)	0.54 (0.39, 0.68)	−0.0289 (−0.29)	0.0008 (0.60)
Senegal	0.38 (0.24, 0.51)	−0.4027 (−1.73)	0.0084 (2.79)	0.38 (0.24, 0.52)	−0.3206 (−1.48)	0.0068 (2.44)	0.51 (0.34, 0.67)	−0.0793 (−0.50)	0.0016 (0.79)
South Africa	0.37 (0.22, 0.52)	−0.9884 (−3.81)	0.0164 (4.85)	0.17 (0.01, 0.33)	−0.7896 (−8.70)	0.0129 (10.60)	0.34 (0.21, 0.47)	−0.1684 (−0.95)	0.0032 (1.39)
Sudan	0.41 (0.29, 0.54)	−0.5250 (−1.55)	0.0085 (1.92)	0.45 (0.32, 0.57)	−1.0093 (−2.94)	0.0162 (3.65)	0.35 (0.22, 0.48)	0.4540 (4.03)	−0.0075 (−5.12)
Tanzania	0.39 (0.22, 0.56)	−0.6903 (−3.13)	0.0113 (3.94)	0.41 (0.24, 0.57)	−0.6844 (−2.97)	0.0119 (4.01)	0.40 (0.24, 0.56)	−0.0020 (−0.01)	−0.0006 (−0.28)
Tunisia	0.30 (0.17, 0.42)	−1.0054 (−5.14)	0.0170 (6.60)	0.37 (0.24, 0.50)	−0.9363 (−3.78)	0.0162 (5.02)	0.42 (0.27, 0.58)	−0.0873 (−0.50)	0.0010 (0.44)
Uganda	0.58 (0.41, 0.76)	−0.8968 (−1.93)	0.0141 (2.32)	0.48 (0.32, 0.65)	−0.8757 (−2.52)	0.0147 (3.25)	0.48 (0.32, 0.65)	0.0270 (0.34)	−0.0006 (−0.52)
Zambia	0.28 (0.15, 0.41)	−0.4044 (−2.09)	0.0072 (2.86)	0.37 (0.22, 0.52)	−0.2876 (−1.42)	0.0052 (1.97)	0.37 (0.22, 0.52)	−0.0920 (−0.54)	0.0019 (0.83)
Zimbabwe	0.24 (0.11, 0.38)	−0.5374 (−2.75)	0.0094 (3.66)	0.30 (0.14, 0.45)	−0.4260 (−2.30)	0.0076 (3.14)	0.30 (0.14, 0.45)	−0.1163 (−1.24)	0.0020 (1.55)

Note: Significant linear trend coefficients (intercept or trend) at a 5% level one-sided test (t > 1.64) are in bold with t-statistics in parentheses. For fractional d values, standard errors are in parentheses.

, the results are presented for only the case of intercept with trend. Evidence of long memory and long-range dependence, i.e., $0<d<1$, are found in maximum and minimum temperatures, with $d$ less than 0.5 in a number of countries and fairly above 0.5 in others. The highest bound values for $d$ are 0.72 (Rwanda) and 0.76 (Uganda) in the case of maximum temperature, respectively, and these values correspond to $d$ values 0.43 (0.27, 0.60) and 0.48 (0.32, 0.65), respectively, for minimum temperatures. In the maximum temperature, evidence of $d$ fairly above the long memory stationary range (i.e., $d>0.5$) is found in Kenya, Madagascar, Rwanda, and Uganda, while in the case of minimum temperature, we have Benin, Burkina Faso, Ghana, and Madagascar. These results imply that long memory exists generally in maximum and minimum temperature distributions even though the upper bound of the confidence limit shows that some estimates might be in the long-range dependence range, which is still close to 0.5. Differing persistence estimates explain the dynamics of temperature predictions, not in terms of trend often expected in climatological studies, but in terms of the inherent correlations of current observations to past lagged historical values, large enough to compare the present climate with the climate of the same regions over many decades. In that case, using only the linear trend approach such as that employed in [33] could lead to bias due to the ignorance of exploring the (long memory) time series properties of the climatological observations.

Also, the temperature range series, which is the difference between the maximum and minimum temperatures, display long memory as well in a number of countries, but with an upper bound limit above 0.5 in many cases. Table 3 also indicates 29 cases of significant trends in the case of maximum temperatures, and 33 cases for the minimum temperatures, all of which with significant positive coefficients, while only nine countries show significant trends in the range: three with a positive value (Lesotho, Morocco, and Botswana) and five with a negative trend (Sudan, Burkina Faso, Nigeria, Egypt, Kenya, and Central Africa).

For clarity,

Table 4. Summary of Results in Table 3.

Country	Evidence of Significant Trend Increase	Evidence of dRange < min (dMax.Temp, dMin.Temp)
Angola	√	√
Benin	√
Botswana	√	√
Burkina Faso	√
Cameroon	√	√
Central Afr. Rep.	√	√
Chad	√	√
Congo	√	√
Cote d’Ivoire	√
Egypt	√	√
Gabon	√	√
Ghana	√
Guinea	√
Guinea-Bissau	√
Kenya	√	√
Lesotho	√
Liberia
Libya	√	√
Madagascar	√	√
Malawi	√	√
Mali	√
Mauritania	√
Morocco	√
Namibia	√	√
Niger	√
Nigeria	√	√
Rwanda	√
Sierra Leone
Senegal	√
South Africa	√
Sudan	√	√
Tanzania	√
Tunisia	√
Uganda	√	√
Zambia	√
Zimbabwe	√	√

summarizes the results in Table 3 for the cases where the $d$ value for the range series is less than either or both $d$ values for maximum and minimum temperatures. These countries include Angola, Botswana, Central African Republic, Chad, Congo, Egypt, Gabon, Kenya, Libya, Madagascar, Malawi, Namibia, Nigeria, Sudan, Uganda, and Zimbabwe. These are the countries in which maximum and minimum temperatures are likely to have long-run relationships but the high confidence band for the range series poses suspicions, which requires further robust analyses before one concludes the long-run relationship existing between the pair.

The framework of fractional integration employed here also allows us to simultaneously test for positive trends in the series under investigation, as we know that significant positive trends in temperature series suggest an evidence of global warming induced by temperature increases. In Table 3, positive and significant trend coefficients are found in 29 countries for the case of the maximum temperature, and in 33 countries in the case of the minimum temperature. Thus, in Table 4, it is determined that evidence of temperature increase is observed in 34 countries, that is, all except Liberia and Sierra Leone.

In order to further establish the long-run relationship between maximum and minimum temperature series, we carried out homogeneity of fractional integration orders, where we ignore the confidence band since the test is defined in the frequency domain using periodogram bands. The estimation of $d$ parameter is based on Local Whittle (LW) estimators and the significant difference in paired values of $d$ are tested based on the approach described earlier in Equations (7) and (8). Estimates of ${\widehat{T}}_{xy}$ statistics, as given in [30] are presented in

Table 5. Results of homogeneity of paired persistence parameters for maximum and minimum temperatures.

Country	${\mathit{T}}^{0.5}$	${\mathit{T}}^{0.6}$
Angola	0.1315	0.2008
Benin	1.0788	0.3417
Botswana	0.3511	0.2472
Burkina Faso	1.9117	0.7278
Cameroon	0.1519	0.7277
Central Afr. Rep.	0.3209	0.3103
Chad	0.4145	0.4604
Congo	0.0107	0.0224
Cote d’Ivoire	0.7076	0.2825
Egypt	0.2899	0.2687
Gabon	0.0356	0.0143
Ghana	1.1170	0.0722
Guinea	0.1387	0.5569
Guinea-Bissau	0.1917	0.0568
Kenya	0.4196	0.0586
Lesotho	0.7969	0.7003
Liberia	0.0343	0.0833
Libya	0.1445	0.3202
Madagascar	0.0066	0.0013
Malawi	0.0669	0.8570
Mali	1.1013	0.6679
Mauritania	0.5987	0.4710
Morocco	0.7275	0.9893
Namibia	0.1210	0.4668
Niger	0.1434	0.4195
Nigeria	0.5054	0.7256
Rwanda	0.2099	0.6325
Sierra Leone	0.0190	0.3437
Senegal	0.0281	0.2062
South Africa	0.4934	0.6006
Sudan	0.4931	0.3506
Tanzania	0.0358	0.6058
Tunisia	0.9987	0.1570
Uganda	0.3072	0.4192
Zambia	0.0084	0.5026
Zimbabwe	0.0262	0.4947

Recall that the homogeneity of fractional d is normally distributed; therefore, the two-sided test is rejected based on a critical value of 1.96 at a 5% level.

, where none of these estimates are significant at 5% level. Recall that the test is asymptotically normally distributed with 1.96 as its two-sided rejection value, and all these estimates are below the value. Evidence of homogeneity in all the pairs (maximum and minimum temperature pairs) further supports the possibility of a long-run relationship, based on fractional cointegration in the co-movement of maximum and minimum temperatures in the 36 African countries under investigation.

We further extend the analysis by using fractional cointegration, and following now, the two-step approach developed in [49]. Thus, we first conduct the regression of one of the variables (maximum) against the other (minimum). However, instead of using OLS regressions either in the time or in the frequency domain, we follow Nielsen [50] and perform the narrow-band frequency domain least square (NBFDLS) estimation approach, using as bandwidth numbers m = T^0.5 and T^0.6. The estimated regression coefficients are displayed in

Table 6. Estimated regression coefficients for the NBFDLS (narrow-band frequency domain least square).

Country	${\mathit{T}}^{0.5}$	${\mathit{T}}^{0.6}$
Angola	1.0598	1.0343
Benin	0.5121	0.4858
Botswana	1.1830	1.1676
Burkina Faso	0.5179	0.5152
Cameroon	0.5366	0.5421
Central Afr. Rep.	0.8510	0.8574
Chad	0.9659	0.9600
Congo	0.9994	0.9991
Cote d’Ivoire	0.7146	0.7051
Egypt	0.9012	0.9053
Gabon	0.9992	0.9996
Ghana	0.5931	0.5708
Guinea	1.1052	1.0813
Guinea-Bissau	1.0649	1.0491
Kenya	0.9676	0.9627
Lesotho	1.2112	1.2209
Liberia	0.9692	0.9693
Libya	0.9775	0.9809
Madagascar	1.0008	1.0007
Malawi	1.0256	0.9424
Mali	0.7598	0.7629
Mauritania	0.8452	0.8394
Morocco	1.1145	1.0847
Namibia	0.9024	0.9077
Niger	0.8349	0.8087
Nigeria	0.6811	0.6637
Rwanda	1.0121	0.9834
Sierra Leone	1.0469	1.0342
Senegal	1.0694	1.0512
South Africa	1.1596	1.1726
Sudan	0.6717	0.6733
Tanzania	0.9103	0.8871
Tunisia	0.9855	0.9785
Uganda	0.9589	0.9506
Zambia	1.0194	0.9536
Zimbabwe	1.1875	1.1152

. In the second step, we estimated the order of integration in the residuals of the estimated relationships by using Whittle estimates in the frequency domain. Results are reported across

Table 7. Estimates of d in the NBFDLS regression.

Country	m = T0.5	m = T0.6	Evidence of d Smaller than in Individual Series
			m = T0.5	m = T0.6
Angola	0.14 (−0.05, 0.42) +	0.15 (−0.03, 0.43) +	√	√
Benin	0.44 (0.26, 0.75)	0.46 (0.26, 0.75)		√
Botswana	−0.20 (−0.41, 0.11) +	0.11 (−0.16, 0.43) +	√	√
Burkina Faso	0.43 (0.19, 0.88)	0.43 (0.19, 0.88)		√
Cameroon	0.06 (−0.10, 0.31) +	0.06 (−0.12, 0.32) +	√	√
Central Afr. Rep.	0.31 (0.13, 0.57)	0.31 (0.15, 0.57)	√	√
Chad	0.51 (0.30, 0.82)	0.51 (0.30, 0.81)
Congo	0.00 (−0.19, 0.29) +	0.02 (−0.19, 0.28) +	√	√
Cote d’Ivoire	0.48 (0.27, 0.80)	0.47 (0.26, 0.79)
Egypt	0.42 (0.29, 0.61)	0.42 (0.29, 0.58)
Gabon	−0.10 (−0.28, 0.18) +	−0.08 (−0.27, 0.19) +	√	√
Ghana	0.42 (0.14, 0.77)	0.42 (0.12, 0.78)
Guinea	0.64 (0.38, 1.00)	0.63 (0.36, 0.98)
Guinea-Bissau	0.53 (0.20, 0.96)	0.57 (0.30, 0.91)
Kenya	−0.03 (−0.17, 0.23) +	−0.02 (−0.18, 0.23) +	√	√
Lesotho	0.57 (0.41, 0.77)	0.56 (0.41, 0.77)
Liberia	0.72 (0.43, 1.20)	0.72 (0.43, 1.19)
Libya	0.56 (0.35, 0.82)	0.56 (0.35, 0.83)
Madagascar	−0.13 (−0.32, 0.11) +	−0.12 (−0.31, 0.12) +	√	√
Malawi	0.22 (−0.02, 0.57) +	0.27 (0.04, 0.58)	√	√
Mali	0.46 (0.25, 0.82)	0.48 (0.26, 0.83)
Mauritania	0.26 (−0.01, 0.52) +	0.26 (−0.01, 0.62) +		√
Morocco	0.17 (−0.02, 0.46) +	0.22 (0.05, 0.47)	√	√
Namibia	0.20 (−0.03, 0.59) +	0.20 (−0.04, 0.58) +	√	√
Niger	0.51 (0.30, 0.76)	0.50 (0.28, 0.76)
Nigeria	0.24 (0.08, 0.46)	0.25 (0.08, 0.45)	√	√
Rwanda	0.59 (0.40, 0.89)	0.60 (0.39, 0.71)
Sierra Leone	0.68 (0.38, 1.08)	0.69 (0.40, 1.11)
Senegal	0.42 (0.14, 0.77)	0.43 (0.16, 0.77)
South Africa	0.54 (0.37, 0.76)	0.55 (0.38, 0.74)
Sudan	0.61 (0.45, 0.83)	0.61 (0.46, 0.83)
Tanzania	0.36 (0.12, 0.71)	0.35 (0.13, 0.72)	√	√
Tunisia	0.30 (0.15, 0.57)	0.30 (0.15, 0.59)		√
Uganda	0.28 (0.02, 0.62)	0.29 (0.03, 0.62)	√	√
Zambia	0.44 (0.29, 0.66)	0.46 (0.32, 0.65)
Zimbabwe	0.10 (−0.04, 0.31) +	0.14 (0.00, 0.33)	√	√

Note: ⁺ indicates evidence of I(d = 0) in the cointegrating residuals, and these are 11 countries, while evidence of $I(d>0)$ in the cointegrating residuals are 19 less 11 countries.

.

The results are similar in the two cases in relation to the bandwidth numbers. Evidence of I(0) residuals, thus supporting short memory in the long-run equilibrium relationship, is found in the cases of Angola, Botswana, Cameroon, Congo, Gabon, Kenya, Madagascar, Mauritania, Namibia, and Zimbabwe. If m = T^0.5, this hypothesis is also supported by Malawi and Morocco. Thus, for these groups, our results support the hypothesis of cointegration with a rapid reversion of the series to a long-run equilibrium relationship. On the other extreme end, evidence of nonstationary I(1) is found for Liberia and Sierra Leone for the two bandwidth numbers, and also for Ghana, if m = T^0.5. In all the other countries, the estimate of the differencing parameter is in the interval (0, 1), and evidence of cointegration (in the sense that the order of integration of the residuals is lower than the minimum of the two individual series) is found in the cases of Angola, Botswana, Cameroon, Central African Republic, Congo, Gabon, Kenya, Madagascar, Malawi, Morocco, Namibia, Nigeria, Tanzania, Uganda and Zimbabwe for the two bandwidth numbers, but also for Benin, Burkina Faso, Mauritania, and Tunisia if m = T^0.6. Thus, the countries with no evidence of cointegration are Chad, Cote d’Ivoire, Egypt, Ghana, Guinea, Guinea Bissau, Lesotho, Liberia, Libya, Mali, Niger, Rwanda, Sierra Leone, Senegal, South Africa, Sudan, and Zambia. Among the 19 countries listed in Table 7 with evidence of cointegration, 11 countries display short memory equilibrium relationships between their maximum and minimum temperatures, i.e., $I\left(0\right)$ evidence. These countries include Angola, Botswana, Cameroon, Congo, Gabon, Kenya, Madagascar, Mauritania, Morocco, Namibia, and Zimbabwe, while the remaining eight countries indicate long memory cointegration, i.e., $I(d>0)$.

5. Conclusions

This paper investigates persistence and linear trends in the maximum and minimum annual average temperatures in 36 African countries. The statistical distribution of maximum and minimum temperature series, with the diurnal range in the climatological study as they act as an important factor driving global warming, have gingered our interest. Historical datasets from 1901 to 2021 are analyzed with the annual range series. The results first establish long-term memory in maximum and minimum temperatures over the historic years, implying that the temperature series is often strongly correlated with its past lag values. This is a persistence property, often measured as fractional integration. It assists in uncovering the correlation property of this series, classified as long memory, mean-reverting and non-mean-reverting, and these have implications for erratic and predicted climatic series. Thus, long-term memory observed in this paper further indicates the possibility of temperatures in Africa being predicted for future values. The trend analysis shows evidence of trend shifts in the plots and these are revealed further in the positive significant trend coefficients with an insignificant positive trend in the range series. Note that the trend analysis allows one in making future predictions, but the approach used in this paper checking future predictions based on fractional integration is relatively novel and hardly adopted in climatological studies. Few papers along this line are those of [23] and, [6,36,38], among others.

Our results support the hypothesis of fractional cointegration. This implies that both maximum and minimum temperatures follow a long-run equilibrium relationship with shocks in the range displaying transitory effects and not producing permanent discrepancies between the maximum and minimum temperatures. Also, 17 countries among the 36 African countries are at a very high risk of climate change due to the absence of long-term co-movement in the maximum and minimum temperatures in those countries, compared to other countries with mild effect. Although most African countries are prone to the effect of climatic change as the econometric findings reveal, some regions of the continents are fairer than others.

Findings in this paper are of relevance for climatological studies in a number of ways. It allows for the proper understanding of historical temperature patterns in Africa, which is crucial for predicting and mitigating the impacts of climate change. Thus, it helps in studying the large-scale climate patterns that influence Africa’s climate in its different regions (see [51]). Understanding these patterns and their potential impacts on different parts of Africa is essential for developing effective adaptation and mitigation strategies. Additionally, research on large-scale climate patterns in Africa can contribute to global climate models, improving the accuracy of climate projections and enhancing our understanding of the global climate system.

As a final issue, we should note that the last century was a particularly convulsive era for humankind; due to this, issues such as heterogeneity (changes in the variance) and stability (structural breaks) in the data should also be taken into account, noting that some authors have found that long memory and nonlinearities and breaks are issues which are intimately related ([52,53]; etc.). Thus, nonlinear deterministic trend structures, based, for instance, on Chebyshev polynomial in time [54], Fourier functions [55], or neural networks [56] could be examined in these data, while still under the assumption of long-range dependence. Work in this line is now in progress.