Future Climate Prediction Based on Support Vector Machine Optimization in Tianjin, China
Abstract
1. Introduction
2. Materials and Methods
2.1. Description of the Study Area
2.2. Meteorological Data
2.3. Methods
2.3.1. LARS-WG Model Approach
2.3.2. SVM
2.4. Statistical Evaluation Criterions
3. Results and Discussions
3.1. LARS-WG
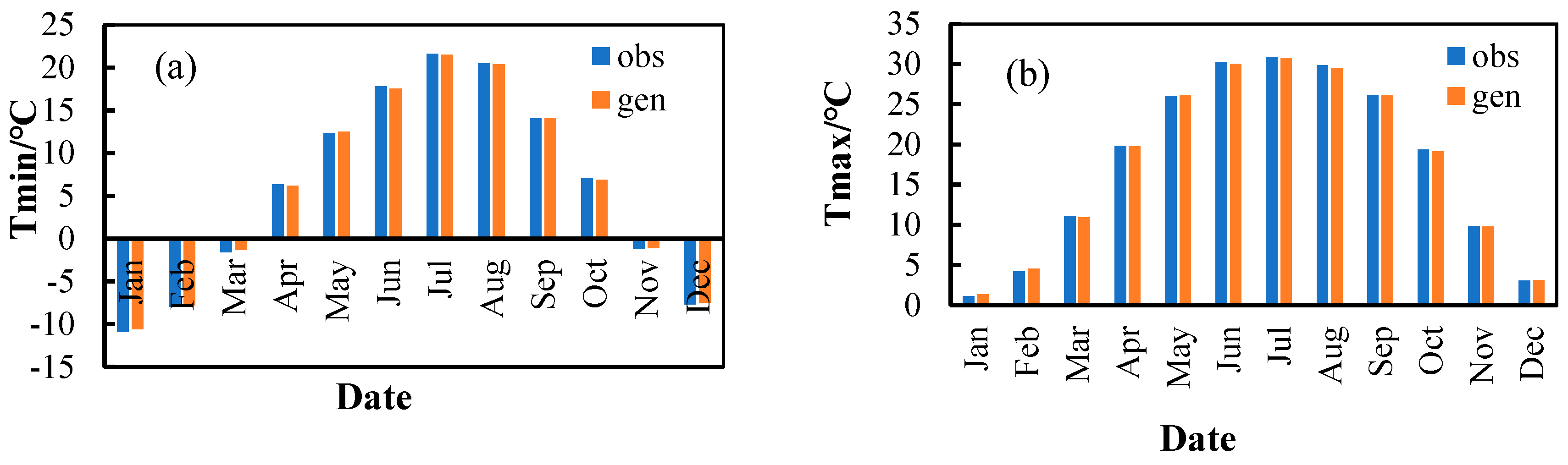
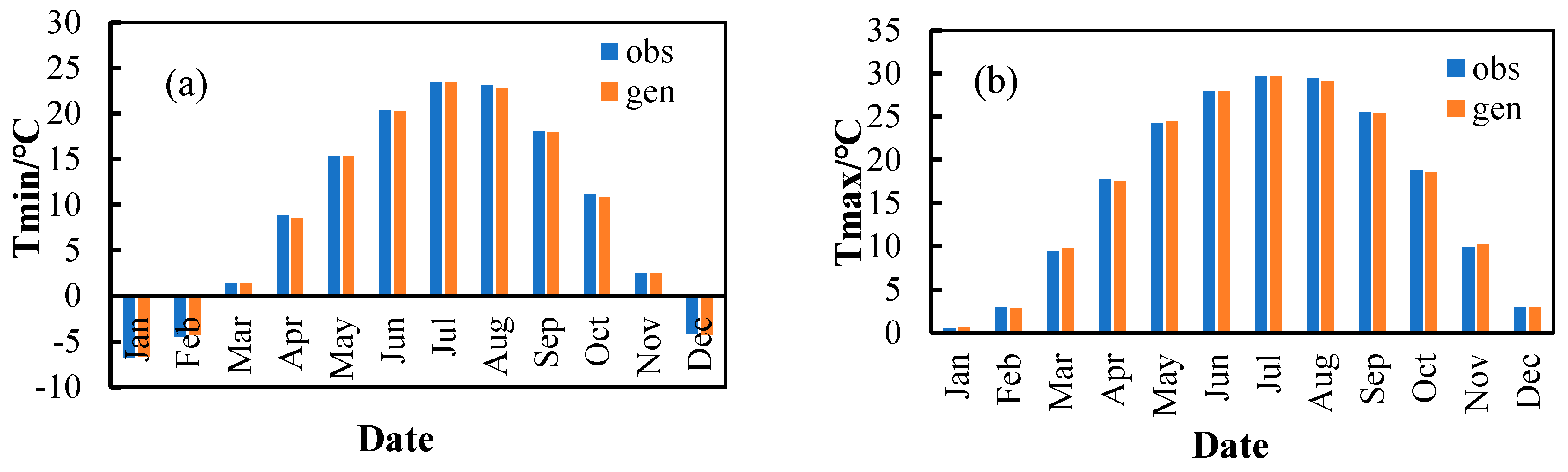
3.1.1. Baseline Data Comparison
3.1.2. Future Climate Projections
3.2. SVM
3.2.1. SVM Operation
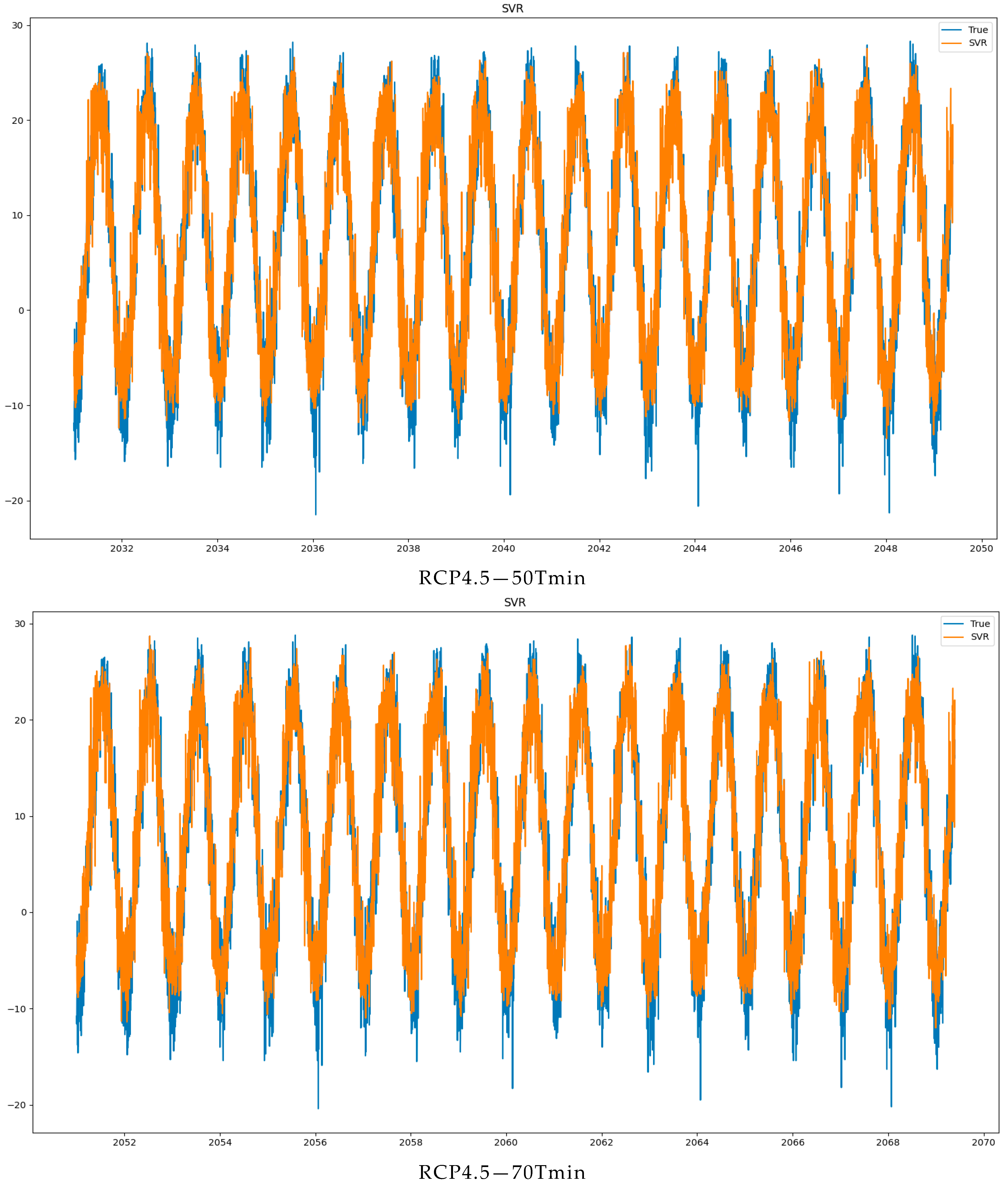
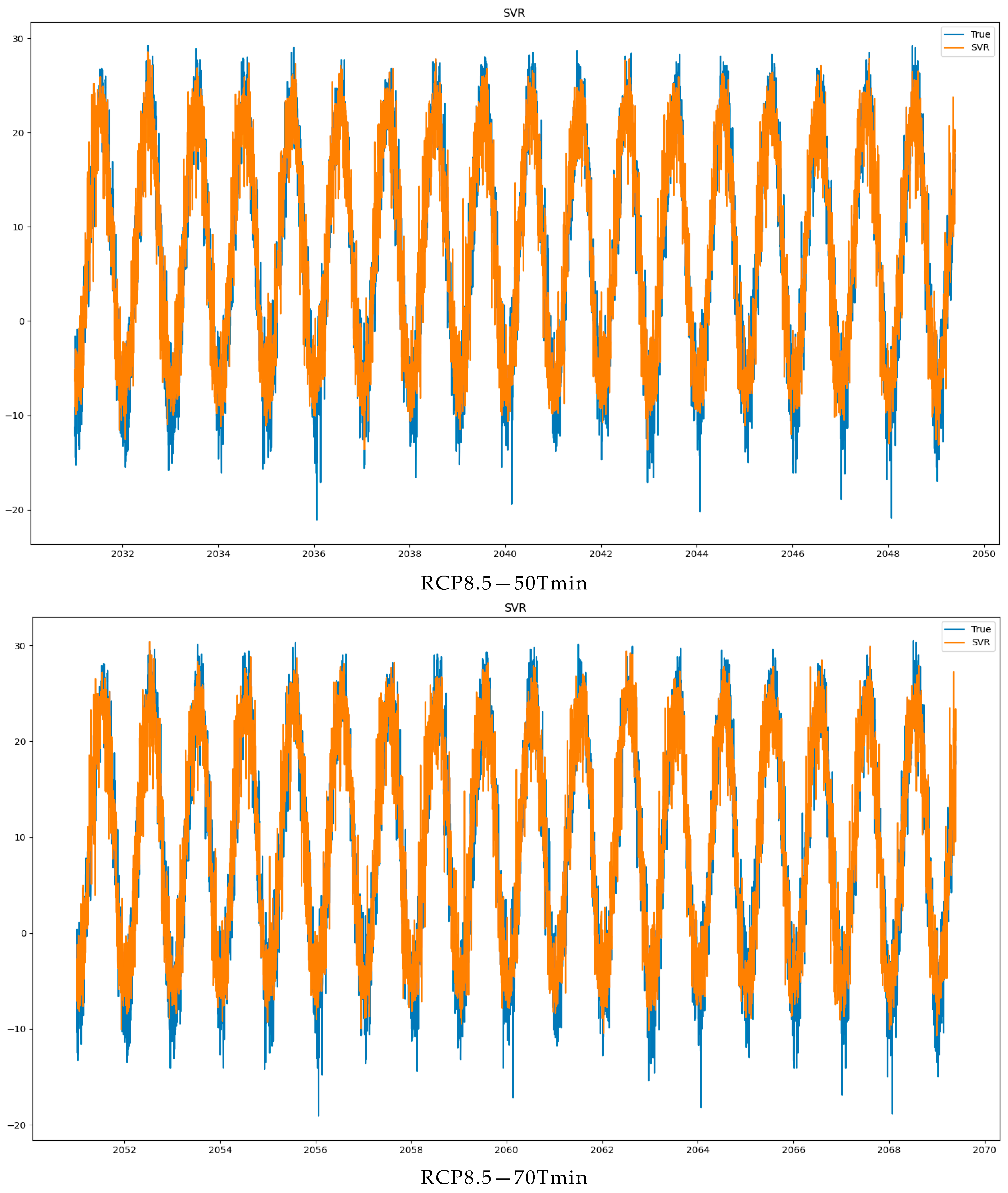
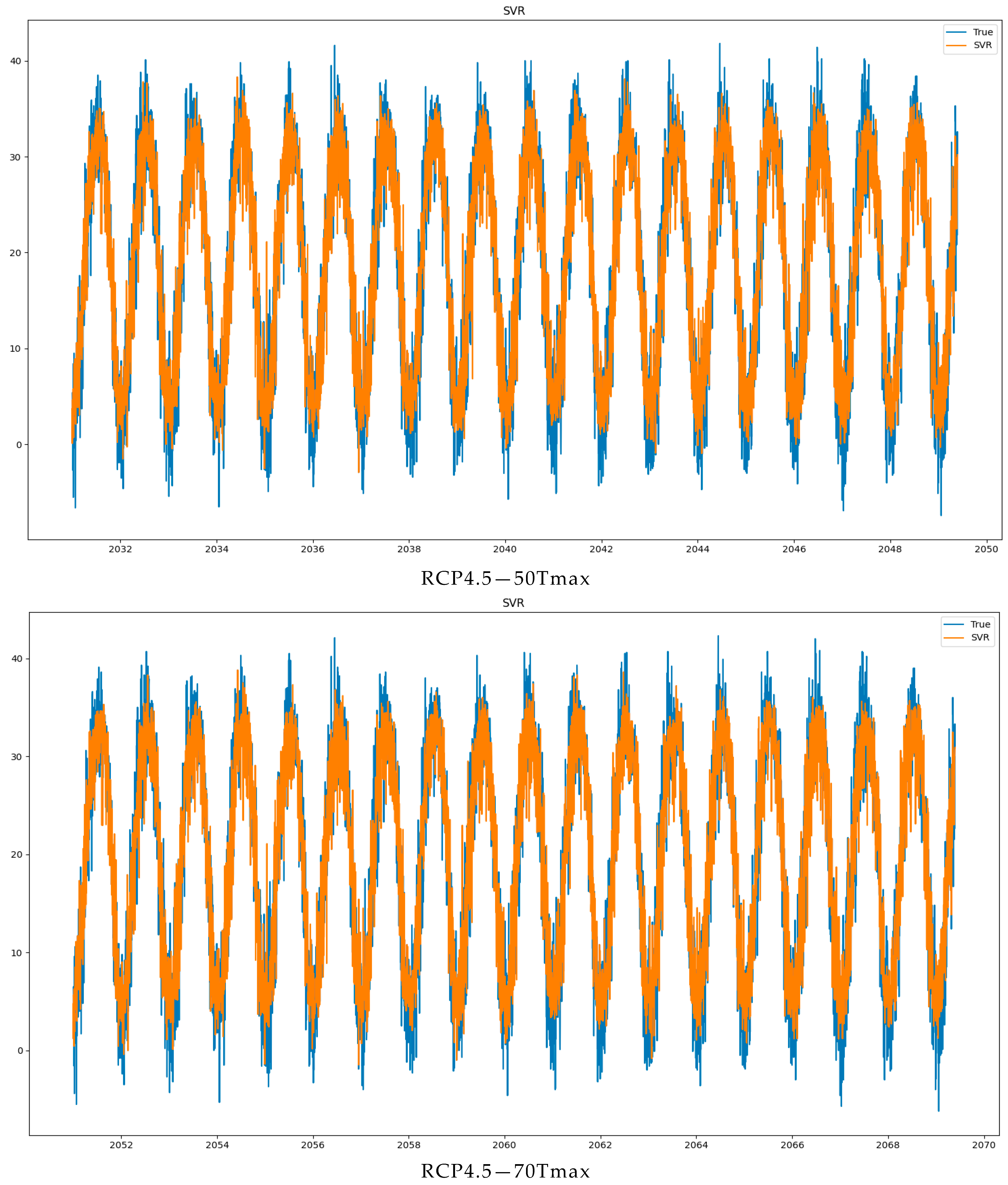
3.2.2. Future Climate Optimization Based on SVM
4. Limitations and Outlooks
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sun, W.; Li, Q.; Huang, B.; Cheng, J.; Song, Z.; Li, H.; Dong, W.; Zhai, P.; Jones, P. The Assessment of Global Surface Temperature Change from 1850s: The C-LSAT 2.0 Ensemble and the CMST-Interim Datasets. Adv. Atmos. Sci. 2021, 38, 875–888. [Google Scholar] [CrossRef]
- IPCC. Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Intergovernmental panel on climate Change, working group I contribution to the IPCC fifth assessment report (AR5); Stocker, T.F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., Eds.; Cambridge University Press: New York, NY, USA, 2013; p. 1535. [Google Scholar]
- Anderson, T.R.; Hawkins, E.; Jones, P.D. CO2, the greenhouse effect and global warming: From the pioneering work of Arrhenius and Callendar to today’s earth system models. Endeavour 2016, 40, 178–187. [Google Scholar] [CrossRef] [PubMed]
- Saddique, N.; Bernhofer, C.; Kronenberg, R.; Usman, M. Downscaling of CMIP5 models output by using statistical models in a data scarce mountain environment (Mangla Dam Watershed), Northern Pakistan. Asia-Pac. J. Atmos. Sci. 2019, 55, 719–735. [Google Scholar] [CrossRef]
- Wang, J.; Liu, Y.; Ding, Y.; Wu, P.; Zhu, Z.; Xu, Y.; Qi, L. Impacts of climate anomalies on the interannual and interdecadal variability of autumn and winter haze in North China: A review. Int. J. Climatol. 2020, 40, 4309–4325. [Google Scholar] [CrossRef]
- Semenov, M.; Shewry, P. Modelling predicts that heat stress and not drought will limit wheat yield in Europe. Nat. Preced. 2010. [Google Scholar] [CrossRef]
- Zhang, J.; Yang, X.H.; Li, Y.Q. A refined rank set pair analysis model based on wavelet analysis for predicting temperature series. Int. J. Numer. Methods Heat Fluid Flow 2015, 25, 974–985. [Google Scholar] [CrossRef]
- Taylor, K.E.; Stouffer, R.J.; Meehl, G.A. An overview of CMIP5 and the experiment design. Bull. Am. Meteorol. Soc. 2012, 93, 485–498. [Google Scholar] [CrossRef]
- Wilks, D.S. Multisite downscaling of daily precipitation with a stochastic weather generator. Clim. Res. 1999, 11, 125–136. [Google Scholar] [CrossRef]
- Semenov, M.A.; Brooks, R.J.; Barrow, E.M.; Richardson, C.W. Comparison of the WGEN and LARS-WG stochastic weather generators for diverse climates. Clim. Res. 1998, 10, 95–107. [Google Scholar] [CrossRef]
- Charles, B.C.; Elijah, P.; Vernon, R.N.C. Climate change impact on maize (Zea mays L.) yield using crop simulation and statistical downscaling models: A review. Sci. Res. Essays 2017, 12, 167–187. [Google Scholar] [CrossRef]
- Moghadam, S.H.; Ashofteh, P.S.; Loáiciga, H.A. Investigating the performance of data mining, lumped, and distributed models in runoff projected under climate change. J. Hydrol. 2023, 617, 128992. [Google Scholar] [CrossRef]
- Ahmadi, M.; Etedali, H.R.; Elbeltagi, A. Evaluation of the effect of climate change on maize water footprint under RCPs scenarios in Qazvin plain, Iran. Agric. Water Manag. 2021, 254, 106969. [Google Scholar] [CrossRef]
- Seifi, A.J.; Baghanam, A.H.; Asadi, E.; Hassanzadeh, Y.; Sheikhbabaei, A. Assessing the impact of climate change by using LARS-WG, Case Study Zarineh-rud River Basin. In Proceedings of the 3rd Iranian National Conference on Hydrology, Tabriz, Iran, 17–19 September 2019. [Google Scholar]
- Dixit, P.N.; Telleria, R. Advancing the climate data driven crop-modeling studies in the dry areas of Northern Syria and Lebanon: An important first step for assessing impact of future climate. Sci. Total Environ. 2015, 511, 562–575. [Google Scholar] [CrossRef]
- Wang, H.; Wang, L.; Yan, G.; Bai, H.; Zhao, Y.; Ju, M.; Chen, L. Assessment and Prediction of Extreme Temperature Indices in the North China Plain by CMIP6 Climate Model. Appl. Sci. 2022, 12, 7201. [Google Scholar] [CrossRef]
- Gos, M.; Krzyszczak, J.; Baranowski, P.; Murat, M.; Malinowska, I. Combined TBATS and SVM model of minimum and maximum air temperatures applied to wheat yield prediction at different locations in Europe. Agric. For. Meteorol. 2020, 281, 107827. [Google Scholar] [CrossRef]
- Alam, M.S.; Barbour, S.L.; Huang, M.; Li, Y. Using statistical and dynamical downscaling to assess climate change impacts on mine reclamation cover water balances. Mine Water Environ. 2020, 39, 699–715. [Google Scholar] [CrossRef]
- Šípek, V.; Daňhelka, J. Modification of input datasets for the ensemble streamflow prediction based on large-scale climatic indices and weather generator. J. Hydrol. 2015, 528, 720–733. [Google Scholar] [CrossRef]
- Ripendra, A.; Haimanote, B.; Ali, F. Analysis of potential future climate and climate extremes in the brazos headwaters basin, texas. Water 2016, 8, 603. [Google Scholar]
- Roshani, A.; Hamidi, M. Groundwater level fluctuations in coastal aquifer: Using artificial neural networks to predict the impacts of climatical cmip6 scenarios. Water Resour. Manag. 2022, 36, 3981–4001. [Google Scholar] [CrossRef]
- Safavi, H.R.; Sajjadi, S.M.; Raghibi, V. Assessment of climate change impacts on climate variables using probabilistic ensemble modeling and trend analysis. Theor. Appl. Climatol. 2017, 130, 635–653. [Google Scholar] [CrossRef]
- Yoosefdoost, I.; Khasheisiuki, A.; Tabari, H.; Mohammadrezapour, O.; Tsakiris, G. Runoff simulation under future climate change conditions: Performance comparison of data-mining algorithms and conceptual models. Water Resour. Manag. 2022, 36, 1191–1215. [Google Scholar] [CrossRef]
- Cortes, C. Support-Vector Networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Kim, Y.; Hong, S. Very Short-term prediction of weather radar-based rainfall distribution and intensity over the Korean Peninsula using convolutional long short-term memory network. Asia-Pac. J. Atmos. Sci. 2022, 58, 489–506. [Google Scholar] [CrossRef]
- Smith, D.M.; Scaife, A.A.; Hawkins, E.; Bilbao, R.; Boer, G.J.; Caian, M.; Yeager, S. Predicted chance that global warming will temporarily exceed 1.5 °C. Geo. Res. Let. 2018, 45, 11–895. [Google Scholar] [CrossRef]
- Tong, S.; Ebi, K. Preventing and mitigating health risks of climate change. Environ. Res. 2019, 174, 9–13. [Google Scholar] [CrossRef]
- Entao, Y. A warmer, wetter and less windy China in the twenty-first century as projected by a nested high-resolution simulation using the Weather Research and Forecasting (WRF) Model. Asia-Pac. J. Atmos. Sci. 2019, 55, 53–74. [Google Scholar] [CrossRef]


| Station | Lat. | Long. | Elev. (m) | Tmax (°C) | Tmin (°C) | P. (mm/year) |
|---|---|---|---|---|---|---|
| Baodi54525 | 39.73 | 117.28 | 4.7 | 40.8 | −27.4 | 672.0 |
| Tianjin54527 | 38.59 | 117.43 | 5.6 | 40.5 | −22.9 | 635.72 |
| Tanggu54623 | 39.06 | 117.10 | 3.3 | 40.9 | −17.1 | 719.51 |
| GCM | Development Institute | Country | RCP |
|---|---|---|---|
| ACCESS1-3 | European Organization for the Exploitation of Meteorological Satellites | European | 2.6, 4.5, 8.5 |
| BCC-CSM1-1 | Beijing Climate Center | China | 4.5, 8.5 |
| CanESM2 | Canadian Centre for Climate Modelling and Analysis | Canada | 2.6, 4.5, 8.5 |
| CMCC-CM | China Meteorological Administration | China | 4.5, 8.5 |
| CNRM-CM5 | National Meteorological Research Centre and European Centre for Research and Advanced Training in Scientific Computing | France | 4.5, 8.5 |
| CSIRO-MK36 | Commonwealth Scientific and Industrial Research Organization | Australia | 2.6, 4.5, 8.5 |
| EC-EARTH | European Commission—Joint Research Centre | European | 4.5, 8.5 |
| Had-GEM2-ES | Hadley Centre Global Environment | England | 2.6, 4.5, 8.5 |
| KS-Test for Daily Tmin Distributions | Effective N | KS Statistic | p-Value | KS-Test for Daily Tmax Distributions | Effective N | KS Statistic | p-Value |
|---|---|---|---|---|---|---|---|
| J | 11.5 | 0 | 1 | J | 11.5 | 0.052 | 1 |
| F | 11.5 | 0.053 | 1 | F | 11.5 | 0.052 | 1 |
| M | 11.5 | 0 | 1 | M | 11.5 | 0.053 | 1 |
| A | 11.5 | 0.053 | 1 | A | 11.5 | 0.053 | 1 |
| M | 11.5 | 0.053 | 1 | M | 11.5 | 0.053 | 1 |
| J | 11.5 | 0.053 | 1 | J | 11.5 | 0.053 | 1 |
| J | 11.5 | 0.053 | 1 | J | 11.5 | 0.053 | 1 |
| A | 11.5 | 0.053 | 1 | A | 11.5 | 0.106 | 0.999 |
| S | 11.5 | 0.053 | 1 | S | 11.5 | 0.053 | 1 |
| O | 11.5 | 0.053 | 1 | O | 11.5 | 0.053 | 1 |
| N | 11.5 | 0.052 | 1 | N | 11.5 | 0.053 | 1 |
| D | 11.5 | 0.033 | 1 | D | 11.5 | 0.053 | 1 |
| KS-Test for Daily Tmin Distributions | Effective N | KS Statistic | p-Value | KS-Test for Daily Tmax Distributions | Effective N | KS Statistic | p-Value |
|---|---|---|---|---|---|---|---|
| J | 11.5 | 0.053 | 1 | J | 11.5 | 0.053 | 1 |
| F | 11.5 | 0.053 | 1 | F | 11.5 | 0.053 | 1 |
| M | 11.5 | 0.053 | 1 | M | 11.5 | 0.053 | 1 |
| A | 11.5 | 0.053 | 1 | A | 11.5 | 0.053 | 1 |
| M | 11.5 | 0.053 | 1 | M | 11.5 | 0.053 | 1 |
| J | 11.5 | 0.053 | 1 | J | 11.5 | 0.053 | 1 |
| J | 11.5 | 0.053 | 1 | J | 11.5 | 0.053 | 1 |
| A | 11.5 | 0.106 | 0.999 | A | 11.5 | 0.106 | 0.999 |
| S | 11.5 | 0.053 | 1 | S | 11.5 | 0.053 | 1 |
| O | 11.5 | 0.053 | 1 | O | 11.5 | 0.053 | 1 |
| N | 11.5 | 0.053 | 1 | N | 11.5 | 0.053 | 1 |
| D | 11.5 | 0.053 | 1 | D | 11.5 | 0.053 | 1 |
| KS-Test for Daily Tmin Distributions | Effective N | KS Statistic | p-Value | KS-Test for Daily Tmax Distributions | Effective N | KS Statistic | p-Value |
|---|---|---|---|---|---|---|---|
| J | 11.5 | 0.033 | 1 | J | 11.5 | 0.053 | 1 |
| F | 11.5 | 0.053 | 1 | F | 11.5 | 0.053 | 1 |
| M | 11.5 | 0.053 | 1 | M | 11.5 | 0 | 1 |
| A | 11.5 | 0.053 | 1 | A | 11.5 | 0.053 | 1 |
| M | 11.5 | 0.052 | 1 | M | 11.5 | 0.052 | 1 |
| J | 11.5 | 0.106 | 0.999 | J | 11.5 | 0.053 | 1 |
| J | 11.5 | 0.053 | 1 | J | 11.5 | 0.053 | 1 |
| A | 11.5 | 0.106 | 0.999 | A | 11.5 | 0.106 | 0.999 |
| S | 11.5 | 0.053 | 1 | S | 11.5 | 0.105 | 0.999 |
| O | 11.5 | 0.053 | 1 | O | 11.5 | 0.053 | 1 |
| N | 11.5 | 0 | 1 | N | 11.5 | 0.053 | 1 |
| D | 11.5 | 0.01 | 1 | D | 11.5 | 0.053 | 1 |
| GCM | RCP | Baodi | Tianjin | Tanggu | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Tmax | Tmin | Tmax | Tmin | Tmax | Tmin | ||||||||
| RMSE | R2 | RMSE | R2 | RMSE | R2 | RMSE | R2 | RMSE | R2 | RMSE | R2 | ||
| ACCESS1-3 | RCP4.5 | 5.19 | 0.80 | 4.39 | 0.86 | 5.24 | 0.79 | 4.01 | 0.87 | 5.02 | 0.80 | 4.07 | 0.86 |
| RCP8.5 | 5.20 | 0.80 | 4.41 | 0.86 | 5.26 | 0.79 | 4.02 | 0.87 | 5.03 | 0.80 | 4.09 | 0.86 | |
| BCC-CSM1-1 | RCP4.5 | 5.27 | 0.79 | 4.45 | 0.85 | 5.30 | 0.79 | 4.08 | 0.87 | 5.09 | 0.80 | 4.11 | 0.86 |
| RCP8.5 | 5.26 | 0.79 | 4.41 | 0.85 | 5.28 | 0.79 | 4.08 | 0.87 | 5.04 | 0.80 | 4.09 | 0.86 | |
| CanESM2 | RCP4.5 | 5.30 | 0.79 | 4.49 | 0.85 | 5.32 | 0.78 | 4.10 | 0.87 | 5.12 | 0.79 | 4.17 | 0.86 |
| RCP8.5 | 5.26 | 0.79 | 4.40 | 0.85 | 5.27 | 0.79 | 4.08 | 0.87 | 5.05 | 0.80 | 4.11 | 0.86 | |
| CMCC-CM | RCP4.5 | 5.27 | 0.79 | 4.43 | 0.85 | 5.29 | 0.79 | 4.09 | 0.87 | 5.05 | 0.80 | 4.10 | 0.86 |
| RCP8.5 | 5.18 | 0.80 | 4.39 | 0.85 | 5.22 | 0.79 | 4.07 | 0.87 | 5.00 | 0.80 | 4.07 | 0.86 | |
| CNRM-CM5 | RCP4.5 | 5.25 | 0.79 | 4.48 | 0.85 | 5.29 | 0.79 | 4.06 | 0.87 | 5.10 | 0.80 | 4.13 | 0.86 |
| RCP8.5 | 5.22 | 0.79 | 4.44 | 0.85 | 5.26 | 0.79 | 4.05 | 0.87 | 5.05 | 0.80 | 4.10 | 0.86 | |
| CSIRO-MK36 | RCP4.5 | 5.22 | 0.80 | 4.44 | 0.85 | 5.26 | 0.79 | 4.04 | 0.87 | 5.03 | 0.80 | 4.07 | 0.86 |
| RCP8.5 | 5.21 | 0.80 | 4.40 | 0.84 | 5.27 | 0.79 | 4.05 | 0.87 | 5.05 | 0.80 | 4.07 | 0.86 | |
| EC-EARTH | RCP4.5 | 5.23 | 0.80 | 4.45 | 0.85 | 5.27 | 0.79 | 4.05 | 0.87 | 5.07 | 0.80 | 4.11 | 0.86 |
| RCP8.5 | 5.21 | 0.80 | 4.41 | 0.86 | 5.25 | 0.79 | 4.04 | 0.87 | 5.03 | 0.80 | 4.08 | 0.86 | |
| Had GEM2-ES | RCP4.5 | 5.21 | 0.80 | 4.41 | 0.86 | 5.22 | 0.79 | 4.08 | 0.87 | 4.98 | 0.80 | 4.06 | 0.86 |
| RCP8.5 | 5.21 | 0.80 | 4.41 | 0.86 | 5.22 | 0.79 | 4.12 | 0.87 | 5.01 | 0.80 | 4.08 | 0.86 | |
| Jan | Feb | Mar | Apr | May | Jun | Jul | Aug | Sep | Oct | Nov | Dec | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1-RCP45-50 | −9.3 | −6 | 0.5 | 7.4 | 13.9 | 19 | 22.9 | 21.9 | 15.7 | 8.1 | −0.13 | −6.4 |
| 1-RCP45-70 | −8.2 | −4.9 | 1.6 | 8.4 | 14.7 | 19.6 | 23.5 | 22.6 | 16.4 | 8.8 | 0.77 | −5.3 |
| 1-RCP85-50 | −8.9 | −5.9 | 0.6 | 7.6 | 14.3 | 19.8 | 23.9 | 22.6 | 16.1 | 8.4 | 0.35 | −5.7 |
| 1-RCP85-70 | −6.9 | −3.8 | 2.6 | 9.5 | 16.2 | 21.3 | 25.2 | 24 | 17.8 | 10.3 | 2.08 | −4 |
| 2-RCP45-50 | −8.5 | −6.1 | 0.7 | 7.8 | 14 | 19 | 23.1 | 22.3 | 16.1 | 8.6 | 0.49 | −5.2 |
| 2-RCP45-70 | −7.7 | −5.3 | 1.3 | 8.5 | 15.1 | 20.4 | 24.6 | 23.6 | 17.1 | 9.5 | 1.46 | −4.4 |
| 2-RCP85-50 | −8.5 | −5.7 | 1 | 8 | 14.3 | 19.5 | 23.6 | 22.5 | 16.2 | 8.6 | 0.56 | −5.4 |
| 2-RCP85-70 | −6.9 | −4.4 | 2 | 9 | 15.5 | 20.9 | 25.2 | 24.4 | 18 | 10.3 | 2 | −3.8 |
| 3-RCP45-50 | −9.7 | −6.7 | 0.03 | 7.1 | 13.7 | 18.7 | 22.5 | 21.5 | 15.4 | 7.9 | 0.02 | −6.2 |
| 3-RCP45-70 | −9.2 | −6.2 | 0.4 | 7.7 | 14.2 | 19.1 | 22.9 | 22.2 | 16.1 | 8.6 | 0.55 | −5.8 |
| 3-RCP85-50 | −9.5 | −6.8 | 0.04 | 7.6 | 14.4 | 19.3 | 22.9 | 21.9 | 15.9 | 8.5 | 0.49 | −5.9 |
| 3-RCP85-70 | −8.3 | −5.6 | 1.18 | 8.6 | 15.2 | 20.2 | 24.2 | 23.4 | 17.3 | 9.8 | 1.7 | −4.7 |
| 4-RCP45-50 | −8.2 | −5.6 | 0.84 | 8.3 | 14.9 | 19.8 | 23.5 | 22.3 | 16.3 | 9.1 | 1.22 | −5.1 |
| 4-RCP45-70 | −7.4 | −4.3 | 1.86 | 9.1 | 15.9 | 20.8 | 24.2 | 23.1 | 17.2 | 10 | 1.84 | −4.8 |
| 4-RCP85-50 | −8.1 | −5.3 | 1.56 | 8.8 | 15.1 | 20 | 23.8 | 22.9 | 16.8 | 9.4 | 1.44 | −4.7 |
| 4-RCP85-70 | −5.4 | −2.4 | 4.1 | 10.8 | 16.8 | 21.5 | 25.2 | 24.2 | 18.4 | 11.2 | 3.33 | −2.4 |
| Jan | Feb | Mar | Apr | May | Jun | Jul | Aug | Sep | Oct | Nov | Dec | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1-RCP45-50 | 2.8 | 6.5 | 12.7 | 20.7 | 27.4 | 31.6 | 32.4 | 31 | 27.4 | 20.1 | 10.9 | 4.3 |
| 1-RCP45-70 | 3.9 | 7.6 | 13.8 | 21.8 | 28.1 | 32.2 | 33 | 31.7 | 28.1 | 20.8 | 11.8 | 5.4 |
| 1-RCP85-50 | 3.2 | 6.6 | 12.8 | 21 | 27.7 | 32.4 | 33.4 | 31.6 | 27.8 | 20.5 | 11.3 | 5 |
| 1-RCP85-70 | 5.2 | 8.7 | 14.8 | 22.9 | 29.6 | 34 | 34.7 | 33 | 29.6 | 22.4 | 13.1 | 6.6 |
| 2-RCP45-50 | 3.6 | 6.3 | 12.8 | 21.3 | 27.3 | 31.2 | 32.5 | 31.6 | 28.3 | 21.4 | 12.5 | 6 |
| 2-RCP45-70 | 4 | 6.7 | 13.4 | 22.3 | 28.7 | 33.1 | 34.7 | 33.4 | 29.6 | 22.9 | 13.9 | 6.8 |
| 2-RCP85-50 | 3.7 | 6.7 | 13 | 21.1 | 27.7 | 32 | 32.9 | 31.3 | 27.9 | 21.2 | 12.6 | 6 |
| 2-RCP85-70 | 4.9 | 7.7 | 14 | 22.4 | 28.8 | 33.2 | 34.9 | 34 | 30.6 | 23.6 | 14.4 | 7.4 |
| 3-RCP45-50 | 2.4 | 5.8 | 12.2 | 20.5 | 27.1 | 31.3 | 32 | 30.5 | 27.1 | 20 | 11 | 4.5 |
| 3-RCP45-70 | 3 | 6.2 | 12.6 | 21.1 | 27.7 | 31.6 | 32.5 | 31.2 | 27.8 | 20.7 | 11.6 | 4.9 |
| 3-RCP85-50 | 2.7 | 5.7 | 12.2 | 21 | 27.9 | 31.8 | 32.4 | 30.9 | 27.6 | 20.6 | 11.5 | 4.8 |
| 3-RCP85-70 | 3.9 | 6.9 | 13.3 | 22 | 28.6 | 32.8 | 33.7 | 32.4 | 29 | 21.9 | 12.7 | 6 |
| 4-RCP45-50 | 2.7 | 6.2 | 13.1 | 22.4 | 28.7 | 32.5 | 33.2 | 32.3 | 28.5 | 20.9 | 11.4 | 5 |
| 4-RCP45-70 | 4.7 | 8.7 | 14.7 | 23.3 | 29.9 | 33.6 | 33.5 | 32.4 | 29 | 21.5 | 12.3 | 6.3 |
| 4-RCP85-50 | 3.1 | 6.6 | 13.6 | 22.3 | 28.9 | 32.8 | 33.7 | 32.4 | 28.8 | 21.3 | 12 | 5.3 |
| 4-RCP85-70 | 5.7 | 9.2 | 16 | 23.9 | 30 | 34.1 | 34.9 | 33.6 | 30.4 | 22.8 | 13.4 | 7.4 |
| Jan | Feb | Mar | Apr | May | Jun | Jul | Aug | Sep | Oct | Nov | Dec | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1-RCP45-50 | −6.3 | −3.45 | 2.63 | 9.77 | 16.23 | 21 | 24.2 | 23.35 | 17.94 | 10.69 | 2.41 | −3.76 |
| 1-RCP45-70 | −5.2 | 2.43 | 3.7 | 10.77 | 16.88 | 21.45 | 24.78 | 24.1 | 18.71 | 11.44 | 3.32 | −2.66 |
| 1-RCP85-50 | −6 | −3.44 | 2.7 | 9.95 | 16.51 | 21.71 | 25.18 | 23.92 | 18.31 | 11.02 | 2.86 | −3.13 |
| 1-RCP85-70 | −4.1 | −1.33 | 4.72 | 11.96 | 18.4 | 23.26 | 26.54 | 25.49 | 20.19 | 13 | 4.65 | −1.52 |
| 2-RCP45-50 | −5.6 | −3.37 | 2.82 | 10.08 | 16.2 | 20.8 | 24.22 | 23.65 | 18.44 | 11.26 | 3.02 | −2.79 |
| 2-RCP45-70 | −4.8 | −2.58 | 3.58 | 10.91 | 17.3 | 22.23 | 25.80 | 24.9 | 19.41 | 12.26 | 4.05 | −1.96 |
| 2-RCP85-50 | −5.5 | −2.94 | 3.19 | 10.33 | 16.62 | 21.42 | 24.77 | 23.84 | 18.5 | 11.37 | 3.15 | −2.86 |
| 2-RCP85-70 | −4 | −1.62 | 4.29 | 11.38 | 17.78 | 22.71 | 26.38 | 23.74 | 20.31 | 13.01 | 4.58 | −1.38 |
| 3-RCP45-50 | −6.6 | −4.03 | 2.34 | 9.53 | 15.93 | 20.61 | 23.77 | 22.97 | 17.72 | 10.61 | 2.60 | −3.56 |
| 3-RCP45-70 | −6.1 | −3.53 | 2.68 | 10.07 | 16.42 | 20.91 | 24.22 | 23.68 | 18.43 | 11.29 | 3.14 | −3.14 |
| 3-RCP85-50 | −6.4 | 4.05 | 2.23 | 9.90 | 16.51 | 21 | 23.98 | 23.24 | 18.2 | 11.19 | 3.05 | −3.24 |
| 3-RCP85-70 | −5.2 | −2.56 | 3.39 | 10.89 | 17.33 | 21.96 | 25.28 | 24.7 | 19.58 | 12.44 | 4.21 | −2.09 |
| 4-RCP45-50 | −5.7 | −3.4 | 2.97 | 10.47 | 16.72 | 21.2 | 24.39 | 23.62 | 18.39 | 11.29 | 3.30 | −2.64 |
| 4-RCP45-70 | −5 | −2.17 | 4.02 | 11.36 | 17.79 | 22.24 | 25.17 | 24.37 | 19.35 | 12.23 | 3.92 | −2.30 |
| 4-RCP85-50 | −5.3 | −2.77 | 3.54 | 10.84 | 17.01 | 21.53 | 24.74 | 24 | 18.88 | 11.85 | 3.77 | −2.34 |
| 4-RCP85-70 | −2.5 | 0.16 | 6.06 | 12.84 | 18.72 | 23.11 | 26.18 | 25.41 | 20.55 | 13.7 | 5.71 | 0.01 |
| Jan | Feb | Mar | Apr | May | Jun | Jul | Aug | Sep | Oct | Nov | Dec | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1-RCP45-50 | 3.1 | 6.57 | 13.24 | 21.47 | 27.77 | 31.15 | 32.69 | 31.44 | 27.42 | 20.71 | 11.53 | 4.88 |
| 1-RCP45-70 | 4.2 | 7.6 | 14.31 | 22.51 | 28.40 | 31.56 | 33.22 | 32.18 | 28.21 | 21.44 | 12.44 | 5.98 |
| 1-RCP85-50 | 3.4 | 6.58 | 13.31 | 21.66 | 28 | 31.87 | 33.62 | 32 | 27.78 | 21.03 | 11.97 | 5.5 |
| 1-RCP85-70 | 5.3 | 8.69 | 15.32 | 23.68 | 29.92 | 33.42 | 34.9 | 33.57 | 29.69 | 23.05 | 13.78 | 7.13 |
| 2-RCP45-50 | 3.9 | 6.47 | 13.41 | 21.98 | 27.77 | 30.74 | 32.62 | 31.97 | 28.36 | 21.99 | 13.12 | 6.51 |
| 2-RCP45-70 | 4.3 | 6.87 | 14.01 | 22.98 | 29.12 | 32.68 | 34.87 | 33.7 | 29.73 | 23.56 | 14.57 | 7.31 |
| 2-RCP85-50 | 4.1 | 6.99 | 13.64 | 21.83 | 28.13 | 31.59 | 33.02 | 31.73 | 28.09 | 21.97 | 13.32 | 6.62 |
| 2-RCP85-70 | 5.1 | 7.90 | 14.70 | 23.11 | 29.15 | 32.69 | 35.02 | 34.37 | 30.69 | 24.23 | 14.99 | 7.86 |
| 3-RCP45-50 | 2.8 | 5.98 | 12.85 | 21.26 | 27.48 | 30.75 | 32.21 | 31.05 | 27.22 | 20.61 | 11.75 | 5.07 |
| 3-RCP45-70 | 3.3 | 6.48 | 13.28 | 21.82 | 27.98 | 31.01 | 32.66 | 31.76 | 27.93 | 21.31 | 12.29 | 5.5 |
| 3-RCP85-50 | 3 | 5.96 | 12.81 | 21.64 | 28.11 | 31.14 | 32.42 | 31.32 | 27.7 | 21.23 | 12.20 | 3.38 |
| 3-RCP85-70 | 4.2 | 7.15 | 13.98 | 22.64 | 28.88 | 32.08 | 33.72 | 32.78 | 29.09 | 22.46 | 13.35 | 6.53 |
| 4-RCP45-50 | 3.6 | 6.78 | 14.11 | 22.92 | 29.03 | 32.02 | 33.46 | 32.45 | 28.56 | 21.5 | 12.25 | 5.74 |
| 4-RCP45-70 | 5.6 | 9.33 | 15.94 | 23.97 | 30.3 | 33.16 | 33.79 | 32.59 | 29.07 | 22.23 | 13.30 | 7.19 |
| 4-RCP85-50 | 3.7 | 7.2 | 14.55 | 23.17 | 30.15 | 32.14 | 33.72 | 32.67 | 28.73 | 21.81 | 12.63 | 5.96 |
| 4-RCP85-70 | 6.5 | 9.99 | 16.94 | 24.81 | 30.49 | 33.65 | 35.03 | 34.04 | 30.48 | 23.48 | 14.16 | 8.19 |
| Jan | Feb | Mar | Apr | May | Jun | Jul | Aug | Sep | Oct | Nov | Dec | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1-RCP45-50 | −5.15 | −2.39 | 3.04 | 9.97 | 16.6 | 21.77 | 25 | 24.46 | 19.54 | 12.08 | 3.64 | −3.36 |
| 1-RCP45-70 | −4.07 | −1.4 | 4.1 | 10.97 | 17.25 | 22.23 | 25.58 | 25.28 | 20.36 | 12.85 | 4.57 | −2.23 |
| 1-RCP85-50 | −4.81 | −2.41 | 3.11 | 10.15 | 16.86 | 22.47 | 25.95 | 25.06 | 19.91 | 12.39 | 4.09 | −2.73 |
| 1-RCP85-70 | −2.97 | −1.33 | 5.14 | 12.16 | 18.72 | 23.98 | 27.3 | 26.69 | 21.8 | 14.45 | 5.92 | −1.12 |
| 2-RCP45-50 | −4.38 | −2.18 | 3.24 | 10.21 | 16.54 | 21.51 | 24.83 | 24.65 | 19.98 | 12.63 | 4.24 | −2.46 |
| 2-RCP45-70 | −3.64 | −1.37 | 4.07 | 11.10 | 17.68 | 22.96 | 26.43 | 25.90 | 20.97 | 13.66 | 5.33 | −1.61 |
| 2-RCP85-50 | −4.35 | −1.79 | 3.6 | 10.49 | 17.03 | 22.19 | 25.42 | 24.85 | 20.06 | 12.78 | 4.42 | −2.51 |
| 2-RCP85-70 | −2.80 | −0.42 | 4.77 | 11.60 | 18.17 | 23.43 | 26.99 | 26.73 | 21.85 | 14.41 | 5.85 | −1.03 |
| 3-RCP45-50 | −5.37 | −2.88 | 2.7 | 9.75 | 16.30 | 21.34 | 24.48 | 24.09 | 19.33 | 11.95 | 3.80 | −3.11 |
| 3-RCP45-70 | −4.84 | −2.36 | 3.16 | 10.27 | 16.75 | 21.65 | 24.92 | 24.75 | 19.99 | 12.60 | 4.31 | −2.71 |
| 3-RCP85-50 | −5.12 | −2.82 | 2.73 | 10.06 | 16.79 | 21.64 | 24.57 | 24.23 | 19.71 | 12.47 | 4.21 | −2.81 |
| 3-RCP85-70 | −3.97 | −1.66 | 3.86 | 11.03 | 17.56 | 22.55 | 25.81 | 25.66 | 21.08 | 13.69 | 5.33 | −1.69 |
| 4-RCP45-50 | −4.42 | −2.16 | 3.45 | 10.65 | 17.07 | 21.96 | 25.11 | 24.74 | 20.05 | 12.73 | 4.57 | −2.18 |
| 4-RCP45-70 | −3.72 | −0.89 | 4.58 | 11.57 | 18.16 | 23.06 | 25.93 | 25.51 | 21.04 | 13.66 | 5.22 | −1.83 |
| 4-RCP85-50 | −4.04 | −1.49 | 4.09 | 11.02 | 17.33 | 22.24 | 25.40 | 25.04 | 20.44 | 13.19 | 4.97 | −1.92 |
| 4-RCP85-70 | −1.20 | 1.45 | 6.59 | 12.98 | 19.02 | 23.83 | 26.86 | 26.49 | 22.15 | 15.10 | 6.91 | 0.44 |
| Jan | Feb | Mar | Apr | May | Jun | Jul | Aug | Sep | Oct | Nov | Dec | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1-RCP45-50 | 1.91 | 5 | 11.31 | 18.67 | 25.75 | 29.83 | 31.42 | 30.90 | 26.79 | 19.92 | 11.03 | 4.08 |
| 1-RCP45-70 | 2.99 | 5.98 | 12.37 | 19.68 | 26.39 | 30.29 | 32.01 | 31.72 | 27.61 | 20.68 | 11.97 | 5.20 |
| 1-RCP85-50 | 2.25 | 4.97 | 11.37 | 18.86 | 25.97 | 30.51 | 32.38 | 31.50 | 27.12 | 20.23 | 11.49 | 4.71 |
| 1-RCP85-70 | 4.09 | 7.05 | 13.40 | 20.86 | 27.86 | 32.04 | 33.73 | 33.13 | 29.14 | 22.31 | 13.32 | 6.32 |
| 2-RCP45-50 | 2.79 | 5.01 | 11.53 | 19.12 | 25.80 | 29.53 | 31.26 | 31.32 | 27.59 | 21.06 | 12.50 | 5.74 |
| 2-RCP45-70 | 3.21 | 5.40 | 12.11 | 20.11 | 27.18 | 31.48 | 33.53 | 33.02 | 28.96 | 22.64 | 13.94 | 6.55 |
| 2-RCP85-50 | 2.98 | 5.53 | 11.76 | 19.36 | 26.18 | 30.32 | 31.74 | 31.12 | 27.40 | 21.13 | 12.75 | 5.88 |
| 2-RCP85-70 | 4.02 | 6.42 | 12.84 | 20.25 | 27.14 | 31.44 | 33.63 | 33.69 | 29.90 | 23.30 | 14.35 | 7.07 |
| 3-RCP45-50 | 1.69 | 4.50 | 10.98 | 18.45 | 25.46 | 29.41 | 30.90 | 30.52 | 26.58 | 19.78 | 11.17 | 4.32 |
| 3-RCP45-70 | 2.22 | 5.02 | 11.42 | 18.97 | 25.93 | 29.71 | 31.35 | 31.19 | 27.25 | 20.43 | 11.69 | 4.73 |
| 3-RCP85-50 | 1.94 | 4.55 | 10.97 | 18.76 | 25.99 | 29.70 | 31.00 | 30.67 | 26.98 | 20.32 | 11.60 | 4.63 |
| 3-RCP85-70 | 3.10 | 5.72 | 12.11 | 19.73 | 26.74 | 30.61 | 32.23 | 32.10 | 28.35 | 21.52 | 12.72 | 5.74 |
| 4-RCP45-50 | 2.79 | 5.67 | 12.47 | 20.15 | 27.08 | 30.76 | 32.16 | 31.92 | 27.95 | 20.76 | 11.77 | 5.13 |
| 4-RCP45-70 | 4.83 | 8.24 | 14.37 | 21.31 | 28.30 | 31.81 | 32.53 | 32.10 | 28.52 | 21.54 | 12.90 | 6.66 |
| 4-RCP85-50 | 2.94 | 6.14 | 12.95 | 20.41 | 27.10 | 30.81 | 32.35 | 32.04 | 28 | 20.94 | 12.10 | 5.31 |
| 4-RCP85-70 | 5.81 | 9.03 | 15.4 | 22.19 | 28.59 | 32.40 | 33.73 | 33.47 | 29.87 | 22.73 | 13.77 | 7.63 |
| Station | T | R2 | RMSE |
|---|---|---|---|
| Baodi | Tmin | 0.868 | 2.917 |
| Tmax | 0.877 | 2.66 | |
| Tianjin | Tmin | 0.871 | 2.68 |
| Tmax | 0.889 | 2.56 | |
| Tanggu | Tmin | 0.893 | 2.47 |
| Tmax | 0.903 | 2.36 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Wang, X.; Li, X.; Liu, W.; Yang, Y. Future Climate Prediction Based on Support Vector Machine Optimization in Tianjin, China. Atmosphere 2023, 14, 1235. https://doi.org/10.3390/atmos14081235
Wang Y, Wang X, Li X, Liu W, Yang Y. Future Climate Prediction Based on Support Vector Machine Optimization in Tianjin, China. Atmosphere. 2023; 14(8):1235. https://doi.org/10.3390/atmos14081235
Chicago/Turabian StyleWang, Yang, Xijun Wang, Xiaoling Li, Wei Liu, and Yi Yang. 2023. "Future Climate Prediction Based on Support Vector Machine Optimization in Tianjin, China" Atmosphere 14, no. 8: 1235. https://doi.org/10.3390/atmos14081235
APA StyleWang, Y., Wang, X., Li, X., Liu, W., & Yang, Y. (2023). Future Climate Prediction Based on Support Vector Machine Optimization in Tianjin, China. Atmosphere, 14(8), 1235. https://doi.org/10.3390/atmos14081235





