PWV Inversion Model Based on Random Forest and the Trend of Its Conversion Rate with Precipitation in Hubei from 1960 to 2020

Abstract

In the context of anomalous global climate change and the frequent occurrence of droughts and floods, studying trends in the conversion rate between precipitable water vapor (PWV) and actual precipitation in a certain region can help in analyzing the causes of these natural disasters. This paper examines the variation trend in the conversion rate between PWV and actual precipitation on a monthly scale in Hubei from 1960 to 2020. To estimate historical PWV data, we propose a new method for estimating PWV using water vapor pressure based on the RF algorithm. The new method was evaluated by radiosonde data and improved the accuracy by 1 mm over the traditional method in Hubei. Based on this method, we extrapolate the monthly average PWV in Hubei from 1960 to 2020 and analyze the conversion rate between PWV and precipitation during this period. Our results showed that there was no obvious cyclical pattern in the conversion rate in either the longitude or latitude directions. In Hubei, where the topography varies significantly in the longitude direction, the conversion rate is influenced by topography, with the smallest conversion rate being in the transition zone between the mountainous region of western Hubei and the Jianghan Plain. In the latitudinal direction, the conversion rate decreases with increasing latitude.

1. Introduction

While the proportion of water in the atmosphere fluctuates between 0% and 4% [1], the energy changes that occur due to phase transitions can exert significant impacts on diverse weather processes and a broad spectrum of climatic phenomena. Precipitation is a complex process that involves the phase change of water in the atmosphere. When a sufficient amount of water vapor is present, the upward movement of air carries the water vapor to higher altitudes where it is cooled, leading to the formation of clouds. The water droplets within the cloud grow in size and weight through condensation, coalescence, or collision with other droplets. The water vapor in the cloud remains supersaturated due to a constant supply of water vapor, which facilitates continued condensation and the growth of cloud droplets. Ultimately, the cloud droplets become heavy enough to fall to the ground as raindrops, thus completing the process of precipitation. Precipitation is associated with a number of factors [2,3,4,5], and it is worth noting that the precipitation process is closely linked to the atmospheric water vapor content, which is commonly measured by precipitable water vapor (PWV). However, not all PWV is transformed into actual rainfall. Therefore, a comprehensive analysis of the conversion rate pattern between PWV and actual precipitation over an extended time series in a specific region is necessary to gain a better understanding of the precipitation characteristics and the potential for artificial precipitation in that area.

There have been several investigations into the relationship between the precipitable water vapor (PWV) and actual precipitation. Yang and Qiu [6] proposed a PWV estimation method based on water vapor pressure for the China region, while Li and Zhang [7] utilized water vapor pressure data from 44 meteorological stations around the Tianshan Mountains in Xinjiang to derive PWV. They analyzed the pattern of the conversion rate between PWV and precipitation in the Tianshan region from 1970 to 2000, indicating the potential for artificial rainfall in the area. Chen et al. [8] conducted a study on the conversion rate between PWV and precipitation in Linying, Henan Province, and found that the rate was as low as 6% in summer and autumn. Li et al. [9] discovered that the conversion rate of summer precipitation in the Yellow River Basin was generally low. Zhou et al. [10] conducted an analysis on the correlation between the conversion rate of precipitation and precipitable water vapor (PWV) at 11 meteorological stations in Bayingoleng Prefecture, Xinjiang. Their findings revealed that the maximum conversion rate of precipitation occurred during the summer season. Similarly, Fan et al. [11] carried out a study on the relationship between the conversion rate of precipitation and PWV in Xinjiang from 2001 to 2010. They utilized the National Centers for Environmental Prediction (NCEP) PWV data and monthly precipitation data from 52 meteorological stations in Xinjiang. Their results indicated that the conversion rate was highest during summer and lowest during winter. Li et al. [12] also employed NCEP PWV data and actual precipitation data to analyze the precipitation conversion rate in Hangzhou over the past 66 years. Their study revealed that the conversion rate in the southern part of Hangzhou was high, while that in the northern part was low. It is essential to note that the PWV data used in these studies were derived partly from traditional estimation methods, such as Yang and Qiu [6], which were established based on limited data in the early stages of the country with limited accuracy in local areas. In addition, many scholars have found that PWV is closely related to rainfall and can be used as one of the indicators of rainfall forecasts [13,14,15]. Additionally, the PWV data were also obtained from NCEP reanalysis data, which have a spatial resolution of 1° × 1°. However, the accuracy of PWV in areas with large topographic variations is limited, and NCEP PWV may not be suitable for such areas.

The present study aims to examine the trends in the conversion rate between precipitable water vapor (PWV) and precipitation in Hubei from 1960 to 2020. However, obtaining early PWV values poses a significant challenge. To address this issue, this study utilizes data from 2018 to establish a mapping relationship between water vapor pressure and PWV based on the random forest (RF) algorithm to derive historical PWV values. RF can effectively solve the overfitting problem and does not require feature selection. The studies in [16,17] use various machine learning algorithms including RF to model PWV-related elements and show that RF can achieve better results than the backpropagation neural network (BPNN) and the generalized regression neural network (GRNN) with a shorter training time, so RF is used for the modelling in this paper.

Hubei is situated in the subtropical monsoon zone, where precipitation is abundant, but the monthly distribution is uneven, and inter-annual variability is substantial. Drought disasters often occur in months with little rainfall [18]. Dong et al. [19] discovered that the frequency of drought in Hubei from 2001 to 2010 was higher than in other historical periods, and the drought area showed an increasing trend. Furthermore, some scholars have found that the probability of drought disasters in Hubei in different seasons ranged between 15% and 30% [20]. Artificial rainfall is an effective method to mitigate drought hazards. However, its potential efficacy is contingent on the water vapor content in the atmosphere and its conversion rate to actual precipitation.

2. Study Area and Methodology

The study area, comprising Hubei Province, is delineated in Figure 1, with latitude ranging from 29° N to 33°30′ N and longitude ranging from 108° E to 116°30′ E. The geographical features of Hubei are characterized by mountainous terrain in the west and plains in the east, with the Yangtze River and its tributary, the Han River, flowing from west to east, connecting the two regions. The Jianghan region is the predominant meteorological subdivision in Hubei, intersecting with several other regions in China, but the variation in the precipitation and PWV conversion rate in this region remains understudied. Therefore, this study aims to conduct a comprehensive analysis of PWV, actual precipitation, and their conversion rate from 1960 to 2020 in Hubei Province to provide a better understanding of the precipitation climate and potential in the region. The map in Figure 1 shows the locations of the meteorological stations, including both national and local data provided by the China Meteorological Administration. The red dots in the map represent the meteorological stations, which are densely distributed in the Jianghan Plain and sparsely scattered in the mountainous areas of western Hubei.

In this paper, the monthly average PWV and monthly average precipitation were taken as the research object, and the conversion rate was defined as the ratio of the monthly average precipitation to monthly average PWV.

$$\mathrm{Conversion} \mathrm{Rate}=\frac{\mathrm{m}\mathrm{o}\mathrm{n}\mathrm{t}\mathrm{h}\mathrm{l}\mathrm{y} \mathrm{a}\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{a}\mathrm{g}\mathrm{e} \mathrm{p}\mathrm{r}\mathrm{e}\mathrm{c}\mathrm{i}\mathrm{p}\mathrm{i}\mathrm{t}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}}{\mathrm{m}\mathrm{o}\mathrm{n}\mathrm{t}\mathrm{h}\mathrm{l}\mathrm{y} \mathrm{a}\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{a}\mathrm{g}\mathrm{e} \mathrm{P}\mathrm{W}\mathrm{V}}\times 100\%$$

(1)

Due to the lack of historical PWV data, it was necessary to use some methods to recover the early PWV data. Yang and Qiu [6] proposed an empirical formula expressing PWV as a quadratic function of water vapor pressure e, namely:

$$\mathrm{PWV}={\mathrm{a}}_0+{\mathrm{a}}_1^{}\mathrm{e}+{\mathrm{a}}_2{\mathrm{e}}^2$$

(2)

where PWV is in mm; e is the surface pressure in hPa; ${\mathrm{a}}_0,{\mathrm{a}}_1,{\mathrm{a}}_2$ are empirical parameters, and a₂ is usually equal to 0, except in south China.

For the other parameters,

$${\mathrm{a}}_0=\left\{\begin{array}{c}0.03\exp (-1.39{\mathrm{H}}^2+2.74\mathrm{H}+0.15)\\ 0.04\exp (0.6\mathrm{H})-{\mathrm{d}}_1+{\mathrm{d}}_2\\ -0.02\end{array}\right.\begin{array}{c}(\mathrm{Outside} \mathrm{of} \mathrm{the} \text{Qinghai-Tibet} \mathrm{Plateau},\varphi \ge 33°)\\ (\mathrm{Outside} \mathrm{of} \mathrm{the} \text{Qinghai-Tibet} \mathrm{Plateau},\varphi <33°)\\ (\mathrm{Inside} \mathrm{of} \mathrm{the} \text{Qinghai-Tibet} \mathrm{Plateau})\end{array}$$

$${\mathrm{a}}_1=\left\{\begin{array}{c}0.17+{\mathrm{d}}_3\\ (0.20-{\mathrm{d}}_3){\mathrm{d}}_4\\ 0.185\exp (0.11{\mathrm{H}}^2-0.955\mathrm{H}+1.98)\end{array}\right.\begin{array}{c}(\mathrm{Outside} \mathrm{of} \mathrm{the} \text{Qinghai-Tibet} \mathrm{Plateau},\varphi \ge 33°)\\ (\mathrm{Outside} \mathrm{of} \mathrm{the} \text{Qinghai-Tibet} \mathrm{Plateau},\varphi <33°)\\ \left(\mathrm{Inside} \mathrm{of} \mathrm{the} \text{Qinghai-Tibet} \mathrm{Plateau}\right)\end{array}$$

where

$$\begin{array}{l}{\mathrm{d}}_1=\frac{0.05}{{(\varphi -25.0)}^2+0.25}\\ {\mathrm{d}}_2=\left\{\begin{array}{c}0\\ -0.9\end{array}\right.\begin{array}{c}(\varphi >20°)\\ (\varphi \le 20°)\end{array}\\ {\mathrm{d}}_3=\frac{0.066}{{(\varphi -33)}^2+4.41}\\ {\mathrm{d}}_4=\left\{\begin{array}{l}1.0\\ 1.3\end{array}\right.\begin{array}{ll}& \begin{array}{l}({\mathrm{a}}_2=0)\\ ({\mathrm{a}}_2\ne 0)\end{array}\end{array}\end{array}$$

where $\varphi$ is the geographical latitude in degrees; and H is the altitude in km.

3. PWV Estimation Method Based on RF Algorithm

The PWV estimation method proposed by Yang and Qiu [6] only utilized 28 stations in 1993. In the whole of China, Yang’s method only used twenty-eight stations for modelling, and only one station exists in the study area of this paper because the modelling data was too limited, so this paper suggests that the method may not be applicable in specific areas. This section establishes a new PWV estimation method based on the RF algorithm using the PWV products and water vapor pressure data in 2018 provided by the China Meteorological Administration. There are 74 GNSS stations and weather stations co-located in the study area (that is, the horizontal distance between the GNSS station and weather station is within 3 km, and the height difference is within 100 m [15]). Within the range of a horizontal distance of 3 km and an elevation difference of 100 m, the nearest PWV data were selected as the PWV at the location of the meteorological station. The water vapor pressure at the PWV observation time was obtained by linear interpolation. Equation (3) was used to attribute PWV to the meteorological station location, thus completing the spatial and temporal matching of the PWV data to the water vapor pressure data.

$${\mathrm{PWV}}_{\mathrm{h}1}{=\mathrm{PWV}}_{\mathrm{h}2}·\exp (\frac{{\mathrm{h}}_1-{\mathrm{h}}_2}{-2000})$$

(3)

where PWVh1 and PWVh2 are the PWV at heights h₁ and h₂, respectively, and the unit of h₁ and h₂ is m.

Yang and Qiu [6] found that there was a linear relationship between PWV and water vapor pressure, e, in Hubei Province, namely:

$$\mathrm{PWV}=\mathrm{k}\times \mathrm{e}+\mathrm{b}$$

(4)

where k is the slope, b is the intercept, and k and b are related to the station position.

From this, we can model it in two different schemes. The two schemes are independent of each other. The structure of the two schemes is shown in Figure 2. The first scheme was used to fit the slope k and intercept b of the GNSS stations and meteorological stations one by one and take them as the output parameters of the RF algorithm, respectively, and to take the longitude, latitude, and elevation of the stations as the input parameters of the RF algorithm. The estimation models of slope k and intercept b were established, respectively, so that k and b at any position in the study area could be obtained. Finally, PWV was calculated by Formula (4) combined with water vapor pressure (Figure 2a). The second option directly calculates PWV using longitude, latitude, elevation, and water vapor pressure, e, as the input data to the RF algorithm (Figure 2b). As shown in Figure 2b, each month’s data were modeled separately so that there were 12 models that applied to different months.

The sources of the GNSS PWV modelling data used in this paper were consistent with those mentioned in the literature [17], which were provided by China Meteorological Administration. The GNSS observation data were solved by the GAMIT software to obtain the GNSS ZTD (zenith total delay), which consisted of two parts: the zenith hydrostatic delay (ZHD) and the zenith wet delay (ZWD). The ZHD can be calculated accurately by the Saastamoinen model. Ultimately the ZWD was converted to PWV based on a dimensionless coefficient related to the weighted average temperature T_m.

The model was ultimately used to calculate the PWV data in Hubei from 1960 to 2020. In this section, data from three radiosonde stations (shown as yellow pentagrams in Figure 1) for 1978 and 2004 were used to test the accuracy of the model in estimating PWV while using the method of Yang and Qiu [6] (hereafter referred to as Yang’s method) as a comparison. The results of the accuracy are shown in

Table 1. Accuracy of various methods for estimating PWV (unit: mm).

Year		Yang’s Method	Scheme I	Scheme II
2004	Bias	3.6	−0.7	−0.5
	STD	7	6.5	7.3
	RMS	7.9	6.5	7.3
	R	0.9	0.92	0.89
1978	Bias	2.8	−1.1	−1.0
	STD	11.9	11	10.3
	RMS	12.2	11.1	10.4
	R	0.8	0.81	0.84
All	Bias	3.3	−0.9	−0.7
	STD	9.4	8.7	8.8
	RMS	9.9	8.7	8.9
	R	0.85	0.87	0.87

. The data for the three radiosonde stations were obtained from the University of Wyoming providing data including the specific humidity q, pressure p, and PWV. The water vapor pressure at the radiosonde station was calculated according to Equation (5) [21].

$${\mathrm{P}}_{\mathrm{w}}=\frac{\mathrm{p}\times \mathrm{q}}{0.622}$$

(5)

where p is the pressure in Pa; and q is the specific humidity in g/g.

The empirical formula can only obtain the valuation of PWV, and this paper used the integral method to calculate the real value of PWV, which was used to evaluate the accuracy of the PWV valuation. The PWV integration method based on sounding station data is as follows:

$$\mathrm{PWV}={\displaystyle \underset{0}{\overset{\mathrm{p}}{\int }}\frac{\mathrm{q}}{{\rho }_{\mathrm{w}}\mathrm{g}}}\mathrm{d}\mathrm{P}$$

(6)

where g is the acceleration of gravity; and ${\mathrm{\rho }}_{\mathrm{w}}$ is the density of liquid water.

As shown in Table 1, when comparing the 1978 and 2004 accuracies, it can be seen that there were limitations in inverting the historic PWV data using all three methods. Table 1 shows that there was a large systematic error between the results of the Yang method and the radiosonde stations in 1978 and 2004, while the systematic errors between the other two methods and the radiosonde stations were smaller in 2004 and slightly larger in 1978, indicating the limitations of the Yang method in Hubei. The STD for Scheme I was smaller than that obtained using the Yang method, and the correlation coefficient R was larger than that obtained using the Yang method in both 1978 and 2004, whereas the STD and R for Scheme II were smaller and larger than those obtained using the Yang method in 1978, but became larger and smaller in 2004, indicating that the performance of Scheme I was more stable. Although the STD of the Yang method in 2004 was smaller than that of Scheme II, the RMS was larger due to the large systematic error between the Yang method and the radiosonde station. In 1978, Scheme II had the smallest systematic difference, STD and RMS, and the largest correlation coefficient, suggesting that Scheme II may be more suitable for the inversion of older PWV values and had some limitations for the inversion of more recent PWV values.

In general, Scheme I was the most stable of the three methods. For a better recovery of historical PWV, Scheme I was used to invert the PWV values in Hubei from 1960 to 2020. To discuss the variation patterns of the precipitation, PWV, and conversion rate in the longitude and latitude directions, this section divides the strips at 0.5° intervals along the longitude and latitude directions, respectively. In order to succinctly reflect the precipitation, PWV, and conversion rates within the strips, the corresponding values within our strips were averaged.

Before dividing the strips, we conducted a series of tests on the resolution of the strips from 0.1° to 2.0°, with an increase of 0.2° each time. It was found that if the resolution was too small, the stations in the strip were sparse and could not be evenly distributed to reflect the characteristics of the strip. Combined with the experiments, we found that a resolution of 0.5 reflected the most obvious pattern, so we set the resolution of the strip to 0.5°.

4. Variation Trend of PWV and Precipitation Conversion Rate in Hubei Province

4.1. Longitude Direction

To analyze the conversion rate between precipitation and PWV in the longitude direction, the study area was divided into 17 strips, and the time series of the conversion rates for each strip from 1960 to 2020 are presented in Figure 3. Although there was no clear cyclical pattern in the conversion rate within the individual strips, the pattern of the variation was similar between the strips. During the study period, the conversion rates ranged from 0% to 20% for most months. However, there were two periods when the conversion rate was above average, namely from 108° E to 109° E in 1982 and from 113°30′ E to 116°30′ E in 2020, which coincided with the time period of precipitation anomalies. Overall, the strips in the longitude direction exhibited the highest conversion rates in summer and relatively lower rates in winter and spring. Notably, the study area showed low conversion rates in winter.

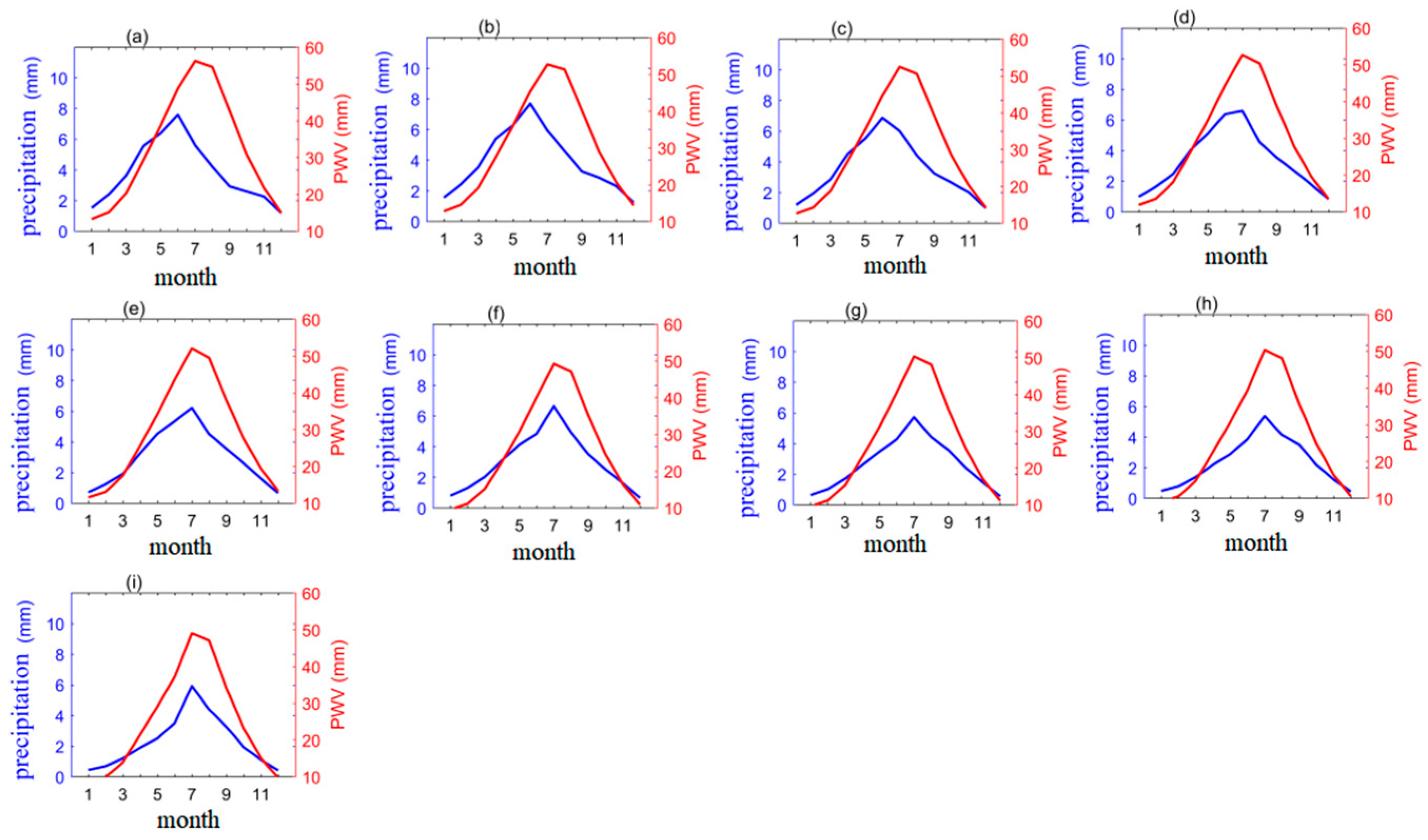
Figure 4 illustrates the variation in the precipitation and PWV in the longitude direction for each decade, with each value in the figure representing the average value of the 120 months in that decade. The region between 108° E and 110°30′ E is primarily mountainous, with the highest peak in Hubei province, Shennongding, being located at its edge. The average elevation in the region is around 2000 m. As shown in the left part of Figure 4, the precipitation in this region has remained relatively stable across the decades. However, within the strip 110°30′ E–111° E, the elevation of the study area drops rapidly, resulting in minimal precipitation values across all decades. The drop in elevation slows down in the strip at 111° E–111°30′ E, while precipitation reached its maximum value in this strip. The Suizao Corridor, situated between the Wudang Mountains and the Dahong Mountains, lies between 111°30′ E and 113° E and opens towards the south, connecting to the Jianghan Plain. The line of the precipitation change decreased rapidly from its maximum value at 111° E to 111°30′ E, resulting in grooves appearing in the position of the Suizao Corridor. To the east of 113° E lies the Jianghan Plain, which is flat terrain. At this point, the precipitation increased from west to east, reaching its maximum value at the edge of the Dabie Mountain (116° E) before beginning to decline. The overall pattern of the variation in rainfall in the longitude direction from the 1960s to the 2010s can be summarized as falling, rising to a maximum value during the study period, falling to a minimum value during the study period, rising, and rising.

The right part of Figure 4 depicts the longitudinal variation in PWV over the decades. The strip spanning from 108° E–108°30′ E is situated on the eastern side of the Sichuan Basin and is characterized by a gradual increase in elevation from west to east. The PWV of all the decades attained its maximum within this strip. The PWV experienced a decline between 108°30′ E and 110°30′ E, but the regional fluctuations were minimal, with variations of approximately 1 mm. The minimum PWV was recorded at strip 110°30′ E–111° E, where the highest peak of the study area, Shennongding, is located. As the altitude decreases steeply, PWV reached its peak in the strip 111° E–111°30′ E and then started to decrease. The range from 111°30′ E to 114° E exhibited a general upward trend, albeit with less dramatic PWV variations. The strip 113°30′ E–114° E recorded the highest PWV value, which then droped sharply to a minimum value in the strip 114° E–114°30′ E. Subsequently, PWV showed a gradual increase with increasing longitude.

A comparison of PWV values over several decades indicated that the changes were similar between the 1960s and 1970s. In the 1980s, there was a slightly larger increase, which was followed by another slight increase in the 1990s. In the region between 108°30′ E and 111° E, the PWV value in the 2000s was higher than in the 1990s, while in other areas, the two decades were comparable. In the 2010s, there was a slight decrease in PWV compared to the 2000s. In summary, PWV showed a gradual increase with each decade, which was followed by a decline in the 2010s.

Figure 5 illustrates the changes in the conversion rate between precipitation and PWV in the longitude direction over the decades. The conversion rate variation line exhibited a saddle-shaped pattern, with the lowest conversion rates being found between 111°30′ E and 113° E. This region corresponds to the Suizao Corridor, which is located between Wudang Mountain and Dahong Mountain. Interestingly, the bottom of the saddle of the conversion line is located in this region despite its PWV not being significantly lower than other areas. To the west of the Suizao Corridor lies the mountainous area of western Hubei, where the conversion rate generally increased and then decreased with longitude. The highest conversion rate values were recorded between 109°30′ E and 110°30′ E, where Shennongding, the highest elevation in the study area, is located. Moving eastward, the conversion rate increased until the maximum value was obtained at 115°30′ E–116° E, which is located at the western edge of the Dabie Mountains. Upon entering the Dabie Mountain area, the conversion rate decreased in most decades. Despite having the lowest conversion rate, the Suizao Corridor possessed greater potential for artificial rainfall enhancement.

By comparing the conversion rates between the different decades, it was found that the conversion rates in the 1960s and 1970s were comparable, whereas the conversion rate in the 1980s was slightly higher than that in the 1970s. Between 108° E and 112°30′ E, the conversion rate in the 1990s was slightly lower than that in the 1980s, while in the rest of the region, it was comparable. The difference between the conversion rates in the 2000s and the 1990s was relatively small. Between 108° E and 111° E, the conversion rate in the 2010s was slightly higher than that in the 2000s, while in the remaining region, the conversion rate in the 2000s was slightly higher than that in the 2010s. It is worth noting that only up to 15% of the PWV was converted into actual precipitation in each decade, as shown in Figure 5.

Figure 6 displays the mean values of precipitation and PWV by month for each strip in the longitude direction between 1960 and 2020. The precipitation and PWV of all the strips in the study area exhibited a single-peaked distribution pattern, with both reaching their maximum in summer between 108° E and 115°30′ E. In this region, both precipitation and PWV reached their peak in July. However, between 115°30′ E and 116°30′ E, the maximum value of PWV usually lagged behind precipitation by one month.

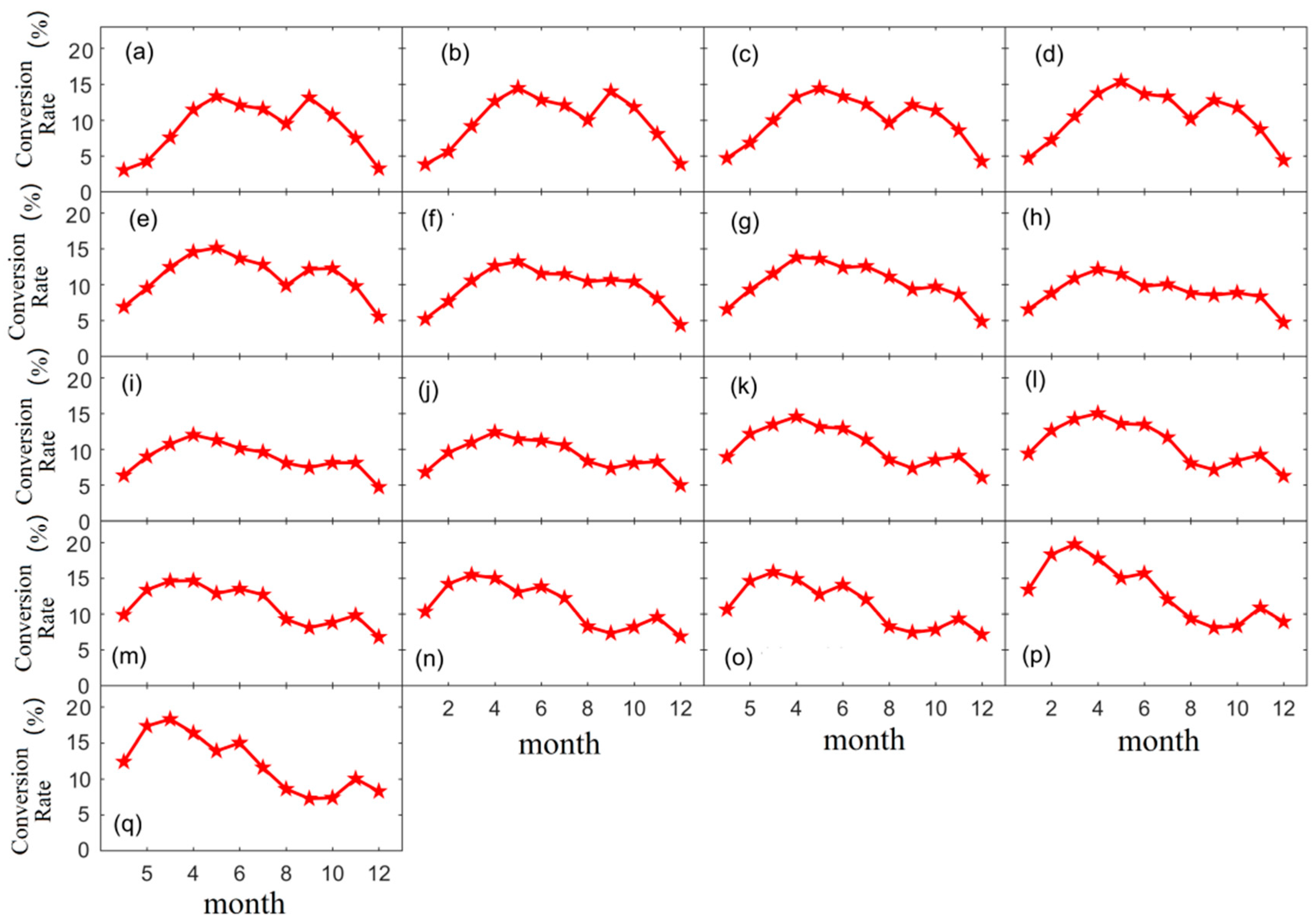
Figure 7 displays the time variation series of the conversion rate in the study period by month in the longitude direction. Between 108° E and 110°30′ E, mostly in the mountainous areas of western Hubei, the conversion rate exhibited an M-shaped pattern, with the minimum value occurring in August. In the transition zone between the mountainous areas of western Hubei and the Jianghan Plain, between 110°30′ E and 112°30′ E, the conversion rate in August and September was not significantly lower than that in the neighboring months, and the conversion rate from April to October fluctuated within a small range. In the region east of 112°30′ E, a clear turning point was reached in September. The conversion rate began to decline after reaching the maximum value in June, and the downward trend did not stop until September. The conversion rates increased slightly from September to November, but less than in previous months.

4.2. Latitude Direction

The topography of the study area exhibits a marked elevation gradient from west to east. The longitudinal division of the region into strips provided valuable insights into the impact of the topographic features on the precipitation, PWV and conversion rates. Conversely, the strips demarcated by latitude demonstrated a relatively uniform elevation profile. Situated within a subtropical monsoon climate zone, the study area is subject to the seasonal influence of Pacific Ocean monsoons, which transport water vapor from lower to higher latitudes during the summer months, and Siberian monsoons, which bring cold air from higher latitudes to lower latitudes in winter. Accordingly, the latitudinal bands served to illustrate the impact of climatic variables on the precipitation, PWV, and conversion rates.

The study area was partitioned into nine longitudinal strips, each spanning 30′ in latitude. The mean conversion rate within each strip for each month was computed and analyzed separately. Figure 8 displays the temporal evolution of the conversion rate between precipitation and PWV for each latitude strip spanning the period from 1960 to 2020. Remarkably, no discernible cyclical pattern was detected in the long-term conversion rate time series. Between 30°30′ N and 33°30′ N, the conversion rates ranged between 0% and 15% for the vast majority of months, while in the region located between 29° N and 30°30′ N, the conversion rates exceeded 15% for a considerable number of months. Importantly, this region coincides with the Hubei section of the Yangtze River, indicating that PWV translated into actual precipitation to a greater extent in this area.

To investigate the latitudinal variability of precipitation and PWV across different decades, the mean values of precipitation and PWV were computed over 120 months within each strip in the latitude direction, as illustrated in Figure 9. The analysis revealed a discernible decreasing trend in precipitation with increasing latitude. Specifically, in the Hubei section of the Yangtze River (29° N to 30°30′ N), the precipitation in the 1970s was slightly higher than that of the 1960s, but it was lower than that of the 1960s in the remaining study area. Across all the strips, precipitation was higher in the 1980s than in the 1970s and 1960s. Comparing precipitation in the 1990s with that of the 1980s, the former was higher than the latter only between 29° N and 30°30′ N, where a severe flooding disaster occurred in 1998. Precipitation in the study area during the 2000s was comparable to that of the 1960s. Notably, in the 2010s, the precipitation in the region between 30° N and 33°30′ N reached its minimum value in the study period, while in other regions, it fell between the levels observed in the 1970s and 1990s. The variation in precipitation in the Hubei section of the Yangtze River (29° N to 30°30′ N) across the different decades can be summarized as follows: from the 1960s to the 1990s, the precipitation gradually increased, whereas in the 2000s, it suddenly decreased to a minimum and then increased again in the 2010s.

Analogous to precipitation, PWV also exhibited a decreasing trend with increasing latitude across all decades, albeit with varying rates of decline in different regions. Notably, the rate of the decrease in PWV was faster between strips 29° N–30° N and strip 31° N–32° N, and it was slightly slower between 30° N and 31° N. Interestingly, PWV increased slightly from strip 31°30′ N–32° N to strip 32° N–32°30′ N before subsequently decreasing again with increasing latitude. Comparing the PWV strips in the latitude direction across the different decades, it was observed that the PWV amounts in the 1960s, 1970s, and 1980s were similar, while the PWV amount in the 1990s was higher than that of the 1980s. The PWV amount in the 2000s was comparable to that of the 1990s, while the PWV amount in the 2010s was lower than that of the 2000s.

Figure 10 displays the temporal evolution of the conversion rate between precipitation and PWV across the different decades in the latitude direction. Overall, a discernible decreasing trend was observed in the conversion rate with increasing latitude. Notably, the conversion rate reached its maximum value within the strip 29°30′ N–30° N. However, as the latitude increased, the conversion rate began to decrease until it reached its minimum value at strip 31° N–31°30′ N. Subsequently, the conversion rate increased slightly in the strip 31°30′ N–32° N before decreasing again.

An investigation into the rates of conversion across the different decades in the latitude direction of the strips revealed that the conversion rate in the 1970s was notably higher than that of the 1960s between the latitudes of 29° N and 30°30′ N. In the other regions, the two decades demonstrated comparable conversion rates. Notably, the conversion rates in the 1980s displayed a higher rate than in the 1970s across all the strips. In the 1990s, the conversion rates were higher than in the 1980s solely between the latitudes of 29° N and 30°30′ N, but they were lower in all the other regions. Conversely, the conversion rates in the 2000s were smaller than those of the 1990s. In the 2010s, the conversion rate was higher than that of the 2000s in the regions below 31° N, lower than in the 2000s in the regions above 31°30′ N, and comparable to the 2000s in the strip of 31° N–31°30′ N.

Figure 11 depicts a time series of the mean precipitation and PWV values for the strips by month in each latitude direction. Generally, the PWV and precipitation images are characterized by single-peaked patterns. Notably, between the latitudes of 29° N and 30°30′ N, where the Hubei section of the Yangtze River is located, the maximum value of PWV was observed in July, while the maximum value of precipitation was observed in June, with a one-month lag between the two peak values. In contrast, in the other regions, the maximum values of both PWV and precipitation coincided in July.

Figure 12 illustrates the monthly variation in the strip conversion rate in each latitude direction. The conversion rate images bounded by the strip 30°30′ N–31° 30′ N could be classified into two categories. Notably, between the latitudes of 29° N and 30°30′ N, where the Yangtze River flows in Hubei Province, the conversion rate reached a minimum value of approximately 5% in September. In this region, the conversion rate gradually increased from January to April with a decelerating growth rate that reached a maximum in April. Subsequently, the conversion rate gradually decreased from April to September with a decelerating deceleration rate. The conversion rate between 29° N and 30°30′ N slightly increased from September to November before decreasing again in December.

In comparison to the strip 29° N–30°30′ N, the conversion rate of the strip 30°30′ N–31° N during the transition stage of the image slightly increased in September, and the conversion rate image gradually exhibited an upward convex shape. In the region between the latitudes of 31° N and 33°30′ N, the conversion rate gradually increased from January to June with a decelerating growth rate. Following June, the growth rate decelerated further, resulting in a gradual decrease in the conversion rate.

5. Conclusions

The PWV estimation model proposed by Yang and Qiu [6] was developed with limited information and may have limitations in specific regions. To address this, a new PWV estimation method was established in this paper, which was applicable to Hubei Province. This method utilized PWV products and water vapor pressure data from the China Meteorological Administration and applied the random forest method. Compared to the conventional method, the new method demonstrated an improved accuracy of PWV estimation by approximately 1 mm.

Using the new PWV estimation method and monthly mean water vapor pressure data, we estimated the monthly mean PWV values in Hubei Province from 1960 to 2020. We combined these data with the monthly mean precipitation data provided by the China Meteorological Administration to discuss the conversion rate between PWV and precipitation and the potential of artificial precipitation during drought disasters. To account for the influence of topographic and climate factors, the study area was divided into seventeen and nine bands with intervals of 0°30′ in the longitude and latitude directions, respectively. Our results showed that there was no obvious periodic rule in either the latitude or longitude directions for precipitation or the conversion rate, while PWV demonstrated interannual periodic change characteristics. Our analysis of the longitude direction revealed the lowest conversion rate along the Suizao Corridor (111°30′ E to 113° E), while the PWV value was not abnormal. The conversion rates in the mountainous areas of western Hubei followed the trend of the average elevation, with high conversion rates being found where the average altitude was high and low conversion rates where it was low. Within the Jianghan Plain, the conversion rate increased with increasing longitude. In the latitude direction, the conversion rate decreased with increasing latitude, and the variation trend of PWV and precipitation was consistent with the conversion rate. Notably, between 29° N and 30°30′ N, i.e., the section of the Yangtze River that flows through Hubei, achieved maximum precipitation, PWV, and conversion rates in the 1990s, which coincided with a major flood in the Yangtze basin in 1998.

We counted the mean values of precipitation, PWV, and conversion rates for different months and found that images of PWV and precipitation showed a single-peaked distribution in both the longitude and latitude directions. Our analysis in the longitude direction revealed that the maximum value of PWV occurred one month later than the maximum value of precipitation in the area east of 115°30′ E (the Dabei Mountain area), while the maximum value of both PWV and precipitation was obtained in the same month in the area west of 115°30′ E. In the latitude analysis, we found that the maximum PWV value appeared one month later than the maximum precipitation value in the Hubei section of the Yangtze River between 29° N and 30°30′ N. In both the longitude and latitude directions, only 15% of the PWV in a month could be converted into actual precipitation in the study area. This indicated that although the actual water vapor content was abundant, it translated less into actual rainfall. The study area, especially in the Suizao Corridor, has a greater potential for artificial rainfall during drought disasters.