Next Article in Journal
Material Substitution Strategies for Energy Reduction and Greenhouse Gas Emission in Cement Manufacturing
Next Article in Special Issue
21st Century Warming, Site Aspect, and Reversal of Age-Related Growth Decline in Shortleaf Pine (Pinus echinata) in North Carolina, USA
Previous Article in Journal
Atmospheric and Ionospheric Effects of La Palma Volcano 2021 Eruption
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Atmosphere
Volume 14
Issue 8
10.3390/atmos14081199
atmosphere-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Tree Rings as Proxies of Historical Runoff in a National Park in Northern Mexico: A Major Ecosystem Service Provider

by
José Villanueva-Díaz
1,*,
Arian Correa-Díaz
2,
Luis Ubaldo Castruita-Esparza
3,
Jesús Valentín Gutiérrez-García
2,
Aldo Rafael Martínez-Sifuentes
1 and
Fátima del Rocío Reyes-Camarillo
1
1
Centro Nacional de Investigación Disciplinaria en Relación Agua, Suelo, Planta, Atmósfera CENID-RASPA, INIFAP, Durango 35140, Mexico
2
Centro Nacional de Investigación Disciplinaria en Conservación y Mejoramiento de Ecosistemas Forestales CENID-COMEF, INIFAP, Ciudad de Mexico 04010, Mexico
3
Facultad de Ciencias Agrícolas y Forestales, Universidad Autónoma de Chihuahua, Chihuahua 33000, Mexico
*
Author to whom correspondence should be addressed.
Atmosphere 2023, 14(8), 1199; https://doi.org/10.3390/atmos14081199
Submission received: 14 June 2023 / Revised: 17 July 2023 / Accepted: 19 July 2023 / Published: 26 July 2023
(This article belongs to the Special Issue Paleoclimate Reconstruction (2nd Edition))
Browse Figures
Versions Notes

Abstract

:
A dendrochronological network of conifers (Pinus leiophylla, Pinus cembroides, Pinus engelmannii) was developed in the Cumbres de Majalca National Park (CMNP) in Chihuahua, Mexico, to reconstruct historical runoff patterns and examine the impact of ocean–atmosphere phenomena. The CMNP plays a vital role as a runoff source for Conchos River tributaries and groundwater recharge for Chihuahua City and nearby populations. The ring-width chronologies displayed a common signal from 1859 to 2021, with the highest association found between P. engelmannii and P. leiophylla (r = 0.65) and the lowest between P. cembroides and P. engelmannii (r = 0.55). The first principal component explained 75.7% of the variance, and among the species, P. leiophylla exhibited the highest correlation (0.624, p < 0.05) with the accumulated streamflow records from the previous November to July, allowing the construction of a bootstrapped model for runoff reconstruction. The reconstructed streamflow spanned from 1859 to 2014, with an average of 2.732 × 108 m3. Periods of low runoff occurred in 1860–1880, 1940–1960, and 1994–2014, while extreme wet years with high runoff occurred in 1865, 1884, and 1987. The interannual streamflow variability correlated significantly with ENSO indices (SOI, MEI, TRI, and sea surface temperature anomalies), particularly during the winter–spring seasons, indicating that warm phases of the ENSO increased precipitation and runoff. The analysis of return periods revealed probabilities for specific runoff volumes, enabling stakeholders to use the information to develop effective strategies for sustainable water allocation and utilization in the region.

1. Introduction

The low availability of water resources in the north of Mexico, particularly in the state of Chihuahua, constitutes one of the factors that historically has limited food production and consequently favored regional famines and epidemics and triggered social conflicts [1,2]. Several studies have determined the interannual variability of Chihuahua for at least the last three hundred years [3,4,5], where extreme droughts have been a common feature with an increasing trend in the coming years, as suggested by climate models of global warming [6,7,8]. Historical droughts of great intensity during the 20th century in Chihuahua were reported in the 1930s, 1950s, and 1990s, where one of the most intense began in 1992 and extended until 2003 [9]. During the 21st century, the years 2011 and 2013 were extremely dry, affecting food production, causing livestock deaths, and diminishing the resilience of forests in the state of Chihuahua and other states in the north and central parts of Mexico [10,11]. Before this period, historical archives documented the presence of severe droughts in the 1810s, 1790s, 1770s, 1750s, and 1720s [2]. Dendroclimatic reconstructions also detect intense droughts in previous periods such as the 1670s, 1570s, and 1490s [12,13,14], with severe impacts on forest ecosystems [15].
The transnational Conchos Basin, which is part of the hydrological region RH-24 Río Bravo–Conchos, comprises approximately 32% of the surface area of the state of Chihuahua and contributes to the production of water over an area of about 77,000 km2. However, this area has not been sufficient to meet the water demand of nearly one million inhabitants settled along the 560 km of Conchos River’s mainstream, where there are also serious pollution problems [16]. Some dendroclimatic studies have been carried out involving the entire Conchos basin, but understanding the hydroclimatic variability in the RH-24 sub-basins is essential for analyzing their contribution in terms of water yield, fluctuations in its availability, and measures required for a sustainable management of this resource, as well as for the conservation of ecosystems where the water resource is produced.
The tributaries that give place to the Conchos River begin in the foothills of the Sierra Madre Occidental in the state limits of Chihuahua and Durango. This region is dominated by mixed-conifer forests, whose species may last for several centuries and produce well-defined annual rings sensitive to climate, particularly precipitation. The lack of extended and confident hydroclimatic records in this basin prevents a proper understanding of the interannual and long-term hydroclimatic variability of the Conchos basin, whose water yield is used for agriculture purposes in the borderland region of Mexico and the United States [5,17].
Given the presence of climatically sensitive tree species in mountainous areas of Chihuahua, this study focused on developing a network of dendrochronological series of conifers growing in the protected area of “Cumbres de Majalca National Park, Chihuahua, Mexico (CMNP)”, one of the Conchos River’s sub-basins. The tree-ring network could then be used as a “proxy” for developing a streamflow reconstruction, which represents the main runoff source for some of the dams located in the lower basin of the Conchos River. In addition, they constitute an important source of water for irrigation and groundwater recharge for the aquifers that feed the state capital of Chihuahua, Mexico. Thus, the objective of this study was to use tree-ring series as a proxy to analyze the interannual and multi-year streamflow variability that has historically characterized the CMNP mountain system, define its trend and return periods, and analyze the influence that ocean–atmosphere modes exert on this variability.

2. Materials and Methods

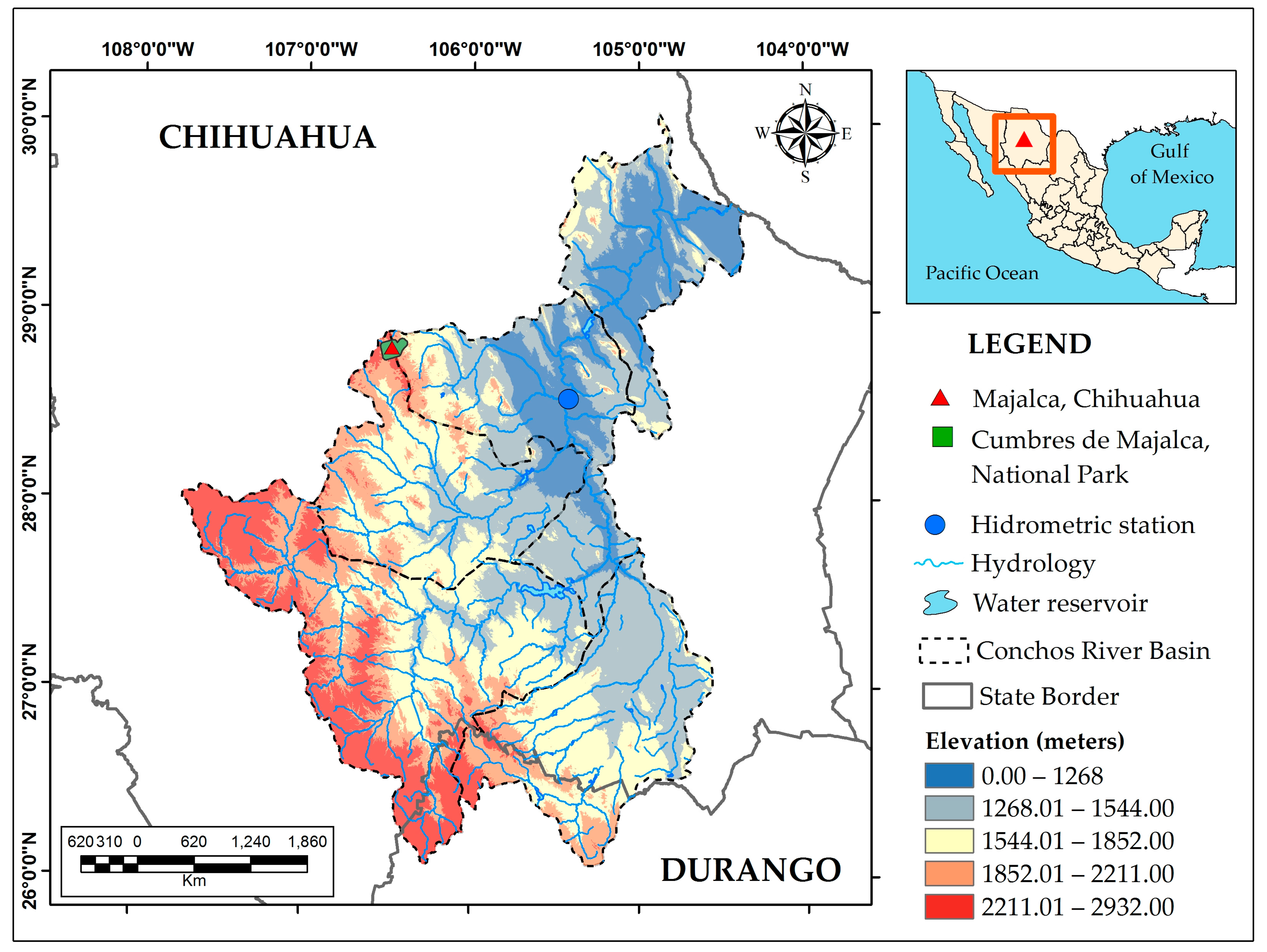
2.1. Study Area

The study site is located within the mountain range called “Cumbres de Majalca”, or Cumbres de Majalca National Park (CMNP), a protected natural area currently managed by the National Commission of Protected Natural Areas (CONANP). In physiographic terms, it is in the transitional zone of two large provinces: to the west, the Sierra Madre Occidental, and to the east, the Sierra and Valleys provinces, dominated by volcanic rocks and separated by elevated inter-mountain valleys. The elevation of the area ranges from 2100 to 2600 m. The eastern portion of the park is transversed by the Majalca Canyon stream, which originates in the Cumbres de Majalca at elevations of 1800 to 2300 m at its eastern end. The CMNP is the origin of the Sacramento River, which drains into the Chuviscar River before reaching Chihuahua City [18]. The climate is semiarid, with an average temperature of 13.9 °C, ranging from 4.8 to 21.6 °C, and an annual precipitation of 345 mm, which falls particularly from July to August in the summer season [18].
The CMNP belongs to the Rio Conchos basin, integrated by three hydrological sub-basins: the Guerachi River sub-basin, the Majalca Canyon sub-basin, and the La Fortuna sub-basin, with areas of 15,521, 4515, and 536 hectares, respectively (Figure 1) [19]. The CMNP includes the watershed and high recharge zone of two hydrological basins, where vegetation cover plays a preponderant role in the hydrological cycle and conservation of biodiversity. Its proper functionality allows the supply and recharge of aquifers that feed the rivers, a substantive basis for the agricultural activities of communities settled at the foot of the mountain range and for most of the urban, suburban, and industrial areas of the municipality and capital of Chihuahua [9].
As the CMNP is located in the transitional zone between the Sierra and Valleys provinces, it favors the presence of several plant communities, dominated by steppe vegetation at lower elevations composed of different grasses and shrubs (Juniperus monosperma) and temperate forest at higher elevations with the dominance of an oak-pine association [20]. The most important conifer species are Pinus cembroides Zucc., Pinus engelmannii Carr., and Pinus leiophylla Schl. & Cham. The conservation of plant communities along with specific species of fauna such as the American black bear (Ursus amaericanus) is of major concern to guarantee the provision of environmental services, among them biodiversity, amenity, runoff for the Sacramento and Chuviscar rivers, and groundwater recharge for the aquifers that supply water for Chihuahua City and nearby municipalities [18].

2.2. Dendrochronological Methods

Increment cores and cross-sections were obtained from mature trees of P. cembroides, P. engelmannii, and P. leiophylla within CMNP. At least two increment cores per tree were obtained from 45 trees of P. cembroides, 23 of P. engelmannii, and 60 of P. leiophylla. All samples were processed using conventional dendrochronological techniques [21]. Quality control for dating and tree-ring standardization was carried out using the dplR package in R [22]. To eliminate age-related trends and other factors unrelated to climate, we employed negative exponential curves to detrend the raw measurements [23]. Thus, we computed the tree-ring width indices (RWIs) (according to tree species) by ratio, dividing the raw measurements by the values from the fitted curve. To build a species-level chronology, we averaged the RWIs using Tukey’s biweight robust mean. We also calculated dendrochronological statistics such as intercorrelation series, Rbar, autocorrelation, Expressed Population Signal (EPS), and Subsample Signal Strength (SSS).

2.3. Hydrometric Records and Data Filling

We used daily hydrometric records from the Surface Water Data Bank [24] to obtain historical runoff data from gauge station 24226, also known as Las Burras (28°32′45″ N–105°25′20″, 1120 masl), located in the Rio Conchos basin (Figure 1). The station is located on the Conchos River, 6 km downstream from the confluence with the Bachimba stream and 2 km before the confluence with the Chuviscar River. Daily runoff data are available from 1949 to 2014; however, missing values were found, mainly during the period 2004–2008.
To address missing records in the runoff data, we utilized the imputeTS package in R, which offers several imputation methods. It is difficult to identify a single method that is universally the best, as the efficacy of the algorithms relies on the characteristics of each time series. Typically, for most time series, the na.kalman, na.interpolation, and na.seadec algorithms tend to produce the best results [25].
In this study, we utilized the na.interpolation algorithm with the “stine” option to impute missing values in the runoff series. The Stineman interpolation method employs a second-order polynomial function (parabola) to interpolate between two adjacent points of the time series. This method adjusts the curvature of the parabola based on the slope of the adjacent points, which allows a better estimation of missing data in comparison with simpler methods such as linear interpolation. For more information on the theoretical basis of imputation algorithms, please see [26].

2.4. Reconstruction Approach and Bootstrapping the Final Model

A correlation matrix was computed between monthly historical runoff data and species-level chronologies using a bootstrap Pearson correlation with the treeclim package to determine the best period for association between variables [27]. Furthermore, to account for a common signal between tree species within CMNP, we performed a Principal Component Analysis (PCA) and selected the first component (PC1, 76% of variance retained) for the same analysis. We tested single chronologies, pooled PC1 (PC1, 76% of common variance), and stepwise regression procedures (using species-level chronologies) for the runoff reconstruction, considering the period with the highest association. The best approach was selected according to adjusted R2, Akaike Information Criteria (AIC), and a Variance inflation factor (VIF) lower than five, when appropriate. Residuals for all models were inspected for normality, trend, and autocorrelation.
Once we selected the best approach, we ran a 1000 bootstrap regression to provide a more accurate inference among predictors. In this case, we used bootstrapping with resampling, which results in multiple replicates of the original data. This procedure is recommended when small databases are used and the data does not come from a normal distribution [28]. We followed the calibration–verification procedure, using 60% of the data for calibration and the rest for verification, and if reconstruction statistics were adequate (Reduction of error—RE, Sign test—ST, and Root mean squared error—RMSE), the whole period of recorded data was used to build the final model.

2.5. Return Periods of Historical Runoff at CMNP

We estimated the return periods of historical runoff by fitting various probability distribution functions (Gumbel, Normal, Log-Normal, and Gamma) using the software Ax + b, version 13 [29]. The selection of the most appropriate function was based on the Square Error, Kolmogorov–Smirnov, Chi-square, and Anderson–Darling tests.

2.6. Ocean–Atmosphere Phenomena

We determined the influence of different circulation phenomena on the variability of the reconstructed volumes, correlating the historical runoff with the El Niño–Southern Oscillation (ENSO), through different indices of this phenomenon such as the Southern Oscillation Index (SOI), Multivariate ENSO Index (MEI), Tropical Rainfall Index (TRI), and sea surface temperature anomalies (SST). Other analyzed phenomena were the Pacific Decadal Oscillation (PDO) and the Atlantic Multidecadal Oscillation (AMO).

3. Results

3.1. Tree-Ring Chronologies at Species Level

Pinus leiophylla had the highest intercorrelation value (0.69), while P. engelmannii had the lowest (0.53), but all tree species had values above the reference threshold (0.3281) (Table 1). The longest series within CMNP was for P. cembroides, with 366 years (1656–2021), while the shortest was for P. leiophylla, with 163 years (Figure 2). The parameters related to the amount of signal captured by the sample respecting a master chronology (EPS and SSS) showed reliable values for climate reconstruction purposes (e.g., EPS > 0.85). Notably, P. leiophylla had the highest signal-to-noise ratio, more than double that of P. cembroides.
The three chronologies were statistically correlated among them (p < 0.01) [Supplemental material Table S1]. For instance, the highest association was found between P. engelmannii and P. leiophylla (r = 0.65), while the lowest correlation was between P. cembroides and P. engelmannii (r = 0.55). This was confirmed by the high percentage of explained variance by the first component (PC1 = 75.7%), which confirmed high synchrony in the ring-width series among tree species (Figure 3a). Notably, the second component (PC2 = 14.3%) showed two separate groups, one including P. engelmannii and P. leiophylla and a second one exclusively for P. cembroides (Figure 3b).

3.2. Hydrometric Records and Imputed Data

Overall, we found high agreement between the observed and imputed data, as the Pearson correlation coefficient (COR) was 0.97, indicating a strong positive correlation. The performance metrics of mean squared error (MSE) and Mean Absolute Error (MAE) were 148.37 and 0.89, respectively. This suggests that the model used is effective in imputing missing data in the runoff records. Furthermore, it is important to mention that imputed data only represented 13.71% of the total hydrometric records (24,106) (Figure 4a).
The average annual runoff was 6.341 × 108 m3 year−1, with notably dry periods during the mid- and late 20th century. For example, the lowest record was found in 2001 (5.723 × 107 m3 year−1). A noticeable period below the average was found from 1994 onwards, except 2008, which had the highest streamflow record (2.712 × 109 m3 year−1) (Figure 4b).

3.3. Correlation between Tree-Ring Indexes and Monthly Hydrometric Records

The period with the highest association between monthly hydrometric records and tree-ring information was the accumulated runoff from the previous November to July of the current year (November-July, hereafter). At species level, Pinus leiophylla had the highest correlation (r = 0.624, p < 0.05), followed by PC1 (r = 0.546, p < 0.05) and Pinus cembroides (r = 0.390, p < 0.05) (Table 2). The period November-July represents, on average, 53.68% of the total annual runoff and involves important periods for tree growth, such as the previous winter, spring, and beginning of the summer season.

3.4. Comparison among Approaches for Historical Reconstruction of Runoff

The species-level chronologies, as well as the PC1 chronology, were significant factors in explaining the November-July runoff, with higher performance observed for Pinus leiophylla and the common signal extracted by the PC1 (R2 = 0.372 and R2 = 0.281, respectively) (Table 3). The pooled model, which included all tree species chronologies, did not find Pinus cembroides to be a significant factor. This finding was further confirmed by the stepwise procedure, which discarded Pinus cembroides due to collinearity issues with the rest of the chronologies (VIF > 5). Therefore, based on R2 and AIC, the best model for reconstruction purposes was obtained through the stepwise procedure, utilizing Pinus leiophylla and Pinus engelmannii as explanatory factors (Table 3). This model accounted for more than 40% of the variance in the November-July runoff while also demonstrating no heteroscedasticity problems (p = 0.898) and having normally distributed residuals (p = 0.277).

3.5. Calibration, Verification, and Bootstrapping of the Final Model

For calibration purposes, we utilized the subperiod of 1950 to 1988, while the verification covered from 1989 to 2014. Both periods yielded statistically significant results, explaining a runoff variance ranging from 38% to 44.5%. The Pearson correlation coefficient ranged from 0.64 during the calibration period to 0.70 during the verification period. Additionally, metrics such as RE and ST demonstrated positive values, indicating satisfactory reconstruction skills (Table 4).
Given the previous results, we used the whole period (1950–2014) to develop a bootstrapped reconstruction model for the historical runoff in CMNP. The dependent variable in this model was the November-July runoff, while the independent variables consisted of species-level chronologies of Pinus engelmannii and Pinus leiophylla.
The final model was as follows:
Yi = 1.428 × 108 − 2.121 × 108 β1i + 3.536 × 108 β2i
where Yi is the November-July runoff of year i and β1 and β2 are the tree-ring width indices for P. engelmannii and P. leiophylla, respectively. Note that the parameters correspond to the median of 1000 models (Figure 5a). The bootstrapped R2, R2adjusted, and AIC for the final model were 0.43, 0.41, and 2617.26, respectively. The lower AIC value suggests that the model is a better fit compared to alternative models. The statistics indicate that the model explains approximately 43% of the variance in the nov-Jul runoff and that the model’s goodness of fit is relatively high. Although the tree-ring data show a sharp decrease from 1994 onwards, the predicted values of runoff were not as low as the recorded data, which probably suggests lower synchrony during the last few decades (Figure 5b,c).
The reconstructed runoff from November to July, spanning the period from 1859 to 2014, had an average of 2.732 × 108 m3, which is slightly lower than the average from the available data from the gauge station (2.918 × 108 m3). Notably, periods of low runoff were observed from 1860 to 1880, 1940 to 1960, and 1994 to 2014, with specific years being 1860 (0.564 × 108 m3), 1877 (0.846 × 108 m3), 1948 (1.29 × 108 m3), and 2009 (1.42 × 108 m3). On the other hand, years with extremely high runoff events were identified in 1865, 1884, and 1987, with increases of 63.5%, 121.97%, and 174.72%, respectively, compared to the historical average. The last period with consistently above-average runoff (a wet period) was observed from 1983 to 1989 (Figure 6).

3.6. Return Periods

According to the analysis, the Gumbel distribution provided the best fit for the historical runoff in CMNP. Based on this, we can infer that there is a 50-year return period for events with a volume of 5.532 × 108 m3 (p = 0.019), which is approximately twice the historical average (Figure 7a). Similarly, there is a 20-year return period for runoffs that are 60% higher than the average (p = 0.051). Overall, we can state that there is a 90% probability of having runoffs above 1.506 × 108 m3, a 50% probability of runoffs being above 2.633 × 108 m3, and a 10% probability of runoffs being above 3.959 × 108 m3 (Figure 7b and Table 5).

3.7. Association with Circulatory Phenomena

The comparative analysis between the reconstructed runoff and PDO showed a high correlation for the period Jan-Sep (r = 0.42), indicating cooler sea surface temperatures along the Pacific coast and increased rainfall in northern Mexico; these results were confirmed by the positive correlation with SST from the previous September to June (r = 0.37). Positive correlations were also found with MEI (r = 0.37) and TRI (r = 0.39), mainly during the previous year’s conditions up until the end of winter (Table 6). The AMO index exhibited a significant negative correlation for the previous year (September to December, r = −0.33) (Table 6).

4. Discussion

4.1. The Importance of the Tree-Ring Series in the Study of Ecosystem Services in the Region

Our research suggests that beyond classical ecosystem services such as timber production, carbon sequestration, or oxygen release, pine species, particularly through their annual rings, represent a proxy to study the natural variability of hydrological services such as runoff, which is a major topic in the region [23]. The integration of tree-ring series from different species to generate representative regional series has been a common practice for the development of various dendroclimatic studies in northern Mexico, sometimes even with chronologies that have a separation of more than 200 km [36,37]. In this case, P. leiophylla exhibited the highest series intercorrelation and signal-to-noise ratio (r = 0.69, SNR = 33.94, Table 1), reflecting the influence of a common limiting factor in the CMNP, even surpassing P. cembroides, which is a tree species with high dendrochronological potential in the region [38,39].
P. leiophylla has a very wide range of distribution, extending from northwestern Mexico southward along the Sierra Madre Occidental [40]. This opens the possibility of using this species in a dendrochronological network for hydrological reconstruction in the zone. It is important to mention that all tree species exhibited similar interannual and multidecadal variation, as confirmed by the significant correlations among them (up to r = 0.65) and the high proportion of common variance retained by the first principal component (PC1 = 75.7%, Figure 3a,b).

4.2. The Runoff of the Gauge Station Las Burras and Its Correlation with the Tree-Ring Chronologies

Overall, the imputation procedure yielded good results, aiding in the estimation of missing data in the hydrometric records of gauge station 24226 Las Burras. For instance, we calculated higher correlations between the observed and calculated data (r = 0.97, Figure 4a). However, in the future, it is important to complement these imputation methods with precipitation records or other auxiliary variables to help detect extreme events that may have occurred, as well as consider the use of multivariate algorithms for imputing missing data. These algorithms provide similar results and, in some cases, offer improved performance without the additional drawbacks of time and computational requirements, particularly when time is explicitly treated as a variable [41]. In the case of the streamflow dataset from gauge station 24226, it was determined that, to select the most suitable imputation algorithm, additional knowledge about the characteristics of the watershed, such as climate and flood event periods, is required. For example, in 2008, an extreme waterspout occurred, impacting nearby localities near Chihuahua (https://www.elheraldodechihuahua.com.mx/local/parral/se-cumplen-13-anos-de-la-tromba-del-2008-en-parral-noticias-danos-clima-destruccion-7147702.html; accessed on 21 April 2023). Fortunately, this event coincided with the restart of the operation and the availability of data from the gauge station. Otherwise, it would have been impossible to impute the data considering only the previous months (Figure 4b).
The response of the tree-ring series to the runoff from November to July may be associated with a strong connection to the accumulated precipitation from the previous winter to spring (Table 2). This relationship has been well documented in the region [3,12,14,42,43]. Winter–spring precipitation in this region generally occurs at low intensity and often as snow, a situation that favors the process of water infiltration and accumulation in the soil profile. The relatively lower evaporation compared to other seasons with higher insolation allows a significant amount of this moisture to be available at the beginning of the growing season. This, in turn, promotes radial growth in most conifers in the southwestern United States of America and northern Mexico [23,44,45]. The increase in winter–spring precipitation in this region is also influenced by cold fronts [46] and circulatory phenomena, particularly El Niño in its warm phase [30].

4.3. The Historical Reconstruction of the Runoff in the Cumbres de Majalca National Park

Among all the statistical models evaluated, the stepwise procedure yielded the best results, exhibiting the highest R2 and lowest AIC (Table 3). However, due to collinearity issues, the P. cembroides information had to be excluded. Despite this limitation, the model still demonstrated significant predictive power, capturing a substantial portion of the runoff variance (≈40%) (Table 4). Unlike traditional reconstructions that rely on a single model, our approach utilized a bootstrap procedure, which allowed us to estimate robust coefficients, as depicted in Figure 5, resulting in more precise reconstruction values [39].
The runoff reconstruction from November to July covered 155 years, indicating severe low values during the periods of 1860 to 1880, 1940 to 1960, and 1994 to 2014 (Figure 6). These droughts occurred simultaneously in the northwest of Chihuahua [47] and Durango [37] and extended to parts of the southwestern United States of America [45,48,49]. The reconstructed series showed periods of up to seven consecutive years of drought, with runoff volumes below the recorded average. For example, the runoff during the periods 1892–1894 and 1994–1996 accounted for only around 50% of the average seasonal volume that typically occurs from November to July. The drought from the last period extended until 2003 and has been one of the longest recorded in Chihuahua [50]. However, it is important to mention that the developed reconstruction does not include runoff data from August to October, which represent 51% of the annual runoff. This situation could introduce some bias when determining drought years in this region. For example, this caused the extreme peaks of runoff observed in Figure 4a,b but not observed in the reconstruction as they were recorded mostly in September.
The analysis of return periods revealed a low probability, less than 20%, of experiencing historical runoffs of 4.287 × 108 m3 or more. This value is almost 50% higher than the average recorded at gauge station 2426 from 1950 to 2014. Conversely, there is an even lower probability, less than 0.01%, of finding runoffs below 1.43 × 108 m3 (Table 5). These findings have important implications for water resource management, particularly for designing water-use programs for agricultural and human consumption purposes. By using the lowest estimates as a baseline for water availability, stakeholders can develop effective strategies to ensure sustainable water allocation and utilization.

4.4. The Ocean–Atmospheric Modes and Their Influence on the Runoff

The hydroclimatic variability of northern Mexico is influenced by different atmospheric circulatory modes, where the El Niño–Southern Oscillation (ENSO), the Pacific Decadal Oscillation (PDO), the Atlantic Multidecadal Oscillation, and other atmospheric phenomena play a major role in the interannual variability of dominant climatic conditions that characterize this region [7,30,49,51]. Our results indicated a positive correlation with the ENSO for the reconstructed SOI (from the previous December to the current February), TRI, and MEI from January to February (Table 6). This response suggests that the warm phase of the ENSO (more negative values of this index) favors an increase in winter–spring precipitation in this region, and consequently, it is reflected in a greater radial growth and, thus, in the runoff in CMNP.
The teleconnection of the ENSO is stronger in the southwestern United States and northern Mexico, where the warm phase (El Niño) of this phenomenon favors greater precipitation in the winter–spring seasons, whereas in the cold phase (La Niña), precipitation is reduced [30]. Similarly, the PDO, an El Niño-like pattern of Pacific climate variability [52], in its positive phase has been found to produce a positive effect on precipitation [53]. In this case, we found a positive association during the period from January to September (r = 0.42). Conversely, our results indicate a negative correlation with AMO and the reconstructed SOI (Table 6). If we compare this response to the northwest part of the state, the relationship between the SOI and earlywood indices was −0.4, very similar to the one obtained in this study. However, for the western portion of Chihuahua, in its border area with the states of Sonora and Durango, this value was −0.55 [12]. Finally, the positive correlation with TRI (r = 0.39) suggests a direct influence of temperature anomalies on precipitation in the tropical Pacific region [32].

5. Conclusions

A dendrochronological network of tree-ring chronologies of P. cembroides, P. engelmannii, and P. leiophylla was developed in the Cumbres de Majalca National Park to analyze its historical hydroclimatic variability. This area is an important source of water recharge for the aquifers that feed the capital city of Chihuahua and contributes to the streamflow of the Chuviscar River, a tributary of the Conchos River (a hydrological system of transnational importance).
The dendrochronological series had a common climatic signal as indicated by the first principal component explaining 75.7% of the common variance; however, the P. leiophylla chronology with greater interseries correlation indicated a better association with gauge records from the recorded station 24226, located in a tributary of the Conchos River. Using a bootstrapped model, a streamflow reconstruction was developed for the accumulated runoff from November to July, covering the last 155 years (1859–2014). This reconstruction incorporated data from P. leiophylla and P. engelmannii. The results revealed significant interannual variability, with periods of extremely low runoff observed from 1860 to 1880, 1940 to 1960, and 1994 to 2014. The historical runoff was influenced by ocean–atmosphere phenomena such as the El Niño–Southern Oscillation (ENSO) during the winter–spring season. Additionally, the Pacific Decadal Oscillation (PDO) exerted its influence from January to September, while the Atlantic Multidecadal Oscillation (AMO) had an impact from September to December of the previous year.

Supplementary Materials

The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/atmos14081199/s1: Table S1: Correlation matrix between chronologies.

Author Contributions

Conceptualization, J.V.-D., A.C.-D. and L.U.C.-E.; Methodology, J.V.-D., L.U.C.-E., A.R.M.-S. and F.d.R.R.-C.; Software: J.V.-D., A.C.-D. and J.V.G.-G.; Formal analysis, J.V.-D., A.C.-D. and J.V.G.-G.; Writing—original draft preparation, J.V.-D., A.C.-D. and L.U.C.-E.; Writing—review and editing, J.V.-D., A.C.-D., J.V.G.-G. and A.R.M.-S.; Funding acquisition, J.V.-D. All authors have read and agreed to the published version of the manuscript.

Funding

The present study was funded by CONACYT CB-2016-01-283134 “Mexican dendrochronological network: hydroclimatic and ecological applications”.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Acknowledgments

We acknowledge the support provided by Emilia Raquel Pérez-Evangelista in dating of wood material.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Escobar-Ohmstede, A. Las sequías y sus impactos en las sociedades del México decimonónico, 1856–1900. In Historia y Desastres en América Latina; García-Acosta, V., Ed.; Estudios Sociales en Prevención de Desastres en América Latina; Centro de Investigaciones y Estudios Superiores en Antropología Social: Ciudad de México, México, 1997; Volume II. [Google Scholar]
  2. Endfield, G.H.; Fernández, I. Decades of drought, years of hunger: Archival investigations of multiple year droughts in late colonial Chihuahua. Clim. Chang. 2006, 75, 391–419. [Google Scholar] [CrossRef]
  3. Díaz, S.C.; Therrell, M.D.; Stahle, D.W.; Cleaveland, M.K. Chihuahua winter-spring precipitation reconstructed from tree-rings, 1647–1992. Clim. Res. 2002, 72, 237–244. [Google Scholar] [CrossRef] [Green Version]
  4. Villanueva, D.J.; Cerano, P.; Constante, G.; Stahle, D.W.; Estrada, A.; Tostado Plascencia, M.M. Variabilidad hidroclimática histórica del norte de México inferida con anillos de crecimiento de Douglas-fir. Rev. Mex. Cienc. Agrícolas. Publ. Espec. 2011, 2, 221–234. [Google Scholar]
  5. Martínez-Sifuentes, A.R.; Villanueva-Díaz, J.; Estrada-Ávalos, J.; Trucíos-Caciano, R.; Carlón-Allende, T.; Castruita-Esparza, L.U. Two Centuries of Drought History in the Center of Chihuahua, Mexico. Forests 2022, 13, 921. [Google Scholar] [CrossRef]
  6. Seager, R.; Ting, M.; Davis, M.; Cane, M.; Nike, N.; Nakumara, J.; Lie, C.; Cook, E.; Stahle, D.W. Mexican drought: An observational modeling and tree ring study of variability and climate change. Atmósfera 2009, 22, 1–31. [Google Scholar]
  7. Mendez, M.; Magaña, V. Regional aspects of prolonged meteorological droughts over Mexico and Central America. Am. Meteorol. Soc. 2010, 23, 1175–1188. [Google Scholar] [CrossRef] [Green Version]
  8. Magaña, V.; Zermeno, D.; Neri, C. Climate change scenarios and potential impacts on water availability in northern Mexico. Clim. Res. 2012, 51, 171–184. [Google Scholar] [CrossRef] [Green Version]
  9. Junta Central de Agua y Saneamiento del Estado de Chihuahua. Análisis Sobre el Uso y Manejo de Recursos Hidráulicos en el Estado de Chihuahua; Junta Central de Agua y Saneamiento del Estado de Chihuahua: Chihuahua, Mexico, 2005; 10p. [Google Scholar]
  10. Domínguez, J. Revisión histórica de las sequías en México: De la explicación divina a la incorporación de la ciencia. Tecnol. Cienc. Agua 2016, 7, 77–93. [Google Scholar]
  11. Castruita-Esparza, L.U.; Silva, L.C.R.; Gómez-Guerrero, A.; Villanueva-Díaz, J.; Correa-Díaz, A.; Horwath, W.R. Coping with Extreme Events: Growth and Water-Use Efficiency of Trees in Western Mexico during the Driest and Wettest Periods of the Past One Hundred Sixty Years. J. Geophys. Res. Biogeosciences 2019, 124, 3419–3431. [Google Scholar] [CrossRef]
  12. Villanueva, D.J.; Fulé, P.Z.; Cerano Paredes, J.; Estrada Ávalos, J.; Sánchez Cohen, I. Reconstrucción de la precipitación estacional para el barlovento de la Sierra Madre Occidental con anillos de crecimiento de Pseudotsuga menziesii (Mirb.) Franco. Cienc. For. México 2009, 34, 37–69. [Google Scholar]
  13. Woodhouse, C.A.; Stahle, D.W.; Villanueva Díaz, J. Rio Grande and Rio Conchos water supply variability over past 500 years. Clim. Res. 2012, 51, 147–158. [Google Scholar] [CrossRef] [Green Version]
  14. Villanueva-Díaz, J.; Castruita Esparza, L.; Martínez-Sifuentes, A.; Loera-Chaparro, R.; Estrada-Ávalos, J. Chihuahua southwestern hydroclimatic variability inferred with coniferous growth rings. Rev. Chapingo Ser. Cienc. For. Ambiente 2020, 26, 373–389. [Google Scholar] [CrossRef]
  15. Correa-Díaz, A.; Villanueva-Díaz, J.; Gómez-Guerrero, A.; Martínez-Bautista, H.; Castruita-Esparza, L.U.; Horwath, W.R.; Silva, L.C.R. A comprehensive resilience assessment of Mexican tree species and their relationship with drought events over the last century. Glob. Chang. Biol. 2023, 29, 3652–3666. [Google Scholar] [CrossRef] [PubMed]
  16. Rubio, A.H.; Felix, V.O.; Alanís, H.; Flores, M.J.; Rubio, A.H.; Felix, V.O.; Alanís, H.; Flores, M.J. Influencia del manejo de los recursos en la contaminación del Río Conchos y funcionalidad de sus áreas ribereñas; Conocimiento indispensable para la salud humana y la sustentabilidad ambiental. In Informe Técnico 2002; Comisión Nacional Forestal: Ciudad de México, Mexico, 2002. [Google Scholar]
  17. Romero-Blake, A. Impactos socioeconómicos de la sequía en la cuenca del río Conchos. In Expresiones Territoriales Latinoamericanas; Nieves-Guebara, M., Cortez-Ruiz, C., Eds.; UAM-X, CSH: Ciudad de Mexico, Mexico, 2014; pp. 197–233, 238. [Google Scholar]
  18. CONANP. Programa de Manejo Parque Nacional Cumbres de Majalca; CONANP: Chihuahua, Mexico, 2016; 252p. [Google Scholar]
  19. INEGI. Síntesis Geográfica del Estado de Chihuahua; INEGI: Ciudad de Mexico, Mexico, 2003; 145p. [Google Scholar]
  20. Estrada-Castillón, E.; Jurado, E.; Navar, J.J.; Jiménez-Pérez, J.; García-Ocañas, F. Plant associations of Cumbres de Majalca Nationa Park, Chihuahua, Mexico. Southwest. Nat. 2003, 48, 177–187. [Google Scholar] [CrossRef]
  21. Stokes, M.A.; Smiley, T.L. An Introduction to Tree-Ring Dating; University of Chicago Press: Chicago, IL, USA, 1968. [Google Scholar]
  22. Bunn, A.G. A dendrochronology program library in R (dplR). Dendrochronologia 2008, 26, 115–124. [Google Scholar] [CrossRef]
  23. Fritts, H.C. Tree Rings and Climate; Academic Press: London, UK, 1976; 567p. [Google Scholar]
  24. IMTA. Banco Nacional de Datos de Aguas Superficiales (BANDAS); Instituto Mexicano de Tecnología del Agua: Jiutepec, Mexico, 2006; Available online: http://hidrosuperf.imta.mx/bandas/ (accessed on 1 January 2020).
  25. Moritz, S.; Bartz, D.T. imputeTS: Time series missing value imputation in R. R J. 2017, 9, 207. [Google Scholar] [CrossRef] [Green Version]
  26. Moritz, S.; Bartz, D. Package ImputeTS. 2017. Available online: http://cran.r-project.org/web/packages/imputeTS/imputeTS.pdf (accessed on 2 May 2023).
  27. Zang, C.; Biondi, F. Treeclim: An R package for the numerical calibration of proxy-climate relationships. Ecography 2015, 38, 431–436. [Google Scholar] [CrossRef]
  28. Faraway, J.J. Extending the Linear Model with R: Generalized Linear, Mixed Effects and Nonparametric Regression Models; CRC Press: Boca Raton, FL, USA; Taylor & Francis Group: Oxfordshire, UK, 2016. [Google Scholar]
  29. Merlos, M.; Villegas, F. Manual de Usuario del Programa AX+B, Versión 1.3. 2017. Available online: https://www.hydrobits.com/programas/ax_b.html (accessed on 2 May 2023).
  30. Stahle, D.W.; D’Arrigo, R.D.; Krusic, P.J.; Cleaveland, M.K.; Cook, E.R.; Allan, R.J.; Cole, J.E.; Dunbar, R.B.; Therrell, M.D. Experimental dendroclimatic reconstruction of the southern oscillation. Bull. Am. Meteorol. Soc. 1998, 79, 2137–2152. [Google Scholar] [CrossRef]
  31. Wolter, K.; Timlin, M.S. El Niño Southern Oscillation behavior since 1871 as diagnosed in an extended multivariate ENSO index (MEI.ext). Int. J. Climatol. 2011, 31, 1074–1087. [Google Scholar] [CrossRef]
  32. Wright, P.B. Persistance of rainfall anomalies in the Central Pacific. Nature 1979, 277, 371–374. [Google Scholar] [CrossRef]
  33. Mantua, N.J.; Hare, S.R.; Zhang, Y.; Wallace, J.M.; Francis, R.C. A Pacific interdecadal climate oscillation with impacts on salmon production. Bull. Am. Meteorol. Soc. 1997, 78, 1069–1079. [Google Scholar] [CrossRef]
  34. Van Oldenborgh, G.J.; Te Raa, L.A.; Dijkstra, H.A.; Philip, S.Y. Frequency- or amplitude-dependent effects of the Atlantic meridional overturning on the tropical Pacific Ocean. Ocean. Sci. 2009, 5, 293–301. [Google Scholar] [CrossRef] [Green Version]
  35. Huang, B.; Banzon, V.F.; Freeman, E.; Lawrimore, J.; Liu, W.; Peterson, T.C.; Smith, T.M.; Thorne, P.W.; Woodruff, S.D.; Zhang, H.-M. Extended Reconstructed Sea Surface Temperature (ERSST); Version 4; NOAA National Centers for Environmental Information: Asheville, NC, USA, 2015. [Google Scholar] [CrossRef]
  36. Villanueva Díaz, J.; Cerano Paredes, J.; Gómez Guerrero, A.; Castruita Esparza, L.U.; Stahle, D.W.; Ruiz Corral, J.A. Volúmenes reconstruidos en presas del Valle del Yaqui con anillos anuales de coníferas. Rev. Mex. Cienc. Agrícolas. Pub. Esp. 2014, 10, 1977–1991. [Google Scholar]
  37. Martínez-Sifuentes, A.R.; Villanueva-Díaz, J.; Correa-Díaz, A.; Estrada-Ávalos, J.; Trucíos-Caciano, R.; Estrada-Arellano, J.R.; Cardoza-Martínez, G.F.; Garza-Martínez, M.Á. Dendroclimatic reconstruction of precipitation and temperature for the Mayo River basin in northwestern Mexico. Trees 2022, 36, 835–847. [Google Scholar] [CrossRef]
  38. Constante-García, V.; Villanueva-Díaz, J.; Cerano-Paredes, J.; Cornejo-Oviedo, E.; Valencia-Manzo, S. Dendrocronología de Pinus cembroides Zucc. y reconstrucción de precipitación estacional para el sureste de Coahuila. Rev. Cienc. For. México 2009, 34, 17–39. [Google Scholar]
  39. Villanueva-Díaz, J.; Estrada-Ávalos, J.; Martínez-Sifuentes, A.R.; Correa-Díaz, A.; Meko, D.M.; Castruita-Esparza, L.U.; Cerano-Paredes, J. Historic Variability of the Water Inflow to the Lazaro Cardenas Dam and Water Allocation in the Irrigation District 017, Comarca Lagunera, Mexico. Forests 2022, 13, 2057. [Google Scholar] [CrossRef]
  40. Perry, J.P. The Pines of Mexico and Central America; Timber Press: Portland, OR, USA, 1991. [Google Scholar]
  41. Baddoo, T.D.; Li, Z.; Odai, S.N.; Boni, K.R.C.; Nooni, I.K.; Andam-Akorful, S.A. Comparison of missing data infilling mechanisms for recovering a real-world single station streamflow observation. Int. J. Environ. Res. Public Health 2021, 18, 8375. [Google Scholar] [CrossRef]
  42. Cleaveland, M.K.; Stahle, D.W.; Therrell, M.D.; Villanueva-Diaz, J.; Burns, B.T. Tree-ring reconstructed precipitation and tropical teleconnections in Durango, Mexico. Clim. Chang. 2003, 59, 369–388. [Google Scholar] [CrossRef]
  43. Cerano-Paredes, J.; Villanueva-Díaz, J.; Valdez-Cepeda, R.D.; Arreola-Ávila, J.G.; Constante-García, V. Constante-García. El Niño Oscilación del Sur y sus efectos en la precipitación en la parte alta de la cuenca del río Nazas. Rev. Chapingo Ser. Cienc. For. Ambiente Publ. Espec. 2011, XVII, 207–215. [Google Scholar]
  44. Vaganov, E.A.; Anchukaitis, K.J.; Evans, M.N. How well understood are the processes that create dendroclimatic records? A mechanistic model of the climatic control on conifer tree-ring growth dynamics. In Development in Paleoenvironmental Research; Hughes, M.K., Swetnam, T.W., Diaz, H.F., Eds.; Springer: New York, NY, USA, 2011; Volume 11, pp. 37–75, 340p. [Google Scholar]
  45. Torbenson, M.C.A.; Stahle, D.W.; Howard, I.M.; Burnette, D.I.; Griffin, D.; Villanueva-Diaz, J.; Cook, B.I. Drought relief reversal over North America from 1500 to 2016. Earth Interact. 2021, 25, 94–107. [Google Scholar] [CrossRef]
  46. Magaña, V.; Pérez, J.L.; Vázquez, J.L.; Carrizosa, E.; Pérez. El Niño y el clima. In Los Impactos del Niño en México; Rueda, V., Ed.; Secretaria de Educación Pública, Consejo Nacional de Ciencia y Tecnología: Ciudad de Mexico, Mexico, 1999; pp. 23–68. [Google Scholar]
  47. Villanueva Díaz, J.; Cerano Paredes, J.; Fulé, P.Z.; Cortés Montaño, C.; Vázquez Selem, L.; Yocom, L.L.; Ruiz-Corral, J.A. Cuatro Siglos de Variabilidad Hidroclimática en el Noroeste de Chihuahua; Investigaciones Geográficas, Boletín del Instituto de Geografía: Ciudad de Mexico, Mexico, 2015; ISSN 0188-461. [Google Scholar] [CrossRef] [Green Version]
  48. Swetnam, T.W.; Betancourt, J.L. Mesoscale disturbances and ecological response to decadal climate variability in the American Southwest. J. Clim. 1998, 11, 3128–3147. [Google Scholar] [CrossRef]
  49. Stahle, D.W.; Cook, E.R.; Burnette, D.J.; Torbenson, M.C.A.; Howard, I.M.; Griffin, D.; Crawford, C.J. Dynamics, Variability, and Change in Seasonal Precipitation Reconstructions for North America. J. Clim. 2020, 33, 3173–3195. [Google Scholar] [CrossRef]
  50. Núñez-López, D.; Muñoz-Robles, A.; Reyes-Gómez, V.M.; Velasco-Velasco, I.; Gadsden-Esparza, H. Caracterización de las sequías a diversas escalas de tiempo en Chihuahua, México. Agrociencia 2007, 41, 253–262. [Google Scholar]
  51. Torbenson, M.C.A.; Stahle, D.W.; Howard, J.M.; Burnette, D.J.; Villanueva-Diaz, J.; Cook, E.R.; Griffin, D. Multidecadal modulation of the ENSO teleconnection to precipitation and tree growth over subtropical North America. Paleoceonography Paleoclimatology 2019, 34, 886–900. [Google Scholar] [CrossRef]
  52. Zhang, Y.; Wallace, J.M.; Battisti, D.S. ENSO-like interdecadal variability. 1900–1993. J. Clim. 1997, 10, 1004–1020. [Google Scholar] [CrossRef]
  53. Méndez-González, J.; Ramírez-Leyva, A.; Cornejo-Oviedo, E.; Zárate-Lupercio, A.; Cavazos-Pérez, T. Teleconexiones de la Oscilación Decadal del Pacífico (PDO) a la precipitación y temperatura en México. Investig. Geográficas Boletín Inst. Geogr. UNAM 2010, 73, 57–70. [Google Scholar]
Atmosphere 14 01199 g001 550
Figure 1. Geographical location of the Cumbres de Majalca National Park, Chihuahua, Mexico, and gauge station 24226 Las Burras, which records the streamflow of one of the tributaries of the Conchos River.
Figure 1. Geographical location of the Cumbres de Majalca National Park, Chihuahua, Mexico, and gauge station 24226 Las Burras, which records the streamflow of one of the tributaries of the Conchos River.
Atmosphere 14 01199 g001
Atmosphere 14 01199 g002 550
Figure 2. Ring-width index (RWI) chronologies of tree species within the Cumbres de Majalca National Park. The red line represents a decadal spline to highlight low-frequency events.
Figure 2. Ring-width index (RWI) chronologies of tree species within the Cumbres de Majalca National Park. The red line represents a decadal spline to highlight low-frequency events.
Atmosphere 14 01199 g002
Atmosphere 14 01199 g003 550
Figure 3. Principal Component Analysis of ring-width chronologies (RWI) at the Cumbres de Majalca National Park. (a) Scree-plot and (b) variable factor map for species-level chronologies.
Figure 3. Principal Component Analysis of ring-width chronologies (RWI) at the Cumbres de Majalca National Park. (a) Scree-plot and (b) variable factor map for species-level chronologies.
Atmosphere 14 01199 g003
Atmosphere 14 01199 g004 550
Figure 4. (a) Daily streamflow and (b) annual runoff from gauge station 24226 Las Burras. Black and red colors represent the observed and imputed data in panel (a). The blue and red years represent, respectively, the highest and lowest records for the annual streamflow in panel (b).
Figure 4. (a) Daily streamflow and (b) annual runoff from gauge station 24226 Las Burras. Black and red colors represent the observed and imputed data in panel (a). The blue and red years represent, respectively, the highest and lowest records for the annual streamflow in panel (b).
Atmosphere 14 01199 g004
Atmosphere 14 01199 g005 550
Figure 5. (a) Bootstrapped coefficients: light color corresponds to 0.025 and 0.975 quantiles, while dark corresponds to 0.25 and 0.75 quantiles; the black vertical line is the median for the 1000 replicates. (b) Scatterplot between observed and predicted runoffs from November to July; the equation represents the average model for all replicates. The red lines are the linear regression for each replicate. (c) Predicted runoff from November to July at each replicate (light-gray lines) and observed data from gauge station 24226 Las Burras (black line).
Figure 5. (a) Bootstrapped coefficients: light color corresponds to 0.025 and 0.975 quantiles, while dark corresponds to 0.25 and 0.75 quantiles; the black vertical line is the median for the 1000 replicates. (b) Scatterplot between observed and predicted runoffs from November to July; the equation represents the average model for all replicates. The red lines are the linear regression for each replicate. (c) Predicted runoff from November to July at each replicate (light-gray lines) and observed data from gauge station 24226 Las Burras (black line).
Atmosphere 14 01199 g005
Atmosphere 14 01199 g006 550
Figure 6. Seasonal reconstruction (November-July) of runoff events occurring in the catchment area of the basin at the Cumbres de Majalca National Park and concentrated at the hydrological station 24226 Las Burras, Chihuahua. The black line is the mean from the bootstrapped reconstructions (light-gray lines). The dashed horizontal line corresponds to the average historical runoff (1859–2014), while the blue line is the recorded average at the Las Burras hydrological station from 1950 to 2014. The red line represents a decadal spline to highlight low-frequency events (wet and dry periods).
Figure 6. Seasonal reconstruction (November-July) of runoff events occurring in the catchment area of the basin at the Cumbres de Majalca National Park and concentrated at the hydrological station 24226 Las Burras, Chihuahua. The black line is the mean from the bootstrapped reconstructions (light-gray lines). The dashed horizontal line corresponds to the average historical runoff (1859–2014), while the blue line is the recorded average at the Las Burras hydrological station from 1950 to 2014. The red line represents a decadal spline to highlight low-frequency events (wet and dry periods).
Atmosphere 14 01199 g006
Atmosphere 14 01199 g007 550
Figure 7. (a) Fit of distribution function to historical runoff data (1859–2014). The red line represents the best fit, which is the Gumbel distribution, while the gray lines represent the rest of the functions (Normal, Log-Normal, Fréchet, Exponential, and Gamma). (b) Accumulated probability based on the Gumbel distribution.
Figure 7. (a) Fit of distribution function to historical runoff data (1859–2014). The red line represents the best fit, which is the Gumbel distribution, while the gray lines represent the rest of the functions (Normal, Log-Normal, Fréchet, Exponential, and Gamma). (b) Accumulated probability based on the Gumbel distribution.
Atmosphere 14 01199 g007
Table
Table 1. Dendrochronological parameters of the total ring-width series located within the Cumbres de Majalca National Park.
Table 1. Dendrochronological parameters of the total ring-width series located within the Cumbres de Majalca National Park.
Tree SpeciesPeriodLength (Years)n (Cores)Intercorrelation (Standard Deviation)RbarEPS 1SNR 2SSS 3
Pinus cembroides1656–2021366960628 (0.106)0.4210.98625.6690.868
Pinus engelmannii1807–2021215460.528 (0.149)0.3170.9557.8210.892
Pinus leiophylla1859–20211631300.694 (0.122)0.5250.99333.9360.910
1 Expressed Population Signal (EPS) quantifies how well a chronology based on a finite number of trees represents a hypothetical true chronology; 2 signal-to-noise ratio (SNR) is a measure of the common signal intensity; 3 Subsample Signal Strength (SSS) is a measure of the amount of signal captured by a subsample of cores.
Table
Table 2. Bootstrapped Pearson correlation between tree-ring chronologies and monthly runoff from gauge station 24226 Las Burras (n = 1000). Correlations are statistically significant at p < 0.05; NS means not significant. Note that Prev. and Curr. refer to months from the previous and current years, respectively.
Table 2. Bootstrapped Pearson correlation between tree-ring chronologies and monthly runoff from gauge station 24226 Las Burras (n = 1000). Correlations are statistically significant at p < 0.05; NS means not significant. Note that Prev. and Curr. refer to months from the previous and current years, respectively.
MonthPinus cembroidesPinus engelmanniiPinus leiophyllaPrincipal component 1
Prev. sepNS0.330NSNS
Prev. octNSNSNSNS
Prev. nov0.3400.3220.4590.428
Prev. dec0.3860.3020.4970.463
Curr. Jan0.266NS0.4140.362
Curr. Feb0.279NS0.4330.365
Curr. Mar0.3370.2770.5600.478
Curr. Apr0.3550.3430.6810.567
Curr. May0.3010.2940.6140.500
Curr. Jun0.4500.3140.6160.555
Curr. Jul0.3400.4000.5880.523
Curr. AugNSNSNSNS
Curr. SepNSNSNSNS
Curr. OctNSNSNSNS
∑ nov-Jul0.3900.3510.6240.546
Table
Table 3. Statistical comparison among different models explaining the seasonal runoff November-July with tree-ring information. * p < 0.05, ** p < 0.01, and *** p < 0.001. Note that superscript numbers indicate the rank according to AIC.
Table 3. Statistical comparison among different models explaining the seasonal runoff November-July with tree-ring information. * p < 0.05, ** p < 0.01, and *** p < 0.001. Note that superscript numbers indicate the rank according to AIC.
ModelVariablesEstimatesT Valuep-ValueR2R2adjustedAIC
Single tree speciesP. cembroides1.952 × 1083.2790.0017 **0.1890.1322647.1
P. leiophylla2.556 × 1086.237<0.0001 ***0.3820.3722626.1
P. engelmannii2.332 × 1082.8980.0052 **0.1180.1042649.2
Principal component modelPC11.723 × 1085.095<0.0001 ***0.2920.2812634.9
Pooled modelP. cembroides−5.181 × 107−0.6930.4910.4240.3962626.1
P. leiophylla3.733 × 1085.271<0.0001 ***
P. engelmannii−1.879 × 108−2.8110.015 *
Stepwise modelP. leiophylla3.493 × 1085.676<0.0001 ***0.4120.4012624.3
P. engelmannii−2.026 × 108−2.0040.041 *
Table
Table 4. Verification statistics in the calibration and verification periods.
Table 4. Verification statistics in the calibration and verification periods.
PeriodR2R2adjustedPearson CorrelationRE 1ST 2RMSE 3
Calibration (1950–1988)0.413 *0.380 *0.642 *0.413 *39 *9.298 × 107
Verification (1989–2014)0.490 *0.445 *0.700 *0.49 *25 *1.295 × 108
1 RE = Reduction of error (positive values indicate that the model has predictive skills); 2 ST = Sign test (relates the number of agreements and disagreements between the observed and reconstructed); 3 RMSE = Root mean squared error; * values are significant (p < 0.05).
Table
Table 5. Probability of occurrence of runoff volumes that can occur in the sub-basins of the CMNP and be recorded at gauge station 24226 Las Burras.
Table 5. Probability of occurrence of runoff volumes that can occur in the sub-basins of the CMNP and be recorded at gauge station 24226 Las Burras.
Probability (%)Average (m3)MinimumMaximumn
<204.287 × 1083.451 × 1087.505 × 10831
20.0–39.93.132 × 1082.852 × 1083.447 × 10831
40.0–59.92.658 × 1082.456 × 1082.846 × 10832
60.0–79.92.157 × 1081.852 × 1082.447 × 10831
80.0–99.91.430 × 1080.564 × 1081.849 × 10831
Table
Table 6. Association among different circulation phenomena indices and the reconstructed runoff nov-Jul in CMNP, Chihuahua.
Table 6. Association among different circulation phenomena indices and the reconstructed runoff nov-Jul in CMNP, Chihuahua.
IndexMonthsPeriod (n)Pearson CorrelationProbability
SOI reconstructed 1prev. dec—Feb1859–1977 (119)−0.331p < 0.01
MEI 2Jan–Feb1871–2005 (135)0.373p < 0.01
TRI 3prev. sep—Feb1894–1995 (102)0.386p < 0.01
PDO 4Jan–Sep1900–2014 (115)0.416p < 0.01
AMO 5prev. sep—prev. dec1859–2014 (156)−0.333p < 0.01
SST 6prev. sep—Jun1859–2014 (156)0.373p < 0.01
1 SOI—Southern Oscillation Index [30]; 2 MEI—Multivariate ENSO Index [31]; 3 TRI—Tropical Rainfall Index [32]; 4 PDO—Pacific Decadal Oscillation [33]; 5 AMO—Atlantic Multidecadal Oscillation index [34]; 6 SST—sea surface temperature [35]. Months in lowercase letters correspond to the previous year, whereas months in capital letters correspond to the current year.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Villanueva-Díaz, J.; Correa-Díaz, A.; Castruita-Esparza, L.U.; Gutiérrez-García, J.V.; Martínez-Sifuentes, A.R.; Reyes-Camarillo, F.d.R. Tree Rings as Proxies of Historical Runoff in a National Park in Northern Mexico: A Major Ecosystem Service Provider. Atmosphere 2023, 14, 1199. https://doi.org/10.3390/atmos14081199

AMA Style

Villanueva-Díaz J, Correa-Díaz A, Castruita-Esparza LU, Gutiérrez-García JV, Martínez-Sifuentes AR, Reyes-Camarillo FdR. Tree Rings as Proxies of Historical Runoff in a National Park in Northern Mexico: A Major Ecosystem Service Provider. Atmosphere. 2023; 14(8):1199. https://doi.org/10.3390/atmos14081199

Chicago/Turabian Style

Villanueva-Díaz, José, Arian Correa-Díaz, Luis Ubaldo Castruita-Esparza, Jesús Valentín Gutiérrez-García, Aldo Rafael Martínez-Sifuentes, and Fátima del Rocío Reyes-Camarillo. 2023. "Tree Rings as Proxies of Historical Runoff in a National Park in Northern Mexico: A Major Ecosystem Service Provider" Atmosphere 14, no. 8: 1199. https://doi.org/10.3390/atmos14081199

APA Style

Villanueva-Díaz, J., Correa-Díaz, A., Castruita-Esparza, L. U., Gutiérrez-García, J. V., Martínez-Sifuentes, A. R., & Reyes-Camarillo, F. d. R. (2023). Tree Rings as Proxies of Historical Runoff in a National Park in Northern Mexico: A Major Ecosystem Service Provider. Atmosphere, 14(8), 1199. https://doi.org/10.3390/atmos14081199

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop