Abstract
In order to improve the calculation accuracy of the rainfall probability distribution in related applications, this study aimed to select a theoretical function from applicable functions for three classes of the class-conditional probability density function (CCPD) of hourly rainfall series. The three applicable functions are generalized gamma distribution (GΓD), generalized normal distribution (GND), and Weibull distribution. For the reason that it is hard to distinguish the advantages and disadvantages of the three functions by the probability plot and error analysis of fitted values, optimization criteria are proposed, which are the Bayesian information criterion (BIC) and the estimated accuracy of both the annual average rainfall (AAR) and the annual average continuous rainfall (AACR). The results show that by using three applicable functions in 15 regions, the relative fitting deviations for CCPD1 were less than 2.3% and less than 3.3% for ln(CCPD1). The goodness-of-fit values were all above 0.98 for CCPD1 and greater than 0.94 for ln(CCPD1). The fitting effect of the Weibull distribution was relatively poor from the perspective of the probability plot and error analysis of the fitted values, while the three applicable functions could be used to fit CCPD. GΓD had the highest fitting accuracy for the three classes of CCPDs, but there is concern about overfitting due to its broad spectrum. GND, with fewer parameters, had comparable performance to GΓD, and when fitting CCPD1 using GND, the mean relative fitting deviation was 0.6%, the coefficient of determination was 0.999, and for ln(CCPD1), they were 1.45% and 0.989. At the same time, GND performed well in estimating the AARs, with an 8.6% relative error and a 0.92 correlation coefficient in the fifteen regions, indicating that GND can well reflect the spatial variation characteristics of the AAR. Moreover, the function form of GND is simple. GND follows the parsimonious principle, and it is suitable for the whole domain. Therefore, GND is recommended as the theoretical density function based on the optimization criteria. The genetic algorithm was adopted to obtain the approximate solution of the parameters through optimization, which can simplify the derivation and calculation steps. The multiplicative and additive fitting errors were both used in the objective functions, which gave comprehensive consideration to both ends of the fitting curve.
1. Introduction
With increasing greenhouse gases, it is widely accepted that precipitation intensity is increasing, but the frequency is decreasing. It has been confirmed by climate models that extreme precipitation under global warming has not simply manifested as an increase in the total rainfall amount. Instead, the unevenness of precipitation has increased, and extreme precipitation accounts for a larger proportion of the total precipitation, which may exacerbate impacts such as flooding and drought [1,2]. Dai et al. [3] explored the mechanism for the decreasing frequency of precipitation using a weather model to forecast the hourly rainfall in North America, and their conclusions were similar. That is, the reduction in the overall precipitation frequency in the warm season has mainly been due to the decrease in light-to-moderate precipitation events, while intense precipitation events have increased, and dry spells have become longer and more frequent. Thus, the study of the probability density function (PDF) of rainfall appears to be important. The rainfall PDF has been applied in many fields, such as the compilation of rainstorm intensity formulas in engineering designs [4,5], the estimation of the probable maximum rainfall (PMP) in hydraulic engineering designs [6,7], the probability (or frequency) matching method in the interpretation application of numerical weather models [8,9,10], climate models [11,12], and quantitative rainfall estimation [13,14,15,16,17], weather generators in stochastic hydrology [18,19], the forecast of hazards such as flood, droughts, and landslides [20,21,22,23,24,25], rainfall downscaling [26,27,28,29], and filling in missing rainfall data [30,31]. However, there are problems with the rainfall PDF.
Problem 1: The rainstorm intensity formula is an important part of the technical specifications for engineering, water supply, and drainage designs. In terms of the distribution curve of urban design rainstorm frequency, there have been many academic debates and discussions among many scholars [4,5,32]. There is no consensus on a unified model of the theoretical distribution function. In the national standard of Design criterion for outdoors drainage, released in 2014 in China, the exponential distribution and Pearson Ⅲ distribution are recommended as the theoretical distribution. In the Technical Guidelines for Urban Rainstorm Intensity Formula and Design Rainstorm Profile, released in 2014 in China, the Pearson type III and Gumbel distribution functions are recommended. The Gumbel and log-normal distribution functions are preferred in the United States. Although the rainstorm intensity formula has been questioned, its crudeness has been ignored, as it is mainly used in engineering designs with a focus on a return period of 2–20 years. Since the release of the Notice on Revising the Rainstorm Intensity Formula in 2014 in China, this crudeness still exists, and the gap between demand and supply has widened. The development progress of relevant local standards and specifications is limited due to the lack of more advanced technology.
Problem 2: There are multiple mathematical expressions for the probability distribution, such as the cumulative probability distribution function (CDF) or PDF, the survival distribution function (SDF), or the return period. As for the rainfall probability distribution, a lot of investigations have been conducted on the selection of the applicable function, sampling method, fitting method, optimal parameters, and time scale [33,34,35,36,37,38]. Regarding rainfall probability distribution, the current prevailing method is annual maximum sampling (AMS) and extreme value sampling (EVS), with a focus on the daily precipitation and its CDF. For example, Papalexiou and Koutsoyiannis [39] conducted a survey with a large number of stations and reference functions for comparison. After an extensive analysis of approximately 170,000 monthly daily precipitation records from more than 14,000 stations over the globe, the research indicated that the generalized gamma distribution (GΓD) and Burr type XII distribution performed well in describing daily precipitation. Gu et al. [40] carried out fitting tests and evaluated the goodness of fit for seven potential probability distribution functions based on the daily precipitation data in China. It was revealed that the KAP distribution was the most universal, while the Pearson type Ⅲ (P-Ⅲ) distribution function was more optimal for daily precipitation fitting. A few preferred distribution functions given by various scholars have different directions and different opinions, but none of them have obvious advantages, and it is difficult to make a preference choice.
Problem 3: The imperfection of the daily rainfall PDF is attributed mainly to the constraints of the sampling size by many scholars. These constraints can be improved by hourly rainfall data because this sampling size is 24 times greater than that of daily rainfall data. Under the condition that the spatio-temporal resolution of the observation data is obviously improved, the constraints will disappear with hourly rainfall data. However, the hourly rainfall PDF is even worse than that of daily rainfall, so few studies have focused on it. Wang XY. et al. [41] analyzed the characteristics of hourly extreme rainfall in the Beijing–Tianjin–Hebei region and selected the most suitable frequency distribution based on the ZDIST criterion of a Monte Carlo simulation. It was found that the performance of five frequency distribution functions varied in different zones, where the generalized extreme value distribution (GEV) performed better. However, the fitting accuracy was limited by the method of moments (MoM), resulting in inconspicuous advantages of the recommended optimal functions. Wang L. et al. [42] investigated the rainfall distribution by the gamma function based on the hourly rainfall in the wet season in Northwest China and analyzed the impact of station elevation on the rainfall. Wang BY. et al. [43] used the P-Ⅲ distribution function to fit the PDF for hourly rainfall at the gauges in the Sichuan Province of China and calculated the probability distribution pattern and their maximum values under different return periods of hourly rainfall. The maximum likelihood estimation (MLE) was used to calculate the parameters in [42,43].
Problem 4: MLE is one of the most frequently used classical fitting methods to solve the parameters. Others are the MoM and the principle of maximum entropy (POME). Singh and Guo [44] used the POME to estimate the parameters of various CDFs and compared the performances of MLE and MoM. It was found that the POME performed better. In addition, Krylov et al. [45] proposed the method of logarithmic cumulants (MoLC) for parameter estimation, which is a substitute for the MLE and MoM methods. Li and Liu [46] suggested that the MoLC also has limitations in estimating the parameters of the GΓD. For example, there are limitations of the logarithmic cumulants of the second and third orders of the sample data. Thus, the parameter separation method has become an urgent problem to be solved. For instance, the method based on the scale-independent shape estimation (SISE) equation was used [47,48,49]. However, the methods mentioned above also have their own limitations, which are described in Section 3.2 in detail.
Problem 5: Although the rainfall CDF, or PDF, has been studied for a long time, there are arguments on the theoretical distribution function at present. Many researchers believe that there is no one PDF applicable worldwide due to regional differences and limited samples. Researchers prefer to use their own familiar functions rather than searching for a unified model, while the latter is an international difficulty. During the study of the PDF, problems, including unsatisfactory fitting accuracy and limited applicability, still exist. On the other hand, a few scholars have abandoned the extreme value theory and have tried to study the PDF using the whole rain sample, that is, the whole rain domain. For example, Zhang and Ding [50] used daily precipitation data to establish a gamma distribution model of precipitation in different statistical periods, and they proposed an improved maximum likelihood estimation method to obtain a theoretical distribution model of precipitation on different days of each month. Gamma distribution is currently the most widely used rain PDF, but there are different opinions on gamma distribution [19,51], and Ye et al. [52] showed that P-Ⅲ and kappa distributions performed better than gamma distribution for both the point and catchment rainfall on wet days. Shoji [53] determined that log-normal distribution performed well in fitting the statistical distribution of hourly, daily, and annual precipitation, exponential distribution was more suitable for monthly precipitation, and Weibull distribution performed well in fitting hourly and monthly precipitation. However, the results were limited due to the short records of data. Exponential distribution is a light-tailed distribution, but log-normal distribution is a heavily heavy-tailed distribution. Li C. et al. [54] proposed a hybrid probability distribution to simulate the full spectrum of the precipitation amount to solve the problem of underestimating the extreme values in a weather generator, where the head and tail of the daily precipitation amount are processed by different functions. Similarly, Li Z. et al. [19] preferred mixed exponential distribution to five other probability distributions for simulating daily precipitation in the north of Canada when using PDF with a hybrid function. There is a difference in the Loess Plateau in China [55]. Hybrid distribution is the best because none of the tested distributions were able to simulate all of the observed statistical characteristics of precipitation. However, we think that hybrid probability distribution is the best way to deal with PDF if there should be no other way, because it puts more emphasis on practicality rather than theory. These studies have reformed the sampling method, but its method has not improved, and the applicability of the preferred distribution was not acceptable. Therefore, these innovations did not solve the problems. The preferred functions in the previous studies do not represent the theoretical function, and some are even inapplicable. There has been no consensus on a unified model of the theoretical distribution function. The PDF can be calculated by some methods but not with high precision. Perhaps the problem is hidden in the multiple links of the whole chain, which consists of the screening of an applicable function, sampling, fitting, parameter testing, setting the preference criterion, and an optimal function and needs to be renovated. Among these, the key lies in the strict optimization criterion once the sample size is large enough. Criteria with a coarse scale do not make a preferred function stand out and may make an unsuitable function the preferred function, but strict criteria with a fine scale do not.
For trying to solve the existing problem, the links of fitting, parameter optimization, and the optimal function criterion were reformed. In our study, the criteria were separated into two parts: parameter optimization and optimal function criteria. The new parameter optimization takes both ends of the head and tail into account by error analysis and parametric check. According to the parameter optimization, the empirical functions were fitted separately using the three kinds of applicable functions that had been screened out. Then, the optimal function criteria containing three parts were put forward to select the optimal density function. Finally, the optimal function was recommended as the theoretical density function by the three criteria. It can be used to fit the PDF of hourly rainfall with high accuracy and suits the three CCPD classes and all fifteen regions. If using daily rainfall, the sample size is often restricted, but it is not with hourly rainfall. We believe that the high-accuracy PDF of hourly rainfall may bring an advantage to the PDF of daily rainfall, because the PDF of a multiple temporal scale is correlative. In-depth research on the rainfall PDF using fine data will help also optimize the rainstorm intensity formula. If an eigenvalue algorithm that is more scientific and reliable for rare rainfall events is developed, it will have great significance in improving the capabilities of urban disaster prevention and mitigation, flood control, and drainage.
2. Study Area and Datasets
The study area chosen is in the southeast of the Hu Huanyong Line. In 1935, the Hu Huanyong Line—a line from Heihe in Heilongjiang Province to Tengchong in Yunnan Province—was put forward based on China’s population distribution. Figure 1 shows China’s average annual rainfall and isohyets of 400 mm and 800 mm. The Hu Huanyong Line is drawn with a green line in Figure 1. It roughly represents a 400 mm iso-precipitation line, the dry–wet boundary, and it is related to the distribution of waterlogging, economy, vegetation, agriculture, and civilization in China. At the same time, it is also related to the rain gauges. Southeast of this line, rainstorms and flood disasters are prone to happen, and the rain gauge net was established earlier, with higher density and finer data.
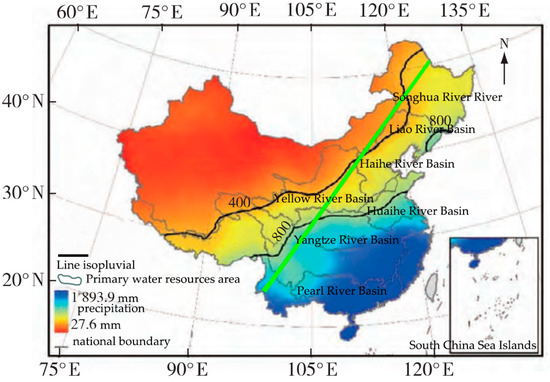
Figure 1.
China’s average annual rainfall and isohyets of 400 mm and 800 mm (quoted from [56]). The green line is the Hu Huanyong Line, which was added later.
All data used in this study were from national meteorological stations. The data from the regional gauge were used only to fill in missing data. The data consisted of the hourly rainfall, quality control codes (QCCs), and observation times. They were obtained from the China Integrated Meteorological Information Sharing System (CMISS). The rain data were correct and passed the quality control when their QCCs were equal to 0, 3, or 4. When the QCCs were equal to 7 or 9, it means that the data had no QC, but they were still useful. As for the other QCC scores, the data were treated as lost. A QCC of 7 or 9 may happen at the early stage of a station being established or in the winter in northern China and rarely happens in southern China. When the QCC was 7 or 9, another QC had to be set by executing an extreme value check. If the data did not pass this check, a spatial consistency check and temporal consistency check were carried out to determine whether rain occurred. If there was no rain, the missing data were recovered as 0. If there was rain, the missing data were recovered according to the temporal series and surrounding gauge data; otherwise, it was hard to determine whether rain occurred, and the missing data were treated as lost data. The lost data were filled in arbitrarily using random models based on a certain PDF.
The empirical function of probability density (PDEF) relies heavily on the size of the sample, because some values may be zero as singular values when there are fewer rainfall samples. The more stations and the larger the scanning radius, the larger the size of the sample. However, the larger the scanning radius, the larger the rainfall variation and the worse the rainfall consistency. The balance point is between the radius and the consistency. Thus, the criteria for selecting the regions were as follows: (1) a circular area was selected as a region in each province (or municipality or autonomous region), and the central point was close to the provincial center; (2) the number of stations in the regions was greater than 12; (3) the radius was roughly the minimum radius according to the distribution of the stations, and the radius was obtained as the latitude and longitude from the regional center; (4) if a region crossed a dense area of rainfall isohyets, the radius was reduced, and the number of stations was less than 12; (5) the deadline of obtaining the data was 20 April 2023. All stations had to start measuring and were obtained from the China Integrated Meteorological Information Sharing System (CIMISS) before 21 April 2009 to confirm the data of 14 years; (6) the regions with a rate of lost records larger than 4% were ignored for the statistical accuracy and completeness of the PDEFs.
After some regions of northern provinces were omitted according to the criteria (6) including three northeast provinces and Shandong, Hebei, and Beijing–Tianjin, fifteen regions were selected, whose locations and ranges are shown in Figure 2 (the base map was taken from the map of China No. GS(2022)4316). In all fifteen regions, the annual average rainfall (AAR) was greater than 600 mm, and they were prone to rainstorm and flood disasters. In the omitted regions, the AAR rates were about 400~700 mm, and the observed rain data were not good enough.
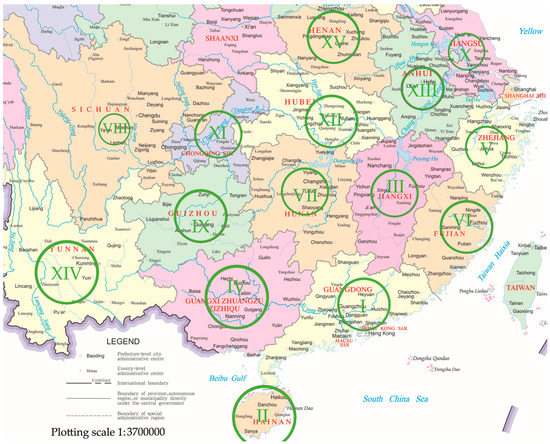
Figure 2.
Location and range of each region (base map was taken from map of China No.GS(2022)4316).
There are four distinctive seasons in all fifteen regions. Winter is cold and dry, with northerly winds blowing from the interior of Eurasia. In the summer, the prevailing southeast wind from the Pacific and southwest wind from the Indian Ocean are warm and humid and rainy and hot at the same time. Except for the XIV region in Henan Province, which is in a subhumid climate zone and has a temperate monsoon climate, all other regions are in humid climate zones and have a sub-tropical monsoon climate. Table 1, which was sorted according to the AAR, gives the geographical scope, the lost data ratio, the number of stations, and the AAR rates of the fifteen circular regions. As shown in Table 1, the AAR rates were larger than 800 mm in all regions except the XIV region. There were 11 regions where the AAR was larger than 1000 mm, and the maximum AAR was 1930 mm in the I region in Guangdong Province. The percentage of data lost was less than 4% in all fifteen regions, and the maximum, average, and minimum values were 3.91%, 1.08%, and 0.01%. There are 202 stations in the fifteen regions.

Table 1.
Geographical scope, data lost ratio, number of stations, and AAR in each circular region.
3. Methodology
3.1. Object of Study
Three classes of the class-conditional probability density (CCPD) of hourly rainfall were defined [57]. Then, the applicability of multiple functions was theoretically explored, and three kinds of applicable functions of the CCPD were deduced and screened out [58]. These included GΓD, generalized normal distribution (GND), and Weibull distribution. However, the appropriateness of these applicable functions still needed to be analyzed by some criteria to achieve the optimal function of the theoretical density function.
In this study, the fitting object was the CCPD, which refers to the probability density of a certain class of states or a certain condition. For example, CCPD1 is the first class of CCPD, which corresponds to the rain conditions. Some studies aim at non-zero rainfall; that is, data without rain are excluded from the data series. In this case, the density function is named CCPD1. In the domain of CCPD1, which is a subdomain of the domain of the PDF, CCPD1 has a multiplying relationship in its domain with the PDF. CCPD2 refers to the second class of the CCPD, corresponding to the continuous rainfall condition, and CCPD3 is the third class of the CCPD and corresponds to the state of rainfall duration. In the following text, the PDF of rainfall conditions is studied using these three classes of CCPDs.
The method of sampling adopted the whole rain sample instead of the AMS and EVS, because the AMS and EVS break the PDF curve trend between normal rain and extreme rain, and it was difficult to statistically accurately obtain the PDF when there were fewer examples of extreme rain.
The statistical method and processing flow of the empirical functions of CCPDs were omitted. The following describes the fitting method, including why the genetic algorithm (GA) and the objective function, which is the parameter optimization criterion for the probability density function, were selected. The objective function was in the same formula as for three CCPDs. Subsequently, the optimization criterion of the theoretical density function was used to select the preferred model among the multiple functions.
3.2. Fitting Method
The commonly used methods for estimating the parameters of PDFs need to establish simultaneous equations, for which there may be no solution or multiple solutions. In addition, the solution to establishing simultaneous equations is to obtain the form of the exact solution, but the parameters obtained are only the exact solution of the simultaneous equations and are still an approximate solution to the fitting problem. The main reasons for such problems are as follows.
Appropriateness of candidate functions. In each case where the theoretical function is uncertain and the sample size is limited, the appropriateness of the candidate functions is always worth discussing. For inappropriate functions, it is difficult for the obtained parameter solutions to fit both the head and tail of the PDF curve, or there may be no solution.
Calculation methods. For theoretical density functions and their forms after logarithmic transformation, many functions cannot satisfy the independence of the parameters simultaneously. At this time, the establishment of an equation set is unreasonable. That is, the step of establishing a likelihood equation set by using derivation after the partial derivative of the parameters is obtained is inappropriate when the parameters lack independence.
Statistical error. There are errors in the coefficients and their related statistics in equations, which are sourced from the observational and statistical errors of empirical functions. Statistical errors are mainly affected by the limited size of observation samples. In addition, the statistical errors of variables and independent variables in the discretization process of independent variables also have an impact.
Limited sample size. Some studies have shown that the fitting accuracy of these methods is highly dependent on the sample size. For the small occurrence probability of extreme rainfall, the scarcity of statistical samples leads to a poor smoothness of the empirical function curve and a rough classification for rainfall grades. The problem mentioned above is more obvious when using the extreme value method, which may lead to larger fitting deviations, limited fitting accuracy, and a questionable fitting method.
Calculation steps. The calculation processes of these five methods are complex with numerous steps. Since the PDF is a nonlinear equation, the deviation will gradually accumulate and be enlarged with the calculation steps.
Therefore, the approximate solution of fitting for the CCPD can be obtained directly through mathematical methods, such as parameter optimization and numerical approximation. For example, the genetic algorithm (GA) can simplify the derivation and corresponding calculation process, enhance the universality, and improve the fitting accuracy. Therefore, the GA was selected to search for the optimal solution of multi-objective parameters by comprehensively considering the multiplicative and additive errors, so as to give consideration to the head and tail of the curve and improve the overall fitting accuracy.
In this study, represents the empirical function of a certain type of CCPD in the region M (M = 1, 2,……, 15), and represents its fitting function. The independent variable of the three classes of CCPDs corresponds to the hourly rainfall (HR), the rainfall amount during the hourly continuous rainfall (HCR) process, and the duration of the HCR (HoCR), respectively. The domains are defined as x1 ≥ 0.1 mm in CCPD1, x2 ≥ 0.2 mm in CCPD2, and x3 ≥ 2 h in CCPD3. In view of the fitting parameters, the power exponent is expressed by (0 < n <1), is the shape parameter, and is related to the scale parameter ().
The objective functions for the three classes of CCPDs were set as
where is the root-mean-square error (RMSE) operator. ERMS(PM) and ERMS_[ln(PM)] represent the relative fitting deviations in the additive and multiplicative error models, respectively, which are the RMSE operator of the normalized or . SSE is the variance of the fitting deviation with the weight of the echo bins, and N is the number of bins divided by the -axis. Φ represents the fitting deviation of and Φ , and its contribution to the deviation is mainly determined by the head of the curve, contributing a little to the middle of the curve and zero to the tail of the curve. When a multiplicative error model is selected, , the contribution to the deviation is related to the relative deviation of each data point, and it contributes more at the tail of the curve than at the head because is larger at the tail, while Φ approaches zero. By setting the objective function in this way, the relative deviation of each data point can be taken into account. Specifically, for the data points at the end of the curve, with the CCPD approaching zero, the fitting accuracy can be effectively improved, so that both ends of the curve can be comprehensively considered.
Figure 3 gives the weights of three CCPD classes in each bin while calculating the objective functions. The weight series was set by artificial experience, taking care of error at the tail of the empirical function, and with the purpose of easing the contradiction between the head and the tail of the fitting curve. It can be adjusted if a better overall result is looked for.
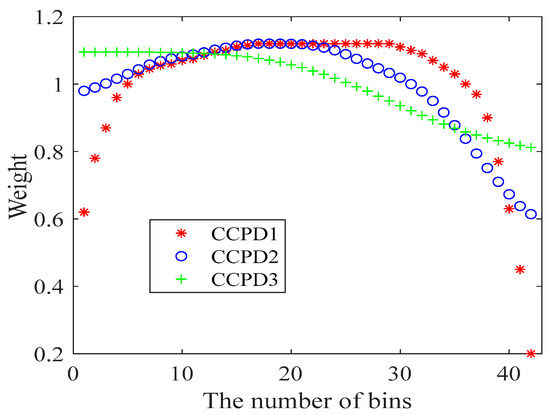
Figure 3.
The weight of three CCPD classes in each bin when calculating the objective functions.
In the engineering field and under extreme rainfall, the tail should be given more attention, and then the weight of ERMS_ is larger. In our opinion, the two weights must be moderate. If the gap becomes too large, the improvement in the fitting accuracy may be limited, and the optimal function may be distorted. Choosing an appropriate theoretical density function that considers both the head and tail is more important because the PDF must be limited by the condition that its integral is 1. Therefore, the weights of ERMS_ and ERMS were not set.
3.3. Optimal Criteria for Theoretical Density Function
The Kolmogorov–Smirnov (KS) test was used to test the applicability of the functions, which was featured as a low standard. The KS goodness-of-fit test is not recommended because it is inaccurate even with three corrections. The KS test is similar to the inferior Shapiro–Wilk (SW) and Jarque–Bera(JB) tests. Test results of the JB and KS tests on geopotential height have been very different [51,59]. Instead of the KS test, the coefficient of determination, that is, the goodness of fit, and the probability plot have been adopted by many researchers and were used to verify the fitting effect in our study. In addition, the objective function Obj, which contains two fitting deviation models, was mentioned in the above section, and it was used in the GA for parameter optimization. To a certain extent, the Obj can be used for fitting the capability assessment of functions, too.
After the parameters of the 3 applicable functions in the 15 regions were optimized, the coefficient of determination and the probability plot were calculated to verify the fitting effect. However, the application of these was still inadequate for analyzing the fitting results. When the functions were fitted with high accuracy, the fitting deviation was affected by the observation error, so the optimal function may not correspond to the minimum Obj or the maximum goodness of fit, and the entire probability plot looks good. It was meaningless to compare the statistical indicators and analyze the probability plot, as it was difficult to select a winner among the three applicable functions. It was necessary to adopt stricter objective criteria for judging the optimal function in contrast to previous studies. Therefore, the following three criteria were proposed. According to these criteria, this study aimed to select an optimal theoretical function among the three applicable functions.
- (1)
- Bayesian information criterion (BIC)
The BIC [60], or the Akaike information criterion (AIC) [61], is commonly used to determine the optimal function. A distribution function with the minimum BIC value might score high and is regarded as the preferred one. For parameter estimation, the likelihood function is usually taken as the objective function. The accuracy of the model can be continuously improved under conditions with enough parameters and training data, but an overfitting problem may occur with increasing model complexity. Therefore, it is essential to balance the complexity of the model and the description capability of the model on a dataset. The specific formula is as follows:
where represents the likelihood function, represents the parameter set, is the number of model parameters, and represents the number of bins; N1, N2, and N3 are equal to 41, 42, and 42, respectively. is a penalty term, which helps avoid the overfitting problem caused by the high complexity of the model when seeking balanced point between the precision and the number of parameters to approach the optimal model.
- (2)
- Estimation accuracy of AAR
The observed AAR can be obtained using the rainfall data from each region, and it is expressed as . A series of can be obtained when there are multiple regions.
The AAR can also be estimated by the fitting parameters of CCPD1, and it is denoted as . Using the GND in the fifteen regions, thewas obtained. Thewas similar. HY = 365.2422 × 24 is the number of hours in a year, PHR is the hourly rain frequency, and the can be calculated as follows:
where and represent the expected values of the GΓD and GND functions, respectively, and are the GND parameters obtained by GA, and , and are the GΓD parameters.
According to the formula above, the series of was obtained for the whole region using the GND or GΓD. The relative error between the and the can express the estimation accuracy of the AAR. The correlation coefficient between the series of and reflects the ability to describe the regional variation characteristics. Therefore, two indexes of the CCPD1 optimization criteria stand out. One is the relative deviation between the and . The other is the correlation coefficient between the series of and . Comparing them, the function with a smaller relative error and higher correlation coefficient scored higher.
- (3)
- Estimation accuracy of annual average continuous rainfall
The AAR corresponded to CCPD1. Similarly, the annual average continuous rainfall (AACR) corresponded to CCPD2. Similar to the calculation method of , the AACR can also be estimated by CCPD2. The relative error and correlation coefficient of the AACR estimation are used to express the estimation accuracy, which can be regarded as preference criterion of CCPD2.
The average number of hours of annual rain can be obtained using CCPD3. However, in our study, the empirical function of CCPD3 was not smooth enough because the rain sample size was limited (see Figure 4), so the calculation using CCPD3 was omitted because the error would have been large.
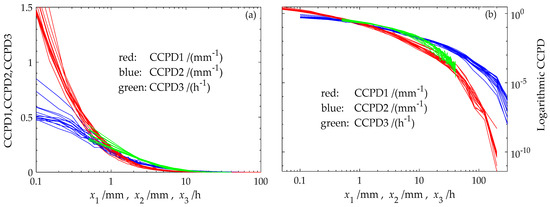
Figure 4.
Empirical functions of the three classes of CCPDs (a) and their logarithm functions (b).
4. Results
4.1. Empirical Function of Three CCPD Classes
Figure 4 shows the empirical function distributions of the three types of CCPDs in 14 regions. All of the curves are convex and decreasing in Figure 4a and concave and decreasing in Figure 4b. According to these and other characteristics, three distributions were chosen as applicable functions by filtering using theoretical derivation [58].
In Figure 4, the rainfall series along the x-axis is divided into bins with variable widths for CCPD1 and CCPD2. Table 2 lists 41, 42, and 42 bins for CCPD1, CCPD2, and CCPD3, respectively. In the empirical function, the bins at the head with rainfall below 0.1~2.5 and 0.2~2.6 mm were set with a 0.1 mm equal width for and , because the sample sizes in this rainfall interval were large, and the resolution of rainfall observation was 0.1 mm. For the rainfall above 2.5 and 2.6 mm, the bin width was incremental due to the decrease in the sample size with and . Regarding CCPD3, is the duration of hourly continuous rainfall, and the design of equal width with the width of 1 h. In Figure 4, is divided into 42 bins with a one-hour width.

Table 2.
The rainfall bins of CCPD1, CCPD2, and forty-two hourly bins of CCPD3.
4.2. Fitting Plot of Three CCPD Classes
The objective functions Obj of CCPD1 of the IV region (in GuangXi Zhuang Autonomous Region) were the largest among all 15 regions when the GΓD was used for the fit, and that of the I region (in GuangDong Province) was the largest when the GND was used. So the IV and I regions were chosen to show the PDF fitting plot. Figure 5 shows the empirical function and fitting function using the GΓD (Figure 5a), GND (Figure 5b), and Weibull (Figure 5c) distribution of CCPD1 in the I Region, and Figure 5d–f show those of the IⅤ Region. The other regions were not plotted. In Figure 5, the left blue y-axis represents the CCPDs, and the right red y-axis represents the natural logarithm values of the CCPDs. It is the same in Figure 6 and Figure 7. It can be seen that CCPD1 and its natural logarithm ln (CCPD1) have high coincidence with the fitting functions by the GΓD and GND and Weibull distribution, revealing that the three applicable functions fit CCPD1 well.
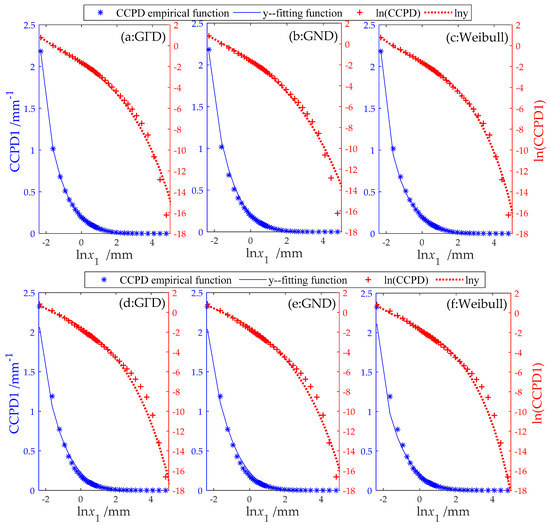
Figure 5.
The empirical function and the fitting function of CCPD1 (blue dot and line reference the left blue y-axis) and their logarithmic function (red dot and line reference the right red y-axis). (a–c) for I region; (d–f) for IV region.
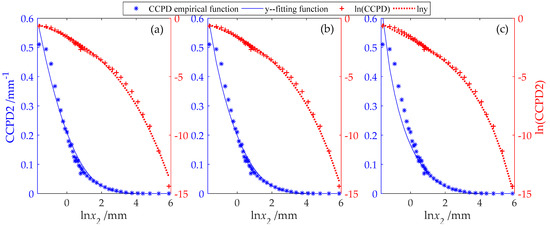
Figure 6.
The empirical function and fitting function of CCPD2 in the XIII region (blue dot and line reference the left blue y-axis) and their logarithmic function (red dot and line reference the right red y-axis) by the (a) GΓD, (b) GND, and (c) Weibull distribution.
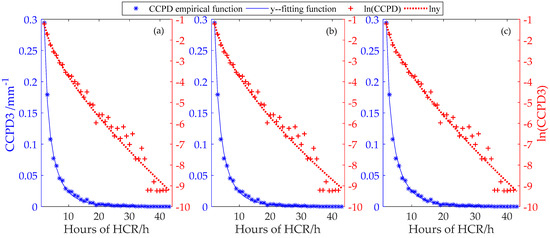
Figure 7.
The empirical function and the fitting function of CCPD2 in XV region (blue dot and line reference the left blue y-axis) and their logarithmic function (red dot and line reference the right red y-axis) by the (a) GΓD, (b) GND, and (c) Weibull distribution.
Among the 15 regions, the objective functions Obj of CCPD2 in the XIII region were the largest, and the Obj of CCPD3 in the XV region were the largest. Thus, the XIII region in Anhui Province and the XV region in Henan Province were chosen to draw a PDF fitting plot. Figure 6 shows the fitting results of the GΓD, GND, and Weibull distribution on CCPD2 in the XIII regions, and Figure 7 shows it on CCPD3 in the XV regions. Similar to the results of CCPD1, all three of the distribution effectively fit CCPD2 and CCPD3.
It is obvious that the smoothness of the CCPD2 and CCPD3 curve is poor, and that of CCPD3 is the worst. The reason is that the sample size was about four to six times smaller than that of CCPD1 because the mean duration of the HCR was about 4~6 h.
Other than the two cases above, the other regions were not plotted. It can be concluded that the three-parameter Weibull distribution performed relatively poorly compared to the GΓD and GND because there are larger deviations between the empirical function and the fitting function at the head of the curve (weak rainfall section). This point can be seen more clearly in the error analysis below.
4.3. Fitting Error Analysis of Three CCPD Classes
The fitting effect was roughly analyzed by observing the PDF fitting plot and more carefully based on the error analysis and goodness-of-fit table. Table 3 shows the objective function Obj, fitting error, and the coefficient of determination of CCPD1 in the fifteen regions. The fitting error contains Er0 and Er1, which are similar to the ERMS and ERMS of Obj except that Er0 and Er1 do not contain the weight series as statistics. Er0 represents the relative fitting deviations in the additive models and Er1 in the multiplicative error models. The coefficients of determination, that is, the goodness of fit, were denoted as R2 and Rln2, respectively, corresponding to CCPD1 and ln(CCPD1). The x-axis shifted to the left by 0.06 mm in the fitting process. The fitting parameters of CCPD1 in the 15 regions are provided for readers to refer to and verify in Table A1 (see Appendix A). In Table 3, it can be seen that the relative fitting deviations of CCPD1 in the 15 regions were less than 2.3%, and the relative fitting deviations of ln (CCPD1) were less than 3.3%. The coefficients of determination were all above 0.98 for CCPD1 and greater than 0.94 for ln(CCPD1). Therefore, the three distributions containing three-parameter Weibull distribution had good fitting capability for CCPD1. As shown in Table 3, the GΓD and GND were better than the three-parameter Weibull distribution for a smaller ERMS and ERMS_ and a larger R2 and Rln2. Comparing the Er0 and Er1 of GΓD with GND revealed that the GΓD performed better due to its broad spectrum (GND is a special type of GΓD). In order by fitting effect, the first was GΓD, the second was GND, and the last was Weibull distribution. In addition, with respect to the deviation and the coefficients of determination, GΓD and GND were comparable in their fitting accuracy.

Table 3.
The objective function, fitting error, and coefficient of determination of CCPD1 in fifteen regions.
The fitting parameters of CCPD2 and CCPD3 in the 15 regions are given in Table A2 and Table A3. Table A4 and Table A5 show the fitting of statistical values (the objective function, error, and goodness of fit) of the three fitting functions of CCPD2 and CCPD3 in the fifteen regions. As shown in Table A4 and Table A5, the conclusion is the same as before: Weibull distribution had the worse fitting ability compared to GΓD or GND, and the fitting performance of GΓD was slightly better than GND. Moreover, all of the errors were less than 7%, and each goodness of fit was larger than 0.93. The ERMS, R2, and Rln2 using GΓD were approximately the same as using GND.
By this time, the competitiveness of the Weibull distribution was less than the GΓD and GND. The discussion about the Weibull distribution is not discussed below. Between the GΓD and GND, ERMS and ERMS had small differences, but R2 and Rln2 were almost the same. Is GΓD with three arguments an optimal function by a slim margin rather than GND with two arguments? No, the winner is still uncertain.
4.4. Analysis on the Selection of Theoretical Density Function
The above analysis shows that the fitting accuracies of GΓD and GND were relatively higher for the three CCPD classes, and the fitting deviation was affected by the observation error. In this section, a comparative analysis is conducted to select an optimal theoretical density function according to the three criteria mentioned in Section 3.3.
Table 4 shows the BIC values of the GΓD, GND, and Weibull distribution in each region. It was found that the BIC values of the GND were generally lower than the BIC values of the GΓD. GΓD won zero times, while GND won 14 times among 15 regions for CCPD1. Meanwhile, GND gained a complete victory for CCPD2, as it did for CCPD3. This indicates that GND can be the optimal function and is more appropriate for CCPD. As is known, GND is a special kind of GΓD, while GΓD has a broader spectrum due to more parameters. If GND and GΓD are comparable in their fitting accuracy, overfitting may be a concern when using GΓD if the observation error is not excluded.

Table 4.
Bayesian information criterion (BIC) values for GΓD, GND, and Weibull distribution in each region.
AIC had similar ability to BIC, with a lower penalty term than BIC. Table A6 presents the AIC values and proves that GND was again superior.
Figure 8a shows the observed AARs and their estimation using GΓD and GND. The observed AARs were calculated by the mean rainfall of all the stations in a region during a 14-year observation period. It can be seen that the estimated values by the two functions were close to the observed AARs in each region. Additionally, it can be seen that the regions’ mean value is farthest to the right, and the estimation value is almost equal using GΓD or GND. That is, GΓD and GND had a stronger ability to estimate the AACRs with spatial variation. In addition, the estimated relative errors in the XII, XIII, and XV regions were larger than the other regions because the ratio of the lost data was larger in those regions. Figure 8b shows the AACRs and their estimation regarding only continuous rain. Similar to Figure 8a, it shows that GΓD and GND can also be used to estimate AACRs.
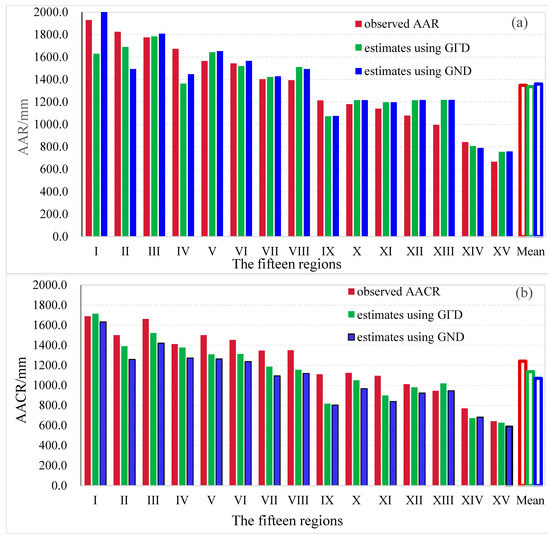
Figure 8.
The observed AARs (a) and AACRs (b) and their estimation using GΓD and GND.
Table 5 shows the relative errors and correlation coefficients of the estimated and observed AARs and AACRs in each region. Comparing GND with GΓD using the four values in the table, GND wins three out of four times. As shown in this table, the correlation coefficients of the AACRs were both approximately 0.95 and approximately 0.92 for the AAR. These results indicate that the estimated value using both GΓD and GND can well reflect the spatial variation characteristics of the AAR and AACR in different regions. In addition, the mean relative error was about 8.7% in the estimated AARs using both GΓD and GND, and in the estimated AARs, it was 9.7% using GΓD and 13.6% using GND. Therefore, both GΓD and GND were used to estimate the AAR. The AACR estimated error was larger than that of the AAR because the sample size was about four to six times smaller. Both could have been used to estimate the AACR if the rain sample size was long enough.

Table 5.
The relative error and correlation coefficient between the estimated and observed values of AAR and AACR.
GND was suitable for all of the domains that were larger than 0, and suitable for three CCPD classes and all fifteen regions. In addition to high accuracy, universality was also high. GND has a simple function form and two parameters that are a special type of GΓD. Although GΓD had a slightly higher accuracy for fitting the hourly rainfall probability distribution than the GND, it might have a risk of overfitting. GND can calculate less and obtain more than GΓD. Using GND to fit the rainfall PDF follows the parsimonious principle.
In short, GND is comparable to GΓD and can be used to fit CCPD with high accuracy and universality. Therefore, the GND is recommended as the optimal theoretical density function following the parsimonious principle.
5. Conclusions and Discussion
There has been no consensus on the unified model of a theoretical distribution function, although a lot of research has been carried out on rainfall probability distributions for a long time. Perhaps the problem is hidden in the multiple links of the whole chain, which contains screening applicable functions, sampling, fitting, parameter testing, setting the preference criterion, and the optimal function, which needs to be renovated. Among these, the key lies in the preference criterion, which must be on a strict scale when the rain sample size is big enough.
Three criteria are proposed in this study when fitting has high precision and it is hard to select by the probability plot. These are the BIC and the estimation accuracy of both the AAR and AACR. The criteria, which are on a stricter scale than previous studies, aim to select an optimal theoretical function among the applicable functions.
Using three applicable functions in 15 regions, the relative fitting deviations on CCPD1 were less than 2.3%, and the relative fitting deviations of ln(CCPD1) were less than 3.3%. The coefficients of determination were all above 0.98 for CCPD1 and greater than 0.94 for ln(CCPD1). GΓD, GND, and Weibull distribution could well fit the three classes of CCPDs with high accuracy, but the fitting performance of the Weibull distribution was relatively poor according to the probability plot and error analysis.
GΓD had the highest fitting accuracy for the three classes of CCPDs, but there is a worry about the overfitting phenomenon due to its broad spectrum. While the fitting performance of GND with fewer parameters is comparable to that of GΓD, GND is recommended as the theoretical density function according to the optimal criteria. The function form of GND is simple. For the rainfall PDF, GND follows the parsimonious principle, and it is suitable for the whole domain. For fitting CCPD1 using GND, the mean relative fitting deviation was 0.6%, and the coefficient of determination was 0.999; for ln (CCPD1), these values were 1.45% and 0.989, respectively.
Some parameter estimation methods for probability distribution functions seem to obtain accurate solutions, but these solutions are approximate solutions for the fitting problems due to parameter independence, error effect, the applicability of functions, and other problems. The genetic algorithm was selected to obtain the approximate solution for the parameters through optimization. The parameter optimization criterion is the objective function of the genetic algorithm. This can simplify the derivation and calculation steps. In the objective functions, both the multiplicative and additive fitting errors are considered. So, both ends of the fitting curve can be fitted with high accuracy.
GND performed well in fitting the AARs with an 8.6% relative error, and the correlation coefficient between the estimated and observed AARs was 0.92 among the fifteen regions, indicating that GND can well reflect the spatial variation characteristics of the AAR.
The period of observational data that we used was too short to provide information on climate statistics. So, the ability of our statistical rainfall PDF parameters to represent climate values is limited. The curve smoothness of the CCPD3 and CCPD2 empirical function was not enough, so the fitting error was large, and the estimated error of the AACR was large. It was assumed that this should be improved by using the data of regional gauges. The data quality of the national station is good, and the period is longer, but there are more regional gauge data because of the higher spatial density. So, how to make use of regional gauge data for big data statistics with fine quality control will be a challenge for us. In addition, the GA had a defect, which is that the parameter solution may have been obtained from the local optimal instead of the global optimal, even though genetic variation and large population numbers were used to search global optimal solutions as much as possible. Although it has been found that GND has high accuracy and strong universality for the fitting of hourly precipitation, it is still necessary to further discuss the universality of GND on daily, monthly, seasonal, sub-hour, and sub-day rainfall. In addition, it is worth exploring the universality of CCPD classification in more regions too. We look forward to working with scholars interested in this topic to solve the international problem of an “accepted unified model” as soon as possible.
Author Contributions
Methodology, Software, Data, Writing, Review, T.S.; Writing, Review & Editing, Y.X. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Meteorological Science and Technology Development Fund of Hubei Province in China (2021Y03, 2022Y26, 2022Y06), the Basic Research Fund of WHIHR (202204, 202210, 202306, 202314), the National and Provincial Coordination (CXFZ2022J018, CXFZ2022-J019), the Hubei Provincial Natural Science Foundation (2022CFD129, 2018CFB706).
Institutional Review Board Statement
Not applicable for our studies did not require ethical approval.
Informed Consent Statement
Not applicable for our studies not involving humans.
Data Availability Statement
We are grateful to the developers of the China Integrated Meteorological Information Sharing System (CMISS) for the precipitation datasets. We obtained the hourly rainfall data at these stations from the interface of the Meteorological Unified Service Interface Community service of the CIMISS [62,63]. The meteorological data from the CIMISS are classified according to the national standard of China GB/T 40153-2021 [64]. A quality control procedure was performed on the rainfall data [65]. The CIMISS server in Hubei Province stopped running and was upgraded to the meteorological big data cloud platform “Tianqing” in November 2022. To access “Tianqing”, one must obtain permission by strictly registering by their real name and submit the data list they require.
Acknowledgments
We would like to thank the China Integrated Meteorological Information Sharing System (CMISS) for providing the study datasets.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
Fitting parameters of three functions for CCPD1 in fifteen regions.
Table A1.
Fitting parameters of three functions for CCPD1 in fifteen regions.
| Region | GND | GΓD | Weibull | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Code | Location | b11 | n11 | a12 | b12 | n12 | c13 | b13 | n13 |
| I | GuangDong | 4.2757 | 0.2662 | 1.5926 | 1.8499 | 0.3894 | 0.0108 | 0.9657 | 0.5116 |
| II | HaiNan | 4.5377 | 0.2444 | 2.4887 | 2.7613 | 0.3036 | 0.0652 | 0.9999 | 0.4814 |
| III | JiangXi | 3.5873 | 0.3203 | 2.5255 | 2.9033 | 0.3500 | 0.0051 | 1.0938 | 0.5279 |
| IV | GuangXi | 4.5118 | 0.2632 | 3.3774 | 4.0347 | 0.2777 | 0.0099 | 1.1617 | 0.4910 |
| V | ZheJiang | 3.2007 | 0.3626 | 2.3770 | 2.7578 | 0.3883 | 0.0027 | 1.1280 | 0.5582 |
| VI | FuJian | 3.6819 | 0.3114 | 2.5480 | 2.9276 | 0.3456 | 0.0046 | 1.1089 | 0.5178 |
| VII | HuNan | 3.8541 | 0.3199 | 2.4643 | 3.0722 | 0.3540 | 0.0066 | 1.3616 | 0.5220 |
| VIII | SiChuan | 4.5108 | 0.2857 | 7.4568 | 9.0707 | 0.2074 | 0.0063 | 1.8997 | 0.4694 |
| IX | GuiZhou | 5.3934 | 0.2543 | 6.8078 | 8.7822 | 0.2022 | 0.0128 | 2.0776 | 0.4624 |
| X | JiangSu | 3.3306 | 0.3423 | 3.0705 | 3.5003 | 0.3346 | 0.0018 | 1.1071 | 0.5353 |
| XI | ChongQing | 3.7542 | 0.3358 | 3.0986 | 3.8978 | 0.3300 | 0.0055 | 1.4681 | 0.5262 |
| XII | HuBei | 3.4818 | 0.3300 | 3.1928 | 3.6668 | 0.3222 | 0.0027 | 1.1350 | 0.5257 |
| XIII | AnHui | 3.4735 | 0.3308 | 3.4970 | 4.0128 | 0.3096 | 0.0019 | 1.1642 | 0.5210 |
| XIV | YunNan | 3.6738 | 0.3343 | 1.4807 | 1.8646 | 0.4430 | 0.0101 | 1.2038 | 0.5493 |
| XV | HeNan | 3.4022 | 0.3442 | 2.5497 | 2.9907 | 0.3654 | 0.0048 | 1.1357 | 0.5478 |

Table A2.
Fitting parameters of three functions for CCPD2 in fifteen regions.
Table A2.
Fitting parameters of three functions for CCPD2 in fifteen regions.
| Region | GND | GΓD | Weibull | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Code | Location | b21 | n21 | a22 | b22 | n22 | c23 | b23 | n23 |
| I | GuangDong | 2.1622 | 0.3057 | 4.1959 | 2.9496 | 0.2673 | −0.0357 | 0.2275 | 0.5398 |
| II | HaiNan | 2.2677 | 0.3029 | 6.0911 | 4.7203 | 0.2205 | −0.0312 | 0.2547 | 0.5347 |
| III | JiangXi | 2.1459 | 0.3186 | 4.8208 | 3.6162 | 0.2541 | −0.0314 | 0.2649 | 0.5423 |
| Iv | GuangXi | 2.3828 | 0.2991 | 8.8620 | 7.3830 | 0.1844 | −0.0224 | 0.2676 | 0.5202 |
| V | ZheJiang | 1.8736 | 0.3523 | 3.9639 | 2.8422 | 0.2962 | −0.0406 | 0.2756 | 0.5604 |
| VI | FuJian | 2.2007 | 0.3161 | 8.4726 | 6.9833 | 0.1943 | −0.0265 | 0.2668 | 0.5312 |
| VII | HuNan | 2.3085 | 0.3193 | 7.8272 | 6.6216 | 0.2022 | −0.0095 | 0.3010 | 0.5370 |
| VIII | SiChuan | 2.7388 | 0.2964 | 8.8259 | 7.9232 | 0.1884 | 0.0120 | 0.3406 | 0.5199 |
| IX | GuiZhou | 3.0451 | 0.2891 | 8.5237 | 7.9993 | 0.1915 | 0.0228 | 0.3973 | 0.5132 |
| X | JiangSu | 2.2272 | 0.3116 | 8.4893 | 6.9716 | 0.1915 | −0.0313 | 0.2676 | 0.5272 |
| XI | ChongQing | 2.1071 | 0.3494 | 7.8589 | 6.7282 | 0.2117 | −0.0113 | 0.3312 | 0.5555 |
| XII | HuBei | 2.0793 | 0.3294 | 8.5756 | 7.0602 | 0.1970 | −0.0297 | 0.2693 | 0.5415 |
| XIII | AnHui | 2.3178 | 0.3073 | 8.2362 | 6.8292 | 0.1937 | −0.0254 | 0.2791 | 0.5227 |
| XIV | YunNan | 1.5961 | 0.4000 | 2.6707 | 1.7348 | 0.3907 | −0.0319 | 0.2785 | 0.6013 |
| XV | HeNan | 2.3991 | 0.3025 | 8.3451 | 6.9924 | 0.1918 | −0.0173 | 0.2810 | 0.5213 |

Table A3.
Fitting parameters of three functions for CCPD3 in fifteen regions.
Table A3.
Fitting parameters of three functions for CCPD3 in fifteen regions.
| Region | GND | GΓD | Weibull | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Code | Location | b31 | n31 | a32 | b32 | n32 | c33 | b33 | n33 |
| I | GuangDong | 1.3230 | 0.5304 | 2.6339 | 1.9273 | 0.4698 | 0.1329 | 0.4113 | 0.7251 |
| II | HaiNan | 1.6270 | 0.4743 | 4.4013 | 3.6180 | 0.3590 | 0.1437 | 0.4564 | 0.6813 |
| III | JiangXi | 0.9522 | 0.5787 | 2.0025 | 1.1545 | 0.5426 | 0.1029 | 0.3015 | 0.7627 |
| Iv | GuangXi | 1.6492 | 0.4620 | 2.5451 | 1.9299 | 0.4421 | 0.1166 | 0.4620 | 0.6551 |
| V | ZheJiang | 0.8511 | 0.6029 | 1.9242 | 1.0406 | 0.5648 | 0.0936 | 0.2851 | 0.7763 |
| VI | FuJian | 1.1248 | 0.5475 | 2.7135 | 1.8305 | 0.4638 | 0.1260 | 0.3376 | 0.7413 |
| VII | HuNan | 0.9120 | 0.5919 | 2.2055 | 1.2912 | 0.5277 | 0.0955 | 0.3030 | 0.7663 |
| VIII | SiChuan | 0.6296 | 0.7073 | 1.1838 | 0.4840 | 0.7634 | 0.0533 | 0.2915 | 0.8321 |
| IX | GuiZhou | 1.0557 | 0.5828 | 2.4910 | 1.6528 | 0.5028 | 0.0865 | 0.3773 | 0.7482 |
| X | JiangSu | 0.8835 | 0.5934 | 1.5018 | 0.7552 | 0.6240 | 0.0929 | 0.2887 | 0.7727 |
| XI | ChongQing | 0.7400 | 0.6576 | 1.4637 | 0.7019 | 0.6682 | 0.0812 | 0.2957 | 0.8096 |
| XII | HuBei | 0.7786 | 0.6390 | 1.4989 | 0.7332 | 0.6513 | 0.0920 | 0.2923 | 0.8018 |
| XIII | AnHui | 0.9603 | 0.5734 | 1.4864 | 0.7770 | 0.6137 | 0.0942 | 0.3008 | 0.7560 |
| XIV | YunNan | 1.5623 | 0.5045 | 2.4727 | 1.9426 | 0.4756 | 0.1529 | 0.4720 | 0.7119 |
| XV | HeNan | 0.7608 | 0.6432 | 1.1315 | 0.4828 | 0.7371 | 0.0868 | 0.2894 | 0.8004 |

Table A4.
The objective function, fitting error, and determination coefficient of CCPD2 in each region.
Table A4.
The objective function, fitting error, and determination coefficient of CCPD2 in each region.
| Region | GND | GΓD | Weibull | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Code | Location | Obj | Er0 (%) | Er1 (%) | R2 | Rln2 | Obj | Er0 (%) | Er1 (%) | R2 | Rln2 | Obj | Er0 (%) | Er1 (%) | R2 | Rln2 |
| I | GuangDong | 2.89 | 1.72 | 0.94 | 0.995 | 0.997 | 2.86 | 1.60 | 1.02 | 0.995 | 0.996 | 4.73 | 3.12 | 1.85 | 0.983 | 0.987 |
| II | HaiNan | 3.79 | 2.24 | 1.42 | 0.991 | 0.992 | 3.72 | 1.96 | 1.69 | 0.993 | 0.988 | 5.31 | 3.60 | 1.82 | 0.978 | 0.986 |
| III | JiangXi | 4.30 | 2.81 | 1.17 | 0.987 | 0.994 | 4.25 | 2.59 | 1.32 | 0.989 | 0.992 | 5.80 | 4.17 | 1.74 | 0.971 | 0.987 |
| Iv | GuangXi | 4.83 | 3.52 | 1.30 | 0.981 | 0.994 | 3.99 | 2.60 | 1.17 | 0.990 | 0.995 | 7.69 | 5.78 | 2.23 | 0.948 | 0.982 |
| V | ZheJiang | 4.66 | 3.38 | 0.97 | 0.983 | 0.996 | 4.59 | 3.15 | 1.06 | 0.985 | 0.995 | 6.40 | 4.91 | 1.69 | 0.965 | 0.987 |
| VI | FuJian | 4.55 | 3.47 | 1.09 | 0.982 | 0.996 | 3.62 | 2.40 | 1.13 | 0.991 | 0.996 | 7.75 | 5.92 | 1.98 | 0.947 | 0.988 |
| VII | HuNan | 3.92 | 2.66 | 1.14 | 0.988 | 0.995 | 3.47 | 2.02 | 1.21 | 0.993 | 0.994 | 6.58 | 5.07 | 1.67 | 0.957 | 0.989 |
| VIII | SiChuan | 3.56 | 2.24 | 1.37 | 0.990 | 0.993 | 2.46 | 1.24 | 1.09 | 0.997 | 0.996 | 6.85 | 5.12 | 1.98 | 0.949 | 0.986 |
| IX | GuiZhou | 4.23 | 2.43 | 1.76 | 0.989 | 0.987 | 3.24 | 1.41 | 1.67 | 0.996 | 0.989 | 6.89 | 5.34 | 1.66 | 0.945 | 0.989 |
| X | JiangSu | 5.13 | 3.93 | 1.19 | 0.977 | 0.995 | 4.44 | 3.08 | 1.08 | 0.986 | 0.996 | 7.78 | 5.98 | 2.17 | 0.948 | 0.983 |
| XI | ChongQing | 4.38 | 2.77 | 1.49 | 0.988 | 0.990 | 3.54 | 1.81 | 1.45 | 0.995 | 0.991 | 7.28 | 5.55 | 1.86 | 0.951 | 0.984 |
| XII | HuBei | 5.03 | 3.68 | 1.36 | 0.980 | 0.993 | 3.83 | 2.44 | 1.19 | 0.991 | 0.995 | 8.30 | 6.28 | 2.28 | 0.943 | 0.981 |
| XIII | AnHui | 5.85 | 4.46 | 1.35 | 0.972 | 0.994 | 5.26 | 3.67 | 1.52 | 0.981 | 0.992 | 8.23 | 6.49 | 1.83 | 0.940 | 0.989 |
| XIV | YunNan | 2.55 | 1.65 | 0.81 | 0.996 | 0.998 | 2.48 | 1.55 | 0.84 | 0.996 | 0.997 | 5.39 | 4.16 | 1.33 | 0.972 | 0.993 |
| XV | HeNan | 5.48 | 4.24 | 1.15 | 0.972 | 0.996 | 4.97 | 3.55 | 1.25 | 0.980 | 0.995 | 7.97 | 6.31 | 1.78 | 0.938 | 0.989 |
| Maximum/Minimum | 5.85 | 4.46 | 1.76 | 0.972 | 0.987 | 5.26 | 3.67 | 1.69 | 0.980 | 0.988 | 8.30 | 6.49 | 2.28 | 0.938 | 0.981 | |
| average | 4.34 | 3.01 | 1.23 | 0.985 | 0.994 | 3.78 | 2.34 | 1.25 | 0.991 | 0.994 | 6.87 | 5.18 | 1.86 | 0.956 | 0.987 | |

Table A5.
The objective function, fitting error, and determination coefficient of CCPD3 in each region.
Table A5.
The objective function, fitting error, and determination coefficient of CCPD3 in each region.
| Region | GND | GΓD | Weibull | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Code | Location | Obj | Er0 (%) | Er1 (%) | R2 | Rln2 | Obj | Er0 (%) | Er1 (%) | R2 | Rln2 | Obj | Er0 (%) | Er1 (%) | R2 | Rln2 |
| I | GuangDong | 3.81 | 0.86 | 3.28 | 0.998 | 0.981 | 3.24 | 0.32 | 3.30 | 1.000 | 0.981 | 3.94 | 0.77 | 3.39 | 0.998 | 0.980 |
| II | HaiNan | 4.16 | 1.43 | 2.32 | 0.993 | 0.989 | 3.18 | 0.44 | 2.45 | 0.999 | 0.988 | 4.10 | 1.15 | 2.73 | 0.996 | 0.985 |
| III | JiangXi | 3.07 | 0.33 | 2.81 | 1.000 | 0.989 | 3.00 | 0.27 | 2.84 | 1.000 | 0.988 | 3.39 | 0.48 | 2.89 | 0.999 | 0.988 |
| Iv | GuangXi | 3.35 | 1.28 | 2.13 | 0.995 | 0.993 | 2.96 | 0.90 | 2.18 | 0.997 | 0.992 | 4.04 | 1.36 | 2.76 | 0.994 | 0.988 |
| V | ZheJiang | 2.67 | 0.42 | 2.46 | 0.999 | 0.992 | 2.60 | 0.34 | 2.49 | 1.000 | 0.991 | 3.02 | 0.73 | 2.46 | 0.998 | 0.992 |
| VI | FuJian | 3.15 | 0.70 | 2.34 | 0.999 | 0.991 | 2.68 | 0.18 | 2.38 | 1.000 | 0.990 | 3.24 | 0.86 | 2.36 | 0.998 | 0.991 |
| VII | HuNan | 2.81 | 0.41 | 2.66 | 1.000 | 0.990 | 2.55 | 0.22 | 2.57 | 1.000 | 0.991 | 3.47 | 0.69 | 3.07 | 0.999 | 0.987 |
| VIII | SiChuan | 3.99 | 0.83 | 3.40 | 0.998 | 0.983 | 3.91 | 0.74 | 3.42 | 0.998 | 0.983 | 3.70 | 0.44 | 3.54 | 0.999 | 0.981 |
| IX | GuiZhou | 3.79 | 0.55 | 3.30 | 0.999 | 0.986 | 3.45 | 0.39 | 3.12 | 1.000 | 0.988 | 4.71 | 0.62 | 4.14 | 0.999 | 0.978 |
| X | JiangSu | 3.45 | 0.51 | 3.36 | 0.999 | 0.981 | 3.42 | 0.50 | 3.33 | 0.999 | 0.982 | 3.18 | 0.36 | 3.24 | 1.000 | 0.983 |
| XI | ChongQing | 3.19 | 0.47 | 2.89 | 0.999 | 0.990 | 3.17 | 0.45 | 2.90 | 0.999 | 0.990 | 3.24 | 0.26 | 3.18 | 1.000 | 0.988 |
| XII | HuBei | 3.45 | 0.37 | 2.76 | 1.000 | 0.986 | 3.45 | 0.37 | 2.78 | 1.000 | 0.986 | 3.42 | 0.37 | 2.94 | 1.000 | 0.985 |
| XIII | AnHui | 4.09 | 0.61 | 3.49 | 0.999 | 0.985 | 4.02 | 0.57 | 3.41 | 0.999 | 0.985 | 3.52 | 0.32 | 3.14 | 1.000 | 0.988 |
| XIV | YunNan | 5.31 | 1.16 | 2.92 | 0.995 | 0.976 | 4.85 | 0.69 | 3.10 | 0.998 | 0.973 | 5.11 | 0.76 | 3.50 | 0.998 | 0.966 |
| XV | HeNan | 5.84 | 1.00 | 5.22 | 0.997 | 0.965 | 5.69 | 0.98 | 5.05 | 0.997 | 0.967 | 5.40 | 0.99 | 4.74 | 0.997 | 0.971 |
| Maximum/Minimum | 5.84 | 1.43 | 5.22 | 0.993 | 0.965 | 5.69 | 0.98 | 5.05 | 0.997 | 0.967 | 5.40 | 1.36 | 4.74 | 0.994 | 0.966 | |
| average | 3.74 | 0.73 | 3.02 | 0.998 | 0.985 | 3.48 | 0.49 | 3.02 | 0.999 | 0.985 | 3.83 | 0.68 | 3.21 | 0.998 | 0.983 | |

Table A6.
Akaike information criterion (AIC) values for GΓD, GND, and Weibull in each region.
Table A6.
Akaike information criterion (AIC) values for GΓD, GND, and Weibull in each region.
| Class | Win Rate | Function | I | II | III | IV | V | VI | VII | VIII | IX | X | XI | XII | XIII | XIV | XV |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0/15 | GΓD | 0.0 | 1.7 | −2.9 | 1.4 | −0.1 | −2.4 | −1.3 | −1.6 | 0.8 | −0.6 | 0.2 | −1.4 | −1.7 | −0.2 | 0.6 | |
| CCPD1 | 12/15 | GND | 1.4 | 0.0 | −3.4 | 0.4 | −2.0 | −2.2 | −2.8 | −3.1 | −1.0 | −2.7 | −1.8 | −3.3 | −3.7 | −1.6 | −1.3 |
| 3/15 | Weibull | −1.5 | −0.7 | −1.5 | 2.4 | 1.1 | −2.4 | 4.1 | 5.6 | 6.6 | 1.1 | 5.4 | 0.0 | 0.1 | 3.1 | 1.8 | |
| 0/15 | GΓD | 1.4 | 2.2 | 3.0 | 0.9 | 2.9 | −0.3 | 2.3 | 1.1 | 2.6 | 1.2 | 3.7 | 1.4 | 1.1 | 1.0 | 0.7 | |
| CCPD2 | 15/15 | GND | −1.0 | −0.7 | 0.4 | −2.0 | 0.4 | −3.8 | −0.9 | −1.7 | 0.1 | −1.8 | 0.6 | −1.7 | −2.1 | −0.9 | −2.5 |
| 0/15 | Weibull | 13.6 | 13.1 | 13.1 | 12.5 | 13.5 | 12.9 | 12.6 | 11.6 | 10.7 | 12.7 | 12.7 | 13.1 | 12.4 | 14.7 | 12.4 | |
| 0/15 | GΓD | −0.4 | −1.4 | −1.8 | −2.7 | −2.6 | −1.7 | −3.0 | −0.2 | −0.8 | −0.7 | −1.6 | −0.3 | −2.3 | 2.3 | 1.9 | |
| CCPD3 | 15/15 | GND | −2.5 | −3.7 | −3.8 | −4.8 | −4.7 | −4.0 | −4.9 | −2.2 | −2.6 | −2.7 | −3.6 | −2.3 | −4.1 | 0.3 | 0.0 |
| 0/15 | Weibull | 14.5 | 13.1 | 16.9 | 12.6 | 17.4 | 15.8 | 16.9 | 18.4 | 15.8 | 17.2 | 17.9 | 17.8 | 16.7 | 13.5 | 17.7 |
References
- Pendergrass, A.G.; Hartmann, D.L. Changes in the Distribution of Rain Frequency and Intensity in Response to Global Warming. J. Clim. 2014, 27, 8372–8383. [Google Scholar] [CrossRef]
- Pendergrass, A.G.; Knutti, R. The uneven nature of daily precipitation and its change. Geophys. Res. Lett. 2018, 45, 11980–11988. [Google Scholar] [CrossRef]
- Dai, A.; Rasmussen, R.M.; Liu, C.; Ikeda, K.; Prein, A.F. A new mechanism for warm-season precipitation response to global warming based on convection-permitting simulations. Clim. Dyn. 2020, 55, 343–368. [Google Scholar] [CrossRef]
- Mei, C.; Liu, J.H.; Wang, H.; Xiang, C.; Zhou, J. Review on Urban Design Rainstorm. Chin. Sci. Bull. 2017, 62, 3873–3884. [Google Scholar] [CrossRef]
- Liu, J.; Zhou, H.; Lu, C.H.; Gao, C. A Review on Recent Advances of Urban Rainfall Intensity-Duration-Frequency Relationships. Adv. Water Sci. 2018, 29, 898–910. [Google Scholar]
- Lin, B.Z.; Lan, P.; Zhang, Y.H.; Lin, Z.C.; Chen, X.Y. Review on estimation of probable maximum precipitation estimation. J. Hydraul. Eng. 2018, 49, 92–102,114. [Google Scholar]
- Clark, C.; Dent, J.L. New Estimates of 24-h Probable Maximum Precipitation (PMP) for the British Isles. J. Geosci. Environ. Prot. 2021, 9, 209–228. [Google Scholar] [CrossRef]
- Liu, L.; Chen, J.; Cheng, L.; Lin, C.; Wu, Z. Study of the ensemble-based forecast of extremely heavy rainfalls in China: Experiments for July 2011 cases. Acta Meteorol. Sin. 2013, 71, 853–866. [Google Scholar] [CrossRef]
- Benkaci, T.; Mezenner, N.; Dechemi, N. Exploration of maximum likelihood method in extreme rainfall forecasting using four probability distributions-The case of northern Algeria. Larhyss J. 2020, 43, 57–72. [Google Scholar]
- Su, X.; Yuan, H.L.; Zhu, Y.J. A comparative study of four objective quantitative precipitation forecast calibration methods. Acta Meteorol. Sin. 2021, 79, 132–149. [Google Scholar] [CrossRef]
- Watterson, I.G.; Dix, M.R. Effective sensitivity and heat capacity in the response of climate models to greenhouse gas and aerosol forcings. Q. J. R. Meteorol. Soc. 2005, 131, 259–279. [Google Scholar] [CrossRef]
- Yoo, C.; Jung, K.S.; Kim, T.W. Rainfall frequency analysis using a mixed Gamma distribution: Evaluation of the global warming effect on daily rainfall. Hydrol. Process. 2005, 19, 3851–3861. [Google Scholar] [CrossRef]
- Falkovich, A.; Lord, S.; Treadon, R. A new methodology of rainfall retrievals from indirect measurements. Meteorol. Atmos. Phys. 2000, 75, 217–232. [Google Scholar] [CrossRef]
- Yu, J.J.; Shen, Y.; Pan, Y.; Zhao, P.; Zhou, Z. Improvement of probabilistic density matching method on satellite precipitation data over China. J. Appl. Meteorol. 2013, 24, 544–553. [Google Scholar]
- Shen, Y.; Pan, Y.; Yu, J.J. Quality evaluation of regional hourly precipitation fusion products in China. J. Atmos. Sci. 2013, 36, 37–46. [Google Scholar]
- Pulkkinen, S.; Koistinen, J.; Kuitunen, T.; Harri, A.-M. Probabilistic radar-gauge merging by multivariate spatiotemporal techniques. J. Hydrol. 2016, 542, 662–678. [Google Scholar] [CrossRef]
- Pan, Y.; Gu, J.X.; Xu, B. Research and application progress of multi-source precipitation data fusion. Adv. Meteorol. Sci. Technol. 2018, 8, 143–152. [Google Scholar]
- Watterson, I.G.; Dix, M.R. Simulated changes due to global warming in daily precipitation means and extremes and their interpretation using the gamma distribution. J. Geophys. Res. 2003, 108, 4379. [Google Scholar] [CrossRef]
- Li, Z.; Brissette, F.; Chen, J. Finding the most appropriate precipitation probability distribution for stochastic weather generation and hydrological modelling in Nordic watersheds. Hydrol. Process. 2013, 27, 3718–3729. [Google Scholar] [CrossRef]
- Yuan, W.; Fu, L.; Gao, Q. Study on extreme precipitation probability distribution-based estimation model of early warning index for mountain torrent disaster. Water Resour. Hydropower Eng. 2019, 50, 17–24. [Google Scholar]
- Zarei, A.R. Evaluation of effect of Markov order on the accuracy of drought forecasting Based on SPEI index using Markov Chain method. Watershed Eng. Manag. 2019, 11, 88–100. [Google Scholar]
- Li, S.; Liu, S.; Zhu, Y.; Zhang, J. Applicability of weather generator based on dry and wet spells (WGDWS) in five climate regions of China. Trans. Chin. Soc. Agric. Eng. 2022, 38, 75–83. Available online: http://www.tcsae.org/10.11975/j.issn.1002-6819.2022.03.009 (accessed on 12 June 2023). [CrossRef]
- Zhou, J.Z.; Wang, Y.R.; Feng, K.X.; Yang, X.; Fang, W.; Jing, Q.F.; Cha, G.; He, Z.Z.; Jia, B.J.; Wu, H. A Hydrological Forecasting Method and System Considering Rainfall Grade. China Patent CN111126699A, 8 May 2020. (In Chinese). [Google Scholar]
- Xiang, X.L.; Sun, W.F.; Tan, C.X.; Hou, C.T.; Ren, H.F.; Liu, M.J. Calculation method of instability probability of rainfall-type landslide. Geol. Bull. China 2020, 37, 176–181. (In Chinese) [Google Scholar]
- van Dijk, A.; Meesters, A.; Schellekens, J.; Bruijnzeel, L. A two-parameter exponential rainfall depth-intensity distribution applied to runoff and erosion modelling. J. Hydrol. 2004, 300, 155–171. [Google Scholar] [CrossRef]
- Michelangeli, P.A.; Vrac, M.; Loukos, H. Probabilistic downscaling approaches: Application to wind cumulative distribution functions. Geophys. Res. Lett. 2009, 36, 163–182. [Google Scholar] [CrossRef]
- Zhou, L.; Jiang, Z.H. Future changes in precipitation over Hunan Province based on CMIP5 simulations using the statistical downscaling method of transform cumulative distribution function. Acta Meteorol. Sin. 2017, 75, 223–235. [Google Scholar] [CrossRef]
- Chen, J.; Chen, H.; Guo, S. Multi-site precipitation downscaling using a stochastic weather generator. Clim. Dyn. 2018, 50, 1975–1992. [Google Scholar] [CrossRef]
- Wu, W.; Liang, Z.; Liu, X. Projection of the daily precipitation using CDF-T method at meteorological observation site scale. Plateau Meteorol. 2018, 37, 796–805. [Google Scholar]
- Teegaravapu, R.S.V. Statistical corrections of spatially interpolated missing precipitation data estimates. Hydrol. Process 2014, 28, 3789–3808. [Google Scholar] [CrossRef]
- Mohammad, T.S.; Ali Rezazadeh, J.; Andrew, K. Assessment of different methods for estimation of missing data in precipitation studies. Hydrol. Res. 2016, 48, 1032–1044. [Google Scholar] [CrossRef]
- Deng, P.D. One’s again on problems in urban storm statistics. Water Wastewater Eng. 1998, 24, 15–19. [Google Scholar] [CrossRef]
- Su, B.D.; Jiang, T. Distribution characteristics of precipitation extreme time series in the Yangtze River Basin. Lake Sci. 2008, 20, 125–130. [Google Scholar]
- Zhang, Y.H.; Wang, S.X.; Liu, K.L.; Chen, Q.H. Applicability Analysis of Rainfall Extremes with Different Probability Distribution Functions. Sci. Geogr. Sin. 2015, 35, 1460–1467. [Google Scholar]
- Ghanmi, H.; Bargaoui, Z.; Mallet, C. Estimation of intensity-duration-frequency relationships according to the property of scale invariance and regionalization analysis in a Mediterranean coastal area. J. Hydrol. 2016, 541, 38–49. [Google Scholar] [CrossRef]
- Song, X.M.; Zhang, J.Y.; Kong, F.Z. Probability Distribution of Extreme Precipitation in Beijing Based on Extreme Value Theory. Sci. China Sci. Technol. 2018, 48, 639–650. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, X.R.; Cheng, B.Y.; Sun, J.; Liao, D.Q. Application of generalized extreme value distribution model to short-duration extreme precipitation in Chongqing. Meteor. Mon. 2019, 45, 820–830. [Google Scholar] [CrossRef]
- Progênio, M.F.; Blanco, C. Cumulative distribution function of daily rainfall in the Tocantins–Araguaia hydrographic region, Amazon, Brazil. Nat. Resour. Model. 2020, 38, e12264. [Google Scholar] [CrossRef]
- Papalexiou, S.M.; Koutsoyiannis, D. A global survey on the seasonal variation of the marginal distribution of daily precipitation. Adv. Water Resour. 2016, 94, 131–145. [Google Scholar] [CrossRef]
- Gu, X.Z.; Ye, L.; Zhao, T.T.G.; Aoyang, W.Y.; Zhang, C. Probability distribution of daily precipitation in China. J. Hydraul. Eng. 2021, 52, 1248–1262, (In Chinese with English Abstract). [Google Scholar]
- Wang, X.Y.; Jiang, W.G.; Deng, Y.; Jiang, Z.J. Characteristic Analysis and Fatalness of Disaster-inducing Factors Assessment of Hourly Extreme Rainfall in Different Return Periods of Beijing-Tianjin-Hebei Region. Geogr. Res. 2020, 39, 2581–2592. [Google Scholar]
- Wang, L.; Chen, R.S.; Song, Y.X. Study of statistical characteristics of wet season hourly rainfall at Hulu watershed with Γ function in Qilian Mountains. Adv. Earth Sci. 2016, 31, 840–848. [Google Scholar]
- Wang, B.Y.; Zhao, L.N.; Xu, H.; Liu, Y. Probability Distribution and Partition of Hourly Rainfall During the Rainy Season over Sichuan Province. Torrential Rain Disasters 2018, 37, 115–123. [Google Scholar]
- Singh, V.P.; Guo, H. Parameter Estimations for 3-parameter Generalized Pareto Distribution by the Principle of Maximum Entropy (POME). Hydrol. Sci. J. 1995, 40, 165–181. [Google Scholar] [CrossRef]
- Krylov, V.A.; Moser, G.; Serpico, S.B.; Zerubia, J. On the Method of Logarithmic Cumulants for Parametric Probability Density Function Estimation. IEEE Trans. Image Process. 2013, 22, 3791–3806. [Google Scholar] [CrossRef] [PubMed]
- Li, H.C.; Liu, C.A. Multitexture Model of Multilook Polarimetric SAR Data Based on Generalized Gamma Distribution. In Proceedings of the IEEE International Geoscience & Remote Sensing Symposium, Beijing, China, 10–15 July 2016; pp. 174–177. [Google Scholar]
- Qin, X.X.; Gao, G.; Zhou, S.L.; Zou, H.X. Method on Parameters Estimation of Generalized Gamma Distribution Based on SISE (scale-independent-shape-estimation) Equation. J. Electron. Inf. Technol. 2012, 34, 1860–1865. [Google Scholar] [CrossRef]
- Song, K.S. Asymptotic Relative Efficiency and Exact Variance Stabilizing Transformation for the Generalized Gaussian Distribution. IEEE Trans. Inf. Theory 2013, 59, 4389–4396. [Google Scholar] [CrossRef]
- Zhang, S.S.; Dong, Y.Y.; Qiao, Y.X. A Novel Target Detection Algorithm with Generalized Gamma Distribution in SAR Images. J. Nav. Aeronaut. Astronaut. Univ. 2020, 35, 167–175. [Google Scholar]
- Zhang, Y.; Ding, Y. A General Gamma probability model for Precipitation in various periods. Acta Meteorol. Sin. 1991, 49, 80–84. [Google Scholar] [CrossRef]
- Vlček, O.; HuthIs, R. Daily precipitation Gamma-distributed?: Adverse effects of an incorrect use of the Kolmogorov–Smirnov test. Atmos. Res. 2009, 93, 759–766. [Google Scholar] [CrossRef]
- Ye, L.; Hanson, L.S.; Ding, P.; Wang, D.; Vogel, R.M. The probability distribution of daily precipitation at the point and catchment scales in the United States. Hydrol. Earth Syst. Sci. 2018, 22, 6519–6531. [Google Scholar] [CrossRef]
- Shoji, T.; Kitaura, H. Statistical and geostatistical analysis of rainfall in central Japan. Comput. Geosci. 2006, 32, 1007–1024. [Google Scholar] [CrossRef]
- Li, C.; Singh, V.P.; Mishra, A.K. Simulation of the entire range of daily precipitation using a hybrid probability distribution. Water Resour. Res. 2012, 48, W03521. [Google Scholar] [CrossRef]
- Li, Z.; Brissette, F.; Chen, J. Assessing the applicability of six precipitation probability distribution models on the Loess Plateau of China. Int. J. Climatol. 2014, 34, 462–471. [Google Scholar] [CrossRef]
- Yuan, Z.; Yan, D.H.; Yang, Z.Y.; Yin, J.; Yuan, Y. Research on temporal and spatial change of 400 mm and 800 mm rainfall contours of China in 1961–2000. Adv. Water Sci. 2014, 25, 494–502. [Google Scholar] [CrossRef]
- Shen, T.Y.; Liu, J.; Xiang, Y.H.; Qi, H.X.; Ying, Z.Y.; Wang, J.C. Partition Comparison and Fitting Function of Class Conditional Probability Density of Hourly Rainfall. Torrential Rain Disasters 2021, 40, 664–674. [Google Scholar] [CrossRef]
- Shen, T.; Xiang, Y.; Liao, Y.; Qi, H.; Wang, J.; Yu, D. Function applicability to class conditional probability density of hourly rainfall. J. Lake Sci. 2023, 35, 743–754. [Google Scholar] [CrossRef]
- Steinskog, D.J.; Tjøstheim, D.B.; Kvamstø, N.G. A Cautionary Note on the Use of the Kolmogorov–Smirnov Test for Normality. Mon. Weather. Rev. 2007, 135, 1151–1157. [Google Scholar] [CrossRef]
- Schwarz, G. Estimating the dimension of a model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Xiong, A.Y.; Zhao, F.; Wang, Y.; Zhang, X.; Feng, G.; Li, D.; Tan, X.; Qiang, M. Design and implementation of national integrated meteorological information sharing system. J. Appl. Meteorol. 2015, 26, 500–512. [Google Scholar]
- Fang, Z.; Anyuan, X.; Xiaoying, Z.; Li, D.; Ying, W.; Qiang, M.; Xin, Y.; Xiaohua, T.; Feng, G. Technical characteristics of architecture design of national integrated meteorological information sharing platform. J. Appl. Meteorol. 2017, 28, 750–758. [Google Scholar]
- GB/T 40153-2021; Classification and Coding of Meteorological Data. The State Administration for Market Regulation. Standardization Administration of the State: Beijing, China, 2021.
- Ren, Z.H.; Zhang, Z.F.; Sun, C.; Liu, Y.M.; Li, J.; Ju, X.H.; Zhao, Y.F.; Li, Z.P.; Zhang, W.; Li, H.K.; et al. Development of Three-Step Quality Control System of Real-Time Observation Data from AWS in China. Meteorol. Mon. 2015, 41, 1268–1277. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).