Abstract
In recent decades, the United States has experienced changing patterns of extreme temperature. Although much progress has been made, delineating the change in synoptic surface temperature variability (SSTV) and understanding its potential causes remain to be pursued. In this study, we seek to provide a quantitative description of the change in SSTV in the past seven decades across the US and its potential relevant physical factors. To achieve this goal, we develop a spatiotemporally local analysis method based on the ensemble empirical mode decomposition that bypasses the stationary assumption and makes it possible to continuously track the change in SSTV in the spatiotemporal domain. We have found that the change in SSTV across the US is spatially inhomogeneous and temporally non-uniform. The change in the SSTV amplitude ranges from −36% to 39% across the continental United States, Northern Mexico, and surrounding oceans. Higher altitudes and surrounding regions generally see an increase in variability, while elsewhere over land, a reduction is observed, creating a three-band zonal structure across the continental United States. Generally, increases in variability are observed in the subtropics. The shape of the spatiotemporal evolution of SSTV implies that the topography of the United States may play an important role in altering synoptic-scale variability.
1. Introduction
With the continuing human-produced greenhouse gas input into the atmosphere, the Earth’s climate has been warming at an unprecedented pace and in a spatiotemporally non-uniform fashion [1,2,3], especially in the high-latitude regions where warming is the most dramatic [4,5,6,7]. Associated with this slowly spatiotemporally varying warming, synoptic-scale weather variability at the mid-latitudes has also been changing, and with the reduced meridional temperature gradient caused by polar warming amplification, the synoptic variability generated by meridional advection is anticipated to reduce as the globe continues to warm [8,9,10]. However, the precondition that led to the theoretical arguments in these studies [8,9,10] is that the enhanced polar warming is not caused by the meridional heat transport materialized by the synoptic-scale variability. If the latter is the major contributor to the polar warming amplification [5], a valid counterargument may also be that increased synoptic variability is necessary to maintain the polar warming amplification. The conflict between these two arguments remains to be resolved. Adding to this challenge is the fact that the change in the synoptic variability may be spatially non-uniform.
It is indeed these difficulties that led to this study. However, this study is not targeted at resolving the two contradicting arguments; rather, it is focused on quantifying the spatiotemporal change in the synoptic surface temperature variability (SSTV) using a newly developed nonlinear nonstationary method based on multi-dimensional ensemble empirical mode decomposition (MEEMD) [11,12,13]. Previous studies have chronicled future changes in temperature variability in a multitude of ways, from calculating the standard deviation of monthly temperature anomalies [14] to feature tracking algorithms [15]. These methods generally contain piece-wise stationary assumptions, and the results may be significantly distorted by the multi-decadal variability contained in both the SSTV amplitude variability and the multi-decadal variability of the surface temperature itself. With MEEMD, we can track the variability and change in the amplitude of SSTV and obtain the temporal evolution of the SSTC itself. By applying a nonlinear nonstationary trend-defining method [16], we can extract the spatiotemporal evolution of the amplitude of SSTV. The fine structure of the amplitude evolution of SSTV obtained will help us to determine some physical factors that contribute to the variability and change in the amplitude of SSTV, potentially providing observational evidence to verify the correctness of competing theories.
An additional purpose of this study is to commemorate Prof. Duzheng Ye (also known as Tu-Cheng Yeh), one of the founding fathers of modern meteorological and climate sciences in China and one of the pioneers who initiated the global collaboration in understanding climate change and its impact on future human wellness. Prof. Ye was a student of Carl-Gustaf Rossby and widely considered one of the main figures of the famous Chicago School of Meteorology. His legendary works include, but are not limited to, studies on the development of mid-latitude waves (synoptic variability) and their propagation, the role of topography, especially the Tibetan Plateau in shaping the weather and climate of eastern Asia, and how global climate change has been modulating the weather and climate. All authors of this study can be considered academic descendants of his and have benefitted either directly or indirectly from his guidance. This study, to a significant degree, touches all these aforementioned areas. Other papers in this collection may introduce some other renowned works of Prof. Ye.
2. Data and Method
2.1. Data
This study has two sets of data: surface air temperature (SAT) and surface topography. The temperature data are from the daily averaged NCEP/NCAR Reanalysis 1 project available through NOAA’s Physical Sciences Laboratory (PSL) website (https://psl.noaa.gov/data/gridded/data.ncep.reanalysis.html) (accessed on 1 September 2019). The horizontal resolution is 2.5° × 2.5° [17]. The region of interest for this study covers a region bordered by 20° N and 50° N lines in the meridional direction and 60° W and 140° W lines in the zonal direction, encompassing the continental United States as well as parts of the surrounding oceans, Canada, and Mexico. Our analysis uses the data from 1 January 1948 to 31 December 2018, a span of 71 years.
The topography data were obtained from the European Centre for Medium-Range Weather Forecasts (ECMWF) ERA-Interim 1 reanalysis project [18]. The data cover the entire globe, with a resolution of 0.125° × 0.125°. These data were averaged over the 2.5° × 2.5° grid spacing, consistent with the spatial locations of the temperature data.
2.2. Method
A challenging question that remains in our research community is how to quantify systematic change (the monotonic trend) in synoptic variability. Traditionally, we calculate statistical quantities, such as variance or standard deviation, for this purpose. However, this approach leads to a dilemma: to track the non-stationarity of synoptic variability and its potential influence by global climate change, we calculate statistical quantities from either piece-wised sections or running sections of a prescribed length of a time series of synoptic variability. It is well known that even for a stationary time series that contains randomness, the statistical quantities calculated from a limited number of samples can contain uncertainty, as the law of large numbers has stated, let alone nonstationary time series. To some degree, this is a manifestation of Heisenberg’s uncertainty principle when the principle is applied to statistical studies. Therefore, when a prescribed piece-wised section of a limited number of samples is applied, the obtained statistical quantities often contain large variability of different timescales caused by the randomness of weather variability and are sensitive to the length of the sections one selects or prescribes, even in the case of stationary processes. The selection of a longer section can reduce the variability and uncertainty of the calculated statistics for stationary processes but leads to the calculated statistical quantities not extending to the two data ends. The longer the data section, the larger the portion of undefined statistical quantities. For non-stationary series, this approach can cause even larger uncertainty. Thus, alternative methods need to be developed.
The method developed here takes advantage of the recent advancements in the adaptive and temporally local analysis of nonlinear nonstationary time series, the empirical mode decomposition (EMD) [11]-based methods [12,13,16]. In this study, EEMD [12] is applied to an SAT time series of a given spatial grid. This time series is decomposed in terms of a set of oscillatory components and a monotonic trend. All these oscillatory components are natural waves of different timescales with amplitude and frequency modulations. Since EEMD is an effective dyadic filter bank, usually, the first component has an averaged period of 3 data points governed by the added white noise in the EEMD algorithm, the second has 6 data points, and so on. Figure 1 presents an example of such a decomposition of the SAT time series near Boston, Massachusetts, USA. The first component, to a significant degree, captures the day-to-day variability [19,20] contained in the SAT time series, while the second, which is highlighted in red and overlapped by a shining blue line, is the synoptic variability with an average period of 6 days. The following four components are sub-seasonal variability, followed by the seasonal cycle, and the lumped inter-annual and longer time scale variability (including the trend).
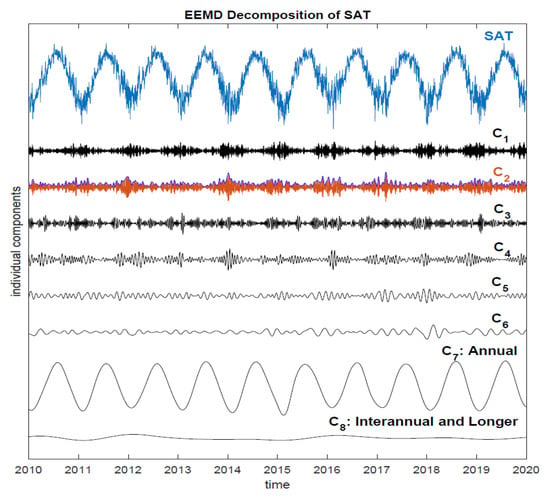
Figure 1.
The decomposition of the SAT near Boston, MA, USA. The top navy-blue line is the original SAT time series, and the black and red lines are individual EEMD components of the SAT with their mean periods from about three days and up. In the figure, the amplitude of different timescale variability is in proportion, and each component has a zero mean. The shining blue line that connects the maxima of the second component is the amplitude of the second component.
The EEMD decomposition enables us to isolate typical SSTV, the second component of SAT. Since EMD/EEMD is based on defining upper and lower envelopes that pass-through maxima and minima of a time series, respectively, the varying amplitude of SSTV that encompasses the length of a time series can be well defined. However, this amplitude still contains variability of timescales at least double that of SSTV. Thus, refining needs to be carried out. To achieve this goal, we applied EEMD to this amplitude again, which is shown in Figure 2. After all the oscillatory components of different times scales were removed, we obtained the nonlinear trend [16] that is either monotonic or contains only one internal extremum, as the bold red line for Boston SSTV, which is also shown in the enlarged Figure 3. It can be verified that the mean value of the trend of the amplitude is about 1.13 times the standard deviation of the overall synoptic component, and this proportional number fits the ratios of the amplitude and the standard deviation for individual piece-wised sections well, provided all sections are a few decades long. In this sense, our new method overcomes the dilemma that traditional statistical methods face. It is also noted that the extracted trend in Figure 3 is also visually appealing to the human eye, which serves as the first judgment of the correctness of data analysis.
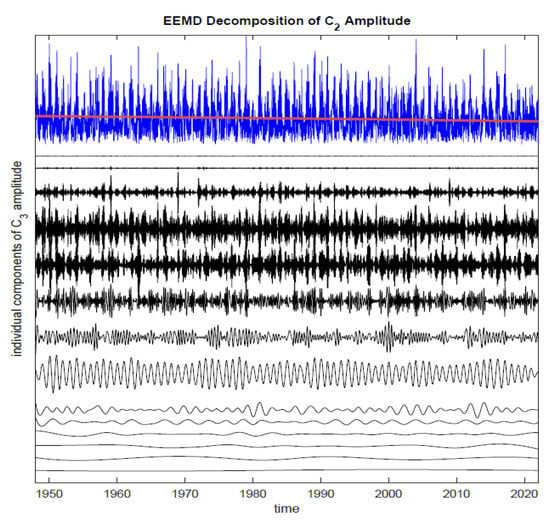
Figure 2.
The decomposition of the amplitude of synoptic variability. The shining blue line is the amplitude, the black lines are all EEMD components of the SSTV amplitude, and the red line is the trend.

Figure 3.
The enlarged top section of Figure 2.
It is noted again that the trend in this study is nonlinear and nonstationary [2,16], not a traditional linear trend. The time-varying nature of this secure trend allows us to derive the accumulated change of any given time with respect to a reference time, as well as the changing rate of the secure trend at any given time. With this isolated trend, denoted as A(t), we can now systematically quantify how synoptic variability has been evolving by defining a standardized amplitude change ratio, i.e.,
where represents a reference time selected. In this study, this reference time is selected as 1 January 1948, the starting date of the reanalysis data.
The above calculation procedure is applied to all the spatial grid points within the selected domain to obtain the spatiotemporal evolution of the SSTV amplitude evolution.
3. Results
Figure 4 plots the normalized accumulated SSTV amplitude change, P(t), for the decades following the referenced decade, 1948 to 1958. By 1968, we can already see an emerging spatial pattern that persists throughout later decades. In the zonal direction, this pattern is marked by an increase in variability over the ocean off the western coast of the US, a decrease over California and Baja California, an increase over much of the Rocky Mountain region, a decrease in the central longitudinal regions of the US, and an increase again over the southeast US. In the meridional direction, the pattern shows a north–south contrast. In the subtropical region, an increase in SSTV amplitude prevails, while in the mid-latitude, a decrease in SSTV amplitude extends from the Great Plains to the Great Lakes.

Figure 4.
The normalized accumulated SSTV amplitude change, P(t), from the referenced decade ending in 1958. The year label on each panel represents the end of a decade. All panels used the same color scheme of percentage-wise reduction/increment scale.
The pattern continues to develop with time, with small-spatial scale structures fading and those of larger spatial scale becoming more dominant. One of the more notable regions is the southeast US, where the increase in SSTV amplitude in earlier decades transitions to a reduction in SSTV amplitude by 2018. The result of this reversal is that almost all land to the east of the Rocky Mountains is dominated by a decrease in SSTV amplitude, though a notable exception occurs near the Appalachian Mountains, where the early period increase in SSTV amplitude, though reduced compared to early decades, persists.
From 1948 to 2018, there is a significant reduction in SSTV amplitude over much of the central United States, extending northward into Canada, a trend that began in 1968 and has persisted through to 2018. The entire eastern half of the continental United States has seen a reduction in variability over these seven decades. The largest reduction of 36.5% occurs just off the coast of Washington. The reduction in variability is not confined to the eastern US, as reductions are observed along much of the west coast as well. Among the regions with the greatest reductions are the Great Lakes, Northeast, and Southern Plains. Notably, this does not include Mexico, Arizona, or the Rocky Mountain region, where an intensification of a region of increasing variability has occurred. Overall, the total change in variability from 1948 to 2018 over the entire area analyzed is a reduction of 3.33%, due to much of the regional increases/decreases canceling each other out.
The continuous change in SSTV variability, as illustrated by the bold red line in Figure 3, provides an opportunity to quantify the instantaneous change rate of SSTV amplitude, , by taking the temporal derivative of the normalized amplitude change rate. Since the SSTV amplitude trend at any spatial grid is slowly varying, can be well approximated by , where is one decade. Figure 5 presents the instantaneous change rate of SSTV for the years 1963, 1973, 1983, 1993, 2003, and 2013. Again, a large-scale spatiotemporal evolution pattern emerges. Of the surrounding oceans of the continental US, the Pacific Ocean experienced a sharp SSTV amplitude increase in the 1960s and a reduced increasing rate in the 1970s and the 1980s, followed by a mild SSTV amplitude reduction and an intensified SSTV amplitude reduction. This change contrasts with the Atlantic Ocean, where initial changes in both directions are observed, gradually transitioning to a large region of increased variability. Over the continental US, the increment in the SSTV amplitude has been generally steady in the Rocky Mountain region through all decades, although the area of increment expands in all directions. The southeast US shares a similar evolution of SSTV amplitude to the Pacific Ocean, but generally with smaller changing rates, apart from the strong reductions in 2013 covering much of South Carolina. In the regions of the continental US, other than the Rocky Mountains and the southeast US, the changing SSTV amplitude changing rates are mostly negative and mild. The maximum decadal change rate of amplitude is about 12% in the Pacific Ocean region off the west coast of the US.
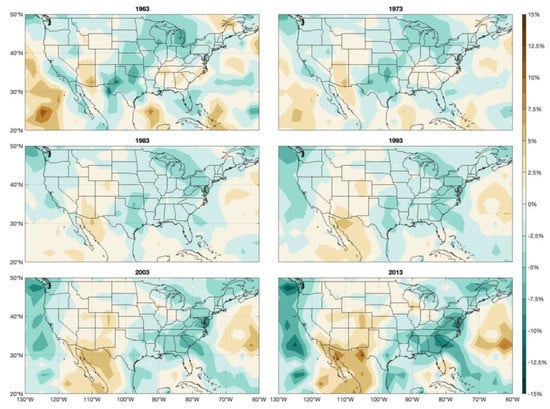
Figure 5.
The decade-wise normalized accumulated SSTV amplitude change for the years 1963, 1973, 1983, 1993, 2003, and 2013. All panels used the same color scheme of percentage-wise reduction/increment scale.
The results presented in both Figure 4 and Figure 5 point to the topography of the United States affecting the SSTV amplitude evolution over the past seven decades. To quantify this, we calculated the correlation between the accumulated SSTV amplitude rate of change (the bottom right panel of Figure 4) and the topography of the continental US, which is shown in Figure 6. The correlation coefficient is 0.52. To test whether this correlation coefficient is statistically significant, we designed a Monte Carlo method by repeatedly randomizing either spatial topography data or the normalized accumulated SSTV amplitude changes and calculating the correlation coefficient. The result showed that the correlation coefficient of 0.52 is statistically significant at the 99% confidence level.
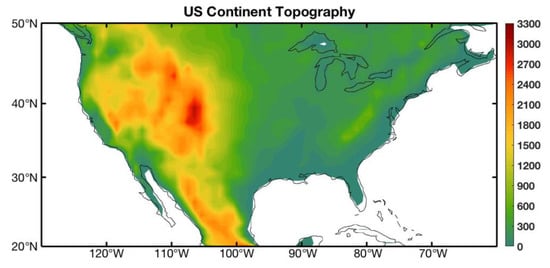
Figure 6.
The topography of the continental US. The unit in the color bar is meters above sea level. It is noted that the slight mismatch of the coastal line with the topography display is caused by the grossed horizontal resolution of the topography.
4. Summary and Discussions
In recent years, the world has been experiencing a significant increase in extreme weather events. It is widely suspected that these events are tied closely to global warming in the past century, with a significant number of diagnosis and modeling studies supporting this argument. However, most of these studies used traditional statistical methods that have deficiencies in terms of quantifying the nonlinear nonstationary synoptic variability. An improvement in the methodologies can significantly reduce uncertainty.
In this study, we developed a new analysis method to quantify the nonstationary change in synoptic temperature variability in the last seven decades. The method takes advantage of the most recent progress in nonlinear nonstationary time series analysis, especially the EEMD-based methods for isolating spatiotemporal evolutions of spatiotemporal fields of different spatiotemporal scales. By applying the newly developed method to surface temperature data, we first isolated the nonstationary synoptic-scale surface temperature variability, then tracked its spatiotemporal evolution, and finally extracted important factors that may contribute to the observed SSTV change.
We found that the SSTV change over the US is spatially inhomogeneous and temporally non-uniform. The accumulated maximum changes with respect to the late 1940s reached levels of a 39% increase in the mountainous regions and a 36% reduction in the lowlands. The spatial structure appears to have a zonal three-band structure across the continental United States. In addition to this, increases in variability are observed in the subtropics. We also calculated the correlation between the change in SSTV amplitude and the topography over the USA and found that this relationship is robust. The evolution of the SSTV amplitude is significantly different over land and oceans, with the former regions steadier and the latter region containing a significant change in the changing rate over time.
The most important role of synoptic variability in the mid-latitudes is to provide a carrier to transport heat from low latitudes to high latitudes, and its amplitude is modulated by the meridional temperature gradient. It is also known that the polar region has warmed much more than the lower latitudes in the past seven decades as the globe continues to warm. This inhomogeneous global warming reduces the meridional temperature gradient and infers a reduction in the amplitude of synoptic variability. This result has been confirmed in the lowlands of the continental US but not in the mountainous regions in our study, implying that the evolution of regional synoptic variability in the presence of warming is beyond our current understanding. While our study provides a piece of unambiguous evidence that topography and land–sea contrast are key factors to modify the above dynamical argument, how topography and land–sea contrast affects the SSTV amplitude remains to be investigated.
Author Contributions
Conceptualization, Z.W. and X.Z.; Formal analysis, M.S., J.S., F.Y. and Z.W.; Funding acquisition, Z.W. and X.Z.; Investigation, M.S., F.Y. and Z.W.; Methodology, J.S. and Z.W.; Project administration, Z.W.; Resources, Z.W.; Software, Z.W.; Supervision, Z.W.; Validation, J.S. and F.Y.; Visualization, M.S., J.S. and Z.W.; Writing—original draft, M.S. and Z.W.; Writing—review and editing, X.Z. and Z.W. All authors have read and agreed to the published version of the manuscript.
Funding
M.S., J.S., F.Y. and Z.W. were supported by the US National Science Foundation, grant AGS-1723300. X.Z. was supported by the National Natural Science Foundation of China, grant 91337218.
Data Availability Statement
The temperature data are from the daily averaged NCEP/NCAR Reanalysis 1 project available through NOAA’s Physical Sciences Laboratory (PSL) website (https://psl.noaa.gov/data/gridded/data.ncep.reanalysis.html) (accessed on 1 September 2019). The topography data were obtained from the European Centre for Medium-Range Weather Forecasts (ECMWF) ERA-Interim 1 reanalysis project [18].
Conflicts of Interest
The authors declare no conflict of interest.
References
- Masson-Delmotte, V.; Zhai, P.; Pirani, A.; Connors, S.L.; Péan, C.; Berger, S.; Caud, N.; Chen, Y.; Goldfarb, L.; Gomis, M.I.; et al. Climate change 2021: The physical science basis. In Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2021; Volume 2. [Google Scholar]
- Wu, Z.; Huang, N.E.; Wallace, J.M.; Smoliak, B.V.; Chen, X. On the time-varying trend in global-mean surface temperature. Clim. Dyn. 2011, 37, 759–773. [Google Scholar] [CrossRef]
- Ji, F.; Wu, Z.; Huang, J.; Chassignet, E.P. Evolution of land surface air temperature trend. Nat. Clim. Chang. 2014, 4, 462–466. [Google Scholar] [CrossRef]
- Holland, M.M.; Bitz, C.M. Polar amplification of climate change in coupled models. Clim. Dyn. 2003, 21, 221–232. [Google Scholar] [CrossRef]
- Cai, M. Dynamical amplification of polar warming. Geophys. Res. Lett. 2005, 32, L22710. [Google Scholar] [CrossRef]
- Bekryaev, R.V.; Polyakov, I.V.; Alexeev, V.A. Role of polar amplification in long-term surface air temperature variations and modern Arctic warming. J. Clim. 2010, 23, 3888–3906. [Google Scholar] [CrossRef]
- Taylor, P.C.; Cai, M.; Hu, A.; Meehl, J.; Washington, W.; Zhang, G.J. A decomposition of feedback contributions to polar warming amplification. J. Clim. 2013, 26, 7023–7043. [Google Scholar] [CrossRef]
- Hassanzadeh, P.; Kuang, Z.; Farrell, B.F. Responses of midlatitude blocks and wave amplitude to changes in the meridional temperature gradient in an idealized dry GCM. Geophys. Res. Lett. 2014, 41, 5223–5232. [Google Scholar] [CrossRef]
- Schneider, T.; Bischoff, T.; Płotka, H. Physics of changes in synoptic midlatitude temperature variability. J. Clim. 2015, 28, 2312–2331. [Google Scholar] [CrossRef]
- Cattiaux, J.; Peings, Y.; Saint-Martin, D.; Trou-Kechout, N.; Vavrus, S.J. Sinuosity of midlatitude atmospheric flow in a warming world. Geophys. Res. Lett. 2016, 43, 8259–8268. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E.; Chen, X. The multi-dimensional ensemble empirical mode decomposition method. Adv. Adapt. Data Anal. 2009, 1, 339–372. [Google Scholar] [CrossRef]
- Bathiany, S.; Dakos, V.; Scheffer, M.; Lenton, T.M. Climate models predict increasing temperature variability in poor countries. Sci. Adv. 2018, 4, eaar5809. [Google Scholar] [CrossRef] [PubMed]
- Tamarin-Brodsky, T.; Hodges, K.; Hoskins, B.J.; Shepherd, T.G. Changes in Northern Hemisphere temperature variability shaped by regional warming patterns. Nat. Geosci. 2020, 13, 414–421. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E.; Long, S.R.; Peng, C.K. On the trend, detrending, and variability of nonlinear and nonstationary time series. Proc. Natl. Acad. Sci. USA 2007, 104, 14889–14894. [Google Scholar] [CrossRef] [PubMed]
- Kalnay, E.; Kanamitsu, M.; Kistler, R.; Collins, W.; Deaven, D.; Gandin, L.; Iredell, M.; Saha, S.; White, G.; Woollen, J.; et al. The NCEP/NCAR 40-year reanalysis project. Bull. Am. Meteorol. Soc. 1996, 77, 437–472. [Google Scholar] [CrossRef]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, D.P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Wu, F.T.; Fu, C.; Qian, Y.; Gao, Y.; Wang, S.Y. High-frequency daily temperature variability in China and its relationship to large-scale circulation. Int. J. Climatol. 2017, 37, 570–582. [Google Scholar] [CrossRef]
- Liu, Q.; Tan, Z.-M.; Sun, J.; Hou, Y.; Fu, C.; Wu, Z. Changing rapid weather variability increases influenza epidemic risk in a warming climate. Environ. Res. Lett. 2020, 15, 044004. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).