Comparison of Clouds and Cloud Feedback between AMIP5 and AMIP6

Abstract

We examine the changes in clouds and cloud feedback between Phase 5 (AMIP5) and Phase 6 (AMIP6) of the Atmospheric Model Intercomparison Project. Each model is perturbed by uniformly increasing the sea surface temperature by 4 K. The simulated cloud fraction, the perturbed states and cloud radiative kernels are used to derive cloud feedback in the shortwave (SW), longwave (LW) and their sum (Net). Compared to AMIP5, the cloud fraction in AMIP6 increases by 9.1%, while the perturbation leads to a 0.25% decrease. The Net cloud feedback at the top of the atmosphere (TOA) is almost double (174%). Statistical tests support that this change is mainly due to an increase in the surface SW cloud feedback caused by optically thick, middle and low clouds. The contribution of the atmospheric Net component (12%) stems from the increase in the atmospheric LW cloud feedback, likely to play a role in weakening (strengthening) the northward (southward) meridional atmospheric energy transport, while the opposite is true for the surface LW and Net cloud feedback in the meridional oceanic energy transport. The substantial increase in cloud feedback at the TOA primarily contributes to the higher climate sensitivity. The cloud feedback spread in AMIP6 is comparable to that in AMIP5.

1. Introduction

In the last three decades, both observations and General Circulation Models (GCMs) have indicated that the largest uncertainty in climate simulations resides within cloud feedback [1]. In climate modeling, cloud feedback indeed exhibits the largest intermodel spread of all feedbacks, and is highly correlated with the equilibrium/effective climate sensitivity (ECS), an important indicator of future climate trends [2]. The Intergovernmental Panel on Climate Change (IPCC) Sixth Assessment Report (AR6) was recently finalized [3]. It concluded that improved knowledge of climate processes, paleoclimate evidence and the response of the climate system to increasing radiative forcing gives a best estimate of ECS of 3 °C, with a very likely range of 2 °C to 5 °C. The likely range (2.5–4 °C) is narrower than that in AR5 (1.5–4.5 °C) [4,5], but some of the Coupled Model Intercomparison Project Phase 6 (CMIP6) climate models have either high (>5 °C) or low (<2 °C) ECS, which also simulate past global surface temperature changes outside the range of proxy-based reconstructions for the coldest and warmest reference periods. The ensemble-mean global surface temperature change obtained from the CMIP6 historical simulations assessed in AR6 is within 0.2 °C of the observations over most of the historical periods. Additionally, the observed warming is within the very likely range of the CMIP6 ensemble, but some models simulate warming that is either above or below the assessed, very likely range of observed warming [4,5]. The AR6 differs from previous reports because it does not directly use climate model estimates of ECS (and transient climate response, TCR) in the assessed ranges of climate sensitivity. Indeed, the AR6 uses “observational constraints” to select a subset of CMIP6 for its warming projections (i.e., the projection is not entirely based on CMIP6 projection). Zelinka et al. [2] show that ECS > 5 K for 4 of the 27 CMIP6 models and ECS < 2 K for one model only. In comparison, none of the 28 Coupled Model Intercomparison Project Phase 5 (CMIP5) models have such excessive ECS values. Forster et al. [6] concluded that one-third of the CMIP6 models exhibit a higher ECS than did the CMIP5 models, and those with CMIP6 models showing the highest warming are unlikely to be representative of real-world conditions. Additionally, it is reported that CMIP6 projections of global surface temperature should not be exclusively relied on for policy-relevant decisions. Scafetta [7] argued that the real ECS could lie between 1 and 2 °C, which implies moderate warming for the next decades. Subsequently [8], he identified a subset of seventeen best-performing CMIP6 GCMs for which the ECS ranges between 1.8 and 3.0 °C and the TCR between 1.2 and 1.8 °C. He further observed that if the global warming reported by the climate records is overestimated due to urban heat contamination and other local, non-climatic biases, the real ECS and TCR may be significantly lower than what is produced by the CMIP6 GCMs, causing the CMIP6 GCMs to be invalidated.

Even if the IPCC has used a subset of the CMIP6 models to construct more rational, observation-constrained results to produce the final AR6 reports to better serve the policymakers and society, the higher-ECS problem remains to be investigated and resolved. A number of authors have published their results to explain the causes of the problem using various approaches. Wang et al. [9] have found that the observed warming with hemispheric asymmetry (which is correct) during the mid to late 20th century is more consistent with low ECS (weak aerosol indirect effect) models. Mülmenstädt et al. [10] have hypothesized that underestimating negative warming-cloud-lifetime feedbacks contributes to larger greenhouse warming in CMIP6 models. To test the hypothesis, they used a single climate model to better simulate warm-rain probability and found that the cloud lifetime feedback is nearly three times larger than that in the original CMIP6 model. This fact suggests that model errors in cloud-precipitation processes may bias cloud feedbacks by as much as the CMIP5-to-CMIP6 ECS difference. They have concluded that reliable climate model projections, therefore, require improved realism in cloud processes guided by process-oriented observations and observational constraints. The highly biased ECS values in some CMIP6 models are indicative of a failing component in the model simulations, along with other pitfalls, such as the double Intertropical Convergence Zone (double-ITCZ) problem already present in CMIP3 and CMIP5 [11]. However, despite all the model issues, clouds are arguably the most intriguing and challenging components of the climate system [12].

With the new Coupled Model Intercomparison Project Phase 7 (CMIP7) in its planning stage (e.g., [13]), the models still cannot simulate clouds directly, so they rely on known physics and observations to estimate cloud properties and behavior. It is therefore necessary to explore extensively the simulated clouds and cloud feedback, and understand the differences between CMIP5 and CMIP6 in order to gain insights on potential improvements for future models, including CMIP7.

In this study, we analyze results obtained with Atmospheric Model Intercomparison Project (AMIP) models. In this simplified version of the CMIP models, the ocean is prescribed as opposed to being let to interact with the atmosphere. Because of their computational efficiency, AMIP experiments provide an ideal test bed to investigate the physical mechanisms of cloud feedbacks in CMIP models [14,15].

We also exploit cloud radiative kernels (CRKs), which are based on the partitioning of clouds into 49 types of a 2D histogram, and that have been used to study cloud feedback since they were first introduced by Zelinka et al. [16]. The advantage of using CRKs to calculate cloud feedback is that the cloud feedback derived from cloud changes (relative to mean-state clouds) is clearly defined for all the 49 cloud types produced with the International Satellite Cloud Climatology Project (ISCCP) Simulation (ISCCP-Sim) in AMIP models (see Section 2). In the simulation, clouds are defined on the joint 2D histogram of seven cloud optical depth (τ) and seven cloud top pressure (CTP) values. However, the cloud feedback is traditionally computed (and defined) only at the top of the atmosphere (TOA), i.e., for the entire earth–atmosphere system. As the physical responses of the surface and the atmosphere to cloud-feedback-caused radiative effects are quite different, it is necessary to characterize their individual roles in the feedback chains. The radiation code (ISCCP-FH [17]) used to compute radiative flux profiles provides CRKs [18], which in turn can be used to decompose the TOA cloud feedback into its surface and atmospheric components. In this paper, the ISCCP-FH CRKs for the TOA, the surface (SFC) and atmosphere (ATM) are used to calculate the TOA, SFC and ATM cloud feedback [18]. The AMIP5 and AMIP6 “amip4k” experiment results (see Section 2) and the ISCCP-Sim cloud datasets are used to derive cloud feedback at the TOA, at SFC and in ATM using the ISCCP-FH CRKs. This strategy allows us to compare the evolution of clouds and cloud feedback in AMIP5 to AMIP6. The paper proceeds as follows. Section 2 compares mean cloud fraction (CF) and cloud-fraction changes (CFCs, with respect to mean state) between AMIP5 and AMIP6 models. Section 3 and Section 4 compare their associated global and zonal mean cloud feedback, respectively. Section 5 explores the spatial distribution of the differences in cloud feedback between AMIP5 and AMIP6. Section 6 summarizes the study and draws the conclusions.

2. Comparison of Cloud Fraction and Cloud Fraction Changes

As CF and CFCs are the basis for calculating and understanding cloud feedback, we start by comparing CF between AMIP5 and AMIP6 models. The CF datasets are from the control runs that give the mean-state CF. The control run is constrained with observed sea surface temperature (SST) and sea ice concentrations, and the associated amip4k simulation is prescribed with SST uniformly increased by 4 K over the ice-free oceans (see [19] for AMIP5 and [20] for AMIP6). The CFC is obtained by differencing amip4k- and control-run CFs, normalized by the change in global-mean surface air temperature. All of the AMIP5 and AMIP6 experiment results (i.e., the 2D histograms of the monthly averages of the ISCCP-Sim cloud datasets) were provided by Zelinka (see [15]).

Table 1. List of the 9 AMIP6 and 10 AMIP5 models whose amip4k experiment results are used in the study. The CMIP counterparts of the AMIP models (which are the atmospheric component) are listed in Zelinka et al. [2].

No.	AMIP6 Models	Abbr.
1	CCSM4.r1i1p1, National Center for Atmospheric Research, USA	n4
2	CNRM-CM5.r1i1p1, Centre National de Recherches Météorol., France	c5
3	CanAM4.r1i1p1, Canadian Centre for Clim. Modelling and Analysis, Canada	ca
4	HadGEM2-A.r1i1p1, Hadley Centre Global Environment, UK	h2
5	IPSL-CM5A-LR.r1i1p1, Institute Pierre Simon Laplace, France	ia
6	IPSL-CM5B-LR.r1i1p1, Institute Pierre Simon Laplace, France	ib
7	MIROC5.r1i1p1, University of Tokyo, Japan	m5
8	MPI-ESM-LR.r1i1p1, Max Planck Institute for Meteorology, Germany	mp
9	MRI-CGCM3.r1i1p1, Max Planck Institute for Meteorology, Germany	mr
	AMIP5 models
1	BCC-CSM2-MR.r1i1p1f1, Beijing Climate Center Climate System, China	bc
2	CESM2.r1i1p1f1, National Center for Atmospheric Research, USA	ce
3	CNRM-CM6-1.r1i1p1f2, Centre National de Recherches Météorol., France	c6
4	CanESM5.r1i1p2f1, Canadian Earth System, Canada	cs
5	E3SM-1-0.r2i1p1f1, the US Department of Energy, USA	e3
6	GFDL-CM4.r1i1p1f1, NOAA/Geophysical Fluid Dynamics Laboratory, USA	gd
7	HadGEM3-GC31-LL.r5i1p1f3, Hadley Centre Global Environment, UK	h3
8	IPSL-CM6A-LR.r1i1p1f1, Institute Pierre Simon Laplace, France	i6
9	MIROC6.r1i1p1f1, University of Tokyo, Japan	m6
10	MRI-ESM2-0.r1i1p1f1, Meteorol. Research Institute Earth System, Japan	mi

lists the 9 AMIP6 and 10 AMIP5 models used in this study. The ISCCP-Sim cloud datasets are defined in the form of 2D histograms binned in seven values of τ by seven values of CTP, forming 49 cloud types. The datasets have a spatial resolution of 2.5° in longitude and 2.0° in latitude.

Figure 1 shows global, annual and ensemble mean CF and CFCs for AMIP5, AMIP6 and their differences, calculated by subtracting the AMIP5 CF and CFCs from those of AMIP6. This same definition also applies to the other parameters discussed below. It is seen that the total global-mean CF (CFC) is increased (decreased) by 9.1% (0.25%/K) going from AMIP5 to AMIP6, as indicated in the titles of the bottom panels. The increase in the global-mean CF to 63% (middle left panel) for AMIP6 from 54% for AMIP5 (top left panel) suggests an improvement, based on the comparison among the 5-year, 2B-GEOPROF-LIDAR P2_R04 and 2B-TAU P_R04 datasets from the CloudSat and CALIPSO Data Processing Center, the 33-year ISCCP-H products and the 10-year CERES FluxByCldTyp-Day/Month (Terra-Aqua-MODIS) Ed4.1 products. The global-mean CFs are 61%, 69% and 66%, respectively (not shown). The mean of the three observational CFs is 65%, i.e., close to the AMIP6 CF. The bottom left panel in Figure 1 shows that AMIP6 CF increases in most bins, and the largest increase appears in low-τ, high clouds and medium-τ, low-to-middle clouds. By contrast, most of the CFCs (bottom right panel) are negative, with the largest for the bin of CTP between 800 and 680 hPa for 3.6 < τ < 9.4. The decrease in the global-mean CFCs has complex implications for the changes in cloud feedback, which can improve or worsen climate model predictions depending on the specific cloud type and model itself.

Note that, although the CF representation in AMIP6 models is improved in matching the observations (based on snapshots of cloud state), the present-day state alone is an insufficient constraint for cloud modeling [10]. Being produced by the dynamic and thermodynamic processes in the atmosphere, it is the CFC that determines the cloud feedback.

Since this study focuses on the differences between AMIP6 and AMIP5, we supply the statistical test of the null hypothesis (zero difference) at a 95% confidence level with the simultaneous alternative hypothesis for the difference between AMIP6 and AMIP5 using Student’s t-distribution (t-test) method (e.g., [21]). The test assumes that AMIP6 and AMIP5 are independent of each other, and that their distributions are normal. Indicating with the population means for AMIP5 and AMIP6, we have the following:

Null Hypothesis, H₀: μ₁ = μ₂
Alternative Hypothesis, H_a: μ₁ ≠ μ₂

(1)

With the significance level (α = 5%), we can obtain the critical value, t_α/2, if the degree of freedom, df, is known. The values of df are calculated by

$$df=\frac{{\left[\left(s_1^2/n_1\right)+\left(s_2^2/n_2\right)\right]}^2}{\frac{{\left(s_1^2/n_1\right)}^2}{n_1-1}+\frac{{\left(s_2^2/n_1\right)}^2}{n_2-1}}$$

(2)

where s₁ and s₂ are the standard deviations of the individual AMIP6 and AMIP5 models, and n₁ and n₂ are their sample sizes, usually equal to 10 and 9 (for the 10 AMIP5 and 9 AMIP6 models). The nearest integer obtained by rounding down df is used to obtain t_α/2 from its table of values. The value of the test, t, is then given by the following:

$$t=\frac{{\overline{x}}_1-{\overline{x}}_2}{\sqrt{{(s}_1^2/n_1)-(s_2^2/n_1)}}$$

(3)

where ${\overline{x}}_1$ and ${\overline{x}}_2$ are the sample means for AMIP6 and AMIP5, respectively.

If the test yields |t| < t_α/2, t falls in the not-reject region of H₀ (implying that the difference between AMIP6 and AMIP5 is insignificant); otherwise, t falls in the reject region of H₀, i.e., H_a is statistically true.

Applying Equations (1)–(3) to each bin for the global mean difference between AMIP6 and AMIP5 models in Figure 1, we obtain that all the CF difference bins (bottom left panel) are insignificant. For the CFC differences, there are instead seven significant bins (indicated by crosses in the bottom right panel) corresponding to optically thick, middle and low clouds and optically thin/medium-high clouds. The same method is applied to all other relevant figures and the results are indicated therein (see captions).

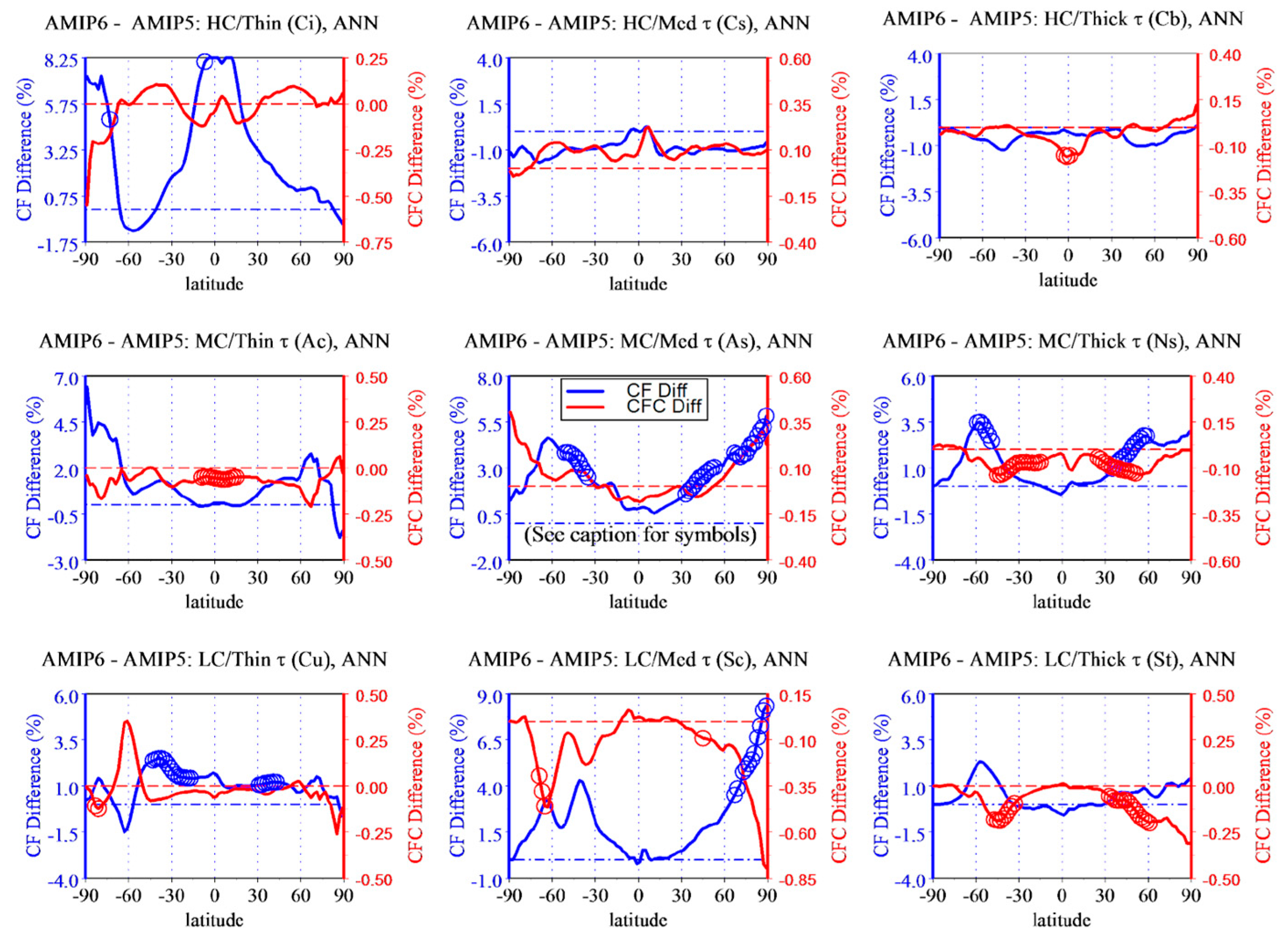
To offer more detailed comparisons based on cloud type, the original 49 cloud types are reduced to 9 cloud types by partitioning them according to (i) low (τ < 3.55), medium (3.55 ≤ τ < 22.6) and thick (22.6 ≤ τ < ≤ 379) optical depth and (ii) high-level (50 < CTP < 440 hPa), middle-level (440 < CTP < 680 hPa) and low-level (680 < CTP < 1000 hPa) clouds. These cloud classes are (in order of thin, medium and thick τ for each CTP interval): Cumulus (Cu), Stratocumulus (Sc) and Stratus (St) for low clouds (LCs), Altocumulus (Ac), Altostratus (As) and Nimbostratus (Ns) for middle clouds (MLs) and Cirrus (Ci), Cirrostratus (Cs) and Deep Convection (Cb, historically used for Cumulonimbus) for high clouds (HCs) (Figure 20 in [22]).

Figure 2 shows the zonal-mean difference for ensemble and annual mean AMIPs for both CF (blue line) and CFC (red line), and for each of the nine cloud types. For the majority of CF (CFC), the differences are positive (negative). The largest CF changes (~10%) from AMIP5 to AMIP6 appear in the tropical and polar regions for Ci and in the Northern polar regions for Sc, while changes at high latitudes for most cloud types are moderate (up to ~4%). Most of the CFC differences are <0.5%/K, except for Ci in the Southern polar regions and for Sc at both Northern and Southern high latitudes (up to 0.75%/K). It is worth noting that the CF and CFC differences are largely anticorrelated for seven cloud types regarding the zonal means, and for eight cloud types for all the grid cells on the global map. The highest correlation coefficients are R = −0.76 and R = −0.91 for Sc for all the grid cells and the zonal means, respectively. The overall correlation for all the types of clouds and grid cells is R = −0.35. The spatial distribution of the anticorrelation is apparent for most cloud types, with the most representative being Sc, but some level of positive correlation also appears in several regions for a few cloud types, especially Cs (not shown). We also see that significant zonal-mean differences between AMIP6 and AMIP5 appear mainly in extratropical zones for middle and low clouds; a few exceptions occur in some tropical zones for middle and high clouds.

Before presenting the results on cloud feedbacks in the next section, we look at what the CFC results alone tell about the cloud feedback uncertainty and the spread, which is one of the important indicators of the performance of a group of models. Zhang et al. [18] used a statistical method to estimate the cloud feedback uncertainty and quantify uncertainty and spread based on the modulus mean difference and standard deviation of their CFCs and CRKs. We apply the method to the CFCs relative to the two groups of 10 AMIP5 and 9 AMIP6 models. The CFC root-mean-square (RMS) values for the two groups are 0.206 and 0.205%/K, respectively, which can essentially represent the cloud feedback uncertainty because more than 98% of it is contributed by the CFC RMS [18]. Since the difference in AMIP6 and AMIP5 RMS is negligible (~0.5%), it seems that the spread of the AMIP6 models has virtually not improved compared to AMIP5 models.

3. Global-Mean Cloud Feedback from AMIP5 to AMIP6

As both the CFC and ISCCP-FH CRK datasets are presented as monthly mean, 7-τ by 7-CTP histograms with a spatial resolution of 2.5° longitude × 2.0° latitude, we can directly calculate the monthly mean cloud feedback at the TOA and SFC and in ATM using Equation (2e) in [18], which is rewritten here (Equation (4)) for convenience:

$$\begin{array}{ll}FDB{K}_{cld\_TOA}\hfill & =\frac{1}{dTs}{\displaystyle \sum _{i=1}^{49}CRKto{a}_i\times CF{C}_i}\\ & =\frac{1}{dTs}{\displaystyle \sum _{i=1}^{49}CRKsf{c}_i\times CF{C}_i}+\frac{1}{dTs}{\displaystyle \sum _{i=1}^{49}CRKat{m}_i\times CF{C}_i}\\ & =FDB{K}_{cld\_SFC}+FDB{K}_{cld\_ATM}\end{array}$$

(4)

where FDBK stands for cloud feedback and CRK for cloud kernel. The subscripts indicate the TOA, SFC or ATM components, dT_s is the global-mean surface air temperature change from mean to perturbed state and j is the index for summation over the 49 histogram bins. The calculation is performed for each type (bin) of clouds, each grid cell and each month for each AMIP model. Equation (4) explicitly shows how the TOA cloud feedback is partitioned into its SFC and ATM components.

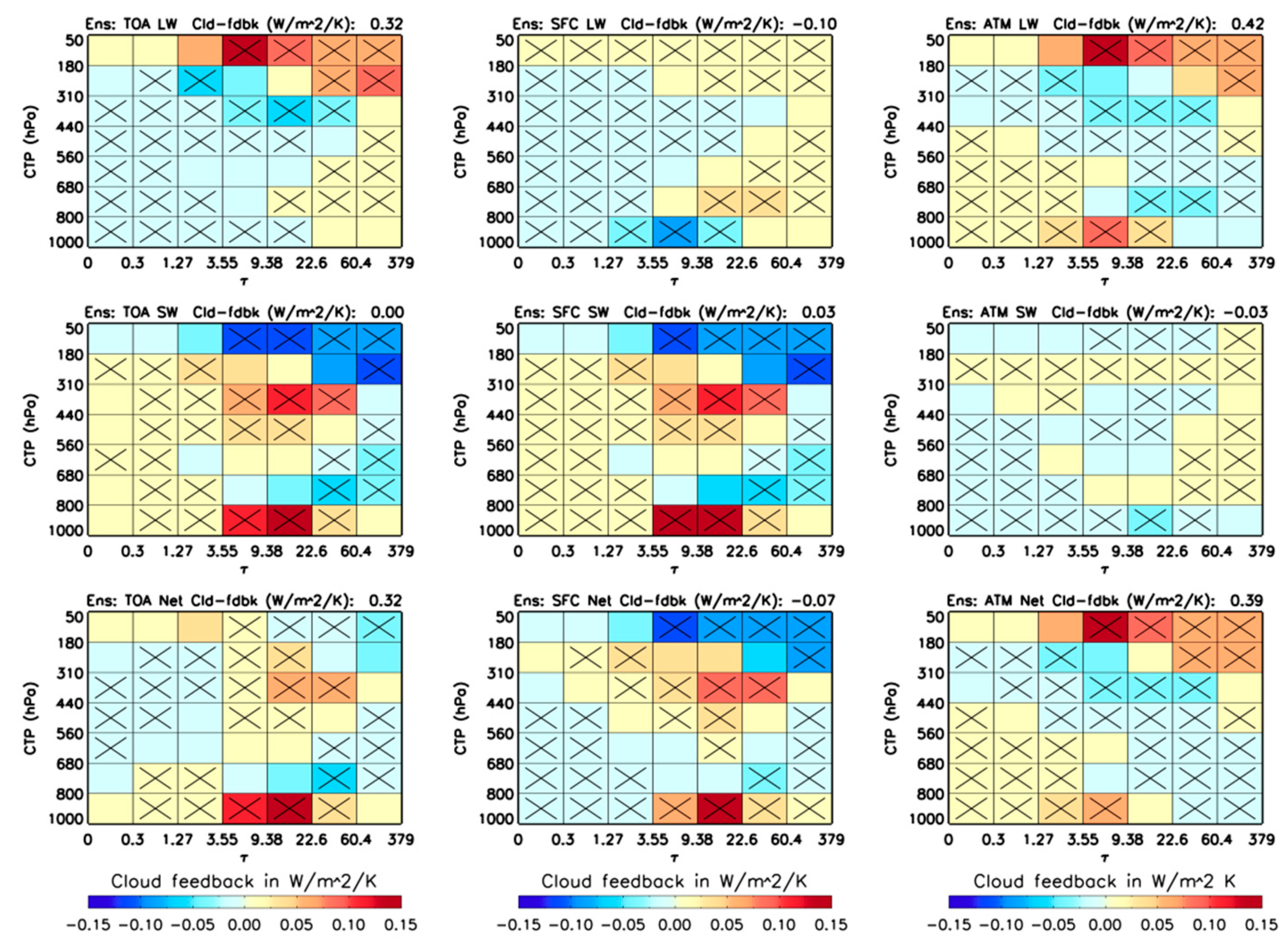
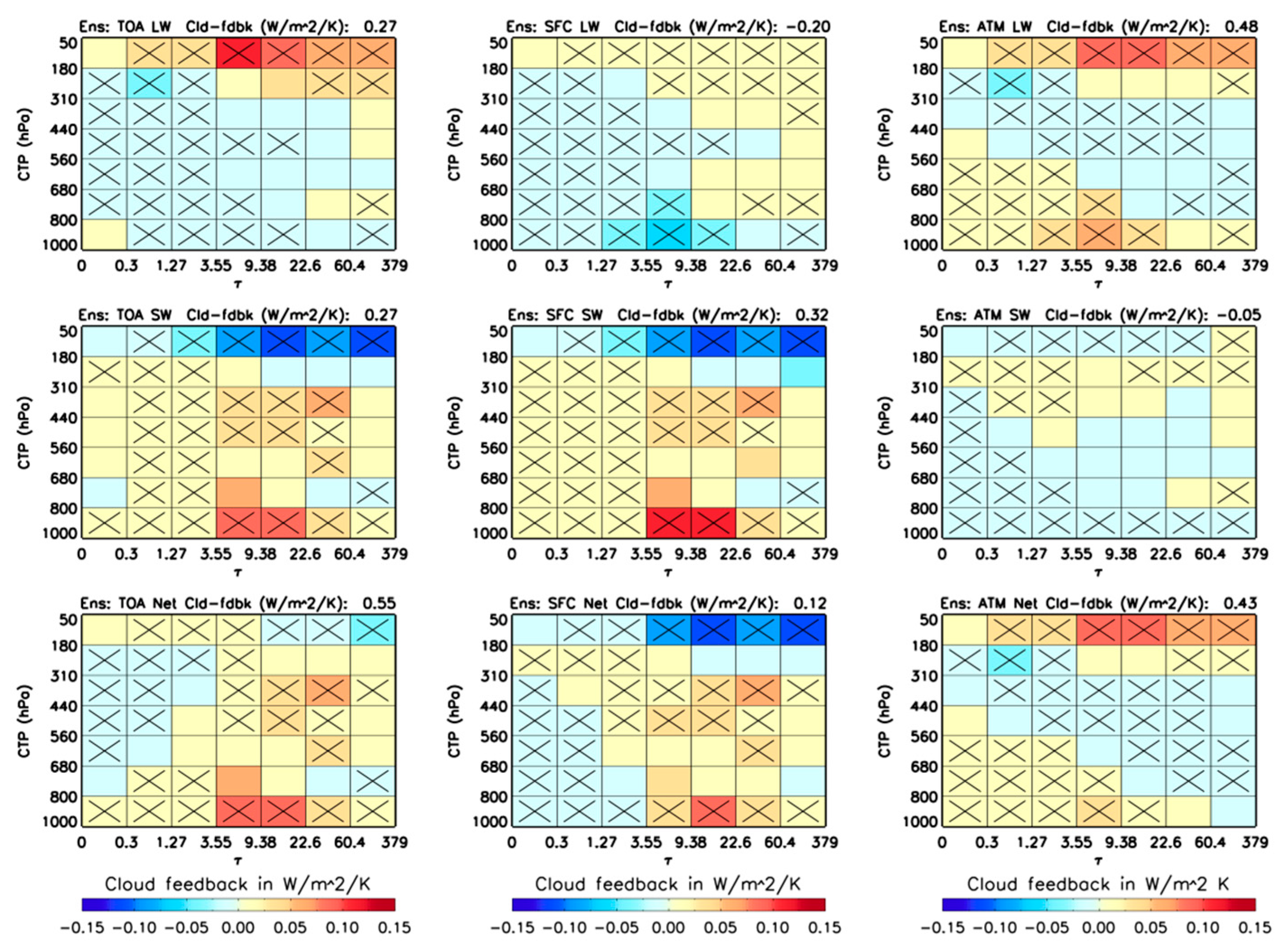
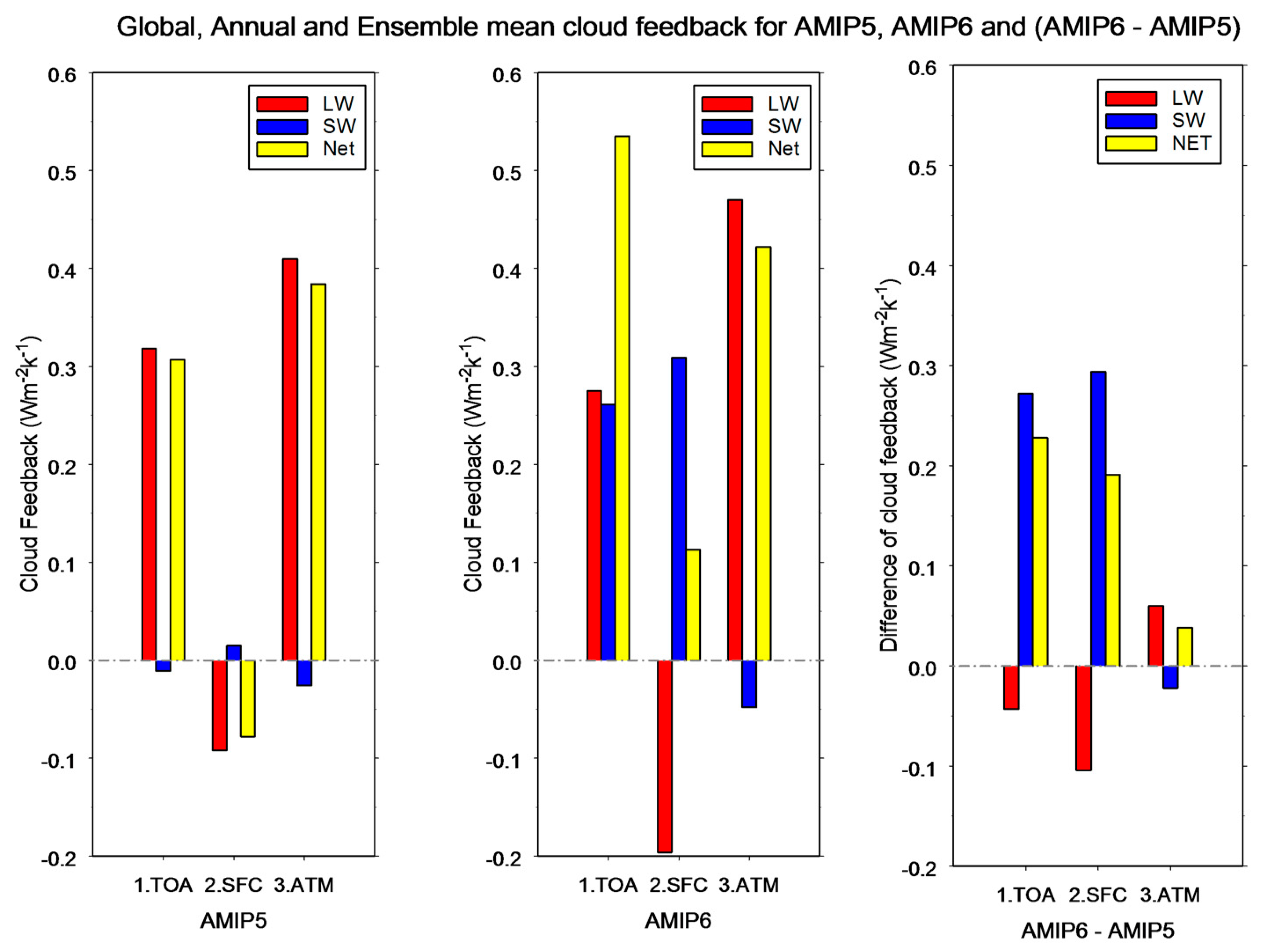
The resulting global, ensemble and annual mean cloud feedback for the 49 histogram bins show that the majority (≥80%) of individual models for both AMIP5 and AMIP6 (Figure 3 and Figure 4) agree in sign. The most noticeable aspect is that the longwave (LW) cloud feedback in the ATM is substantially larger than that at the TOA. Figure 5 shows the global, annual and ensemble mean cloud feedback for LW, shortwave (SW) and their sum (Net) at the TOA and SFC, and in the ATM for AMIP5, AMIP6 and their differences. Both AMIP5 and AMIP6 have positive LW cloud feedback in the ATM, larger than that at the TOA by 29% and 71%, respectively. They are offset by the negative LW cloud feedback at the SFC to maintain their sums (the TOA LW cloud feedback), which is slightly smaller for AMIP6 (0.28 Wm⁻²K⁻¹) than for AMIP5 (0.32 Wm⁻²K⁻¹). The SW cloud feedback for AMIP5 is nearly negligible (small and negative for the TOA and ATM cloud feedback, small and positive for the SFC cloud feedback), but it is substantially increased at the TOA and SFC in AMIP6. As a result, the TOA Net cloud feedback from AMIP5 to AMIP6 is increased by 74%, entirely contributed by the SW cloud feedback, even though it has been compensated by the LW feedback. However, the evident differences of the LW, SW and Net cloud feedback for total clouds in the global mean (right panel in Figure 5) are statistically insignificant.

The large increase in the Net cloud feedback is strongly (positively) correlated with the total feedback parameter and ECS [23]. Because AMIP itself does not directly output ECS values, we have examined the results of the CMIP models in [2], since the AMIP models are their atmosphere component. The mean ECS of the CMIP6 associated with AMIP6 is 4.4 K; that of CMIP5 associated with AMIP5 is 3.4 K (see Table 1). Therefore, the substantial increase (74%) in the TOA cloud feedback is a primary contributor to the highly biased ECS [2] (the best estimate is 3.0 K, see Section 1) in some CMIP6 models.

The substantially large, positive LW (and consequently, Net for both AMIP5 and AMIP6) cloud feedback in the atmosphere would heat the atmosphere and amplify (under the amip4k scenario) global warming, further enhancing the positive feedback. This effect is physically different from the general (simplistic) view that feedback processes scale with global-mean surface temperature independent of the spatial pattern of warming [23]. For AMIP6, the SFC SW cloud feedback is larger than the TOA’s by 18% (which is offset by the ATM SW cloud feedback by the same amount to preserve the TOA value). After compensation by the negative SFC LW cloud feedback, the Net SFC cloud feedback for AMIP6 is 0.11 Wm⁻²K⁻¹, which shows a substantial increase compared to AMIP5 (−0.078 Wm⁻²K⁻¹). Since the SFC Net cloud feedback directly heats/cools the surface to raise (reduce) the surface temperature, it may also increase (decrease) climate sensitivity in a more direct way.

The global-mean cloud feedback can only give an overall view of cloud feedback, and the statistical significance of the difference in cloud feedback may be degraded by spatial averaging. More detailed spatial characteristics are needed to understand the evolution of cloud feedback from AMIP5 to AMIP6, which are presented in the following two sections (Section 4 and Section 5).

4. Zonal Mean Cloud Feedback from AMIP5 to AMIP6

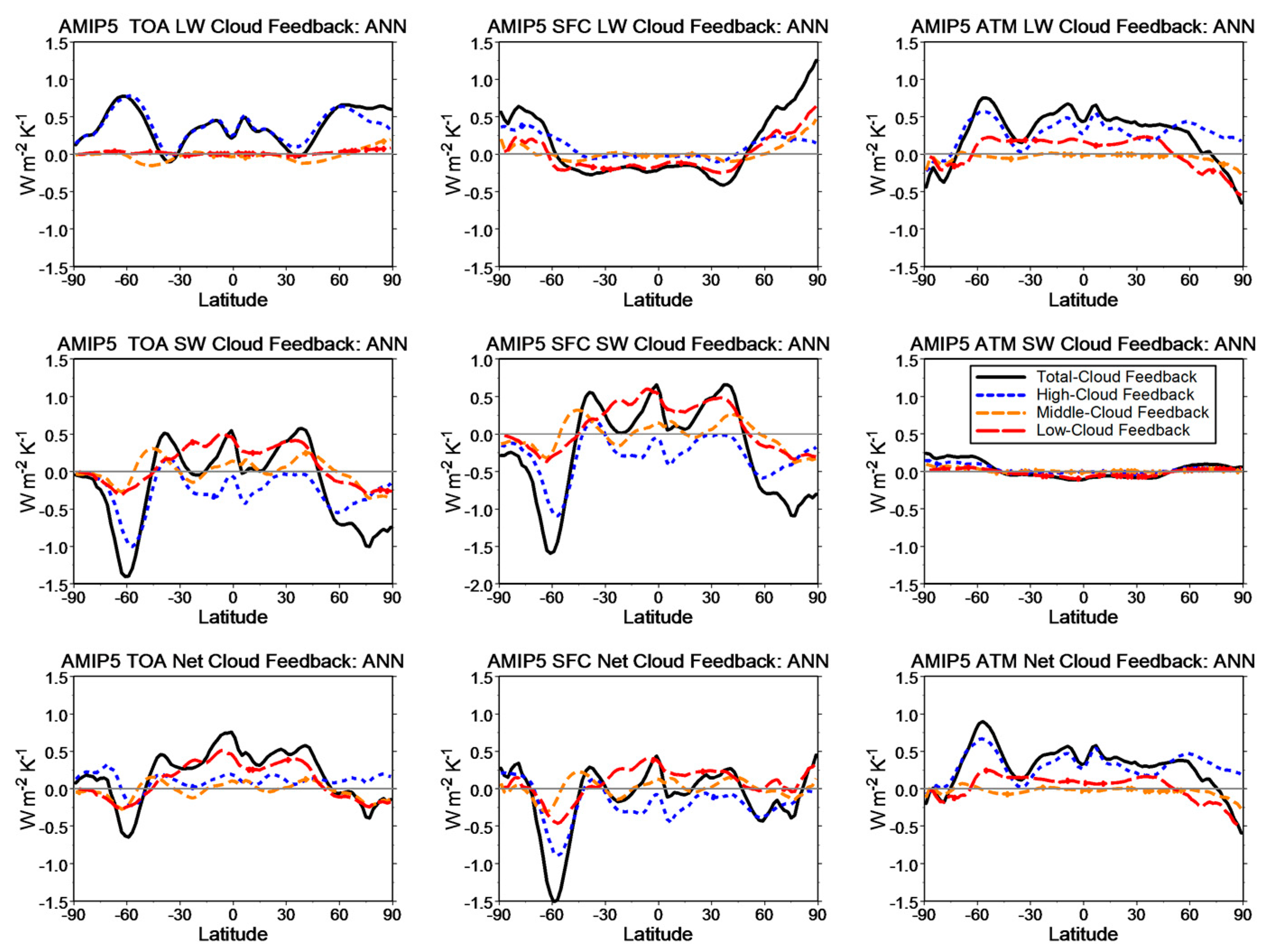
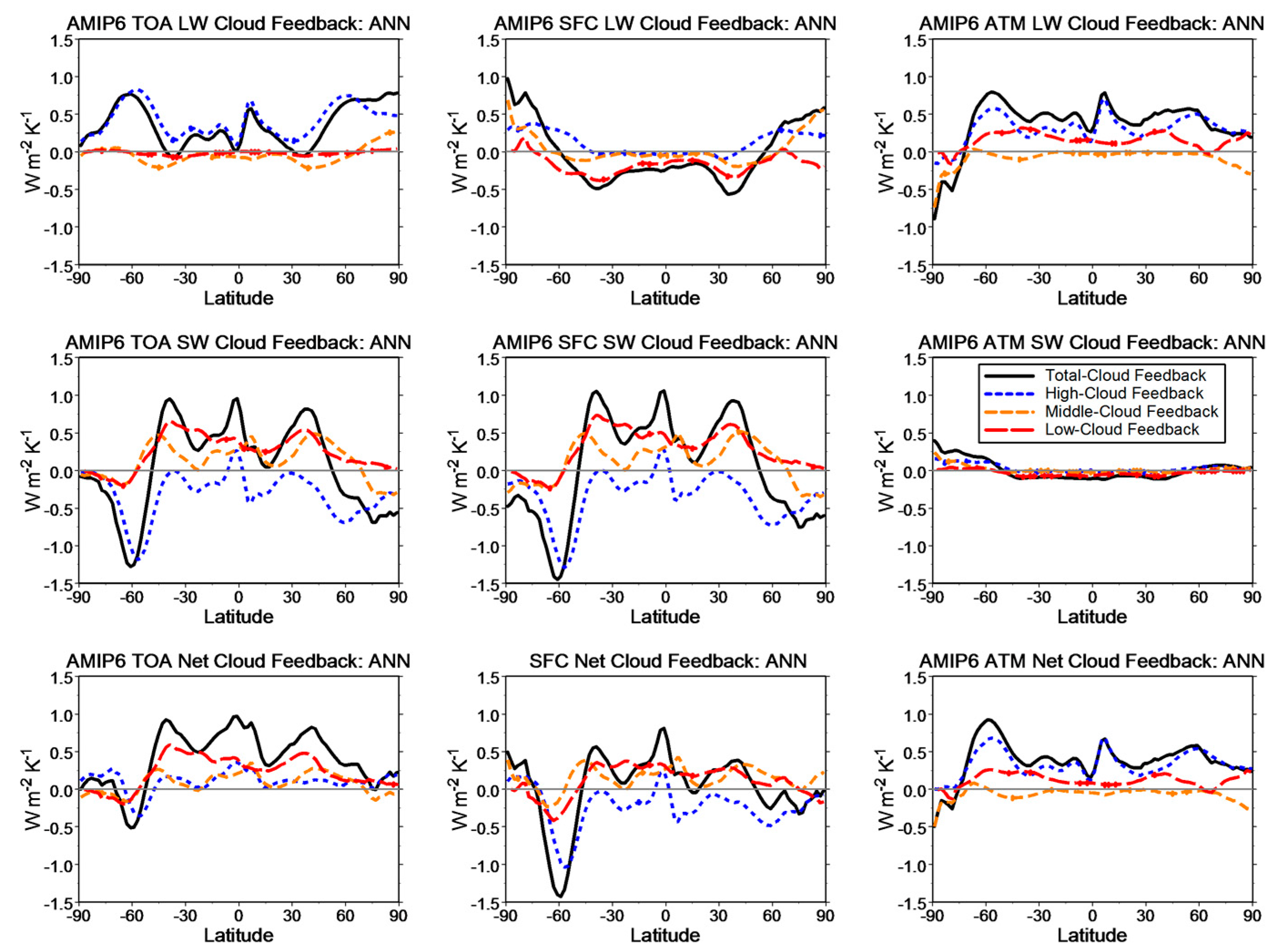
The cloud feedback presents various spatial inhomogeneities over latitudinal zones. Figure 6 and Figure 7 show the zonal-mean LW, SW and Net cloud feedback for high, middle, low and total clouds, at the TOA and SFC and in ATM, for AMIP5 and AMIP6, respectively. These results are consistent with the previous findings based on the ensemble, annual mean cloud feedback from CMIP3/CFMIP1 models [18]. Namely, (i) the near-zero low cloud feedback for the TOA LW results from a nearly complete compensation of the sizeable low cloud feedback at the SFC and in the ATM, and (ii) the smaller high cloud feedback in the TOA Net cloud feedback may be explained by the compensating effect of either the SFC and ATM Net cloud feedback or the TOA LW and SW cloud feedback [16,18]. These considerations can be applied to the cloud-feedback component of other GCMs. The complex radiative and thermodynamic effects of the SFC and ATM cloud-feedback components happening in the real atmosphere–earth system cannot be revealed by the analysis of the apparent TOA cloud feedback alone, because their individual physical effects cannot be combined in a simple way to form the cloud feedback at the TOA. The use of the SFC and ATM CRKs to separate these components is therefore indispensable, and innovative model experiments (that fall beyond the scope of this study) may finally reveal the physical role of these “hidden” effects.

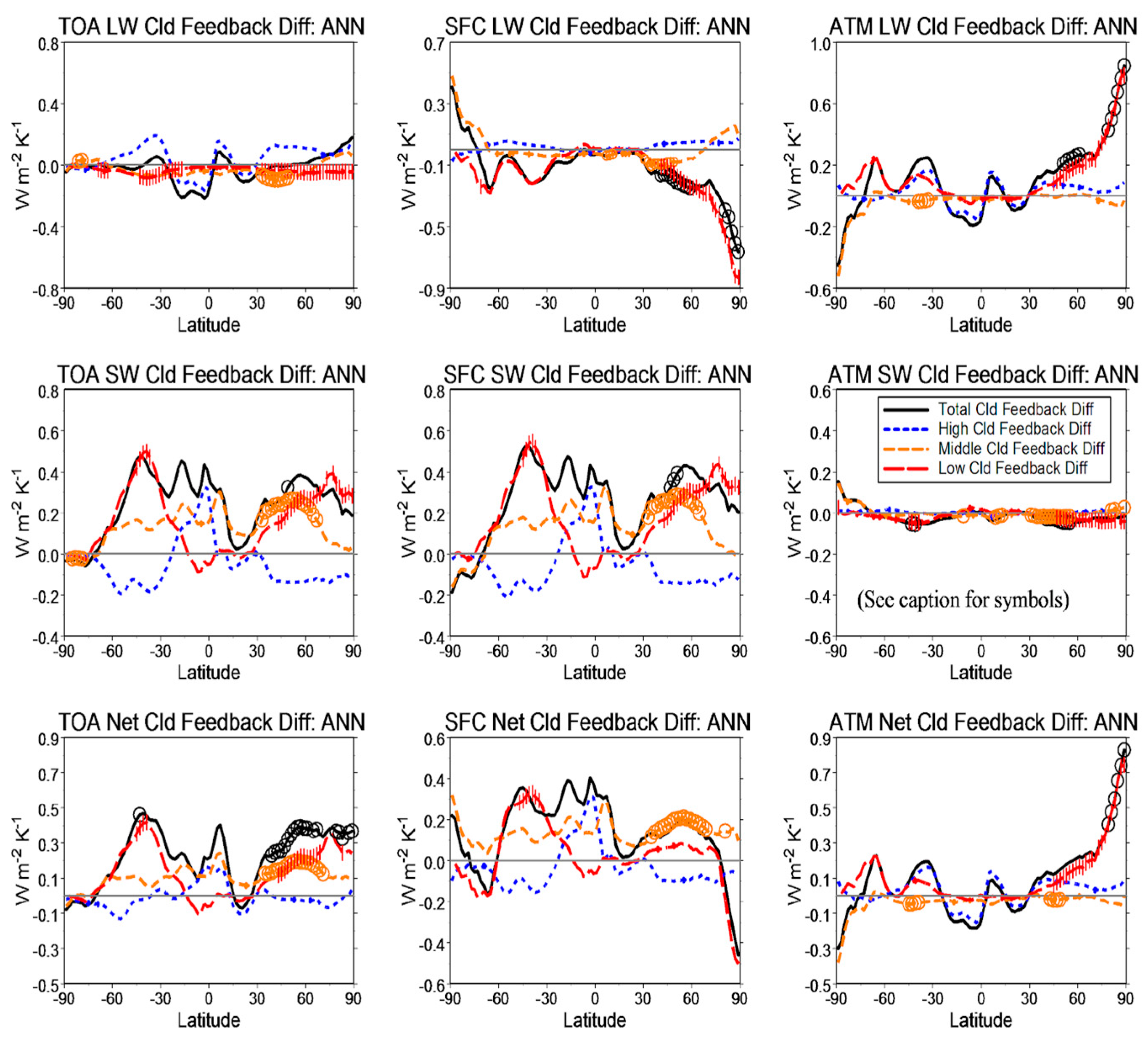
Figure 8 shows the zonal mean of the cloud feedback difference. The large SFC and ATM LW cloud feedback differences (up to ~0.8 Wm⁻² K⁻¹) are contributed by low clouds at high latitudes, but they almost entirely compensate each other when adding them to form the TOA LW cloud feedback difference. This is also reflected in the TOA Net cloud feedback. The middle and high cloud feedback differences of the TOA SW and Net come largely from the SFC contribution, mainly at high latitudes in both hemispheres but also in tropical zones. Overall, the Net cloud feedback (bottom left panel) increases nearly everywhere, with peaks in the tropics, at mid-to-high latitudes of the northern hemisphere and at midlatitudes of the southern hemisphere. Figure 8 also shows that all the zonal-mean, high cloud feedback differences are insignificant. The significant zonal-mean cloud feedback differences mainly appear in the northern mid-to-high latitudes, but also in some tropical and other extratropical zones.

Cloud feedback may also change the net radiative energy distribution in the zonal average, which may cause changes in energy transport from the tropics to the polar regions. Figure 8 indicates that relative to AMIP5, the cloud radiative effects of the AMIP6 ATM LW cloud feedback (top right panel) have a positive (negative) gradient over mid-to-high latitudes for the northern (southern) hemisphere, which implies a weakening (strengthening) of the northward (southward) meridional atmospheric energy transport. This fact is also manifested in the ATM Net cloud feedback (bottom right panel), yet only to a smaller degree because of the compensation between the opposite effects of the ATM SW cloud feedback (right middle panel). Based on similar arguments, the opposite role is likely to be played by the AMIP6’s SFC LW (and Net) cloud feedback with respect to the meridional oceanic energy transport (cf. [18,24]), caused by the meridional gradient of cloud radiative effects resulting from the cloud feedback [25]. A precise quantification of all changes in the meridional energy transport due to changes in the cloud feedback requires further data processing, which will be the object of future investigations.

5. Spatial Features of Global Cloud Feedback from AMIP5 to AMIP6

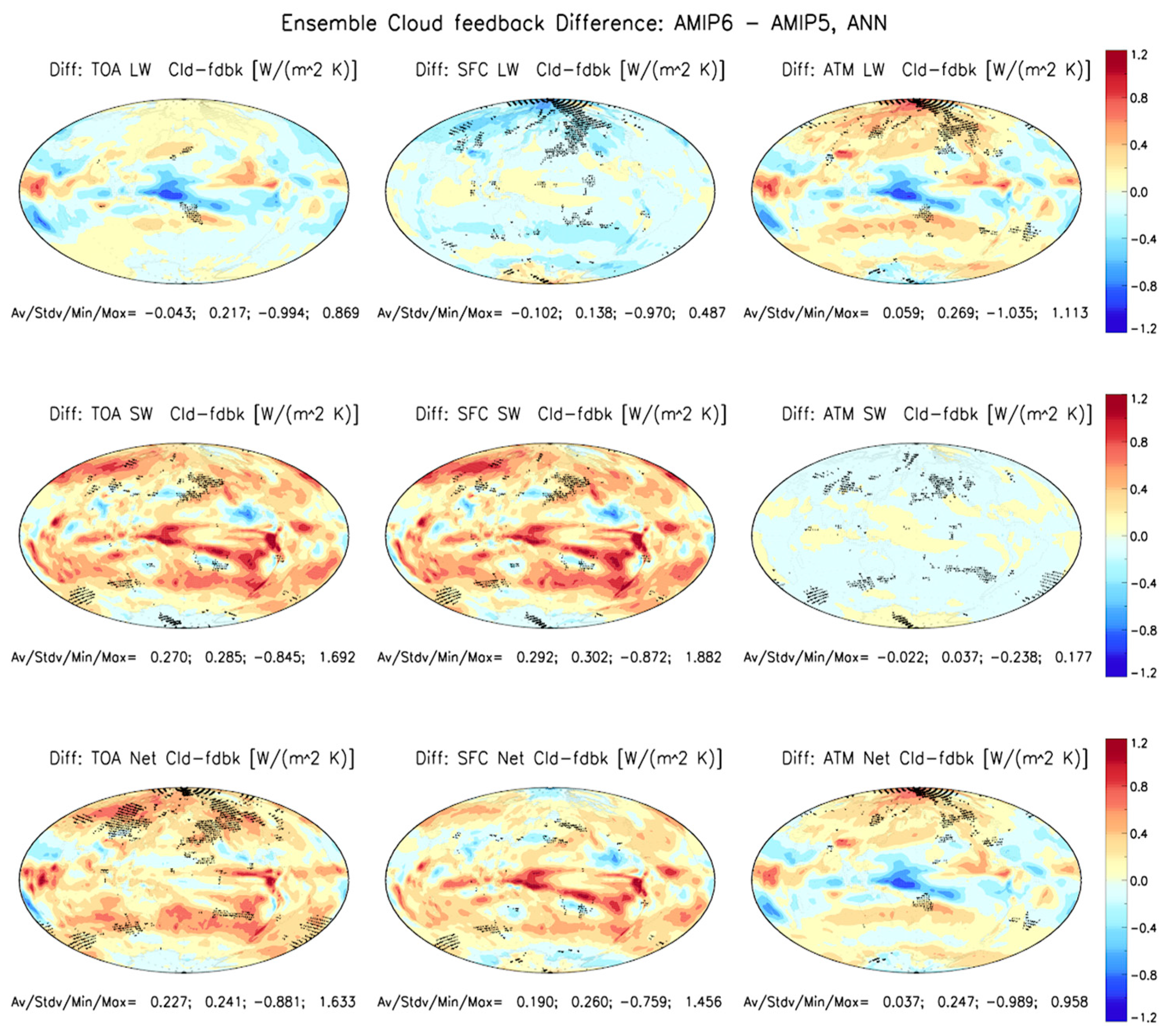
After comparing the zonal cloud feedback in AMIP5 and AMIP6, we turn to explore their spatial distribution on a global map for different cloud types in order to gain insight into the regional details. Figure 9 presents the difference in the total cloud feedback (sum of cloud feedback in all 49 bins) between AMIP6 and AMIP5 for LW, SW and Net cloud feedback at the TOA and SFC and in ATM (cf. Figure 5 and Figure 8). The global-mean statistics show that 83% of the TOA Net cloud feedback increase (0.23 Wm⁻²K⁻¹) is contributed by the SFC Net cloud feedback increase (0.19 Wm⁻²K⁻¹), which originates from the compensation between the SFC SW cloud feedback increase (0.29 Wm⁻²K⁻¹) and the SFC LW cloud feedback decrease (−0.10 Wm⁻²K⁻¹). In Figure 9, the regions (grid cells) with a significant cloud feedback difference are more or less sparse except (i) the north polar region for LW at the SFC and in the ATM, the Net at the TOA and in the ATM; (ii) the other northern high latitudes for all the nine panels; and (iii) the southern middle latitudes for most of the nine panels.

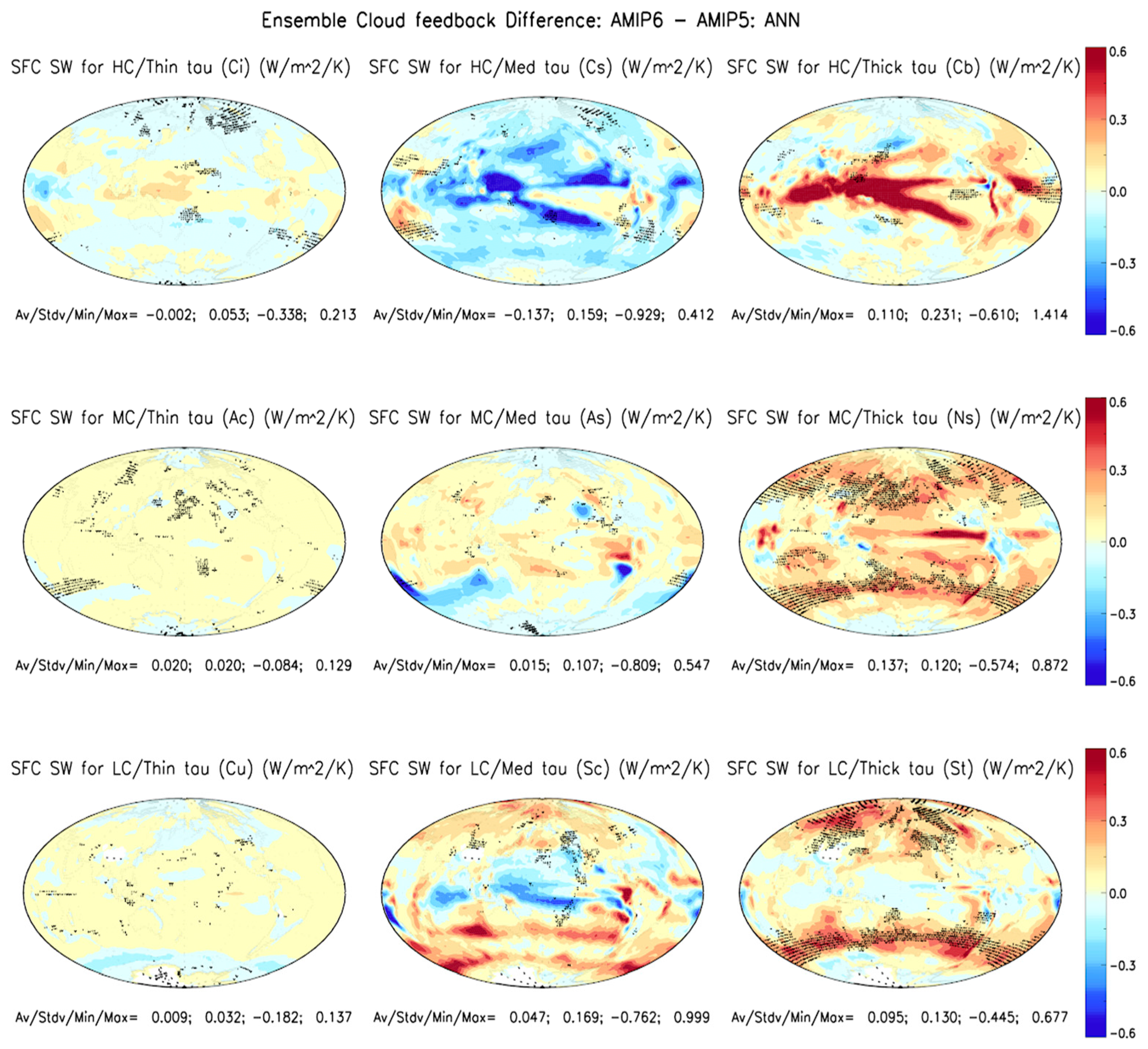
Regarding the link between the SFC SW cloud feedback change and cloud type, Figure 10 shows that it is mainly contributed by thick clouds (Ns, Cb and St in order of strength of 0.14, 0.11 and 0.10 Wm⁻²K⁻¹), but are partially compensated by Cs (−0.14 Wm⁻²K⁻¹). Because the SFC SW cloud radiative kernel is negative for all the histogram bins [18], the sign of the SFC SW cloud feedback is opposite to that of CFCs. At a grid-cell level, we see that more significant difference regions forming dense latitudinal bands appear for middle and low, optically thick clouds, which are the cause of the increase in the TOA SW and Net cloud feedback, as mentioned before.

Figure 11 shows the difference in annual and ensemble mean CFCs in the same layout as Figure 10. The regional sign correspondence between the SFC SW cloud feedback difference in Figure 10 and the CFC difference in Figure 11 for each cloud type can be exactly matched, but the magnitude varies depending on the strength of the individual SFC SW kernels as well as on the magnitude of the CFC differences. Generally speaking, the SFC SW CRK increases with increasing τ (and slightly with decreasing cloud altitude). For high clouds, the increase in the AMIP6’s SFC SW cloud feedback from deep convection (Cb) clouds is substantially larger over the ITCZ and the South Pacific Convergence Zone (SPCZ), but also largely offset by that of the feedback difference due to Cs. As a result, there appear to be small and positive, high-cloud feedback differences (up to 0.3 Wm⁻²K⁻¹) over the south tropical region and small negative cloud feedback differences at high latitudes as shown by the zonal mean (middle panel of the second column in Figure 8). For middle clouds, the SFC SW cloud feedback difference for Ns in Figure 10 is positive over almost the entire globe except for some continental areas. After small compensation by negative SFC SW cloud feedback differences due to As over some oceanic areas (mainly at mid-latitudes), its zonal mean maintains a roughly constant positive value of ~0.2 (Wm⁻²K⁻¹) from ~60° S to ~60° N (Figure 8). For low clouds, the positive SFC SW cloud feedback difference mainly comes from St and Sc over southern mid-latitude and northern mid-to-high-latitude oceanic areas, with small negative values around the equator (Figure 8 and Figure 10). In Figure 11, we see the similar bands that correspond to the bands in Figure 10, which well explains why Figure 10′s bands appear in Ns and St.

Based on spaceborne active remote sensing, Mülmenstädt et al. [10] are able to construct a close proxy to the cloud-precipitation process rate and conclude that the warm clouds precipitate too readily in the test CMIP6 model, potentially leading to underestimated negative cloud-lifetime feedbacks, particularly for the southern ocean. In addition, Qin et al. [15] have extensively studied the relationship between CMIP and AMIP models. They have compared radiative feedbacks between amip4K and coupled experiments in CMIP5 and CMIP6 models, and analyzed the global-mean values, spatial distribution and breakdown into individual cloud feedback components. They concluded that, overall, these results confirm the utility of atmosphere-only experiments, particularly to study cloud feedbacks, which are the dominant source of inter-model spread in climate sensitivity. They also concluded that amip4K experiments successfully capture most of the coupled model diversity in global-mean cloud amount, altitude, and optical depth feedback components for all clouds. Therefore, the implication is that the CFCs of the AMIP6 models for the warm clouds are biased low (larger and negative) relative to the AMIP5 models, particularly over the southern ocean, because frequent raining of the warm clouds would lead to smaller CFCs (Figure 11). This seems to be the case for Ns, Sc and St, and they thus contribute to large positive cloud feedback over the southern midlatitude ocean (Figure 10), which is the primary cause of the overestimate of the cloud feedback and high ECS in the AMIP6/CMIP6 models.

This example demonstrates how we can obtain detailed spatial distributions of the cloud feedback changes due to individual cloud types and to what extent they contribute to the total SW cloud feedback changes at the SFC (central panel of Figure 9). In addition, the significance test for the difference between AMIP6 and AMIP5, along with the rest of the detailed analysis at the grid-cell level for nine cloud types, offers a new method to analyze the model differences and shed light on potential improvement. A similar analysis can be applied to any other total cloud feedback (Figure 9) for SW, LW and Net at the TOA and SFC and in the ATM to provide a new way to increase our understanding of cloud feedback so as to improve the cloud feedback representation in climate models. Based on Figure 10, climate modelers may explore different ways to constrain changes in CFCs associated with different cloud types and different regions, to reduce climate sensitivity in AMIP6/CMIP6 based on the cloud feedback mechanism [23].

6. Summary and Conclusions

The purpose of this study is to understand the evolution of clouds and cloud feedback from AMIP5 to AMIP6 by comparing their amip4k experimental results based on 10 AMIP5 and 9 AMIP6 models. This exercise is useful for providing insights for GCM improvements. The detailed comparison considers global and zonal means, and the spatial distribution of CF, CFCs and their CRK-derived cloud feedback at the TOA and SFC and in the ATM for different cloud types when applicable.

Compared to AMIP5, the annual ensemble and global mean of CF increase by 9.0% in AMIP6, while the CFC global average decreases by 0.25%. The majority of cloud types contributes positive (negative) CF (CFC) differences. The increase in the global-mean CF may be regarded as an improvement as it leads to a closer match with the observations, but the effects of CFCs on cloud feedback are complex (e.g., a simple increase in CFCs for a cloud type may cause either increase or decrease in the net cloud feedback or ECS). The increase in cloud feedback for AMIP6 is dominated by optically thick- and medium-τ clouds, and causes higher ECS in some CMIP6 models. The changes in CF and CFCs are largely (or for the majority of the cloud types) anticorrelated, which may be useful to refine cloud models based on cloud feedback mechanisms [23].

The characteristics of the zonal-mean cloud feedback of both AMIP5 and AMIP6 are consistent with previous findings [18]. Namely, the very small, low-cloud feedback of the TOA LW and the small, high-cloud feedback of the TOA Net do not reflect the real, sizable ATM and SFC cloud feedbacks because of the compensation effects between these two components. Such characteristics are likely to manifest in the majority of current GCMs. Analyzing the SFC and ATM components separately allows us to elucidate intricacies that cannot be revealed by analyzing the TOA cloud feedback alone, because the atmosphere and the surface have quite different physical responses to the cloud feedback. Even within the same atmosphere, the radiative warming (cooling) caused by the cloud feedback in the upper atmosphere tends to stabilize (destabilize) the atmosphere, while the situation is reversed in the lower atmosphere. On the other hand, the surface warming (cooling) caused by the SFC cloud feedback may more directly increase (decrease) the surface temperature (and, therefore, the ECS). The partition of the TOA cloud feedback into its atmospheric and surface contributions is also instrumental for studying ECS estimates, the intermodal spreads and, in general, how the TOA cloud feedback functions in the real world.

We also made the null hypothesis test to estimate if the differences between AMIP6 and AMIP5 (as shown in those figures) are statistically significant. The test was conducted for the various differences from global to zonal mean to the original grid-cell level for clouds, from total/all clouds to individual cloud types. The test at the original grid-cell level and for cloud types seems more fundamental in understanding and improving future models, while all the averages generally degraded the significance levels.

Based on the comparison of the annual ensemble means, the changes in cloud feedback from AMIP5 to AMIP6 may be summarized as follows:

1. The TOA Net cloud feedback in AMIP6 is almost double (174%) compared to that of AMIP5. The increase (74%) is contributed mainly by the SFC Net component (62%), followed by the ATM Net counterpart (12%). The former is entirely due to the increase in SFC SW cloud feedback, albeit partially compensated by a decrease in SFC LW cloud feedback. The latter is entirely due to an increase in the ATM LW cloud feedback, partially compensated by a decrease in the ATM SW cloud feedback;

2. The large zonal-mean SFC and ATM LW cloud feedback differences (up to ~0.8 Wm⁻² K⁻¹) are contributed by low clouds that appear at (especially Northern) high latitudes, but they almost entirely compensate when calculating the TOA LW cloud feedback difference (Figure 8);

3. The middle- and high-cloud feedback differences of the TOA SW are dominated by the SFC component. They mainly appear at (especially northern) high latitudes and, to a smaller degree, in tropical zones (Figure 8);

4. The increase in SFC SW cloud feedback is mainly contributed by optically thick, middle- and low-level clouds. Noticeably, the strong SFC SW cloud feedback over the ITCZ and SPCZ from optically thick, high-level clouds (Cb and Cs) is nearly compensated by the LW counterparts (Figure 10);

5. Partitioning the total SFC SW cloud feedback difference into the nine cloud types (Section 5) offers a way to investigate the cloud feedback changes between AMIP5 and AMIP6 in regional details for all the individual cloud types. The impact on cloud feedback mechanisms (e.g., [23]) is useful for modelers to improve cloud models;

6. Based on the study by Mülmenstädt et al. [10], the large negative CFC difference of Ns, Sc and St between AMIP6 and AMIP5 is likely a manifest of the too-frequent warm cloud raining in AMIP6 models that leads to smaller warm cloud amount, especially over the southern ocean, contributing to the large positive cloud feedback (Figure 10), which is the primary cause of the overestimate of the cloud feedback and high ECS in the AMIP6/CMIP6 models;

7. With respect to AMIP5, the AMIP6 ATM LW (and Net) cloud feedback is likely to play a role in weakening (strengthening) the northward (southward) meridional atmospheric energy transport, while the opposite role is likely to be played by the AMIP6’s surface LW and Net cloud feedback for the meridional oceanic energy transport;

8. The cloud feedback spread in AMIP6 is compared to that in AMIP5;

9. Using the null hypothesis test to establish the significance of all the relevant differences between AMIP6 and AMIP5 sheds new light on the analysis of changes in clouds and cloud feedback between the two model groups. The results are consistent with the other conclusions, especially for middle and low, optically thick clouds that cause the substantial increase in the AMIP6 TOA Net cloud feedback. A strong, positive cloud feedback difference takes place over most extratropical regions due to the negative CFC difference (Figure 10 and Figure 11). However, caution must be exercised because the assumptions for the test are not strictly satisfied since about half of AMIP6 models (see Table 1) belong to the same breed as AMIP5, so the two model groups are not strictly independent.

Finally, we would like to stress that the conclusions from this study are largely applicable to the study of fully coupled simulations, e.g., to evaluate the TOA cloud feedback under abrupt-4xCO2 scenarios for CMIPs [15] and improve the highly biased ECS in some CMIP6 models in perspective of the upcoming CMIP7 models.