The Role of Water Vapor Observations in Satellite Rainfall Detection Highlighted by a Deep Learning Approach
Abstract
1. Introduction
2. Materials and Methods
2.1. Development Dataset and Benchmark Satellite Rainfall Products
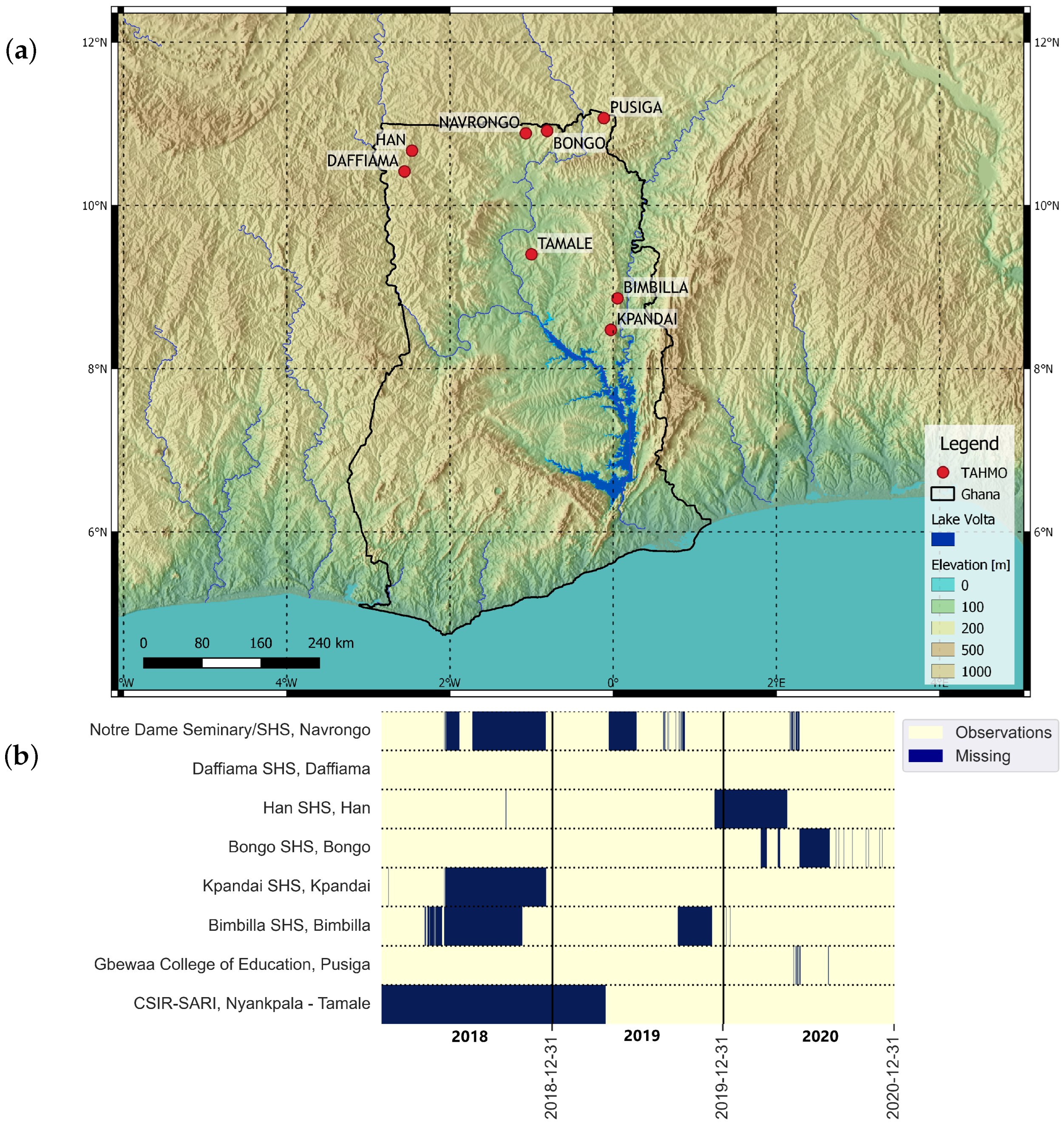
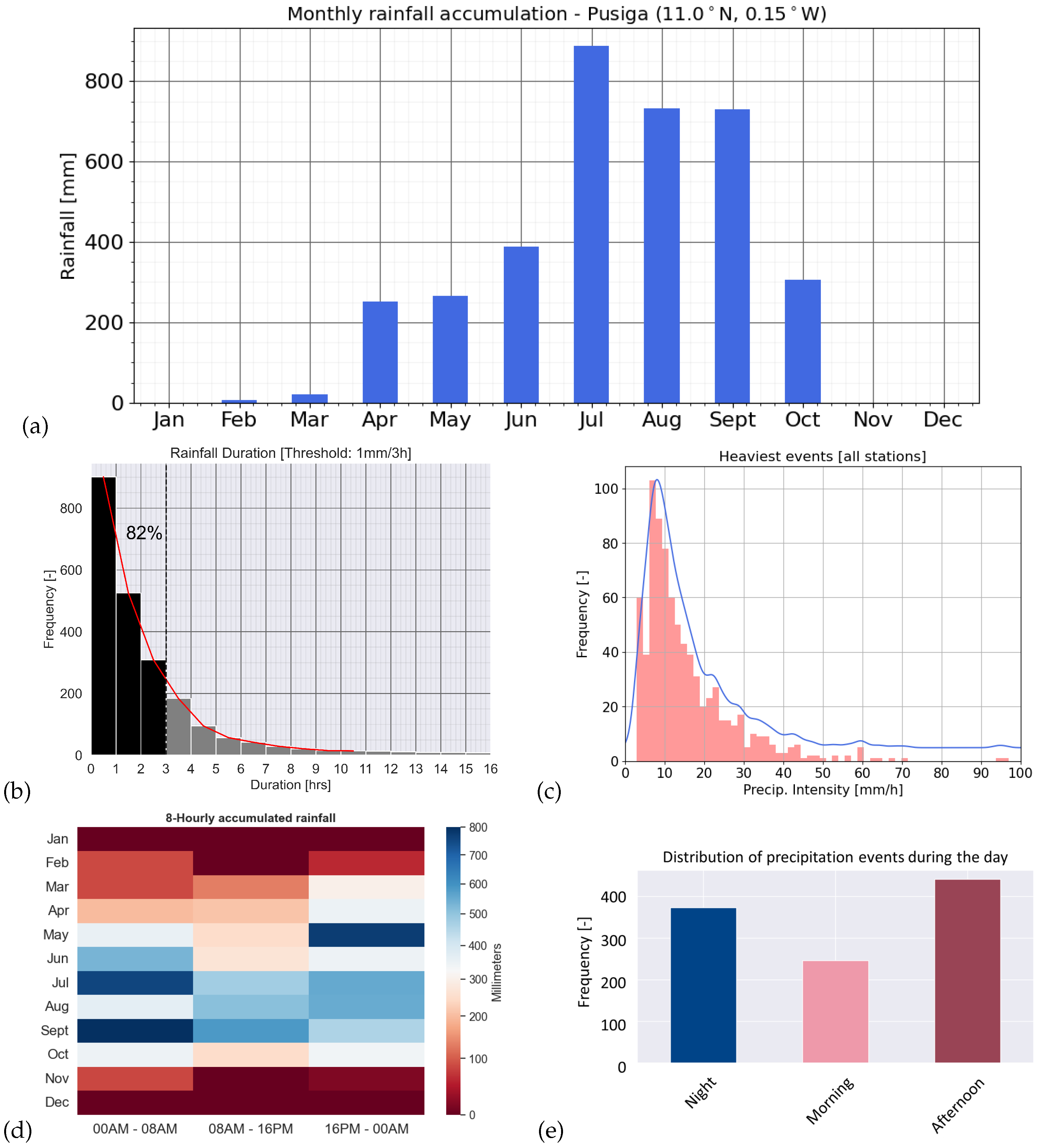
2.2. Study Area: North of Ghana
2.3. Data Preprocessing
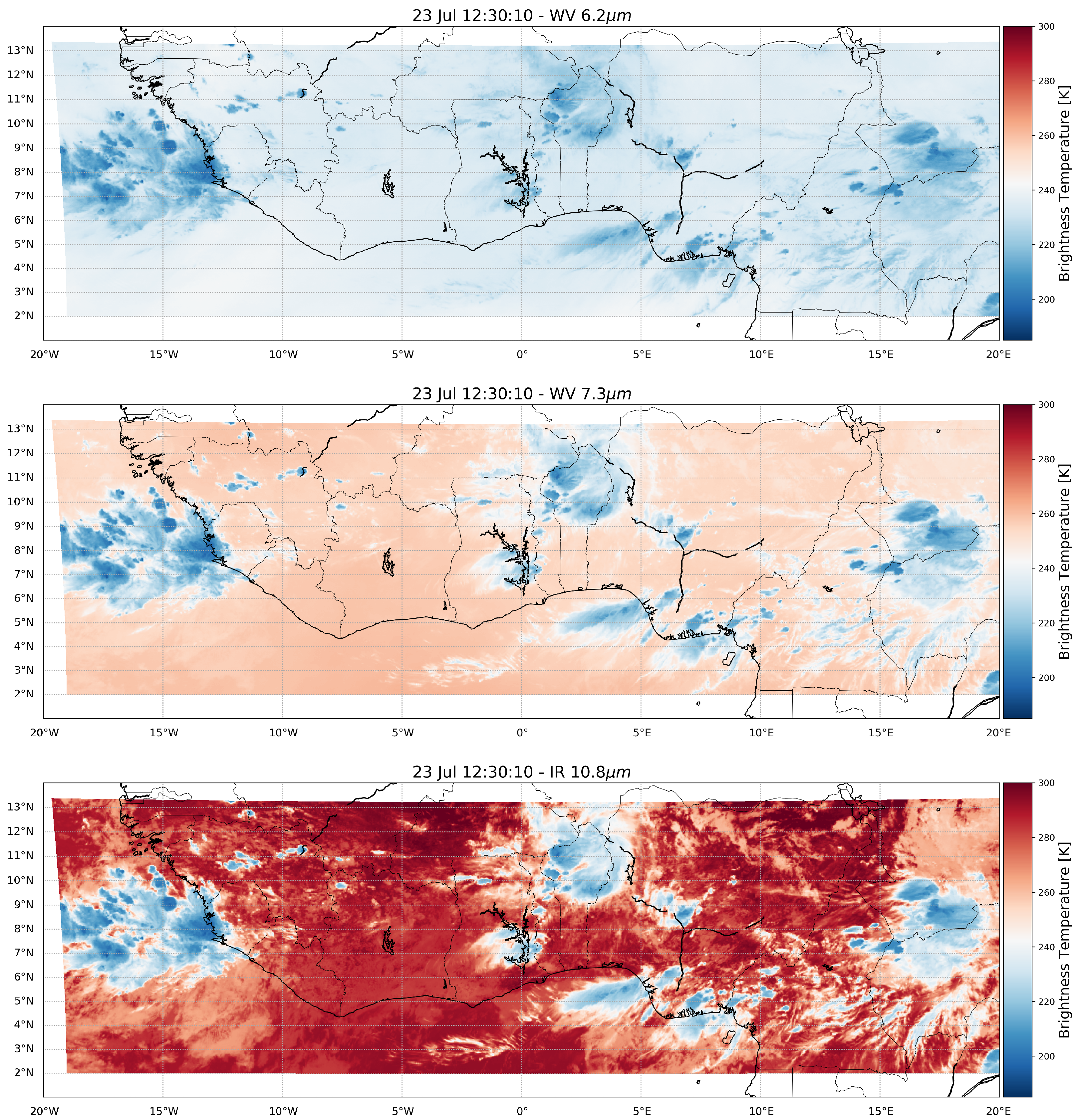
2.4. Satellite Data Analysis
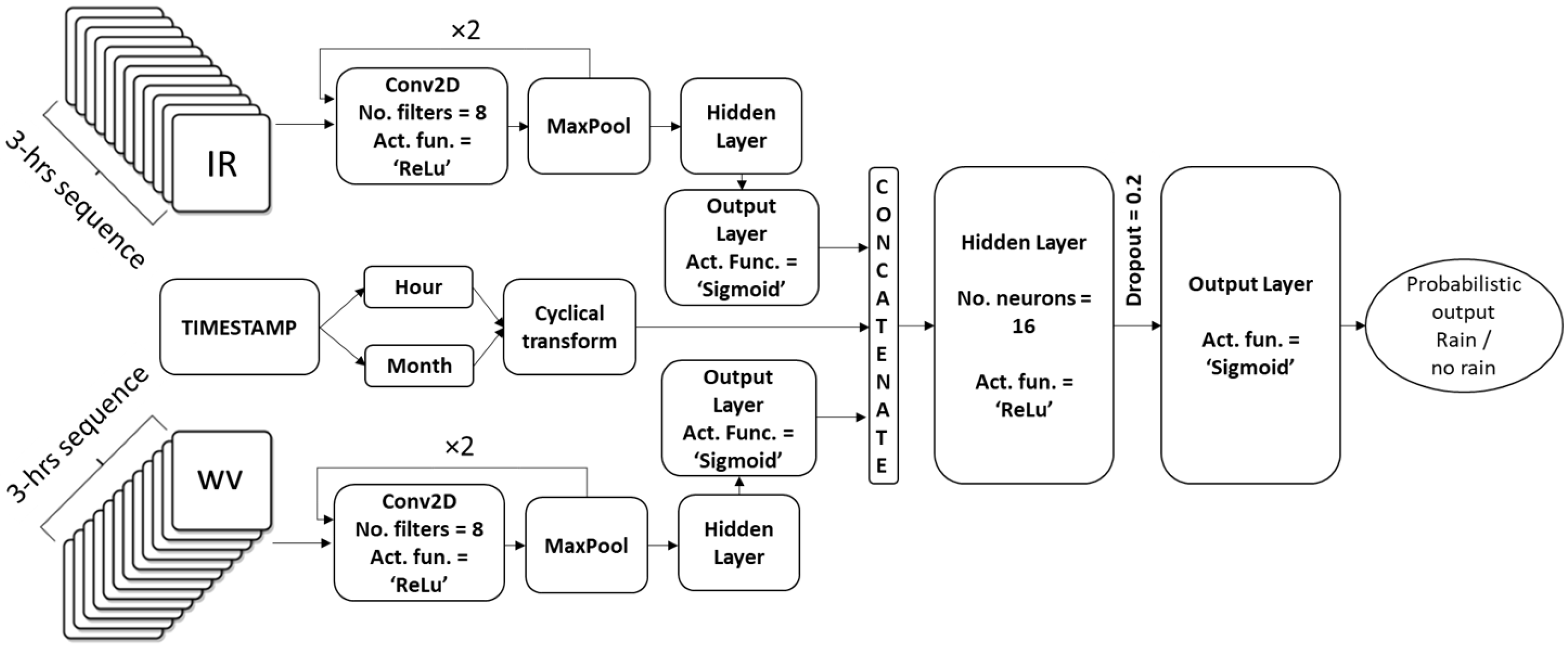
2.5. Model Development
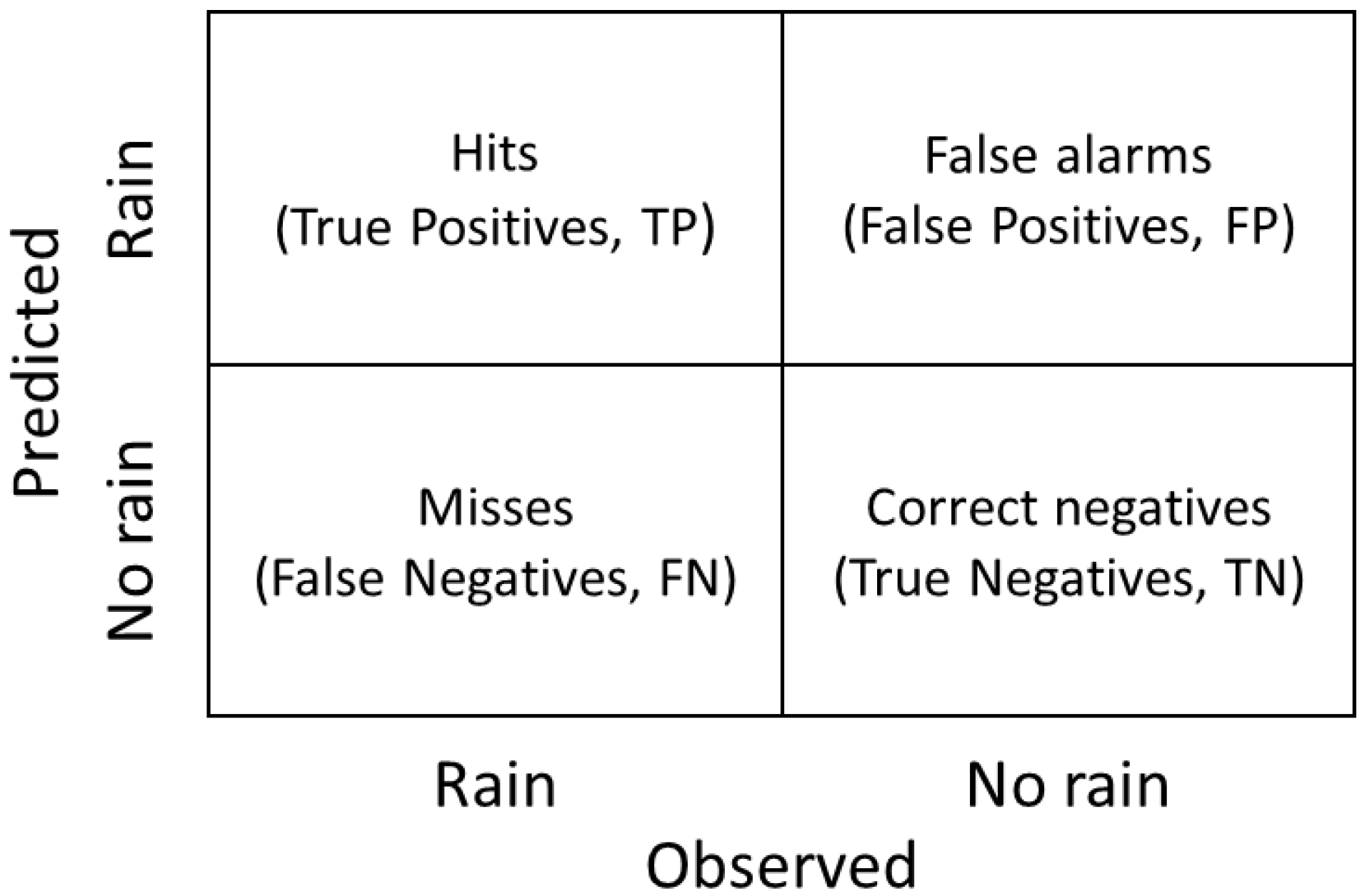
2.6. Performance Evaluation and Assessment of Data Contribution
- Very light rain: 1 mm/3 h 1 mm/h;
- Light rain: 1 mm/h 2.5 mm/h;
- Moderate rain: 2.5 mm/h 7.6 mm/h;
- Heavy rain: 7.6 mm/h.
3. Results
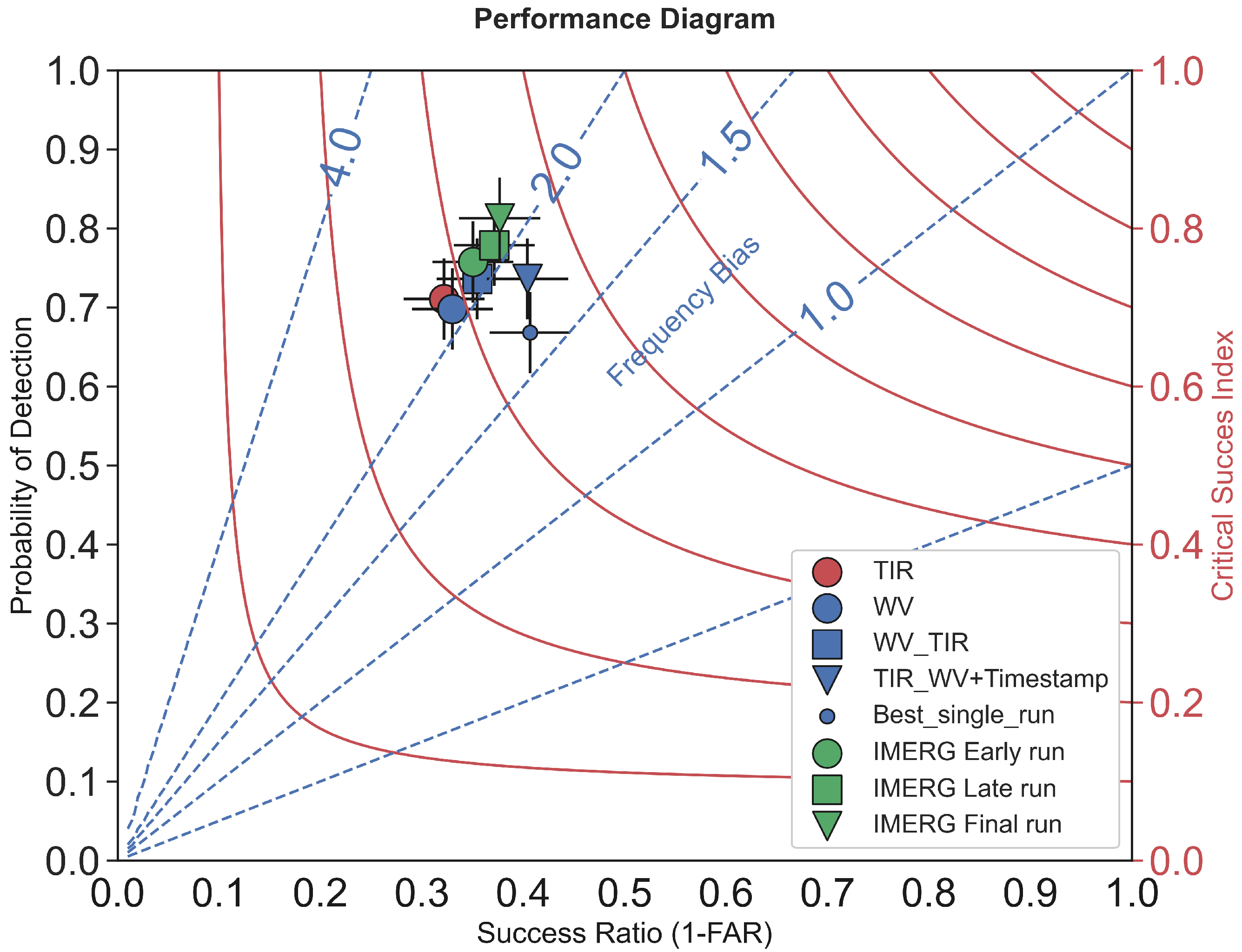
3.1. Model Performance on the Independent Test Dataset
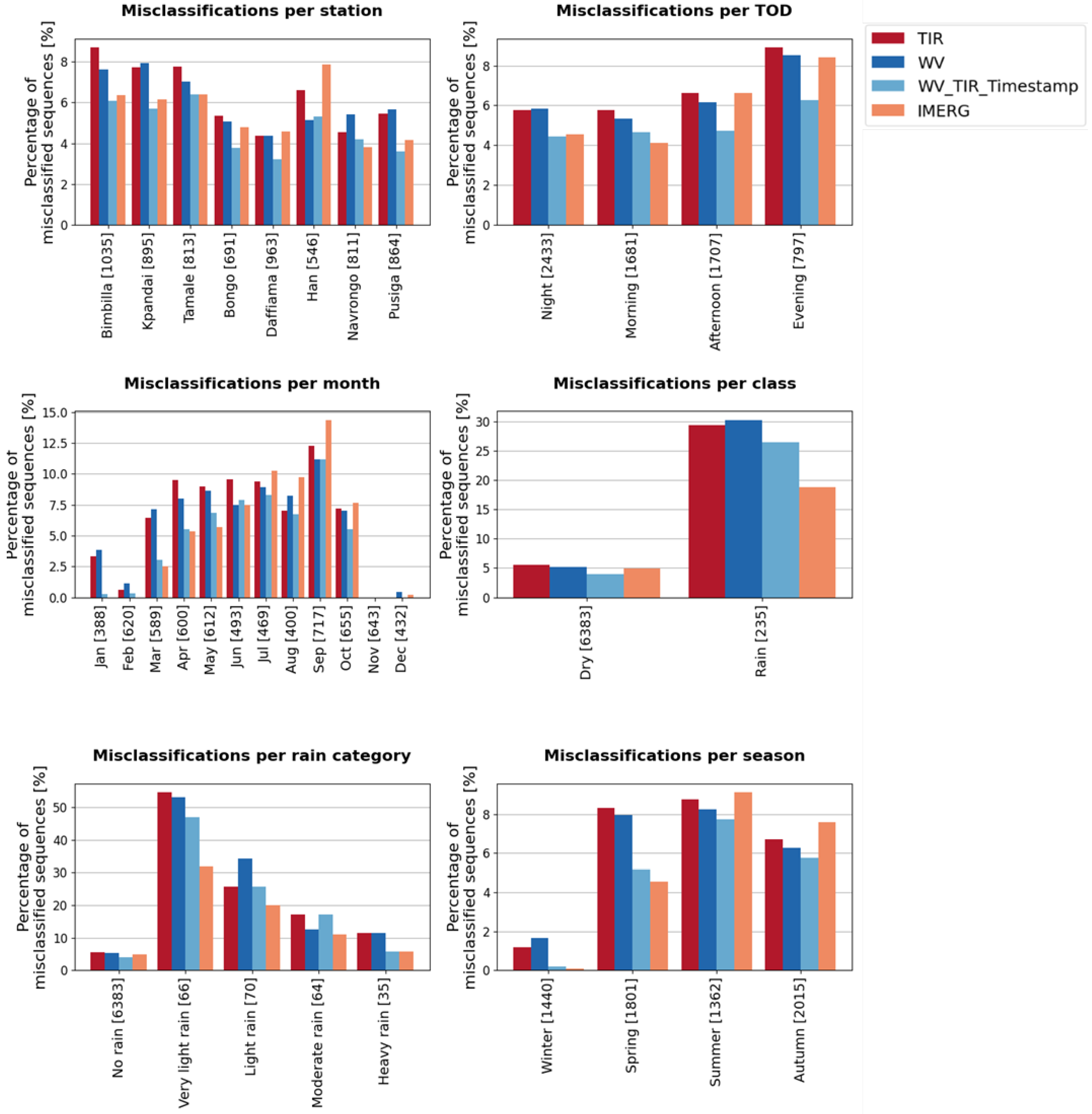
3.2. Misclassification Analysis
3.3. Pixel Analysis Comparison
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. Pixel Analysis

Appendix A.2. Dry Slots
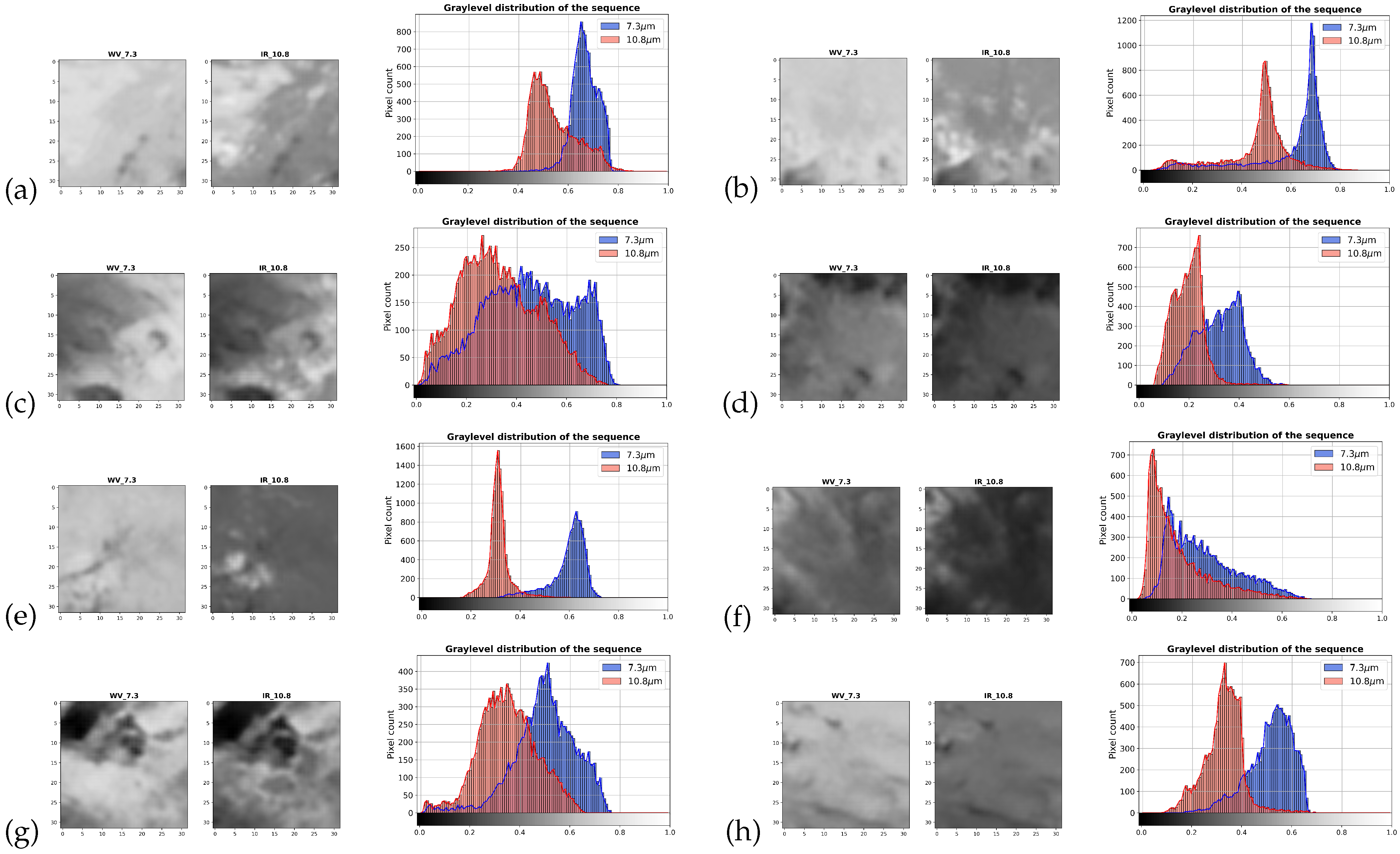
| Event | Ground Truth | TIR | WV | TIR + WV | TIR + WV + Timestamp |
|---|---|---|---|---|---|
| (a) Bimbilla, 2020.09.07, 09 h | 0 | 0.51 | 0.03 | 0.007 | 0.17 |
| (b) Bimbilla, 2020.09.12, 06 h | 0 | 0.56 | 0.54 | 0.23 | 0.39 |
| (c) Han, 2020.10.01, 15 h | 0 | 0.73 | 0.34 | 0.42 | 0.33 |
| (d) Bongo, 2020.04.10, 15 h | 0 | 0.66 | 0.28 | 0.49 | 0.38 |
| (e) Bongo, 2020.05.09, 12 h | 0 | 0.41 | 0.11 | 0.32 | 0.35 |
| (f) Daffiama, 2020.05.15, 15 h | 0 | 0.74 | 0.28 | 0.47 | 0.25 |
| (g) Tamale, 2020.06.14, 12 h | 0 | 0.52 | 0.09 | 0.29 | 0.23 |
| (h) Navrongo, 2020.06.20, 15 h | 0 | 0.45 | 0.04 | 0.35 | 0.50 |
Appendix A.3. Dry Intrusions
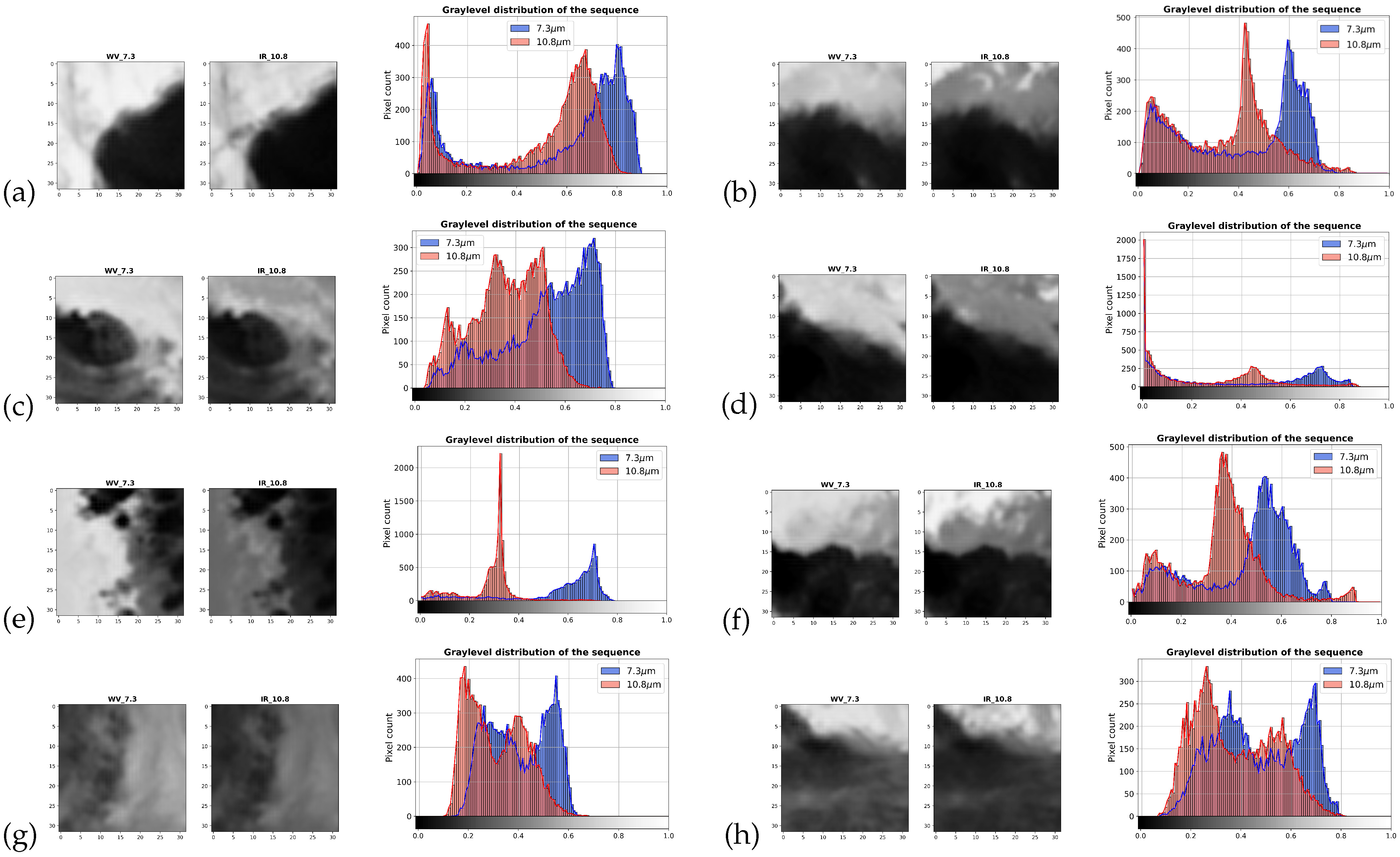
| Event | Ground Truth | TIR | WV | TIR + WV | TIR + WV + Timestamp |
|---|---|---|---|---|---|
| (a) Bimbilla, 2020.03.22, 15 h | 0 | 0.57 | 0.14 | 0.67 | 0.17 |
| (b) Bimbilla, 2020.05.06, 21 h | 0 | 0.92 | 0.45 | 0.64 | 0.23 |
| (c) Bimbilla, 2020.07.26, 12 h | 1 | 0.51 | 0.26 | 0.75 | 0.78 |
| (d) Bimbilla, 2020.09.30, 15 h | 0 | 0.77 | 0.69 | 0.46 | 0.59 |
| (e) Navrongo, 2020.05.17, 12 h | 0 | 0.81 | 0.41 | 0.69 | 0.48 |
| (f) Pusiga, 2020.05.06, 00 h | 0 | 0.50 | 0.34 | 0.24 | 0.29 |
| (g) Pusiga, 2020.07.15, 03 h | 0 | 0.51 | 0.37 | 0.46 | 0.54 |
| (h) Bongo, 2020.09.25, 12 h | 0 | 0.62 | 0.27 | 0.44 | 0.44 |
Appendix A.4. Low-Level Moisture
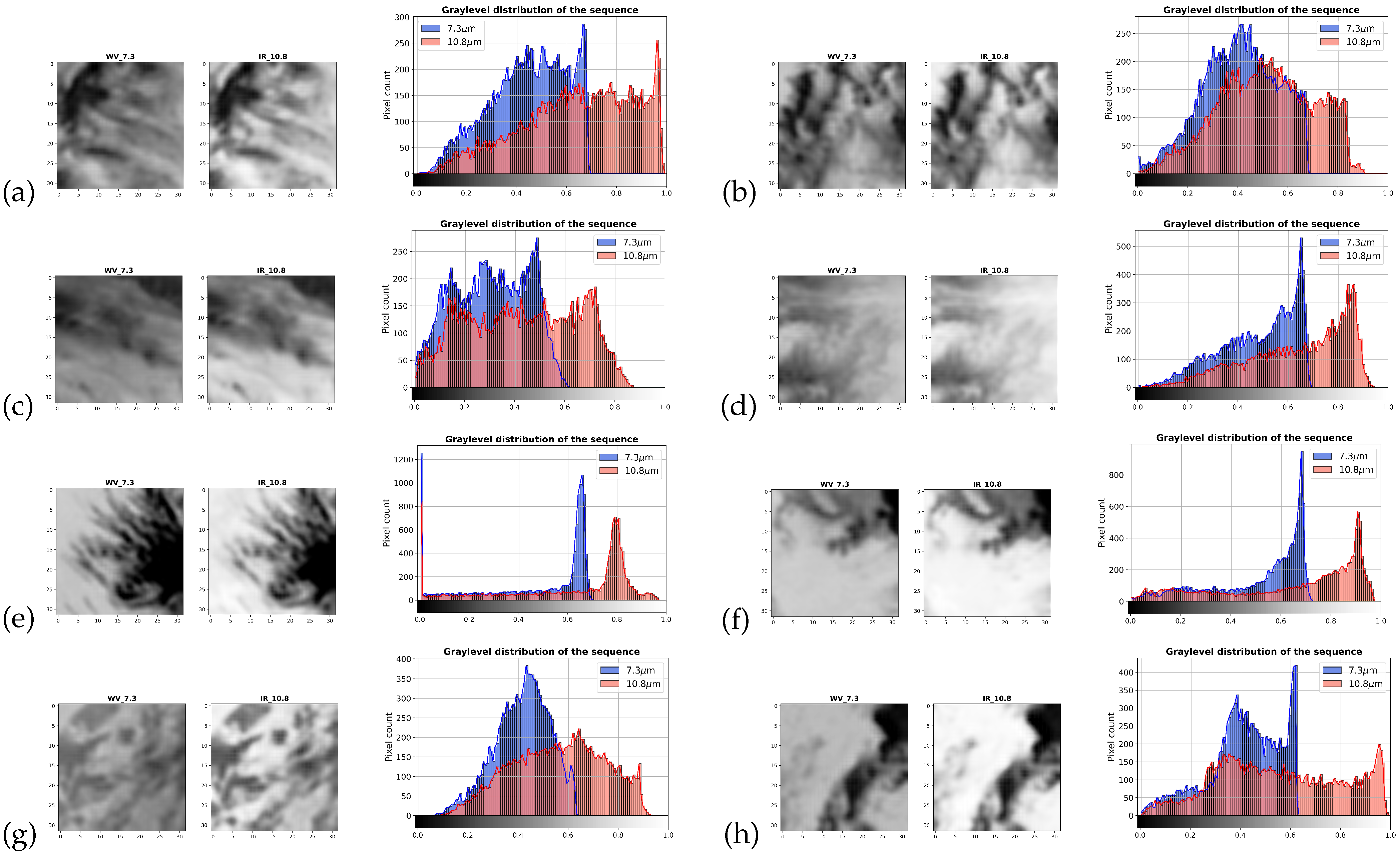
| Event | Ground Truth | TIR | WV | TIR + WV | TIR + WV + Timestamp |
|---|---|---|---|---|---|
| (a) Bimbilla, 2020.02.11, 18 h | 0 | 0.42 | 0.83 | 0.28 | 0.30 |
| (b) Bimbilla, 2020.12.22, 12 h | 0 | 0.41 | 0.65 | 0.37 | 0.18 |
| (c) Daffiama, 2020.01.22, 21 h | 0 | 0.28 | 0.54 | 0.20 | 0.02 |
| (d) Daffiama, 2020.01.23, 06 h | 0 | 0.22 | 0.66 | 0.14 | <0.01 |
| (e) Kpandai, 2020.01.25, 00 h | 0 | 0.43 | 0.58 | 0.18 | 0.02 |
| (f) Kpandai, 2020.10.21, 00 h | 0 | 0.30 | 0.63 | 0.37 | 0.23 |
| (g) Navrongo, 2020.02.12, 00 h | 0 | 0.07 | 0.50 | 0.24 | <0.01 |
| (h) Pusiga, 2020.02.11, 18 h | 0 | 0.08 | 0.55 | 0.24 | 0.05 |
References
- FAO. Ghana at a Glance. Available online: https://www.fao.org/ghana/fao-in-ghana/ghana-at-a-glance/en/#:~:text=Agriculture%20contributes%20to%2054%20%25%20of,food%20needs%20of%20the%20country (accessed on 1 December 2022).
- Bechtold, P. Convective Precipitation. Available online: https://confluence.ecmwf.int/display/FUG/9.6+Convective+Precipitation#id-9.6ConvectivePrecipitation-ConvectivePrecipitation (accessed on 1 December 2022).
- Coz, C.L.; van de Giesen, N. Comparison of Rainfall Products over Sub-Saharan Africa. J. Hydrometeorol. 2020, 21, 553–596. [Google Scholar] [CrossRef]
- ESA. Meteosat Third Generation Takes Major Step towards Its First Launch. Available online: https://www.eumetsat.int/meteosat-third-generation (accessed on 1 December 2022).
- Shen, C.; Chen, X.; Laloy, E. Editorial: Broadening the Use of Machine Learning in Hydrology. Front. Water 2021, 3, 681023. [Google Scholar] [CrossRef]
- Tarnavsky, E.; Grimes, D.; Maidment, R.; Black, E.; Allan, R.P.; Stringer, M.; Chadwick, R.; Kayitakire, F. Extension of the TAMSAT satellite-based rainfall monitoring over Africa and from 1983 to present. J. Appl. Meteorol. Climatol. 2014, 53, 2805–2822. [Google Scholar] [CrossRef]
- Funk, C.; Peterson, P.; Landsfeld, M.; Pedreros, D.; Verdin, J.; Shukla, S.; Husak, G.; Rowland, J.; Harrison, L.; Hoell, A.; et al. The climate hazards infrared precipitation with stations—A new environmental record for monitoring extremes. Sci. Data 2015, 2, 150066. [Google Scholar] [CrossRef]
- Dybkjær, G. A simple self-calibrating cold cloud duration technique applied in West Africa and Bangladesh. Geogr. Tidsskr.-Dan. J. Geogr. 2003, 103, 83–97. [Google Scholar] [CrossRef]
- Satgé, F.; Defrance, D.; Sultan, B.; paule Bonnet, M.; Rouche, N.; Pierron, F.; emmanuel Paturel, J.; Satgé, F.; Defrance, D.; Sultan, B.; et al. Evaluation of 23 gridded precipitation datasets across West Africa to cite this version: HAL Id: Hal-02626156. J. Hydrol. 2020, 581, 124412. [Google Scholar] [CrossRef]
- Atiah, W.A.; Amekudzi, L.K.; Aryee, J.N.A.; Preko, K.; Danuor, S.K. Validation of satellite and merged rainfall data over Ghana, West Africa. Atmosphere 2020, 11, 859. [Google Scholar] [CrossRef]
- Estébanez-Camarena, M.; Taormina, R.; van de Giesen, N.; ten Veldhuis, M.C. The Potential of Deep Learning for Satellite Rainfall Detection over Data-Scarce Regions, the West African Savanna. Remote Sens. 2023, 15, 1922. [Google Scholar] [CrossRef]
- Maranan, M.; Fink, A.H.; Knippertzand, P. Rainfall Types over Southern West Africa: Objective Identification, Climatology and Synoptic Environment. Q. J. R. Meteorol. Soc. 2018, 144, 1628–1648. [Google Scholar] [CrossRef]
- Kidd, C.; Huffman, G. Global precipitation measurement. Meteorol. Appl. 2011, 18, 334–353. [Google Scholar] [CrossRef]
- Aoki, P.M. CNNs for Precipitation Estimation from Geostationary Satellite Imagery; Course report: Deep Learning for Computing Vision; Standford University: Stanford, CA, USA, 2017; pp. 1–9. [Google Scholar]
- Moraux, A.; Dewitte, S.; Cornelis, B.; Munteanu, A. Deep learning for precipitation estimation from satellite and rain gauges measurements. Remote Sens. 2019, 11, 2463. [Google Scholar] [CrossRef]
- Barbero, G.; Moisello, U.; Todeschini, S. Evaluation of the Areal Reduction Factor in an Urban Area through Rainfall Records of Limited Length: A Case Study. J. Hydrol. Eng. 2014, 19, 05014016-1. [Google Scholar] [CrossRef]
- Tomassini, L.; Parker, D.; Stirling, A.; Bain, C.; Senior, C.; Milton, S. The interaction between moist diabatic processes and the atmospheric circulation in African Easterly Wave propagation: The interaction between moist processes and circulation in AEWs. Q. J. R. Meteorol. Soc. 2017, 143, 3207–3227. [Google Scholar] [CrossRef]
- Tomassini, L. The Interaction between Moist Convection and the Atmospheric Circulation in the Tropics. Bull. Am. Meteorol. Soc. 2020, 101, E1378–E1396. [Google Scholar] [CrossRef]
- Berry, G.J.; Thorncroft, C. Case Study of an Intense African Easterly Wave. Mon. Weather Rev. 2005, 133, 752–766. [Google Scholar] [CrossRef]
- ESA. MSG’s SEVIRI Instrument; ESA EUMETSAT; ESA: Paris, France, 2016; p. 33. [Google Scholar]
- Selami, N.; Sèze, G.; Gaetani, M.; Grandpeix, J.Y.; Flamant, C.; Cuesta, J.; Noureddine, B. Cloud Cover over the Sahara during the Summer and Associated Circulation Features. Atmosphere 2021, 12, 428. [Google Scholar] [CrossRef]
- van de Giesen, N.; Hut, R.; Selker, J. The Trans-African Hydro-Meteorological Observatory (TAHMO). Wiley Interdiscip. Rev. Water 2014, 1, 341–348. [Google Scholar] [CrossRef]
- Schneider, U.; Becker, A.; Finger, P.; Meyer-Christoffer, A.; Ziese, M.; Rudolf, B. GPCC’s new land surface precipitation climatology based on quality-controlled in situ data and its role in quantifying the global water cycle. Theor. Appl. Climatol. 2014, 115, 15–40. [Google Scholar] [CrossRef]
- Tan, J.; Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J. IMERG V06: Changes to the Morphing Algorithm. J. Atmos. Ocean. Technol. 2019, 36, 2471–2482. [Google Scholar] [CrossRef]
- Windmeijer, P.; Andriesse, W. Inland Valleys in West Africa: An Agro-Ecological Characterization of Rice-Growing Environments; International Institute for Land Reclamation and Improvement: Wageningen, The Netherlands, 1993. [Google Scholar]
- Nicholson, S. The West African Sahel: A Review of Recent Studies on the Rainfall Regime and Its Interannual Variability. ISRN Meteorol. 2013, 2013, 453521. [Google Scholar] [CrossRef]
- Knippertz, P.; Fink, A.H. Dry-Season Precipitation in Tropical West Africa and Its Relation to Forcing from the Extratropics. Mon. Weather Rev. 2008, 136, 3579–3596. [Google Scholar] [CrossRef]
- Schmetz, J.; Pili, P.; Tjemkes, S.; Just, D.; Kerkmann, J.; Rota, S.; Ratier, A. SEVIRI Calibration. Bull. Am. Meteorol. Soc. 2002, ES52–ES53. [Google Scholar] [CrossRef]
- Roebber, P.J. Visualizing Multiple Measures of Forecast Quality. Weather Forecast. 2009, 24, 601–608. [Google Scholar] [CrossRef]
- Karagiannidis, A.; Lagouvardos, K.; Kotroni, V. The use of lightning data and Meteosat Infrared imagery for the nowcasting of lightning activity. Atmos. Res. 2015, 168, 57–69. [Google Scholar] [CrossRef]
- Mitchell, E.D.W.; Vasiloff, S.V.; Stumpf, G.J.; Witt, A.; Eilts, M.D.; Johnson, J.T.; Thomas, K.W. The National Severe Storms Laboratory Tornado Detection Algorithm. Weather Forecast. 1998, 13, 352–366. [Google Scholar] [CrossRef]
- Liu, C.; Zipser, E.J. “Warm Rain” in the Tropics: Seasonal and Regional Distributions Based on 9 yr of TRMM Data. J. Clim. 2009, 22, 767–779. [Google Scholar] [CrossRef]
- Reinares Martínez, I.; Chaboureau, J.P.; Handwerker, J. Warm Rain in Southern West Africa: A Case Study at Savè. Atmosphere 2020, 11, 298. [Google Scholar] [CrossRef]
- Domenikiotis, C.; Spiliotopoulos, M.; Galakou, E.; Dalezios, N. Assessment of the Cold Cloud Duration (Ccd) Methodology for Rainfall Estimation in Central Greece. In Proceedings of the Geographical Information Systems and Remote Sensing: Environmental Applications International Symposium, Volos, Greece, 7–9 November 2003. [Google Scholar]
- Hsu, K.; Karbalee, N.; Braithwaite, D. Improving PERSIANN-CCS Using Passive Microwave Rainfall Estimation. In Satellite Precipitation Measurement. Advances in Global Change Research; Springer: Cham, Switzerland, 2020; pp. 375–391. [Google Scholar] [CrossRef]




| Dataset | Year | Dry Samples | Rain Samples | Total n_Samples | Ratio Dry/Rain |
|---|---|---|---|---|---|
| Training | 2018, 2019, 2020 | 4218 | 1055 | 5273 | 4.0 |
| Validation | 2020 | 6627 | 235 | 6862 | 28.2 |
| Test | 2020 | 6627 | 235 | 6862 | 28.2 |
| Event | Ground Truth | TIR | WV | TIR + WV | TIR + WV + Timestamp |
|---|---|---|---|---|---|
| (a) Kpandai, 30.09.2020, 18 h | 0 | 0.60 | 0.18 | 0.48 | 0.47 |
| (b) Bimbilla, 27.05.2020, 9 h | 0 | 0.51 | 0.10 | 0.42 | 0.21 |
| (c) Tamale, 23.01.2020, 18 h | 0 | 0.42 | 0.64 | 0.32 | 0.14 |
| (d) Pusiga, 27.05.2020, 12 h | 1 | 0.04 | 0.16 | 0.45 | 0.20 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Estébanez-Camarena, M.; Curzi, F.; Taormina, R.; van de Giesen, N.; ten Veldhuis, M.-C. The Role of Water Vapor Observations in Satellite Rainfall Detection Highlighted by a Deep Learning Approach. Atmosphere 2023, 14, 974. https://doi.org/10.3390/atmos14060974
Estébanez-Camarena M, Curzi F, Taormina R, van de Giesen N, ten Veldhuis M-C. The Role of Water Vapor Observations in Satellite Rainfall Detection Highlighted by a Deep Learning Approach. Atmosphere. 2023; 14(6):974. https://doi.org/10.3390/atmos14060974
Chicago/Turabian StyleEstébanez-Camarena, Mónica, Fabio Curzi, Riccardo Taormina, Nick van de Giesen, and Marie-Claire ten Veldhuis. 2023. "The Role of Water Vapor Observations in Satellite Rainfall Detection Highlighted by a Deep Learning Approach" Atmosphere 14, no. 6: 974. https://doi.org/10.3390/atmos14060974
APA StyleEstébanez-Camarena, M., Curzi, F., Taormina, R., van de Giesen, N., & ten Veldhuis, M.-C. (2023). The Role of Water Vapor Observations in Satellite Rainfall Detection Highlighted by a Deep Learning Approach. Atmosphere, 14(6), 974. https://doi.org/10.3390/atmos14060974








