Summary Study on Temperature Calculation Method for Water Accumulation in Permafrost Regions

Abstract

With permafrost degeneration caused by climate change, water accumulation has increased in permafrost regions during recent decades. Water accumulation will deteriorate the existing status of engineering in cold regions. Water accumulation can have a thermal effect on permafrost during its formation, even resulting in failure of the subgrade. Moreover, the thermal effect is related to water temperature. However, temperature variation of water accumulation is complex, and its influencing factors include air temperature, environment, scope of water accumulation and so on. In order to conduct analysis of the damage mechanism of water accumulation on permafrost, it is necessary to explore the internal temperature change of water accumulation. This paper proposes a review of temperature calculation method for water accumulation in cold environment. The thermal calculation method for the space between the air and the water boundary of water accumulation is summarized. Water temperature change of water accumulation of various types is analyzed. The thermal calculation considering phase transformation in water accumulation is discussed, and heat transfer from the bottom of the water accumulation to the underlying soil is further studied. Finally, the key factors that are advantageous for conducting research about the thermal effect of water accumulation in permafrost are proposed to optimize the calculation method.

1. Introduction

Water accumulation is a common engineering phenomenon in cold regions, and water accumulation gradually increases with climate change and permafrost degenerating [1]. Research indicated water accumulation along subgrade sides has increased more than 10-fold in recent years [2]. The forming and development of water accumulation is usually caused by environment factors such as air temperature, geographical environment and soil, and water accumulation can also change the local climate [3]. As a kind of exchange boundary between air and ground, the temperature change of water accumulation is different from permafrost, and water accumulation usually has a thermal effect on permafrost and engineering in cold regions [4]. Moreover, water accumulation along an embankment will also threaten the stability and bearing capacity of subgrade [5].

As a kind of water accumulation, thermokarst lakes have been studied in permafrost areas [6,7,8]. A thermokarst lake always has a thermal impact on the permafrost and engineering around it, increasing and reducing the permafrost temperature and permafrost table, respectively [9,10]. Therefore, a thermokarst lake can make permafrost degenerate and destroy the permafrost engineering, causing thaw settlement and bearing capacity decline [11,12,13,14]. Previous studies show that the temperature of water is a key factors affecting permafrost and thermokarst lakes. Moreover, water depth is also an important factor when analyzing the thermal effect of a lake on permafrost, which can affect the lake bottom temperature. When the water depth is smaller than the frozen depth, temperature at the bottom of the water will be below 0 °C in winter. Conversely, when the water depth is greater than or equal to the frozen thickness, the temperature of the underlying soil will continue to be above 0 °C, making the permafrost thaw [15,16,17,18]. Therefore, the depth of the water and heat transfer in it cannot be neglected.

The recent study of water accumulation in cold regions is mainly focused on thermokarst lakes. It always includes a thermal analysis of the permafrost and embankment, but the heat transfer and temperature change in the lake are ignored. Therefore, this method is not applicable. The water should be treated as a boundary and the heat flux between the air and water and between the water and ground below considered in order to conduct research about the thermal effect of ponds in permafrost regions from the perspective of mechanisms.

This paper reviews previous calculation methods for water temperature in water accumulation. Various kinds of analysis theory, calculation models and methods of determining internal temperature in water accumulation are obtained, which provide the analytical method and basis for the calculation of water temperature in permafrost regions, and then provide reference for the calculation and analysis of water accumulation problems in projects.

2. Thermal Surface Boundary of Water Accumulation

The surface temperature of water accumulation is determined by the heat exchange of the water surface layer, which affects the temperature distribution in the water accumulation. The surface of water in a permafrost region is divided into unfrozen and frozen.

2.1. Unfrozen Surface Boundary

For an unfrozen surface of water, surface temperature calculation has two kinds. One is using the fitting of measured temperature to obtain a periodic function or empirical formula about water temperature at the surface over time [1]. 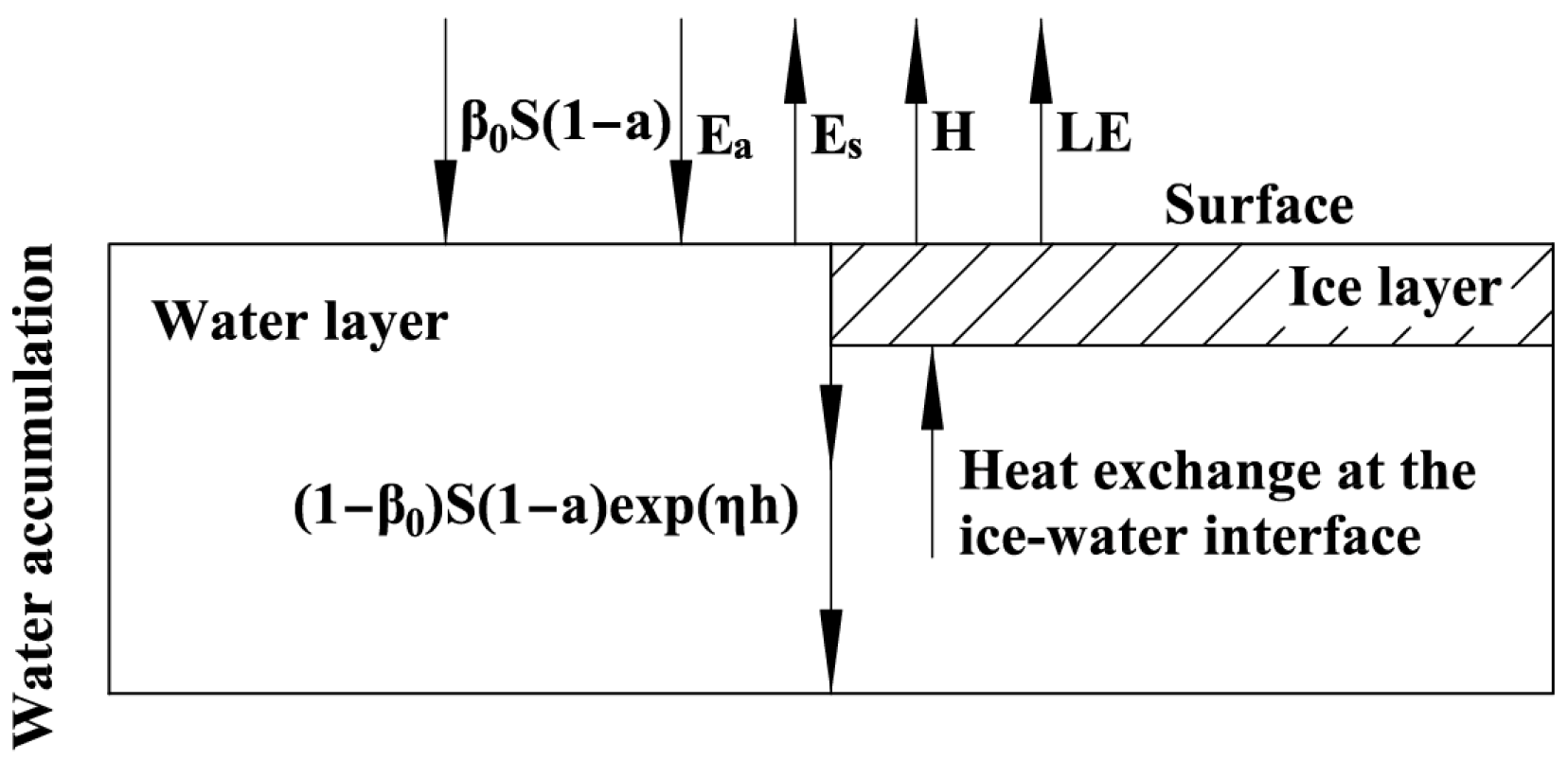The other is calculating energy balance of the water at the surface according to meteorological elements including air temperature, wind speed and radiation [19], as shown in Figure 1.

$S\left(1-\mathrm{a}\right)$exp(ηh) is the solar energy absorbed by depth of water. $\mathsf{\beta }$₀ is the solar absorptivity at the surface. $S\left(1-\mathrm{a}\right)$, $E_a, E_s$, $H$ and $LE$ are the heat exchange factors at the surface of water, which can be explained by the equations below.

A water surface temperature calculation using energy balance is always used in the calculation model for lakes. The equation of heat balance proposed by Stepanenko at the surface of a pond based on meteorological data can be used to calculate the surface temperature of small lakes [19].

$$S\left(1-\mathrm{a}\right)+E_a-E_s-H-LE=-\frac{\lambda }{h}\frac{\partial T}{\partial \xi }$$

(1)

where $S\left(1-\mathrm{a}\right)$ is solar radiation, $E_a$ is atmospheric long-wave radiation, $E_s$ is surface reflection, $H$ is sensible heat, $LE$ is latent heat and $-\frac{\lambda }{h}\frac{\partial T}{\partial \xi }$ is surface temperature considering the change in surface by evaporation.

When the change in surface by evaporation is ignored, the equation above can be expressed as follows.

$$S\left(1-\mathrm{a}\right)+E_a-E_s-H-LE=Q=-\left(k+K\right)\frac{\partial T}{\partial z}$$

(2)

Each heat value in the left side of Equation (2) can be obtained directly by observations and calculated by formulas and different models of lakes [20].

$$H_0=K\left(T_e-T\right)A_s$$

(3)

where $H_0$ is the heat received at the surface of water in unit time, $K$ is the surface heat exchange coefficient, $T_e$ is the equilibrium temperature, $T$ is surface water temperature and $A_s$ is the surface area of the reservoir. $K$ and $T_e$ are expressed as follows:

$$K=15.7+\left(\beta +0.26\right)W_f$$

(4)

$$T_e=T_D+{\beta }_1{H}_s/K$$

(5)

where $\beta$ is the curve slope of water vapor pressure–temperature,$\beta =\left(E_s-E\right)/\left(T_A-T_D\right)$, and $E_s$ and $E$ are saturation and actual vapor pressure, respectively.

$T_e$ and $T_D$ are air temperature and dew point temperature, respectively, $W_f$ is the wind function related to evaporation, ${\beta }_1$ is the absorption coefficient of the water surface for solar radiation, and $H_s$ is the sun radiation reaching water surface.

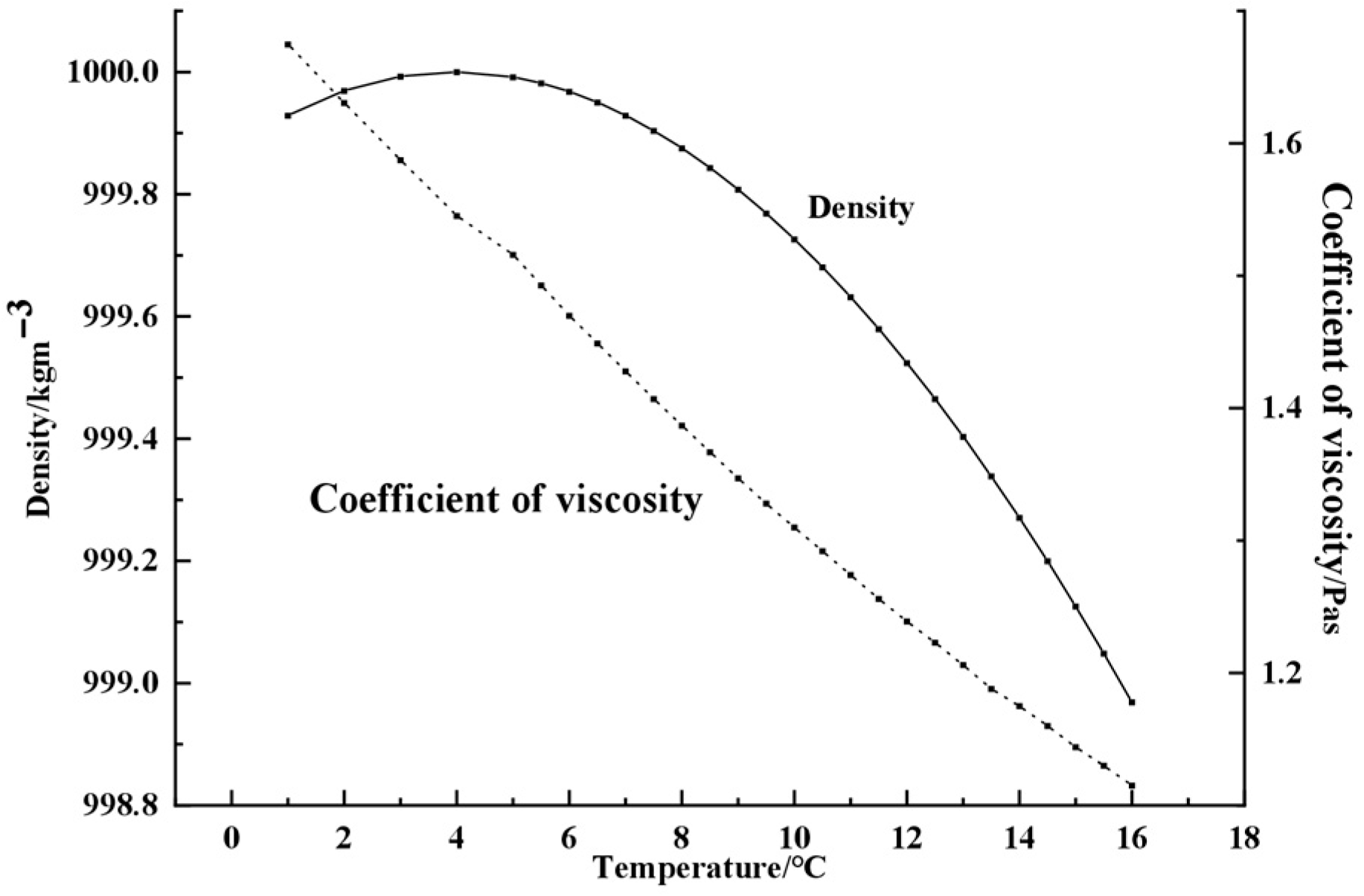
The thermal balance at the surface is also affected by flow conditions of water. Due to the density of water being a function of temperature as shown in Figure 2, according to the difference in water temperature, different densities of water flows into different positions. New energy is brought to the surface layer with water flowing to the surface.

2.2. Frozen Surface Boundary

Ignoring snow, there are two kinds of methods to calculate a thermal boundary at the frozen surface of water: formulas and energy balance. Ashton [21] thought ice surface temperature is same as air temperature. Sydor [22] simulated ice growth through taking the measured water temperature under the ice as the thermal boundary.

In addition, more methods using the energy balance method to calculate the frozen surface of a pond are widely used.

Water is gradually frozen from the surface to lower down as the surface reaches freezing temperature. When water accumulation is completely frozen, heat is transferred from air and soil underwater to ice. When water accumulation is not completely frozen, heat is transferred from high temperature and water to ice. Therefore, there is usually freezing in one direction from up to down and melting in two directions from up and down to the middle position in permafrost regions [23].

Ice–gas and ice–water heat exchanges are important during the process of freezing and melting. These heat exchanges above and the change in water temperature are affected by meteorological factors such as accumulated negative temperature, sunshine and wind speed, and they are controlled by convection and phase transition of water [24]. Therefore, icing time is related to accumulated air temperature, freezing time and the area and depth of water. At the early stage of ice growth, the heat exchange between ice and air temperature is relatively large and the growth rate is fast. As the ice layer becomes thicker, the heat exchange between air and ice is decreased, so the growth rate is stable. Burn found the relationship between ice thickness and mean temperature in winter is linear based on the measured data of Todd Lake in Canada [25].

3. Water Temperature

3.1. Empirical Law

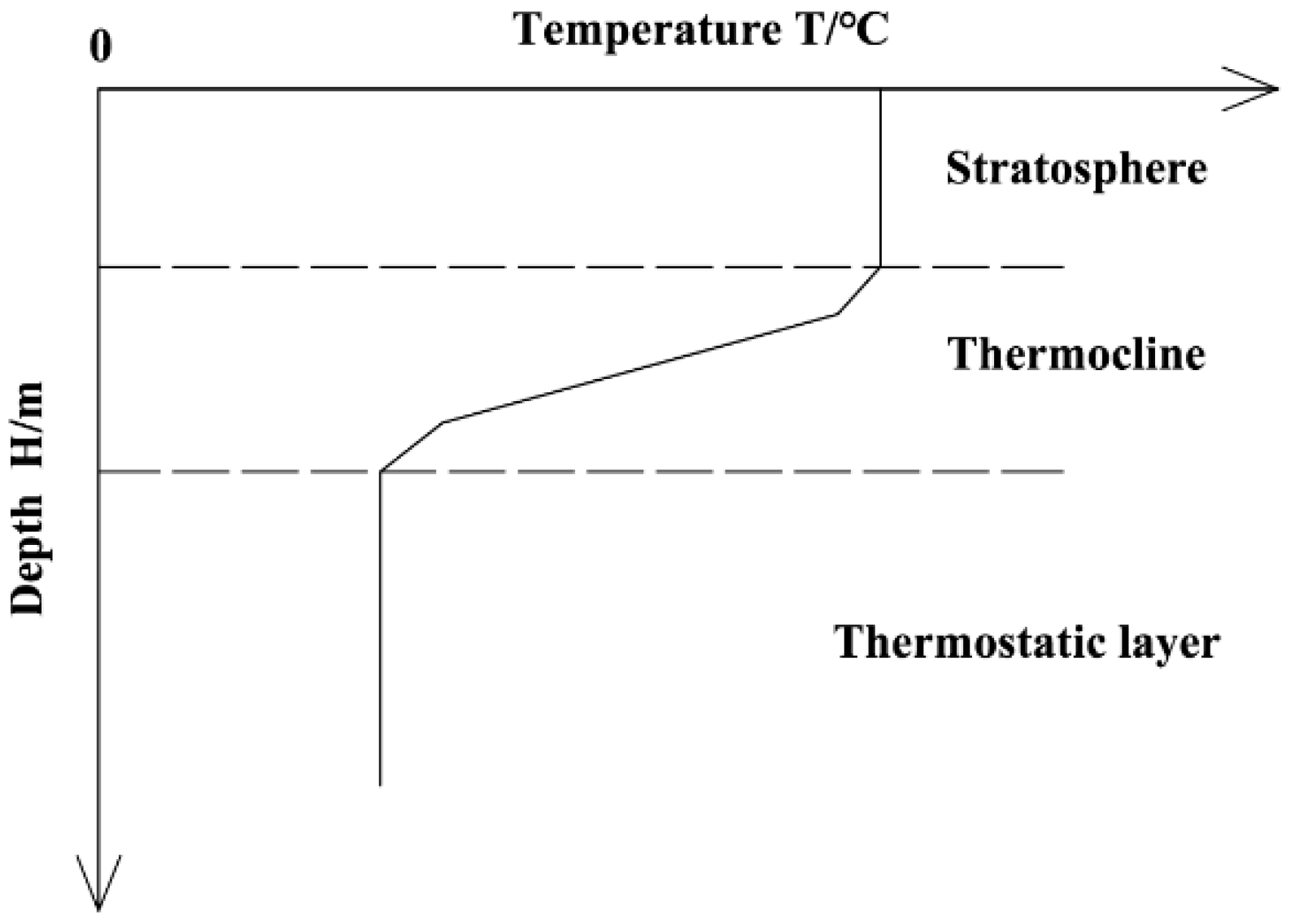
The empirical methods of water temperature calculation can be divided into two types, which are the calculation method based on the boundary temperature of water and the method based on the vertical average temperature of water. The vertical temperature distribution of water is shown as Figure 3. Zhang calculated the vertical water temperature each month, according to the water temperature distribution of reservoir surface and bottom [26].

$$T_y=\left(T_0-T_b\right)e^{\left(-y/x\right)}{}^n+T_b+T_y+T_0+T_b$$

(6)

where $T_y$ is the vertical water temperature related to depth y, $T_0$ is the reservoir surface temperature, $T_b$ is the reservoir bottom temperature and x, n is a function related to month.

Chen [27] observed that the water temperature of the reservoir mainly changed in the vertical direction, especially in summer. The vertical temperature difference can be more than 10 °C, based on the temperature measurement data of Miyun Reservoir in Beijing for two years.

However, the empirical formula of water temperature obtained from measured data has particularity, ignoring the factors such as water flow, local meteorological conditions and wind mixing. However, these factors can be incorporated into a mathematical model by a theoretical method. Because its calculation results are more accurate, the mathematical model method may be more practical and universal.

3.2. Mathematical Model Method

The research on a mathematical model of water accumulation temperature originated in the 1930s [28]. At that time, a large number of measured data on reservoir water temperature were analyzed in the USA, and the stratification of water temperature was mainly reflected in the vertical direction. The diffusion model based on convection–diffusion is based on this assumption, the longitudinal and transverse temperature changes are ignored, vertical water temperature stratification is considered, and all the elements of inflow in the same water layer are basically the same. Based on the convection–diffusion theory, WRE and MIT one-dimensional mathematical models were put forward successively in the 1960s. In this model, it is assumed that the reservoir is composed of mixed homogeneous horizontal isothermal thin layers, the heat transfer only occurs between the adjacent horizontal thin layers, and the external water flows into the water layer with the same density [29,30].

The energy equation is

$$\frac{\partial T}{\partial t}+\frac{\partial }{\partial \mathrm{z}}\left(\frac{T{Q}_V}{A}\right)=\frac{1}{A}\frac{\partial }{\partial z}\left(A{D}_Z\frac{\partial T}{\partial z}\right)+\frac{B}{A}\left(u_i{T}_i-u_{0}T\right)+\frac{1}{\rho AC}\frac{\partial \left(A{\phi }_Z\right)}{\partial z}$$

(7)

where T is the water temperature of unit layer $\left(°\mathrm{C}\right)$, $T_i$ is the inflow temperature $\left(°\mathrm{C}\right)$, A is the unit level area (m²), B is the average width of the unit layer (m), $D_Z$ is the vertical temperature diffusivity (m²/s), $\mathsf{\rho }$ is the density of water (kg/m³), the density of water is a function of temperature, C is the specific heat capacity of water [J/kg °C)], ${\phi }_Z$ is the solar radiation flux (W/m²), $u_i$ is the inflow velocity (m/s), $u_0$ is the outflow velocity (m/s), $Q_V$ is the vertical flow through the upper boundary of the element (m³/s), N is the surface unit, $V_N$ is the volume of surface unit (m³), $Q_{V,N-1}$ is the vertical flow through the interface between layer N and layer N-1 (m³/s), and ${\phi }_N$ is the heat absorbed by the surface water through the water air interface (W/m²).

In the mid- and late 1970s, the distribution of vertical water temperature was proposed, considering the inflow and outflow of the reservoir and the influence of wind based on the total energy. In 1975, Stefan and Ford proposed the MLTM model based on this theory [31]. In 1978, Imberger proposed the DYRESM model [32], suitable for simulating the temperature and salinity changes of reservoirs, and introduced the concept of a mixed layer for the first time, which can simulate the distribution of reservoir inflow and outflow, water temperature and salinity at the same time. Since 1980, the mixed-layer model has been widely used and improved because of its good characteristics of simulating water temperature and water quality. Some models have been applied to the study of water temperature in lakes and other pond types. Although the mixed-layer model increases the migration of turbulent kinetic energy compared with the previous diffusion model, the study of diffusion in the lower layer of a pond is fuzzy and has poor universality. It can be seen from the equation that the key to the water temperature distribution is the selection of the vertical diffusion coefficient. Therefore, the improvement of the water temperature numerical model is embodied in the treatment of the vertical diffusion coefficient. Some models set the vertical diffusion coefficient as constant according to the focus of research problems, more empirical formulas for the vertical diffusion coefficient have been proposed, and various improved water temperature models have been applied.

With the gradual development of a one-dimensional water temperature model, researchers have successively proposed two-dimensional or even three-dimensional water temperature models. The two-dimensional model integrates the input in term of N-S equation transversely and obtains the longitudinal and vertical water temperature distribution. In 1975, Edinger developed the earliest two-dimensional model, LARM [33]. After that, more two-dimensional water temperature models were proposed. Based on the energy balance and the vertical one-dimensional hybrid model, Farrell and Heinz [34] introduced the k-ᵋ model into the simulation of reservoir density flow (the k-ᵋ model is a mathematical treatment of water momentum equation), which can simulate well the characteristics of reservoir density flow, such as submergence, vertical vortex and temperature stratification. Young [35] proposed a two-dimensional model of turbulent diffusion of momentum and heat under different vertical empirical formulas. By using numerical software, a universal multi-dimensional prediction model of reservoir water temperature was established, which considered the factors of water surface heat exchange, reservoir inflow, reservoir discharge, reservoir water level and storage capacity change greatly. The three-dimensional model is based on the turbulence model, which considers the temperature changes in the transverse, longitudinal and vertical directions at the same time, and the heat transport equation and turbulence equation are coupled to solve. Due to the relatively large workload of 3D model calculation, it is not widely used in practice. By comparing the simulated and measured results of water temperature in the water accumulation, it is concluded that the variation in water accumulation temperature is related to its internal diffusion coefficient and indirectly affected by the density of water under the action of temperature. In winter, the bottom temperature of deep water is high, and the heat is transferred to the upper part; in summer, the heat is transferred from the surface to the bottom, and the temperature from the surface to the bottom shows a linear or nonlinear trend. In the process of melting and freezing, the internal temperature stratification is obvious.

4. Phase Change in Water Accumulation

4.1. Empirical Law

The empirical method is based on the measured data, which is from field observation and indoor test data. The method was improved continuously and according to the theory of water flow, thermal conduction and the ice forming [36]. The measured reservoir temperature data showed that the ice temperature near the ice surface is the same as the total radiation on the ice surface, and the closer the water temperature is to the ice bottom, the faster the water temperature decreases [36]. The temperature of static water condition is the main factor affecting ice condition, and ice thickness is linearly related to accumulated hourly negative temperature. Water depth also affects the start time of initial ice formation but has little effect on the thermal change in ice. In the early stage of ice formation, the surface water body loses heat quickly and falls to freezing point to form needle ice. During the freezing period, the bottom layer of the ice layer crystallizes continuously under the heat conduction in the ice and the heat balance in the water to realize the ice growth [37]. In the growth period, the temperature in the ice layer is of basically linear distribution, and the slope of ice temperature increases with the decrease in temperature. The distribution of water temperature under ice during melting is basically unchanged, and the vertical temperature difference is mainly concentrated in the surface water body. It is shown that the water body is in a static state in the experiment, the heat exchange between the ice surface and atmosphere is mainly affected by the temperature and relative humidity, and the icing only occurs at the interface of ice water. In view of the limitations of field measurement and model tests, it cannot be used directly and widely, and the water temperature calculation is nonlinear during phase transition. More mathematical models of water phase transition icing have been proposed.

4.2. Mathematical Model Method

In the ice mathematical model, the development of river ice is better than that of reservoir ice [38]. The first one-dimensional vertical Chen–Orlob water temperature model considering icing was proposed in Carlson 1977. However, due to the lack of stability, it is difficult to simulate the icing and melting process [39]. A CE-QUAL-R1 model was proposed in Ashton 1982 to simulate the water temperature distribution under the ice layer [40]. In 1984, a one-dimensional unsteady river ice model was proposed that takes into account the variation in ice and density during the process [41]. The existing one- and two-dimensional ice mathematical models have developed relatively mature, classic RICE models. Lal and Shen [42] improved, validated, and applied it in practice. Shen also proposed replacing the critical velocity in the RICE model with ice transport capacity and an RECEN model for simulating ice transport and accumulation in ice cap. The temperature distribution models of the water layer and the lower soil layer after freezing under the heat exchange of each meteorological factor and the water accumulation bottom were established [31]. The empirical formulas and parameters in the above model were refined by Fang and Stefan in 1994 [43]. Fang [15] assumed that each water layer produces a heat exchange with the bottom of the water in 1996. The water temperature and ice growth were simulated for a long time. With the development of a one-dimensional model, the two-dimensional icing model has been developed accordingly. Shen [44] proposed two-dimensional river ice mathematical models including hydrodynamic force, ice transport and ice mass conservation. Although the research on river ice models has made great progress, because of the mechanical complexity of rivers, various physical mechanical processes met difficulty, such as hydrodynamic, thermal and phase transition processes. Therefore, there still are many problems in the development of a river ice model.

The study of reservoir ice condition is still in the initial stage. At present, in the reservoir ice model, the Stefan classical assumption is used to determine the ice surface temperature. The ice surface temperature is considered equal to the air temperature, and the water temperature under the ice is linearly assumed [45]. In addition to meteorological conditions, the reservoir capacity and the flow into the reservoir are also the main factors affecting the water temperature of the reservoir. Hence, the ice condition in the reservoir is affected by many factors, such as meteorological conditions, reservoir morphology, operation mode and hydrodynamic conditions, and the icing mechanism is relatively complex [45]. Reservoir surface ice is mostly formed in winter due to the night temperature difference. The surface is less than 0 °C, ice formation begins on the shore, and as the temperature decreases, more ice is gradually formed at the deep level of the reservoir. Xing Fang [23], considering the influence of wind speed, established a lake ice model to calculate the ice thickness by using the heat lost from water cooling.

5. Heat Exchange between the Bottom of Water Accumulation and the Underlying Soil

The research and development regarding water temperature calculation models show that the heat situation in water accumulation depends on the energy exchange between the water and the environment. Therefore, the water, the upper atmosphere and a part of the adjacent soil layer should be taken to determine the complete calculation model. Especially for shallow water, the influence of the heat exchange of the bottom soil layer on the heat distribution in water accumulation cannot be ignored. In the previous calculation methods for water temperature distribution in lakes and reservoirs, the thermal effect of soil layer was also considered. In 1972, the model for calculation of temperature distribution in water and underwater sediment by finite difference method was established [46]. The thermal effects between the water accumulation and the soil layer are also mutual, and especially when studying the influence of water accumulation on nearby projects, the soil layer at the water bottom should be considered in calculation and analysis. Stepanenko [19] used the plant soil model [47] to analyze the heat and water exchange between the pond bottom and the soil. Xing Fang [15] proposed a modified pond model considering the heat exchange between the pond and the bottom sediments, indicating that the change in water bottom temperature can affect the depth of 10 m.

Water depth can affect the degree to which water temperature is affected by external changes and the heat exchange between water bottom and soil. The measured bottom water temperature of a lake shows that the lake edge temperature is lower than that of the inner deep water in the cold season, while the temperature at the lake edge is higher than that of the inner deep water in the warm season. The heat exchange between the lake bottom and the soil layer is greater than that of the internal deep water. The bottom temperature varies in the horizontal direction due to the influence of water depth and heat exchange between water and soil [1]. In the alpine environment, taking a permafrost region as an example, the relationship between water depth and freezing depth will also affect the lower soil layer affected by the heat of a pond, and the temperature of the bottom layer of the pond determines the development of its lower melting zone [5,48]. When the depth of water is less than the freezing depth, the water bottom temperature is less than 0 °C [49]. However, when the water depth is greater than or equal to the freezing depth, the water accumulation in winter is not completely frozen or the bottom of the cold season is frozen, and the temperature is still higher than 0 °C. The long-term effects of the above two scenarios will drive the bottom soil layer of water accumulation to gradually form a melting layer [1]. If the accumulated water does not exist for a long time and the temperature at the bottom has not changed recently, the lower soil layer and the bottom of the pond reach a thermal balance, and the lower melting layer will not develop any more [50,51]. However, if the accumulated water exists for a long time or the bottom temperature changes obviously due to the external temperature, such water will have a great impact on the development of the surrounding permafrost. By measuring and simulating the heat budget at different positions of the water accumulation, it is found that the lower part of the water can form a melt-through zone, and the surrounding permafrost degenerates [1]. The results show that thermokrast lakes in cold region can be regarded as heat sources for the surrounding permafrost [52]. Therefore, the heat exchange between water and soil should be considered in the water temperature calculation model in permafrost regions, and the heat impact caused by water is also affected by the external environment, geological conditions, water accumulation type and other factors.

6. Discussion

There is vertical temperature stratification in water accumulation, which can be divided into mixed type, stable type and transition type by degree of stratification. For the mixed type, the water temperature gradient in the vertical direction is small and the bottom temperature varies little with surface temperature. For the stable type, there are layers of variable temperature, oblique temperature and average temperature from the upper to the lower, and the surface water temperature changes faster than the middle and lower layers. The transition type has the temperature characteristic of the two types above. When the surface is frozen, the ice temperature is distributed with temperature gradient, and the water layer under ice still accords with the distribution characteristics of the above water body.

The water temperature stratification is affected by surface absorption heat, wind speed, solar short-wave radiation, heat conduction and buoyancy convection in water, which are determined by the environment, climate, depth and scale of water accumulation. The surface absorption heat is the power source of water accumulation. The wind speed can affect the kinetic energy of the surface layer diffusing heat to lower layers. The solar short-wave radiation absorbed in every layer affects the internal energy exchange of water, and the density of water is a nonlinear function of temperature. Therefore, when there is an unstable temperature stratification in water accumulation, the difference in density can form a natural buoyancy flow, which causes the water flow and promotes the temperature change. The depth of water not only changes the influence of solar radiation but also changes the effect degree of the surrounding soil. Shallow water is more affected by solar radiation and surrounding soil. The area of water accumulation can affect the flow state and the heat transfer ability of water and the degree of natural buoyancy convection. Moreover, the water temperature distribution is also affected by the inlet and outlet water temperature and velocity. The external forced inflow will cause additional energy and momentum exchange in the water accumulation.

When the water is frozen, the latent heat of phase change between ice and water and the movement of the interface will affect the water temperature distribution. The ice layer belongs to solid heat transfer, and the attenuation coefficient of solar short-wave radiation is different from that of water. Therefore, the influence factors considered in the temperature distribution of water accumulation with the icing process include ice melting period, ice thickness and thermodynamic parameters of ice. The energy transfer process can be affected by the depth and area of the water accumulation. Shallow water is greatly affected by the heat exchange between soil and water, and the water accumulation area will affect the icing sequence of the surface layer.

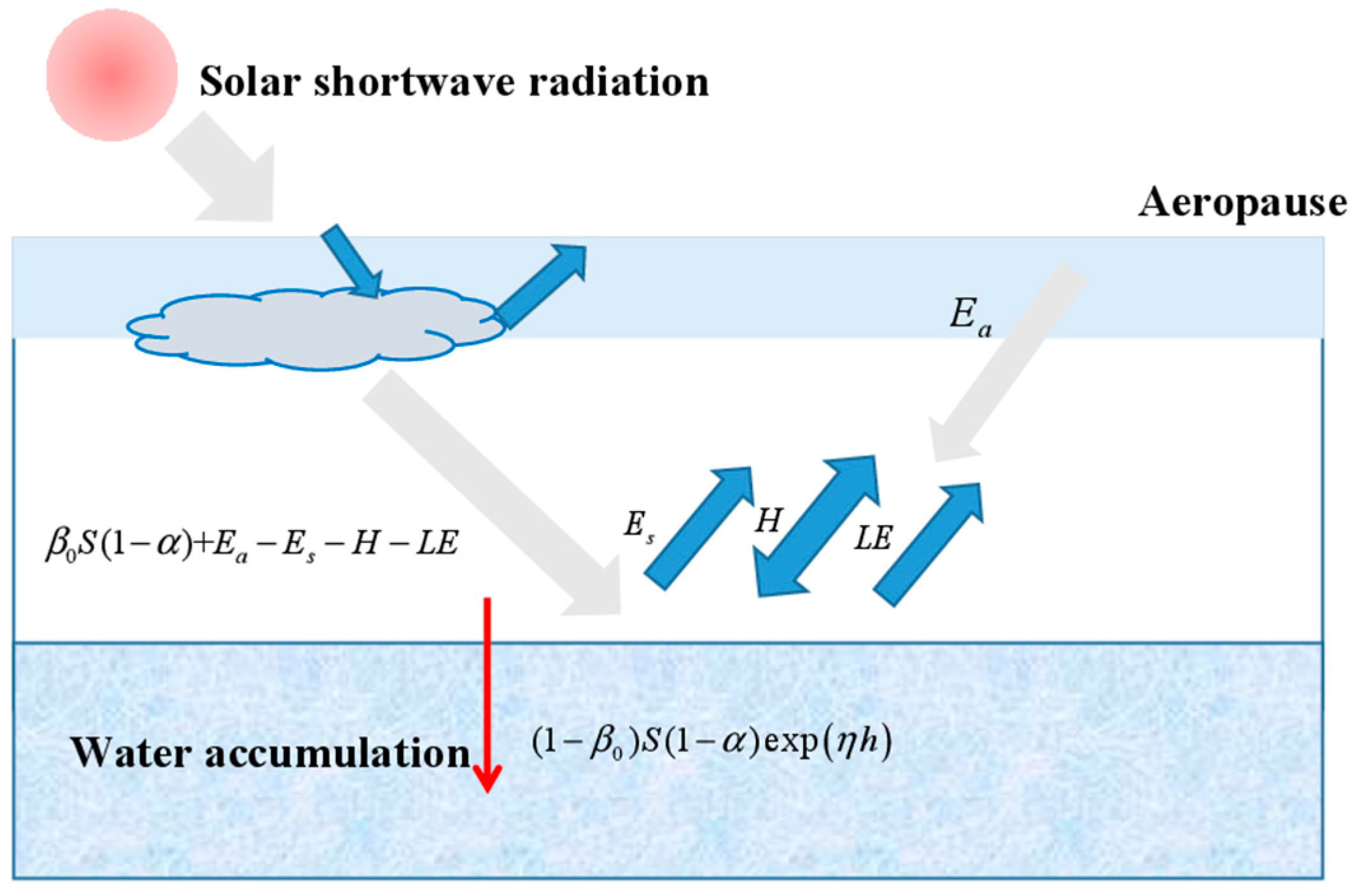
Water accumulation in permafrost regions involves phase transformation. Therefore, the factors above should also be considered in order to calculate water temperature accurately. The key factors in the calculation of water accumulation in cold regions are shown in Figure 4. The variables E_a, E_s, H, LE in the figure has the same means as the Equation (1). They include the energy exchange at the interface of water and air, including the energy exchange between water and air, the heat transfer in water accumulation and the energy exchange between soil and water bottom. For the interface of water and air, it is important to calculate the surface energy balance of water, considering the meteorological elements at the surface. For the heat transfer in water accumulation, it is important to conduct an analysis of water temperature stratification, taking into account the buoyancy flow and the solution of melting and freezing of ice. Moreover, the solar short-wave radiation will be absorbed by each water layer as a heat source in the water accumulation. The heat exchange between water accumulation bottom and permafrost below is key to calculating water temperature.

In addition, the change in water balance is due to evaporation and transpiration in the calculations. Evaporation in cold regions is of great importance in the water balance. In the zone of continental permafrost, evaporation during the warm period of the year often exceeds the amount of precipitation. Only the presence of permafrost contributes to the development and existence of vegetation in these regions. Therefore, taking into account this process is of great importance in such calculations.

7. Conclusions

As a kind of earth boundary, water accumulation changes the energy exchange between atmosphere and soil, affecting the surrounding environment and the stability of projects. In order to deeply analyze its impact on the local environment and engineering, it is necessary to define the response of water accumulation to climatic conditions, that is, to calculate and analyze the internal temperature of water accumulation with time and external conditions. Taking water accumulation as the research object, this paper summarizes the previous methods, mechanisms and application conditions of surface and internal temperature calculation and analysis of water accumulation. However, for the special environment in permafrost regions, the calculation and analysis of water temperature and its impact on frozen soil engineering are still in the initial stage, and there are many problems to be studied in depth.

(1)

It is more practical to calculate the water surface temperature by energy balance method, which includes solar short-wave radiation, net long-wave radiation, sensible heat and latent heat. The mechanisms and influence degrees of various factors acting on the surface temperature of water accumulation can be discussed in depth, which is conducive to accurate prediction of water temperature.

(2)

The depth and area of water accumulation will affect the water temperature distribution. It is necessary to analyze the variation law of water temperature and its influence on the thermal state of the lower soil layer from the perspective of a water accumulation scale.

(3)

Water accumulation in permafrost regions not only affects the environment but also affects the stability of surrounding engineering. Therefore, the impact of water accumulation on soil based on the response of water accumulation to climate under different existing times should be analyzed.