An MCDM Approach to Analytically Identify the Air Pollutants’ Impact on Health
Abstract
1. Introduction
- We propose a modified CRITIC method first in which we use logarithmic criteria for the normalization of criteria/factors taken for the study to make the criteria’s values on the same scale as the criteria taken are in different units with high variability, and Manhattan distance correlation is used to evaluate the non-linear relationships between the criterion which is not captured by the Pearson’s correlation in the CRITIC method;
- After evaluating the criteria weights, we aggregate the results and apply the modified TOPSIS method in which normalization data is taken from the modified CRITIC normalization table itself to avoid bias. Moreover, instead of first making the weighted decision matrix, we first calculate the distance from the normalized data and then multiply it with the weights that we get from the modified CRITIC results, and then the weighted Euclidean distance is calculated;
- A case study is done based on the proposed methodology followed by verification and validation.
2. Air Pollutants and Risks Associated with It
3. Review of a Few MCDM Techniques
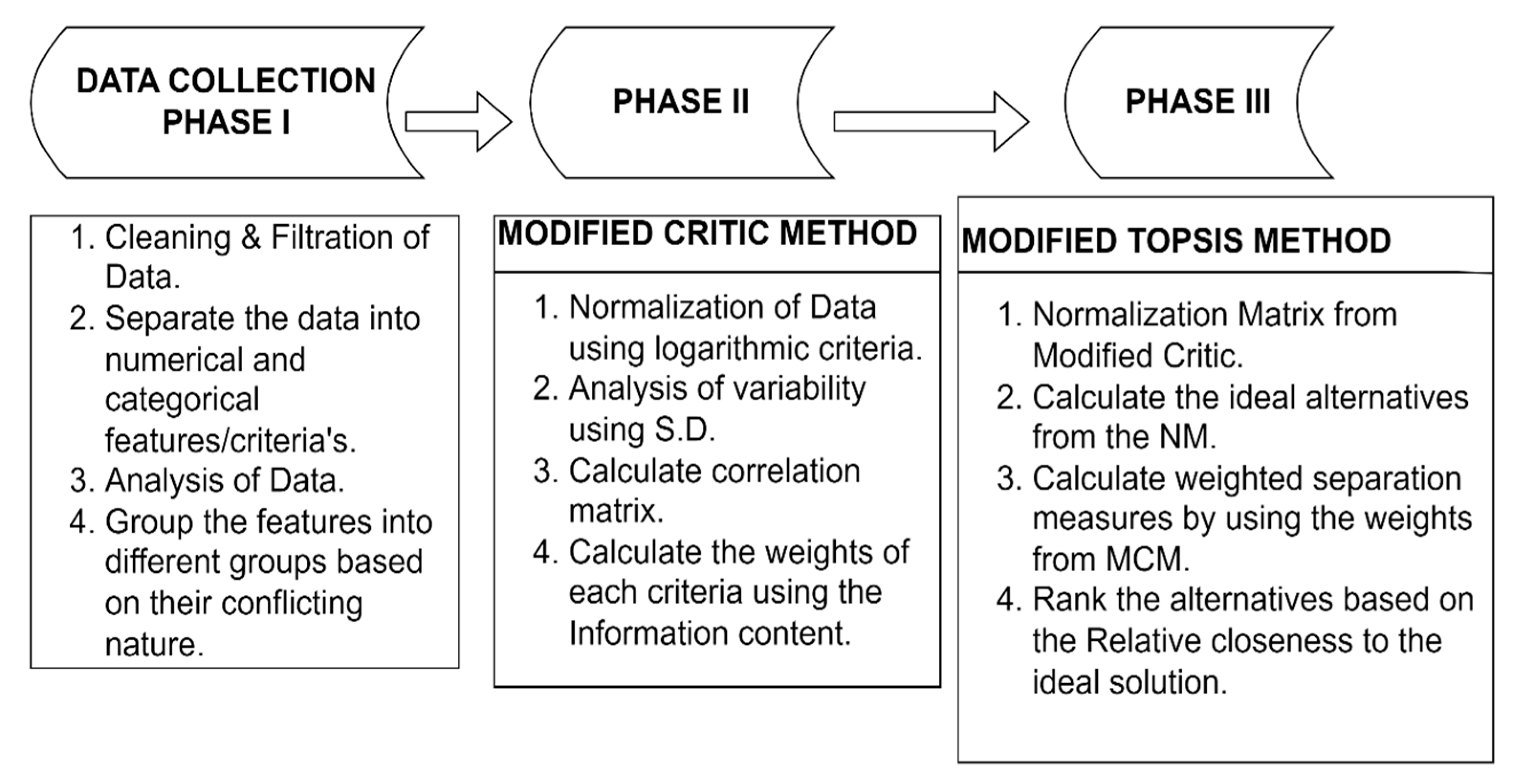
4. Proposed Methodology
4.1. Phase I—Collection and Analysis of Data
4.2. Phase II—Evaluation of Weights Using the Modified Critic Method
- Data is already collected, filtered, and analyzed in Phase I. Let us consider we are dealing with r number of pollutants/criteria in s number of regions. So, the matrix of the Data becomes ;
- Normalization of the data: As the criteria are in different units or scales so normalizing of data is necessary. After normalization, the value lies between 0 and 1. The logarithmic procedure is used for the normalization procedure:
- 3.
- After normalization, standard deviation is calculated for each criterion which will be helpful in analyzing contrast intensity [37]. More standard deviation of the criteria means higher weight associated with the criteria. S.D. is given by the Equation (3):where is the average value of the jth pollutant;
- 4.
- The Manhattan distance correlation matrix is created using the normalization matrix. As the Pearson correlation deals only with the linear data and does not accurately calculate the relationship among the criteria, we are using distance correlation. The process of calculating the distance correlation between the criteria is given below:
- Create a distance matrix for each criterion based on the normalized values attached with all the alternatives taken;
- From the distance matrix, subtract the row and column mean and add the matrix mean, and this procedure is done with each entry of the distance matrix. In the final matrix, the row mean and the column mean of the resultant matrix is zero;
- Multiply the resultant matrix element-wise and by taking the average of the entire matrix, and then the resulting value square root gives the Manhattan distance covariance of and , that is, mdCov ();
- If in the above step, , then mdVar () = mdCov (). Similarly, by using steps (a)–(d), we can calculate other distance covariances and variances;
- 5.
- By using the distance covariances and variances, the correlation matrix [37] is given by Equation (4):
- 6.
- Analyze the distance correlation matrix and figure out the important and redundant criteria based on the values of the matrix;
- 7.
- To get deeper insights into our results and to know about the amount of information each criterion has, the next step is to calculate the information content which is given by
- 8.
- Calculate the weights of each criterion j using Equation (6).
4.3. Phase III—Alternatives Ranking Using the Modified TOPSIS Method
- The normalization matrix data that we evaluated in Phase II using Equation (1) is taken as a normalization matrix for the MODIFIED TOPSIS method;
- By using the normalized matrix, we find the ideal solutions by implementing the following Equations (7) and (8).
- After finding the negative and positive ideal solution, we find the weighted Euclidean distance, and the weights that are used here are taken from the results of the modified CRITIC method. The distance is given by Equations (9) and (10):
- The relative distance of each alternative from its ideal solution is calculated by Equation (11):
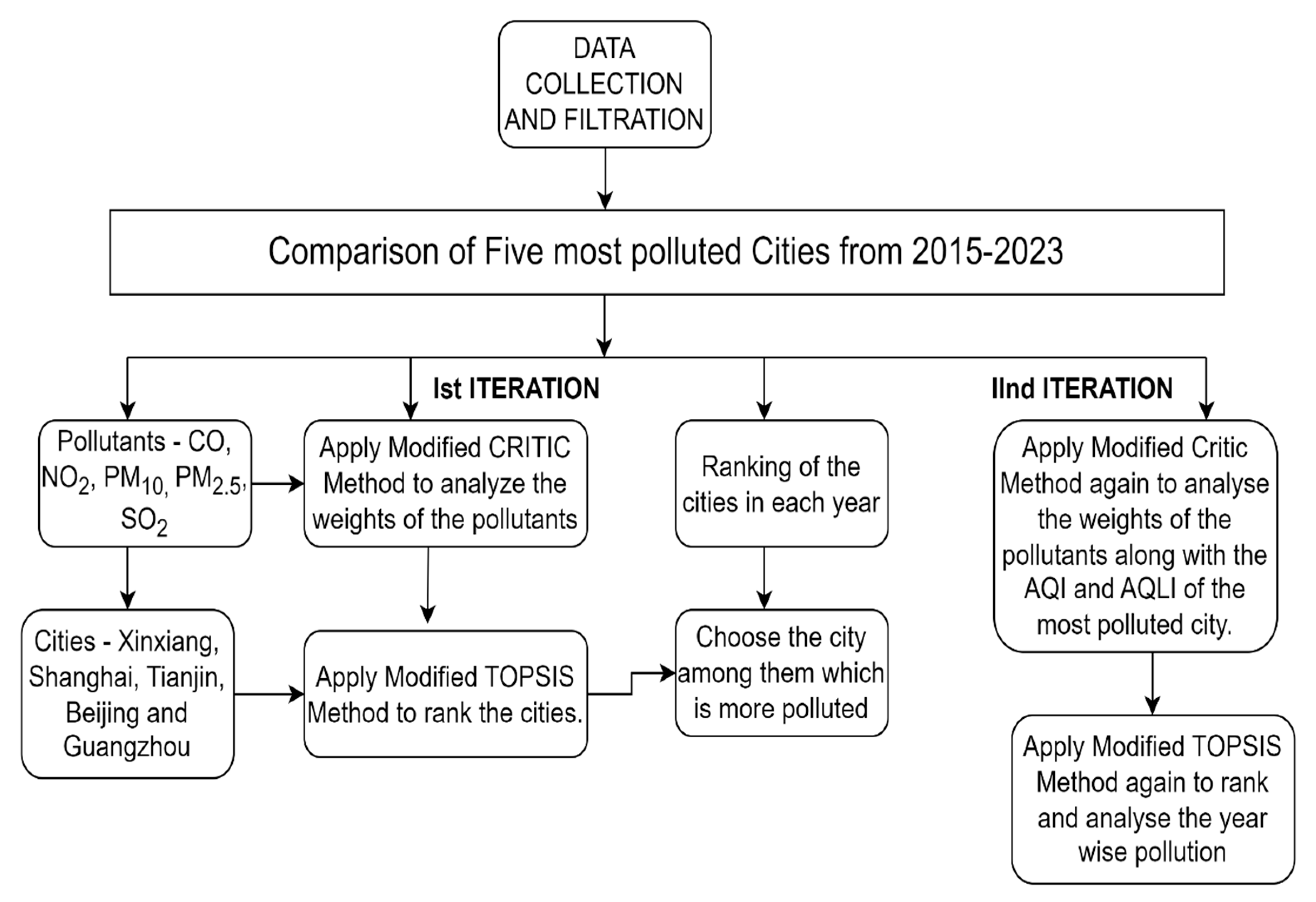
5. Case Study
- Identification of the criteria and alternatives for evaluating the case study. CO, NO2, PM10, PM2.5, SO2 pollutants are taken as criteria which are already discussed in Table 1, and in addition to this, AQI (air quality index) is used for evaluating and identifying the quality of air currently and also used in forecasting the air quality and AQLI (air quality life index) which eventually uses the concentration of air pollutant to know its impact on the life expectancy are also taken as criteria. The alternatives information is given in Table 3. The control of air quality in these megacities has enormous implications for the upcoming development of other Chinese megacities [49].
- Collection and filtration of data on air pollutants, AQI, and AQLI of five different cities of China that are mentioned above from the years 2015 to 2023.
5.1. Ist Iteration
- Creation of the normalized matrix for each year by using the equation of the modified CRITIC method which is shown in Table 4. As CO, NO2, PM10, PM2.5, SO2, and AQI are negative so we are using the logarithmic procedure of normalization for the negative criteria. Table 4 and the subsequent tables below are based on the data from the year 2015;
- Calculate the distance correlation matrix which is shown in Table 5 by using Equation (4). As there is a high distance correlation between the CO–PM10 and similarly between PM10–PM2.5, PM10–SO2, and PM2.5–SO2 which means there is a strong redundancy between these criteria;
- S.D. is calculated to analyze the contrast intensity which is shown in Table 6. The greater the S.D., the greater the contrast intensity which means SO2 followed by CO and PM10 has high contrast intensity;
- The criteria weights for each year are given in Table 9. By analyzing the weights, we can easily find the most contributing pollutant causing air pollution;The modified TOPSIS method is applied to rank the cities of China to find out which city is more polluted;
- Normalization matrix created in the modified CRITIC method is taken for this and from this normalized matrix, we have evaluated the positive and negative ideal solutions by Equations (7) and (8) shown in Table 10;
- After evaluating the ideal solutions, we need to calculate the weighted Euclidean distance by Equations (9) and (10) from the weights that we calculated in step (d). The Euclidean Distance is shown in Table 11.
- The relative distance of each city from its ideal solution is calculated. As all criteria are negative criteria so we need to maximize the distance from a particular alternative. Ci− for Xinxiang, Shanghai, and Tianjin and Beijing are 0.7523, 0.2080, 0.8124, 0.4590, 0.1865 respectively. Moreover, we can see from here that Tianjin is on rank 1 and Xinxiang is on rank 2 followed by others;
- The ranking of the cities for each year is shown in Table 12. From this, we can see that Xinxiang is on rank 1 from the year 2016 to 2023 which means Xinxiang is the most polluted city in China.
5.2. IInd Iteration
- For evaluating the effect of this, repeat steps (a)–(j) of Ist Iteration. As AQLI is the positive criterion so we are using the logarithmic positive criteria for the evaluation;
| CO | NO2 | PM10 | PM2.5 | SO2 | AQI | AQLI | |
| 2015 | 0.060952 | 0.050773 | 0.037982 | 0.035838 | 0.040296 | 0.044905 | 0.231218 |
| 2016 | 0.054615 | 0.052844 | 0.038334 | 0.036963 | 0.039357 | 0.034979 | 0.336427 |
| 2017 | 0.051752 | 0.050302 | 0.040748 | 0.037856 | 0.050399 | 0.035488 | 0.281072 |
| 2018 | 0.057472 | 0.05265 | 0.042146 | 0.038884 | 0.060932 | 0.035835 | 0.251629 |
| 2019 | 0.062559 | 0.050018 | 0.041772 | 0.038759 | 0.072066 | 0.035835 | 0.223001 |
| 2020 | 0.06398 | 0.049932 | 0.041306 | 0.037984 | 0.074427 | 0.035488 | 0.205586 |
| 2021 | 0.063844 | 0.053254 | 0.04372 | 0.040679 | 0.078625 | 0.04306 | 0.203606 |
| 2022 | 0.069988 | 0.063641 | 0.046315 | 0.042556 | 0.083189 | 0.037111 | 0.194428 |
| 2023 | 0.062384 | 0.059265 | 0.041369 | 0.037375 | 0.077293 | 0.035317 | 0.188641 |
| CO | NO2 | PM10 | PM2.5 | SO2 | AQI | |
| 2015 | 0.060952 | 0.050773 | 0.037982 | 0.035838 | 0.040296 | 0.044905 |
| 2016 | 0.054615 | 0.052844 | 0.038334 | 0.036963 | 0.039357 | 0.034979 |
| 2017 | 0.051752 | 0.050302 | 0.040748 | 0.037856 | 0.050399 | 0.035488 |
| 2018 | 0.057472 | 0.05265 | 0.042146 | 0.038884 | 0.060932 | 0.035835 |
| 2019 | 0.062559 | 0.050018 | 0.041772 | 0.038759 | 0.072066 | 0.035835 |
| 2020 | 0.06398 | 0.049932 | 0.041306 | 0.037984 | 0.074427 | 0.035488 |
| 2021 | 0.063844 | 0.053254 | 0.04372 | 0.040679 | 0.078625 | 0.04306 |
| 2022 | 0.069988 | 0.063641 | 0.046315 | 0.042556 | 0.083189 | 0.037111 |
| 2023 | 0.062384 | 0.059265 | 0.041369 | 0.037375 | 0.077293 | 0.035317 |
6. Conclusions
- We first find the cities in China where people are more prone to the effects of this deadly pollution. We have taken five cities, that is, Xinxiang, Shanghai, Tianjin, Beijing, and Guangzhou, and among them, Xinxiang is the city that is most prone to this; therefore, by doing the Ist iteration of our model and along with that we also get the weights of the pollutants which are causing air pollution;
- Moreover, from the IInd iteration, we see that in 2022, Xinxiang experienced the highest air pollution and in 2016, the lowest air pollution which in turn means that life expectancy increases with the improvement in air pollution;
- But it is not always mandatory that whenever air pollution increases, life expectancy decreases as we can see in the years 2015 and 2023 as life expectancy also depends on many factors like the lifestyle of people and genetics other than the environmental impact.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Manisalidis, I.; Stavropoulou, E.; Stavropoulos, A.; Bezirtzoglou, E. Environmental and Health Impacts of Air Pollution: A Review. Front. Public Health 2020, 8, 14. [Google Scholar] [CrossRef] [PubMed]
- Lepeule, J.; Bind, M.A.C.; Baccarelli, A.A. Epigenetic Influences on Associations between Air Pollutants and Lung Function in Elderly Men. N. Engl. J. Med. 2014, 122, 1085–1095. [Google Scholar]
- Pope, C.A.; Burnett, R.T.; Thun, M.J.; Calle, E.E.; Krewski, D.; Ito, K.; Thurston, G.D. Lung Cancer Cardiopulmonary Mortality, and Long-term Exposure to Fine Particulate Air Pollution. JAMA 2002, 287, 1132–1141. [Google Scholar] [CrossRef] [PubMed]
- Tanaka, S. Environmental regulations on air pollution in China and their impact on infant mortality. J. Health Econ. 2015, 42, 90–103. [Google Scholar] [CrossRef]
- Cho, H.S.; Choi, M.J. Effects of Compact Urban Development on Air Pollution: Empirical Evidence from Korea. Sustainability 2014, 6, 5968–5982. [Google Scholar] [CrossRef]
- Liu, H.L.; Shen, Y.S. The Impact of Green Space Changes on Air Pollution and Microclimates: A Case Study of the Taipei Metropolitan Area. Sustainability 2014, 6, 8827–8855. [Google Scholar] [CrossRef]
- Alvarado, M.; Gonzalez, F.; Erskine, P.; Cliff, D.; Heuff, D. A Methodology to Monitor Airborne PM10 Dust Particles Using a Small Unmanned Aerial Vehicle. Sensors 2017, 17, 343. [Google Scholar] [CrossRef]
- Chen, J.K.; Chen, I.S. Using a novel conjunctive MCDM approach based on DEMATEL, fuzzy ANP, and TOPSIS as an innovation support system for Taiwanese higher education. Expert Syst. Appl. 2010, 37, 1981–1990. [Google Scholar] [CrossRef]
- Nduwayezu, J.B.; Ishimwe, T.; Niyibizi, A. Quantification of Air Pollution in Kigali City and Its Environmental and Socio-Economic Impact in Rwanda. Am. J. Environ. Eng. 2015, 5, 106–119. [Google Scholar]
- Fuller, R.; Landrigan, P.J.; Balakrishnan, K.; Bathan, G.; Bose-O’Reilly, S.; Brauer, M.; Caravanos, J.; Chiles, T.; Cohen, A.; Corra, L.; et al. Pollution and Health: A progress update. Lancet Planet Health 2022, 6, E535–E547. [Google Scholar] [CrossRef]
- Pradhan Mantri Ujjwala Yojana. Ministry of Petroleum and Natural Gas. 2016. Available online: https://www.pmuy.gov.in/index.aspx (accessed on 5 January 2023).
- Vallero, D.A. Air Pollution Monitoring Changes to Accompany the Transition from a Control to a Systems Focus. Sustainability 2016, 8, 1216. [Google Scholar] [CrossRef]
- Donga, L.; Liang, H. Spatial analysis on China’s regional air pollutants and CO2 emissions: Emission pattern and regional disparity. Atmos. Environ. 2014, 92, 280–291. [Google Scholar] [CrossRef]
- Taherdoost, H.; Madanchian, M. Multi-Criteria Decision Making (MCDM) Methods and Concepts. Encyclopedia 2023, 3, 77–87. [Google Scholar] [CrossRef]
- Shahsavarani, A.M.; Azad Marz Abadi, E. The Bases, Principles, and Methods of Decision-Making: A review of literature. Int. J. Med. Rev. 2015, 2, 214–225. [Google Scholar]
- Hajduk, S. Multi-Criteria Analysis in the Decision-Making Approach for the Linear Ordering of Urban Transport Based on TOPSIS Technique. Energies 2021, 15, 274. [Google Scholar] [CrossRef]
- Bączkiewicz, A.; Wątróbski, J.; Kizielewicz, B.; Sałabun, W. Towards Objectification of Multi-Criteria Assessments: A Comparative Study on MCDA Methods. In Proceedings of the 2021 16th Conference on Computer Science and Intelligence Systems (FedCSIS), Sofia, Bulgaria, 2–5 September 2021. [Google Scholar] [CrossRef]
- Zeydan, Ö.; Pekkaya, M. Evaluating air quality monitoring stations in Turkey by using multi criteria decision making. Atmos. Pollut. Res. 2021, 12, 101046. [Google Scholar] [CrossRef]
- Giannakitsidou, O.; Giannikos, I.; Chondrou, A. Ranking European countries on the basis of their environmental and circular economy performance: A DEA application in MSW. Waste Manag. 2020, 109, 181–191. [Google Scholar] [CrossRef]
- Hamurcu, M.; Eren, T. Electric Bus Selection with Multicriteria Decision Analysis for Green Transportation. Sustainability 2020, 12, 2777. [Google Scholar] [CrossRef]
- Ghoushchi, S.J.; Ab Rahman, M.N.; Soltanzadeh, M.; Rafique, M.Z.; Marangalo, F.Y.; Ismail, A.R. Assessing Sustainable Passenger Transportation Systems to Address Climate Change Based on MCDM Methods in an Uncertain Environment. Sustainability 2023, 15, 3558. [Google Scholar] [CrossRef]
- Suresh, S.; Modi, R.; Sharma, A.K.; Arisutha, S.; Sillanpää, M. Pre-COVID-19 pandemic: Effects on air quality in the three cities of India using fuzzy MCDM model. J. Environ. Health Sci. Eng. 2022, 20, 41–51. [Google Scholar] [CrossRef]
- Yoon, K.P.; Hwang, C.L. Multiple Attribute Decision Making: An Introduction; Sage Publications: Thousand Oaks, CA, USA, 1995; Volume 104. [Google Scholar]
- Sipahi, S.; Timor, M. The analytic hierarchy process and analytic network process: An overview of applications. Manag. Decis. 2010, 48, 775–808. [Google Scholar] [CrossRef]
- Velasquez, M.; Hester, P.T. An analysis of multi-criteria decision making methods. Int. J. Oper. Res. 2013, 10, 56–66. [Google Scholar]
- Behzadian, M.; Otaghsara, S.K.; Yazdani, M.; Ignatius, J. A state-of the-art survey of TOPSIS applications. Expert Syst. Appl. 2012, 39, 13051–13069. [Google Scholar] [CrossRef]
- Hafezalkotob, A.; Hafezalkotob, A. Extended MULTIMOORA method based on Shannon entropy weight for materials selection. J. Ind. Eng. Int. 2016, 12, 1–13. [Google Scholar] [CrossRef]
- Dymova, L.; Sevastjanov, P.; Tikhonenko, A. An approach to generalization of fuzzy TOPSIS method. Inf. Sci. 2013, 238, 149–162. [Google Scholar] [CrossRef]
- Vanolya, N.M.; Jelokhani-Niaraki, M. The use of subjective–objective weights in GIS-based multi-criteria decision analysis for flood hazard assessment: A case study in Mazandaran, Iran. GeoJournal 2019, 86, 379–398. [Google Scholar] [CrossRef]
- Alemi-Ardakani, M.; Milani, A.S.; Yannacopoulos, S.; Shokouhi, G. On the effect of subjective, objective and combinative weighting in multiple criteria decision making: A case study on impact optimization of composites. Expert Syst. Appl. 2016, 46, 426–438. [Google Scholar] [CrossRef]
- Marković, V.; Stajić, L.; Stević, Ž.; Mitrović, G.; Novarlić, B.; Radojičić, Z. A Novel Integrated Subjective-Objective MCDM Model for Alternative Ranking in Order to Achieve Business Excellence and Sustainability. Symmetry 2020, 12, 164. [Google Scholar] [CrossRef]
- Yerlikaya, M.A.; Tabak, Ç.; Yıldız, K. Logistic Location Selection with Critic-Ahp and Vikor Integrated Approach. Data Sci. Appl. 2019, 2, 21–25. [Google Scholar]
- Krishnan, A.R.; Kasim, M.M.; Hamid, R.; Ghazali, M.F. A Modified CRITIC Method to Estimate the Objective Weights of Decision Criteria. Symmetry 2021, 13, 973. [Google Scholar] [CrossRef]
- Wu, H.W.; Zhen, J.; Zhang, J. Urban rail transit operation safety evaluation based on an improved CRITIC method and cloud model. J. Rail Transp. Plan. Manag. 2020, 16, 100206. [Google Scholar] [CrossRef]
- Žižović, M.; Miljković, B.; Marinković, D. Objective methods for determining criteria weight coefficients: A modification of the CRITIC method. Decis. Mak. Appl. Manag. Eng. 2020, 3, 149–161. [Google Scholar] [CrossRef]
- Diakoulaki, D.; Mavrotas, G.; Papayannakis, L. Determining objective weights in multiple criteria problems: The critic method. Comput. Oper. Res. 1995, 22, 763–770. [Google Scholar] [CrossRef]
- Krishnan, A.R.; Hamid, R.; Kasim, M.M. An Unsupervised Technique to Estimate λ0-Fuzzy Measure Values and Its Application to Multi-criteria Decision Making. In Proceedings of the 2020 IEEE 7th International Conference on Industrial Engineering and Applications (ICIEA), Bangkok, Thailand, 16–21 April 2020; pp. 969–973. [Google Scholar] [CrossRef]
- Li, L.-H.; Mo, R. Production Task Queue Optimization Based on Multi-Attribute Evaluation for Complex Product Assembly Workshop. PLoS ONE 2015, 10, e0134343. [Google Scholar] [CrossRef]
- Peng, X.; Zhang, X.; Luo, Z. Pythagorean fuzzy MCDM method based on CoCoSo and CRITIC with score function for 5G industry evaluation. Artif. Intell. Rev. 2020, 53, 3813–3847. [Google Scholar] [CrossRef]
- EPA—United States Environmental Protection Agency. Available online: https://www.epa.gov/criteria-air-pollutants (accessed on 10 January 2023).
- Burroughs Peña, M.S.; Rollins, A. Environmental exposures and cardiovascular disease: A challenge for health and development in low- and middle-income countries. Cardiol. Clin. 2017, 35, 71–86. [Google Scholar] [CrossRef] [PubMed]
- Environment Protection Authority—Victoria. Available online: https://www.epa.vic.gov.au/ (accessed on 20 January 2023).
- Omoya, F.O.; Ajayi, K.O.; Afolami, O.I.; Odetunde, E.T. Air pollution: Adverse effects on plants, animals, humans, microorganisms and food—A review. Monogr. Atmos. Res. 2018, 33–37. Available online: https://carnasrda.com/wp-content/uploads/2019/06/Omaya-et-al.pdf (accessed on 3 February 2023).
- Whitacre, P. Air Pollution Accounts for 1 in 8 Deaths Worldwide, According to New WHO Estimates; National Institute of Environmental Health Sciences: Durham, NC, USA, 2014. Available online: https://www.niehs.nih.gov/research/programs/geh/geh_newsletter/assets/docs/april14_feature_508.pdf (accessed on 3 February 2023).
- Piasecki, M.; Kostyrko, K. Development of Weighting Scheme for Indoor Air Quality Model Using a Multi-Attribute Decision Making Method. Energies 2020, 13, 3120. [Google Scholar] [CrossRef]
- Chaudhuri, A.; Hu, W. A fast algorithm for computing distance correlation. Comput. Stat. Data Anal. 2019, 135, 15–24. [Google Scholar] [CrossRef]
- Air Quality Open Data Platform, WAQI. Available online: https://aqicn.org/data-platform/covid19/ (accessed on 3 February 2023).
- Ministry of Envirmental Protection of the People’s Republic China. Ambient Air Quality Standards; Ministry of Envirmental Protection of the People’s Republic China: Beijing, China, 2012. [Google Scholar]
- Chan, C.K.; Yao, X. Air pollution in mega cities in China. Atmos. Environ. 2008, 42, 1–42. [Google Scholar] [CrossRef]
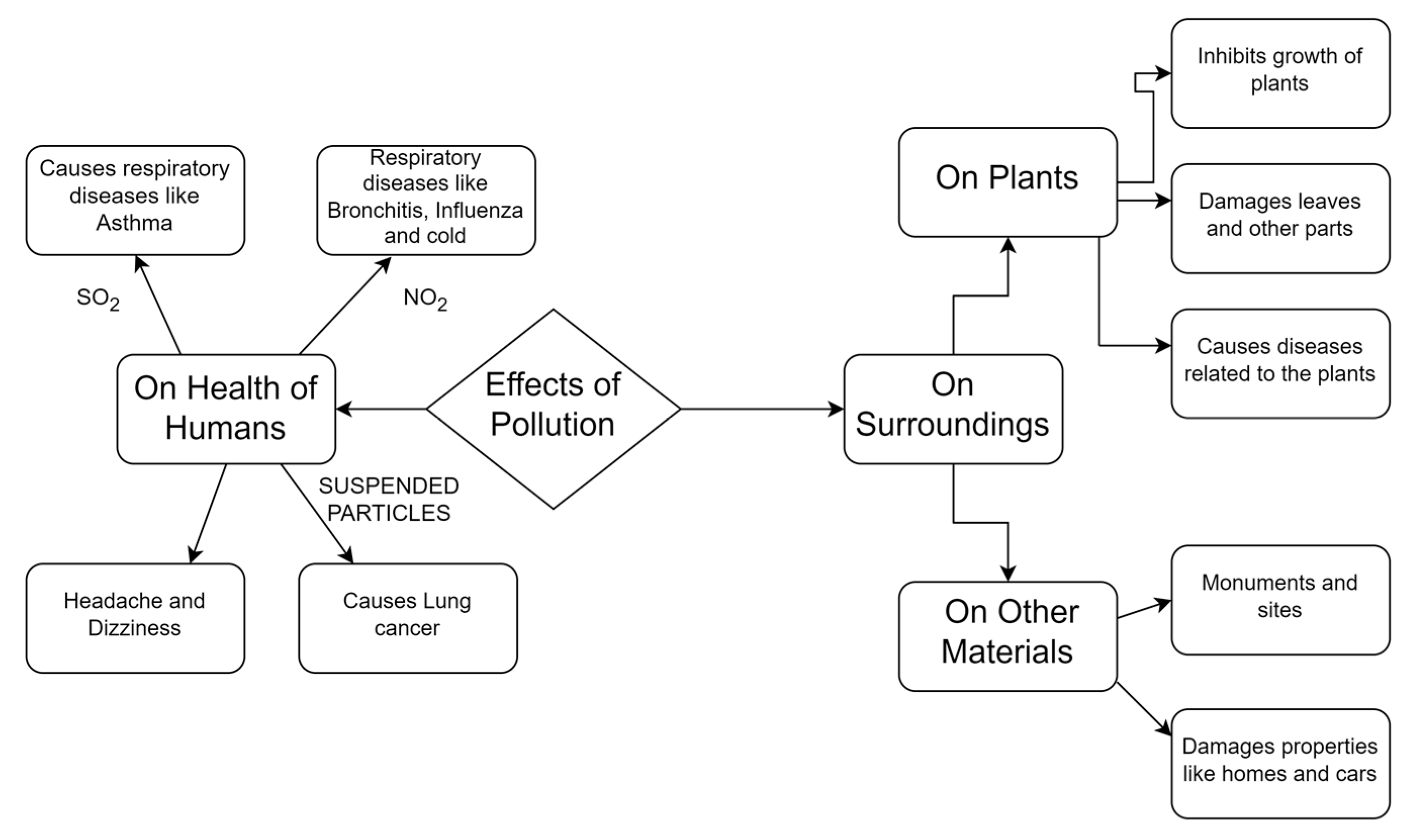
| Pollutant’s Name | Description | Sources | Associated Risk |
|---|---|---|---|
| PM2.5 | Infants and the elderly are mainly affected. It is usually found in smoky areas having a diameter of 0.0025 mm. | Fire smoke, smoke released from wooden heaters, industrial release | Premature mortality, diseases related to the heart or lungs (asthma, bronchitis), coughing, chest pain |
| PM10 | PM 10 particles are present in a dusty area or where smoke is present having a diameter of 0.01 mm or smaller. | Dust is present on roads, release of harmful affluents from industries, and smoke from fire. | respiratory diseases (asthma and COPD (chronic obstructive pulmonary disease), runny nose, irritation in eyes. |
| NO2 | It irritates our throat and lungs. | Vehicles exhaust, industries, coal-fired power stations | Respiratory symptoms like coughing, difficulty in breathing. |
| CO | It interferes with the main parts of the body like the heart and brain by reducing the supply of oxygen. Odorless gas. | Faulty gas heaters, Smoke from wood, burning fossil fuels. | Heart attack, diseases related to the brain, headache, dizziness, |
| SO | Sulfur oxides when reacting with other compounds form small particles which cause particulate air pollution. | coal-fired stations, diesel vehicles, oil refineries | Diseases related to lungs, shortness of breath. |
| Ozone | Both high and low levels of ozone are harmful to our health. Main pollutant in summer smog. | Smoke from bushfires, industries, power stations | Diseases related to the lungs, irritation in the throat. |
| Lead | A soft dense metal which when exposed in air causes diseases specially among young children. | Mining operation smelters, finishing of lead shots, battery recycliing | Weakness of muscles, lower IQ in children, weight loss, abdominal pain, anemia |
| Authors with Year | Method Name | Explanation | Advantages | Disadvantages | Area of Application |
|---|---|---|---|---|---|
| Thomas Saaty (1970) | Analytic hierarchy process (AHP) | The optimal solution is obtained by the pairwise comparison matrix and the data initial data is given by the experts based on the Saaty scale. | Can easily solve bigger size problems, high scalability, an additional tool is not required for the determination of weights of criteria, | More complicated when the number of criteria and alternatives increases, interdependency problem. | Health, policy selection, environment; for choosing different schemes; making strategies |
| Kolodner (1993) | Case-based reasoning (CBR) | It uses past data for making recommendations. | the method improves itself over time and adapts changes to the environment. | If the data is insensitive, it will create problems. | Transportation, finance sector, engineering design |
| Hwang and Yoon (1981) | Technique for order preferences by similarity to ideal solution (TOPSIS) | The ranking is based on the alternative distance to the positive and negative ideal solutions. | New criteria and alternatives do not affect the procedure of applying this method. | Difficulty in the calculation of weights, normalization is necessary for the multi-dimensional problem. | Health, environment, education, management of resources, marketing |
| Ataei et al. (2020) | Ordinal priority approach (OPA) | Priorities of the attributes as well as the ranking of the alternatives are given by the decision maker. It is solved in the form of LPP. | There is no need for the creation of the pairwise comparison matrix, Decision, and normalization Matrix. Experts can comment only on the attribute and alternatives for which they have knowledge. | Biasedness may occur because of different expert views on prioritizing the attributes. | Irrigation planning, logistics, strategies for the management of knowledge |
| Diakoulaki et al. (1995) | Criteria importance through intercriteria correlation (CRITIC) | The main concept of this method is contrast intensity. Pearson correlation is used to find the interrelationship between the criteria. | No need to make a pairwise comparison matrix like in other methods. | It does not work well with nonlinear data. | Resource planning, manufacturer selection problem, health policies |
| Chen Or Lai et al. (1994) | Fuzzy TOPSIS | It is a distance-based method. It uses the theory of fuzzy set and helps in accurately solving more complex problems. | The judgments do not depend on the crisp values. | Difficulty in the calculation of weights, normalization is necessary for the multi-dimensional problem. | Customer evaluation, environmental evaluation, transportation problem |
| Zavadskas et al. (2012) | WASPAS (weighted sum model + weighted product model) | It is used for the ranking of alternatives by considering both positive and negative alternatives. | It considers all types of criteria and optimizes the weighted aggregation function to increase the accuracy of estimation. | Ranking of alternatives changes on changing λ values. | Portfolio selection, policy evaluation, suppliers evaluation |
| K. Yang and et al. (2018), M.R. Mansor and et al. (2014) | AHP + TOPSIS | Weights of the criteria are calculated through AHP and ranking is done by the TOPSIS method. | It overcomes the problem of weight evaluation in TOPSIS. | Requires high computational power even for smaller problems. | Machine selection, selection of software packages, defense |
| P. Saxena et al. (2022), C. Wang et al. (2023) | CRITIC + TOPSIS | Weights of the criteria are calculated through CRITIC and ranking is done by the TOPSIS method. | It overcomes the problem of weight evaluation in TOPSIS. | Does not work well with nonlinear data. | Environment, health, stress prediction, supply chain |
| Name of the Alternatives | Description |
| Xinxiang | Xinxiang (35.18N, 113.52E), in the North China Plain, is approximately 111 km south of the Jing-Jin-Tang region and 80 km north of Zhengzhou. One of the fastest industrializing regions with rapid growth in economy and population which leads to an increase in motor vehicles which in turn increases pollution. |
| Shanghai | Shanghai has a population density of 3816 persons per km2 and a population of over 24 million people. With a GDP of 3.81 trillion RMB, it is located in the Yangtze River Delta, a significant financial and cultural center of the country. It is a vital transportation hub for railways, roadways, and air traffic, as well as a large port on the East China Sea. |
| Tianjin | Tianjin is a major industrial city in the Beijing-Tianjin-Hebei region, as well as one of China’s largest open coastline cities. In recent years, it has also suffered from poor atmospheric conditions. |
| Beijing | Beijing, China’s capital, is located northwest of the Beijing-Tianjin-Hebei region. With the fast rise of industrialization, urbanization, and motorization in recent decades. Beijing’s energy consumption and the resulting numerous pollutant emissions were rising year after year, wreaking havoc on air quality, human health, and the ecosystem. |
| Guangzhou | The PRD region, which includes Guangzhou, is distinguished by export processing businesses as well as finance and other service industries. |
| Cities/Criteria | CO | NO2 | PM10 | PM2.5 | SO2 | AQI |
| Xinxiang | 0.101108 | 0.086303 | 0.054325 | 0.054102 | 0.061883844 | 0.07512127 |
| Shanghai | 0.121268 | 0.086015 | 0.078389 | 0.064908 | 0.120547716 | 0.05668565 |
| Tianjin | 0.086429 | 0.091196 | 0.062825 | 0.059655 | 0.079712187 | 0.05493764 |
| Beijing | 0.099431 | 0.07988 | 0.065816 | 0.06023 | 0.113861987 | 0.05512783 |
| Guangzhou | 0.110895 | 0.087342 | 0.087126 | 0.072958 | 0.137641371 | 0.05936595 |
| CO | NO2 | PM10 | PM2.5 | SO2 | AQI | |
| CO | 1 | 0.691297 | 0.849997 | 0.781232 | 0.751138076 | 0.50576949 |
| NO2 | 0.691297 | 1 | 0.517252 | 0.495016 | 0.576059736 | 0.46127487 |
| PM10 | 0.849997 | 0.517252 | 1 | 0.981398 | 0.912463088 | 0.7203802 |
| PM2.5 | 0.781232 | 0.495016 | 0.981398 | 1 | 0.885899801 | 0.75136965 |
| SO2 | 0.751138 | 0.57606 | 0.912463 | 0.8859 | 1 | 0.74280719 |
| AQI | 0.505769 | 0.461275 | 0.72038 | 0.75137 | 0.742807191 | 1 |
| CO | NO2 | PM10 | PM2.5 | SO2 | AQI | |
| S.D. | 0.013073 | 0.004069 | 0.013018 | 0.007051 | 0.031058107 | 0.00850145 |
| CO | NO2 | PM10 | PM2.5 | SO2 | AQI | |
| Information Content | 0.018570411 | 0.009193 | 0.013259349 | 0.007792 | 0.035146 | 0.015459029 |
| CO | NO2 | PM10 | PM2.5 | SO2 | AQI | |
| Weights (In %) | 18.68 | 9.25 | 13.3 | 7.84 | 35.35 | 15.5 |
| Weights (In %) | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | 2021 | 2022 | 2023 |
| CO | 18.68 | 28 | 17.8 | 21.3 | 14.71 | 20 | 11.1 | 18.88 | 21.78 |
| NO2 | 9.247 | 13.8 | 14.9 | 7.17 | 7.477 | 8.81 | 9.95 | 7.551 | 20.89 |
| PM10 | 13.34 | 13.8 | 15 | 16.1 | 8.189 | 12.3 | 9.58 | 18.43 | 11.59 |
| PM2.5 | 7.837 | 4.76 | 6.41 | 4.88 | 4.763 | 6.75 | 5.28 | 8.48 | 6.24 |
| SO2 | 35.35 | 37.7 | 43.8 | 49.1 | 63.32 | 49.9 | 58.8 | 44.55 | 37.57 |
| AQI | 15.55 | 1.89 | 2.09 | 1.51 | 1.535 | 2.22 | 5.32 | 2.109 | 1.927 |
| CO | NO2 | PM10 | PM2.5 | SO2 | AQI | |
| I− | 0.12126819 | 0.091196 | 0.087126336 | 0.072958 | 0.137641 | 0.075121274 |
| I+ | 0.086428983 | 0.07988 | 0.054325038 | 0.054102 | 0.061884 | 0.054937636 |
| Weighted Euclidean Distance | ED+ | ED− |
| Xinxiang | 0.007266 | 0.022075 |
| Shanghai | 0.021699 | 0.005699 |
| Tianjin | 0.005045 | 0.02185 |
| Beijing | 0.014622 | 0.012406 |
| Guangzhou | 0.022898 | 0.00525 |
| Cities/Rank | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | 2021 | 2022 | 2023 |
| Xinxiang | 2 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| Shanghai | 4 | 5 | 5 | 3 | 4 | 4 | 4 | 4 | 4 |
| Tianjin | 1 | 3 | 2 | 2 | 2 | 2 | 2 | 2 | 2 |
| Beijing | 3 | 4 | 3 | 5 | 5 | 5 | 5 | 5 | 5 |
| Guangzhou | 5 | 2 | 4 | 4 | 3 | 3 | 3 | 3 | 3 |
| Ci-(with AQLI) | Ranking | Ci-(without AQLI) | Ranking | |
| 2015 | 0.33388421 | 4 | 0.758121423 | 3 |
| 2016 | 0.97357736 | 1 | 0.919158752 | 1 |
| 2017 | 0.638267 | 2 | 0.794670799 | 2 |
| 2018 | 0.43769878 | 3 | 0.561303803 | 4 |
| 2019 | 0.24176959 | 5 | 0.328458647 | 5 |
| 2020 | 0.13399072 | 6 | 0.279261706 | 6 |
| 2021 | 0.11606656 | 7 | 0.206971165 | 8 |
| 2022 | 0.04221192 | 9 | 0.08048887 | 9 |
| 2023 | 0.07419227 | 8 | 0.252765256 | 7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bhardwaj, R.; Garg, S. An MCDM Approach to Analytically Identify the Air Pollutants’ Impact on Health. Atmosphere 2023, 14, 909. https://doi.org/10.3390/atmos14060909
Bhardwaj R, Garg S. An MCDM Approach to Analytically Identify the Air Pollutants’ Impact on Health. Atmosphere. 2023; 14(6):909. https://doi.org/10.3390/atmos14060909
Chicago/Turabian StyleBhardwaj, Rashmi, and Shanky Garg. 2023. "An MCDM Approach to Analytically Identify the Air Pollutants’ Impact on Health" Atmosphere 14, no. 6: 909. https://doi.org/10.3390/atmos14060909
APA StyleBhardwaj, R., & Garg, S. (2023). An MCDM Approach to Analytically Identify the Air Pollutants’ Impact on Health. Atmosphere, 14(6), 909. https://doi.org/10.3390/atmos14060909










