Abstract
Aerobiological predictive model development is of increasing interest, despite the distribution and variability of data and the limitations of statistical methods making it highly challenging. The use of concentration thresholds and models, where a binary response allows one to establish the occurrence or non-occurrence of the threshold, have been proposed to reduce difficulties. In this paper, we use logistic regression (logit) and regression trees to predict the daily concentration thresholds (low, medium, high, and very high) of six airborne fungal spore taxa (Alternaria, Cladosporium, Agaricus, Ganoderma, Leptosphaeria, and Pleospora) in eight localities in Catalonia (NE Spain) using data from 1995 to 2014. The predictive potential of these models was analyzed through sensitivity and specificity. The models showed similar results regarding the relationship and influence of the meteorological parameters and fungal spores. Ascospores showed a strong relationship with precipitation and basidiospores with minimum temperature, while conidiospores did not indicate any preferences. Sensitivity (true-positive) and specificity (false-positive) presented highly satisfactory validation results for both models in all thresholds, with an average of 73%. However, seeing as logit offers greater precision when attempting to establish the exceedance of a concentration threshold and is easier to apply, it is proposed as the best predictive model.
1. Introduction
The study of primary biological aerosol particles increases their importance, especially those focused on identifying and quantifying fungal spores [1]. The increasing interest in the utility of fungi as aerobiological particles is usually linked to agriculture and public health, as their presence is linked to phytopathological and allergological diseases [2,3,4]. A review of the spectrum of airborne fungal spores in Europe identified 67 taxa, where Alternaria and Cladosporium were the most common taxa studied due to their spores reporting the highest concentrations in northern Europe [5]. The frequency of analysis of each taxon is related to the interest, importance, or impact it may have on public health, agriculture, or the environment [3,6]. For example, Alternaria is recognized as an allergenic spore type [7], while Ganoderma is recognized as phytopathogenic [8].
In this sense, developing observational predictive models for fungal spores is of great interest [3,9]. Predictions will be of high value for public health, as they allow the susceptible population to self-manage, thus reducing critical allergic episodes and the costs associated with the health system due to moderate and severe allergy episodes [10]. In other sectors, such as agriculture, predictions can help improve understanding and activate the necessary mechanisms for the eminent management of pest infections by phytopathogenic fungi, avoiding partial or total losses in production [11]. Finally, forecasts can also be used for other purposes, such as forest resource management and improving our understanding of ecosystem changes and trends, among other environmental processes [12].
Some of the difficulties linked to developing predictive models include the selection of predictors and the statistical distribution of the data used [3,13,14]. Traditional models require linearity and normality, which are absent in the aerobiology database and asseverated by various studies [3,14,15,16]. As an alternative, the implementation of methods based on machine learning algorithms (MLA) is being increasingly considered, as evidenced by the advent of neural networks, generalized additive models, and vector support machines, among other available techniques [3]. These methodologies offer multiple advantages, such as classification, numerical prediction, and clustering, all of which improve forecasts with respect to modeling [17]. However, interpreting results can be challenging, despite their high fitting level.
For example, neural networks establish a suitable method of classification and regression for environmental processes, but their form of execution is considered a “black box”. The criteria for classification and the impact of independent variables in the model cannot be identified [18]. Likewise, another possible limitation is the high computational requirements of the MLA [18], which only sometimes yields better results than classical methods [19,20].
Another recent alternative is to use concentration thresholds [21,22] to help generate forecasts. Concentration thresholds are mainly established if a determined threshold is reached [23,24,25]. This allows predictions to be much more efficient [26] and simultaneously avoids the problem related to the statistical distribution of aerobiological data [27]. In this sense, the predictive models need nonlinear equations to relate the concentration of fungal spores (dependent variable) and meteorological parameters (independent variable) in the forecast, as logistic regression and regression trees do. These methodologies are characterized by binary responses, which allow us to infer the occurrence or non-occurrence of the event modeled or, in the case of aerobiology, the thresholds modeled.
Logistic regression has been used to predict increases in Annual Integral [13] and daily concentration [28]. Regression trees have only been used to forecast hourly/daily concentrations [29,30,31,32,33,34] and to relate meteorological parameters with concentrations of fungal spores [35]. However, both methodologies have a fundamental binary response. Therefore, the aim of this study was to assess the performance of logistic regression and regression trees as tools to predict the daily concentration thresholds of airborne fungal spores in Catalonia, Spain.
2. Materials and Methods
2.1. Study Area
Catalonia, northeast of Spain, is our study area. It has a Mediterranean climate with warm winters, hot summers, and rainy episodes in autumn and spring. Additionally, this region has a wide diversity of local flora due to varied geomorphology and distances to the sea, which give rise to diverse phytoclimates [36]. Eight aerobiological stations in Catalonia are placed in four phytoclimates. Three stations are localized in urban areas—two of them on the Mediterranean coast (Barcelona and Tarragona), one inland (Girona); three are rural-urban, one on the Mediterranean coast (Roquetes-Tortosa), and two near agricultural areas (Bellaterra and Manresa). Finally, two stations are located in a predominantly rural environment: one in the Pyrenees (Vielha) and one in the Central Catalan Depression (Lleida). More details on the study are shown in Figure 1, while the meteorological conditions and aerobiological stations are elaborated in Figure S1 and Table S1, respectively.
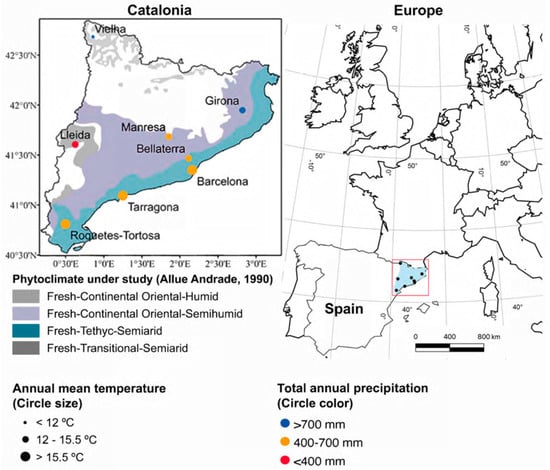
Figure 1.
Geographical situation, meteorological characteristics, and phytoclimates of the aerobiological stations in Catalonia [37].
2.2. Aerobiological and Meteorological Data
The aerobiological database was retrieved from Catalan Aerobiological Network (Xarxa Aerobiològica de Catalunya, XAC). Samples were obtained by employing Hirst traps [38] and analyzed according to the Spanish Aerobiological Network [39]. The terminology applied in this study was derived from Galán et al. [40]. Considering the daily concentration of fungal spores as the number of fungal spores per cubic meter of air (spore/m3), we selected six taxa according to the results of a previous study in the group, applying the gamma model [14], which identified them as the fungal aerobiological taxa most representative of Catalonia. These taxa were Leptosphaeria and Pleospora (ascospores), Agaricus and Ganoderma (basidiospores), and Alternaria and Cladosporium (conidiospores). The aerobiological data used were daily mean concentrations from 1995 to 2014 (details for each station in Table S1). We modeled four concentration thresholds: low, medium, high, and very high. The range of concentration per each threshold and taxa is presented in Table S2 and they correspond to those used by the authors in previous studies [14] and were established based on the expertise of the XAC group and the knowledge related to allergies in Catalonia. Thresholds of airborne biological particles vary with the environmental conditions of the study areas and cannot be universally established. After stating that the high level of diversity of fungi in the air makes it difficult to define the allergenicity of individual fungi and establish clinical thresholds coherent with environmental concentrations of airborne fungal spores, Annes-Hill et al. [5] cited two clinical allergy thresholds for Alternaria (100 spores/m3) and Cladosporium (3000 spores/m3). Both thresholds proposed for northern Europe are out of the range of the concentrations of these spores in our study area.
The meteorological variables considered in this study were as follows: temperature (maximum, minimum, and their squares); rainfall (in the day and one, two, and three previous days); and relative humidity (Table S3 shows a brief justification of the selected predictors). Agencia Estatal de Meteorología and Servei Meteorològic de Catalunya provided the meteorological data. A summary of the parameters is available in Figure S1.
2.3. Statistical Methods
2.3.1. Logistic Regression
The logistic regression model, i.e., logit model, is a modeling technique in which the answer is a probability of occurrence from n potential prediction variables [18]. This model is described in several books on statistics. Hosmer and Lemeshow [41] is the most suitable reference. The generic mathematical equation is as follows:
where x1, …, xn are the predictors or explicative variables, and p is the proportion in which a certain result is observed.
From a mathematical point of view, the logit model is a parametric, additive, and flexible model with a binary response that is easy to interpret, because the sign of parameters indicate the sense (positive or negative) of the relationship and its value shows the predictor weighting in the equation. However, the incorporation or elimination of predictors tends to provoke convergent problems [18,41].
Although the logit model is not optimal for real-time forecasts, it can be used to make predictions regarding critical values through the probabilities of occurrence in the data modeled [13]. However, establishing the critical value for aerobiological data could be a major problem since aerobiological data usually do not follow an ideal symmetric distribution. Possible solutions could be subsampling with the expected proportion desired, true/false case = 0.5 [42], or pondering factors [43]. Nevertheless, these strategies tend to cause a loss of information or change the original database. Consequently, establishing the critical value of the binary response with the percentage of times that the modeled threshold has exceeded in the database is proven to be the most efficient and coherent alleviative strategy [44,45].
2.3.2. Regression Trees
Regression trees operate in the same way as a traditional regression model—using one or more variables or predictors to forecast the modeled variable. However, a regression tree uses a binary classification and hierarchy, generating model regions or subregions with high homogeneity, and then adjusts a traditional linear regression, such as the critical value (as a constant). First, the model cuts the database into two regions from one predictive variable; then, if an answer is not homogenous, take each region and cut them into subregions, and so on, until good homogeneity is obtained in the subregions. The methodology for selecting the predictive variables is diverse but generally based on the impurity in the generated regions [46,47].
The conceptual simplicity of the regression tree gives this method a greater advantage since it facilitates interpretation, serving as a powerful and intuitive tool for the development of models in various areas of knowledge [47]. Mathematically, the regression tree is usually represented as:
where cm is the constant m in the regression region R, x is the predictive variable used to split the observation into n observations, and Rm is the m homogeneity region obtained in the set of n observations that respond to constant regression Cm.
The regression tree is a non-additive and hierarchical methodology that facilitates the interpretation of the results based on the exploration of the data and not on the inference of itself, as in traditional methods. This allows for one or more exploration routes in the database [48]. The first corresponds to descriptive exploration, reducing the data volume in R regions while, at the same time, preserving the characteristics of the sample. In contrast, the second corresponds to an exploratory classification, where the R region should be interpreted in a significative way in the context of the subsampling or hypothesis proposed. Finally, the exploratory generalization analysis allows one to map the predictive variable to the modeled variable through R regions. All this allows for the modeling of future events [48].
Another advantage is that a regression tree is a non-parametric test, meaning that it allows for data exploration without previous knowledge about probabilistic distribution function, likewise reducing the high computational resources needed for its development, storage, and application [48,49]. Additionally, this methodology efficiently uses the characteristics available in the data, generating a more effective classification based on the hierarchical decomposition on which the method is based. Finally, a regression tree can model a one- or bi-modal database and is not affected by missing data [47,48,49]. As a disadvantage, a regression tree favors the predictive variable with high variability in the hierarchical process and, at the same time, has low flexibility regarding the binary answer associated with a classification problem, occasionally resulting in overestimation results. Finally, since it is not an additive model, it is impossible to obtain a significance and relationship between the predictors and the modeled variable [47]. However, it can be solved by analyzing the hierarchy generated by the model. Variables at higher levels indicate a higher incidence of the predictor in the development of the model.
2.3.3. Criteria for the Application of Regression to Modeling
The regression models will be applied to forecast the probability of occurrence of the different concentration thresholds of the airborne fungal spores under study. In determining the threshold occurrence, the critical values were set as the percentage of times the threshold was exceeded in the aerobiological database (details of each critical value are available in Table S4). This is in agreement with the work of Real et al. [50], who elucidated the incidence of the proportions of presence/absence in the model’s success. We previously tested it using the standard value of 0.5 in the regressions. The results showed an overestimation, especially in taxa with a low frequency of appearance or low concentration of the aerobiological database.
To evaluate the potential prediction capacity of the models, sensitivity and specificity parameters were used, which are the most popular parameters in biostatistics for binary response models. Cross-validation is not recommended, especially when a big part of the data has low/null values, because the fraction of expected true positives is lower with respect to the fraction of true-false, increasing the value of cross-validation which is not a good measure of the potential model prediction. As described by De Linares et al. [13] and Vélez-Pereira et al. [28], sensitivity is the percentage of true positives with respect to the total observed positives, and specificity is the percentage of true negatives with respect to the sum of observed negatives. In the present study, these values were calculated for each model, threshold, taxon, and station using the data from the testing period (2012–2014).
As already mentioned, the logit model gives the type (direct or indirect) and significance of each predictor (meteorological parameter) with the modeled variable (concentration threshold). At the same time, the regression tree allows us to infer, from the split level, what is the variable with more influence on the model development (see Figure S2). So, to compare the regression technique, we will use this output.
The calculations were developed with R statistical software, using the GML (Fitting Generalized Linear Models) function to develop the logistic regression and the rpart package to develop the regression trees.
3. Results
Figure 2 shows the signification and kind of relationship between the concentration fungal spore thresholds and the meteorological parameters for each taxon resulting from logistic regression. The values represented on the Y-axis indicate the number of aerobiological stations for which the meteorological variable (X-axis) shows a significative p-value: zero (no station) to eight (all stations). Precipitation shows a greater positive significance in ascospores (Leptosphaeria and Pleospora), as well as minimum temperature, relative humidity, the precipitation of the previous day (for low, medium, and high thresholds), and the precipitation of two days ago (low threshold). Basidiospores (Agaricus and Ganoderma) show that square minimum temperature is the most influential predictor in the airborne spores’ concentration, except in the low threshold, where minimum temperature is most influential. Basidiospores also show a high frequency of positive significance with maximum temperature and humidity, while precipitation is of little significance. Finally, conidiospores (Alternaria and Cladosporium) do not show a main influential predictor. Alternaria shows a high frequency with maximum temperature, while Cladosporium shows a high frequency with the minimum temperature. Humidity is negative to Alternaria and positive to Cladosporium. For this last taxon, the precipitation of previous days also shows a significant positive relationship, especially the precipitation three days ago. More detail on the significance of the logit model is available in the Supplementary Materials (from Tables S5–S10).
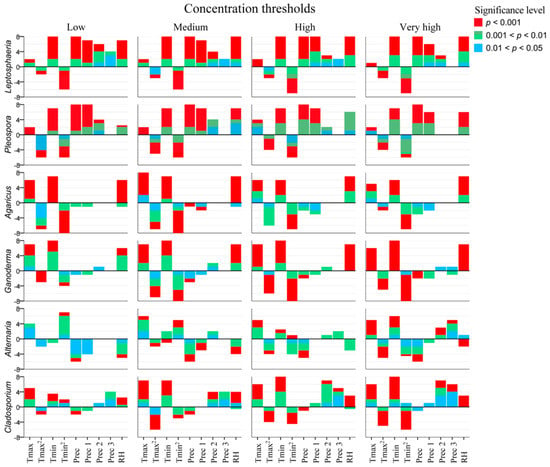
Figure 2.
Frequency and significance level of the predictors (meteorological variables) by fungal spore taxon and concentration threshold were studied by the logistic regression model. Tmax: maximum temperature, Tmax2: squared maximum temperature, Tmin: minimum temperature, Tmin2: squared minimum temperature, Prec: precipitation of the day (≥0.5 mm), Prec 1: Precipitation of the previous day, Prec 2: Precipitation of two days ago, Prec 3: Precipitation of three days ago, RH: relative humidity.
The influence of the predictors on the concentration thresholds produced by the regression trees is illustrated in Figure 3; the Y-axis shows the number of times the predictor occurs in the first four levels of the regression tree model by taxon and threshold. Ascospores and basidiospores show similar results to logit models. However, the influence of precipitation in the previous day on ascospores is notable, especially in Pleospora. In contrast, temperature predictors are the most notable for conidiospores.
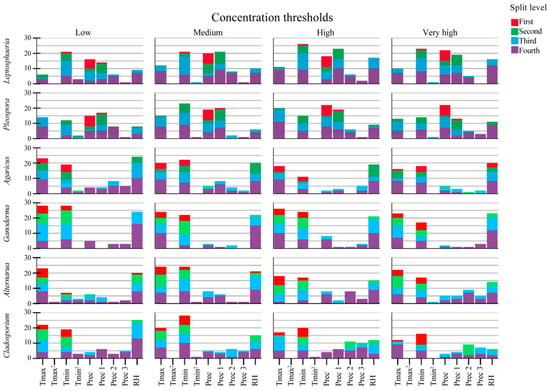
Figure 3.
Frequency split levels of the predictors (meteorological variables) by fungal spore taxa and concentration thresholds studied via regression tree. Tmax: maximum temperature, Tmax2: squared maximum temperature, Tmin: minimum temperature, Tmin2: squared minimum temperature, Prec: precipitation of the day (≥0.5 mm), Prec 1: Precipitation of the previous day, Prec 2: Precipitation of two days ago, Prec 3: Precipitation of three days ago, RH: relative humidity.
Finally, the results for conidiospores show that Alternaria is influenced by the maximum temperature, whereas Cladosporium is influenced by the minimum temperature—the same results as in the logit model. The frequency of the predictor and split values of the regression tree model are available in the Supplementary Materials (from Tables S11–S13).
Regarding the split value established by each regression tree, ascospores show that the split value increases when the concentration threshold is higher. Likewise, greater variations in the minimum temperature and relative humidity are observed in the following sublevels—possibly related to an increase in the concentration threshold of Leptosphaeria and Pleospora, which is consistent with the results reported for the logit model (details in Table S11). Meanwhile, basidiospores present the same behavior, only that the predictor is maximum temperature, increasing split value at the same time as when the concentration threshold increases (details in Table S12). Finally, conidiospores are also consistent with the logit model. Alternaria shows an increase in the maximum temperature split value with increased threshold concentration (details in Table S13).
Table 1 shows the sensitivity and specificity results obtained during the testing models for each taxon, threshold, and station under study. The values show excellent performance in the two models. The logit model varied between 62% and 76% in sensitivity and 72% and 81% in specificity, while the regression tree showed values of sensitivity (68–88%) and specificity (50–69%) that are close to those reported in the logit model but higher in sensitivity and lower in specificity.

Table 1.
Sensitivity and specificity of logistic regression and regression tree per threshold, taxon, and aerobiological station under study.
Ascospores show that Leptosphaeria has higher mean values in both parameters and all models. Likewise, Ganoderma is the basidiospore type with high mean values in both parameters in the two models. Finally, regarding conidiospores, Alternaria shows high values in the logit model in both parameters, while the regression tree shows high values in Cladosporium specificity and Alternaria sensitivity.
The results per concentration thresholds are not consistent. Regarding the logit model, high sensitivity values are observable in the high threshold, while basidiospores and conidiospores show high specificity values in the low threshold. On the other hand, the regression tree shows that only basidiospores and conidiospores matched with respect to the high sensitivity values in low thresholds.
4. Discussion
The high response of ascospores to the precipitation obtained in the logit model and regression tree analyses could be due to fungal spore release being favored by the rain, provoking higher emissions after rain ceased [5,51,52,53,54,55]. Likewise, the results agree with other studies in terms of relative humidity but differ with respect to minimum temperature [56,57,58,59]. However, our results agree with Toscano-Underwood et al. [60], who assert that ascoma can develop in a wide range of temperatures (5–20 °C), but it is optimal between 15 and 20 °C. This is corroborated by Kaczmarek et al. [61], who assert that an increase in temperature is associated with an increasing trend of ascospores in Poland.
In the case of basidiospores, the results related to temperature agree with those shown in other studies [54,62,63,64,65]. In alignment with our results, Hernández et al. [64] evidenced the requirement of temperate temperatures in the sporulation process, although an increase in temperature (warm temperature) limits the process, and this is corroborated by peaks of these taxa during spring and after summer. Additionally, Calderon et al. [66] reported higher concentrations between 20 and 24 °C in dry weather and between 24 and 26 °C in wet conditions. Even the intra-diurnal behavior of some basidiospores shows restrictions because the high values are reported during the night and first hours of the day when the temperature is temperate, and the humidity should be high [67,68]. In the case of Catalonia, the results reported by Vélez-Pereira et al. [69] support the relationship between the presence of basidiospores in the air and temperature because the trend analyzed shows that basidiospores tend to increase annual values when the temperature tends to increase, especially in cold and temperate geographical zones.
The results regarding relative humidity are also similar to other studies [58,62,64,67,68,70,71]. Hasnain et al. [67] and Quintero et al. [70] assert that high humidity and light precipitation facilitate the sporulation of basidiospores. Meanwhile, the low influence of precipitation agrees with the results reported by Gonzálo et al. [72], who confirm that basidium development occurs in periods without rainfall. Burch and Livetin [73] and Quintero et al. [70] stated the same, but with reference to the sporulation process of the basidiospores.
Finally, the results regarding conidiospores are consistent with other studies [74,75,76], in which it is also shown that this type of spore is favored by temperature and lack of precipitation, even though punctual meteorological events could have a different effect on the sporulation process [77,78,79,80]. The predictors used to indicate a relationship between Alternaria and Cladosporium are similar compared to the work of Recio et al. [81], who stated that fluctuation occurs in a short period as a result of temperature variation, which controlled the physiological process of formation, while other meteorological parameters (precipitations and relative humidity) affected the physical process of emission, dispersion, and suspension in the atmosphere.
In comparing the results from the logit model and regression tree, we observed that, in general, the specificity values were high in all thresholds, except in low thresholds in Agaricus of the logit model and Cladosporium and Alternaria in the regression tree. Considering that sensitivity represents the percentage of true positives, the logit model tended to have high sensitivity values, except in the low threshold. These results show that the logistic regression model’s predictions are more accurate when the threshold is reached, while the regression tree’s predictions are more precise when the threshold is not exceeded. It is important to note that the high validation values obtained are not comparable with those of other investigations or published techniques. Classic descriptors such as R2 or root mean square error tend to overestimate the values of the fit due to the high proportion of non-null days that are equal to or close to zero. This could be better explained by analyzing the observed and measured proportions based on the probability of occurrence of the events (presence/absence), where the proportion of values in which the model must establish a true-positive prediction is very low regarding the true-negatives due to a high quantity of concentrations that are close to or equal to zero, thus generating validation values that do not reflect their true predictive power.
A challenge often faced in creating the aforementioned models is the selection of the concentration thresholds for the specified region related to allergy response or pathogenic infections in crops and, likewise, for the taxa studied. In this sense, future research should focus on conducting allergological/phytopathological studies that consider aerobiological records to establish accurate concentration thresholds.
5. Conclusions
Aerobiological predictions based on concentration thresholds facilitate the application of statistical methodologies for constructing observation base models. In this sense, the logistic regression model and regression tree applied in this study are simple and intuitive when it comes to interpreting the results. Both models show similar results regarding the relationship and/or influence of predictors (meteorological parameters) in different simulated thresholds. The validation results show satisfactory values. However, the logistic regression model shows greater precision in estimating the exceedance of the modeled threshold. Considering that it is much easier to apply and store, the logistic regression model is the ideal model for establishing the prediction of thresholds in the aerobiological stations of Catalonia.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/atmos14061016/s1, Figure S1: Monthly averages of the maximum temperature (red boxplot) and minimum temperature ((blue boxplot), total precipitation (green bar), number of days with precipitation (italic number inside the bar), and relative humidity (orange line) of the station under study in the period 1995–2014 [37]; Figure S2: Diagram of the levels and split of a regression tree; Table S1: Details on the geographical and meteorological characteristics of the aerobiological sampling stations, [5,14,82,83,84]; Table S2: Classification, category, and concentration thresholds per fungal spore for Catalonia; Table S3: Arguments for the inclusion of predictors into the models [6,28,68,69,81,85]; Table S4: Critical values used as positive binary answers per taxon-concentration thresholds-aerobiological station; Table S5: Details on the logistic regression coefficient for Leptosphaeria for each aerobiological station and concentration thresholds modeled; Table S6: Details on the logistic regression coefficient for Pleospora for each aerobiological station and concentration threshold modeled; Table S7: Details on the logistic regression coefficient for Agaricus for each aerobiological station and concentration threshold modeled; Table S8: Details on the logistic regression coefficient for Ganoderma for each aerobiological station and concentration threshold modeled; Table S9: Details on the logistic regression coefficient for Alternaria for each aerobiological station and concentration threshold modeled; Table S10: Details on the logistic regression coefficient for Cladosporium for each aerobiological station and concentration threshold modeled; Table S11: First four regression tree split values and frequency for ascospores for each aerobiological station and modeled concentration threshold; Table S12: First four regression tree split values and frequency for basidiospores for each aerobiological station and modeled concentration threshold; Table S13: First four regression tree split values and frequency for conidiospores for each aerobiological station and modeled concentration threshold.
Author Contributions
Conceptualization: A.M.V.-P., C.D.L., M.A.C. and J.B. Methodology: A.M.V.-P. and M.A.C. Formal analysis: A.M.V.-P. Investigation: A.M.V.-P. and C.D.L. Resources: A.M.V.-P. and J.B. Data curation: A.M.V.-P. Writing—original draft preparation: A.M.V.-P. Writing—review and editing: A.M.V.-P., C.D.L., M.A.C. and J.B. Funding acquisition: J.B. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Spanish Ministry of Science and Technology through the project “CGL2012-39523-C02-01/CLI” and by the Administrative Department of Science, Technology and Innovation-COLCIENCIAS (Colombia) through the doctoral fellowship to Andrés M. Vélez-Pereira.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors wish to thank the following entities and projects that made it possible to obtain the database used in this study: Laboratorios LETI PHARMA.; Servei Meteorològic de Catalunya; Diputacions de Barcelona, Girona, and Tarragona; SCAIC; SEAIC; Stallergenes Iberica; J. Uriach y Cia; European Commission for “ENV4-CT98-0755”; Spanish Ministry of Science and Technology I+D+I for “AMB97-0457-CO7-021”, “REN2001-10659-CO3-01”, “BOS2002-03474”, “CGL2004-21166-E”, “CGL2005-07543/CLI”, “GGL2006-12648-CO3-02”, “CGL2009-11205”, “CGL2012-39523-C02-01”, “CTM2017-89565-C2-1-P”, FEDER “A way to build Europe”, and CONSOLIDER CSD 2007_00067 GRACCIE; Catalan Government AGAUR for “2002SGR00059”. “2005SGR00519”, “2009SGR1102”, “2014SGR1274”, and “2017SGR1692”, Andalusian Government for RNM 0110 PAIDI. This research contributes to the “María de Maeztu” Programme for Units of Excellence of the Spanish Ministry of Science and Innovation (CEX2019-000940-M).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Markey, E.; Clancy, J.H.; Martínez-Bracero, M.; Neeson, F.; Sarda-Estève, R.; Baisnée, D.; McGillicuddy, E.J.; Sewell, G.; O’Connor, D.J. A Modified Spectroscopic Approach for the Real-Time Detection of Pollen and Fungal Spores at a Semi-Urban Site Using the WIBS-4+, Part I. Sensors 2022, 22, 8747. [Google Scholar] [CrossRef] [PubMed]
- Camargo, Y.; Henao, D.M.; Vélez-Pereira, A.M. Emisiones Atmosféricas de Origen Biológico; Primera; Fondo Editorial UniMagdalena: Santa Marta, Colombia, 2011; ISBN 978-958-746-037-7. [Google Scholar]
- Vélez-Pereira, A.M.; De Linares, C.; Belmonte, J. Aerobiological modeling I: A review of predictive models. Sci. Total Environ. 2021, 795, 148783. [Google Scholar] [CrossRef] [PubMed]
- Caicedo, Y.C.; Pérez, H.B.; Fuentes, M.M.; Vergara-Vásquez, E.; Vélez-Pereira, A.M. Assessment of fungal aerosols in a public library with natural ventilation. Aerobiologia 2023, 39, 37–50. [Google Scholar] [CrossRef]
- Anees-Hill, S.; Douglas, P.; Pashley, C.H.; Hansell, A.; Marczylo, E.L. A systematic review of outdoor airborne fungal spore seasonality across Europe and the implications for health. Sci. Total Environ. 2022, 818, 151716. [Google Scholar] [CrossRef] [PubMed]
- Vélez-Pereira, A.M.; De Linares, C.; Belmonte, J. Aerobiological modelling II: A review of long-range transport models. Sci. Total Environ. 2022, 845, 157351. [Google Scholar] [CrossRef]
- Sánchez, P.; Vélez-del-Burgo, A.; Suñén, E.; Martínez, J.; Postigo, I. Fungal Allergen and Mold Allergy Diagnosis: Role and Relevance of Alternaria alternata Alt a 1 Protein Family. J. Fungi 2022, 8, 277. [Google Scholar] [CrossRef]
- Jazuli, N.A.; Kamu, A.; Chong, K.P.; Gabda, D.; Hassan, A.; Abu Seman, I.; Ho, C.M. A Review of Factors Affecting Ganoderma Basal Stem Rot Disease Progress in Oil Palm. Plants 2022, 11, 2462. [Google Scholar] [CrossRef]
- Martinez-Bracero, M.; Markey, E.; Clancy, J.H.; McGillicuddy, E.J.; Sewell, G.; O’Connor, D.J. Airborne Fungal Spore Review, New Advances and Automatisation. Atmosphere 2022, 13, 308. [Google Scholar] [CrossRef]
- Komnos, I.D.; Michali, M.C.; Ziavra, N.V.; Katotomichelakis, M.A.; Kastanioudakis, I.G. A Study of Airborne Pollen Grains and Fungal Spores in the Region of Epirus (Northwestern Greece). Cureus 2022, 14. [Google Scholar] [CrossRef]
- Kremneva, O.; Danilov, R.; Gasiyan, K.; Ponomarev, A. Spore-Trapping Device: An Efficient Tool to Manage Fungal Diseases in Winter Wheat Crops. Plants 2023, 12, 391. [Google Scholar] [CrossRef]
- Raza, M.M.; Bebber, D.P. Climate change and plant pathogens. Curr. Opin. Microbiol. 2022, 70, 102233. [Google Scholar] [CrossRef]
- De Linares, C.; Belmonte, J.; Canela, M.; de la Guardia, C.D.; Alba-Sanchez, F.; Sabariego, S.; Alonso-Pérez, S. Dispersal patterns of Alternaria conidia in Spain. Agric. For. Meteorol. 2010, 150, 1491–1500. [Google Scholar] [CrossRef]
- Vélez-Pereira, A.M.; De Linares, C.; Canela, M.; Belmonte, J. Spatial distribution of fungi from the analysis of aerobiological data with a gamma function. Aerobiologia 2021, 37, 461–477. [Google Scholar] [CrossRef]
- Comtois, P. The gamma distribution as the true aerobiological probability density function (PDF). Aerobiologia 2000, 16, 171–176. [Google Scholar] [CrossRef]
- Al-Nesf, M.A.; Gharbi, D.; Mobayed, H.M.; Ali, R.M.; Tuffaha, A.; Dason, B.R.; Adeli, M.; Sattar, H.A.; Trigo, M.d.M. Aerobiological monitoring in a desert type ecosystem: Two sampling stations of two cities (2017–2020) in Qatar. PLoS ONE 2022, 17, e0270975. [Google Scholar] [CrossRef]
- Scheifinger, H.; Belmonte, J.; Buters, J.; Celenk, S.; Damialis, A.; Dechamp, C.; García-Mozo, H.; Gehrig, R.; Grewling, L.; Halley, J.M.; et al. Monitoring, modelling and forecasting of the pollen season. In Allergenic Pollen; Sofiev, M., Bergmann, K.-C., Eds.; Springer: Dordrecht, The Netherlands, 2013; pp. 71–126. ISBN 978-94-007-4880-4. [Google Scholar]
- Tu, J.V. Advantages and disadvantages of using artificial neural networks versus logistic regression for predicting medical outcomes. J. Clin. Epidemiol. 1996, 49, 1225–1231. [Google Scholar] [CrossRef]
- Aznartem, J.; Sánchez, J.M.B.; Lugilde, D.N.; Fernández, C.d.L.; de la Guardia, C.D.; Sánchez, F.A. Forecasting airborne pollen concentration time series with neural and neuro-fuzzy models. Expert Syst. Appl. 2007, 32, 1218–1225. [Google Scholar] [CrossRef]
- Verma, K.S.; Pathak, A.K. A comparative analysis of forecasting methods for aerobiological studies. Asian J. Exp. Sci. 2009, 23, 193–198. [Google Scholar]
- Belmonte, J.; Canela, M.; Guàrdia, R.-A. Comparison between categorical pollen data obtained by Hirst and Cour sampling methods. Aerobiologia 2000, 16, 177–185. [Google Scholar] [CrossRef]
- Belmonte, J.; Canela, M.A.; Guardans, R.; Roure, J.M. Comparison of polllen data obtained by Cour and modified-Durham methods. Pollen Spores 1988, 30, 257–264. [Google Scholar]
- Castellano-Méndez, M.; Aira, M.J.; Iglesias, I.; Jato, V.; González-Manteiga, W. Artificial neural networks as a useful tool to predict the risk level of Betula pollen in the air. Int. J. Biometeorol. 2005, 49, 310–316. [Google Scholar] [CrossRef] [PubMed]
- Makra, L.; Matyasovszky, I.; Thibaudon, M.; Bonini, M. Forecasting ragweed pollen characteristics with nonparametric regression methods over the most polluted areas in Europe. Int. J. Biometeorol. 2011, 55, 361–371. [Google Scholar] [CrossRef] [PubMed]
- Myszkowska, D.; Majewska, R. Pollen grains as allergenic environmental factors–new approach to the forecasting of the pollen concentration during the season. Ann. Agric. Environ. Med. 2014, 21, 681–688. [Google Scholar] [CrossRef] [PubMed]
- Ranzi, A.; Lauriola, P.; Marletto, V.; Zinoni, F. Forecasting airborne pollen concentrations: Development of local models. Aerobiologia 2003, 19, 39–45. [Google Scholar] [CrossRef]
- Cotos-Yáñez, T.R.; Rodríguez-Rajo, F.J.; Jato, V. Short-term prediction of Betula airborne pollen concentration in Vigo (NW Spain) using logistic additive models and partially linear models. Int. J. Biometeorol. 2004, 48, 179–185. [Google Scholar] [CrossRef]
- Vélez-Pereira, A.M.; De Linares, C.; Canela, M.-A.; Belmonte, J. Logistic regression models for predicting daily airborne Alternaria and Cladosporium concentration levels in Catalonia (NE Spain). Int. J. Biometeorol. 2019, 63, 1541–1553. [Google Scholar] [CrossRef]
- Grinn-Gofroń, A.; Strzelczak, A. The effects of meteorological factors on the occurrence of Ganoderma sp. spores in the air. Int. J. Biometeorol. 2011, 55, 235–241. [Google Scholar] [CrossRef]
- Jedryczka, M.; Strzelczak, A.; Grinn-Gofron, A.; Nowak, M.; Wolski, T.; Siwulski, M.; Sobieralski, K.; Kaczmarek, J. Advanced statistical models commonly applied in aerobiology cannot accurately predict the exposure of people to Ganoderma spore-related allergies. Agric. For. Meteorol. 2015, 201, 209–217. [Google Scholar] [CrossRef]
- Sadyś, M.; Skjøth, C.A.; Kennedy, R. Forecasting methodologies for Ganoderma spore concentration using combined statistical approaches and model evaluations. Int. J. Biometeorol. 2016, 60, 489–498. [Google Scholar] [CrossRef]
- Grinn-Gofroń, A.; Strzelczak, A. Hourly predictive artificial neural network and multivariate regression tree models of Alternaria and Cladosporium spore concentrations in Szczecin (Poland). Int. J. Biometeorol. 2009, 53, 555–562. [Google Scholar] [CrossRef]
- Kasprzyk, I.; Grinn-Gofroń, A.; Strzelczak, A.; Wolski, T. Hourly predictive artificial neural network and multivariate regression trees models of Ganoderma spore concentrations in Rzeszów and Szczecin (Poland). Sci. Total Environ. 2011, 409, 949–956. [Google Scholar] [CrossRef]
- O’Connor, D.J.; Sadyś, M.; Skjøth, C.A.; Healy, D.A.; Kennedy, R.; Sodeau, J.R. Atmospheric concentrations of Alternaria, Cladosporium, Ganoderma and Didymella spores monitored in Cork (Ireland) and Worcester (England) during the summer of 2010. Aerobiologia 2014, 30, 397–411. [Google Scholar] [CrossRef]
- Martínez-Bracero, M.; González-Fernández, E.; Wójcik, M.; Alcázar, P.; Fernández-González, M.; Kasprzyk, I.; Rodríguez-Rajo, F.J.; Galán, C. Airborne fungal phytopathological spore assessment in three European vineyards from different bioclimatic areas. Aerobiologia 2020, 36, 715–729. [Google Scholar] [CrossRef]
- Allue Andrade, J.L. Phytoclimatic Atlas of Spain Taxonomies; Instituto Nacional de Investigaciones Agrarias, Ministerio de Agricultura, Pesca y Alimentación: Madrid, Spain, 1990; ISBN 84-7498-362-2. [Google Scholar]
- Vélez-Pereira, A.M. Modelación Espacio-Temporal de Polen y Esporas de Hongos Aerovagantes de Catalunya (1994–2015). Ph.D. Thesis, Universitat Autònoma de Barcelona–Institut de Ciència i Tecnologia Ambiental, Barcelona, Spain, 26 September 2017. [Google Scholar]
- Hirst, J.M. An Automatic Volumetric Spore Trap. Ann. Appl. Biol. 1952, 39, 257–265. [Google Scholar] [CrossRef]
- Galán, C.; Cariñanos, P.; Alcázar, P.; Dominguez, E. Manual de Calidad y Gestión de la Red Española de Aerobiología; Universidad de Córdoba: Cordoba, Spain, 2007. [Google Scholar]
- Galán, C.; Ariatti, A.; Bonini, M.; Clot, B.; Crouzy, B.; Dahl, A.; Fernandez-González, D.; Frenguelli, G.; Gehrig, R.; Isard, S.; et al. Recommended terminology for aerobiological studies. Aerobiologia 2017, 33, 293–295. [Google Scholar] [CrossRef]
- Hosmer, D.W.; Lemeshow, S. Multiple Logistic Regression, 2nd ed.; Wiley Series in Probability and Statistics Texts and References Section; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2000; ISBN 978-0-471-72214-4. [Google Scholar]
- Brito, C.; Crespo, E.G.; Paulo, O.S. Modelling wildlife distributions: Logistic multiple regression vs overlap analysis. Ecography 1999, 22, 251–260. [Google Scholar] [CrossRef]
- Teixeira, J.; Ferrand, N.; Arntzen, J.W. Biogeography of the golden-striped salamander Chioglossa lusitanica: A field survey and spatial modelling approach. Ecography 2001, 24, 618–624. [Google Scholar] [CrossRef]
- Rojas, A.B.; Cotilla, I.; Real, R.; Palomo, L.J. Determinación de las áreas probables de distribución de los mamíferos terrestres en la provincia de Málaga. Galemys 2001, 13, 217–229. [Google Scholar]
- Barbosa, A.M.; Real, R.; Olivero, J.; Vargas, J.M. Otter (Lutra lutra) distribution modeling at two resolution scales suited to conservation planning in the Iberian Peninsula. Biol. Conserv. 2003, 114, 377–387. [Google Scholar] [CrossRef]
- Calle, M.L.; Sánchez-Espigares, J.A. Árboles de clasificación y regresión en la investigación biomédica. Med. Clin. 2007, 129, 702–706. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning—Data Mining, Inference, 2nd ed.; Springer Series in Statistics; Springer: New York, NY, USA, 2009; ISBN 978-0-387-84857-0. [Google Scholar]
- Murthy, S.K. Automatic construction of decision trees from data: A multi-disciplinary survey. Data Min. Knowl. Discov. 1998, 2, 345–389. [Google Scholar] [CrossRef]
- Tzima, F.A.; Karatzas, K.D.; Mitkas, P.A.; Karathanasis, S. Using data-mining techniques for PM 10 forecasting in the metropolitan area of Thessaloniki, Greece. In Proceedings of the 2007 International Joint Conference on Neural Networks, Orlando, FL, USA, 12–17 August 2007; IEEE: Piscataway, CK, USA; pp. 2752–2757. [Google Scholar]
- Real, R.; Barbosa, A.M.; Vargas, J.M. Obtaining environmental favourability functions from logistic regression. Environ. Ecol. Stat. 2006, 13, 237–245. [Google Scholar] [CrossRef]
- Hernández-Trejo, F.; Muñoz, F.R.; Tormo, R.M.; Silva, I.P. Airborne ascospores in Mérida (SW Spain) and the effect of rain and other meteorological parameters on their concentration. Aerobiologia 2012, 28, 13–26. [Google Scholar] [CrossRef]
- Rivera-Mariani, F.E.; Bolaños-Rosero, B. Allergenicity of airborne basidiospores and ascospores: Need for further studies. Aerobiologia 2012, 28, 83–97. [Google Scholar] [CrossRef]
- Rúa-Giraldo, A.L. Aerobiología de las Esporas de Pleosporales en Ambientes intra y Extradomiciliarios de Barcelona. Aplicación a la Clínica en Población Alérgica. Ph.D. Thesis, Universitat Autònoma de Barcelona, Barcelona, Spain, 2013. [Google Scholar]
- Martínez-Bracero, M.; Markey, E.; Clancy, J.H.; Sodeau, J.; O’Connor, D.J. First Long-Time Airborne Fungal Spores Study in Dublin, Ireland (1978–1980). Atmosphere 2022, 13, 313. [Google Scholar] [CrossRef]
- Mantoani, M.C.; Emygdio, A.P.M.; Degobbi, C.; Sapucci, C.R.; Guerra, L.C.C.; Dias, M.A.F.S.; Dias, P.L.S.; Zanetti, R.H.S.; Rodrigues, F.; Araujo, G.G.; et al. Rainfall effects on vertical profiles of airborne fungi over a mixed land-use context at the Brazilian Atlantic Forest biodiversity hotspot. Agric. For. Meteorol. 2023, 331, 109352. [Google Scholar] [CrossRef]
- Díez, A.H.; Sabariego, S.; Gutiérrez, M.B.; Cervigón, P.M. Study of airborne fungal spores in Madrid, Spain. Aerobiologia 2006, 22, 133. [Google Scholar] [CrossRef]
- Oliveira, M.; Ribeiro, H.; Delgado, J.L.; Abreu, I. The effects of meteorological factors on airborne fungal spore concentration in two areas differing in urbanisation level. Int. J. Biometeorol. 2009, 53, 61–73. [Google Scholar] [CrossRef]
- SenGupta, K.; Karmakar, B.; Roy, S.; Kaur, A.; Bhattacharya, S.G. Analyzing airborne fungal concentration in Kolkata, India: Temporal distribution, the effect of atmospheric parameters and health impact. Air Qual. Atmos. Health 2023, 16, 963–984. [Google Scholar] [CrossRef]
- Simović, I.; Matavulj, P.; Šikoparija, B. Manual and automatic quantification of airborne fungal spores during wheat harvest period. Aerobiologia 2023. [Google Scholar] [CrossRef]
- Toscano-Underwood, C.; Huang, Y.J.; Fitt, B.D.L.; Hall, A.M. Effects of temperature on maturation of pseudothecia of Leptosphaeria maculans and L. biglobosa on oilseed rape stem debris. Plant Pathol. 2003, 52, 726–736. [Google Scholar] [CrossRef]
- Kaczmarek, J.; Kedziora, A.; Brachaczek, A.; Latunde-Dada, A.O.; Dakowska, S.; Karg, G.; Jedryczka, M. Effect of climate change on sporulation of the teleomorphs of Leptosphaeria species causing stem canker of brassicas. Aerobiologia 2016, 32, 39–51. [Google Scholar] [CrossRef]
- Craig, R.L.; Levetin, E. Multi-year study of Ganoderma aerobiology. Aerobiologia 2000, 16, 75–81. [Google Scholar] [CrossRef]
- Stępalska, D.; Wołek, J. Intradiurnal periodicity of fungal spore concentrations (Alternaria, Botrytis, Cladosporium, Didymella, Ganoderma) in Cracow, Poland. Aerobiologia 2009, 25, 333–340. [Google Scholar] [CrossRef]
- Hernández, F.T.; Muñoz, A.F.; Tormo, R.M.; Silva, I.P. Airborne spores of basidiomycetes in Merida (SW Spain). Ann. Agric. Environ. Med. 2013, 20, 657–663. [Google Scholar]
- Almaguer, M.; Rojas-Flores, T.I.; Rodríguez-Rajo, F.J.; Aira, M.-J. Airborne basidiospores of Coprinus and Ganoderma in a Caribbean region. Aerobiologia 2014, 30, 197–204. [Google Scholar] [CrossRef]
- Calderon, C.; Lacey, J.; McCartney, H.A.; Rosas, I. Seasonal and diurnal variation of airborne basidiomycete spore concentrations in Mexico city. Grana 1995, 34, 260–268. [Google Scholar] [CrossRef]
- Hasnain, S.M.; Fatima, K.; Al-Frayh, A.; Al-Sedairy, S.T. Prevalence of airborne basidiospores in three coastal cities of Saudi Arabia. Aerobiologia 2005, 21, 139–145. [Google Scholar] [CrossRef]
- Ščevková, J.; Hrabovský, M.; Kováč, J.; Rosa, S. Intradiurnal variation of predominant airborne fungal spore biopollutants in the Central European urban environment. Environ. Sci. Pollut. Res. 2019, 26, 34603–34612. [Google Scholar] [CrossRef]
- Vélez-Pereira, A.M.; De Linares, C.; Delgado, R.; Belmonte, J. Temporal trends of the airborne fungal spores in Catalonia (NE Spain), 1995–2013. Aerobiologia 2016, 32, 23–37. [Google Scholar] [CrossRef]
- Quintero, E.; Rivera-Mariani, F.; Bolaños-Rosero, B. Analysis of environmental factors and their effects on fungal spores in the atmosphere of a tropical urban area (San Juan, Puerto Rico). Aerobiologia 2010, 26, 113–124. [Google Scholar] [CrossRef]
- Li, Y.; Feng, Y.; Shang, Y.; Xu, H.; Xia, R.; Hou, Z.; Pan, S.; Li, L.; Bian, Y.; Zhu, J.; et al. Sexual spores in edible mushroom: Bioactive components, discharge mechanisms and effects on fruiting bodies quality. Food Sci. Hum. Wellness 2023, 12, 2111–2123. [Google Scholar] [CrossRef]
- Gonzálo, M.A.; Paredes, M.M.; Muñoz, A.F.; Tormo, R.; Silva, I. Dinámica de dispersión de basidiosporas en la atmósfera de Badajoz. Rev. Esp. Alergol. Inmunol. Clín. 1997, 12, 294–300. [Google Scholar]
- Burch, M.; Levetin, E. Effects of meteorological conditions on spore plumes. Int. J. Biometeorol. 2002, 46, 107–117. [Google Scholar] [CrossRef]
- Picornell, A.; Rojo, J.; Trigo, M.M.; Ruiz-Mata, R.; Lara, B.; Romero-Morte, J.; Serrano-García, A.; Pérez-Badia, R.; Gutiérrez-Bustillo, M.; Cervigón-Morales, P.; et al. Environmental drivers of the seasonal exposure to airborne Alternaria spores in Spain. Sci. Total Environ. 2022, 823, 153596. [Google Scholar] [CrossRef]
- Olsen, Y.; Skjøth, C.A.; Hertel, O.; Rasmussen, K.; Sigsgaard, T.; Gosewinkel, U. Airborne Cladosporium and Alternaria spore concentrations through 26 years in Copenhagen, Denmark. Aerobiologia 2020, 36, 141–157. [Google Scholar] [CrossRef]
- De Linares, C.; Navarro, D.; Puigdemunt, R.; Belmonte, J. Airborne Alt a 1 Dynamic and Its Relationship with the Airborne Dynamics of Alternaria Conidia and Pleosporales Spores. J. Fungi 2022, 8, 125. [Google Scholar] [CrossRef]
- Grinn-Gofroń, A.; Strzelczak, A. Changes in concentration of Alternaria and Cladosporium spores during summer storms. Int. J. Biometeorol. 2013, 57, 759–768. [Google Scholar] [CrossRef]
- Damialis, A.; Mohammad, A.B.; Halley, J.M.; Gange, A.C. Fungi in a changing world: Growth rates will be elevated, but spore production may decrease in future climates. Int. J. Biometeorol. 2015, 59, 1157–1167. [Google Scholar] [CrossRef]
- Grinn-Gofroń, A.; Bosiacka, B. Effects of meteorological factors on the composition of selected fungal spores in the air. Aerobiologia 2015, 31, 63–72. [Google Scholar] [CrossRef]
- Sousa, L.; Camacho, I.C.; Grinn-Gofroń, A.; Camacho, R. Monitoring of anamorphic fungal spores in Madeira region (Portugal), 2003–2008. Aerobiologia 2016, 32, 303–315. [Google Scholar] [CrossRef]
- Recio, M.; Trigo, M.M.; Docampo, S.; Melgar, M.; García-Sánchez, J.; Bootello, L.; Cabezudo, B. Analysis of the predicting variables for daily and weekly fluctuations of two airborne fungal spores: Alternaria and Cladosporium. Int. J. Biometeorol. 2012, 56, 983–991. [Google Scholar] [CrossRef]
- Frankland, A.W.; Davies, R.R. Allergie Aux Spores de Moisissures En Angleterre. Le Poumon et le cøeur 1965, 21, 11–23. [Google Scholar]
- Gravesen, S. Fungi as a Cause of Allergic Disease. Allergy 1979, 34, 135–154. [Google Scholar] [CrossRef]
- Katotomichelakis, M.; Nikolaidis, C.; Makris, M.; Proimos, E.; Aggelides, X.; Constantinidis, T.C.; Papadakis, C.E.; Danielides, V. Alternaria and Cladosporium Calendar of Western Thrace: Relationship with Allergic Rhinitis Symptoms. Laryngoscope 2016, 126, E51–E56. [Google Scholar] [CrossRef]
- Pace, L.; Boccacci, L.; Casilli, M.; Fattorini, S. Temporal Variations in the Diversity of Airborne Fungal Spores in a Mediterranean High Altitude Site. Atmos. Environ. 2019, 210, 166–170. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).