Abstract
This study analyzes the different impacts of autoconversion of cloud droplets to raindrops (ACR) in a Meiyu front rainfall event by comparing two simulations using different parameterizations (KK00 and LD04) in the Weather Research and Forecasting (WRF) model. The Meiyu frontal clouds are further classified into stratiform and deep-convective cloud categories, and the precipitation and microphysical characteristics of the two simulations are compared with a budget analysis of raindrops. The simulated precipitation, radar composite reflectivity distribution, and rain rate evolution are overall consistent with observations while precipitation is overestimated, especially in the rainfall centers. The intensity and vertical structure of the ACR process between the two simulations are significantly different. The ACR rate in LD04 is larger than that in KK00 and there are two peak heights in LD04 but only one in KK00. Accretion of droplets by raindrops (CLcr), melting of ice-phase particles (ML), evaporation of raindrops (VDrv), and accretion of raindrops by ice-phase particles (CLri) are the dominant pathways to raindrop production. Limited distributional differences can be found in both the deep-convective and stratiform clouds between the two simulations during the growth stage of the Meiyu event. Stronger ACR in LD04 results in less cloud droplet content (Lc), more raindrop content (Lr), and larger raindrop number concentration (Nr) and the effect of ACR on Nr is greater than that on Lr. The ACR process also impacts other microphysical processes indirectly, and the influences vary in the two cloud categories. Less CLcr (especially), ML, and VDrv content, caused by stronger ACR, lead to less raindrop production in the LD04 deep-convective clouds, which is different from stratiform clouds, and finally correct the overestimated rainfall center to better match the observations.
1. Introduction
Clouds contain numerous hydrometeors, including cloud droplets, raindrops, and ice phase particles; the field of cloud microphysics deals with the transformation mechanisms between different hydrometeors and their corresponding dynamic and thermodynamic processes. Moreover, changes in cloud microphysics can modulate dynamical and thermo-dynamical properties [1,2]. Therefore, a reasonable representation of cloud microphysical processes is one of the key factors in providing accurate numerical weather forecasts. Cloud microphysical processes are generally described via parameterization in numerical models. However, due to varying atmospheric conditions, the microphysical characteristics often have large regional differences. Numerical models are also nonlinear and complex. All of these factors lead to challenges in microphysical parameterizations [3,4,5].
A large amount of water evaporates from the land and ocean and is converted into water vapor; the water vapor then condenses on the cloud condensation nucleus (CCN) and becomes a cloud droplet with a small diameter. Larger droplets with larger velocities collide and coalesce with smaller droplets to form raindrops, which is referred to as the autoconversion process of cloud droplets to raindrops (autoconversion process, hereafter) [6,7]. This process is the initial way in which raindrops are formed and is usually the dominant process for generating drizzle in stratiform clouds [8,9,10]. Over the past few decades, many studies on autoconversion parameterizations have been conducted. In consideration of different sensitivity factors, autoconversion parameterizations can be roughly classified into three categories. The first one is a simple single-moment parameterization, proposed by Kessler in 1969 [11], and assumes that the autoconversion rate is correlated linearly with the cloud liquid water content (LWC). The Kessler-type parameterization usually sets an invariable conversion threshold and takes the autoconversion rate to be zero when the LWC is less than the threshold value. The constant setting leads to no autoconversion in clouds with low LWC; so, the precipitation efficiency is underestimated. Conversely, in clouds with high LWC, a large variety of cloud droplets convert to raindrops instantly, resulting in overestimates of the precipitation efficiency [12]. In fact, the collision rate between cloud droplets is inextricably linked to the mean diameter. Manton et al. [13] then came up with the second parameterization, which was a complex two-moment parameterization with independent LWC and cloud droplet number concentration (Nc) variables, and numerous studies were conducted using this formula [14,15,16,17]. This two-moment type of parameterization can reflect the CCN effect and is, therefore, more in line with real microphysical processes. In addition, Berry [18] derived the third type considering three variables: LWC, NC, and spectral dispersion (ε). ε is defined as the ratio of the standard deviation to the mean radius of the cloud droplet spectral distribution to describe the various functions of NC. Since its initial formulation, many scholars have rewritten and built upon Berry’s original formula [19,20,21].
Most of the studies on autoconversion parameterization in numerical models focus primarily on comparing different types or discussing relevant variables in the formula. For example, using a two-dimensional, time-varying, warm-rain cumulus model, Li et al. [22] compared the autoconversion rate among three parameterizations in several types of warm-rain cumulus clouds with different intensities. They found that autoconversion plays a major role in the initial stage of precipitation; further, the accretion of droplets by raindrops contributes more than autoconversion when more raindrops are generated. Xie et al. [23,24] conducted a series of studies to analyze the influence of ε on precipitation under different CCN backgrounds and the relationship between ε and NC; there are other studies on the aerosol indirect effect. Jing et al. [25,26], for instance, incorporated five different autoconversion schemes into individual global climate models (GCMs) to evaluate the warm-rain formation process. Xie et al. [27] investigated how autoconversion affects precipitation with various CCN concentrations. Overall, most of the previous numerical experiments were conducted in warm-rain regions within relatively simple microphysical processes. Most rainstorms, however, are formed in mixed clouds with various kinds of ice-phase particles within a wide range of shapes and densities, which makes the microphysical processes much more complex. Therefore, the targeted study of mixed clouds is important.
The Meiyu front is a climatological phenomenon occurring in eastern Asia every summer that is characterized by a quasi-stationary front. The Meiyu frontal cloud usually presents as an elongated cloud band within some deep-convective centers [28,29,30]. The mixture of stratiform clouds and deep-convective clouds in Meiyu front makes the microphysical processes complex with various ice-phase particles [31,32,33]. During 4–5 July 2020, heavy rainfall occurred in the Meiyu front over the Middle–Lower Yangtze River. In this paper, we conducted two numerical simulations within different autoconversion parameterizations using the Advanced Research Weather Research and Forecasting model (WRF-ARW), version 4.1.1. Model grids were divided into stratiform and deep-convective grids to analyze the influence of the autoconversion process on mixed clouds rainfall via budget analysis of the raindrops.
The rest of this paper is organized as follows: Section 2 provides the data sources, an overview of the Meiyu front heavy rainfall case considered herein, two autoconversion parameterizations, the WRF model setup, and the regime partitioning method. Section 3 presents the results from the simulations and a comparison of the two autoconversion parameterizations. The summary and conclusions are provided in Section 4.
2. Materials and Methods
2.1. Data Sources
There are three types of data used in this paper. (1) The observational precipitation data from 1200 UTC on 4 July 2020 to 1200 UTC on 5 July 2020, which are a combination of the Climate Prediction Center morphing technique (CMORPH) real-time precipitation retrieval and hourly precipitation data from more than 30,000 automatic weather stations in China and are provided by the National Meteorological Information Centre (NMIC) of the China Meteorological Administration (CMA). The products have a 0.1° × 0.1° spatial resolution and an hourly temporal resolution. (2) The radar composite reflectivity data combine the gridded data of all the weather radars in the rainfall region. The data were output in 1 km × 1 km grids every 6 min. (3) The initial conditions and 1-hourly lateral boundaries of the WRF model are obtained from the fifth generation European Centre for Medium-Range Weather Forecasts (ECMWF) atmospheric reanalysis of the global climate (ERA-5, hereafter). The ERA5 data are updated on 0.25° × 0.25° grids on the surface and pressure levels.
2.2. Simulation Configuration
2.2.1. Autoconversion Parameterization
In this study, the cloud microphysical scheme used is the two-moment Morrison scheme [34], which predicts the mixing ratios of five hydrometeors (i.e., cloud droplets, raindrops, ice crystals, snow, and graupel) and the number concentrations of four hydrometeors (all except for cloud droplets). We conducted two simulations with different autoconversion parameterization in this study, and only the autoconversion settings are different between the two simulations. The default autoconversion parameterization in Morrison scheme was written as Khairoutdinov and Kogan [16] (KK00), and the simulation with default autoconversion parameterization was called simulation KK00. The compared simulation used a parameterization written as Liu et al. [7,20,21] (LD04). LD04 parameterization was rewritten into the related autoconversion process in the Fortran code in WRF to conduct simulation LD04. The detailed descriptions of the two parameterizations are as follows:
The KK00 parameterization is a simple power-law expression based on the study by Manton et al. [13], which was initially applied to the marine stratocumulus layer in a large-eddy simulation model. The autoconversion rate (P) is related to both the cloud droplet mixing ratio (QC) and the cloud droplet number concentration (NC); it increases with increasing QC and decreases with increasing NC:
Here, the units of P, QC, and NC are, respectively, kg kg−1 s−1, kg kg−1, and cm−3. The simple expression makes it possible to analytically integrate the microphysical process rates over a probability density function [35]. Yin et al. [36] found that KK00 parameterization was highly dependent on Nc. In low Nc conditions, the autoconversion process is allowable, which might lead to overestimations.
LD04 parameterization considers not only the content of raindrop (Lc) and NC but also ε. It was proposed by Liu et al. [7,20,21] (LD04, hereafter). By using the kinetic potential identified in McGraw et al. [37] to present a theoretical formulation for the mass autoconversion rate, LD04 came up with the new R6 parameterization instead of R4, in which R4 is the mean radius of the fourth moment and widely used in the study of Manton et al. Type [13]. The LD04 parameterization was given by the following theoretical formulation for the mass autoconversion rate.
Here, P is in g cm−3 s−1, P0 is in g cm−3 as the rate function, and T is dimensionless as the threshold function. NC and LC are in cm−3. xc has an analytic formula of xc = 9.7 × 10−17 Nc 3/2 Lc−2. ε is linearly correlated with NC in ε = 0.0005714 NC + 0.271. LD04 parameterization was investigated to be more reliable by Xie et al. [27] for improving the understanding of the AIE compared to the Kessler and Berry parameterization [11,18].
2.2.2. Simulation Design
The initiation and boundary fields were obtained from the ERA-5 reanalysis data. We utilized a one-way triple-nested (9/3 km; the spatial extents of the two model domains are shown in Figure 1) simulation for conducting experiments. There were 51 layers from surface to 10 hPa (see Table 1 for an overview of the simulation design). All settings except for the autoconversion settings in the two simulations were completely identical. All the domains were initialized at 1200 UTC on 4 July and then integrated up to 1200 UTC on 5 July. The forecasts’ products were collected at 5 min intervals.
Figure 1.
Geographical domain used in the WRF model runs. The solid red circle indicates the central point of the outer domain.

Table 1.
Overview of the simulation design.
2.3. Convective/Stratiform Regime Partitioning Method
According to the various dynamic structures and hydrometeor distributions in the mesoscale convective system (MCS), a method adopted by Luo et al. [31] was used to separate the 3-D model grids into clear sky and cloudy regions, which are further classified into shallow-convective, deep-convective, and stratiform regions. If the vertically integrated mass of the five types of hydrometeors in the column from the ground to the top of the model is less than 0.2 kg m−2, the grid is classified as a clear-sky grid; an unclear grid indicates cloudy skies. In the cloudy column, a shallow-convective grid must have a positive vertical-mean air velocity from the surface to the 0 °C level, with a raindrop path less than 0.1 kg m−2, a cloud droplet path greater than 0.1 kg m−2 from the ground to the melting level, and a path of ice-phase particles (including ice crystals, snow, and graupel) from the ground to the model top less than 0.4 kg m−2. A deep-convective grid satisfies at least one of the following two conditions: (1) the maximum cloud updraft strength below the melting level is greater than 5 m s−1 or (2) the surface rain rate is greater than 25 mm h−1. Finally, a grid that does not belong to a clear sky, shallow-convective, or deep-convective grid is regarded as a stratiform grid.
3. Results and Discussion
3.1. Model Evaluation
3.1.1. Precipitation Characteristics
Figure 2 shows the observed and simulated accumulated precipitation distribution from 1200 UTC on 4 July 2020 to 1200 UTC on 5 July 2020. In observation, the distribution presented as a typical Meiyu front precipitation pattern with quasi-linear east–west oriented rain bands in northeastern Hubei Province, southern Anhui Province, and southern Jiangsu Province, and the two rainfall centers exceeding 100 mm were in Hubei and along the boundary of Hubei and Anhui. The main rainfall bands that exceeded 10 mm were located at 29–32° N, 112–122° E (marked with a red dotted box).
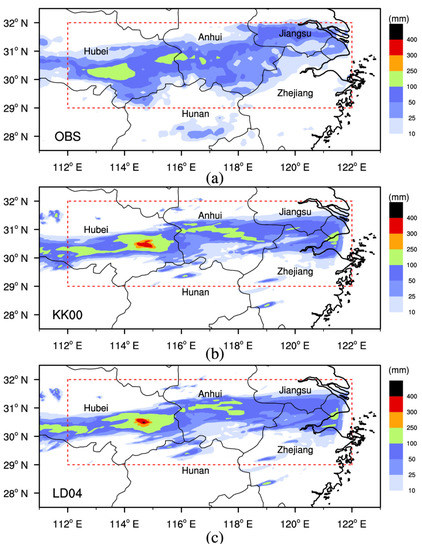
Figure 2.
Distribution of the 24 h accumulated surface rainfall from 1200 UTC on 4 July 2020 to 1200 UTC on 5 July 2020 in the (a) observation, (b) KK00 simulation, (c) LD04 simulation.
All simulated results in this paper are analyzed with the domain 2 output. The main rain belts of the two simulations are basically consistent with the observations within the nearly west–east oriented rain bands. However, the moderate rain and heavy rain belts ranging between 10 and 25 mm are slightly narrower and rainstorms larger than 100 mm are heavier, with the four centers located in south-central Hubei, eastern Hubei, south-central Anhui, and northeastern Zhejiang. Overall, the rainfall band in LD04 is similar to that in KK00 and the main differences appear over magnitudes of 100 mm.
Figure 3 describes the probability distribution of the rain rate (RR) and the temporal evolution of the regionally averaged RR in the main rainfall region (29–32° N, 112–122° E) where the 24 h rainfall is great at approximately 10 mm and the regionally averaged values are computed in this region throughout this article. When the RR is below 18 mm h−1, both simulations slightly underestimate the RR and the LD04 simulation better matches the observations. However, when RR exceeds 18 mm h−1, both simulations overestimate the RR. It is notable that the rain magnitude still differs between the simulations. The temporal evolutions show that the observational RR strengthens from 1800 UTC on 4 July and then weakens after reaching its peak at 0200 UTC on 5 July. Results from the two simulations are similar to the observations; however, the results of the LD04 run are stronger than those of KK00 during most periods, especially in the weakening period after 0600 UTC on 5 July.
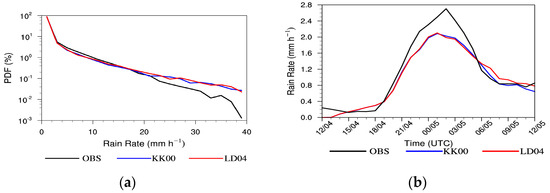
Figure 3.
(a) PDFs of the rain rate and (b) the temporal evolution of the regionally averaged rain rate from 1200 UTC on 4 July to 1200 UTC on 5 July 2020.
3.1.2. Evolution of Radar Composite Reflectivity
To help understand the life cycle of Meiyu front rainfall, Figure 4 shows the time sequence of the observed radar composite reflectivity distribution. At 1500 UTC on 4 July 2020, some echoes were spun up in northeastern Hubei and northeastern Hunan (marked as C1 and C2, respectively). The C1 echoes gradually gained strength but the C2 echoes weakened at 1800 UTC. Subsequently, some new convective echoes developed in southwestern Anhui and along the boundary between Anhui and Jiangsu (C3 and C4, respectively) at 2100 UTC. The three convective echoes (C1, C3, and C4) continued to strengthen and then organize in a quasi-linear fashion from 0000 to 0300 UTC on 5 July 2020. After that, the Meiyu frontal system gradually weakened.
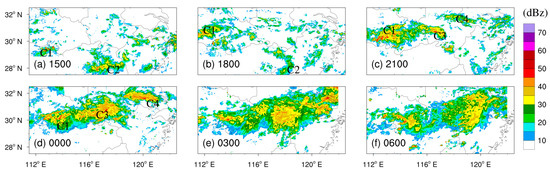
Figure 4.
The observed radar composite reflectivity distribution at (a) 1500 UTC on 4 July, (b) 1800 UTC on 4 July, (c) 2100 UTC on 4 July, (d) 0000 UTC on 5 July, (e) 0300 UTC on 5 July, (f) 0600 UTC on 5 July.
Although there are some differences in the intensities and locations of the radar composite reflectivity between the two simulations, the overall shapes are similar to one another; so, the outputs from the KK00 simulation were selected to be analyzed in Figure 5 (similar to those from the LD04 simulation). At 1500 UTC on 4 July, some convective echoes were initiated in central-eastern Hubei, the border region between Hunan and Zhejiang, and southern Anhui (marked with C1, C2, and C3, respectively). The C1 and C3 echoes developed eastward but the C2 echoes began to weaken at 1800 UTC. Compared with the observations in Figure 4, the simulated C3 echoes in southern Anhui were initialized so early that an excessive regionally averaged precipitation was produced during 1500 to 1800 UTC on 4 July (Figure 3b). After that, the simulated echoes gradually combined into a banded front similar to that in the observations; however, it is also obvious that they were narrower than observations resulting in less regionally averaged rainfall.
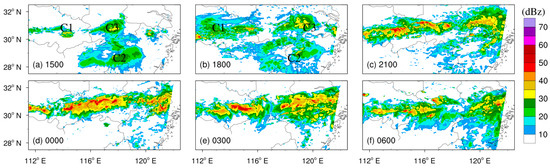
Figure 5.
The radar composite reflectivity distribution from KK00 simulation at (a) 1500 UTC on 4 July, (b) 1800 UTC on 4 July, (c) 2100 UTC on 4 July, (d) 0000 UTC on 5 July, (e) 0300 UTC on 5 July, (f) 0600 UTC on 5 July.
Overall, despite the overestimated rainfall intensity, the distribution of the rainfall, the evolution of the regionally averaged RR, and the distribution of the radar composite reflectivity in the simulations are consistent with the observations; so, the two simulations can reflect the quasi-linear Meiyu event well and can be used for subsequent analysis.
3.2. Autoconversion Analysis
The horizontal and vertical structures of the content of autoconversion are shown in Figure 6. Figure 6a shows that the distributions of the autoconversion content and precipitation are consistent (Figure 2), particularly in the area of maximum value. Obviously, the autoconversion content in the LD04 simulation is significantly larger than that in KK00, which indicates that more cloud droplets convert to raindrops in the LD04 parameterization.
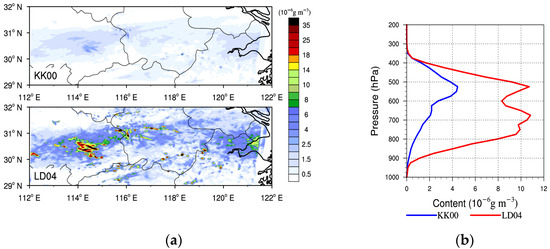
Figure 6.
(a) Simulated distribution of the 24 h accumulated, height-averaged content of autoconversion; (b) the vertical profile of the 24 h accumulated, regionally averaged content of autoconversion.
Figure 6b describes the vertical profile of the 24 h accumulated, regionally averaged content of autoconversion. The results indicate that the autoconversion process mainly occurs below 350 hPa. Another significant difference is that the KK00 parameterization simulates one peak level near 550 hPa with a value of 4.5 × 10−6 g m−3, while LD04 simulates two peaks at 550 hPa and 650 hPa with values of about 11 × 10−6 g m−3, which is two and a half times that of KK00. To verify whether this difference is related to different rainfall events, we conducted the same numerical simulations for two other Meiyu front events (figures not shown) and found that all the events produced the same results: the autoconversion content in the LD04 simulation is greater than that in KK00 and there are two peak levels in the LD04 simulation but only one in KK00. Therefore, we can conclude that the different settings in the autoconversion parameterizations result in these differences.
3.3. Evaluation of Stratiform–Convective Clouds
With the regime partitioning method described in Section 2.3, Figure 7 shows the temporal evolutions of the categorized grid numbers every five minutes.
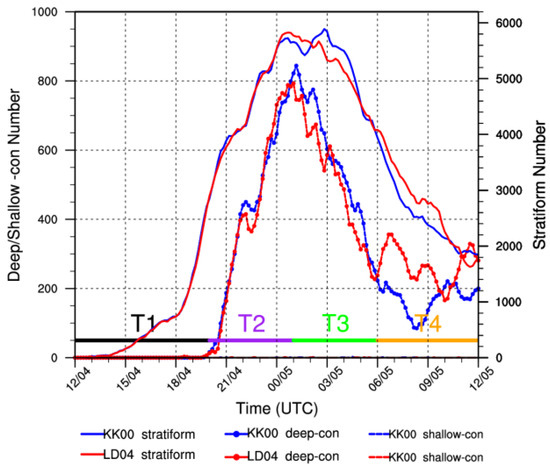
Figure 7.
Temporal evolutions of the stratiform and deep-convective grid numbers. “T1” is the startup stage from 1200 to 2000 UTC on 4 July, “T2” is the growth stage from 2000 UTC on 4 July to 0100 UTC on 5 July. “T3” is the dissipation stage from 0000 to 0600 UTC on 5 July, and “T4” is the redevelopment stage after 0600 UTC on 5 July.
To eliminate the statistical error caused by an inconsistent grid, any times with fewer than twenty grids are regarded as missing times (the total number of grids is 42,675 throughout the statistically analyzed region). It is clear that almost no shallow-convective grids are generated during the entire lifecycle; therefore, they are not analyzed in this paper. Morphologically, the evolution trends are in line with those of the RR (Figure 3b). The stratiform grid numbers between the two simulations are different in four stages: before 0000 UTC on 5 July, there is no significant difference; from 0000 to 0200 UTC on 5 July, the number of grids in LD04 exceeds that in KK00; from 0200 to 0600 UTC on 5 July, the number of grids in LD04 is less than that in KK00; then, the number of grids in LD04 is greater than that in KK00 after 0600 UTC on 5 July. The differences in the deep-convective numbers, similarly, have four stages, which are marked as T1–T4 in Figure 8. The eight hours (1200 to 2000 UTC on 4 July) after the WRF model is initialized are the initial spin-up stage, during which there are almost no deep-convective grids. The second stage from 2000 UTC on 4 July to 0100 UTC on 5 July is the growth stage, in which the convective echoes strengthen gradually and the deep-convective number increase rapidly; however, the difference between the two simulations is small. The third stage from 0000 to 0600 UTC on 5 July is the dissipation stage, in which the echoes weaken and the deep-convective grid number decreases, with that of the LD04 simulation being less than that of KK00. In the fourth stage after 0600 UTC on 5 July, depending on the new echoes in eastern Hubei, the weakened system redevelops to generate more deep-convective clouds, with the number of deep-convective grids in LD04 exceeding that of KK00.
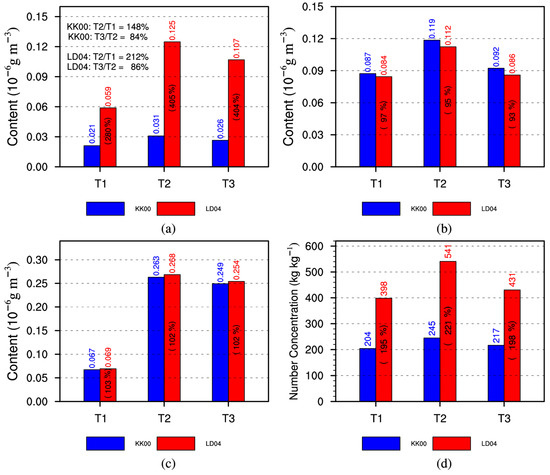
Figure 8.
Regionally and height-averaged hourly content of (a) ACR and the regionally, height-, and time-averaged (b) Lc, (c) Lr, and (d) Nr from T1 to T3 stages.
The strength of the deep-convective clouds is generally related to the strength of the MCS system. T1 to T3 clearly present the Meiyu front lifecycle. This paper later focuses on comparing the microphysical characteristics between the two simulations to analyze how the autoconversion process affects the rainfall on the ground.
3.4. Microphysical Analysis
3.4.1. Comparison of the Raindrop Budget from T1 to T3 Stages
The formula for the rain rate is in the numerical bulk microphysical scheme, where is the air density, is the content of the raindrop, and is the final falling speed of the raindrop. Thus, the change in raindrop content is highly correlated to the RR. In the Morrison scheme, seven types of source and sink terms of raindrop mixing ratio or content (Qr or Lr) are considered, including autoconversion of droplets to form raindrops (ACR, hereafter), accretion of droplets by raindrops (CLcr), melting of ice-phase particles (i.e., snow and graupel) to form raindrops (ML), evaporation of raindrops (VDrv), freezing of raindrops (FR), accretion of raindrops by ice-phase particles (CLri), and riming and splintering from accreted raindrops (RM), among which the first three terms are source terms and the last four terms are sink terms. On the other hand, four types of source and sink terms including Auto, self-collection or breakup of rain (CB), FR, and CLri increase the raindrop number concentration (Nr).
It is clear that the change in the ACR process will have a direct impact on the development of raindrops and cloud droplets, especially at the early stages of precipitation formation [22]. In addition, the formation of surface precipitation is the combined result of various microphysical processes and corresponding thermodynamic and dynamic processes; the change in a single microphysical process can have an indirect effect on other processes [36,38], and the complex interactive and influencing mechanisms between different microphysical processes remain a complication in current cloud microphysics research.
Figure 8 compares the regionally and height-averaged hourly ACR content and the regionally, height-, and time-averaged Lc, Lr, and Nr in the three stages.
Compared with the KK00 simulation, the ACR content in the LD04 simulation is greater in all stages so that the LD04 simulation always has a smaller regionally averaged Lc and a larger regionally averaged Lr and Nr. The ACR content in the LD04 simulation is 280% to 405% of that in KK00; Lc reduces to 93% to 97% of that in KK00; and Lr and Nr increase to 102% to 103% and 195% to 221%, respectively, so that ACR has a larger effect on Nc than Lc. Moreover, the ACR content in the two simulations gradually increases and then decreases, as the RR does (Figure 8a). At the T2 stage, ACR increases rapidly, and the ACR content in the KK00 (LD04) simulation increases to 148% (212%) of that in the T1 stage. In the T3 stage, however, ACR decreases slowly and the ACR content in the KK00 (LD04) simulation decreases to 84% (86%) of that in the T2 stage, which indicates that ACR more heavily influences raindrops in the growth stage. This is similar to the results of Li et al. [22], who found that ACR plays a major role in the early stages of warm-rain-cloud precipitation. However, given the results presented in Figure 7 and Figure 8, the impact of ACR on Meiyu frontal rainfall exists throughout the entire MCS evolution, not only in the early stage.
Figure 9 then compares the other budget terms and the sum of them between the two simulations.
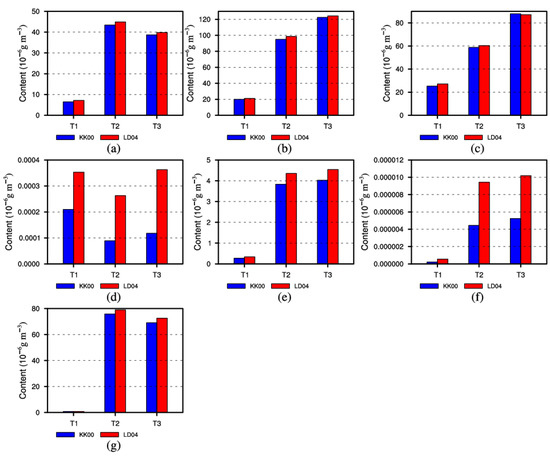
Figure 9.
Same as Figure 8a but for (a) CLcr, (b) ML, (c) VDrv, (d) FR, (e) CLri, (f) RM, and (g) total raindrop source and sink terms.
Four terms—CLcr, ML, VDrv, and CLri—contribute the most, ACR contributes a bit less (Figure 8a), and FR and RM contribute the least. Moreover, as the ACR in the LD04 simulation strengthens, more cloud droplets convert to raindrops; CLcr, ML, FR, CLri, and RM strengthen to different degrees; VDrv also strengthens in the T1 and T2 stages. Overall, the total budget content in the LD04 simulation is larger than that in KK00 (Figure 9g), which increases the raindrop content in LD04 relative to that in KK00.
Alongside the stages of startup, growth, and dissipation, the ACR and CLcr content tend to first increase and then weaken; however, ML, VDrv, CLri, and RM strengthen during the whole cycle of the rainfall. The continual reinforcement of VDrv may be caused by raindrops generated at the previous stage even though the growth of raindrops has slowed down. Further, the continual reinforcement of ML and CLri may be due to the continuous increasing of the ice-phase particles (Figure 10).
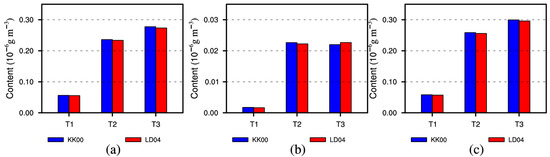
Figure 10.
Same as Figure 8b but for (a) snow, (b) graupel, and (c) total ice particles.
3.4.2. Comparison of Stratiform–Convective Microphysical Characteristics at the T2 Stage
The microphysical characteristics of stratiform and convective clouds in the Meiyu front heavy rainfall tend to be different. For a more detailed comparison, the microphysical characteristics in the growth stages (T2) when ACR content increases rapidly were compared.
Figure 11 shows the vertical profiles of the time- and regionally averaged ACR rate, Qc, Qr, and Nr. In stratiform clouds, the upper peak height of the ACR rate in LD04 and the only peak height in KK00 lie at 550 hPa, the peak value in LD04 is about three times that of KK00, and the lower peak height in LD04 lies at 700 hPa. In deep-convective clouds, the peak height of the ACR rate is at a higher altitude caused by the higher altitude that the updraft in the convective cloud reaches. The upper peak height of the ACR rate in LD04 and the only peak height in KK00 exist at 450–500 hPa, the peak value in LD04 is about 5.5 times that of KK00, and the lower peak height in LD04 lies at 800 hPa. Besides that, the Nr in the LD04 deep-convective clouds achieves two peaks as the ACR rate does; this may be because ACR influences the Nr more so the two-peak characteristic is reflected in the Nr of deep-convective clouds.
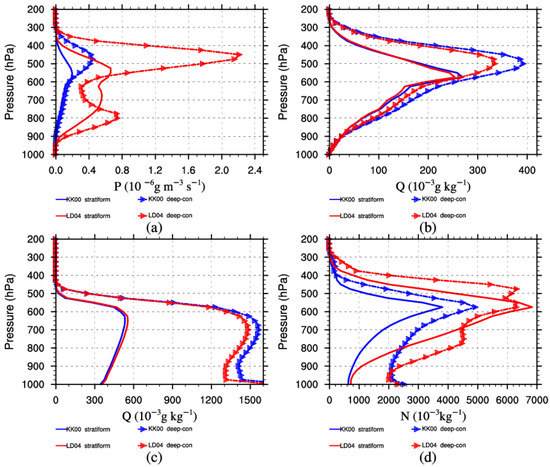
Figure 11.
Vertical profiles of the time- and regionally averaged (a) ACR rate, (b) Qc, (c) Qr, and (d) Nr at the T2 stage.
Figure 11 also indicates that most of the raindrops exist below 400 hPa. Qr in deep-convective clouds has a greater value but a lower peak height at 700 hPa compared with stratiform clouds at about 650 hPa. The previous analysis shows that more ACR content in the LD04 simulation leads to a smaller Lc and larger Lr and Nr in the entire regional average. However, after separating the clouds, it can be seen that a stronger ACR leads to a larger Qr in stratiform clouds but a smaller Qr in deep-convective clouds (Figure 11c). The reason for this fact will be analyzed next.
Since most of the raindrops exist below 400 hPa, we only consider the source and sink terms of raindrops below 400 hPa in this section. Figure 12 compares the vertical profiles of the time- and regionally averaged rates of the source and sink terms in the two regions at the T2 stage. It can be seen that budget terms at different levels play different roles in the growth of raindrops. Basically, from 400 hPa to 550 hPa, CLcr, ML, and CLri are the key processes in both stratiform and deep-convective clouds. However, below the melting level at about 550 hPa, CLcr, ML, and VDrv are the key processes. ML and CLcr contribute more and decrease towards the surface, and VDrv contributes less and changes less as the altitude decreases. In addition, the contribution of microphysical processes is also different between the stratiform and deep-convective clouds. In stratiform clouds, an ML with a maximum value of 1.7 × 10−3 g m−3 s−1 contributes more than a CLcr with a maximum value of 0.51 × 10−3 g m−3 s−1 from 500 hPa to 550 hPa; below 550 hPa, with the rapid decrease in ice-phase particles, ML clearly decreases until CLcr becomes the biggest source below 750 hPa (Figure 12a,c). In deep-convective clouds, the main budget terms increase more in stratiform clouds, especially CLcr, with a peak of 2.2 × 10−3 g m−3 s−1, which is about four times that in stratiform clouds; ML, however, increases less with a peak of 2.7 × 10−3 g m−3 s−1, which is about 1.6 times more than that in stratiform clouds. In other words, in deep-convective clouds, CLcr contributes more than ML to the growth of raindrops at most heights (Figure 12b,d).
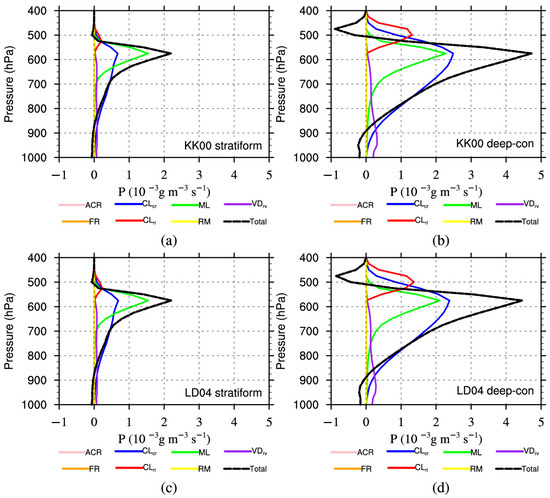
Figure 12.
Vertical profiles of the time- and regionally averaged rate of the raindrop source and sink terms in stratiform and deep-convective regions at the T2 period from (a) stratifrom clouds in KK00 simulation, (b) deep-convective clouds in KK00 simulation, (c) stratifrom clouds in LD04 simulation, (d) deep-convective clouds in LD04 simulation.
To further investigate the difference in raindrop budgets between the two simulations, Figure 13 exhibits the vertical profiles of the time- and regionally averaged rate differences between the two simulations.
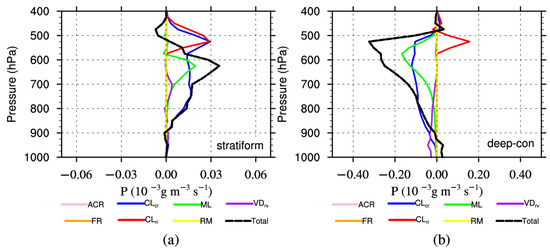
Figure 13.
Vertical profiles of time- and regionally averaged rate of the budget differences in (a) stratiform and (b) deep-convective regions at the T2 stage. “Total” refers to the summation of the seven terms.
The prefix “dif-” is used to represent the differences hereafter; for example, “dif-ACR” indicates the value of the ACR rate in LD04 minus the ACR rate in KK00. In stratiform clouds, from 400 to 550 hPa, the dif-Total rate is negative, and dif-CLcr and dif-CLri are the dominant terms; below 550 hPa, there are positive dif-CLcr, dif-ML, and dif-VDrv rates. The dif-CLcr rate in LD04 contributes the most at most altitudes, resulting in a positive dif-Total rate, meaning more raindrop production in the stratiform clouds compared with KK00, which are consistent with the regional average results (Figure 8c). In deep-convective clouds, dif-CLcr, dif-ML, dif-CLri, and dif-VDrv are still the dominant terms while the dif-Total rate is negative throughout the atmospheric column giving negative dif-CLcr, dif-ML, and dif-VDrv rates. This differs greatly from stratiform clouds. Furthermore, in deep-convective clouds, the dif-ML rate peak exists at about 550 hPa and is greater than the dif-CLri rate; however, below 550 hPa, dif-CLcr (especially) and dif-VDrv become the dominant terms. To sum up, the indirect influences on CLcr (especially), ML, and VDrv by ACR are different to the growth of raindrops in two regions. In deep-convective regions, the smaller CLcr, ML, and VDrv rates in the LD04 simulation compared with those in KK00 are the most critical factors in the smaller Qr.
3.4.3. Comparison of Precipitation at the T2 Stage
Figure 14 compares the distribution of the 5 h accumulated precipitation during the T2 stage. As in the 24 h accumulated precipitation distribution, the simulated 5 h rainfall is still overestimated. The maximum observed precipitation is 110.3 mm, while LD04 and KK00 simulations produce maximum precipitation values of 177.7 mm and 200.7 mm, respectively. The previous analysis indicates that ACR rate in the LD04 simulation is larger than that in the KK00 simulation. However, the former produces relatively better results. Rainfall centers are mainly the result of convective clouds; so, the microphysical processes in the deep-convective clouds play an important role therein. It is clear that the change in ACR indirectly influences other microphysical processes, especially CLcr, which tends to correct the budget terms so that the overestimated rainfall center better approaches the observations.
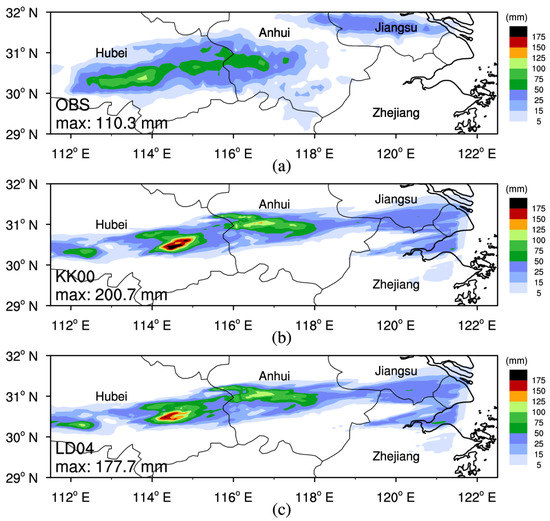
Figure 14.
Distribution of the 5 h accumulated precipitation during the T2 stage from the (a) OBS, (b) KK00 simulation, and (c) LD04 simulation.
4. Summary and Conclusions
Based on the WRF model, this paper analyzes the impact of ACR on a Meiyu rainfall event by comparing two numerical experiments with KK00 and LD04 parameterizations. For the characteristics of the mixed rainfall in the Meiyu frontal system, the Meiyu clouds are divided into stratiform and deep-convective clouds. The precipitation and microphysical characteristics of the two simulations are compared. The key outcomes of the study are highlighted below:
1. In terms of the accumulated precipitation distribution, the evolution of the regionally averaged RR, and the radar composite reflectivity distribution, the results from both simulations are essentially consistent with the observations. However, the simulations overestimate the rainfall intensity, especially in the rainfall centers. The precipitation difference between the two simulations is larger in the rainfall centers.
2. The ACR content in the LD04 simulation is significantly larger than that in KK00 and, in the vertical distribution, there are two maximum heights in the LD04 simulation but only one in KK00.
3. CLcr, ML, VDrv, and CLri are the dominant pathways to the growth of raindrops. Along with the development of the Meiyu system, the ACR and CLcr content tend to first increase and then weaken, but ML, VDrv, and CLri strengthen continuously. The reason for the continual reinforcement of VDrv may be because many cloud droplets still exist that were generated in the previous stage, although the growth of raindrops slowed down, and the reason for the continual reinforcement of ML and CLri may be because the ice-phase particles continue to increase.
4. Changes in a microphysical process will indirectly affect other associated microphysical particles and processes in some way. With stronger ACR compared with the KK00 parameterization, the LD04 parameterization simulates a smaller Lc but a bigger Lr and Nr in the regional and height averages. Further, the effect of ACR on Nr is greater than it is on Lr. In the LD04 simulation, CLcr, ML, and CLri strengthen to some degree and VDrv strengthens in most stages.
5. After the clouds are divided by category, limited distributional differences can be found in both the deep-convective clouds and stratiform clouds between the two simulations during the growth stage of the Meiyu event. Compared with KK00, LD04 simulates narrower deep-convective clouds in the decaying stage.
6. In the growth stage, a stronger ACR process in the LD04 simulation than in the KK00 simulation, results in a smaller (bigger) Qc (Qr) in stratiform clouds but both smaller Qc and Qr in deep-convective clouds. The influences on CLcr (especially), ML, and VDrv caused by ACR indirectly vary in the two regions and, finally, lead to the different influences on raindrop growth. A decrease in CLcr, ML, and VDrv, caused by an increase in ACR, leads to less raindrop production in the LD04 deep-convective clouds, thereby correcting the overestimated rainfall center to better match the observations. In addition, compared with stratiform clouds, the four main raindrop source and sink terms strengthen in deep-convective clouds, especially CLcr.
This paper focuses on the influence of the autoconversion process on mixed clouds’ rainfall via budget analysis of hydrometeors. However, there are still some deficiencies. Precipitation is the comprehensive result of various microphysical, dynamic, and thermodynamic processes, and the microphysical processes also have feedback effects on the dynamic and thermodynamic processes. Due to the limited length of the manuscript, the dynamic and thermodynamic processes were not discussed. In addition, the comparisons were mainly carried out in a regionally averaged or cumulative manner, which may ignore some details. Due to the lack of observations, the simulated microphysical characteristics cannot be compared. In our follow-up work, a more comprehensive analysis will be conducted by utilizing more observational data.
Author Contributions
Conceptualization, Z.K. and Z.Z.; methodology, Z.K.; software, Y.S.; validation, Z.K. and Z.Z.; formal analysis, Y.S.; investigation, Y.H.; data curation, D.H.; writing—original draft preparation, Z.K.; funding acquisition, Y.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (42230612 and 41905071) Science and Technology Funds (2023Y04, 2022Y05, 2021Y05, 2023Y19); the Key projects (2020Q02) of Hubei Meteorological Bureau; and the Joint Open Project of KLME and CIC-FEMD, NUIST (grant number KLME202211).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The precipitation data used in this study were provided by the China Meteorological Administration. The ERA5 reanalysis data used were obtained from European Center for Medium-Range Weather Forecasts (https://cds.climate.copernicus.eu/cdsapp#!/search?text=era5 (accessed on 1 September 2021)). The weather radar data used are available from the corresponding author upon request.
Acknowledgments
The first author is grateful for the support from Guirong Xu and Wen Zhou.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kumar, S.; Hazra, A.; Goswami, B.N. Role of interaction between dynamics, thermodynamics and cloud microphysics on summer monsoon precipitating clouds over the Myanmar Coast and the Western Ghats. Clim. Dyn. 2014, 43, 911–924. [Google Scholar] [CrossRef]
- Thomas, B.; Viswanadhapalli, Y.; Srinivas, C.V.; Dasari, H.P.; Attada, R.; Langodan, S. Cloud resolving simulation of extremely heavy rainfall event over Kerala in August 2018—Sensitivity to microphysics and aerosol feedback. Atmos. Res. 2021, 258, 105613. [Google Scholar] [CrossRef]
- Mohan, P.R.; Srinivas, C.V.; Yesubabu, V.; Baskaran, R.; Venkatraman, B. Simulation of a heavy rainfall event over Chennai in Southeast India using WRF: Sensitivity to microphysics parameterization. Atmos. Res. 2018, 210, 83–99. [Google Scholar] [CrossRef]
- Bao, J.W.; Michelson, S.A.; Grell, E.D. Microphysical process comparison of three microphysics parameterization schemes in the WRF Model for an idealized squall-line case study. Mon. Weather Rev. 2019, 147, 3093–3120. [Google Scholar] [CrossRef]
- Zhou, Z.M.; Deng, Y.; Hu, Y.; Kang, Z.P. Simulating heavy meiyu rainfall: A note on the choice of the model microphysics scheme. Adv. Meteorol. 2020, 2020, 8827071. [Google Scholar] [CrossRef]
- Guo, H.; Liu, Y.; Penner, J.E. Does the threshold representation associated with the autoconversion process matter? Atmos. Chem. Phys. 2008, 8, 1225–1230. [Google Scholar] [CrossRef]
- Liu, Y.G.; Daum, P.H.; McGraw, R. An analytical expression for predicting the critical radius in the autoconversion parameterization. Geophys. Res. Lett. 2004, 31, 6. [Google Scholar] [CrossRef]
- Rotstayn, L.D. On the “tuning” of autoconversion parameterizations in climate models. J. Geophys. Res. Atmos. 2000, 105, 15495–15507. [Google Scholar] [CrossRef]
- Michibata, T.; Takemura, T. Evaluation of autoconversion schemes in a single model framework with satellite observations. J. Geophys. Res. Atmos. 2015, 120, 9570–9590. [Google Scholar] [CrossRef]
- Jing, X.W.; Suzuki, K.; Guo, H.; Goto, D.; Ogura, T.; Koshiro, T.; Mülmenstädt, J. A multimodel study on warm precipitation biases in global models compared to satellite observations. J. Geophys. Res. Atmos. 2017, 122, 11–806. [Google Scholar] [CrossRef]
- Kessler, E. On the distribution and continuity of water substance in atmospheric circulations. In On the Distribution and Continuity of Water Substance in Atmospheric Circulations; Kessler, E., Ed.; Meteorological Monographs; American Meteorological Society: Boston, MA, USA, 1969; pp. 1–84. [Google Scholar]
- Hu, Z.J.; Cai, L. A parameterized numerical simulation of warm rain and salt-seeding in cumulus clouds. Sci. Atmos. Sin. 1979, 3, 334–342. (In Chinese) [Google Scholar]
- Manton, M.J.; Cotton, W.R. Formulation of Approximate Equations for Modeling Moist Deep Convection on the Mesoscale; Atmospheric Science Paper 266; Colorado State University: Fort Collins, CO, USA, 1977; 62p. [Google Scholar]
- Sundqvist, H. A parameterization scheme for non-convective condensation including prediction of cloud water content. Q. J. R. Meteorol. Soc. 1978, 104, 677–690. [Google Scholar] [CrossRef]
- Ziegler, C.L. Retrieval of thermal and microphysical variables in observed convective storms. Part 1: Model development and preliminary testing. J. Atmos. Sci. 1985, 42, 1487–1509. [Google Scholar] [CrossRef]
- Khairoutdinov, M.; Kogan, Y. A new cloud physics parameterization in a large-eddy simulation model of marine stratocumulus. Mon. Weather Rev. 2000, 128, 229–243. [Google Scholar] [CrossRef]
- Morrison, H.C.; Curry, J.A.; Khvorostyanov, V.I. A new double-moment microphysics parameterization for application in cloud and climate models. Part I: Description. J. Atmos. Sci. 2005, 62, 1665–1677. [Google Scholar] [CrossRef]
- Berry, E.X. Modification of the Warm Rain Process. In Proceedings of the First National Conference on Weather Modification, Albany, NY, USA, 28 April–1 May 1968. [Google Scholar]
- Orville, H.D.; Kopp, F.J. Numerical simulation of the life history of a hailstorm. J. Atmos. Sci. 1977, 34, 1596–1618. [Google Scholar] [CrossRef]
- Liu, Y.G.; Daum, P.H. Parameterization of the autoconversion process. Part I: Analytical formulation of the Kessler-type parameterizations. J. Atmos. Sci. 2004, 61, 1539–1548. [Google Scholar] [CrossRef]
- Liu, Y.G.; Daum, P.H.; McGraw, R.L.; Wood, R. Parameterization of the autoconversion process. Part II: Generalization of Sundqvist-type parameterizations. J. Atmos. Sci. 2006, 63, 1103–1109. [Google Scholar] [CrossRef]
- Li, G.C.; Xu, H.Y. The studies of autoconversion rate form cloud water to hydrometeor water in the rain forming process of warm cumulus cloud. Acta Meteorol. Sin. 1988, 3, 376–380. (In Chinese) [Google Scholar]
- Xie, X.N.; Liu, X.D. Effects of spectral dispersion on clouds and precipitation in mesoscale convective systems. J. Geophys. Res. Atmos. 2011, 116, D06202. [Google Scholar] [CrossRef]
- Xie, X.N.; Liu, X.D. Analytical studies of the cloud droplet spectral dispersion influence on the first indirect aerosol effect. Adv. Atmos. Sci. 2013, 30, 1313–1319. [Google Scholar] [CrossRef]
- Jing, X.W.; Suzuki, K. The impact of process-based warm rain constraints on the aerosol indirect effect. Geophys. Res. Lett. 2018, 45, 10–729. [Google Scholar] [CrossRef]
- Jing, X.W.; Suzuki, K.; Michibata, T. The key role of warm rain parameterization in determining the aerosol indirect effect in a global climate model. J. Clim. 2019, 32, 4409–4430. [Google Scholar] [CrossRef]
- Xie, X.N.; Liu, X.D. Aerosol-cloud-precipitation interactions in WRF model: Sensitivity to autoconversion parameterization. J. Meteorol. Res. 2015, 29, 72–81. [Google Scholar] [CrossRef]
- Zhu, S.C.; Yuan, Y.; Wu, Y.; Zhang, Y. Cloud vertical structure of stratiform clouds with embedded convections occurring in the Mei-Yu Front. Atmosphere 2022, 13, 1088. [Google Scholar] [CrossRef]
- Luo, Y.L.; Gong, Y.; Zhang, D.L.D. Initiation and organizational modes of an extreme-rain-producing mesoscale convective system along a mei-yu front in East China. Mon. Weather Rev. 2014, 142, 203–221. [Google Scholar] [CrossRef]
- Ding, Y.H. The major advances and development process of the theory of heavy rainfalls in China. Torr. Rain Dis 2019, 38, 395–406. (In Chinese) [Google Scholar]
- Luo, Y.L.; Wang, Y.J.; Wang, H.Y.; Zheng, Y.J.; Morrison, H. Modeling convective-stratiform precipitation processes on a Mei-Yu front with the Weather Research and Forecasting model: Comparison with observations and sensitivity to cloud microphysics parameterizations. J. Geophys. Res. Atmos. 2010, 115, D18117. [Google Scholar] [CrossRef]
- Liu, L.; Lin, C.Z.; Bai, Y.Q.; He, D.X. Assessing the effects of microphysical scheme on convective and stratiform characteristics in a mei-yu rainfall combining WRF simulation and field campaign observations. Adv. Meteorol. 2020, 2020, 8231320. [Google Scholar] [CrossRef]
- Yang, J.; Zhao, K.; Zheng, Y.Y.; Chen, H.N.; Chen, G. Microphysical Structure of Thunderstorms and Their Lightning Activity During the mei-yu and Post-mei-yu Periods Over Nanjing, Yangtze River Delta. Geophys. Res. Lett. 2022, 49, e2022GL100952. [Google Scholar] [CrossRef]
- Morrison, H.; Thompson, G.; Tatarskii, V. Impact of cloud microphysics on the development of trailing stratiform precipitation in a simulated squall line: Comparison of one-and two-moment schemes. Mon. Weather Rev. 2009, 137, 991–1007. [Google Scholar] [CrossRef]
- Griffin, B.M.; Larson, V.E. Analytic upscaling of a local microphysics scheme. Part II: Simulations. Q. J. Roy. Meteor. Soc. 2013, 139, 58–69. [Google Scholar] [CrossRef]
- Yin, J.F.; Liang, X.D.; Wang, H.; Xue, H.L. Representation of the autoconversion from cloud to rain using a weighted ensemble approach: A case study using WRF v4. 1.3. Geosci. Model Dev. 2022, 15, 771–786. [Google Scholar] [CrossRef]
- McGraw, R.; Liu, Y.G. Kinetic potential and barrier crossing: A model for warm cloud drizzle formation. Phys. Rev. Lett. 2003, 90, 018501. [Google Scholar] [CrossRef]
- Beydoun, H.; Caldwell, P.M.; Stein, E.V.; Wharton, S. Tracing the rain formation pathways in numerical simulations of deep convection. J. Adv. Model. Earth Syst. 2023, 15, e2022MS003413. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).