Evaluation of PBL Parameterization Schemes in WRF Model Predictions during the Dry Season of the Central Amazon Basin
Abstract
1. Introduction
2. Materials and Methods
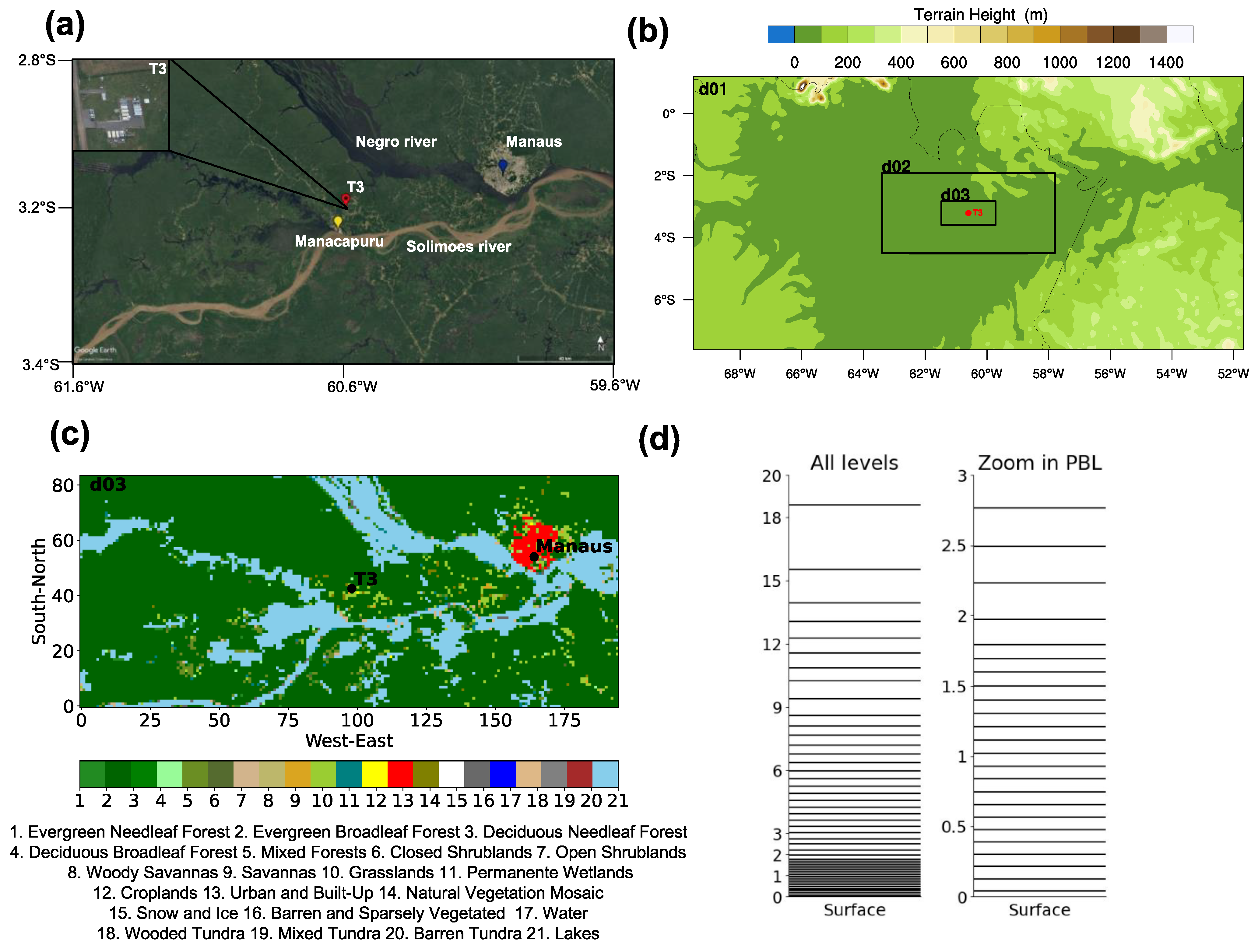
2.1. Study Area and Observational Data
2.2. Numerical Modeling Design
2.3. Evaluated PBL Schemes
2.4. Evaluation Metrics
3. Results
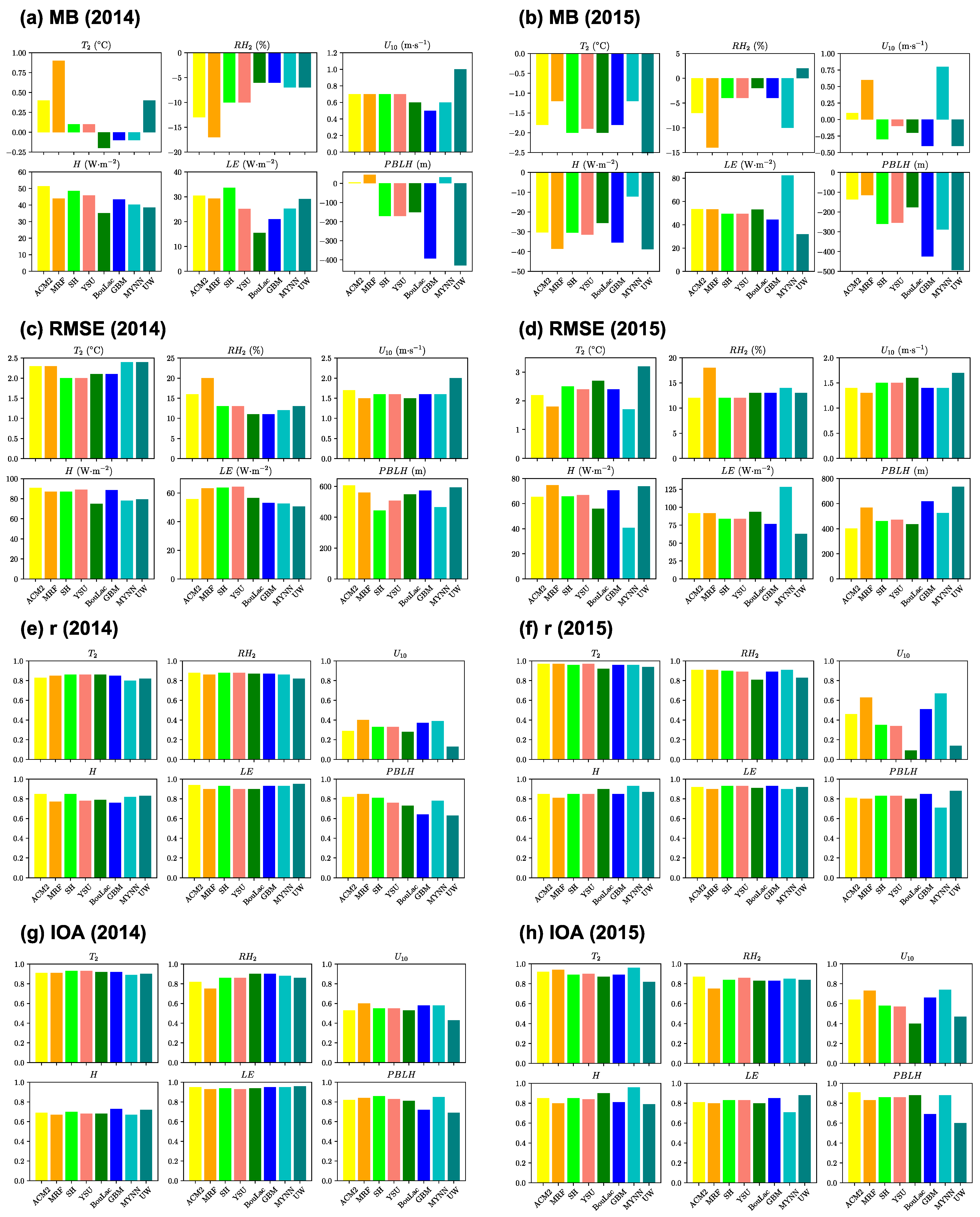
3.1. Comparison of Predicted and Observed Meteorological Variables
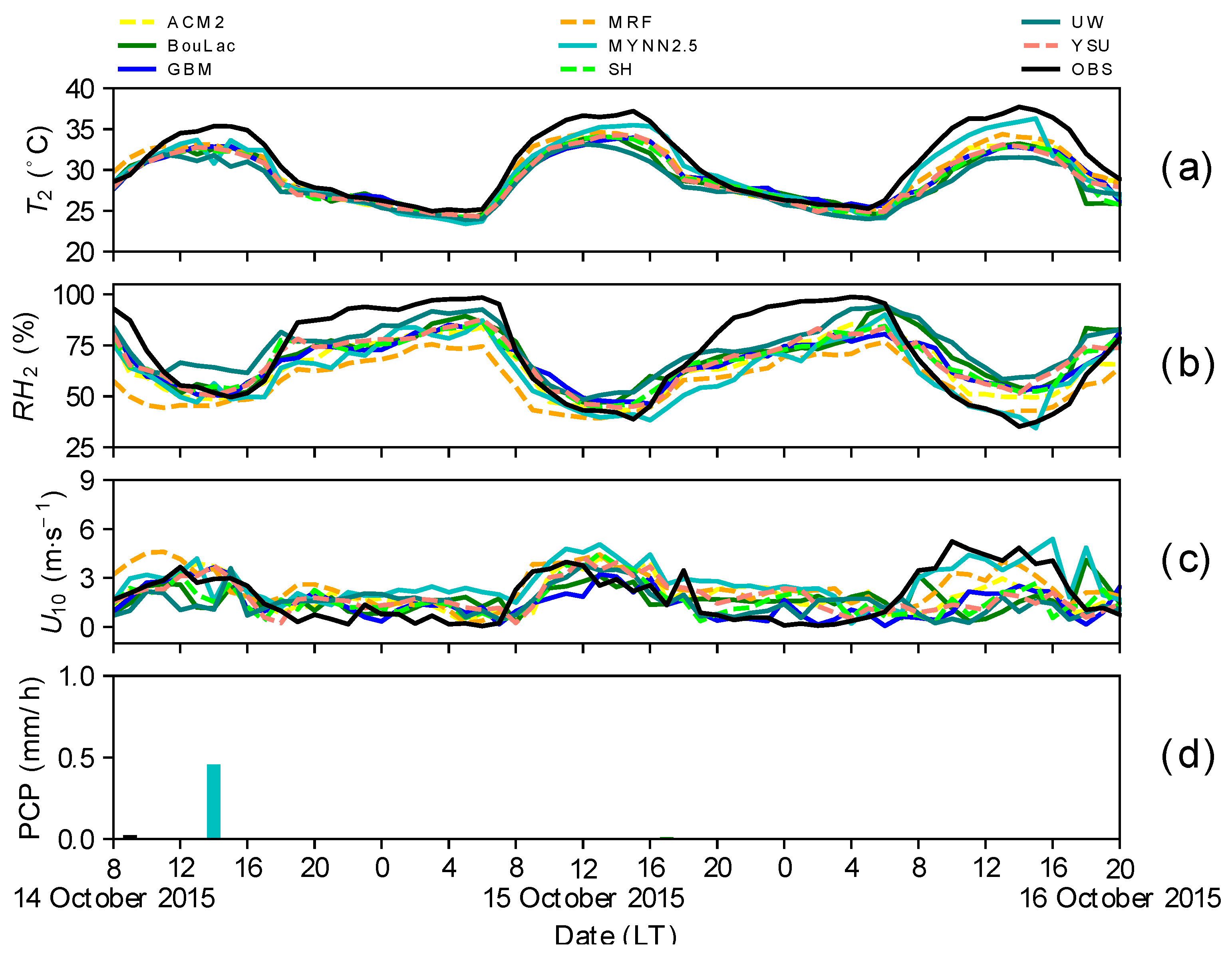
3.1.1. 2014 Dry Period
3.1.2. 2015 Dry Period
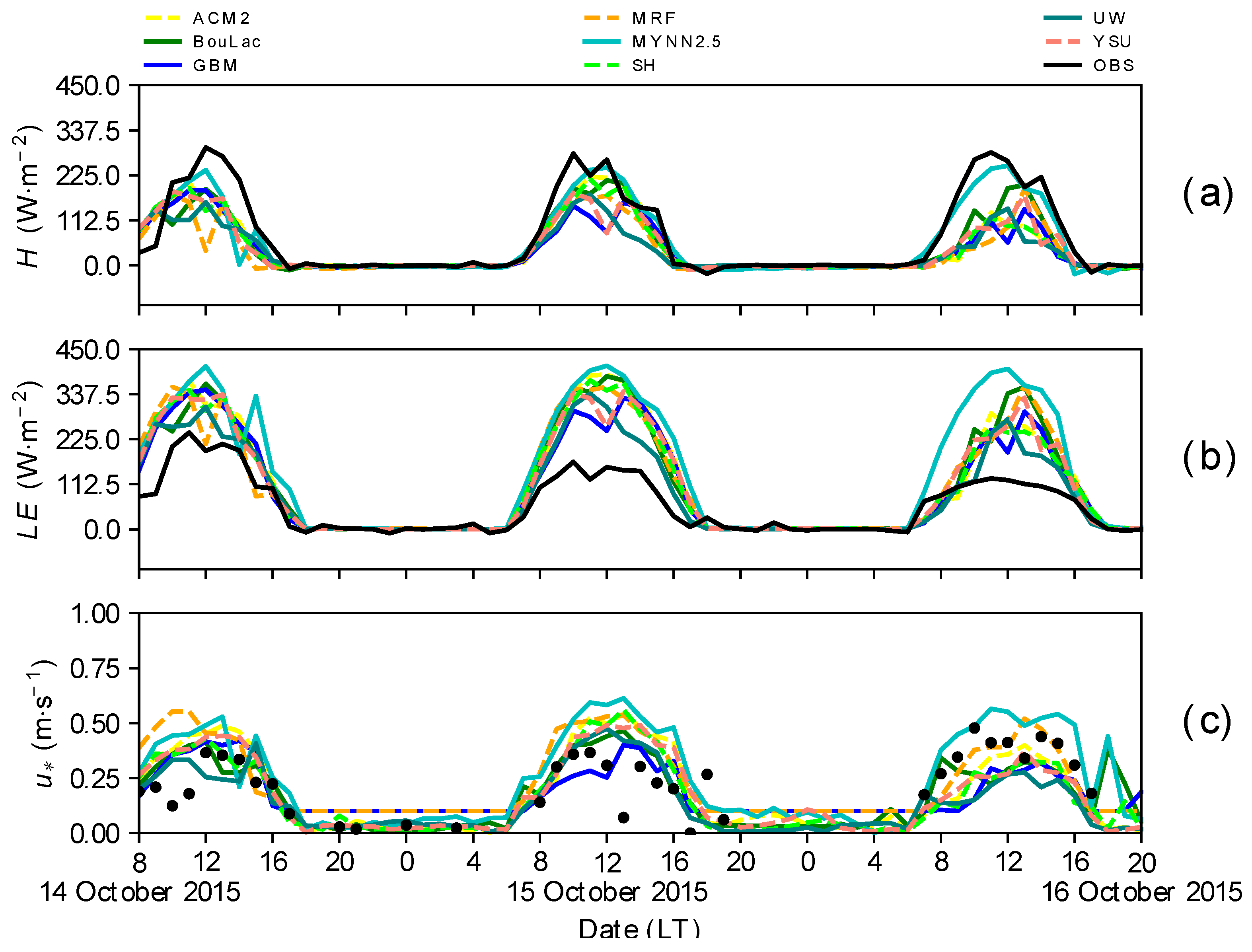
3.2. Comparison of Predicted and Observed Surface Turbulent Fluxes
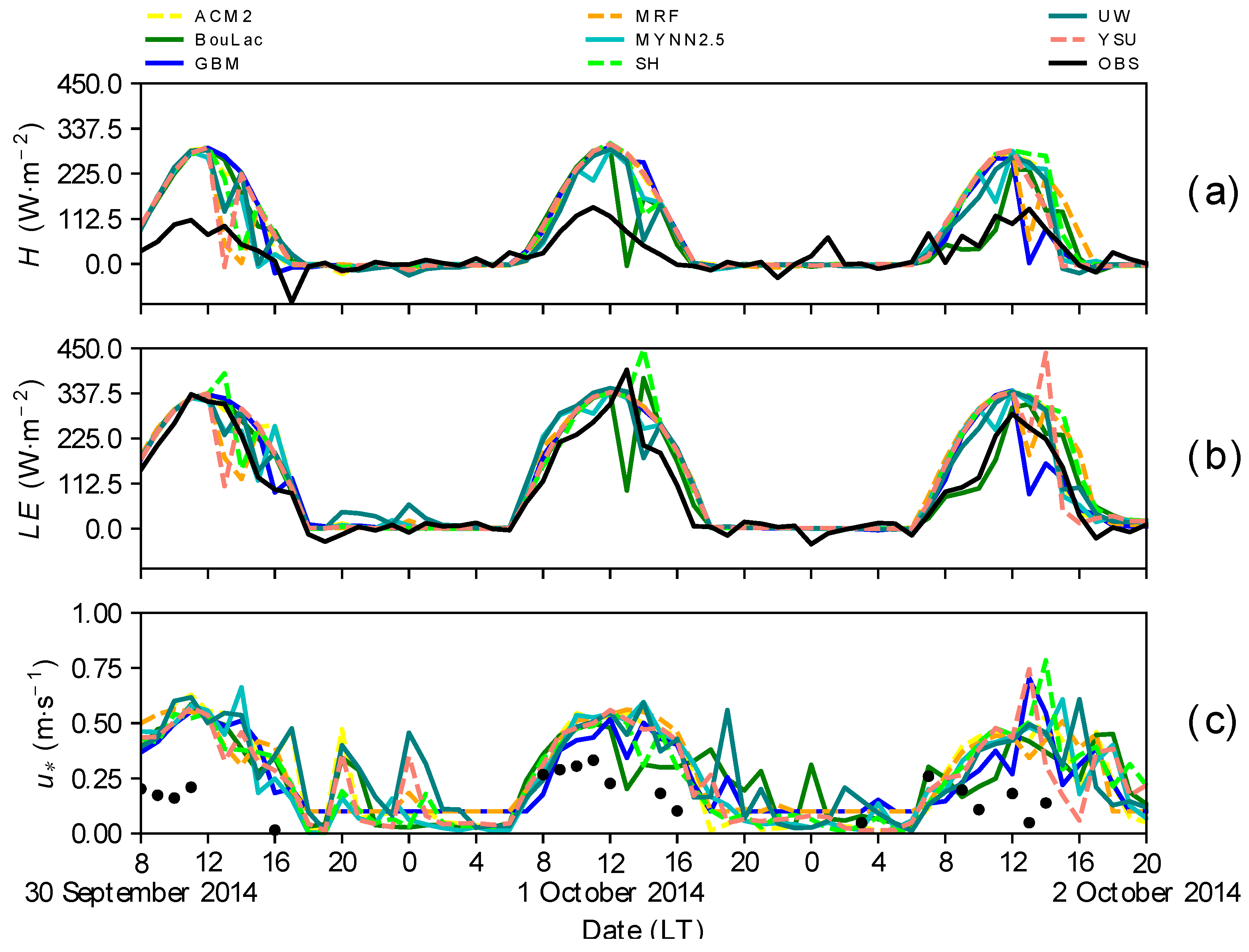
3.2.1. 2014 Dry Period
3.2.2. 2015 Dry Period
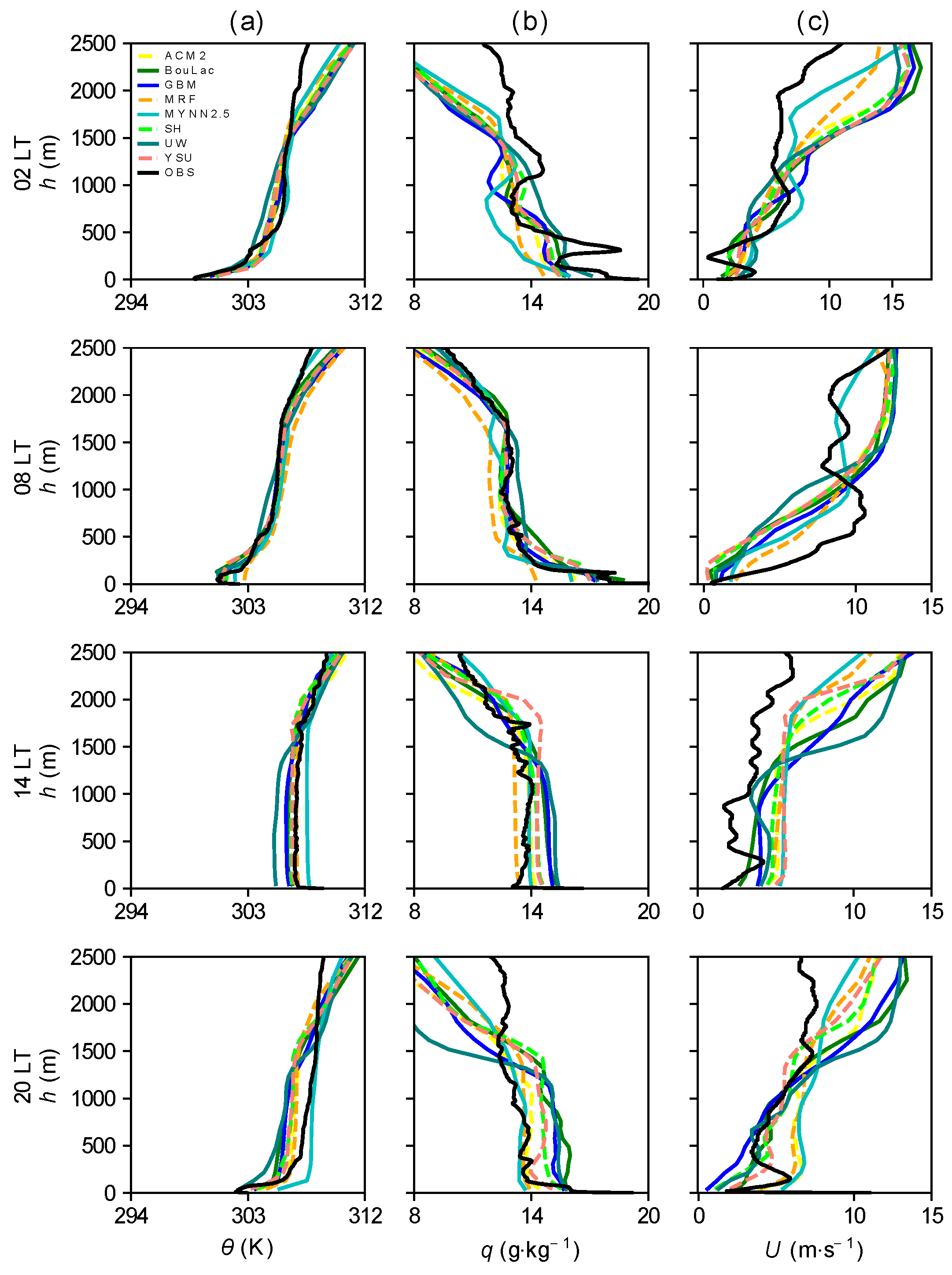
3.3. Comparison of Predicted and Observed PBL Structures
3.3.1. 2014 Dry Period
3.3.2. 2015 Dry Period
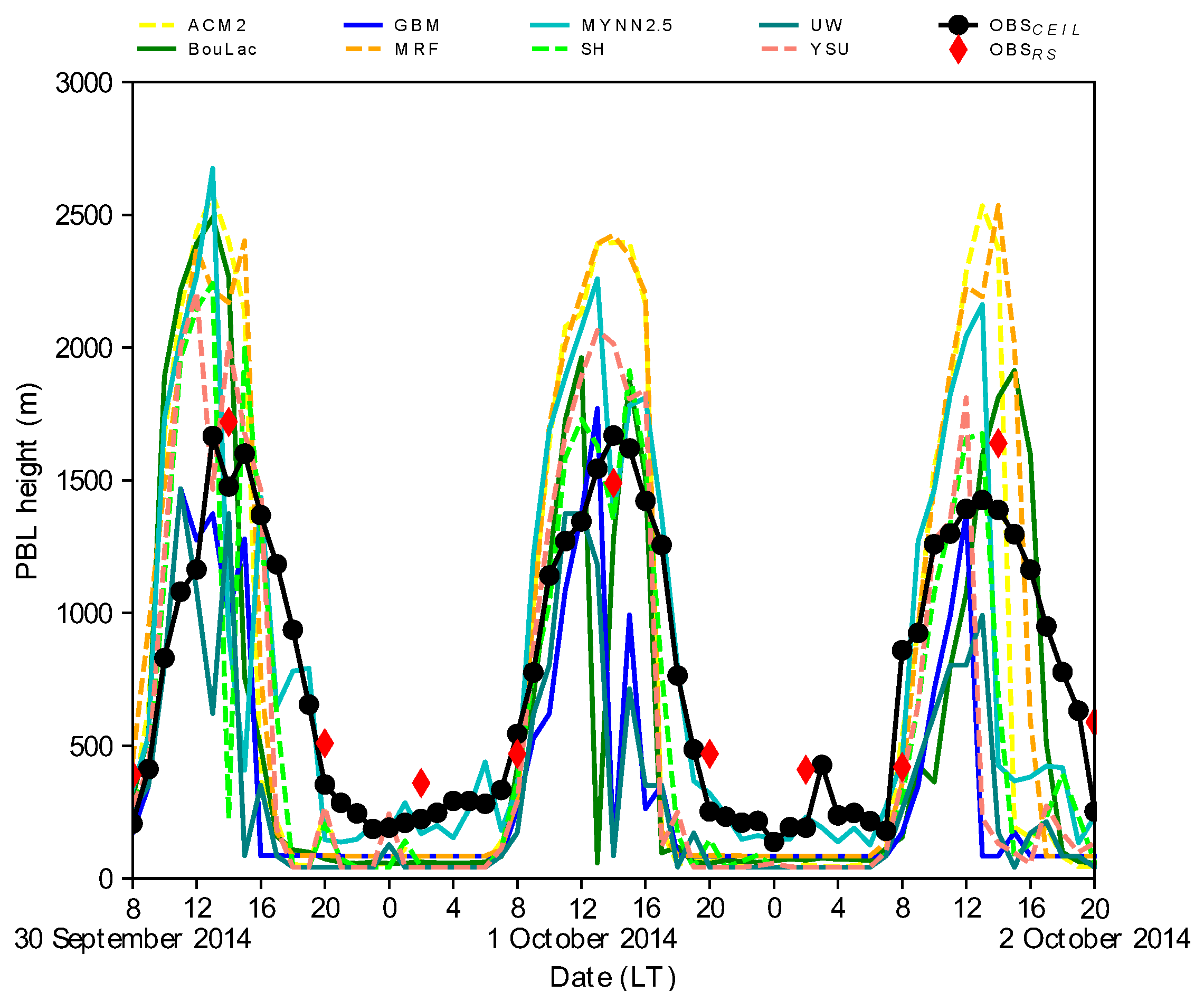
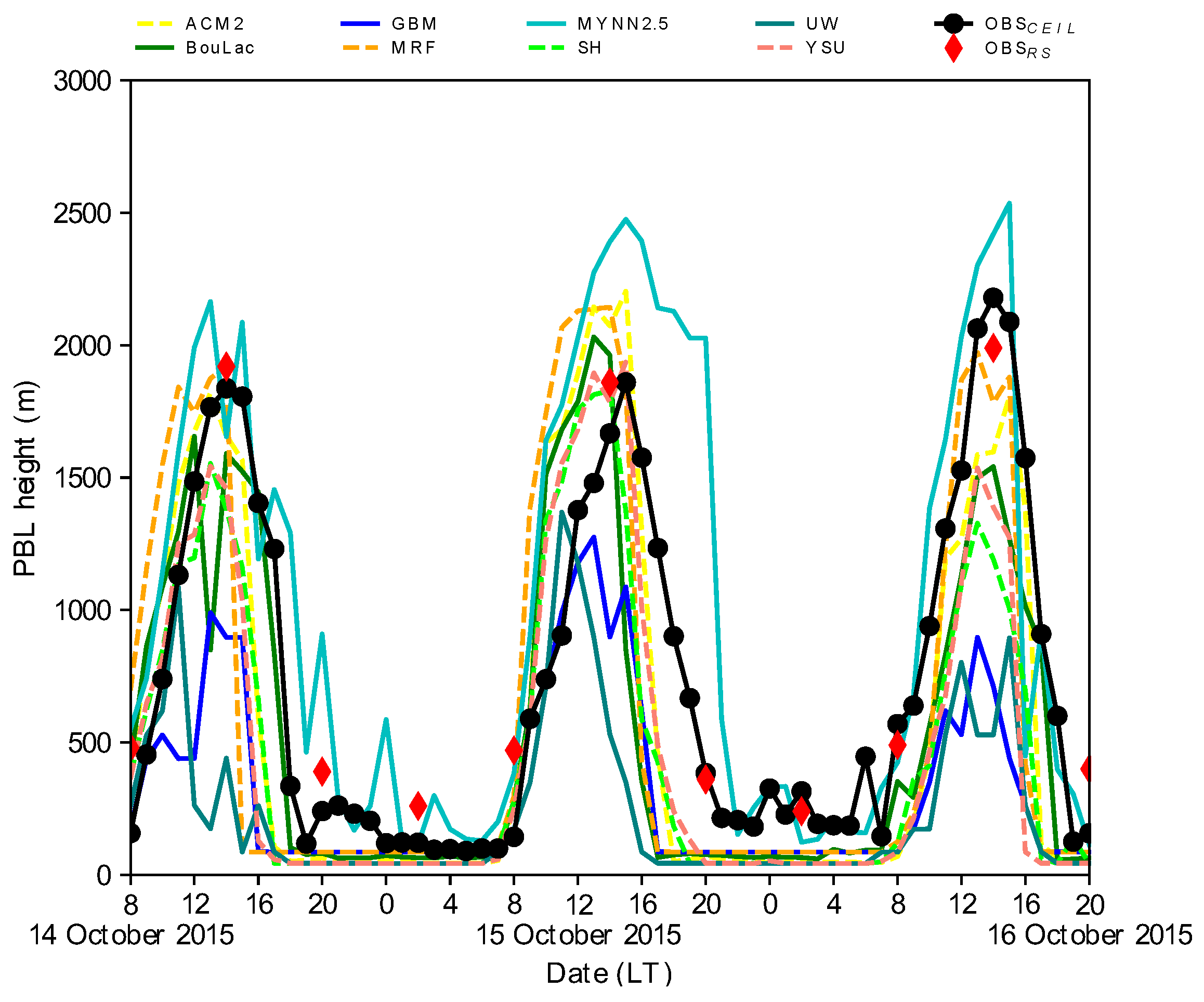
3.4. Comparison of Predicted and Observed PBL Heights
3.4.1. Diurnal Variations of PBL Height
2014 Dry Period
2015 Dry Period
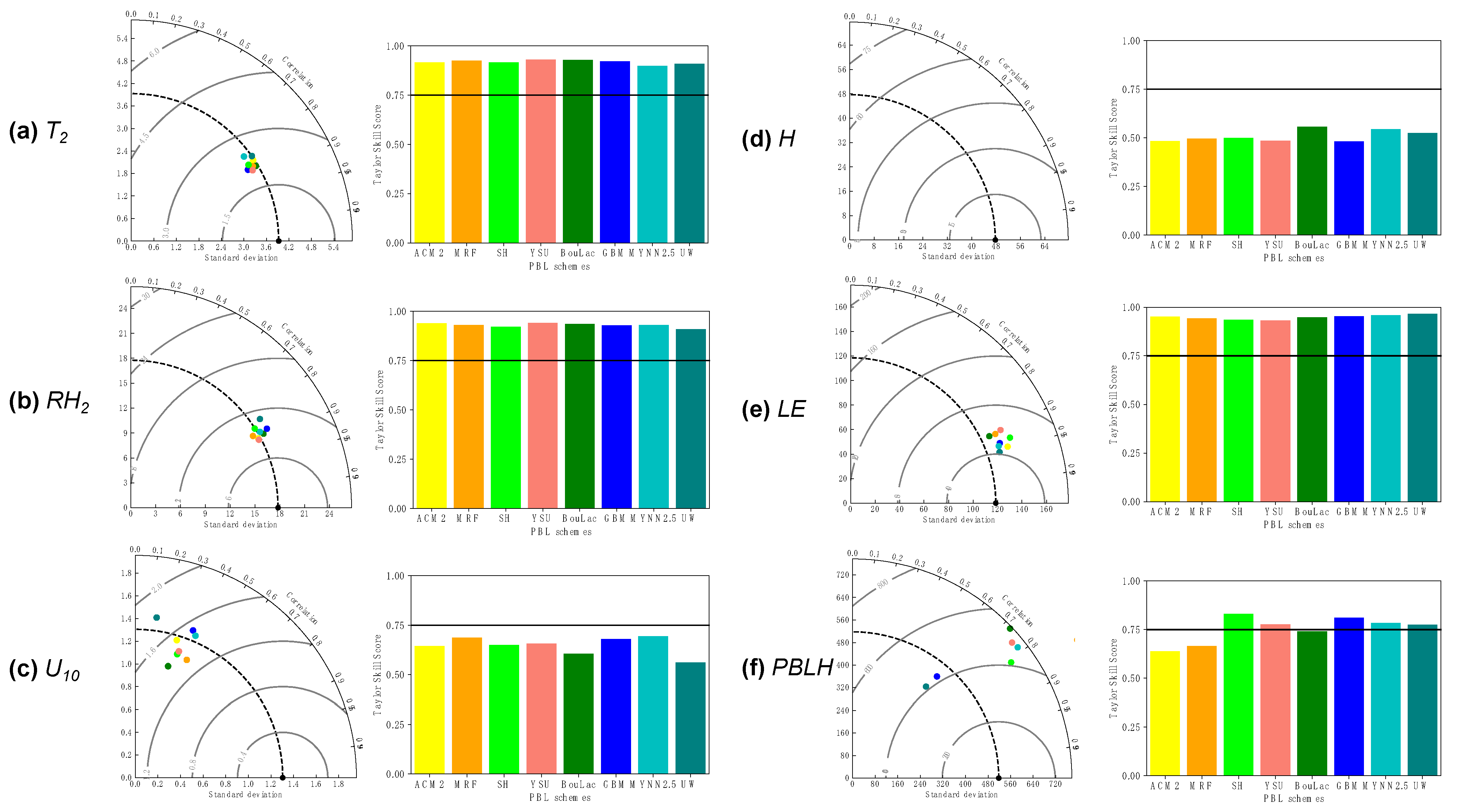
3.5. Performance Analysis
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Soares, P.M.M.; Miranda, P.M.A.; Siebesma, A.P.; Teixeira, J. An eddy-diffusivity/mass-flux parametrization for dry and shallow cumulus convection. Q. J. R. Meteorol. Soc. 2004, 130, 3365–3383. [Google Scholar] [CrossRef]
- Hu, X.-M.; Nielsen-Gammon, J.W.; Zhang, F. Evaluation of Three Planetary Boundary Layer Schemes in the WRF Model. J. Appl. Meteorol. Clim. 2010, 49, 1831–1844. [Google Scholar] [CrossRef]
- Zhang, X. Subgrid Turbulence Mixing. In Uncertainties in Numerical Weather Prediction, 1st ed.; Olafsson, H., Bao, J.-W., Eds.; Elsevier: Amsterdam, The Netherlands, 2021; pp. 205–227. [Google Scholar] [CrossRef]
- de Lange, A.; Naidoo, M.; Garland, R.M.; Dyson, L.L. Sensitivity of meteorological variables on planetary boundary layer parameterization schemes in the WRF-ARW model. Atmos. Res. 2020, 247, 105214. [Google Scholar] [CrossRef]
- Njuki, S.M.; Mannaerts, C.M.; Su, Z. Influence of Planetary Boundary Layer (PBL) Parameterizations in the Weather Research and Forecasting (WRF) Model on the Retrieval of Surface Meteorological Variables over the Kenyan Highlands. Atmosphere 2022, 13, 169. [Google Scholar] [CrossRef]
- de Lange, A.; Naidoo, M.; Garland, R.M.; Dyson, L.L. The sensitivity of simulated surface-level pollution concentrations to WRF-ARW-model PBL parameterisation schemes over the Highveld of South Africa. Atmos. Res. 2021, 254, 105517. [Google Scholar] [CrossRef]
- Yang, J.; Tang, Y.; Han, S.; Liu, J.; Yang, X.; Hao, J. Evaluation and improvement study of the Planetary Boundary-Layer schemes during a high PM2.5 episode in a core city of BTH region, China. Sci. Total Environ. 2020, 765, 142756. [Google Scholar] [CrossRef]
- He, J.; Chen, D.; Gu, Y.; Jia, H.; Zhong, K.; Kang, Y. Evaluation of planetary boundary layer schemes in WRF model for simulating sea-land breeze in Shanghai, China. Atmospheric Res. 2022, 278, 106337. [Google Scholar] [CrossRef]
- Louis, J.-F. A parametric model of vertical eddy fluxes in the atmosphere. Bound.-Layer Meteorol. 1979, 17, 187–202. [Google Scholar] [CrossRef]
- Mellor, G.L.; Yamada, T. Development of a turbulence closure model for geophysical fluid problems. Rev. Geophys. 1982, 20, 851–875. [Google Scholar] [CrossRef]
- Troen, I.B.; Mahrt, L. A simple model of the atmospheric boundary layer; sensitivity to surface evaporation. Bound.-Layer Meteorol. 1986, 37, 129–148. [Google Scholar] [CrossRef]
- Hong, S.Y.; Pan, H.L. Nonlocal boundary layer vertical diffusion in a medium-range forecast model. Mon. Weather Rev. 1996, 124, 2322–2339. [Google Scholar] [CrossRef]
- Sukoriansky, S.; Galperin, B.; Perov, V. Application of a New Spectral Theory of Stably Stratified Turbulence to the Atmospheric Boundary Layer over Sea Ice. Bound.-Layer Meteorol. 2005, 117, 231–257. [Google Scholar] [CrossRef]
- Pleim, J.E. A Combined Local and Nonlocal Closure Model for the Atmospheric Boundary Layer. Part I: Model Description and Testing. J. Appl. Meteorol. Climatol. 2007, 46, 1383–1395. [Google Scholar] [CrossRef]
- Angevine, W.M.; Jiang, H.; Mauritsen, T. Performance of an eddy diffusivity–mass flux scheme for shallow cumulus boundary layers. Mon. Weather Rev. 2010, 138, 2895–2912. [Google Scholar] [CrossRef]
- Shin, H.H.; Hong, S.-Y. Representation of the Subgrid-Scale Turbulent Transport in Convective Boundary Layers at Gray-Zone Resolutions. Mon. Weather Rev. 2015, 143, 250–271. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, Y.; Xue, M. Evaluation of an E–ε and Three Other Boundary Layer Parameterization Schemes in the WRF Model over the Southeast Pacific and the Southern Great Plains. Mon. Weather Rev. 2020, 148, 1121–1145. [Google Scholar] [CrossRef]
- Cohen, A.E.; Cavallo, S.M.; Coniglio, M.C.; Brooks, H.E. A Review of Planetary Boundary Layer Parameterization Schemes and Their Sensitivity in Simulating Southeastern U.S. Cold Season Severe Weather Environments. Weather Forecast. 2015, 30, 591–612. [Google Scholar] [CrossRef]
- Shin, H.H.; Hong, S.-Y. Intercomparison of Planetary Boundary-Layer Parametrizations in the WRF Model for a Single Day from CASES-99. Bound.-Layer Meteorol. 2011, 139, 261–281. [Google Scholar] [CrossRef]
- Wang, W.; Shen, X.; Huang, W. A Comparison of Boundary-Layer Characteristics Simulated Using Different Parametrization Schemes. Bound.-Layer Meteorol. 2016, 161, 375–403. [Google Scholar] [CrossRef]
- Moya-Álvarez, A.S.; Estevan, R.; Kumar, S.; Rojas, J.L.F.; Ticse, J.J.; Martínez-Castro, D.; Silva, Y. Influence of PBL parameterization schemes in WRF_ARW model on short—Range precipitation’s forecasts in the complex orography of Peruvian Central Andes. Atmos. Res. 2020, 233, 104708. [Google Scholar] [CrossRef]
- Jo, H.-Y.; Lee, H.-J.; Jo, Y.-J.; Heo, G.; Lee, M.; Kim, J.-A.; Park, M.-S.; Lee, T.; Kim, S.-W.; Lee, Y.-H.; et al. A case study of heavy PM2.5 secondary formation by N2O5 nocturnal chemistry in Seoul, Korea in January 2018: Model performance and error analysis. Atmos. Res. 2021, 266, 105951. [Google Scholar] [CrossRef]
- Lee, H.-J.; Jo, H.-Y.; Kim, J.-M.; Bak, J.; Park, M.-S.; Kim, J.-K.; Jo, Y.-J.; Kim, C.-H. Nocturnal Boundary Layer Height Uncertainty in Particulate Matter Simulations during the KORUS-AQ Campaign. Remote Sens. 2023, 15, 300. [Google Scholar] [CrossRef]
- Tyagi, B.; Magliulo, V.; Finardi, S.; Gasbarra, D.; Carlucci, P.; Toscano, P.; Zaldei, A.; Riccio, A.; Calori, G.; D’allura, A.; et al. Performance Analysis of Planetary Boundary Layer Parameterization Schemes in WRF Modeling Set Up over Southern Italy. Atmosphere 2018, 9, 272. [Google Scholar] [CrossRef]
- Griffin, S.M.; Otkin, J.A. Evaluating the Impact of Planetary Boundary Layer, Land Surface Model, and Microphysics Parameterization Schemes on Simulated GOES-16 Water Vapor Brightness Temperatures. Atmosphere 2022, 13, 366. [Google Scholar] [CrossRef]
- Shen, W.; Lu, Z.; Ye, G.; Zhang, Y.; Chen, S.; Xu, J. Exploring the Impact of Planetary Boundary Layer Schemes on Rainfall Forecasts for Typhoon Mujigae, 2015. Atmosphere 2022, 13, 220. [Google Scholar] [CrossRef]
- Falasca, S.; Gandolfi, I.; Argentini, S.; Barnaba, F.; Casasanta, G.; Di Liberto, L.; Petenko, I.; Curci, G. Sensitivity of near-surface meteorology to PBL schemes in WRF simulations in a port-industrial area with complex terrain. Atmos. Res. 2021, 264, 105824. [Google Scholar] [CrossRef]
- Zhang, L.; Xin, J.; Yin, Y.; Chang, W.; Xue, M.; Jia, D.; Ma, Y. Understanding the Major Impact of Planetary Boundary Layer Schemes on Simulation of Vertical Wind Structure. Atmosphere 2021, 12, 777. [Google Scholar] [CrossRef]
- Jia, W.; Zhang, X. The role of the planetary boundary layer parameterization schemes on the meteorological and aerosol pollution simulations: A review. Atmos. Res. 2020, 239, 104890. [Google Scholar] [CrossRef]
- Wang, C.; Qian, Y.; Duan, Q.; Huang, M.; Berg, L.K.; Shin, H.H.; Feng, Z.; Yang, B.; Quan, J.; Hong, S.; et al. Assessing the sensitivity of land-atmosphere coupling strength to boundary and surface layer parameters in the WRF model over Amazon. Atmos. Res. 2019, 234, 104738. [Google Scholar] [CrossRef]
- Wang, C.; Qian, Y.; Duan, Q.; Huang, M.; Yang, Z.; Berg, L.K.; Gustafson, W.I.; Feng, Z.; Liu, J.; Quan, J. Quantifying physical parameterization uncertainties associated with land-atmosphere interactions in the WRF model over Amazon. Atmos. Res. 2021, 262, 105761. [Google Scholar] [CrossRef]
- Prein, A.F.; Ge, M.; Valle, A.R.; Wang, D.; Giangrande, S.E. Towards a Unified Setup to Simulate Mid-Latitude and Tropical Mesoscale Convective Systems at Kilometer-Scales. Earth Space Sci. 2022, 9, 8. [Google Scholar] [CrossRef]
- Martin, C.L.; Fitzjarrald, D.; Garstang, M.; Oliveira, A.P.; Greco, S.; Browell, E. Structure and growth of the mixing layer over the Amazonian rain forest. J. Geophys. Res. Atmos. 1988, 93, 1361–1375. [Google Scholar] [CrossRef]
- Betts, A.K.; Fisch, G.; Von Randow, C.; Silva Dias, M.A.F.; Cohen, J.C.P.; Da Silva, R.; Fitzjarrald, D.R. The Amazonian boundary layer and mesoscale circulations. Amazon. Glob. Chang. 2009, 186, 163–181. [Google Scholar] [CrossRef]
- Martin, S.T.; Artaxo, P.; Machado, L.A.T.; Manzi, A.O.; Souza, R.A.F.; Schumacher, C.; Wang, J.; Andreae, M.O.; Barbosa, H.M.J.; Fan, J.; et al. Introduction: Observations and Modeling of the Green Ocean Amazon (GoAmazon2014/5). Atmos. Meas. Tech. 2016, 16, 4785–4797. [Google Scholar] [CrossRef]
- Henkes, A.; Fisch, G.; Machado, L.A.T.; Chaboureau, J.-P. Morning boundary layer conditions for shallow to deep convective cloud evolution during the dry season in the central Amazon. Atmos. Meas. Tech. 2021, 21, 13207–13225. [Google Scholar] [CrossRef]
- Carneiro, R.G.; Fisch, G. Observational analysis of the daily cycle of the planetary boundary layer in the central Amazon during a non-El Niño year and El Niño year (GoAmazon project 2014/5). Atmos. Meas. Tech. 2020, 20, 5547–5558. [Google Scholar] [CrossRef]
- Carneiro, R.; Fisch, G.; Neves, T.; Santos, R.; Santos, C.; Borges, C. Nocturnal Boundary Layer Erosion Analysis in the Amazon Using Large-Eddy Simulation during GoAmazon Project 2014/5. Atmosphere 2021, 12, 240. [Google Scholar] [CrossRef]
- Mather, J.H.; Voyles, J.W. The Arm Climate Research Facility: A Review of Structure and Capabilities. Bull. Am. Meteorol. Soc. 2013, 94, 377–392. [Google Scholar] [CrossRef]
- Kyrouac, J.; Springston, S. Meteorological Measurements Associated with the Aerosol Observing System (AOSMET). 2014. Available online: https://adc.arm.gov/discovery/#/results/instrument_code::aosmet (accessed on 10 October 2021).
- Sullivan, R.; Billesbach, D.; Keeler, E.; Ermold, B. Eddy Correlation Flux Measurement System (30ECOR). 2014. Available online: https://adc.arm.gov/discovery/#/results/instrument_code::30ecor (accessed on 10 October 2021).
- Keeler, E.; Coulter, R.; Kyrouac, J. Balloon-Borne Sounding System (SONDEWNPN). 2014. Available online: https://adc.arm.gov/discovery/#/results/instrument_code::sondewnpn (accessed on 10 October 2021).
- Morris, V.; Briam. Boundary-Layer Height Data with CEIL (CEILPBLHT). 2014. Available online: https://adc.arm.gov/discovery/#/results/instrument_code::ceilpblht (accessed on 10 October 2021).
- Wiegner, M.; Madonna, F.; Binietoglou, I.; Forkel, R.; Gasteiger, J.; Geiß, A.; Pappalardo, G.; Schäfer, K.; Thomas, W. What is the benefit of ceilometers for aerosol remote sensing? An answer from EARLINET. Atmos. Meas. Tech. 2014, 7, 1979–1997. [Google Scholar] [CrossRef]
- Kotthaus, S.; O’Connor, E.; Münkel, C.; Charlton-Perez, C.; Haeffelin, M.; Gabey, A.M.; Grimmond, C.S.B. Recommendations for processing atmospheric attenuated backscatter profiles from Vaisala CL31 ceilometers. Atmos. Meas. Tech. 2016, 9, 3769–3791. [Google Scholar] [CrossRef]
- Geiß, A.; Wiegner, M.; Bonn, B.; Schäfer, K.; Forkel, R.; Von Schneidemesser, E.; Münkel, C.; Chan, K.L.; Nothard, R. Mixing layer height as an indicator for urban air quality? Atmos. Meas. Tech. 2017, 10, 2969–2988. [Google Scholar] [CrossRef]
- Shukla, K.; Phanikumar, D.; Newsom, R.K.; Kumar, K.N.; Ratnam, M.V.; Naja, M.; Singh, N. Estimation of the mixing layer height over a high altitude site in Central Himalayan region by using Doppler lidar. J. Atmos. Sol.-Terr. Phys. 2014, 109, 48–53. [Google Scholar] [CrossRef]
- Geisinger, A.; Behrendt, A.; Wulfmeyer, V.; Strohbach, J.; Förstner, J.; Potthast, R. Development and application of a backscatter lidar forward operator for quantitative validation of aerosol dispersion models and future data assimilation. Atmos. Meas. Tech. 2017, 10, 4705–4726. [Google Scholar] [CrossRef]
- Skamarock, W.C.; Klemp, J.B.; Dudhia, J.; Gill, D.O.; Liu, Z.; Berner, J.; Huang, X.Y. A Description of the Advanced Research WRF Model Version 4.3 (No. NCAR/TN-556+STR). 2021. Available online: https://opensky.ucar.edu/islandora/object/opensky:2898 (accessed on 13 February 2021).
- Broxton, P.D.; Zeng, X.; Sulla-Menashe, D.; Troch, P.A. A Global Land Cover Climatology Using MODIS Data. J. Appl. Meteorol. Clim. 2014, 53, 1593–1605. [Google Scholar] [CrossRef]
- Mukul Tewari, N.C.A.R.; Tewari, M.; Chen, F.; Wang, W.; Dudhia, J.; LeMone, M.; Cuenca, R.H. Implementation and verification of the unified NOAH land surface model in the WRF model. In Proceedings of the 20th Conference on Weather Analysis and Forecasting/16th Conference on Numerical Weather Prediction, Seattle, WA, USA, 10 January 2004. [Google Scholar]
- Iacono, M.J.; Delamere, J.S.; Mlawer, E.J.; Shephard, M.W.; Clough, S.A.; Collins, W.D. Radiative forcing by long-lived greenhouse gases: Calculations with the AER radiative transfer models. J. Geophys. Res. Atmos. 2008, 113, D13103. [Google Scholar] [CrossRef]
- Rogers, E.; Black, T.; Ferrier, B.; Lin, Y.; Parrish, D.; DiMego, G. Changes to the NCEP Meso Eta Analysis and Forecast System: Increase in resolution, new cloud microphysics, modified precipitation assimilation, modified 3DVAR analysis. NWS Tech. Proced. Bull. 2001, 488, 15. [Google Scholar]
- Zhang, C.; Wang, Y. Projected Future Changes of Tropical Cyclone Activity over the Western North and South Pacific in a 20-km-Mesh Regional Climate Model. J. Clim. 2017, 30, 5923–5941. [Google Scholar] [CrossRef]
- Jiménez, P.A.; Dudhia, J.; González-Rouco, J.F.; Navarro, J.; Montávez, J.P.; García-Bustamante, E. A Revised Scheme for the WRF Surface Layer Formulation. Mon. Weather Rev. 2012, 140, 898–918. [Google Scholar] [CrossRef]
- Stull, R.B. An Introduction to Boundary Layer Meteorology; Springer: Berlin/Heidelberg, Germany, 1988; Volume 13. [Google Scholar] [CrossRef]
- Bougeault, P.; Lacarrere, P. Parameterization of orography-induced turbulence in a mesobeta-scale model. Mon. Weather Rev. 1988, 117, 1872–1890. [Google Scholar] [CrossRef]
- Grenier, H.; Bretherton, C.S. A moist PBL parameterization for large-scale models and its application to subtropical cloud-topped marine boundary layers. Mon. Weather Rev. 2001, 129, 357–377. [Google Scholar] [CrossRef]
- Bretherton, C.S.; Park, S. A New Moist Turbulence Parameterization in the Community Atmosphere Model. J. Clim. 2009, 22, 3422–3448. [Google Scholar] [CrossRef]
- Nakanishi, M.; Niino, H. Development of an Improved Turbulence Closure Model for the Atmospheric Boundary Layer. J. Meteorol. Soc. Jpn. Ser. II 2009, 87, 895–912. [Google Scholar] [CrossRef]
- Hong, S.-Y.; Noh, Y.; Dudhia, J. A New Vertical Diffusion Package with an Explicit Treatment of Entrainment Processes. Mon. Weather Rev. 2006, 134, 2318–2341. [Google Scholar] [CrossRef]
- Taylor, K.E. Summarizing multiple aspects of model performance in a single diagram. J. Geophys. Res. Atmos. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]
- Sathyanadh, A.; Prabha, T.V.; Chowdhuri, S.; Balaji, B.; Resmi, E.A.; Karipot, A. Evaluation of PBL parameterization schemes against direct observations during a land depression over Central India. Theor. Appl. Clim. 2021, 144, 253–271. [Google Scholar] [CrossRef]
- Sullivan, R.; Cook, D.; Keeler, E. Surface Energy Balance System (SEBS). 2014. Available online: https://adc.arm.gov/discovery/#/results/instrument_code::sebs (accessed on 12 December 2022).
- Sun, X.; Holmes, H.A.; Osibanjo, O.O.; Sun, Y.; Ivey, C.E. Evaluation of Surface Fluxes in the WRF Model: Case Study for Farmland in Rolling Terrain. Atmosphere 2017, 8, 197. [Google Scholar] [CrossRef]
- Sathyanadh, A.; Prabha, T.V.; Balaji, B.; Resmi, E.; Karipot, A. Evaluation of WRF PBL parameterization schemes against direct observations during a dry event over the Ganges valley. Atmos. Res. 2017, 193, 125–141. [Google Scholar] [CrossRef]




| Indexes | Equations * |
|---|---|
| Mean Bias (MB) | |
| Root mean square error (RMSE) | |
| Correlation coefficient (r) | |
| Index of agreement (IOA) | |
| Taylor skill score (TSS) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mantovani Júnior, J.A.; Aravéquia, J.A.; Carneiro, R.G.; Fisch, G. Evaluation of PBL Parameterization Schemes in WRF Model Predictions during the Dry Season of the Central Amazon Basin. Atmosphere 2023, 14, 850. https://doi.org/10.3390/atmos14050850
Mantovani Júnior JA, Aravéquia JA, Carneiro RG, Fisch G. Evaluation of PBL Parameterization Schemes in WRF Model Predictions during the Dry Season of the Central Amazon Basin. Atmosphere. 2023; 14(5):850. https://doi.org/10.3390/atmos14050850
Chicago/Turabian StyleMantovani Júnior, José Antonio, José Antonio Aravéquia, Rayonil Gomes Carneiro, and Gilberto Fisch. 2023. "Evaluation of PBL Parameterization Schemes in WRF Model Predictions during the Dry Season of the Central Amazon Basin" Atmosphere 14, no. 5: 850. https://doi.org/10.3390/atmos14050850
APA StyleMantovani Júnior, J. A., Aravéquia, J. A., Carneiro, R. G., & Fisch, G. (2023). Evaluation of PBL Parameterization Schemes in WRF Model Predictions during the Dry Season of the Central Amazon Basin. Atmosphere, 14(5), 850. https://doi.org/10.3390/atmos14050850







