Strong Nonideal Electric Fields and Energy Dissipation Observed by MMS within Field-Aligned Current Layers in the Plasma Sheet of the Earth’s Magnetotail
Abstract
1. Introduction
2. Results
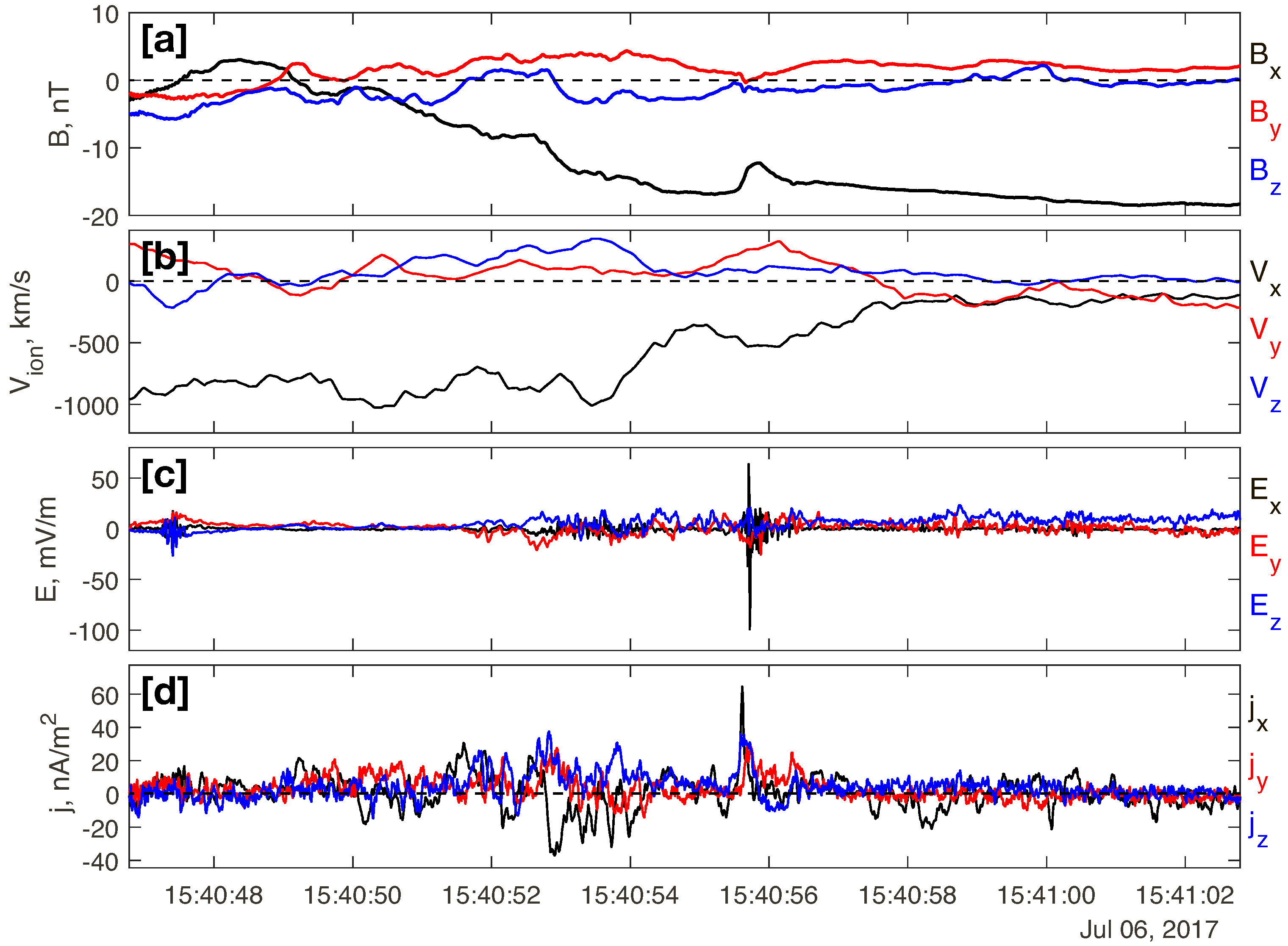
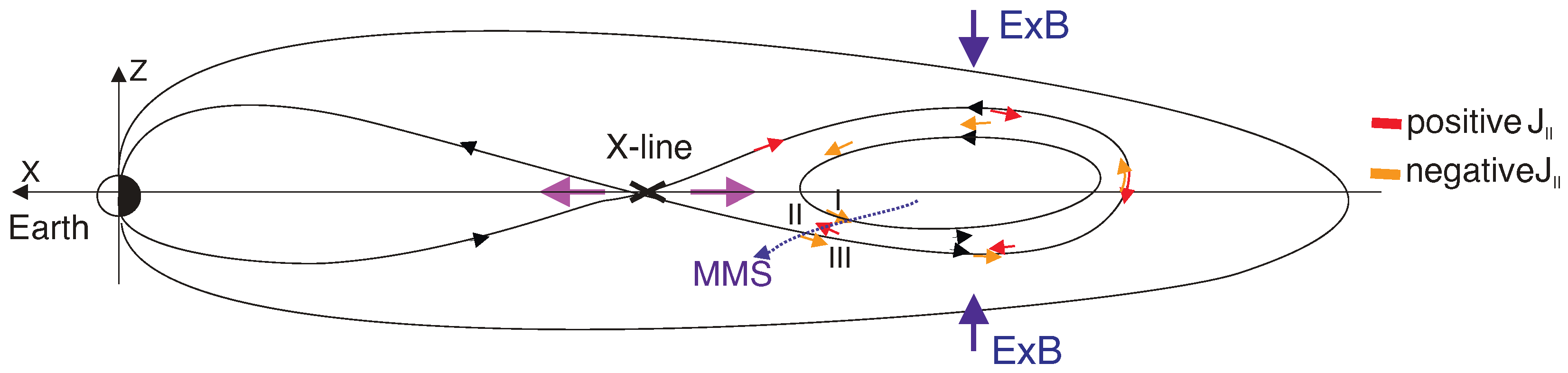
2.1. FACs Observation by the MMS Spacecraft in the Plasma Sheet
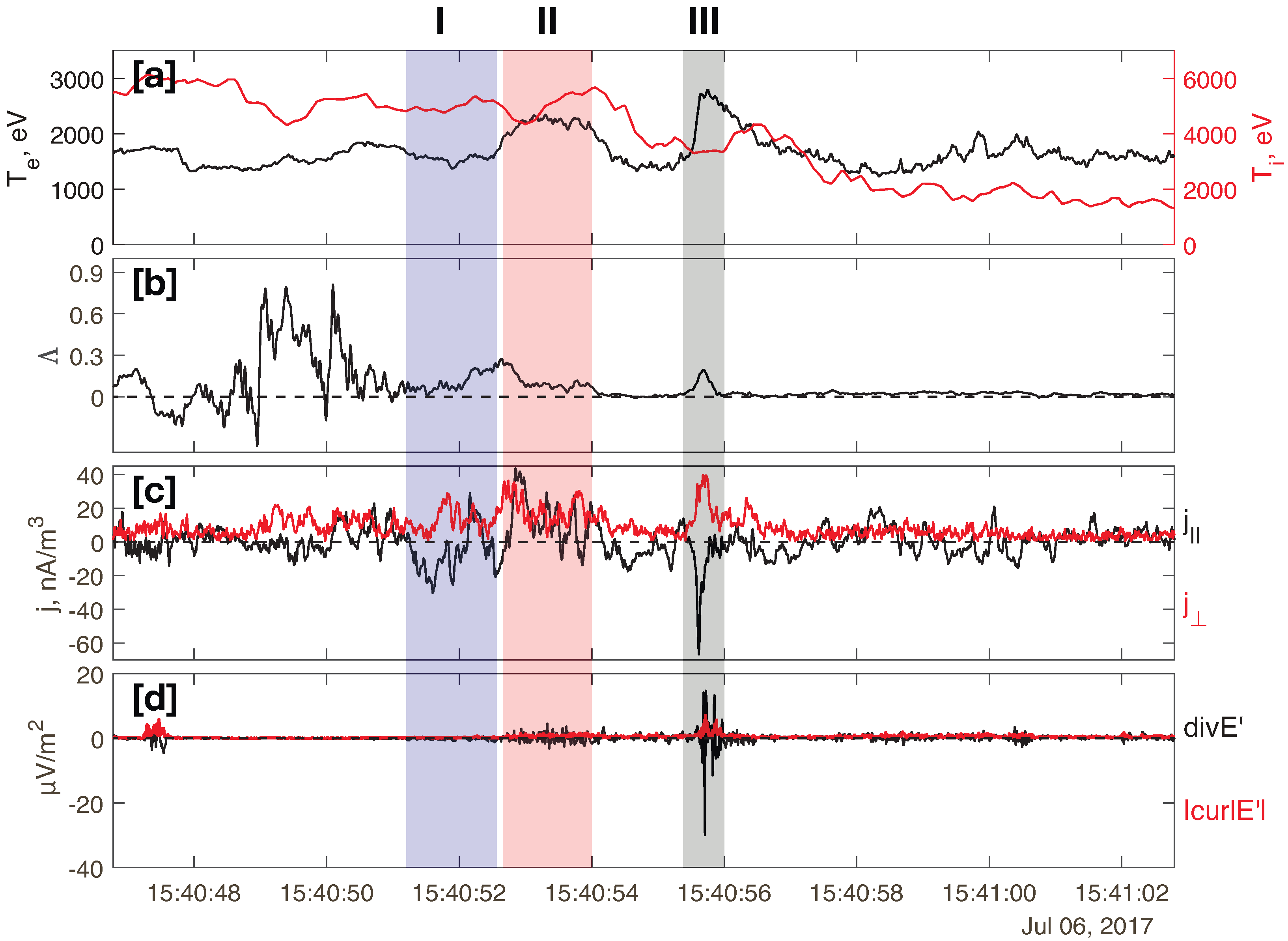
2.2. Energy Dissipation and Electron Heating
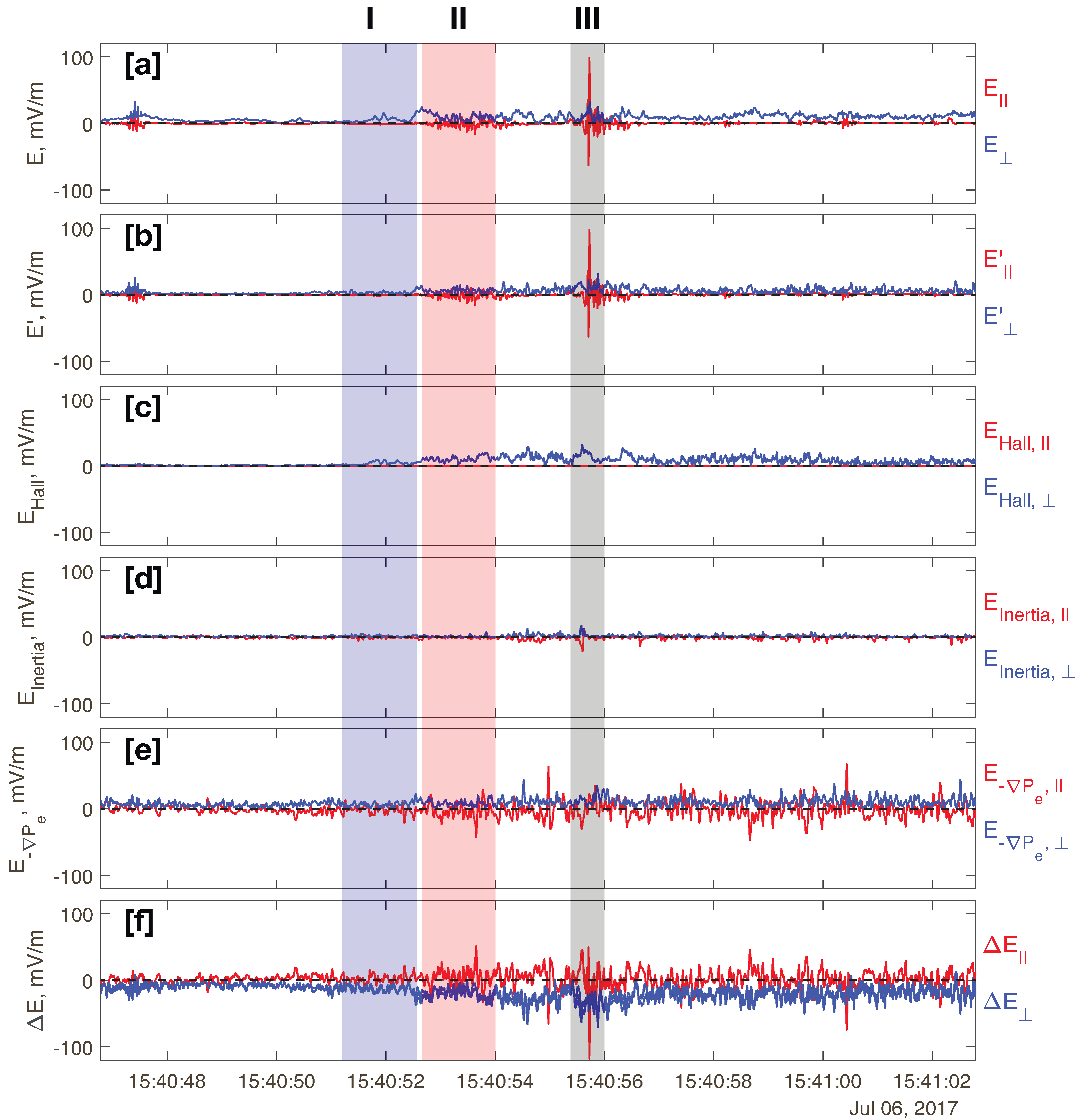
2.3. Ion-Electron Decoupling and the Origin of Strong Electric Fields
3. Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| FAC | Field-aligned current |
| PS | Plasma sheet |
| PSBL | Plasma sheet boundaty layer |
| CS | Current sheet |
| BBF | Bursty bulk flow |
| DF | Dipolization front |
References
- Angelopoulos, V.; Baumjohann, W.; Kennel, C.F.; Coroniti, F.V.; Kivelson, M.G.; Pellat, R.; Walker, R.J.; Lühr, H.; Paschmann, G. Bursty bulk flows in the inner central plasma sheet. J. Geophys. Res. Space Phys. 1992, 97, 4027–4039. [Google Scholar] [CrossRef]
- Sergeev, V.; Runov, A.; Baumjohann, W.; Nakamura, R.; Zhang, T.L.; Volwerk, M.; Balogh, A.; Rème, H.; Sauvaud, J.A.; André, M.; et al. Current sheet flapping motion and structure observed by Cluster. Geophys. Res. Lett. 2003, 30. [Google Scholar] [CrossRef]
- Runov, A.; Nakamura, R.; Baumjohann, W.; Treumann, R.A.; Zhang, T.L.; Volwerk, M.; Vörös, Z.; Balogh, A.; Glaßmeier, K.H.; Klecker, B.; et al. Current sheet structure near magnetic X-line observed by Cluster. Geophys. Res. Lett. 2003, 30. [Google Scholar] [CrossRef]
- Runov, A.; Angelopoulos, V.; Sitnov, M.I.; Sergeev, V.A.; Bonnell, J.; McFadden, J.P.; Larson, D.; Glassmeier, K.H.; Auster, U. THEMIS observations of an earthward-propagating dipolarization front. Geophys. Res. Lett. 2009, 36. [Google Scholar] [CrossRef]
- Sharma, A.S.; Nakamura, R.; Runov, A.; Grigorenko, E.E.; Hasegawa, H.; Hoshino, M.; Louarn, P.; Owen, C.J.; Petrukovich, A.; Sauvaud, J.A.; et al. Transient and localized processes in the magnetotail: A review. Ann. Geophys. 2008, 26, 955–1006. [Google Scholar] [CrossRef]
- Grigorenko, E.E.; Sauvaud, J.A.; Palin, L.; Jacquey, C.; Zelenyi, L.M. THEMIS observations of the current sheet dynamics in response to the intrusion of the high-velocity plasma flow into the near-Earth magnetotail. J. Geophys. Res. Space Phys. 2014, 119, 6553–6568. [Google Scholar] [CrossRef]
- Fu, H.; Grigorenko, E.E.; Gabrielse, C.; Liu, C.; Lu, S.; Hwang, K.; Zhou, X.; Wang, Z.; Chen, F. Magnetotail dipolarization fronts and particle acceleration: A review. Sci. China Earth Sci. 2020, 63, 235–256. [Google Scholar] [CrossRef]
- Burch, J.; Moore, T.; Torbert, R.; Giles, B. Magnetospheric multiscale overview and science objectives. Space Sci. Rev. 2016, 199, 5–21. [Google Scholar] [CrossRef]
- Phan, T.D.; Eastwood, J.P.; Cassak, P.A.; Øieroset, M.; Gosling, J.T.; Gershman, D.J.; Mozer, F.S.; Shay, M.A.; Fujimoto, M.; Daughton, W.; et al. MMS observations of electron-scale filamentary currents in the reconnection exhaust and near the X line. Geophys. Res. Lett. 2016, 43, 6060–6069. [Google Scholar] [CrossRef]
- Leonenko, M.V.; Grigorenko, E.E.; Zelenyi, L.M.; Malova, H.V.; Malykhin, A.Y.; Popov, V.Y.; Büchner, J. MMS Observations of Super Thin Electron-Scale Current Sheets in the Earth’s Magnetotail. J. Geophys. Res. Space Phys. 2021, 126, e2021JA029641. [Google Scholar] [CrossRef]
- Fujimoto, M.; Nagai, T.; Yokokawa, N.; Yamade, Y.; Mukai, T.; Saito, Y.; Kokubun, S. Tailward electrons at the lobe-plasma sheet interface detected upon dipolarizations. J. Geophys. Res. Space Phys. 2001, 106, 21255–21262. [Google Scholar] [CrossRef]
- Nakamura, R.; Baumjohann, W.; Nagai, T.; Fujimoto, M.; Mukai, T.; Klecker, B.; Treumann, R.; Balogh, A.; Rème, H.; Sauvaud, J.A.; et al. Flow shear near the boundary of the plasma sheet observed by Cluster and Geotail. J. Geophys. Res. Space Phys. 2004, 109. [Google Scholar] [CrossRef]
- Eastman, T.E.; Frank, L.A.; Peterson, W.K.; Lennartsson, W. The plasma sheet boundary layer. J. Geophys. Res. Space Phys. 1984, 89, 1553–1572. [Google Scholar] [CrossRef]
- Frank, L.A. Hot plasmas in the earth’s magnetosphere. In Physics of Solar Planetary Environments, Proceedings of the International Symposium on Solar-Terrestrial Physics, Boulder, CO, USA, 7–18 June 1976; American Geophysical Union: Washington, DC, USA; Volume 2, pp. 685–700.
- Grigorenko, E.; Zelenyi, L.; Dolgonosov, M.; Artemiev, A.; Owen, C.; Sauvaud, J.A.; Hoshino, M.; Hirai, M. Non-adiabatic ion acceleration in the Earth magnetotail and its various manifestations in the plasma sheet boundary layer. Space Sci. Rev. 2011, 164, 133–181. [Google Scholar] [CrossRef]
- Nakamura, R.; Sergeev, V.A.; Baumjohann, W.; Plaschke, F.; Magnes, W.; Fischer, D.; Varsani, A.; Schmid, D.; Nakamura, T.K.M.; Russell, C.T.; et al. Transient, small-scale field-aligned currents in the plasma sheet boundary layer during storm time substorms. Geophys. Res. Lett. 2016, 43, 4841–4849. [Google Scholar] [CrossRef] [PubMed]
- Robert, P.; Dunlop, M.W.; Roux, A.; Chanteur, G. Chap. 16. Accuracy of Current Density Determination. In Analysis Methods for Multi-Spacecraft Data; Pashmann, G., Ed.; ISSI Scientific Report SR-001; University of California: Berkeley, CA, USA, 1998. [Google Scholar]
- Mauk, B.; Blake, J.; Baker, D.; Clemmons, J.; Reeves, G.; Spence, H.E.; Jaskulek, S.; Schlemm, C.; Brown, L.; Cooper, S.; et al. The energetic particle detector (EPD) investigation and the energetic ion spectrometer (EIS) for the magnetospheric multiscale (MMS) mission. Space Sci. Rev. 2016, 199, 471–514. [Google Scholar] [CrossRef]
- Harvey, C.C. Chap. 12. Spatial Gradients and the Volumetric Tensor. In Analysis Methods for Multi-Spacecraft Data; Pashmann, G., Ed.; ISSI Scientific Report SR-001; University of California: Berkeley, CA, USA, 1998. [Google Scholar]
- Pollock, C.; Moore, T.; Jacques, A.; Burch, J.; Gliese, U.; Saito, Y.; Omoto, T.; Avanov, L.; Barrie, A.; Coffey, V.; et al. Fast plasma investigation for magnetospheric multiscale. Space Sci. Rev. 2016, 199, 331–406. [Google Scholar] [CrossRef]
- Büchner, J.; Zelenyi, L.M. Regular and chaotic charged particle motion in magnetotaillike field reversals: 1. Basic theory of trapped motion. J. Geophys. Res. Space Phys. 1989, 94, 11821–11842. [Google Scholar] [CrossRef]
- Bittencourt, J.A. Macroscopic Transport Equations. In Fundamentals of Plasma Physics; Springer: New York, NY, USA, 2004; pp. 193–218. [Google Scholar] [CrossRef]
- Torbert, R.B.; Burch, J.L.; Giles, B.L.; Gershman, D.; Pollock, C.J.; Dorelli, J.; Avanov, L.; Argall, M.R.; Shuster, J.; Strangeway, R.J.; et al. Estimates of terms in Ohm’s law during an encounter with an electron diffusion region. Geophys. Res. Lett. 2016, 43, 5918–5925. [Google Scholar] [CrossRef]
- Grigorenko, E.E.; Runov, A.; Angelopoulos, V.; Zelenyi, L.M. Particle Beams in the Vicinity of Magnetic Separatrix According to Near-Lunar ARTEMIS Observations. J. Geophys. Res. Space Phys. 2019, 124, 1883–1903. [Google Scholar] [CrossRef]
- Zelenyi, L.M.; Malova, H.V.; Grigorenko, E.E.; Popov, V.Y.; Dubinin, E.M. Universal Scaling of Thin Current Sheets. Geophys. Res. Lett. 2020, 47, e2020GL088422. [Google Scholar] [CrossRef]
- Matsumoto, H.; Kojima, H.; Miyatake, T.; Omura, Y.; Okada, M.; Nagano, I.; Tsutsui, M. Electrostatic solitary waves (ESW) in the magnetotail: BEN wave forms observed by GEOTAIL. Geophys. Res. Lett. 1994, 21, 2915–2918. [Google Scholar] [CrossRef]
- Lakhina, G.S.; Singh, S.V.; Kakad, A.P.; Pickett, J.S. Generation of electrostatic solitary waves in the plasma sheet boundary layer. J. Geophys. Res. Space Phys. 2011, 116. [Google Scholar] [CrossRef]
- Li, S.; Zhang, S.; Cai, H.; Yu, S. Concentration of electrostatic solitary waves around magnetic nulls within magnetic reconnection diffusion region: Single-event-based statistics. Earth Planets Space 2014, 66, 1–13. [Google Scholar] [CrossRef]
- Yu, X.; Wang, R.; Lu, Q.; Russell, C.T.; Wang, S. Nonideal Electric Field Observed in the Separatrix Region of a Magnetotail Reconnection Event. Geophys. Res. Lett. 2019, 46, 10744–10753. [Google Scholar] [CrossRef]
- Chen, Z.Z.; Fu, H.S.; Liu, C.M.; Wang, T.Y.; Ergun, R.E.; Cozzani, G.; Huang, S.Y.; Khotyaintsev, Y.V.; Le Contel, O.; Giles, B.L.; et al. Electron-Driven Dissipation in a Tailward Flow Burst. Geophys. Res. Lett. 2019, 46, 5698–5706. [Google Scholar] [CrossRef]
- Huang, S.Y.; Fu, H.S.; Yuan, Z.G.; Zhou, M.; Fu, S.; Deng, X.H.; Sun, W.J.; Pang, Y.; Wang, D.D.; Li, H.M.; et al. Electromagnetic energy conversion at dipolarization fronts: Multispacecraft results. J. Geophys. Res. Space Phys. 2015, 120, 4496–4502. [Google Scholar] [CrossRef]
- Liu, C.M.; Fu, H.S.; Vaivads, A.; Khotyaintsev, Y.V.; Gershman, D.J.; Hwang, K.J.; Chen, Z.Z.; Cao, D.; Xu, Y.; Yang, J.; et al. Electron Jet Detected by MMS at Dipolarization Front. Geophys. Res. Lett. 2018, 45, 556–564. [Google Scholar] [CrossRef]
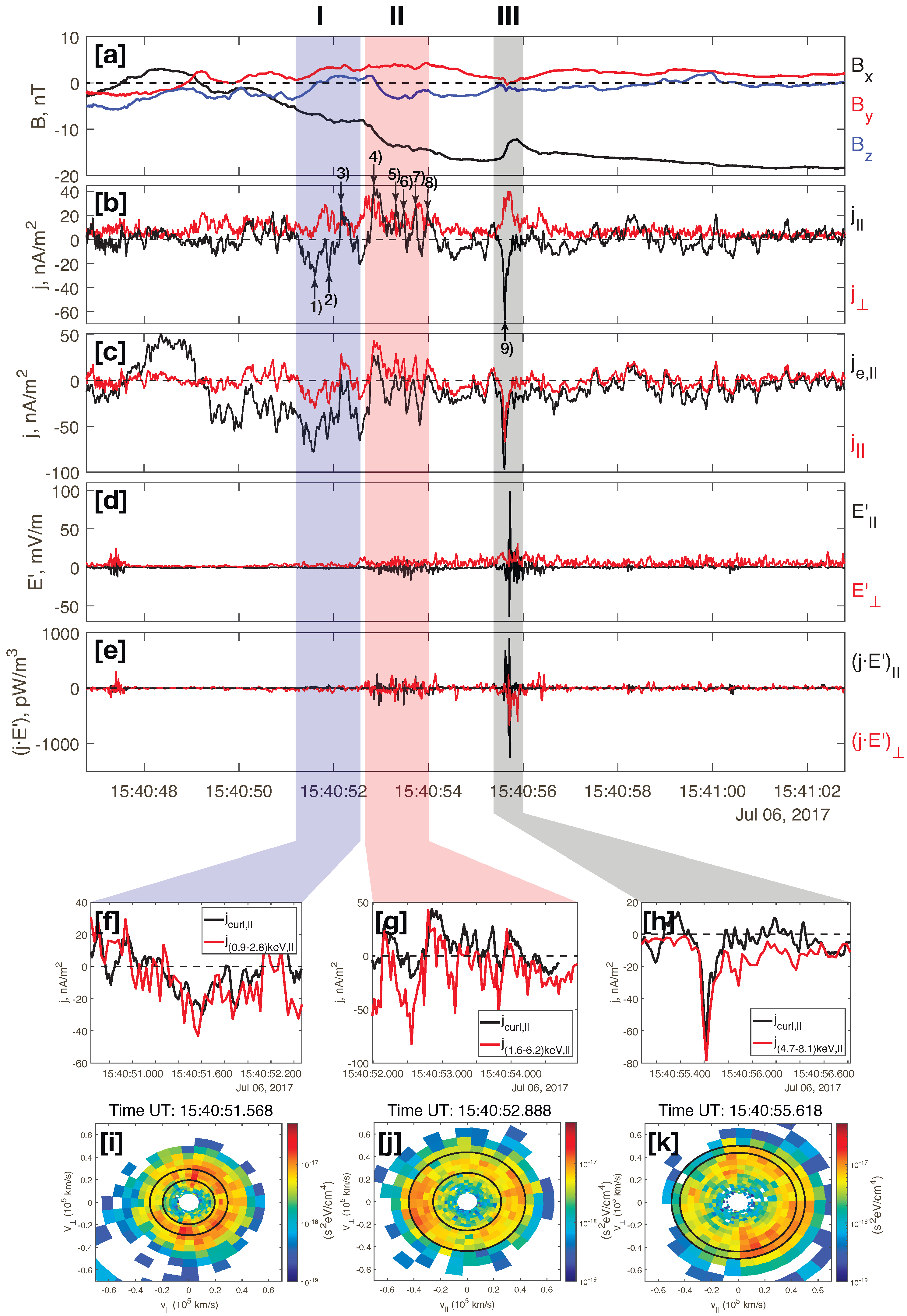
| Time UT | Timing | Timing V, km/s | -Spike Number | , nA/m2 | L, km | , km | , % | |||
|---|---|---|---|---|---|---|---|---|---|---|
| I | 15:40:51.232 15:40:52:545 | [0.48, −0.86, 0.18] | 140 | (1) | −30 | 21 | 23 | 0.9 | 0.3 | 64 |
| (2) | −26 | 6 | 17 | 0.4 | 0.5 | 59 | ||||
| (3) | 29 | 13 | 18 | 0.7 | 0.3 | 47 | ||||
| II | 15:40:52.756 15:40:53:982 | [0.38, −0.82, 0.42] | 130 | (4) | 44 | 13 | 16 | 0.8 | 0.3 | 79 |
| (5) | 30 | 7 | 14 | 0.5 | 0.2 | 72 | ||||
| (6) | 24 | 4 | 13 | 0.3 | 0.1 | 64 | ||||
| (7) | 27 | 5 | 13 | 0.4 | 0.2 | 69 | ||||
| (8) | 24 | 9 | 12 | 0.8 | 0.2 | 67 | ||||
| III | 15:40:55.381 15:40:56:045 | [−0.10, 0.59, −0.80] | 390 | (9) | −67 | 20 | 14 | 1.4 | 0.3 | 22 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Leonenko, M.V.; Grigorenko, E.E.; Zelenyi, L.M. Strong Nonideal Electric Fields and Energy Dissipation Observed by MMS within Field-Aligned Current Layers in the Plasma Sheet of the Earth’s Magnetotail. Atmosphere 2023, 14, 722. https://doi.org/10.3390/atmos14040722
Leonenko MV, Grigorenko EE, Zelenyi LM. Strong Nonideal Electric Fields and Energy Dissipation Observed by MMS within Field-Aligned Current Layers in the Plasma Sheet of the Earth’s Magnetotail. Atmosphere. 2023; 14(4):722. https://doi.org/10.3390/atmos14040722
Chicago/Turabian StyleLeonenko, Makar V., Elena E. Grigorenko, and Lev M. Zelenyi. 2023. "Strong Nonideal Electric Fields and Energy Dissipation Observed by MMS within Field-Aligned Current Layers in the Plasma Sheet of the Earth’s Magnetotail" Atmosphere 14, no. 4: 722. https://doi.org/10.3390/atmos14040722
APA StyleLeonenko, M. V., Grigorenko, E. E., & Zelenyi, L. M. (2023). Strong Nonideal Electric Fields and Energy Dissipation Observed by MMS within Field-Aligned Current Layers in the Plasma Sheet of the Earth’s Magnetotail. Atmosphere, 14(4), 722. https://doi.org/10.3390/atmos14040722






