Potential Predictability of Seasonal Global Precipitation Associated with ENSO and MJO
Abstract
:1. Introduction
2. Data and Methods
2.1. Data
2.2. Identifying the Seasonal Predictable and Unpredictable Components
3. Results
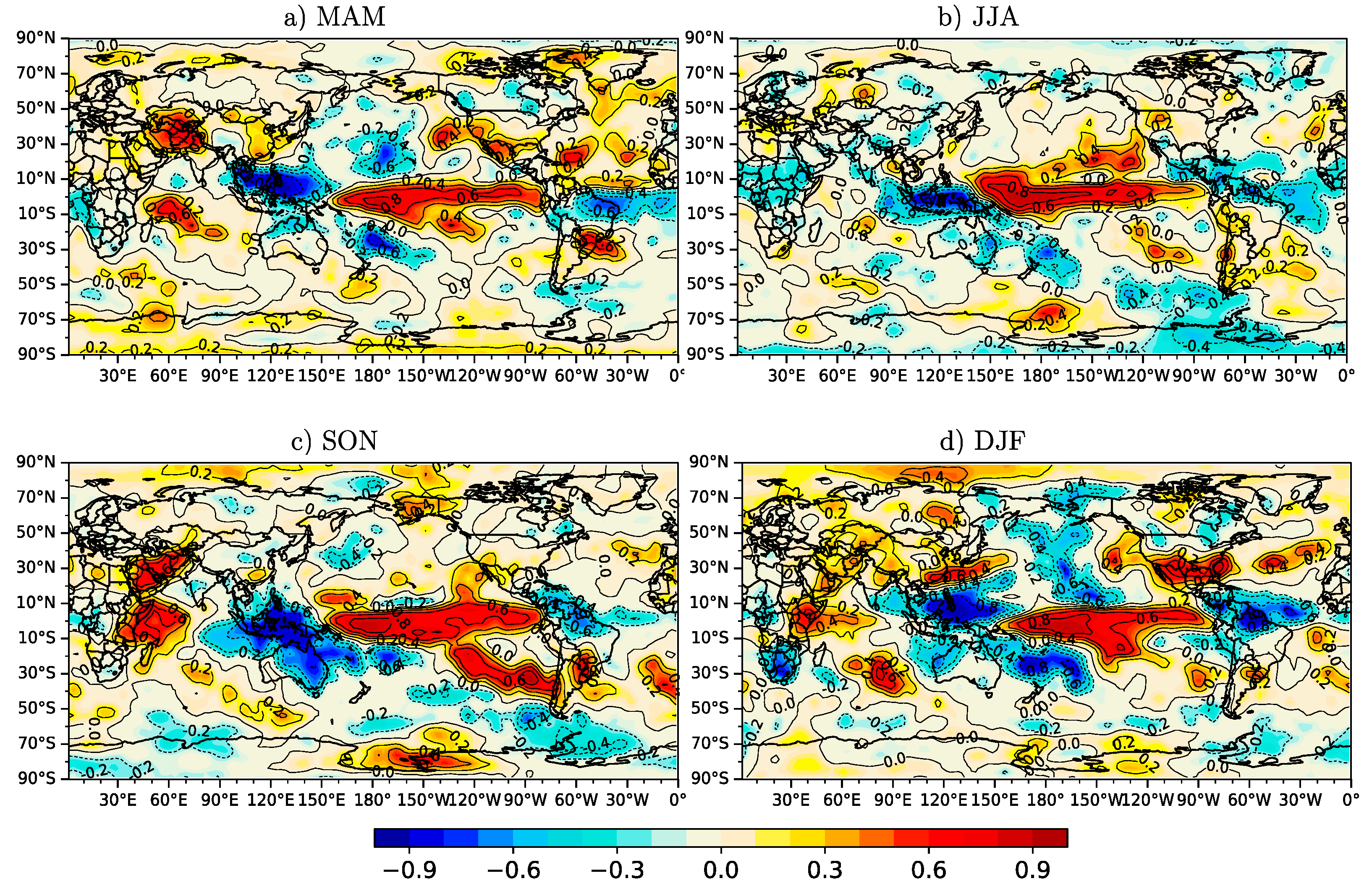
3.1. El Nino-Southern Oscillation
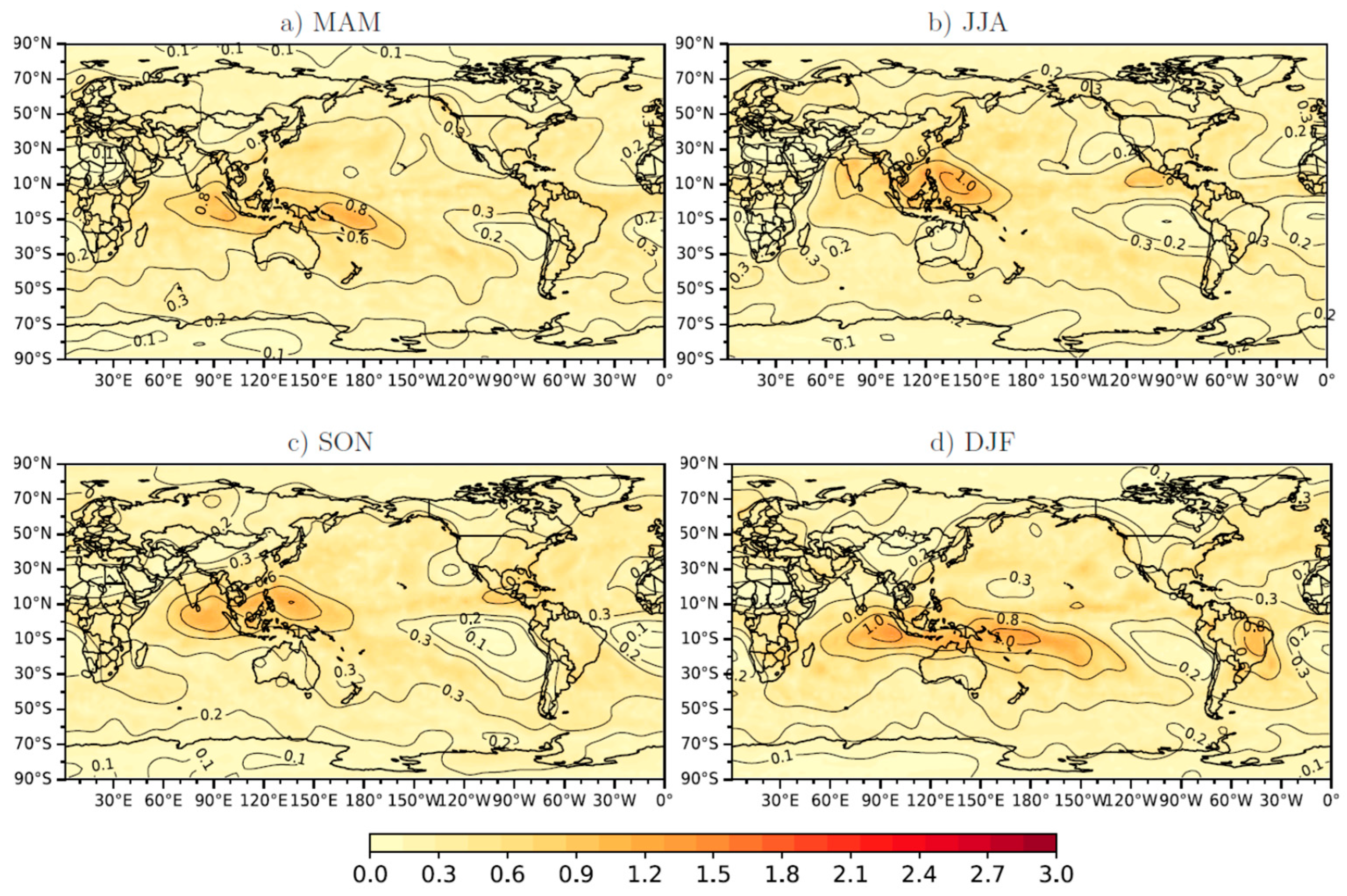
3.2. Madden-Julian Oscillation
3.3. Potential Predictability
4. Discussions on Methodology
5. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
References
- Madden, R.A. Estimates of the natural variability of time averaged sea level pressure. Mon. Wea. Rev. 1976, 104, 942–952. [Google Scholar] [CrossRef]
- Basher, R.E.; Thompson, C.S. Relationship of air temperature in New Zealand to regional anomalies in sea-surface temperature and atmospheric circulation. Int. J. Climatol. 1996, 16, 405–425. [Google Scholar] [CrossRef]
- Zheng, X.; Frederiksen, C.S. Variability of seasonal-mean fields arising from intraseasonal variability: Part I, Methodology. Clim. Dyn. 2004, 23, 177–191. [Google Scholar] [CrossRef]
- Adler, R.F.; Huffman, G.J.; Chang, A.; Ferraro, R.; Xie, P.P.; Janowiak, J.; Rudolf, B.; Schneider, U.; Curtis, S.; Bolvin, D.; et al. The version-2 Global Precipitation Climatology Project (GPCP) monthly precipitation analysis (1979–present). J. Hydrometeor. 2003, 4, 1147–1167. [Google Scholar] [CrossRef]
- Kiladis, G.N.; Dias, J.; Straub, K.H.; Wheeler, M.C.; Tulich, S.N.; Kikuchi, K.; Weickmann, K.M.; Ventrice, M.J. A comparison of OLR and circulation based indices for tracking the MJO. Mon. Wea. Rev. 2014, 142, 1697–1715. [Google Scholar] [CrossRef]
- Ying, K.; Frederiksen, C.S.; Zhao, T.; Zheng, X.; Xiong, Z.; Yi, X.; Li, C. Predictable and unpredictable modes of seasonal mean precipitation over Northeast China. Clim. Dyn. 2018, 50, 3081–3095. [Google Scholar] [CrossRef]
- Zheng, X.; Nakamura, H.; Renwick, J.A. Potential predictability of seasonal means based on monthly time series of meteorological variables. J. Clim. 2000, 13, 2591–2604. [Google Scholar] [CrossRef]
- Zhang, C.; Dong, M. Seasonality in the Madden–Julian Oscillation. J. Clim. 2004, 17, 1369–1380. [Google Scholar] [CrossRef]
- Maloney, E.D.; Kiehl, J.T. MJO-related SST variations over the tropical eastern Pacific during Northern Hemisphere summer. J. Clim. 2002, 15, 675–689. [Google Scholar] [CrossRef]
- Zheng, X.; Frederiksen, C.S. A study of predictable patterns for seasonal forecasting of New Zealand rainfalls. J. Clim. 2006, 19, 3320–3333. [Google Scholar] [CrossRef]
- Ying, K.D.; Jiang, D.; Zheng, X.; Frederiksen, C.S.; Peng, J.; Zhao, T.; Zhong, L. Seasonal predictable source of the East Asian summer monsoon rainfall in addition to the ENSO-AO. Clim. Dyn. 2022, 60, 2459–2480. [Google Scholar] [CrossRef]
- Shukla, J. Comments on “Natural variability and predictability”. Mon. Wea. Rev. 1983, 111, 581–585. [Google Scholar] [CrossRef]
- Trenberth, K.E. Some effects of finite sample size and persistence on meteorological statistics. Part II: Potential predictability. Mon. Wea. Rev. 1984, 112, 2369–2379. [Google Scholar] [CrossRef]
- Zheng, X. Unbiased estimation of autocorrelations of daily meteorological variables. J. Clim. 1996, 9, 2197–2203. [Google Scholar] [CrossRef]
- Jones, R.H. Estimating the variance of time averages. J. Appl. Meteor. 1975, 14, 159–163. [Google Scholar] [CrossRef]
- Delsole, T.; Feng, X. The ‘‘Shukla–Gutzler’’ Method for estimating potential seasonal predictability. Mon. Wea. Rev. 2012, 141, 822–831. [Google Scholar] [CrossRef]
- Madden, R.A.; Shea, D.J.; Katz, R.W.; Kidson, J.W. The potential long-range predictability of precipitation over New Zealand. Int. J. Climatol. 1999, 19, 4. [Google Scholar] [CrossRef]
- Katz, R.W. Precipitation as a chain-dependent process. J. Appl. Meteor. 1977, 16, 671–676. [Google Scholar] [CrossRef]
- Katz, R.W.; Zheng, X. Mixture model for overdispersion of precipitation. J. Clim. 1999, 12, 2528–2537. [Google Scholar] [CrossRef]
- Zheng, X.; Renwick, J.A.; Clark, A. Simulation of multisite precipitation using extended chain-dependent process. Water Resour. Res. 2010, 46, W01504. [Google Scholar] [CrossRef]
- Feng, X.; Houser, P. An examination of potential seasonal predictability in recent reanalysis. Atmo. Sci. Lett. 2014, 15, 266–274. [Google Scholar]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, H.; Zheng, X.; Yuan, J.; Frederiksen, C.S. Potential Predictability of Seasonal Global Precipitation Associated with ENSO and MJO. Atmosphere 2023, 14, 695. https://doi.org/10.3390/atmos14040695
Liu H, Zheng X, Yuan J, Frederiksen CS. Potential Predictability of Seasonal Global Precipitation Associated with ENSO and MJO. Atmosphere. 2023; 14(4):695. https://doi.org/10.3390/atmos14040695
Chicago/Turabian StyleLiu, Haibo, Xiaogu Zheng, Jing Yuan, and Carsten S. Frederiksen. 2023. "Potential Predictability of Seasonal Global Precipitation Associated with ENSO and MJO" Atmosphere 14, no. 4: 695. https://doi.org/10.3390/atmos14040695
APA StyleLiu, H., Zheng, X., Yuan, J., & Frederiksen, C. S. (2023). Potential Predictability of Seasonal Global Precipitation Associated with ENSO and MJO. Atmosphere, 14(4), 695. https://doi.org/10.3390/atmos14040695





