Abstract
Anthropogenic climate change poses a significant threat to both natural and social systems worldwide. In this study, we aim to identify regions most impacted by climate change using the National Centers for Environmental Prediction and the National Center for Atmospheric Research (NCEP-NCAR) reanalysis of near-surface daily air temperature data spanning 73 years (1948–2020). We develop a novel climate network framework to identify “hot spots”, regions that exhibit significant impact or impacted characteristics. Specifically, we use the node degree, a fundamental feature of the network, to measure the influence of each region and analyze its trend over time using the Mann–Kendall test. Our findings reveal that the majority of land areas experiencing increasing degrees are more closely connected to other regions, while the ocean shows the opposite trend due to weakened oceanic circulations. In particular, the degree in the central Pacific Ocean’s El Niño region is significantly reduced. Notably, we identify three “hot spots” in East Asia, South America, and North Africa, respectively, with intensive increasing network degree fields. Additionally, we find that the hot spot in East Asia is teleconnected to remote regions, such as the South Pacific, Siberia, and North America, with stronger teleconnections in recent years. This provides a new perspective for assessing the planetary impacts of anthropogenic global warming. By using a novel climate network framework, our study highlights regions that are most vulnerable to the effects of climate change and emphasizes the importance of understanding network structures to assess the global impacts of anthropogenic climate change.
1. Introduction
The anthropogenic production of greenhouse gases has been identified as the primary driver of climate change [1,2,3], resulting in a range of destabilizing consequences including glacial melting, sea level rise, and unprecedented extreme weather events, such as intense heat waves and catastrophic floods [4,5,6,7]. Global warming, the most prominent indicator of climate change, has emerged as a pressing global issue with the potential to affect a range of ecosystem variables [8,9,10]. Scientific studies have revealed that global warming, caused by the increasing concentration of greenhouse gases in the atmosphere, has resulted in a notable rise in extreme temperatures worldwide. These extreme temperatures can cause harm to humans and other living organisms, leading to serious health concerns and even fatalities in some cases [11,12]. In response, this growing threat of abrupt and irreversible climate changes compels broader societal, political, and economic engagements to perform early actions to reduce climate-related damages [13].
Currently, there is a significant focus on the issue of global warming and the consequential effects on the environment. To investigate global warming, researchers have developed comprehensive dynamical models and statistical methods [14,15,16]. For example, studies have been conducted to evaluate the impact of global warming on Atlantic circulation and have highlighted the potential collapse of Atlantic thermohaline circulation [9,17]. The influence of global warming on the Amazon rainforest has also been examined, and it has been reported that the reduction of the Amazon rainforest may lead to potential dieback of the forest [18]. Huybrechts et al. [19] have discovered that global warming can result in the decay of Greenland’s ice sheet. Global warming has the potential to trigger the Qinghai-Tibet Plateau to become a new “tipping point” [20]. Furthermore, Shawky et al. [21] estimated the land surface temperature trend over South Asia via an MK test and Sen’s slope estimator. Their analysis also identified potential factors that could be influencing temperature changes in the region. Ghaderpour et al. [22] discovered gradual warming and declining annual precipitation in Italy via spectral and wavelet analyses. Li at al. [23] investigated the role of climate change and anthropogenic activities on vegetation and land cover in China via residual analysis and correlation analysis. However, there are still many uncertainties regarding the understanding of the effects of global warming on some specific regions. Therefore, it is necessary to develop new approaches to fill this gap.
In recent years, the field of network science has rapidly developed and has proven to be a valuable tool for investigating the dynamic and structural properties of real systems in a variety of disciplines including physics, biology, and social sciences [24,25,26]. Within the context of climate science, the concept of complex networks has been successfully applied. For example, Yamazaki et al. constructed a time-evolving climate network using sea surface temperature data from the Pacific region and discovered a significant reduction in network degree during El Niño periods [27]. The method of climate network has also been used to identify the weakening of tropical circulation in recent years [14,28]. Furthermore, complex network methods have been employed to predict El Niño events up to one year in advance [29,30,31]. Boers et al. made a significant breakthrough in the understanding and forecasting of extreme rainfall events by using event synchronization network analysis [32,33], while Fan et al. successfully predicted Indian monsoon rainfall six months in advance by constructing a series of dynamic physical climate networks based on global near-surface temperature fields [34]. In summary, complex network analysis is an effective method for exploring the physical and statistical laws of the earth system [35].
Using climate network to reveal the impacts of global warming has certain advantages over traditional statistical analysis methods regarding nonlinear feedbacks and complex mechanisms of climate system. The hot spots under the effect of global warming can be further quantified, thus reflecting the nature of global warming more comprehensively. Currently, numerous methods, including machine learning, deep learning, and wavelet analysis have been employed to study climate change and its influential factors, as documented in several studies [36,37,38]. However, there has been relatively little research on the use of climate networks for this purpose. Here, an approach based on climate network is developed.
This study aims to reveal hot spots under the effects of global warming using the climate networks approach. We have identified three main objectives for our research:
- (1)
- Investigating the tendencies of climate network measures, such as the degree, under the effects of global warming.
- (2)
- Identifying hot spots with an intensive increase in climate network measures over time.
- (3)
- Revealing critical regions that influence the identified hot spots under the effects of global warming.
2. Materials and Methods
2.1. Data
In this study, we employ the National Centers for Environmental Prediction (NCEP) and the National Center for Atmospheric Research (NCAR) reanalysis of near-surface (sig995 level) daily air temperature data, which is provided on a 2.5° × 2.5° spatial grid with daily temporal resolution [39]. The dataset covers the time period from 1948 to 2020 and comprises 10,512 nodes, with each node corresponding to a time series length of 73 × 365 days. Leap days were excluded from the dataset to simplify the analysis. To construct the network, we selected 726 nodes distributed approximately uniformly over the globe [40].
2.2. Methods
For each node , we first removed the trend by calculating the daily atmospheric temperature anomaly value . This was done by subtracting the climate average from the actual temperature value of each calendar day in different years and then dividing by the climate standard deviation [28]. To avoid the effect of global warming, we calculated the average and standard deviation of climate states for three time windows (we divided the data of 72 years into three 24-year time windows). Note that since we used the calculation method with the time delay, the first climate network is constructed in 1949 but not 1948.
We constructed a climate network for each calendar year and computed the time-delayed cross-correlation functions. For a given time delay τ, the link strength between each pair of nodes and was measured by the cross-correlation. The correlation time series between node and is:
where the bar denotes an average over the past 365 days, according to
We considered the time lag of ∈ [−200, 200] days. Here, was defined.
Next, we defined the positive strength of the link between each pair of nodes and in the network as below:
where max represents the maximum in the range of [−200, 200] days; mean and std are the mean and standard deviation of the cross-correlation function, respectively. Meanwhile, we identified the value of the highest peak in the cross-correlation function and denoted the corresponding time lag of this peak as [30]. When the time lag was positive ( > 0), the direction of the link was from to .
After that, we sorted the links in decreasing order of strength and then added one by one according to the strength ; we first chose the most important link with the highest weight, then the second strongest link and so on. In the current study, we considered the top 5% of weights as significant links. We calculated the adjacency matrix and determined the direction of each link according to the sign of the maximum value in the cross-correlation function corresponding to the time delay .
2.3. Network Measures
In this study, the interaction mode of the climate network was defined as the network degree. Each node has two different degrees: The in-degree, , and out-degree, . The in-degree is the number of incoming links, and the out-degree is the number of outgoing links.
where is the amount of nodes in the network and is the adjacency matrix as defied in Equation (4).
For each node , we constructed its in-degree and out-degree time series by counting the number of incoming and outgoing links to this node for each calendar year. A region with an increasing in-degree (out-degree) with year indicates that it is more influenced by (more influences) other regions such that we identified the region as a “hot spot”, which is more vulnerable to and significantly affected by global warming.
2.4. Mann–Kenddall Test
Here, the Mann–Kendall test is employed to test the significance of the degree time series. The Mann–Kendall trend test is a rank correlation test between the ranks of observations and their time series [41,42]. It is one of the most popular statistical significance evaluation methods used to test the trend of climate series; its significance is not affected by the actual distribution of the data.
3. Results
First, we calculated the cross-correlation and the weight by Equations (1) and (2) for any two nodes. To obtain significant links, we determined the threshold (red line) based on the top 5% level of probability density function (PDF) of as shown in Figure 1a. To determine the significance and reality of the correlations in our original data, we compared our results to those of a shuffled dataset where the time series of each node was randomized without any correlation between nodes. Specifically, we shuffled the time series of each node while keeping the order of 365 days per year unchanged. We repeated this process 100 times and recalculated for each shuffled dataset. Since the shuffled data mitigates the correlation between time series, any false correlation we calculated from the shuffled data would be lower than the true correlation found in the original data. The yellow curve in Figure 1a shows the PDF of for the shuffled data for 1949. It can be clearly found that the shuffled data has lost many relatively large values in comparison to that of real data due to being shuffled data. Only less than 5% of the shuffled data can be larger than the threshold . Thus, this suggests that the network we have built is not artificial. We also show an example of PDF for 1971 in Figure 1b. All results are robust and quite similar for different years.
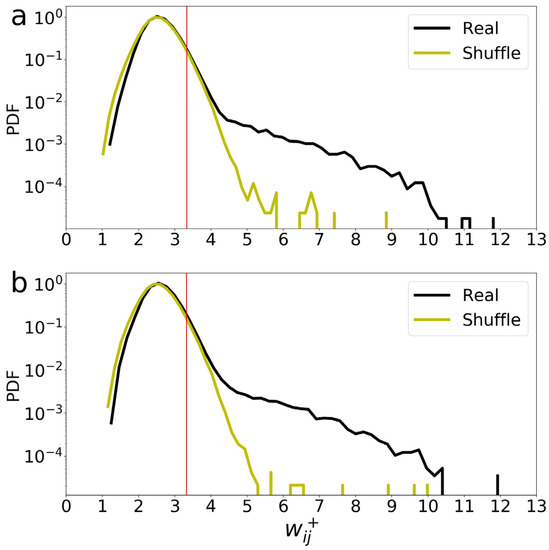
Figure 1.
The probability density function (PDF) of two examples for (a) 1949 and (b) 1971. Red line represents the threshold value for 1949 and for 1971, the top 5% level of PDF for real data, which is also higher than the 95% confidence level of shuffled data.
Next, we calculated in- and out-degrees based on Equation (5) and showed the maps of in- and out-degree distributions for 1949 and 2020 in Figure 2. We found that the in-degree has large values in the mid-latitude regions, especially for the southern hemisphere for both years in Figure 2a,b. For the out-degree field, similar results are also observed as shown in Figure 2c,d. Actually, the large weight is dominated by high frequency waves such as Rossby waves. Rossby waves are mainly located in the mid-latitude regions and are stronger in the southern hemisphere. In comparison to the mid-latitude region, weather waves have lower frequencies in the equatorial region such that the degrees are smaller. These results are consistent with previous studies [43,44].
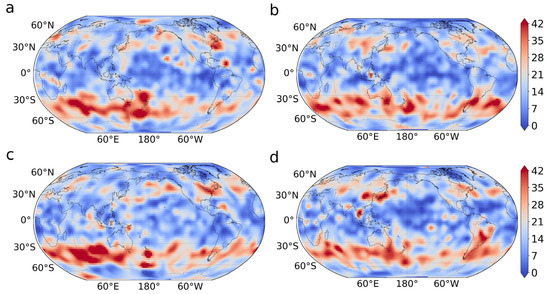
Figure 2.
Maps of in-degree distribution for (a) 1949 and (b) 2020. Maps of out-degree distribution for (c) 1949 and (d) 2020. The color bar stands for the nodes’ degree.
Then we tested the tendency of time series of degrees from 1949 to 2020 according to the MK test method (Materials and Methods) and calculated the Pearson correlation coefficient between the degree and year. Figure 3a,b show the tendency results for the in-degree and out-degree, respectively. Here, we take the significance level of 99% for the MK test, and the triangles shown in Figure 3 indicate that they pass the significance test. Notably, the black upper triangles indicate that the degrees of these nodes increase significantly with year; however, the black lower triangles indicate the significant decreasing trends. These increasing and decreasing trends are also depicted by the positive (red) and negative (blue) values of the Pearson correlation coefficients in Figure 3. Interestingly, we find that most of the land area has increasing in- and out-degrees (see Figure 3a,b). This implies that the inland regions tend to be more strongly connected to others, which suggests they are climate-sensitive areas under global warming. The regions with significantly enhanced degrees are mainly concentrated in East Asia, South America, and North Africa. For the ocean, the trends are the opposite, whereas most of the in- and out-degrees are decreasing. The underlying mechanism for the weakening trend is associated with the weakened ocean circulations [45]. In particular, we find that this weakening of in-degree is very significant in the El Niño basin region as shown in Figure 3a.
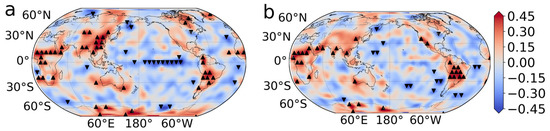
Figure 3.
Tendency of (a) in-degree and (b) out-degree from 1949 to 2020. Colors represent the Pearson correlation coefficient between the degree and year. The black upper triangle indicates that the degree time series at this node is significantly increased with year, and the black lower triangle indicates that it is significantly decreased according to the MK test with the 99% confidence level.
Next, according to Figure 3, we select and show three examples of “hot spots” with significant increasing in-degrees, which are more influenced by other regions under global warming. Figure 4a shows three hot spots highlighted by black boxes. They are located in East Asia, North Africa, and South America, respectively. In Figure 4b, we find that the time series of in-degree significantly increases with year for the hot spot in East Asia. The Pearson correlation coefficient r is 0.49, and the slope k is 0.17 per year. Figure 4c shows the increasing trend with coefficient r = 0.45 and slope k = 0.13 for North Africa. For the hot spot in South America, Figure 4d shows that the in-degree has abruptly increased in recent years. The coefficient r is 0.38, and the slope k is 0.12 for the entire period.
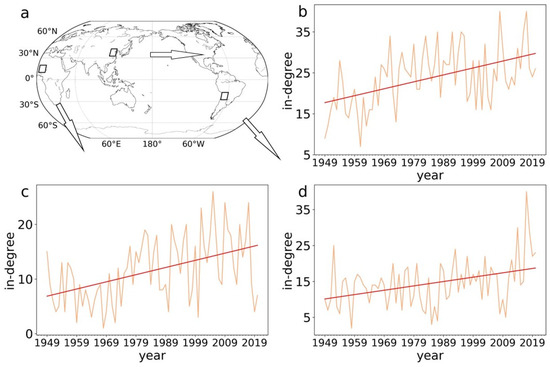
Figure 4.
Examples of time series of in-degree from 1949 to 2020 for three hot spots in (b) East Asia, (c) North Africa, and (d) South America, respectively. The black boxes show the selected hot spots (a). The red lines are the best-fitted linear lines. Each arrow in panel (a) points to subgraph (b), (c), and (d), respectively.
To deeply understand which regions are linked to the hot spots, we here focus on the hot spot in East Asia and compare the probability of emergence of links to the hot spot between two different periods. We take out the links of the first 24 years (1949–1972) and the last 24 years (1997–2020), separately. Then we calculate the sum of incoming (outgoing) links to (from) the hot spot in East Asia divided by 24 for each node globally to obtain the probability map for 1949–1972 and 1997–2020, respectively, as shown in Figure 5a–d. We find that the nodes with the high probabilities of incoming links to the hot spot are mostly located in East Asia and surrounding areas (see Figure 5a). This is since these nodes are much closer to the hot spot in East Asia and, thus, more susceptible to the influence of the hot spot. Figure 5b shows the probability distribution for the outgoing link from the hot spot. The red cluster in Figure 5b shifts to the east relative to that of Figure 5a. This is due to the fact that, in the middle latitudes of the Northern Hemisphere, the air flow is mainly eastward. High probability values related to the hot spot are observed not only for the neighbors, but also for a small number of remote areas (see Figure 5a,b). For the most recent 24 years (1997–2020), we find that there are more remote areas with high probability values in comparison to the first 24 years (1949–1972), as shown in Figure 5c,d). To further show the differences between the two periods, we use the probability of 1997–2020 minus that of 1949–1972, as shown in Figure 5e,f. The difference is significant when the values are above 1/8 (with 99% significance level). In this way, we obtain 15 nodes that are significantly influenced, and 13 of them have the positive difference values, Figure 5e. There are 18/21 nodes with positive differences in Figure 5f. It further demonstrates that more areas are connected to the hot spot in East Asia in recent years in comparison to that of early years. We find that the probabilities of incoming links from the South Pacific, Siberia, and the Rocky Mountains in North America to the hot spot in East Asia have greatly increased to >0.125 for 1997–2020, and the probabilities for 1949–1972 are only zero. Moreover, the probability of outgoing links from the hot spot in East Asia to South Asia is found to be greatly increased in recent years (see Figure 5f)
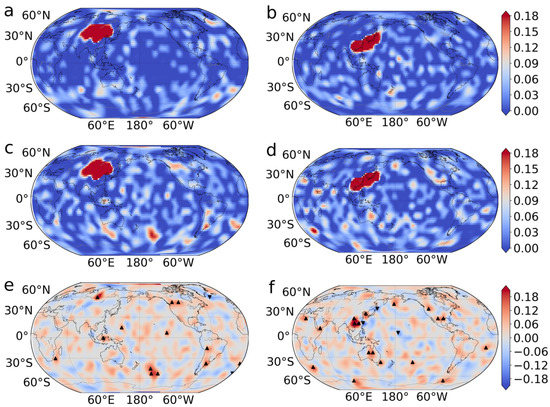
Figure 5.
Probability maps of emergence of (a) incoming links to the hot spot in East Asia and (b) outgoing links from the hot spot in East Asia for 1949–1972 years. (c,d) The same as (a) and (b), but for 1997–2020 years. The differences of the probability between 1949–1972 and 1997–2020 for (e) the incoming link and (f) the outgoing link, respectively. The black triangles in (e,f) indicate that the differences of the probability between 1949–1972 and 1997–2020 are at least 1/8 (with a 99% significance level).
4. Discussion
In recent years, the MK test has become a popular tool for studying climate change in different regions. For instance, Shawky et al. [21] used the MK test to estimate spatiotemporal changes in land surface temperature over South Asia, However, many of these studies have focused solely on individual regions without considering potential teleconnections between different regions, which can have significant impacts on climate patterns under global warming.
One example of a teleconnection is the Asia–North America pathway, which has been identified in several studies as a route for Rossby wave energy and extreme weather events to propagate from East Asia to North America [46]. Zhu et al. [47] proposed a new paradigm for summertime rainfall variation over the continental United States and showed a close relationship between East Asian monsoon precipitation and summer precipitation in the continental United States. Malloy et al. [48] indicated that the East Asian monsoon can excite a trans-Pacific Rossby column, further confirming this Asia–North America rainfall pattern. In addition, Wang et al. [49] examined successive extreme precipitation events across different regions, including India–Sri Lanka flooding, East Asian blizzard, and Canadian floods and found that they are connected by an Asia–North America teleconnection. Importantly, our study indicates that such teleconnection may become stronger under global warming, leading to more frequent and intense extreme weather events.
5. Conclusions
We have developed a climate network-based approach to investigate the impact of global warming on critical regions. To do this, we analyzed reanalysis (sig995 level) of near-surface daily air temperature data for different years and quantified the interactions between nodes using link weight to measure the interaction strength. The in- and out- degrees of a node served as indicators for the number and strength of incoming and outgoing links to and from it. We used the MK significance test to assess the degree parameter trends and elucidated changes in some crucial regions over the past 70 years under global warming. An increased in-degree or out-degree with time in a region indicated that it either influenced or was more strongly influenced by other regions under global warming, hence identifying it as a “hot spot”.
Our findings indicated that on land, the in-degree and out-degree increased with time, in regions such as East Asia, South America, and North Africa passing the MK significance test, possibly due to global warming. In contrast, the in-degree and out-degree in most ocean areas decreased, and, in particular, the in-degree in the central Pacific Ocean’s El Niño region significantly reduced due to weakened ocean circulations.
We presented three examples of hot spots on land, focusing on the East Asian hot spot, and identified the key regions connected to it with an increased probability under global warming. We found that in the most recent 24 years (1997–2020), more areas such as the South Pacific, Siberia, and North America were teleconnected to the East Asian hot spot than in the first 24 years (1949–1972). Moreover, the outgoing links from the East Asian hot spot to South Asia substantially increased in recent years. Further studies are needed to explore the mechanisms influencing the network evolution in these key areas and determine the risk assessment of global warming.
Author Contributions
Conceptualization, Y.Z., J.F. and W.L.; methodology, H.K., Y.Z. and J.F.; software, H.K. and P.Y.; validation, H.K. and P.Y.; formal analysis, H.K. and P.Y.; investigation, H.K. and P.Y.; resources, Y.Z. and J.F.; data curation, H.K.; writing—original draft preparation, H.K. and P.Y.; writing—review and editing, Y.Z., J.F. and W.L.; visualization, H.K.; supervision, Y.Z. and W.L.; project administration, Y.Z. and W.L.; funding acquisition, Y.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Fundamental Research Program of Yunnan Province (No. CB22052C173A), the National Natural Science Foundation of China (No. 61573173), and the Yunnan Academician Workstation of Wang Jingxiu (202005AF150025). J.F acknowledges the support by the National Natural Science Foundation of China (Grant No. 12205025, 12275020, 12135003).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data/reanalysis that supports the findings of this study are publicly available online: NCEP/NCAR reanalysis near-surface (sig995 level) daily air temperature data [39], https://www.esrl.noaa.gov/psd/data/gridded/data.ncep.reanalysis.derived.surface.html, accessed on 14 September 2022.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Christopher, B.F.; Barros, V.; Stocker, T.F.; Dahe, Q. Managing the Risks of Extreme Events and Disasters to Advance Climate Change Adaptation: Special Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Marcia, M. Climate Change Impacts. Science 2013, 341, 435. [Google Scholar]
- Hunt, A.; Watkiss, P. Climate change impacts and adaptation in cities: A review of the literature. Clim. Chang. 2010, 104, 13–49. [Google Scholar] [CrossRef]
- Jansson, J.K.; Hofmockel, K.S. Soil microbiomes and climate change. Nat. Rev. Microbiol. 2020, 18, 35–46. [Google Scholar] [CrossRef] [PubMed]
- Kirilenko, A.P.; Sedjo, R.A. Climate Change Impacts on Forestry. Proc. Natl. Acad. Sci. USA 2007, 104, 19697–19702. [Google Scholar] [CrossRef] [PubMed]
- Ray, D.K.; West, P.C.; Clark, M.; Gerber, J.S.; Prishchepov, A.V.; Chatterjee, S. Climate change has likely already affected global food production. PLoS ONE 2019, 14, e0217148. [Google Scholar] [CrossRef]
- Hinkel, J.; Aerts, J.C.H.; Brown, S.; Jiménez, J.A.; Lincke, D.; Nicholls, R.J.; Scussolini, P.; Sanchez-Arcilla, A.; Vafeidis, A.; Addo, K.A. The Ability of Societies to Adapt to Twenty-First-Century Sea-Level Rise. Nat. Clim. Change 2018, 8, 570–578. [Google Scholar] [CrossRef]
- Pachauri, R.K.; Myles, R.A.; Vicente, R.B.; John, B.; Wolfgang, C.; Renate, C.; John, A.C.; Leon, C.; Qin, D.; Purnamita, D. Climate Change 2014: Synthesis Report. Contribution of Working Groups I, Ii and Iii to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Ipcc: Geneva, Switzerland, 2014. [Google Scholar]
- Caesar, L.; Rahmstorf, S.; Robinson, A.; Feulner, G.; Saba, V. Observed fingerprint of a weakening Atlantic Ocean overturning circulation. Nature 2018, 556, 191–196. [Google Scholar] [CrossRef]
- Min, S.-K.; Zhang, X.; Zwiers, F.W.; Hegerl, G.C. Human contribution to more-intense precipitation extremes. Nature 2011, 470, 378–381. [Google Scholar] [CrossRef]
- Karzani, M.; Ghavidel, Y.; Farajzadeh, M. Temporal Changes in Lethal Temperatures Above 50 °C in the Northern Hemisphere. Pure Appl. Geophys. 2022, 179, 3377–3390. [Google Scholar] [CrossRef]
- Zerafati, H.; Ghavidel, Y.; Farajzadeh, M. Historical reconstruction and statistical survey on long-term temporal changes in temperatures above 50 °C in West Asia. Arab. J. Geosci. 2021, 14, 2242. [Google Scholar] [CrossRef]
- Falkner, R. The Paris Agreement and the new logic of international climate politics. Int. Aff. 2016, 92, 1107–1125. [Google Scholar] [CrossRef]
- Geng, Z.; Zhang, Y.; Lu, B.; Fan, J.; Zhao, Z.; Chen, X. Network-Synchronization Analysis Reveals the Weakening Tropical Circulations. Geophys. Res. Lett. 2021, 48, e2021GL093582. [Google Scholar] [CrossRef]
- Akhter, M.N.; Mekhilef, S.; Mokhlis, H.; Shah, N.M. Review on forecasting of photovoltaic power generation based on machine learning and metaheuristic techniques. IET Renew. Power Gener. 2019, 13, 1009–1023. [Google Scholar] [CrossRef]
- Al-Ghussain, L. Global warming: Review on driving forces and mitigation. Environ. Prog. Sustain. Energy 2018, 38, 13–21. [Google Scholar] [CrossRef]
- Rahmstorf, S.; Ganopolski, A. Long-Term Global Warming Scenarios Computed with an Efficient Coupled Climate Model. Clim. Chang. 1999, 43, 353–367. [Google Scholar] [CrossRef]
- Cox, P.M.; Richard, A.B.; Chris, D.J.; Steven, A.S.; Ian, J.T. Acceleration of Global Warming Due to Carbon-Cycle Feedbacks in a Coupled Climate Model. Nature 2000, 408, 184–187. [Google Scholar] [CrossRef] [PubMed]
- Huybrechts, P.; De Wolde, J. The Dynamic Response of the Greenland and Antarctic Ice Sheets to Multiple-Century Climatic Warming. J. Clim. 1999, 12, 2169–2188. [Google Scholar] [CrossRef]
- Liu, T.; Chen, D.; Yang, L.; Meng, J.; Wang, Z.; Ludescher, J.; Fan, J.; Yang, S.; Chen, D.; Kurths, J.; et al. Teleconnections among tipping elements in the Earth system. Nat. Clim. Chang. 2023, 13, 67–74. [Google Scholar] [CrossRef]
- Shawky, M.; Ahmed, M.R.; Ghaderpour, E.; Gupta, A.; Achari, G.; Dewan, A.; Hassan, Q.K. Remote sensing-derived land surface temperature trends over South Asia. Ecol. Inform. 2023, 74, 101969. [Google Scholar] [CrossRef]
- Ghaderpour, E.; Mazzanti, P.; Mugnozza, G.S.; Bozzano, F. Coherency and phase delay analyses between land cover and climate across Italy via the least-squares wavelet software. Int. J. Appl. Earth Obs. Geoinf. 2023, 118, 103241. [Google Scholar] [CrossRef]
- Li, M.; Qin, Y.; Zhang, T.; Zhou, X.; Yi, G.; Bie, X.; Li, J.; Gao, Y. Climate Change and Anthropogenic Activity Co-Driven Vegetation Coverage Increase in the Three-North Shelter Forest Region of China. Remote Sens. 2023, 15, 1509. [Google Scholar] [CrossRef]
- Watts, D.J.; Strogatz, S.H. Collective dynamics of ‘small-world’ networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef]
- Barabási, A.; Réka, A. Emergence of Scaling in Random Networks. Science 1999, 286, 509–512. [Google Scholar] [CrossRef] [PubMed]
- Blondel, V.D.; Jean-Loup, G.; Renaud, L.; Etienne, L. Fast Unfolding of Communities in Large Networks. J. Stat. Mech. Theory Exp. 2008, 2008, P10008. [Google Scholar] [CrossRef]
- Yamasaki, K.; Gozolchiani, A.; Havlin, S. Climate Networks around the Globe are Significantly Affected by El Niño. Phys. Rev. Lett. 2008, 100, 228501. [Google Scholar] [CrossRef] [PubMed]
- Fan, J.; Meng, J.; Ashkenazy, Y.; Havlin, S.; Schellnhuber, H.J. Climate network percolation reveals the expansion and weakening of the tropical component under global warming. Proc. Natl. Acad. Sci. USA 2018, 115, E12128–E12134. [Google Scholar] [CrossRef]
- Ludescher, J.; Gozolchiani, A.; Bogachev, M.I.; Bunde, A.; Havlin, S.; Schellnhuber, H.J. Very Early Warning of Next El Niño. Proc. Natl. Acad. Sci. USA 2014, 111, 2064–2066. [Google Scholar] [CrossRef]
- Fan, J.; Meng, J.; Ashkenazy, Y.; Havlin, S.; Schellnhuber, H.J. Network analysis reveals strongly localized impacts of El Niño. Proc. Natl. Acad. Sci. USA 2017, 114, 7543–7548. [Google Scholar] [CrossRef]
- Meng, J.; Fan, J.; Ashkenazy, Y.; Bunde, A.; Havlin, S. Forecasting the magnitude and onset of El Niño based on climate network. New J. Phys. 2018, 20, 043036. [Google Scholar] [CrossRef]
- Boers, N.; Bookhagen, B.; Barbosa, H.M.J.; Marwan, N.; Kurths, J.; Marengo, J.A. Prediction of extreme floods in the eastern Central Andes based on a complex networks approach. Nat. Commun. 2014, 5, 5199. [Google Scholar] [CrossRef]
- Boers, N.; Bedartha, G.; Aljoscha, R.; Bodo, B.; Brian, H.; Jürgen, K. Complex Networks Reveal Global Pattern of Extreme-Rainfall Teleconnections. Nature 2019, 566, 373–377. [Google Scholar] [CrossRef] [PubMed]
- Jingfang, F.; Meng, J.; Ludescher, J.; Zhaoyuan, L.; Surovyatkina, E.; Xiaosong, C.; Jürgen, K.; Schellnhuber, H.J. Network-Based Approach and Climate Change Benefits for Forecasting the Amount of Indian Monsoon Rainfall. J. Clim. 2022, 35, 1009–1020. [Google Scholar]
- Fan, J.; Meng, J.; Ludescher, J.; Chen, X.; Ashkenazy, Y.; Kurths, J.; Havlin, S.; Schellnhuber, H.J. Statistical physics approaches to the complex Earth system. Phys. Rep. 2020, 896, 1–84. [Google Scholar] [CrossRef] [PubMed]
- Reichstein, M.; Camps-Valls, G.; Stevens, B.; Jung, M.; Denzler, J.; Carvalhais, N.; Prabhat. Deep learning and process understanding for data-driven Earth system science. Nature 2019, 566, 195–204. [Google Scholar] [CrossRef] [PubMed]
- Rolnick, D.; Donti, P.L.; Kaack, L.H.; Kochanski, K.; Lacoste, A.; Sankaran, K.; Ross, A.S.; Milojevic-Dupont, N.; Jaques, N.; Waldman-Brown, A.; et al. Tackling Climate Change with Machine Learning. ACM Comput. Surv. 2022, 55, 1–96. [Google Scholar] [CrossRef]
- Wu, L.; Wang, S.; Bai, X.; Chen, F.; Li, C.; Ran, C.; Zhang, S. Identifying the Multi-Scale Influences of Climate Factors on Runoff Changes in a Typical Karst Watershed Using Wavelet Analysis. Land 2022, 11, 1284. [Google Scholar] [CrossRef]
- Kalnay, E.; Kanamitsu, M.R.; Kistler, W.; Collins, D.; Deaven, L.; Gandin, M.; Iredell, S.; Saha, G.; White, J.; Woollen, Y.; et al. The Ncep/Ncar 40-Year Reanalysis Project. Bull. Am. Meteorol. Soc. 1996, 77, 437–472. [Google Scholar] [CrossRef]
- Gozolchiani, A.; Havlin, S.; Yamasaki, K. Emergence of El Niño as an Autonomous Component in the Climate Network. Phys. Rev. Lett. 2011, 107, 148501. [Google Scholar] [CrossRef]
- Mann, H.B. Nonparametric Tests against Trend. Econom. J. Econom. Soc. 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods; Griffin Press: Salisbury, UK, 1948. [Google Scholar]
- Wang, Y.; Gozolchiani, A.; Ashkenazy, Y.; Berezin, Y.; Guez, O.; Havlin, S. Dominant Imprint of Rossby Waves in the Climate Network. Phys. Rev. Lett. 2013, 111, 138501. [Google Scholar] [CrossRef]
- Guez, O.C.; Gozolchiani, A.; Havlin, S. Influence of autocorrelation on the topology of the climate network. Phys. Rev. E 2014, 90, 062814. [Google Scholar] [CrossRef] [PubMed]
- Vecchi, G.A.; Soden, B. Global Warming and the Weakening of the Tropical Circulation. J. Clim. 2007, 20, 4316–4340. [Google Scholar] [CrossRef]
- Yu, B.; Lin, H. Modification of the wintertime Pacific–North American pattern related North American climate anomalies by the Asian–Bering–North American teleconnection. Clim. Dyn. 2019, 53, 313–328. [Google Scholar] [CrossRef]
- Zhiwei, Z.; Tim, L. A New Paradigm for Continental U.S. Summer Rainfall Variability: Asia–North America Teleconnection. J. Clim. 2016, 29, 7313–7327. [Google Scholar]
- Kelsey, M.; Kirtman, B.P. The Summer Asia–North America Teleconnection and Its Modulation by Enso in Community Atmosphere Model, Version 5 (Cam5). Clim. Dyn. 2022, 59, 2213–2230. [Google Scholar]
- Bin Wang, B.; Lee, M.-Y.; Xie, Z.; Lu, M.; Pan, M. A new Asian/North American teleconnection linking clustered extreme precipitation from Indian to Canada. Npj Clim. Atmos. Sci. 2022, 5, 90. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).