Modeling Tool for Estimating Carbon Dioxide Fluxes over a Non-Uniform Boreal Peatland
Abstract
1. Introduction
2. Methods
2.1. Field Observations
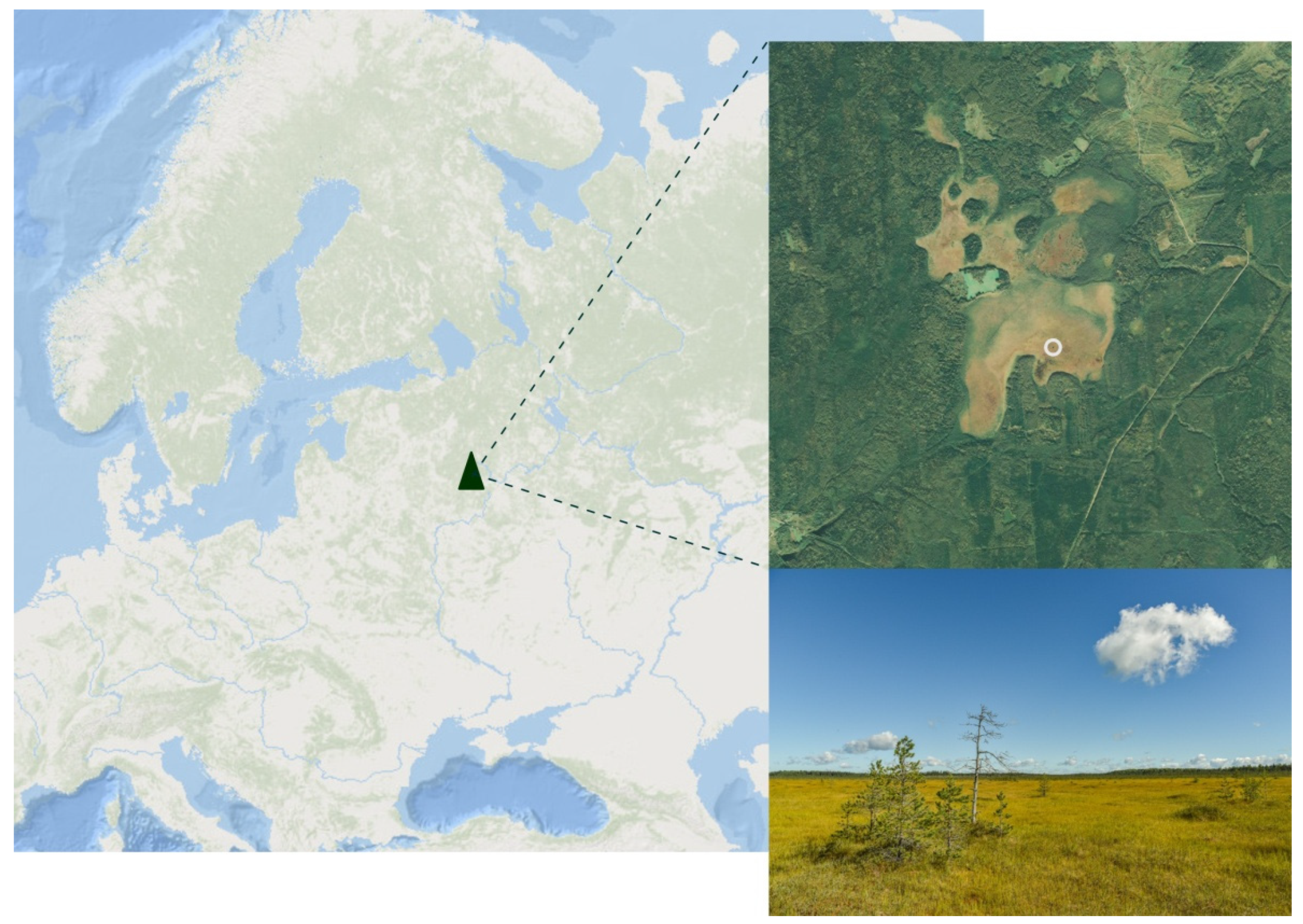
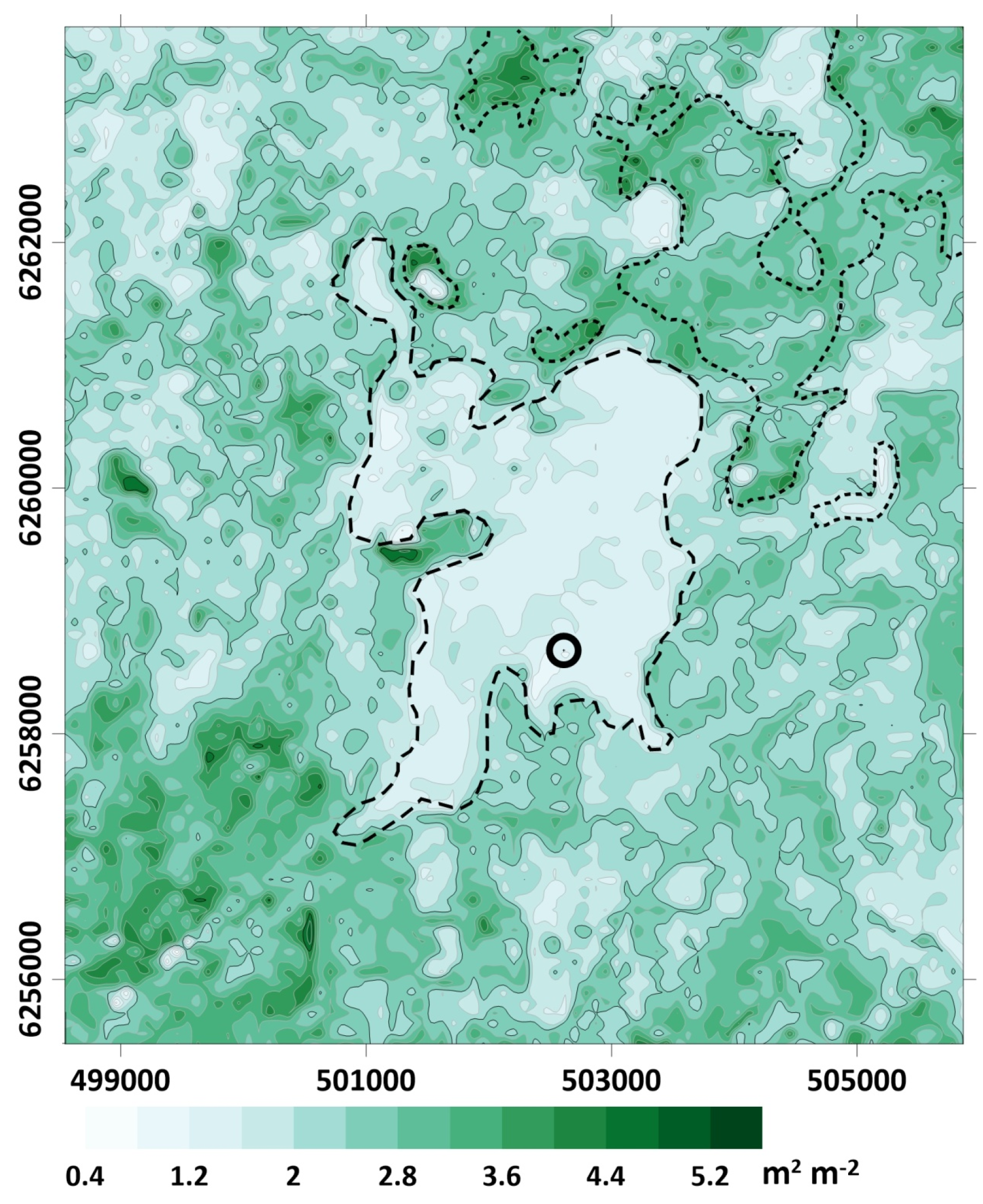
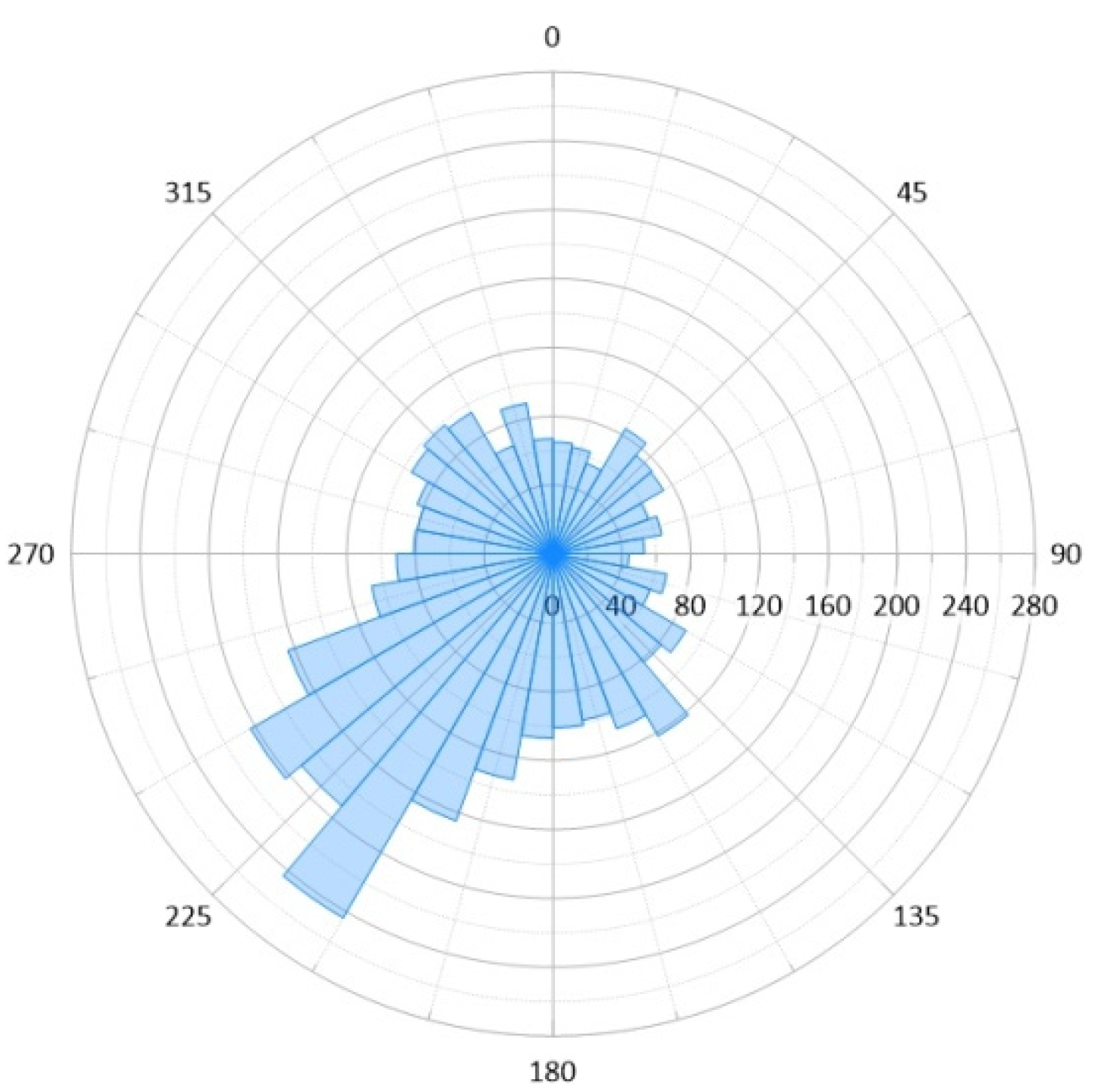
2.1.1. Experimental Site
2.1.2. Flux Measurements
2.2. Modeling of CO2 Transport in the Atmospheric Boundary Layer
2.2.1. Airflow Model
2.2.2. Modeling of the CO2 Emission, Uptake, and Turbulent Transfer
2.2.3. Model Initialization and Solution
3. Results and Discussion
3.1. Spatial Distributions of Wind Speed and Turbulent Kinetic Energy within the Modeling Domain
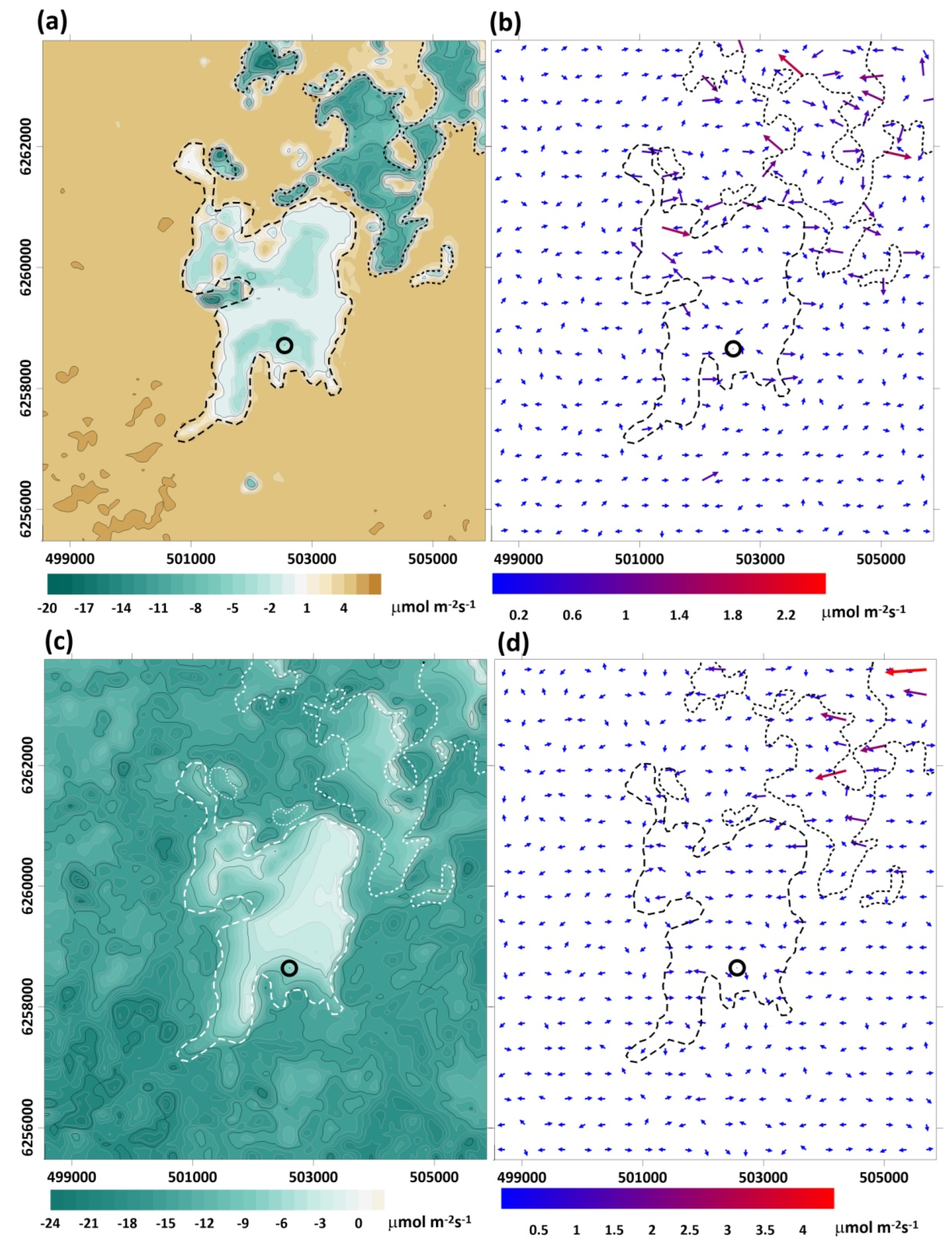
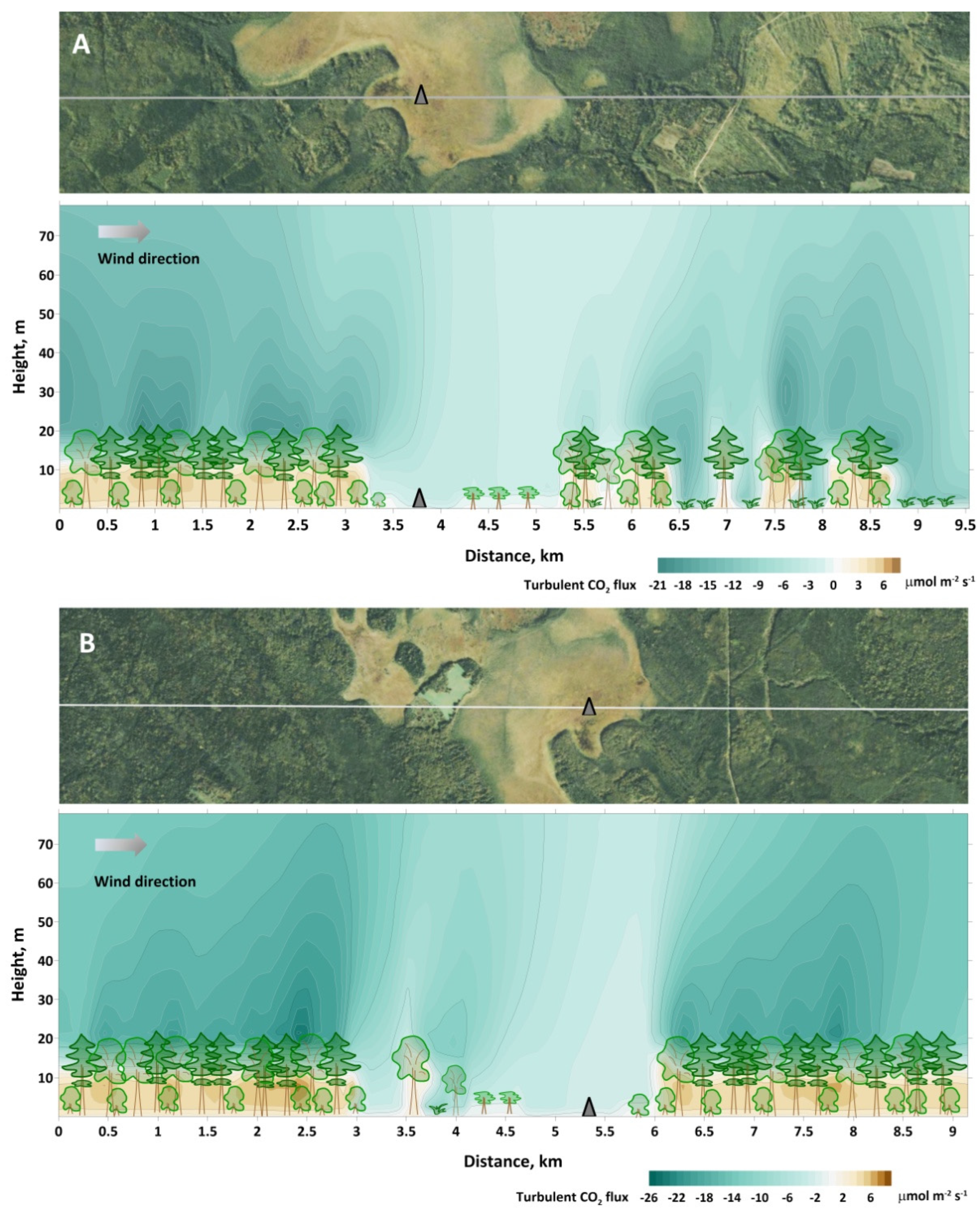
3.2. Spatial Patterns of CO2 Fluxes within the Modeling Domain
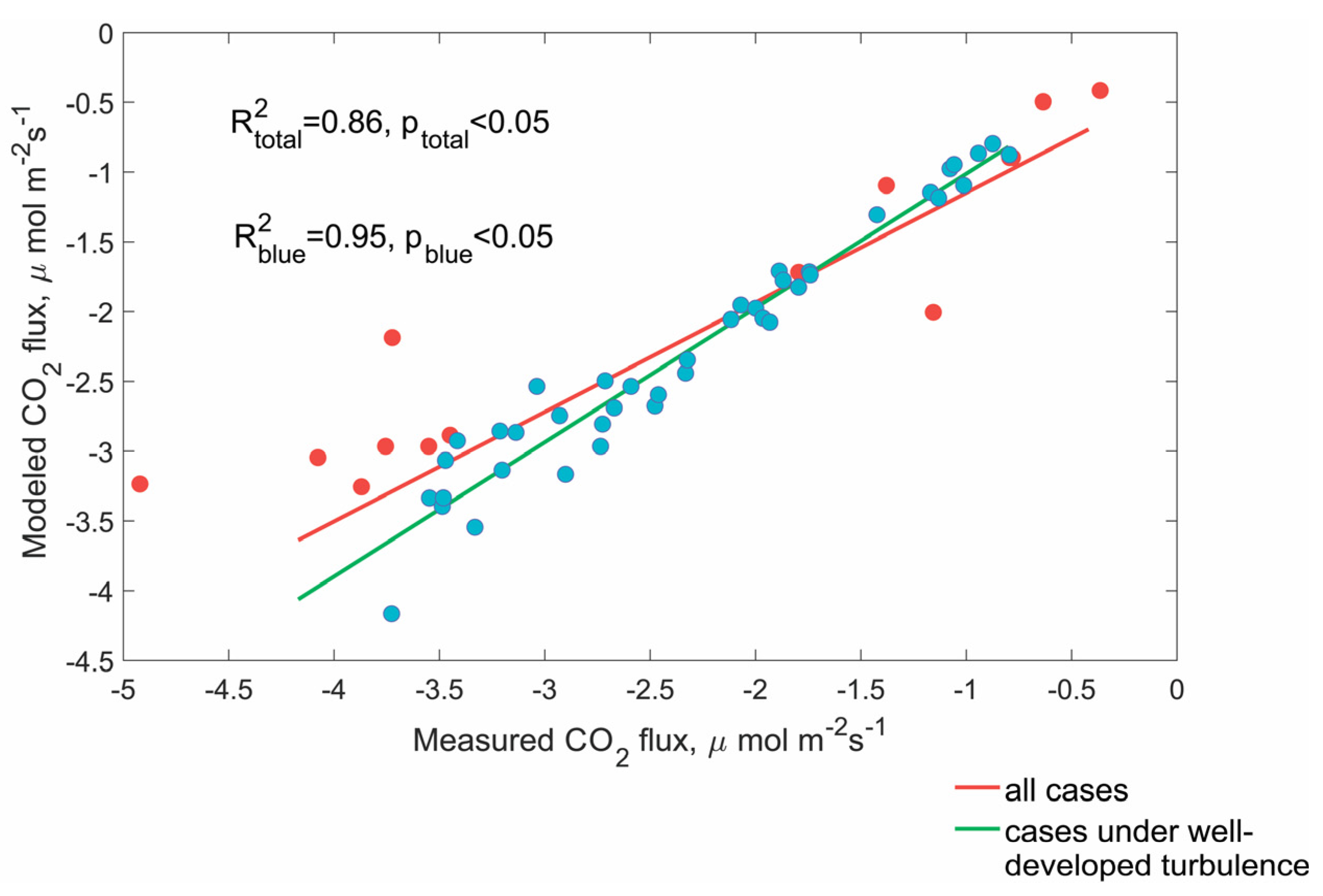
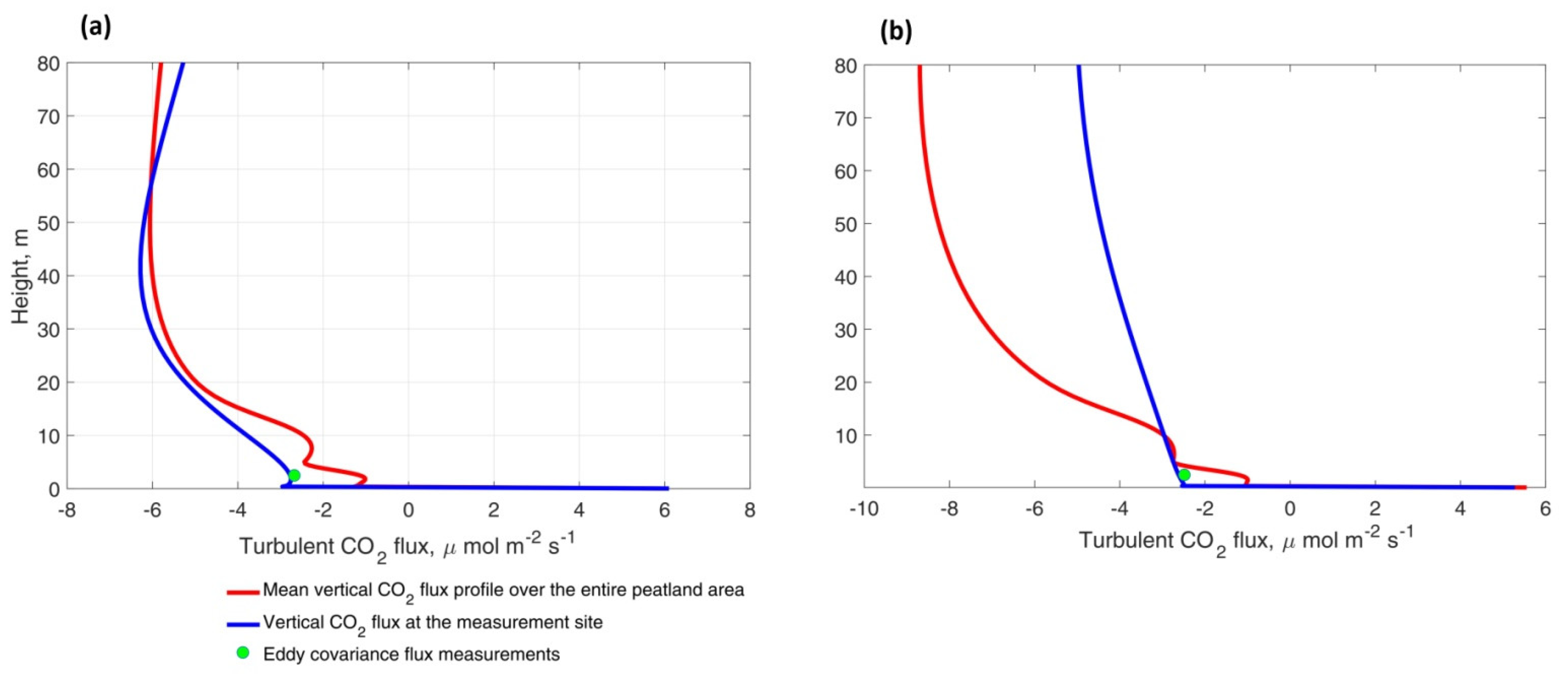
3.3. Comparison of the Model Simulation and Eddy Covariance CO2 Flux Measurements
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pörtner, H.-O.; Roberts, D.C.; Tignor, M.; Poloczanska, E.S.; Mintenbeck, K.; Alegría, A.; Craig, M.; Langsdorf, S.; Löschke, S.; Möller, V.; et al. (Eds.) IPCC, 2022: Climate Change 2022: Impacts, Adaptation, and Vulnerability; Contribution of Working Group II to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2022; 3056p. [Google Scholar]
- Yue, X.-L.; Gao, Q.-X. Contributions of natural systems and human activity to greenhouse gas emissions. Adv. Clim. Change Res. 2018, 9, 243–252. [Google Scholar] [CrossRef]
- Dong, F.; Qin, C.; Zhang, X.; Zhao, X.; Pan, Y.; Gao, Y.; Zhu, J.; Li, Y. Towards Carbon Neutrality: The Impact of Renewable Energy Development on Carbon Emission Efficiency. Int. J. Environ. Res. Public Health 2021, 18, 13284. [Google Scholar] [CrossRef] [PubMed]
- Bonan, G.B. Forests and climate change: Forcings, feedbacks, and the climate benefits of forests. Science 2008, 320, 1444–1449. [Google Scholar] [CrossRef] [PubMed]
- Friedlingstein, P.; O’Sullivan, M.; Jones, M.W.; Andrew, R.M.; Gregor, L.; Hauck, J.; Le Quéré, C.; Luijkx, I.T.; Olsen, A.; Peters, G.P.; et al. Global Carbon Budget. Earth Syst. Sci. Data 2022, 14, 4811–4900. [Google Scholar] [CrossRef]
- Khalil, K.; Mary, B.; Renault, P. Nitrous oxide production by nitrification and denitrification in soil aggregates as affected by O2 concentration. Soil Biol. Biochem. 2004, 36, 687–699. [Google Scholar] [CrossRef]
- Aubinet, M.; Vesala, T.; Papale, D. Eddy Covariance: A Practical Guide to Measurement and Data Analysis; Springer: Dordrecht, The Netherlands, 2012; p. 438. [Google Scholar]
- Pumpanen, J.; Kolari, P.; Ilvesniemi, H.; Minkkinen, K.; Vesala, T.; Niinisto, S.; Lohila, A.; Larmola, T.; Morero, M.; Pihlatie, M.; et al. Comparison of different chamber techniques for measuring soil CO2 efflux. Agric. For. Meteorol. 2004, 123, 159–176. [Google Scholar] [CrossRef]
- Foken, T. The energy balance closure problem: An overview. Ecol. Appl. 2008, 18, 1351–1367. [Google Scholar] [CrossRef]
- Sogachev, A.; Panferov, O.; Ahrends, B.; Doering, C.; Jørgensen, H.E. Numerical assessment of the effect of forest structure changes on CO2 flux footprints for the flux tower in Solling, Germany. Agric. For. Meteorol. 2011, 151, 746–754. [Google Scholar] [CrossRef]
- Vesala, T.; Huotari, J.; Rannik, Ü.; Suni, T.; Smolander, S.; Sogachev, A.; Launiainen, S.; Ojala, A. Eddy covariance measurements of carbon exchange and latent and sensible heat fluxes over a boreal lake for a full open-water period. J. Geophys. Res. Atmos. 2006, 111, D11101. [Google Scholar] [CrossRef]
- Sellers, P.; Dickinson, R.E.; Randall, D.A.; Betts, A.K.; Hall, F.G.; Berry, J.A.; Collatz, G.J.; Denning, A.S.; Mooney, H.A.; Nobre, C.A.; et al. Modeling the exchanges of energy, water, and carbon between continents and the atmosphere. Science 1997, 275, 502–509. [Google Scholar] [CrossRef]
- Vager, B.; Nadezhina, E. Atmospheric Boundary Layer in Conditions of Horizontal Non-Uniformity; Gidrometeoizdat: Leningrad, Russia, 1979. (In Russian) [Google Scholar]
- Penenko, V.; Aloyan, A. Models and Methods for Environmental Protection Problems; Science Publications: Moscow, Russia, 1985. (In Russian) [Google Scholar]
- Sogachev, A.; Panferov, O. Modification of two-equation models to account for plant drug. Bound. Layer Meteorol. 2006, 121, 229–266. [Google Scholar] [CrossRef]
- Sullivan, P.P.; McWilliams, J.C.; Moeng, C.-H. A subgrid-scale model for large-eddy simulation of planetary boundary-layer flows. Bound. Layer Meteorol. 1994, 71, 247–276. [Google Scholar] [CrossRef]
- Warner, T.T. Numerical Weather and Climate Prediction; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Stull, R.B. An introduction to Boundary Layer Meteorology; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1988. [Google Scholar] [CrossRef]
- Garrat, J. The Atmospheric Boundary Layer; Cambridge University Press: Cambridge, UK, 1992. [Google Scholar]
- Wyngaard, J.C. Turbulence in the Atmosphere; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Raupach, M.R.; Finnigan, J.J. Single-layer models of evaporation from plant canopy are incorrect but useful, whereas multilayer models are correct but useless: Discuss. Aust. J. Plant Physiol. 1988, 15, 705–716. [Google Scholar] [CrossRef]
- Olchev, A.; Radler, K.; Sogachev, A.; Panferov, O.; Gravenhorst, G. Application of a three-dimensional model for assessing effects of small clear-cuttings on radiation and soil temperature. Ecol. Model. 2009, 220, 3046–3056. [Google Scholar] [CrossRef]
- Payne, R.J.; Malysheva, E.; Tsyganov, A.; Pampura, T.; Novenko, E.; Volkova, E.; Babeshko, K.; Mazei, Y. A multi-proxy record of Holocene environmental change, peatland development and carbon accumulation from Staroselsky Moch peatland, Russia. Holocene 2016, 26, 314–326. [Google Scholar] [CrossRef]
- Peel, M.C.; Finlayson, B.L.; McMahon, T.A. Updated world map of the Koppen-Geiger climate classification. Hydrol. Earth Syst. Sci. 2007, 11, 1633–1644. [Google Scholar] [CrossRef]
- Novenko, E.Y.; Olchev, A.V. Early Holocene vegetation and climate dynamics in the central part of the East European Plain (Russia). Quat. Int. 2015, 388, 12–22. [Google Scholar] [CrossRef]
- Papale, D.; Reichstein, M.; Aubinet, M.; Canfora, E.; Bernhofer, C.; Kutsch, W.; Longdoz, B.; Rambal, S.; Valentini, R.; Vesala, T.; et al. Towards a standardized processing of Net Ecosystem Exchange measured with eddy covariance technique: Algorithms and uncertainty estimation. Biogeosciences 2006, 3, 571–583. [Google Scholar] [CrossRef]
- Kljun, N.; Calanca, P.; Rotach, M.W.; Schmid, H.P. A simple parameterization for flux footprint predictions. Bound. Layer Meteorol. 2004, 112, 503–523. [Google Scholar] [CrossRef]
- Dubov, A.S.; Bykova, L.P.; Marunich, S.V. Turbulence in Vegetation Canopy; Gidrometeoizdat: Leningrad, Russia, 1978. (In Russian) [Google Scholar]
- Sogachev, A.; Menzhulin, G.V.; Heimann, M.; Lloyd, J. A simple three-dimensional canopy-planetary boundary layer simulation model for scalar concentrations and fluxes. Tellus 2002, 54B, 784–819. [Google Scholar]
- Sorbjan, Z. Structure of the Atmospheric Boundary Layer; Prentice-Hall: Englewood Cliffs, NJ, USA, 1989. [Google Scholar]
- Katul, G.G.; Mahrt, L.; Poggi, D.; Sanz, C. One- and two-equation models for canopy turbulence. Bound. Layer Meteorol. 2004, 113, 81–109. [Google Scholar] [CrossRef]
- Mamkin, V.V.; Mukhartova, Y.V.; Diachenko, M.S.; Kurbatova, J.A. Three-year variability of energy and carbon dioxide fluxes at clear-cut forest site in the European Southern Taiga. Geogr. Environ. Sustain. 2019, 1, 197–212. [Google Scholar] [CrossRef]
- Olchev, A.V.; Mukhartova, Y.V.; Levashova, N.T.; Volkova, E.M.; Ryzhova, M.S.; Mangura, P.A. The influence of the spatial heterogeneity of vegetation cover and surface topography on vertical CO2 fluxes within the atmospheric surface layer. Izv. Atmos. Ocean. Phys. 2017, 53, 539–549. [Google Scholar] [CrossRef]
- Sanz, C. A note on k-ε modelling of vegetation canopy airflows. Bound. Layer Meteorol. 2003, 108, 191–197. [Google Scholar] [CrossRef]
- Pope, S.B. Turbulent Flows; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Wilcox, D.C. Turbulence Modeling for CFD; DCW Industries, Inc.: La Canada, CA, USA, 1998. [Google Scholar]
- Kolmogorov, A. Turbulence flow equations of an uncompressible fluid. Trans. USSR Acad. Sci. Book Phys. 1942, 6, 56–58. [Google Scholar]
- Seginer, I.; Mulhearn, P.J.; Bradley, E.F.; Finnigan, J.J. Turbulent flow in a model plant canopy. Bound. Layer Meteorol. 1976, 10, 423–453. [Google Scholar] [CrossRef]
- Sogachev, A. A Note on Two-Equation Closure Modelling of Canopy Flow. Bound. Layer Meteorol. 2009, 130, 423–435. [Google Scholar] [CrossRef]
- Mamkin, V.; Kurbatova, J.; Avilov, V.; Mukhartova, Y.; Krupenko, A.; Ivanov, D.; Levashova, N.; Olchev, A. Changes in net ecosystem exchange of CO2, latent and sensible heat fluxes in a recently clear-cut spruce forest in western Russia: Results from an experimental and modeling analysis. Environ. Res. Lett. 2016, 11, 125012. [Google Scholar] [CrossRef]
- Mukhartova, Y.V.; Dyachenko, M.S.; Mangura, P.A.; Mamkin, V.V.; Kurbatova, J.A.; Olchev, A.V. Application of a three-dimensional model to assess the effect of clear-cutting on carbon dioxide exchange at the soil-vegetation-atmosphere interface. IOP Conf. Ser. Earth Environ. Sci. 2019, 368, 012036. [Google Scholar] [CrossRef]
- Mukhartova, Y.V.; Mangura, P.A.; Levashova, N.T.; Olchev, A.V. Selection of boundary conditions for modeling the turbulent exchange process within the atmospheric surface layer. Comput. Res. Model. 2018, 10, 27–46. (In Russian) [Google Scholar] [CrossRef]
- Chen, H.; Sun, S.; Zhang, T. Energy Stability Analysis of Some Fully Discrete Numerical Schemes for Incompressible Navier-Stokes Equations on Staggered Grids. J. Sci. Comput. 2018, 75, 427–456. [Google Scholar] [CrossRef]
- Belotserkovskiy, O.M. Numerical Modeling in Continuum Mechanics; Fiziko-Matematicheskaya Literatura: Moscow, Russia, 1994. (In Russian) [Google Scholar]
- Mamkin, V.; Kurbatova, J.; Avilov, V.; Ivanov, D.; Kuricheva, O.; Varlagin, A.; Yaseneva, I.; Olchev, A. Energy and CO2 exchange in an undisturbed spruce forest and clear-cut in the Southern Taiga. Agric. For. Meteorol. 2019, 265, 252–268. [Google Scholar] [CrossRef]
- Belov, A.A.; Kalitkin, N.N. Evolutionary factorization and superfast relaxation count. Math. Model. Comput. Simul. 2015, 7, 103–116. [Google Scholar] [CrossRef]
- Belov, A.A.; Kalitkin, N.N.; Kuzmina, L.V. Modeling of chemical kinetics in gases. Math. Model. Comput. Simul. 2017, 9, 24–39. [Google Scholar] [CrossRef]
- Mukhartova, Y.; Postylyakov, O.; Davydova, M.; Zakharova, S. High-detailed tropospheric transport of NOx from ground sources: Comparison of model data and satellite imagery. In Proceedings of the Remote Sensing of Clouds and the Atmosphere XXVI, Online, 13–17 September 2021; p. 1185906. [Google Scholar]
- Flesch, T.K.; Prueger, J.H.; Hatfield, J.L. Turbulent Schmidt number from a tracer experiment. Agric. For. Meteorol. 2002, 111, 299–307. [Google Scholar] [CrossRef]
- Ball, J.T.; Woodrow, I.E.; Berry, J.A. A Model Predicting Stomatal Conductance and its Contribution to the Control of Photosynthesis under Different Environmental Conditions. In Progress in Photosynthesis Research; Springer: Dordrecht, The Netherlands, 1987; pp. 221–224. [Google Scholar]
- Leuning, R. A critical appraisal of a combined stomatal-photosynthesis model for C3 plants. Plant Cell Environ. 1995, 18, 339–355. [Google Scholar] [CrossRef]
- Oltchev, A.; Ibrom, A.; Constantin, J.; Falk, M.; Richter, I.; Morgenstern, K.; Joo, Y.; Kreilein, H.; Gravenhorst, G. Stomatal and surface conductance of a spruce forest: Model simulation and field measurements. J. Phys. Chem. Earth 1998, 23, 453–458. [Google Scholar] [CrossRef]
- Lloyd, J.; Taylor, J.A. On the temperature dependence of soil respiration. Funct. Ecol. 1994, 8, 315–323. [Google Scholar] [CrossRef]
- Blanken, P.D.; Williams, M.W.; Burns, S.P.; Monson, R.K.; Knowles, J.; Chowanski, K.; Ackerman, T. A comparison of water and carbon dioxide exchange at a windy alpine tundra and subalpine forest site near Niwot Ridge, Colorado. Biogeochemistry 2009, 95, 61–76. [Google Scholar] [CrossRef]
- Feigenwinter, C.; Bernhofer, C.; Eichelmann, U.; Heinesch, B.; Hertel, M.; Janous, D.; Kolle, O.; Lagergren, F.; Lindroth, A.; Minerbi, S.; et al. Comparison of horizontal and vertical advective CO2 fluxes at three forest sites. Agric. For. Meteorol. 2008, 148, 12–24. [Google Scholar] [CrossRef]
- Leuning, R.; Zegelin, S.J.; Jones, K.; Keith, H.; Hughes, D. Measurement of horizontal and vertical advection of CO2 within a forest canopy. Agric. For. Meteorol. 2008, 148, 1777–1797. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 Global Reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Kurbatova, J.; Li, C.; Varlagin, A.; Xiao, X.; Vygodskaya, N. Modeling carbon dynamics in two adjacent spruce forests with different soil conditions in Russia. Biogeosciences 2008, 5, 969–980. [Google Scholar] [CrossRef]
- Belcher, S.E.; Finnigan, J.J.; Harman, I.N. Flows through forest canopies in complex terrain. Ecol. Appl. 2008, 18, 1436–1453. [Google Scholar] [CrossRef]
- Detto, M.; Katul, G.G.; Siqueira, M.; Juang, J.H.; Stoy, P.C. The structure of turbulence near a tall forest edge: The backward facing step flow analogy revisited. Ecol. Appl. 2008, 18, 1420–1435. [Google Scholar] [CrossRef]
- Panferov, O.; Sogachev, A. Influence of gap size on wind damage variables in a forest. Agric. For. Meteorol. 2008, 148, 1869–1881. [Google Scholar] [CrossRef]
- An, L.; Wang, J.; Xiong, N.; Wang, Y.; You, J.; Li, H. Assessment of permeability windbreak forests with different porosities based on laser scanning and computational fluid dynamics. Remote Sens. 2022, 14, 3331. [Google Scholar] [CrossRef]
- Carey, J.C.; Tang, J.; Templer, P.H.; Kroeger, K.D.; Crowther, T.W.; Burton, A.J.; Dukes, J.S.; Emmett, B.; Frey, S.D.; Heskel, M.A.; et al. Temperature response of soil respiration largely unaltered with experimental warming. Proc. Natl. Acad. Sci. USA 2016, 113, 13797–13802. [Google Scholar] [CrossRef] [PubMed]
- Pridacha, V.B.; Sazonova, T.A.; Novichonok, E.V.; Semin, D.E.; Tkachenko, Y.N.; Pekkoev, A.N.; Timofeeva, V.V.; Bakhmet, O.N.; Olchev, A.V. Clear-cutting impacts nutrient, carbon and water exchange parameters in woody plants in an east Fennoscandian pine forest. Plant Soil 2021, 466, 317–336. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mukhartova, I.; Kurbatova, J.; Tarasov, D.; Gibadullin, R.; Sogachev, A.; Olchev, A. Modeling Tool for Estimating Carbon Dioxide Fluxes over a Non-Uniform Boreal Peatland. Atmosphere 2023, 14, 625. https://doi.org/10.3390/atmos14040625
Mukhartova I, Kurbatova J, Tarasov D, Gibadullin R, Sogachev A, Olchev A. Modeling Tool for Estimating Carbon Dioxide Fluxes over a Non-Uniform Boreal Peatland. Atmosphere. 2023; 14(4):625. https://doi.org/10.3390/atmos14040625
Chicago/Turabian StyleMukhartova, Iuliia, Julia Kurbatova, Denis Tarasov, Ravil Gibadullin, Andrey Sogachev, and Alexander Olchev. 2023. "Modeling Tool for Estimating Carbon Dioxide Fluxes over a Non-Uniform Boreal Peatland" Atmosphere 14, no. 4: 625. https://doi.org/10.3390/atmos14040625
APA StyleMukhartova, I., Kurbatova, J., Tarasov, D., Gibadullin, R., Sogachev, A., & Olchev, A. (2023). Modeling Tool for Estimating Carbon Dioxide Fluxes over a Non-Uniform Boreal Peatland. Atmosphere, 14(4), 625. https://doi.org/10.3390/atmos14040625





