Abstract
Hybrid Electric Vehicles (HEVs) are a prominent solution for reducing CO2 emissions from transport in Europe. They are equipped with at least two propulsion energy converters, an Internal Combustion Engine (ICE) and one or more Electric Machines (EMs), operated in a way to exploit synergies and achieve fuel efficiency. Because of the variety in configurations and strategies, the use of simulation is essential for vehicle development and characterisation of energy consumption. This paper introduces a novel simulation approach to estimate the CO2 emissions from different hybrid architectures (series, parallel, power-split) and electrification degrees (mild, full, plug-in and range extender) that is relatively simple, flexible and accurate. The approach identifies the optimal power split between the energy converters for any given time in a driving cycle according to three evaluation levels: supervisor, ICE manager and optimiser. The latter relies on the Equivalent Consumption Minimisation Strategy (ECMS) and the limitations imposed by the other two layers. Six light-duty HEVs with different hybrid architectures were tested to support the development of the approach. The results show an indicative accuracy of ±5%, enabling to run assessments of hybrid powertrain solutions and supporting regulatory and consumer information initiatives.
1. Introduction
The European Climate Law [1] calls for the European Union to become climate-neutral by 2050, stipulating that all sectors contribute to this end. The transport sector, particularly road transport, is a significant contributor of greenhouse gases, and its CO2 emissions have increased in the past decades. New policies that are being formed will significantly affect both Light-Duty (LD) and Heavy-Duty (HD) vehicles in the near future. In this context, Hybrid Electric Vehicles (HEV) represent an effective and market-ready solution to immediately start reducing (not eliminating) tailpipe CO2 emissions meanwhile paving the way for zero-emissions technologies necessary for achieving a climate-neutral transport system; simultaneously, they are capable of keeping the criteria pollutants well below the regulated limit values. Hybridised vehicles can be quickly deployed as they do not require significant changes in the infrastructure or in the drivers’ habits compared to conventional pure-ICE vehicles. Since these benefits come at a competitive and sustainable price, often supported by incentives at national or regional levels, it could be assumed that HEV market share will increase in the years to come. While the already established technologies are becoming more cost-effective, newer and much cheaper hybrid solutions (e.g., mild hybrids) appear in the market, pushing further market shares [2]. In 2021 hybrid vehicles accounted for 28% of the EU light-duty vehicle market, experiencing a fast rise and confirming the market’s and users’ acceptance of this propulsion system [3,4,5].
Hybrid powertrains are characterised by the presence of both an ICE and one or more EMs. A challenging aspect to be modelled on HEVs is the Charge-Sustaining (CS) operating mode, which is the only way mild and full hybrids can be operated; it consists of an operation logic that increases the overall system (ICE and electrics) energy efficiency by keeping the propulsion battery balanced over the long term. On the other hand, Plug-in and Range Extenders (REx) hybrids are featured by an additional operating mode, the Charge-Depleting (CD), whose target is not necessarily that of maximising the overall system efficiency but rather that of achieving pure electric driving to the extent possible, and simultaneously minimise the tailpipe pollutants and CO2 emissions. Although this study focuses mainly on the modelling of the CS operation, a simple approach towards the modelling of the CD operation is also briefly discussed [6,7].
HEVs use either the ICE, the EMs or a combination thereof to deliver the power needed to support propulsion at the wheels. The power is assigned to the energy converters depending on the total power demand and quantities defining the powertrain status: temperatures, rotational speeds and, most importantly, the battery State of Charge (SoC). To keep the latter within the boundaries of the CS operation (narrow band around a reference point), and to ensure the most efficient operation is achieved, HEVs are equipped with controllers deploying sophisticated proprietary control strategies [8]. These are frequently developed on the basis of well-known global optimisation algorithms, e.g., Dynamic Programming (DP) or Pontryagin Minimum Principle (PMP), which are then implemented at vehicle-level using simplifying assumptions (local optimisation) to reduce the computational effort required; the most commonly adopted strategy with these characteristics is the Equivalent Consumption Minimisation Strategy (ECMS) [9,10,11]. The latter is used to evaluate, for each time instant, the cost associated with fuel consumption and the virtual cost related to using battery energy, quantified by a dedicated equivalence factor; the algorithm finally selects the powertrain solution that returns the minimum equivalent consumption. It enables for a cycle-independent optimisation, given that appropriate equivalence factors are used [12,13,14]. Additional reasons favouring the selection of the ECMS stand in its adaptability towards innovative hybrid powertrain solutions that might differ significantly from the most common HEVs (e.g., fuel-cell-based powertrains [15]) and the possibility of adding elements to the optimisation cost function (e.g., pollutants emissions or durability effects [16]) to obtain a more comprehensive solution.
Understanding the CO2 emissions these vehicles exhibit under different operating conditions (route, driving style, ambient temperature, traffic conditions) is essential for objectively quantifying their benefits under real-world use. Unfortunately, this is hindered by the higher level of complexity associated with hybrid powertrains, requiring the development of dedicated simulation tools that are able to deal with such complexity [17,18]. In this study, the applicability of a generalised ECMS-based hybrid controller [19] in a generalised vehicle simulation tool is assessed; such an approach does not use many of the inputs and real-time quantities that are required and used by proprietary control strategies, enabling the simulation of a large variety of vehicles by providing only a reduced set of data. Physical constraints such as rotational speed and power limits of driveline components are also considered, and unrealistic operating conditions are excluded from the set that is provided to the optimiser [12]. The goal is to develop a simulation approach to predict realistic instantaneous operating conditions resembling those of the actual vehicle, but even more importantly, to capture the average vehicle efficiency over a trip for a large portion of the vehicles in the European fleet. In this first stage, the approach is developed and evaluated based on the fuel consumption and CO2 emissions results from laboratory results (WLTC tests) to create the common framework for the different hybrid architectures and simulate the realistic powertrain conditions, which reflects the achievements of this work. The novelty elements are the easy adaptability to different powertrain architectures and the opportunity to run vehicle simulations requiring a smaller amount of input data compared to other tools. In a later stage, the approach can be extended to cover the more complex and diverse real-world conditions and become a useful tool for understanding the real-world fuel consumption gap.
To this aim, six HEVs were tested following the WLTP provisions in the laboratories of the European Commission’s Joint Research Centre (JRC) and the tailpipe CO2 emissions were measured, together with other relevant powertrain quantities (electrical and mechanical power in different locations, battery SoC, temperatures, rotational speeds and others). The experimental findings were used to conceptualise, develop and refine the simulation strategy. Finally, the newly developed simulation tool was validated against test results not used during development.
2. Materials and Methods
2.1. Simulation Framework
This section describes the generic time-based modelling approach adopted for calculating energy consumption (EC) and fuel consumption (FC) from HEVs. Firstly, the approach selected for solving the longitudinal vehicle dynamics is presented and discussed. Secondly, the powertrain model is presented and the main differences from the most common implementations for conventional vehicles are highlighted. Thirdly, the electrical components of hybrid electric powertrains and the associated Electric Energy Consumption (EEC) modelling are presented. Lastly, the developed generic control strategy identifying the powertrain operating condition in each moment of the driving cycle is described.
2.2. Vehicle Energy and Fuel Consumption Calculation Principles
As far as vehicle simulation is concerned, a backwards-looking approach was selected [9]. For each time instant characterised in the time-based simulation, the first step is to calculate the mechanical power needed at wheels to follow the considered driving profile (see Appendix A for details). From the latter, the engine fuel consumption is obtained using a powertrain model that considers the driveline layout and components losses to calculate the amount of power that the ICE has to deliver to meet the demand at wheels. To calculate the fuel consumption, according to Guzzella et al. [9], three different approaches might be adopted on ICE conventional vehicles, ordered for increasing level of detail and accuracy: the average operating point approach, the quasi-static approach and the dynamic approach. While the first one requires the full driving cycle to be known a priori to shrink the full envelope of engine operating conditions into one representative operating point, the second applies the same concept on short time-intervals in which the vehicle speed, acceleration and slope can be considered constant. Lastly, the third approach is based on a mathematical formulation of the powertrain model using equations raising the level of complexity; the extra-effort is justified only in case the faster effects of the system dynamics are of interest (affecting drivability, comfort, pollutant emissions and other aspects). In conclusion, the quasi-static approach represents the most efficient way to capture the slower effects of the system dynamics, relevant for the characterisation of the fuel consumption, without unnecessarily increasing the level of complexity [9].
The most relevant drawbacks of the pure backwards-looking approach are associated with the assumption that the vehicle speed profile is always met (actual power limitations are not considered) and that the accelerator and brake pedal signals are typically absent, hindering the development of vehicle control systems. The most relevant drawback of the quasi-static approach is that steady-state efficiency maps are used, and the actual dynamics of the system is not taken into account. On the other side, the combination of backwards-looking and quasi-static approaches allows obtaining reasonable accuracy by keeping the computational effort limited [11].
2.3. Hybrid Powertrain Operating Conditions and Architectures
Depending on the electrification levels (mild, full, plug-in and REx hybrids), the EMs positioning and their characteristics, different powertrain operating conditions could be achieved:
- Electric Propulsion (EP)
- Regenerative Braking (RB)
- Charging (CH)
- Electric Assist (EA)
EP is operated when the powertrain layout allows the ICE to be switched off and the EMs to sustain propulsion entirely. RB condition is operated when the motive power becomes negative (during significant vehicle decelerations and/or downhill drive) and the EMs can absorb power to regenerate electricity; in this condition, the ICE can either be on or off, depending on the powertrain characteristics, current status and control logic. The CH condition is operated when the ICE is active and provides extra power to generate electricity through the EMs; the overall electric energy balance is positive, and the propulsion battery is recharged. Finally, EA condition is operated when the motive power request is high, or anyhow above the optimal load point for the ICE, and both thermal and electric power are used to sustain the propulsion; as a consequence, the overall electric energy balance is negative, and the propulsion battery is depleted. It is essential to clarify that not all HEVs can fully exploit the operating conditions listed above; for example, certain mild hybrids are significantly limited in EP and RB compared to full or plug-in hybrids [20]. Capturing the instantaneous operating condition and its boundaries proves crucial to model the energy efficiency and calculate the fuel consumption and battery State of Charge (SoC) evolution over time.
The way the propulsion energy converters interact with each other defines the hybrid architecture [9,21]:
- parallel
- series
- power-split.
Parallel hybrids are the most similar to conventional pure-ICE vehicles, as both categories typically have the ICE mechanically coupled with the wheels through a gearbox. In this configuration, both the ICE and the EMs are able to propel the wheels; the latter are either connected to the same ICE driveline and/or mounted in a dedicated driveline (e.g., electrically driven axle to achieve electric all-wheel drive). When a gearbox with different speed reductions is employed, the ICE speed typically depends on the wheel speed and driving conditions; the optimal gear is identified, and a fixed ICE speed is found. The only degree of freedom for optimisation is selecting the ICE load point. On the other hand, series hybrids are similar to Battery Electric Vehicles (BEVs), as the EMs entirely sustain the propulsion needs because the mechanical coupling between the ICE and the wheels is missing. The ICE is only used as an Electric Energy (EE) generator to recharge the propulsion battery or to directly supply the propulsion EMs when propulsive power is requested (by-passing the storage phase). To enable this operation, the powertrain has to be equipped with at least two EMs, one mechanically coupled to the ICE, acting as a generator, and one (or more) to the wheels, acting as propulsion motor(s). Differently from parallel hybrids, series hybrids can also select the desired ICE speed, beside the desired ICE load point, as a consequence of the missing mechanical link with the wheels. This provides an additional degree of freedom for optimisation, with a greater flexibility towards the operation of the ICE in the region of highest efficiency. Many parallel hybrids are, in principle, able to achieve series operation, too; the necessary condition to make this happen is the presence of two EMs, one upstream and one downstream of the ICE clutch; the latter can therefore be opened to separate the propulsion driveline with the ICE-generator system. In the market there are vehicles whose powertrain is structured in such a way to achieve both series and parallel operation, and their controller selects either one or the other depending on the driving condition. For low-speed and low motive power requests, either EP or series ICE-assisted operation are preferred; parallel operation is adopted otherwise, exploiting a mechanically efficient coupling between the ICE and the wheels, maybe through a simplified (or even single-speed) gearbox. Especially when cruising at high-speed, the parallel operation is more efficient since the series operation is affected by higher losses due to multiple energy conversions.
The powertrain configuration described, referred to as series-parallel architecture in this study, is included among the investigated technical solutions. Finally, the power-split hybrids are vehicles whose powertrain is equipped with a specific transmission type, referred to as the Planetary Powers-split Device (PPD). These powertrains are typically equipped with two EMs, one of them closer to the wheels and mostly used as a propulsion motor, while the other is mounted on another end of the PPD, referred to as the Planetary Side (PS). The EM here mounted is typically used as a generator, although sometimes, and for very specific operating conditions, it operates as a motor (when the rotation direction reverses as the result of vehicle speed and ICE speed) and forces the other EM to switch its preferred operation too. This powertrain configuration can simultaneously achieve parallel and series operation, since part of the ICE torque is transmitted to the wheels by the PPD, whereas the remaining ICE torque is transmitted to the EM on the PS. As a consequence, the ICE power is partly used for direct vehicle propulsion and partly transformed into EE by the EM acting as a generator, which alternatively supplies the other EM acting as a motor or recharges the propulsion battery. The PPD is capable of selecting the most appropriate energy conversion pattern depending on the current driving condition and can also achieve pure-ICE operation in specific conditions; additionally, it can select the desired ICE speed like series hybrids. This complex powertrain design enables the selection of very efficient operating conditions in many different use cases.
2.4. Powertrain Model
To cover the largest variety of hybrid powertrain layouts, a generalised hybrid powertrain model was developed that includes all the EMs in the different positions of the driveline (described later) [22]. The layout is presented in Figure 1.
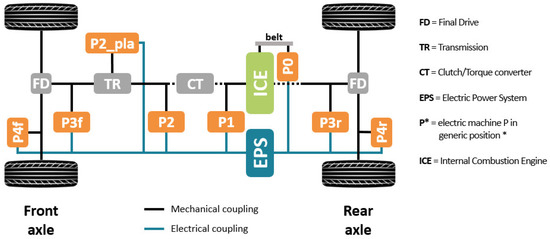
Figure 1.
Generic hybrid powertrain model [22].
In the picture, mechanical couplings that might or might not be present depending on the specific vehicle solutions are drawn with dashed lines. For example, series architectures do not have any mechanical coupling between the ICE and the driveline, whereas parallel and power-split have. For simplicity, the ICE is always assumed to be connected to the front axle (front-wheel-drive) or both (all-wheel-drive); vehicles with ICE delivering power to the rear axle (rear-wheel-drive) is seen as a front-wheel-drive vehicle by the model.
Apart from the Final Drive (FD), the Transmission (TR), the Clutch/Torque Converter (CT) and the ICE, which are typically included in the driveline of all pure-ICE vehicles, additional components were considered for covering the different hybridisation solutions. In addition to the Service Battery (SB), which is the electrical energy storage used to supply the low-voltage electrical consumers and the ICE starter, the Traction Battery (TB) was also included, which is designed to provide and store electrical energy for supporting propulsion, charging through ICE power and regenerative braking. These two electrical energy storages are part of the Electric Power System (EPS), which enables the exchange of electrical power with the different EMs of the hybrid powertrain and the electrical consumers. The EMs are energy converters transforming the mechanical power into electrical power, or vice versa, therefore constituting the connection point between the mechanic and the electric systems. The positioning of the EM, generally referred to as , is described according to the following convention:
- → the EM is connected to the ICE belt
- → the EM is connected to the ICE crankshaft
- → the EM is upstream of the transmission
- → the EM is connected to the planetary side (explained below)
- → the EM is upstream of the final drive (front or rear)
- → the EM is mounted on the wheels (front or rear, one on each wheel of the axle)
EM only applies to HEVs equipped with a planetary power-split device. For hybrid vehicles equipped with this type of motor, it is implied that the powertrain architecture is of the power-split type; the transmission is, therefore, a planetary gearset with three gears (sun, carrier, and ring), attached to three different sides: the ICE, the FD and PS. The latter is where the is mounted; this side is typically the one connected to the sun gear of the planetary gearset.
2.4.1. Electric Machines
Although there are several EMs types (synchronous vs asynchronous, AC vs DC), their performance can be modelled by means of a 0D approach using efficiency maps [22]. A very common approach is to use a map such as the one presented in Figure 2 (left subplot), where the EM rotational speed and torque are used to interpolate the efficiency value [11]. The relationship between electrical and mechanical power is
where and are the EM electrical and mechanical power (both positive when the EM is propelling), is the overall EM efficiency which includes the losses of the conversion from DC to AC (for AC EMs), and lastly and are the rotational speed and torque of the EM. In order to coherently consider the conversion losses when the EM operates as motor or generator, is powered to the sign of the mechanical power; this way, the resulting multiplication factor is smaller than one when converting from mechanical to electrical energy and vice versa. A scaling approach could be used as proposed in [23] to generate a generic EM efficiency map. An existing EM efficiency map can be normalised dividing the speed and torque setpoint by the respective speed of rated power and maximum torque. When a new efficiency map has to be produced, the rated speed and torque are used to rescale the default normalised map. For the generation of the full load curve, it can be assumed that two different regions characterise the EM for the operation, the constant torque and the constant power region, as shown in Figure 2 (left subplot) [24]. This implies that the right boundary of the constant torque region coincides with the left boundary of the constant power region; therefore, the rated power point (the minimum speed at which the maximum rated power is achieved) is also a maximum torque point. Consequently, the entire full load curve can be obtained by defining EM rated power and maximum torque. Lastly, the maximum efficiency can also be scaled from the normalised map using the dependency between maximum efficiency and rated power [24] proposed by Larsson M. and presented in Figure 2 (right subplot).
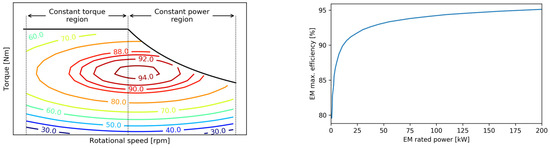
Figure 2.
EM efficiency and generic full load curve (left) and maximum efficiency as function of rated power (right). Right figure based on Larsson [24] and authors’ further elaboration.
2.4.2. Mechanical Power Balance Equations
A distinction was made between the ICE power used for propulsion of the wheels and the part used to charge the TB [22]. The part that contributes to wheels propulsion is used in the following equation, which is obtained balancing the power at wheels
where and are the ICE mechanical power and the respective driveline efficiency factor that is used for propulsion at the wheels, is the mechanical power and the respective driveline efficiency factor for EM PX, also in this case used for propulsion at the wheels, finally is a Boolean variable indicating whether EM PX is able to contribute to the propulsive needs in the current situation (depends on the clutch status). Equation (2) also applies when the wheel power is negative, and the power flow is reversed (the driveline efficiency factor has to be adjusted accordingly). The part of ICE power that is used to charge the TB is used in the following equation, which is obtained balancing the power at the ICE, excluding the part used for propulsion:
where is the part of ICE power that is absorbed by the EMs acting as generators, and are the mechanical power from the EMs that are acting as generators and the respective efficiency seen by the power flowing from the ICE, finally is a Boolean variable indicating whether EM PX is able to contribute to TB charging through the ICE (also depends on the ICE clutch status). The total power from the ICE is finally calculated as follows:
The formulation of the problem allows to cover also those HEVs that simultaneously have one EM acting as a generator and one another as a motor (surely the case for series and power-split hybrids). To create all the possible power combinations, an array with ICE power outputs ranging from zero to the maximum power can be created, using the desired resolution (compromising between the expected accuracy and the computational requirements). The ICE zero power output is the solution associated with EP mode, therefore only the EMs fulfil the propulsive needs by balancing Equation (2). When ICE power is bigger than zero, the hybrid architecture has to be taken into consideration to distribute the power to the EMs coherently. For series hybrids is always zero; additionally, the lack of a mechanical coupling between the ICE and the wheels implies that the EMs used for propulsion are only P2, P3 and P4 (front and rear), whereas for charging only the P0 and P1 are used. For power-split hybrids, is obtained using the fundamental equations of the planetary gearset [9,25]; in this powertrain layout, the EM P2_PLA torque is linearly dependent from the torque entering the ICE side of the gearset and the power output will depend on the rotational speed of the component. The EM P2_PLA torque is calculated as follows:
where is the torque at the ICE side of the planetary gearset, is the fundamental ratio of the planetary gearset and is the torque reduction or multiplication factor of a possible reduction gear between the EM and the planetary gearset (if absent, ). The rotational speed of the P2_PLA is calculated as follows:
where and are the rotational speed of the ICE and FC sides of the planetary gearset, respectively. Finally, the P2_PLA power is obtained from torque and speed. For parallel architectures, the rotational speed of the components is fixed; therefore, the ECMS simply selects the optimal ICE load that returns the optimal FC. For series and power-split hybrids, the power combinations generated will have to be associated to both different loads and rotational speeds for the ICE. Additionally, for those vehicles that can run both in series and parallel mode, one set of power combinations should be produced for each propulsion mode and evaluated by the ECMS; the solution associated to the propulsion with smaller FC shall be selected.
2.5. Electric Power System
Besides the control strategy, the other main difference between the simulation of conventional and hybrid vehicles is in the electrics, here generally referred to as the Electric Power System (EPS) [22]. HEVs are equipped with the following additional components, which are part of the EPS: one or more EMs, the TB, the DC/DC converter and the SB (see Figure 3 below).
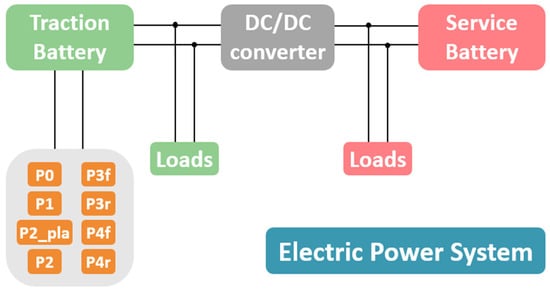
Figure 3.
Generic Electric Power System model [22].
2.5.1. Electrical Power Balance Equation
Given the EPS layout, the electrical power balance on the HV system is obtained as follows [22]:
where is the electrical power at TB terminals, is the electrical power absorbed or generated by EM PX, is the electrical power going to the DC/DC converter to supply the LV system and is the load from all HV consumers (e.g., heaters, air conditioning system, etc.). The DC/DC converter and the LV side of the system are briefly discussed in Appendix B, whereas the most relevant part, the TB, is discussed below.
2.5.2. Traction Battery
The TB model consists of two sub-models. The first deals with identifying the voltage-current combination that allows delivery of the desired power output; the identified values depend on the battery State of Charge (SoC) and efficiency. The second one calculates the battery SoC evolution, using the outputs of the first sub-model (specifically, the battery current).
To simulate the TB efficiency and dynamics, the Equivalent Circuit Battery Model (ECBM) was chosen, which models the battery as an electrical circuit consisting of a voltage source, the Open Circuit Voltage (OCV), plus resistors and capacitors [22,26]. The required battery power is given as input to the model, which returns the compatible voltage–current combination (depending on the actual conditions) and the internally generated heat (linking to TB efficiency). The OCV is normally assumed to be function of SoC only, whereas for resistors and capacitors the influence of temperature and current are also taken into account [27] depending on the desired level of accuracy. The model is applied either at cell-level or battery-level (seeing the whole battery as a unique cell); the former solution has the advantage that literature data can be used for defining the parameters of the electrical circuit when the battery technology is known. The circuit presented in Figure 4 is defined zero-order ECBM due to the presence of only one resistor and the lack of Resistor–Capacitor circuits. The equations relevant to the ECBM are presented in Appendix B.
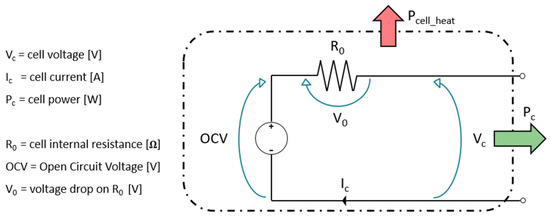
Figure 4.
Equivalent Circuit Battery Model—Battery cell modelling [22].
Details on the ECBM model used in this work and the underlying assumptions can be found in [22]. In this work, the same modelling approach was adopted by taking literature data as exemplified in Figure 5, for OCV (left subplot) and internal resistance (right subplot), and enabling the possibility to calibrate such base-models using experimental data and achieve a close match of the actual battery performance.
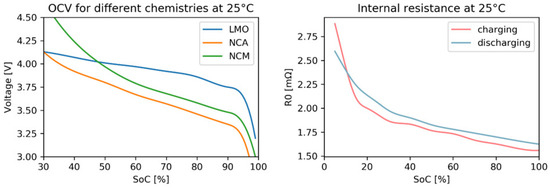
Figure 5.
SoC–OCV curves for different battery chemistries (left) [28] and battery cell internal resistance as a function of SoC and operation (right) [22]. Left figure based on Bharathraj et al. [28] and authors’ further elaboration.
The instantaneous SoC is calculated through the Coulomb Counting method as presented in [22]:
where is the initial SoC, is the charging or coulombic efficiency (often assumed unitary) and is the battery capacity in Ah [9].
2.6. Generic Control Strategy
This section presents the generic control strategy that can be used to simulate different powertrain electrification levels. Depending on the instantaneous motive power request and the hybrid powertrain status, the strategy decides how to operate the ICE and the EMs. The decision is taken at the end of an evaluation process consisting of three steps, taken at the three different levels of the control strategy: Supervisor, ICE Manager and Optimiser. These concepts are introduced in the following sections. The TB power is calculated according to the solution selected, which defines the power output (and, in some cases, the rotational speed) for ICE and EMs. The battery model is then executed to calculate the current intensity needed to supply or absorb the required electric power; the TB SoC for the next calculation loop is subsequently obtained by integrating the instantaneous battery current through Equation (8). At the beginning and at the end of every calculation loop, the other variables defining the powertrain status are updated or calculated (e.g., temperatures, timers, Boolean variables, etc.).
2.6.1. Supervisor
The Supervisor can be used to impose a choice and prioritise the system self-sustainment (balance SoC) and/or propulsion needs, for example when the TB SoC is outside of the acceptancy boundaries, or when the driving conditions are such that no optimisation should be applied, and a predefined solution can be selected [22]. The Supervisor’s logic is presented in the domain sketched in Figure 6 where, in addition to the powertrain operating modes presented in the introduction (EP, RB, CH and EA) an additional one is introduced (HY = Hybrid), which actually represents a no-choice situation.
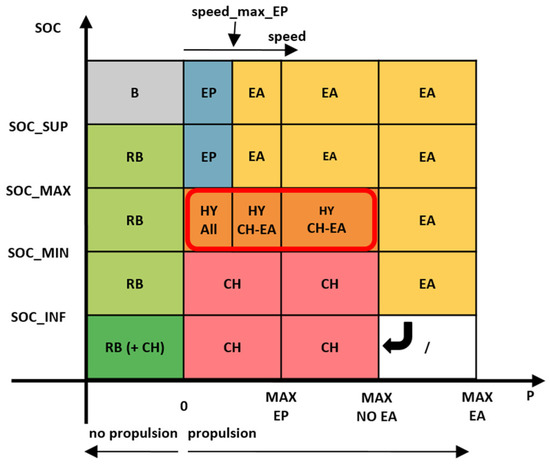
Figure 6.
Supervisor logic [22].
The threshold used in the x-axis, reporting the motive power P, are: zero (to distinguish between propulsion and no propulsion), MAX EP (the maximum power in electric propulsion), MAX NO EA (the maximum power achievable without combining the propulsion of ICE and EMs, electric assist) and MAX EA (the maximum power with EA). The thresholds used in the y-axis, reporting the TB SoC, are: SoC_MIN and SoC_MAX, defining the standard SoC swing window, SoC_INF and SoC_SUP, the minimum and maximum values for SoC below and above which aggressive SoC recovery strategies should be implemented. The coloured boxes in the domain represent all the possible states of the Supervisor, corresponding to different powertrain operation choices, but only one of those is actuated depending on the instantaneous conditions. The decision might consist of a reduced set of operating conditions (only CH, only EP, etc.) to be evaluated by the ICE manager and Optimiser, the next controllers taking action in the iteration step, and impose immediately the ICE state (on or off). Further details to the supervisor evaluations and how these affect the powertrain solution can be found in [22].
2.6.2. ICE Manager
The ICE Manager deals with the warm-up and the limitations of the ICE, either related to Stop-Start (SS) or other aspects. When the conditions require that the ICE is warmed up, the ICE activation is required, and the next steps of the evaluation will not consider any ICE-off solution. Regarding SS, strategies control the on/off time windows duration (e.g., the minimum time the ICE stays active after being activated) or activation/deactivation thresholds (ICE activation based on vehicle speed and/or power request) are implemented. Other limitations might be implemented as well, for example the maximum rotational speed at which the ICE can be switched off because of a drop in the power request; this might prevent unwanted deactivations when the ICE is spinning fast after an acceleration and subsequently, the accelerator pedal is released for a short time.
Following the logical flow presented in Figure 7, the ICE Manager assigns values to three Boolean variables: warming_up, keep_ice_active, consider_switching_off_ice. When needed, the ICE can always be activated (or kept active) to prioritise the propulsion and the operational needs (e.g., warm-up). When a warm-up is required, the ICE manager sets warming_up and keep_ice_active to true.
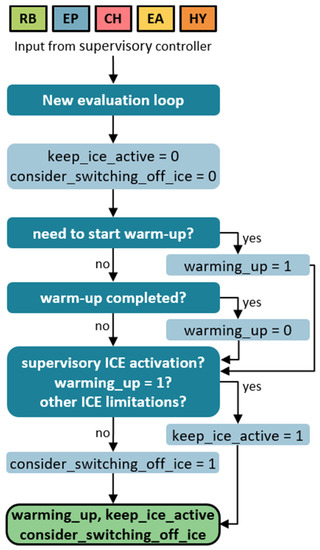
Figure 7.
ICE Manager logic [22].
When there is no need for a warm-up, but the ICE has to be activated or stay active due to a Supervisor choice or other limitation (e.g., exceeded speed limit for EP, ICE having to fulfil a minimum activation time, etc.), then keep_ice_active is set to true. When neither the warm-up nor other conditions require the ICE to be active, then the Boolean variable consider_switching_off_ice is set to true. This last Boolean variable represents the possibility of switching off the ICE, compatibly with the powertrain status, but the Optimiser finally takes the decision whether to have ICE on or off.
2.6.3. Optimiser
As described in the previous sections and in [22], the decisions taken by the Supervisor and the ICE Manager affect the size of the envelope of solutions that the Optimiser evaluates (see Figure 8); for example, all ICE-off solutions will be discarded in case the Supervisor is forcing a charge event (CH) or the ICE needs to warm-up. In order to avoid oscillations in the control or powertrain unphysical behaviour (e.g., too steep power build-up), additional solutions might be excluded from the set that is given to the Optimiser. Within this set, the most efficient operating condition is identified by means of the Equivalent Consumption Minimisation Strategy (ECMS), which was firstly introduced by Paganelli et al. [19] and is nowadays widely adopted for all the different hybrid types (parallel, series and power-split) [29]. The ICE, EMs and TB limitations are considered for every calculation loop, and a set of ICE/ EMs power solutions is created. The ECMS uses a cost function that considers, for each solution, the cost associated to ICE fuel usage and battery virtual fuel usage and selects the one that minimises the equivalent consumption to obtain the optimal ICE and TB power levels. From the former, the instantaneous FC and CO2 emissions are calculated, whereas from the latter the TB current intensity is obtained (using the ECBM); finally, the SoC is updated (using Equation (8)).
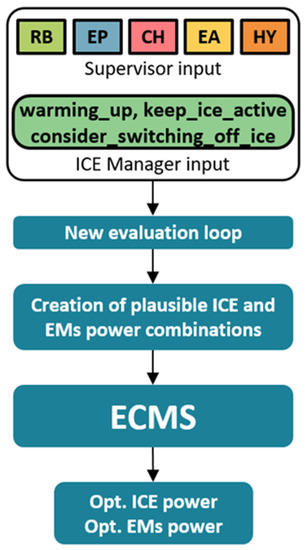
Figure 8.
Optimiser logic [22].
As described in [22], the cost function for the optimisation is written as
where and are the FC of the ICE and the virtual FC associated with the use of electrical power from the TB, which expands into
where is the equivalence factor defining the virtual cost (in terms of fuel) associated with using electrical power, is the electrical power from the TB and LHV is the Low Heating Value of the fuel. The TB equivalent fuel consumption () is negative for charging operation, reducing the overall cost, and vice versa. For any given driving condition, there is an optimal equivalence factor enabling that the SoC is maintained in the long-term, but such value is not trivial to identify. The value assumed for should be as close as possible to in order to simulate successfully the operation of the real vehicle [30]. To limit the side effects of an imprecise assumption, the cost associated to using battery power () can be dynamically adjusted by using an equivalence factor that depends on the SoC deviation from the reference value for CS operation. The following -SoC dependency can be implemented as proposed by Onori et al. [31]:
where is the constant equivalence factor and is the cost adjustment factor. The latter can be defined as follows:
where represents the reference SoC value, the maximum wanted deviation from the reference SoC value, the entity of the adjustment of s on the boundaries (e.g., = 0.1 corresponds to a 10% increase of s when the SoC is deviating from by ); finally, is a parameter allowing to obtain different responses for the adjustment of s as shown in Figure 9. The possibility to adjust s from the constant value does not reduce the importance of finding , but rather limits the side effects of the biased optimisation caused by a wrong value for the current driving conditions, preventing the SoC to go either very high or very low.
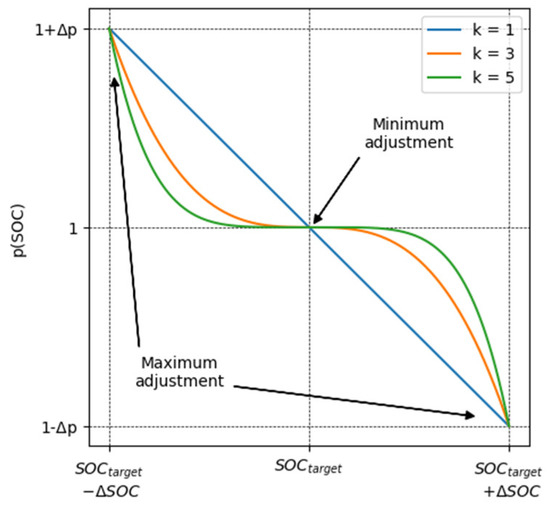
Figure 9.
Cost of electric energy as a function of SoC. Based on [31] and authors’ further elaboration.
3. Results and Discussion
3.1. Model Validation
The strategy presented in the previous sections was tested and validated on a newly developed vehicle simulation tool. For the validation, experimental data collected in the Vehicle Emission LAboratories (VELAs) of the JRC were used. Six vehicles, with different powertrain architectures and electrification degrees, were considered (see Table 1). The architecture (series, series/parallel, parallel and power-split), the electrification level (mild, full, plug-in, range extender), the segment and the indicative electric power ratio are reported in Table 2. The latter is obtained as the sum of the rated power of the EMs used for propulsion divided by the rated power of the ICE; the result is truncated to the first decimal. The vehicle enumeration follows the order in which they were tested. Lastly, the EMs configuration (number and location) is described in Table 3; graphical representations of the powertrains are visible in Figure A1 in Appendix C.

Table 1.
Powertrain architecture and electrification degree of the tested vehicles (unlikely or unrealistic configurations marked with a dash).

Table 2.
Vehicles naming and description.

Table 3.
Vehicles electric machines configuration.
3.2. Validation Scheme
The cases are set up by filling out an input file with the following data: the vehicle specifications and the time-series of the driving profile (time, vehicle speed, road slope). The former are used to generate the vehicle and powertrain models, whereas the latter are passed to the simulation loop, performing iterations over each time instant to solve the powertrain model and identify the operating condition (rotational speed and torque of ICE and EMs, currents and voltages of electrical components). If no additional time-series are provided other than the driving profile, the tool selects default or literature data for the submodels, otherwise, a calibration of the submodels is attempted based on the provided data, e.g., of the TB internal resistance R0 and OCV curve based on the experimental battery current and voltage [32] and of the ICE fuel consumption map based on the experimental ICE power and instantaneous fuel consumption.
3.3. Discussion
3.3.1. Absolute CO2 Emissions
This section presents and discusses the simulation results obtained with the vehicle simulation tool over a cold-start WLTC. The comparison of absolute CO2 emissions between experimental and simulated results is presented in Figure 10, corrected for the vehicle electricity balance to account for the CO2 difference caused by EE gain or loss between the start and the end of the cycle. As can be seen, the deviation from the experimental value (vertical distance from the black bisection line) remains limited and consistent throughout all vehicles and CO2 emissions ranges, from low (~100 g/km) to high (~180 g/km) values. The biggest absolute errors are on Vehicle 1, where the tool underestimates by 6.7 g/km, and on Vehicle 4, where it overestimates by 4.1 g/km. The average error from all simulations is −1.4 g/km and the standard deviation is 3.5 g/km.
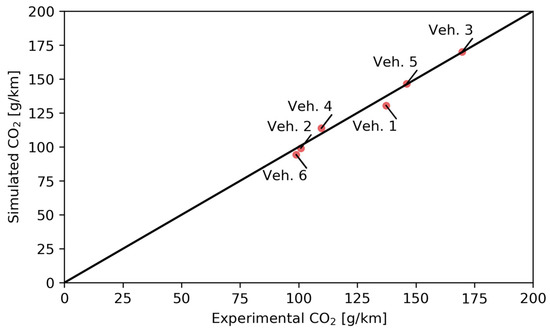
Figure 10.
Comparison of absolute balanced CO2 emissions between experimental and simulation results.
3.3.2. Simulation Accuracy
To further examine the vehicle simulation results, the ICE-on time, the ICE average power (when active), the TB ΔSoC and the normalised CO2 emissions are presented in detail for each vehicle. The CO2 emissions values were normalised on the experimental reference to enable visualising the relative error and cross-comparing among vehicles; therefore, the presented experimental reference result is always 100% and the per cent deviation obtained in simulation is easily visualised. All results are reported in Figure 11. In most cases, the ICE activation time is very close to that of experiments, except for Vehicle 1 (the series REx). For this specific case, the optimisation strategy selects a more aggressive operating condition than that of the real vehicle, since the ICE is operated at a higher average load; consequently, during each ICE-on phase the TB is more quickly charged, and the ICE stays active for a smaller time. Despite the different choice for the powertrain operation, the results are consistent and the ΔSoC is similar to the experimental one. Vehicle 6 also experiences a non-negligible discrepancy in the ICE activation time (more than 100 s) and consequently in the average ICE power. Due to the additional degree of freedom that can be exploited both by Vehicle 1 (series) and Vehicle 6 (power-split) in the selection of the most efficient ICE operating condition (ICE speed is not a constrain in the optimiser), the results are largely affected by the ICE fuel consumption map used for the simulation.
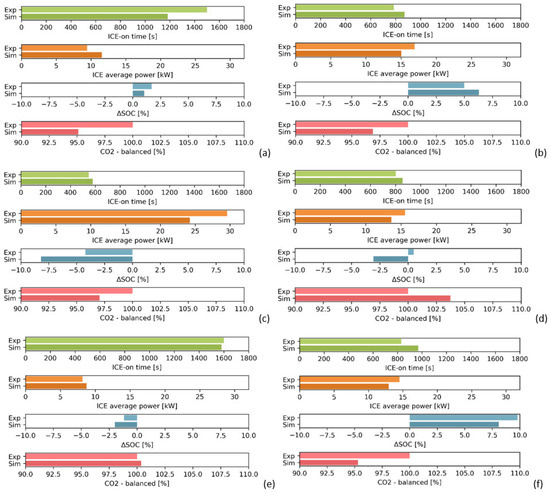
Figure 11.
Simulation results for (a): Vehicle 1 (series REx), (b): Vehicle 2 (parallel full hybrid), (c): Vehicle 3 (series-parallel plug-in hybrid), (d): Vehicle 4 (parallel plug-in hybrid), (e): Vehicle 5 (parallel mild hybrid), (f): Simulation results for Vehicle 6 (power-split full hybrid).
One aspect that needs to be discussed is modelling the possible asymmetry in the EE use between charging and discharging operation, which was experienced with Vehicle 5. This vehicle constitutes an exception from the other cases considered because of the lower electrification degree (mild). In this hybrid configuration, the EM (a P0 with rated power of few kW) is used mostly to generate electricity and recharge the battery through regenerative braking or ICE-assisted charging. Very rarely, the energy is drawn from the TB to operate the P0 EM as a motor; when this happens, it is because the TB SoC is above a certain threshold, higher than the typical reference value, and the motive power request is significant (EA is not adopted for smooth accelerations). As a consequence, it is concluded that for mild hybrid applications, the EM power is subject to optimisation only when specific conditions are met, most likely to limit the electric assist operation that would bring the small capacity TB to deplete rapidly. Considering the limited electric capabilities, a simpler strategy might be adopted instead of a proper optimiser (e.g., ECMS), for example a combination of decisional trees and fixed values for the operation of the electrical components (e.g., constant torque for the EM). These aspects of the real control logic of the vehicle were discovered by analysing the experimental data but are further confirmed by the literature on the mild-hybrid control strategy topic [33,34]. Furthermore, in this mild-hybrid application, the maximum power reached by the P0 in generator mode differs from that of motoring mode; during regenerative braking, the maximum EM power can be reached, whereas for electric assist phases the EM power is limited to approximately one-fourth of that amount. This aspect was captured in the simulation environment by imposing a different TB power limitation for the charging and the discharging phase, therefore affecting the selection of the powertrain operating condition and achieving the said asymmetric characteristic. Despite the differences listed in the previous analysis, the ECMS still provides an accurate result for mild hybrid applications; this allows avoiding the implementation of ad-hoc control strategies that would likely require significant data analysis, coding and tuning of the calibration parameters. No critical points are found for Vehicles 2, 3 and 4, for which all the evaluation parameters fall within the reasonable window of acceptance.
The estimation error is always within ±5%, with an average error of −1.93% and an error standard deviation of 3.07%. The underestimation tendency might be due to some inconsistency in the newly developed vehicle simulation tool, which still needs extensive testing and validation, or by component limitations not represented correctly in the powertrain model and causing more efficient—but non-feasible—operating conditions in simulation. The results are considered satisfactory, and the simulation approach possibly represents a powerful tool for calculating vehicle performance and CO2 emissions.
3.3.3. Comparison Other CO2 Emissions Calculation Tools
To put these results into context and further discuss the designation of this work, a comparison with other tools from the literature was carried out.
The simplest way to calculate CO2 emissions from hybrid vehicles is to use emission factors. They consist of empirical values or functions to obtain the emissions of a specific pollutant or greenhouse gas [35]. Emission factors can be derived by combining (e.g., averaging) the emissions from a set of relevant ad-hoc experiments that cover realistic use-cases [36]; other approaches capture the relationship with a known quantity to obtain more precise results. The methodology proposed by the EMEP/EEA air pollutant emission inventory guidebook [37] uses the average speed and provides different functions depending on the vehicle specifications (segment, EURO standard, fuel injection and aftertreatment technology); the CO2 emissions are then calculated based on the fuel energy consumed. Since CO2 emissions are directly linked to fuel consumed and hence to powertrain efficiency and energy request at the wheels, the emission factors method is limited because of lacking an underlying physics-based model that captures these aspects. A study that compares experimental CO2 emissions from recent plug-in hybrids in charge-sustaining conditions with the EMEP/EEA methodology shows how the latter can deviate by more than 50% [38]. Furthermore, the methodology lacked parameters to obtain CO2 emissions from HEVs powered by diesel engines [37].
On the opposite side, we can identify as the most precise way to calculate CO2 emissions in full vehicle models requiring all specifications (vehicle and components), efficiency/loss maps and thorough modelling of dynamics and vehicle operation. Such models are often developed within simulation frameworks (GT-SUITE, AVL CRUISE, Amesim and others) on a vehicle ad hoc basis with heavy calibration exercises for each component and control strategy. The effort required to obtain all the necessary input data and set up a simulation case is significant, but on the other hand, this opens the possibility of capturing all relevant aspects and reaching accuracy levels of ±1–2% [39].
This work is filling the existing gap in vehicle simulation options, finally enabling to capture HEVs fuel consumption and CO2 emissions with an accuracy of ±5% through a generalised vehicle model and simulation strategy. The relatively easy vehicle-case generation and parametrisation can, in principle, allow to run a large number of simulations with little effort, and create scenarios to support regulatory assessments where hybridised powertrains of different architectures (serial, parallel, serial-parallel, powersplit) and electrification levels (mild, full, plug-in, range extender) represent a much larger part of the fleet.
3.3.4. Real-World Trip Simulation
Although outside the scope described in the introduction section (development of a generalised model and control strategy for HEVs), a Real Driving Emission (RDE) test was simulated to acquire a first understanding of the potential in capturing real-world conditions and quantify how much the accuracy degrades because of the extra unknowns (exact vehicle weight and road load resistance, use of auxiliaries, wind conditions, others). The trip was driven on Vehicle 4 and consists of a mix of urban, rural and motorway conditions (see Figure 12), mild ambient temperature (16 °C average) and starting from a low SoC (charge sustaining). The altitude profile measured from the GPS was used to obtain the road slope and the air drag resistance was adjusted according to the external temperature impacting the air density (correction on the road load F2 parameter from Equation (A5)). The cumulative simulated CO2 emissions (bottom plot in Figure 12) are 9.6% lower than the experimental ones which is expected considering that no extra vehicle auxiliaries were considered in the simulation, meanwhile the air conditioning/heating was active on the tested vehicle. This preliminary result is a good starting point for a follow-up study on the extension of the tool to simulate real-world trip with a good level accuracy for a large variety of HEVs.
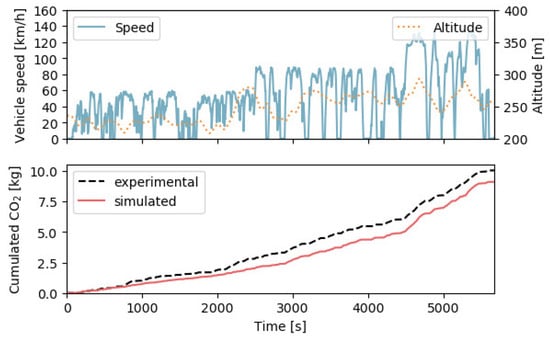
Figure 12.
Vehicle 4: RDE trip characteristics (top) and CO2 emissions results (bottom).
4. Conclusions
A generic HEVs simulation approach that covers the most relevant hybrid architectures currently found in the European market was developed. Flexibility is granted through its generic modelling approach; the hybrid powertrain and its components, including the driveline and the electric power system (low-voltage and high-voltage circuits), and the generic ECMS-based control strategy for the selection of the best operating condition. Dedicated experimental campaigns supported the whole activity. The concepts outlined in this paper were implemented in a newly developed vehicle simulation tool to test its capabilities. Experimental data from six HEVs with different powertrain architecture (series, parallel and power-split) and electrification degrees (mild, full, plug-in and range extender) were collected and used to validate the tool. The results demonstrated robustness in predicting the overall vehicle energy efficiency and CO2 emissions. An accuracy of ±5% was obtained over the WLTP carried out in charge-sustaining conditions, which is considered satisfactory given the generic modelling approach (i.e., the lack of models and features tailored to the specific vehicles), and the limited amount of input data required, which represent the unique feature of the proposed approach.
Furthermore, due to the detailed modelling of the powertrain in terms of components’ performance and limitations, the generic simulation approach also represents a viable option for including HEVs in other simulation environments (e.g., traffic simulation models). The tool will also prove useful for the determination of powertrain conditions from on-road trips, although the modelling approaches will have to be extended and refined in a follow-up study to ensure accuracy under the more diverse boundary conditions that are encountered in the real-world (dependency on temperatures, use of auxiliaries, ageing). As a follow up activity, the simulation framework introduced in this study will be used to analyse and benchmark real-world CO2 emissions values, supporting the actions undertaken by the European Commission to reduce the road transport carbon footprint and verify CO2 emissions and energy consumption.
Author Contributions
Conceptualization, A.T. and G.F.; Data curation, A.T.; Formal analysis, A.T.; Methodology, A.T., G.F. and F.M.; Project administration, G.F.; Supervision, G.F. and F.M.; Visualization, A.T.; Writing—original draft, A.T.; Writing—review & editing, G.F. and F.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data can be made available upon request.
Acknowledgments
The authors acknowledge the JRC Vehicle Emissions Laboratory (VELA) team for their support in carrying out the experimental activities, Luciano Rolando and Alessandro Zanelli for the technical exchange on the simulation and optimisation strategy.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| AC | Alternating Current |
| AD | Air Drag |
| BEV | Battery Electric Vehicle |
| BMS | Battery Management System |
| CD | Charge Depleting |
| CH | Charging |
| CS | Charge Sustaining |
| CT | Clutch/Torque Converter |
| DC | Direct Current |
| EA | Electric Assist |
| EC | Energy Consumption |
| ECBM | Equivalent Circuit Battery Model |
| EE | Electric Energy |
| EEC | Electric Energy Consumption |
| EP | Electric Propulsion |
| EPS | Electric Power System |
| FC | Fuel Consumption |
| FD | Final Drive |
| HD | Heavy-Duty |
| HEV | Hybrid Electric Vehicle |
| HV | High Voltage |
| ICE | Internal Combustion Engine |
| LD | Light-Duty |
| LHV | Low Heating Value |
| LV | Low Voltage |
| OCV | Open Circuit Voltage |
| PPD | Planetary Power-split Device |
| PS | Planetary Side |
| RB | Regenerative Braking |
| RDE | Real Driving Emission |
| RR | Rolling Resistance |
| SB | Service Battery |
| SoC | State of Charge |
| TB | Traction Battery |
| TR | Transmission |
| WLTC | Worldwide harmonised Light vehicles Test Cycles |
| WLTP | Worldwide harmonised Light vehicles Test Procedure |
Appendix A. Vehicle Simulation and Power Calculation
The total resisting force acting on the vehicle is obtained as
where is the Air Drag (AD) force, is the tyres Rolling Resistance (RR) force, is the vehicle inertial force associated with acceleration or deceleration events and is the gravitational force acting on the vehicle when driving uphill or downhill [9,40]. To support chassis dynamometer testing, the air drag and rolling resistance forces are generalised by representing them as a quadratic dependency on vehicle speed:
where is the vehicle speed and , and are the coefficients of the quadratic dependency, typically obtained from a coast-down test and referred to as road load coefficients [41,42,43]. Using the same road loads coefficients for chassis dynamometer measurements and for simulation ensures that the results are comparable. The vehicle inertial force is calculated as
where is the vehicle acceleration, is the vehicle mass and is the inertia of the rotating parts. According to EU Regulation 2017/1151, the inertia of the rotating parts can be obtained as a fixed percent value of the vehicle mass; this value is assumed to be 3% in normal operation, but in case of 2WD chassis dynamometer testing, where one of the two axles is not rotating, a fixed value of 1.5% is assumed [42]. Lastly, the gravitational force is calculated as
where is the gravitational acceleration and is the road gradient.
Combining the equations introduced before, and multiplying everything by the vehicle speed to calculate the power demand, we obtain:
which represents the power needed at the wheels of the vehicle to overcome the resistive forces and support propulsion.
Appendix B. Electrical Power System (EPS)
Appendix B.1. DC/DC Converter
The DC/DC converter enables to transfer energy between the High Voltage (HV) and Low Voltage (LV) circuits. As reported in [22], the DC/DC converter component can be modelled through the following equation (written in such a way to enable the inverse operation too, energy transfer from LV to HV)
where and are the electrical powers on the LV and HV sides of the DC/DC respectively, and is the efficiency of the DC/DC converter. A constant efficiency value of 92.5% is assumed.
Appendix B.2. Service Battery
The SB is the common 12 V electric energy storage mounted on any passenger car, or light commercial vehicle, supplying the locking system, the lights, the dashboard and the other LV electrical consumers. As reported in the previous section, experiments showed that the LV system of HEVs is typically receiving a constant contribution from the DC/DC converter. As a consequence, the SB is typically kept at a target SoC (or slowly brought there through a charging transient) and is not used to supply the LV consumers (or not entirely, at least); therefore, it can be assumed that no significant system optimisation is adopted in this regard and a very simple modelling approach can be adopted. The SB can either be seen as a simple electrical consumer drawing a constant current from the DC/DC converter, and therefore be included in the average LV EE consumption of the vehicle (in the order of 250–500 W from experimental observations), or alternatively be modelled as a battery system characterised by constant voltage (to avoid the need of an ECBM) and a specific operating strategy (e.g., alternating charge–discharge phases or charging to target SoC and maintaining).
Appendix B.3. Equivalent Circuit Battery Model Equations
The following equations are used to express the relationships between cells number and disposition and battery quantities (voltage and current) [22]:
where , , , , and are the power, the voltage and the current of the battery and cell, respectively, is the total number of battery cells, and are the number of cells in series and parallel, respectively. From combining Kirchoff’s voltage law and Ohm’s law, the main governing equations for the ECBM are obtained [22].
which are used to calculate the values of and needed to deliver the required .
Appendix C. Tested Vehicles
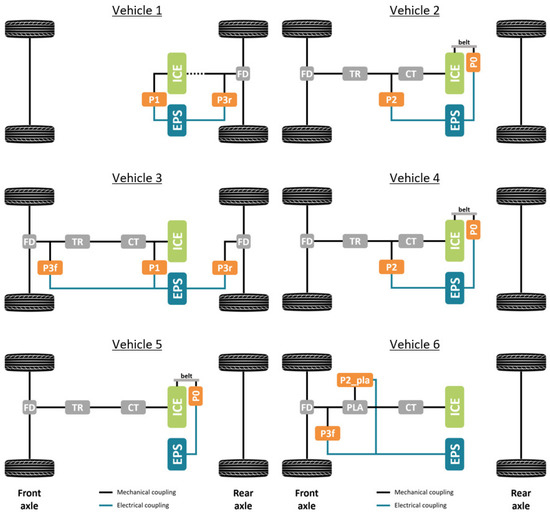
Figure A1.
Powertrain configurations of the tested vehicles [22].
References
- European Commission. Regulation (EU) 2021/1119 of the European Parliament and of the Council of 30 June 2021 Establishing the Framework for Achieving Climate Neutrality and Amending Regulations (EC) No 401/2009 and (EU) 2018/1999 (‘European Climate Law’). 2021. Available online: http://data.europa.eu/eli/reg/2021/1119/oj (accessed on 16 March 2023).
- The International Council on Clean Transportation. Hybrid Vehicles: Technology Development And Cost Reduction. 2015. Available online: https://theicct.org/publication/hybrid-vehicles-trends-in-technology-development-and-cost-reduction (accessed on 16 March 2023).
- ACEA. Fuel Types of New Cars: Petrol 52.3%, Diesel 29.9%, Electric 6.8% Market Share First Quarter of 2020. 2020. Available online: https://www.acea.auto/fuel-pc/fuel-types-of-new-cars-petrol-52-3-diesel-29-9-electric-6-8-market-share-first-quarter-of-2020 (accessed on 16 March 2023).
- ACEA. Fuel Types of New Vans: Diesel 92.8%, Electric 1.2%, Alternative Fuels 1.3% Market Share in 2019. 2020. Available online: https://www.acea.auto/fuel-cv/fuel-types-of-new-vans-diesel-92-8-electric-1-2-alternative-fuels-1-3-market-share-in-2019 (accessed on 16 March 2023).
- ACEA. Fuel Types of New Buses: Diesel 85%, Hybrid 4.8%, Electric 4%, Alternative Fuels 6.2% Share in 2019. 2020. Available online: https://www.acea.auto/fuel-cv/fuel-types-of-new-buses-diesel-85-hybrid-4-8-electric-4-alternative-fuels-6-2-share-in-2019-2 (accessed on 16 March 2023).
- Wisdom, E.; Bannister, C. Modelling and control of hybrid electric vehicles (A comprehensive review). Renew. Sustain. Energy Rev. 2017, 74, 1210–1239. [Google Scholar]
- Denis, N.; Dubois, M.R.; Trovão, J.P.; Desrochers, A. Power Split Strategy Optimization of a Plug-in Parallel Hybrid Electric Vehicle. IEEE Trans. Veh. Technol. 2018, 67, 315–326. [Google Scholar] [CrossRef]
- Çağatay Bayindir, K.; Ali Gözüküçük, M.; Teke, A. A comprehensive overview of hybrid electric vehicle: Powertrain configurations, powertrain control techniques and electronic control units. Energy Convers. Manag. 2011, 52, 1305–10313. [Google Scholar] [CrossRef]
- Guzzella, L.; Sciarretta, A. Vehicle Propulsion Systems—Introduction to Modeling and Optimization, 2nd ed.; Springer: New York, NY, USA, 2005. [Google Scholar]
- Nguyen, A.; Lauber, J.; Dambrine, M. Optimal control based algorithms for energy management of automotive. Energy Convers. Manag. 2014, 87, 410–420. [Google Scholar] [CrossRef]
- Millo, F.; Rolando, L.; Andreata, M. Numerical Simulation for Vehicle Powertrain Development. In The Numerical Analysis—Theory and Application; IntechOpen: London, UK, 2011. [Google Scholar]
- Sciarretta, A.; Back, M.; Guzzella, L. Optimal Control of Parallel Hybrid Electric Vehicles. IEEE Trans. Control Syst. 2004, 12, 352–363. [Google Scholar] [CrossRef]
- A-ECMS: An adaptive algorithm for hybrid electric vehicle energy management. Eur. J. Control 2005, 11, 509–524. [CrossRef]
- Gu, B.; Rizzoni, G. An adaptive algorithm for hybrid electric vehicle energy management based on driving pattern recognition. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Columbus, OH, USA, 30 October–3 November 2006. [Google Scholar]
- Li, H.; Ravey, A.; N’Diaye, A.; Djerdir, A. Online adaptive equivalent consumption minimization strategy for fuel cell hybrid electric vehicle considering power sources degradation. Energy Convers. Manag. 2019, 192, 133–149. [Google Scholar] [CrossRef]
- Finesso, R.; Spessa, E.; Venditti, M. Robust equivalent consumption-based controllers for a dual-mode diesel parallel HEV. Energy Convers. Manag. 2016, 127, 129–139. [Google Scholar] [CrossRef]
- Fontaras, G.; Pistikopoulos, P.; Samaras, Z. Experimental evaluation of hybrid vehicle fuel economy and pollutant emissions over real-world simulation driving cycles. Atmos. Environ. 2008, 42, 4023–4035. [Google Scholar] [CrossRef]
- Frey, H.; Zheng, X.; Hu, J. Variability in Measured Real-World Operational Energy Use and Emission Rates of a Plug-In Hybrid Electric Vehicle. Energies 2020, 13, 1140. [Google Scholar] [CrossRef]
- Paganelli, G.; Guerra, T.; Delprat, S.; Santin, J.; Delhom, M.; Combes, E. Simulation and assessment of power control strategies for a parallel hybrid car. J. Automob. Eng. 2000, 214, 705–717. [Google Scholar] [CrossRef]
- Oh, H.; Lee, J.; Woo, S.; Park, H. Effect of synergistic engine technologies for 48 V mild hybrid electric vehicles. Energy Convers. Manag. 2021, 244, 114515. [Google Scholar] [CrossRef]
- Fuhs, A.E. Hybrid Vehicles and the Future of Personal Transportation; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Tansini, A. Flexible Calculation Approaches to Support the European CO2 Emissions Regulatory Scheme for Road Vehicles. Ph.D. Dissertation, Politecnico di Torino, Turin, Italy, 2020. [Google Scholar]
- DiPierro, G.; Millo, F.; Scassa, M.; Perazzo, A. An Integrated Methodology for 0D Map-Based Powertrain Modelling Applied to a 48 V Mild-Hybrid Diesel Passenger Car; SAE Technical Paper 2018-01-1659; SAE International: Warrendale, PA, USA, 2018. [Google Scholar] [CrossRef]
- Larsson, M. Electric Motors for Vehicle Propulsion; Linköpings Universitet: Linköping, Sweden, 2014. [Google Scholar]
- da Silva, S.F.; Eckert, J.J.; Silva, F.L.; Silva, L.C.; Dedini, F.G. Hybrid Electric Powertrain Design and Control. Ph.D. Dissertation, University of Michigan, Ann Arbor, MI, USA, 2018. Available online: https://theses.hal.science/tel-00863541 (accessed on 16 March 2023).
- Young, K.; Wang, C.; Wang, L.Y.; Strunz, K. Electric Vehicle Battery Technologies. In Electric Vehicle Integration into Modern Power Networks; Springer: New York, NY, USA, 2012; pp. 15–56. [Google Scholar]
- Lee, S.; Cherry, J.; Safoutin, M.; McDonald, J.; Olechiw, M. Modeling and Validation of 48V Mild Hybrid Lithium-Ion Battery Pack. SAE Int. J. Alt. Power 2018, 7, 273–287. [Google Scholar] [CrossRef]
- Bharathraj, S.; Adiga, S.P.; Patil, R.S.; Mayya, K.S.; Song, T.; Sung, Y. An Efficient and Chemistry Independent Analysis to Quantify Resistive and Capacitive Loss Contributions to Battery Degradation. Sci. Rep. 2019, 9, 6576. [Google Scholar] [CrossRef]
- Rolando, L. An Innovative Methodology for the Development of HEVs Energy Management System. Ph.D. Dissertation, Politecnico di Torino, Turin, Italy, 2012. [Google Scholar]
- Millo, F.; Rolando, L.; Fuso, R.; Bergshoeff, E.; Shafiabady, F. Analysis of Different Energy Management Strategies for Complex Hybrid Electric Vehicles. Comput.-Aided Des. Appl. 2014, 11, S1–S10. [Google Scholar] [CrossRef]
- Onori, S.; Serrao, L.; Rizzoni, G. Equivalent Consumption Minimization Strategy. In The Hybrid Electric Vehicles Energy Management Strategies; Springer: New York, NY, USA, 2015; pp. 65–77. [Google Scholar]
- Cubito, C. A Policy-Oriented Vehicle Simulation Approach for Estimating the CO2 Emissions from Hybrid Light Duty Vehicles. Ph.D. Dissertation, Politecnico di Torino, Turin, Italy, 2017. [Google Scholar]
- X-Engineer. Mild Hybrid Electric Vehicle (MHEV)—Control Functions. Available online: https://x-engineer.org/mild-hybrid-electric-vehicle-mhev-control-function/ (accessed on 16 March 2023).
- Ha, S.; Park, T.; Na, W.; Lee, H. Power distribution control algorithm for fuel economy optimization of 48V mild hybrid vehicle. In Proceedings of the International Conference on Modeling and Applied Simulation, Barcelona, Spain, 18–20 September 2017. [Google Scholar]
- Franco, V.; Kousoulidou, M.; Muntean, M.; Ntziachristos, L.; Hausberger, S.; Dilara, P. Road vehicle emission factors development: A review. Atmos. Environ. 2013, 70, 84–97. [Google Scholar] [CrossRef]
- Clairotte, M.; Suarez-Bertoa, R.; Zardini, A.; Giechaskiel, B.; Pavlovic, J.; Valverde, V.; Ciuffo, B.; Astorga, C. Exhaust emission factors of greenhouse gases (GHGs) from European road vehicles. Environ. Sci. Eur. 2020, 32, 1–20. [Google Scholar] [CrossRef]
- EMEP/EEA Air Pollutant Emission Inventory Guidebook 2019: Technical Guidance to Prepare National Emission Inventories; Publications Office of the European Union: Luxembourg, 2019.
- Tansini, A.; Pavlovic, J.; Fontaras, G. Quantifying the real-world CO2 emissions and energy consumption of modern plug-in hybrid vehicles. J. Clean. Prod. 2022, 362, 132191. [Google Scholar] [CrossRef]
- Millo, F.; Rolando, L.; Pulvirenti, L.; Di Pierro, G. A Methodology for the Reverse Engineering of the Energy Management Strategy of a Plug-In Hybrid Electric Vehicle for Virtual Test Rig Development. SAE Int. J. Elec. Veh. 2022, 11, 113–132. [Google Scholar] [CrossRef]
- Tsiakmakis, S.; Fontaras, G.; Anagnostopoulos, K.; Ciuffo, B.; Pavlovic, J.; Marotta, A. A simulation based approach for quantifying CO2 emissions of light duty vehicle fleets. A case study on WLTP introduction. Transp. Res. Procedia. 2017, 25, 3898–3908. [Google Scholar] [CrossRef]
- European Commission. Commission Regulation (EU) 2017/1151 of 1 June 2017. 2017. Available online: http://data.europa.eu/eli/reg/2017/1151/2020-01-25 (accessed on 16 March 2023).
- Pavlovic, J.; Ciuffo, B.; Fontaras, G.; Valverde, V.; Marotta, A. How much difference in type-approval CO2 emissions from passenger cars in Europe can be expected from changing to the new test procedure (NEDC vs. WLTP)? Transp. Res. Part A Policy Pract. 2018, 111, 136–147. [Google Scholar] [CrossRef]
- Komnos, D.; Fontaras, G.; Ntziachristos, L.; Pavlovic, J. An Experimental Methodology for Measuring Resistance Forces of Light-Duty Vehicles under Real-World Conditions and the Impact on Fuel Consumption. In Proceedings of the WCX SAE World Congress Experience, Detroit, MI, USA, 5–7 April 2022. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).