Abstract
Proton exchange membrane fuel cells are a new energy technology with great potential due to advantages such as high efficiency and no pollution. The structure of the gas flow channels has a profound impact on the overall performance of the fuel cell. Different flow channel geometries have their own advantages and disadvantages, and a good understanding of the influence of these structures on performance can provide a reference for the design and improvement of flow channel geometries in various application contexts. Numerical models can be used as a reasonable and reliable tool to evaluate the influence of operating and structural parameters on cell performance and service time by simulating the transport processes of substances and heat as well as electrochemical reactions inside the fuel cell and can be used for the optimisation of cell design. This paper reviews the recent models of proton exchange membrane fuel cells, summarises and analyses the effect of gas flow channels on fuel cells, and organises and concludes efficient design of flow channel structures to enhance PEMFC performance in terms of the cross-section shape, length, width, number of flow channels, and baffle position.
1. Introduction
The proton exchange membrane fuel cell (PEMFC) has gained significant attention as clean energy technologies are sought worldwide for environmental and sustainable development purposes over the past three decades. As devices that use hydrogen as fuel to convert chemical energy directly into electricity, PEMFCs are no longer limited by the Carnot cycle, and water and heat are the only by-products, allowing for higher efficiency and near-zero emissions compared to conventional power generation technologies and direct burning of fossil energy. The composition of a single PEM fuel cell is simple and clear, and individual cells can be easily combined with each other to form different sized stacks to meet demand [1,2]. In addition to these, there are obvious advantages, such as no noise, short start-up times and low operating conditions. These advantages allow for the successful application of PEM fuel cells in many industries, such as aircraft, new energy vehicles, portable energy, and stationary power generation technologies [3]. China currently has close to 6000 fuel cell electric vehicles (FECVs) in its fleet. As of May 2021, over 10,000 FECVs had been purchased in the United States. In Japan, 3520 units had been sold by the end of 2020 [4]. The Mirais from Toyota, the NEXO from Hyundai, and the Maxus EUNIQ 7 from SAIC Motor have also gained considerable market share in the last few years [4,5]. In aviation, the electric unmanned air vehicles powered by PEMFCs have achieved ranges of up to 48 h in laboratory conditions and up to 4 h in low temperature and low-pressure conditions above 5000 m above sea level level [6,7,8].
Besides being a stand-alone source of power, proton exchange membrane fuel cells can also be used in conjunction with other clean energy sources, such as solar and wind power. As renewable energy sources, such as solar and wind power, are unstable and intermittent, the electricity generated using these energy technologies can hardly be utilised directly in a stable and continuous manner in real-life scenarios. PEM fuel cells can be used as energy storage devices together with renewable energy systems to store intermittently generated electricity to increase the availability of solar and wind energy, for example [9,10,11].
While there have been some successful market applications of PEMs as stand-alone power generators and energy storage devices, the relatively high cost of manufacture, the high requirements for the purity of the fuel, and the need for further improvements in mechanical durability have limited the further commercialisation of PEMs. Platinum, the catalyst most commonly used in proton exchange membrane fuel cells, significantly drives up the cost of manufacturing fuel cells. There is thus an urgent need for fuel cell designs that can extend the life of the platinum catalyst and improve the effective use of it. As a power source for transport instruments, mechanical durability is an important performance factor [12].
The single proton exchange membrane fuel cell is usually constructed in a hierarchical structure, with the central layer being a proton exchange membrane through which mainly protons could pass, as shown in Figure 1 [13]. From the centre to the sides are the catalyst layer (CL) of the anode and cathode, the gas diffusion layer (GDL) of two electrodes, and the bipolar plates in order. The membrane, CLs, and GDLs are also together referred to as membrane electrode assemblies (MEA), and the physical structure of these assemblies could be regarded as porous media containing multi-scale pores. The inner surface of the polar plate is mechanically machined with grooves, which are known as gas flow channels (GFCs). The area covered by the flow channels is the so-called flow field. During the operation of the cell, hydrogen and air are transported into the cell along the flow channel and reach the catalyst layer through the gas diffusion layer of anode and cathode, respectively. In the catalyst layer of the anode, the hydrogen molecules are stripped of their electrons and decomposed into protons. The electrons pass through an external circuit to form an electric current. In the catalyst layer of the cathode, the oxygen molecules react with the protons and electrons coming through the proton exchange membrane and the external circuit, respectively, resulting in water and the release of heat. After the reaction has taken place, the water produced is discharged from the cell through the gas flow channels together with the excess gas not involved in the reaction. The formulae for the electrochemical reactions occurring in the cathode and anode are listed in Table 1.
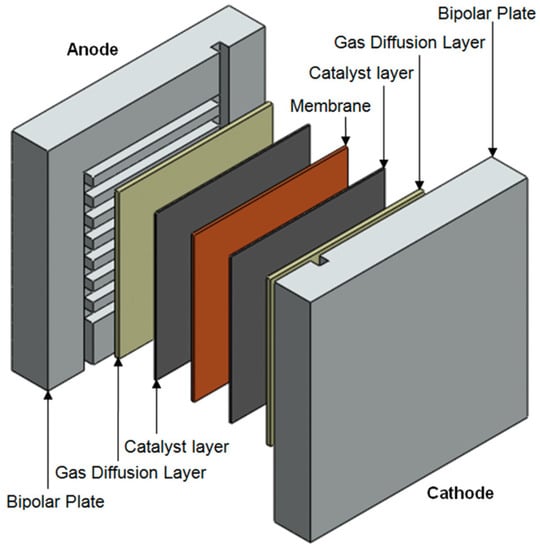
Figure 1.
The layer structure of a proton exchange membrane fuel cell [13].

Table 1.
The electrochemical reaction equations.
The mechanism of operation of PEMFCs clearly demonstrates that the interior of the cell is a complex environment containing various phenomena, such as electrochemical reactions, mass transfer of gases and produced water, heat transfer, and charge transfer. The uniformity and stability of the rate and intensity of the electrochemical reactions are fundamental to the stable current output of the fuel cell, and the current density and output power of the cell are two common and straightforward indicators of cell performance [14]. According to reaction kinetics, the rate of oxygen reduction at the cathode is only one millionth of the rate of hydrogen oxidation at the anode, making the rate of reaction at the cathode a constraint limiting the overall cell efficiency [15]. Moreover, the active surface of the catalyst layer is where the reactions take place, and the retention of the water on the surface isolates the gas reactants from contact with active areas, resulting in a reduction in the reaction rate [16]. The form of the produced water is not fixed and depends on the vapour saturation pressure and temperature. Excessive liquid water left in the cells will cause flooding, which is a great obstacle to mass transfer, resulting in a local gas shortage. The decrease in gas concentration causes degradation of the catalyst and corrosion of the diffusion layer, which seriously impair the durability of the cell [17]. On the other hand, PEM needs to absorb liquid water to maintain ionic conductivity. If the membrane is dehydrated, the output of the fuel cell will drop. Long-term dehydration can make the membrane become brittle or even crack, greatly reducing the service time of the cell [18]. It is therefore essential that the supply of reaction gases is reasonable, adequate, and evenly distributed and that the produced water is discharged in a timely manner. In addition, temperature is also a factor affecting the reaction rate. High temperature will reduce the absorption of PEM to water, while the low vapour saturation pressure corresponding to low temperature increases the possibility of flooding of the gas flow channels [19]. Hence, the thermal conductivity of the cell needs to be carefully considered. Overall, the combined management of gas, water, and heat determines the final performance of the cell.
The significance of the two-phase flow studies in a proton exchange membrane fuel cell is highlighted by the complicated gas–water flow within the flow channels of the fuel cell itself, which should focus on the optimisation of the design of flow channels. The application of visualisation techniques such as X-ray photography, nuclear magnetic resonance imaging, and three-dimensional neutron radiography has helped to gain a better understanding of the distribution and behaviour of the two-phase flow within the fuel cell. However, experimental studies are technically difficult and uneconomical due to the high cost of polymer membranes and platinum catalysts, the unavailability of observation equipment, the difficulty of standardising experimental procedures, and the large amount of time consumed in running experiments. In contrast, numerical simulation of the actual structural dimensions of the fuel cell and the interactions between reaction kinetics, mass and heat transfer, and fluid mechanics not only allows numerical solutions to be obtained in a very short time, but also allows the fundamental parameters to be adjusted as required, saving a great deal of time and cost [4]. Consequently, CFD tools are widely used in the studies of the optimisation of the structural design and performance of fuel cells.
The research results available now contain 1D, 2D, and 3D models of proton exchange membrane fuel cells. The one-dimensional model is easy to solve but can only consider mass transfer in a single direction. Two-dimensional models have been used to simulate the effects of more factors, such as multi-component reaction gases, temperature, humidity, etc., on cell performance. Its applications provide a more accurate simulation of the transfer of water and heat within the cell. Three-dimensional models have been developed to demonstrate intricate flow fields and mass transfer processes between different layered structures within the cell. With the dramatic increase in computing power in recent years, three-dimensional models have gradually become the mainstream of numerical simulation studies of fuel cells. This paper reviews numerical models that have been developed in previous years to simulate multi-phase flows in the gas flow channels of proton exchange membrane fuel cells, with the hope that a compilation of current research achievements will provide a reference for optimisation of modelling and design of proton exchange membrane fuel cells.
2. Comparison of Life-Cycle Emissions of Fuel Cell Electric Vehicles to Internal Combustion Engine Vehicles
Proton exchange membrane fuel cells are seen as a powerful alternative to the internal combustion engine as a propulsion system for vehicles. One reason for the ongoing transition from internal combustion engine vehicles (ICEVs) to fully electrified vehicles in the international passenger car market is the need to fill the gap created by the mismatch between the continuously growing number of vehicles and the shrinking reserves of fossil energy. By 2050, according to one report, the number of light vehicles worldwide will reach 2 billion [20], and the rate of consumption of oil is much faster than that of its production, with data showing that the rate of consumption is accelerating by about per year [21]. Another reason is the emissions resulting from the burning of petroleum-based fuels, which have a nearly irreversible negative impact on the environment. The emissions from vehicle exhausts contribute to both carbon monoxide (CO) and carbon dioxide (CO) emissions, nitrogen oxide (NO) emissions, and particulate emissions such as soot. CO is a major component of global greenhouse gas emissions. According to the U.S. Environmental Protection Agency, of global greenhouse gas emissions are contributed by CO generated by fossil fuels and industrial activities [22]. Moreover, the emissions from the transport sector are now one of the main sources of conventional emissions such as soot and NO. In Europe, around of NO emissions come from the transport sector [23,24,25,26].
As mentioned earlier, the only products attached to the operation of a PEM fuel cell are water and heat, making it possible to call the fuel cell electric vehicles (FECVs) emission-free. However, it does not mean that the use of the fuel cell as a power source for vehicles has no negative effect on the environment. A comparison of air pollution emissions from the petrol and hydrogen-fueled fuel cell vehicles showed that emissions from hydrogen fuel cell vehicles are significantly influenced by the purity of the fuel, in particular, impurities in the hydrogen fuel should be limited to 300 mol/mol for non-hydrogen, 0.2 mol/mol for CO, and 0.004 mol/mol for sulphur compounds [27]. In addition, the current processes of the production, transport, and refuelling of hydrogen are accompanied by emissions. These emissions are more significant for hydrogen than that for petrol and diesel. Figure 2 displays emissions in tonnes from the production of fuel and vehicles for battery electric vehicles (BEVs), fuel cell electric vehicles (FCEVs), and internal combustion vehicles (ICEVs), and it can be seen that the production of FCEVs and the hydrogen fuel generate more than twice the emissions of ICEVs [28]. Therefore, the emissions and impacts on the environment that potentially arise from the use of PEM fuel cells and the internal combustion engine should be discussed and compared in a comprehensive manner, from fuel production to vehicle assembly.
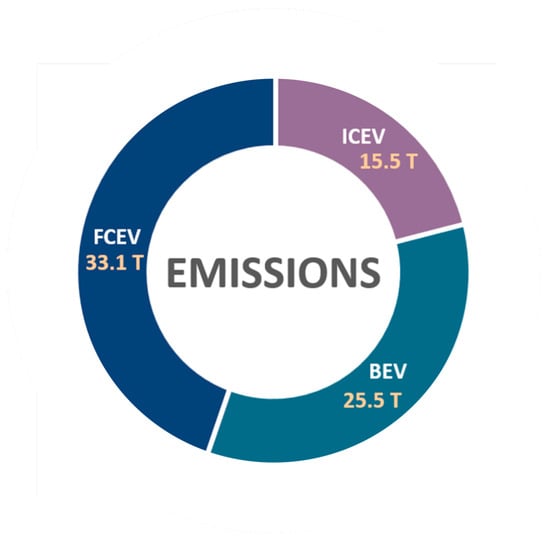
Figure 2.
The emissions from the production of fuel and vehicles for battery electric vehicles, fuel cell electric vehicles, and internal combustion vehicles [28].
One common tool used for comparison is the life-cycle assessment (LCA). This methodology can measure the impact of any energy system on the environment by taking into account all of the emissions generated from the beginning of the process to the end of the process. Dhanushkodi et al. [29] investigated the impact of the FECV on the environment using the life-cycle assessment methodology, focusing on the technologies for the production of hydrogen. The results indicated that the production of hydrogen through wind and solar energy significantly reduced greenhouse gas emissions. The assessment by Buberger et al. [30] stated that even if hydrogen produced from natural gas was used in the fuel cell vehicle, it would still reduce greenhouse gas emissions by approximately compared to the petrol vehicle. Hwang et al. [31] conducted a life-cycle assessment of the fuel cell vehicle and found that the fuel cell vehicles emitted less greenhouse gases compared to the petrol vehicle. Evangelisti et al. [32] compared the results of a comprehensive life-cycle assessment of the fuel cell electric vehicle with those of the battery electric vehicle and the internal combustion engine vehicle and concluded that the production process of the FECV has a larger impact on the environment compared to the other two power sources of the vehicle. Ahmadi and Kjeang [33] investigated the LCA of the hydrogen fuel cell vehicle and the petrol vehicle, considering the emission from both fuel production and vehicle production processes. The conclusions suggested a reduction in total life-cycle greenhouse gases for the FECV compared to the petrol vehicle. A life-cycle assessment of the PEM fuel cell vehicle was developed by Hussain et al. [34]. The results noted that though the PEM fuel cell vehicle produced 8.5 times higher greenhouse gas emissions from hydrogen during the fuel cycle than the internal combustion engine vehicle, the whole life-cycle greenhouse gas emissions of the fuel cell vehicle were 2.6 times lower than that of the internal combustion engine vehicle. Ahmadi et al. [21] found that the driving cycle had an impact on the full life-cycle emissions of hydrogen fuel cell vehicles. Comparing the LCA results for different driving patterns, the motorway driving cycle had the lowest total life-cycle emissions.
Differences in the technologies of the hydrogen production and the power standards in different countries have an impact on the emissions of the fuel cell electric vehicles fuelled by hydrogen. Ahmadi and Kjeang [35] explored the potential of the hydrogen fuel cell vehicle in four of the Canadian provinces through a life-cycle assessment of the vehicle. The results demonstrated that the transition from the petrol vehicle to FCEVs could lead to significant reductions in greenhouse gas emissions in all four provinces. Zamel and Li [36] also examined the impact on the CO emissions of the materials and fuels used to produce vehicles with different power sources in Canada. A full life-cycle assessment of the internal combustion engine vehicle (ICEV) and the fuel cell electric vehicle (FCEV), respectively, showed that the total emissions of the FECV were lower than that of the ICEV. Yang et al. [37] found that the hydrogen production process and fuel cell vehicle mileage affected the greenhouse gas emissions of the vehicles in China. Using the LCA of the fuel cell vehicle, the electric vehicle, and the internal combustion engine vehicle, they concluded that it is necessary to select the appropriate option for the vehicle and fuel based on the driving range. In the scenarios discussed in their study, fuel cell vehicles using hydrogen generated from the electrolysis of wasted hydropower and the coke oven gas had the lowest greenhouse gas emissions when driven over a full life cycle of approximately 75,000 km. In the city of Rosario, Santa Fe Province, Argentina, there are two kinds of technologies for producing hydrogen. One is the ‘green technology’, which is based on renewable resources, such as rapid cut dense poplar trees grown in energy plantations and post-industrial wood residues, such as pallets of wood chips and corn silage, and the other is a ‘grey technology’ based on non-renewable resources, such as the local power grid from the water electrolysis and the natural gas from the steam methane reforming process. Lannuzzi et al. [38] conducted an LCA on local fuel cell buses and found that buses fuelled by ‘green hydrogen’ emit less greenhouse gases than internal combustion vehicles do. Liu et al. [39] performed a well-to-wheel (WTW) emissions analysis on a Toyota Mirai (FECV) and a Mazda3 (ICEV), where the fuel for the Toyota Mirai was hydrogen generated from the fossil energy production pathway and compressed by the US average grid generation mix. The results demonstrated that the WTW greenhouse gas emissions from fuel cell vehicles were 15–45% lower compared to those from internal combustion vehicles and that CO and NO emissions were also lower. Seol et al. [40] investigated the LCA of the internal combustion engine vehicle (petrol), the internal combustion engine vehicle (diesel), and the fuel cell electric vehicle in South Korea, focusing on full life-cycle NO emissions. Both the real driving emission (RDE) of NO from previous studies supported by the South Korean Ministry of Environment and the NO emissions based on the new European driving cycle (NEDC) test procedure were considered in the assessment of the internal combustion engine vehicle (ICEV). The results showed that WTW NO emissions were calculated to be , , and 0.154 g/km for ICEVs (petrol), ICEVs (diesel-euro 6), and ICEVs (diesel-euro 6d-temperature), respectively. In the assessment of the fuel cell electric vehicle, four kinds of hydrogen production technologies were considered. The results indicated that the FECV using hydrogen produced by steam methane reforming as fuel had the lowest full life-cycle NO emissions.
3. Geometric Structure and Parameters of Gas Flow Channels
The gas flow channels located on the bipolar plates are assigned the function of directing the fuel and oxidiser into the reaction zone of the catalyst layer and discharging the product water from the inside of the cell to the outside. It can be said that the shape and arrangement of the channels are important parts of the integrated gas, water, and heat management as they determine the flow state of the substances (hydrogen, oxygen, water vapour, liquid water, etc.) inside the cell which has a profound effect on the ability to get the reactants into the diffusion layer as uniformly as possible and to get the water out as quickly as possible, i.e., the efficiency of the transport and utilisation of the reactants. This is where the study of various designs for the geometry and arrangement of gas flow channels and the search for relationships between structural parameters and cell performance are valuable since the integration of gas, water, and heat management determines the performance of the cell, as already explained. Proper design can reduce the concentration losses incurred in PEMFC at high current density lines, with data showing that it can improve overall cell performance by around 50% [41]. With the consideration of cost and flexibility, the majority of studies on gas flow channels have taken a numerical simulation approach.
The design of the geometry of the gas flow channels has to be considered in terms of the shape of the cross section of the channels, the length and width of channel, the way in which the channels are arranged and combined on the bipolar plates (a reasonable number of channels), and the configuration of the headers at the inlet and outlet. The flow field is formed by multiple channels on the bipolar plates. Depending on the combination and distribution of the channels, regular flow fields include parallel, serpentine, interdigitated, and lattice flow fields. In parallel and serpentine flow fields, the reactant gases are generally transported by diffusion through the straight flow channels. Due to the different flow resistance in each channel of the flow field, the reactants are not uniformly distributed, and the concentration of reactants at the outlet is significantly lower compared to that at the inlet. In addition, there are severe pressure drops. These can limit gas utilisation and water removal capability, leading to loss of performance and shortened service life of the proton exchange membrane fuel cell [42]. The discontinuous design between channels of the interdigitated flow field forces the fuel gas and oxide gas to flow from the gas diffusion layer to the outlet, where a portion of the gas transport becomes forced convection. This improves gas utilisation and facilitates drainage, but the pressure drop is still there [43]. How to optimise the structural geometry of the flow channel in order to overcome these problems has therefore become the main objective of the relevant research.
3.1. The Shape of the Channel Cross Section
The shape of the cross section of the channels has a significant effect on the consumption of reactants and the ability to remove water. Rectangular is the most common shape of the cross section of the channel, and fuel cells using this shape have a higher cell voltage than using other cross-section shapes, which means that the cell can have a higher output [44]. Cells with cross sections that are triangular or semi-circular can increase the fuel consumption at the anode of the cell, which in turn increases the efficiency of the fuel cell. The trapezoidal cross section is useful for the diffusion of the fuel, making it more evenly distributed. Therefore, the cell performance can be improved. The use of the three shapes can also facilitate the removal of liquid water from the channel and the utilisation of oxygen, as the flow rate of reactants has been significantly increased compared to that using rectangular shape [45,46]. Overall, the designs with triangular, trapezoidal, and semi-circular channel cross sections have been found to have better performance than cells with rectangular channel cross sections due to the greatly increased gas flow rate which enhances the ability of PEMFC to remove liquid water and utilise oxygen, as shown in Figure 3 [47]. Using the VOF method, Lorenzini-Gutierrez et al. [48] quantified that a trapezoidal cross section with open angles of and provided better water removal with a relatively stable pressure drop, which could be observed in Figure 4. In addition, the trapezoidal shape as a channel cross section facilitates the diffusion of the reactants into the reflective zone on the central membrane electrode assembly, which has a positive impact on the cell performance. Using the properties of the basic shapes as a basis for the design of a combination of basic shapes as channel cross sections, Mohammedi et al. [49] simulated PEMFC with thirty combined fluid channel cross sections using a 3D CFD model and showed that the cross-sectional shape has a more pronounced effect on cell performance at high current densities. All the cross-sectional shapes containing trapezoids showed better performance than rectangular cross-sectional fuel cells.
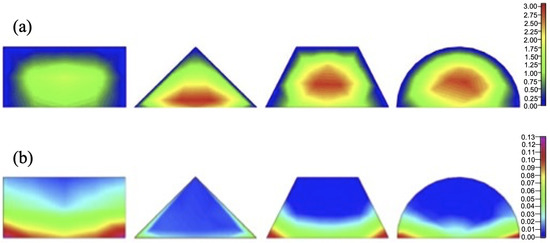
Figure 3.
The distribution of (a) liquid water saturation and (b) flow velocity (m/s) in a channel for various cross-section shapes [47].
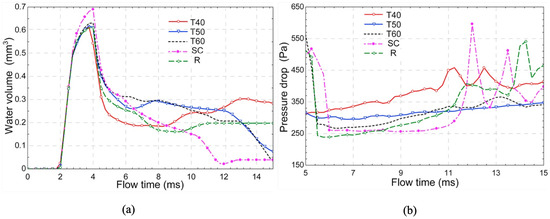
Figure 4.
Variation of (a) the water content within control volume and (b) the two-phase pressure drop during the flow time of 5–15 ms for different channel cross-section geometries [48].
3.2. The Length and Width of the Flow Channel
The part of the flow field between the flow channels, known as the ribs, serves to transfer heat, to collect and conduct current, and to provide some mechanical support for the cell. It is easy to imagine that the width of the flow channels and ribs has a considerable influence on the mass transfer, heat conduction, and electrical conductivity of the cell. To be more specific, the width of the flow channel is related to the transport of fuel gas in the flow field, with a wider flow channel allowing for a smoother flow of the substance. Wide ribs reduce the contact resistance and facilitate the collection of current, while the thermal conductivity and mechanical stability are also better [50]. Hence, a number of geometric parameters, including channel to rib width ratio, flow channel area ratio, and flow channel width ratio, are used to evaluate the effect of flow channel and rib width on the overall performance of the PEMFC. The flow channel area ratio is the ratio of the total flow channel area to the active area of the cell, while the flow channel width ratio is the ratio of the total flow channel width to the width of the entire cell.
Kerkoub et al. [51] used a three-dimensional CFD model to investigate the variation of cell performance in serpentine, parallel, and interdigitated flow fields, respectively, where six different rib width ratios were used. The results in Figure 5 showed that the performance of the serpentine flow field improved by , the interdigitated field by , and the parallel flow field by when the channel-to-rib width ratio was reduced from to . As the channel-to-rib width ratio decreases, the pressure drop and convection under the rib increases, resulting in faster response rates under the rib and more uniform local transport phenomena within the catalyst layer. Qiu et al. [52] investigated the effect of cathode flow channel design on PEM fuel cells. Simulations (see Figure 6) showed that when the channel-to-rib width ratio was kept at one, an increase in channel width generally resulted in an uneven distribution of relative humidity and oxygen concentration within the cell, leading to a decrease in cell performance. Rahimi-Esbo et al. [53] concluded that the best performance of the PEMFC was achieved with a value of 1.5 for the channel-to-rib width ratio.
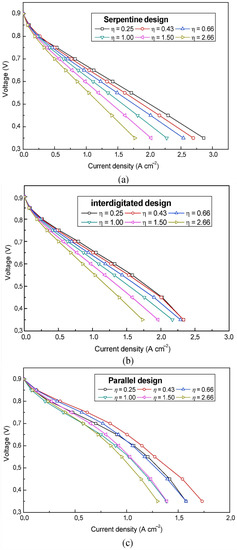
Figure 5.
The polarization curve of PEMFC with different channel-to-rib width ratio in: (a) parallel; (b) serpentine; and (c) interdigitated flow field [51].
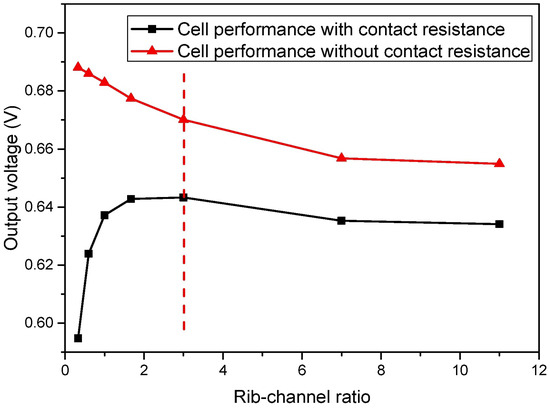
Figure 6.
The performance of PEMFC with different channel-to-rib width ratio at a current density of 600 mA/cm [52].
The increase in the channel area ratio has a beneficial effect on the diffusion transport of the reactant gas, as the contact area between the reactant and the gas diffusion layer is increased, and more hydrogen can be transported directly into the porous media involved in the electrochemical reaction. The performance of the cell is thus improved [54]. The reduced flow channel width ratio accelerates the flow rate of substances in the flow field, again allowing more reactants to participate in the reaction and enhancing the ability to remove water, thereby improving the performance of the cell [55].
Increasing the length of the gas flow path allows convection to be the main way for fuel transport, with higher utilisation compared to diffusion gas. However, short length can contribute to more uniform electrochemical reactions and a reduction in water accumulation in the cell [56,57]. Santamaria et al. [58] simulated two different lengths of interdigitated flow fields using the MUMPS direct solver in COMSOL 4.3 (COMSOL Inc., Stockholm, Sweden), as seen in Figure 7. The results showed that the flow field design with a shorter length produced a higher maximum power. In the case of the longer flow channels, the flow distribution under the rib area (cross-flow) is affected by inhomogeneity, while the shorter case produces relatively uniform cross-flow along its length. The aspect ratio of the channel therefore has to be carefully set when designing the flow field. Cooper et al. [59] investigated the effect of aspect ratio on cell performance in interdigitated flow fields. It was shown in Figure 8 that a significant reduction in current density was observed in the central region of the interdigitated flow field for medium and high aspect ratios, while there is a more uniform current density distribution over the length of the flow field for low aspect ratios. The main cause of power density loss in the cell is the accumulation of liquid water in the flow channels. A low aspect ratio design should be adopted for the PEMFCs with interdigitated flow field or an additional design to remove liquid water if a high aspect ratio is required.
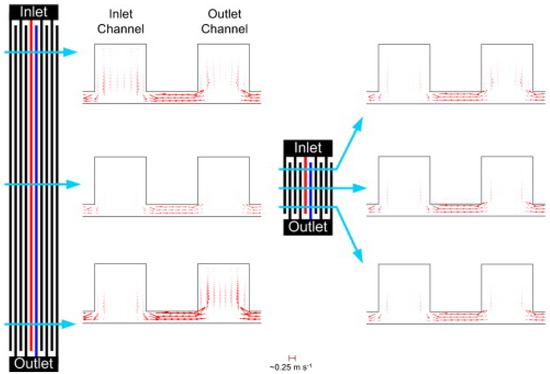
Figure 7.
The cross-sectional views of cross flow velocity at positions of approximately 10%, 50%, and 90% of both long and short interdigitated flow channels [58].
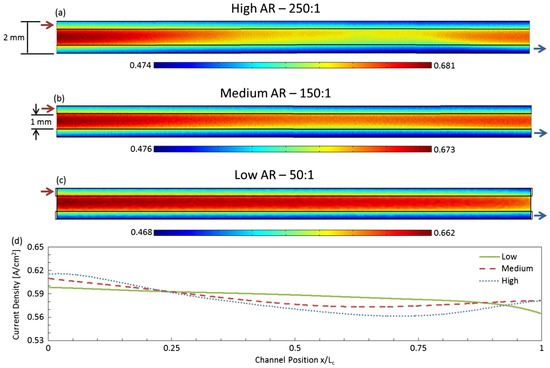
Figure 8.
The current density distribution of PEMFC with a (a) high length to width ratio, a (b) medium length to width ratio, a (c) low length to width ratio, and (d) the current density at positions [59].
3.3. The Number of Gas Flow Channels
The number of gas flow channels also has an effect on the performance of the cell. Limjeerajarus et al. [60] designed six flow fields containing different numbers of channels, including single, three, and five channel serpentine, parallel and three channels in series, and five channels in series, which were investigated using the ANSYS FLUENT 14.0 software (ANSYS, Inc., Canonsburg, PA, USA). Figure 9 shows the simulation result for the distribution of water mass fraction and current density at the cathode. It could be found that for the serpentine flow field, the increase in the number of channels has caused a loss in overall fuel cell performance, whereas for the parallel flow field in series, the increase in the number of channels increases the flow rate of the gas and aids drainage. Boddu et al. [61] instead turned their attention to the effect of the number of channels on the pressure drop and concluded that by increasing the number of channels, the pressure drop could be reduced. It is also noted that Rahimi-Esbo et al. [53] simulated reducing the number of channels for a given channel width and also achieved a reduction in pressure drop.
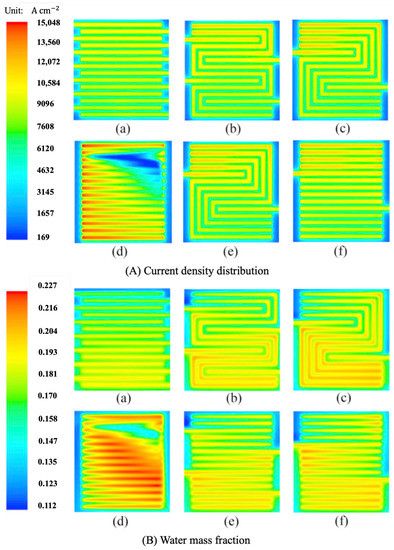
Figure 9.
The distribution of (A) current density and (B) water mass fraction at the cathode of (a) 1S, (b) 3S, (c) 5S, (d) parallel, (e) 3PIS and (f) 5PIS [60].
3.4. Headers at the Inlet and Outlet
The structure and parameters of the inlet and outlet headers of the flow field have a significant effect on the distribution of reactants and liquid water. The results by Hossain et al. [62] for a Z-shaped parallel flow field suggest that decreasing the width of the distribution channel along the inlet increases the gas flow through the transverse channel in the middle of the flow field. In addition, a parallel flow field combining both Z- and U-shaped structures provides a better flow distribution. The geometry of the flow field used in this work is shown in Figure 10. Chen et al. [63] developed a two-dimensional model of the interdigitated flow field and simulated the effect of the width of the head channel at the outlet on the performance of a proton exchange membrane fuel cell. It was found that the PEMFC with narrower head channel width had a more uniform distribution of the amount of oxygen concentration in the cathode, better capacity for drainage, and superior overall performance than the conventional outlet. In the study conducted by Xiong et al. [64], the effect of different widths of the distribution channel at the inlet and the manifold at the outlet of the Z-parallel flow field on the oxygen concentration distribution at the cathode was investigated by simulation. The results show that if the flow rate at the inlet is the same, increasing the width of the manifold at the outlet is of benefit to the increase of the oxygen concentration at the cathode, and the oxygen distribution is more uniform, while increasing the width of the distribution channel at the inlet could disturb the uniformity of oxygen distribution. A tapering design for the inlet header with an appropriate distribution of flow channels can improve the oxygen concentration and oxygen distribution uniformity at the cathode.
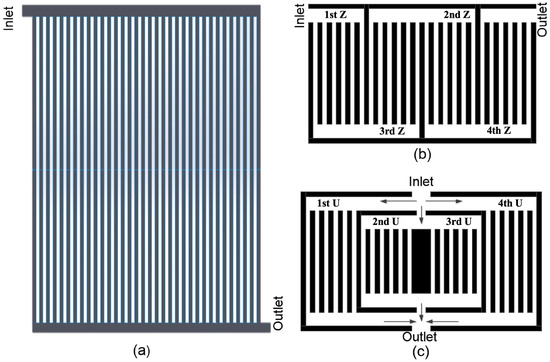
Figure 10.
The geometry of the flow field: (a) conventional Z type; (b) multiple Z type; (c) optimized Z type [62].
4. Morphing in Flow Field Design
Conventional flow fields have distinct advantages and disadvantages. There are also contradictory effects of the geometrical parameters of the gas flow channels on the overall performance of the fuel cell. The optimisation of the flow field design is a matter of making some morphs around these parameters to achieve a balance on demand. Common ideas for morphing include the design of tortuous flow channels while keeping the cross section constant, the design of unfixed or gradual cross sections along the direction of flow, the placement of baffles in the straight flow channels, etc.
4.1. Design of Tortuous Flow Channels
Keeping the cross section constant and changing a straight flow channel to a zigzag, for example sinusoidal, can change the steady flow state of the fluid and help to enhance convection and heat transfer. The study by Saco et al. [65] compared four flow fields: serpentine, serpentine zigzag, parallel, and parallel zigzag flow fields. The results in Figure 11 and Figure 12 indicated that the parallel zigzag flow field had the highest power density of the simulated cases due to effective water management and minimal pressure drop. Atyabi et al. [66] simulated a sinusoidal flow field based on a non-isothermal steady-state multi-phase model using the finite volume method and compared it with a parallel flow field. The maximum velocity and pressure drop of the gas in the sinusoidal and parallel flow fields were 33 m/s and 28 m/s and 1074 Pa and 168 Pa, respectively. The uniformity index of the oxygen mass fraction at the interface between the gas diffusion layer and the catalyst layer was 0.012 and 0.08. The sinusoidal flow field had better water removal characteristics at higher current densities, but the higher pressure drop resulted in more power consumption. Anyanwu et al. [67] investigated the effect of sinusoidal amplitude ratio, radius of curvature, and contact angle on droplet removal in a sinusoidal flow channel by the VOF method. The simulations concluded that the water removal efficiency due to secondary flow caused by sidewall curvature increased with increasing sinusoidal amplitude ratio. The pressure drop and gas flow rate in the sinusoidal flow channel also increased with increasing sinusoidal amplitude ratio.
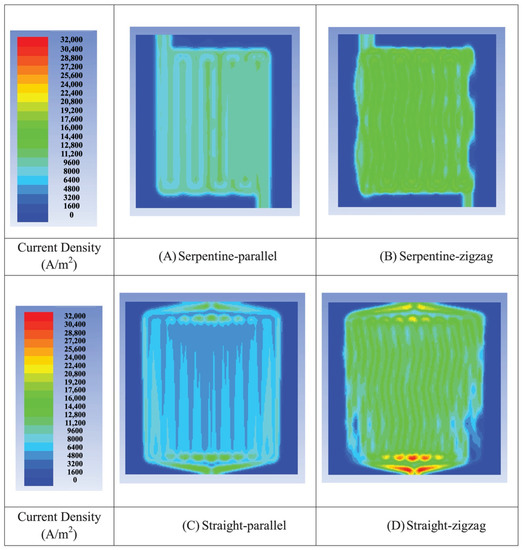
Figure 11.
The current density distribution: (A) serpentine; (B) serpentine zigzag; (C) parallel; (D) parallel zigzag [65].
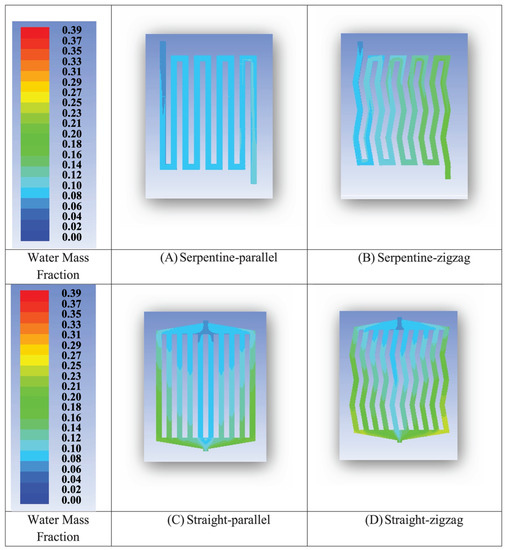
Figure 12.
The water mass fraction distribution: (A) serpentine; (B) serpentine zigzag; (C) parallel; (D) parallel zigzag [65].
Monsaf et al. [68] designed a spiral flow field and investigated the effects of channel width, number of spiral channels, and direction of flow on reactant consumption in a proton exchange membrane fuel cell with such a flow field. The larger the channel to rib width ratio, the larger the contact area between the flow field and the gas diffusion layer, the more reactants penetrated the gas diffusion layer, and the more uniformly the reactants were distributed. The increase in the number of turns of the spiral channel improved the uniformity of the reactant distribution. As Figure 13 shows, when the reactants are injected from the outer side of the spiral flow field and discharged from its inner side, the spiral shape of the channel would generate centrifugal force, thus improving the cell performance. A honeycomb bionic flow field was proposed by Zhang et al. [69]. Compared to parallel and serpentine, a honeycomb flow field has been found to improve cell performance by distributing oxygen more uniformly across the GDL surface, but at the same time, moisture tends to accumulate inside the flow channel leading to flooding.
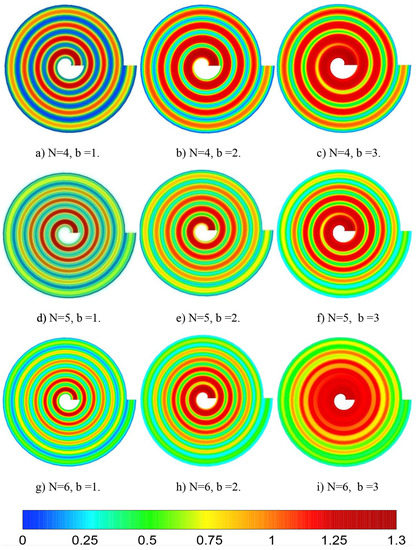
Figure 13.
Hydrogen concentration field [68].
Kloess et al. [70] designed two new flow fields that were inspired by leaves and lungs, which are shown in Figure 14, and compared them with serpentine and interdigitated flow fields. According to the results, a more uniform gas distribution was observed in the leaf and lung flow fields. Subsequently, Ouellette et al. [71] organically combined the concept of enhanced convection under the ribs in an interdigitated flow field with bio-inspiration and analysed the effect on overall performance of the PEMFC where a modified interdigitated flow field based on a tree structure and other non-interdigitated flow field were used at the anode or the cathode in comparison to the serpentine flow field. The combination of the serpentine flow field at the anode and the tree-based interdigitated flow field at the cathode showed the best performance of all discussed combinations. The best homogeneity of the reactants on the surface of the catalyst layer was also achieved, which was attributed to the enhanced convection under the ribs.
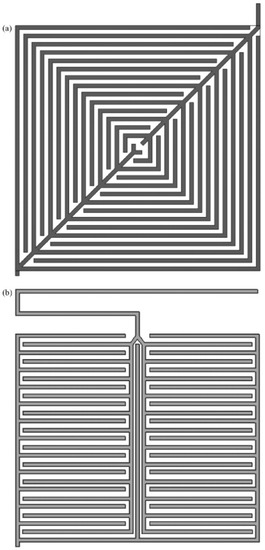
Figure 14.
The novel (a) leaf and (b) lung flow field [70].
4.2. Design of Unfixed Cross Sections
The continuously varied channel cross section along the flow direction interferes with the gas and liquid in the flow channel, causing changes in the flow rate and pressure distribution of the fluid, thus strengthening the mass transfer properties within the flow field. Figure 15 is a contracting and diverging alternately arranged flow field designed by Zehtabiyan-Rezaie et al. [72] in which the vertical ribs of a parallel flow field were inclined at an angle to form flow channels that gradually contract or diverge following the direction of flow. In such a flow field, the pressure distribution was not uniform, and the average pressure in the contracting flow channel was always greater than that in the diverging flow channel. The difference on the pressure between the two created a transverse flow so that oxygen was better distributed over the catalyst layer. The polarisation curves indicated that the optimum inclination angle of the flow channel is . A increase in net output power was obtained compared to a parallel straight field. Wang et al. [73] designed a conical flow field, shown in Figure 16, by gradually reducing the rectangular cross section. The conical flow field was found to increase the flow rate in the outlet zone, thus improving the efficiency of water removal from the cell. Simultaneously, the convection under the ribs between adjacent channels was enhanced by the tapered design, which facilitated the discharge of water accumulated under the ribs, thereby reducing the oxygen concentration difference between the ribs and the channels. With this, the transport of oxygen and cell performance were improved.
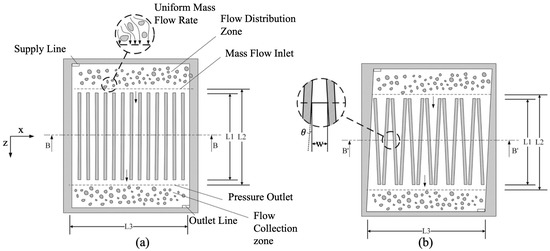
Figure 15.
(a) The conventional parallel flow channels; (b) the contracting and diverging flow field [72].
Figure 16.
The conical flow fields: (a) gradually reduced height; (b) gradually reduced width [73].
Jia et al. [74] changed the flow channel wall of the serpentine flow field to a wavy shape and designed both parallel and symmetrical configurations, simultaneously modifying the path of flow and cross section of the flow channel, as shown in Figure 17. The simulations demonstrated that the serpentine flow field with a wavy cross section could improve the uniformity of the temperature of the membrane. The best uniformity was achieved with the symmetrical configuration. In the parallel configuration, uniformity of membrane temperature could be improved by increasing the amplitude. Ramin et al. [75] investigated the effect of depressions at different cross sections of bipolar plates on the performance of PEMFC using a three-dimensional non-isothermal model. It was found, as seen in Figure 18, that a flow channel with two depressions of 8 mm in length was the optimum design. This design also improved the distribution of oxygen and water across the catalyst layer of the cathode, thus reducing the cathodic overpotential of the cell.
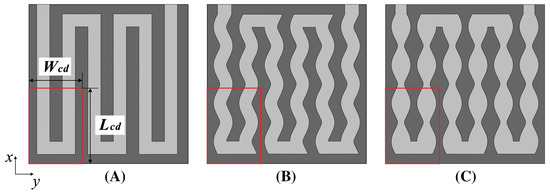
Figure 17.
The serpentine flow field with (A) straight wall; (B) parallel wavy wall; (C) symmetrical wavy wall [74].
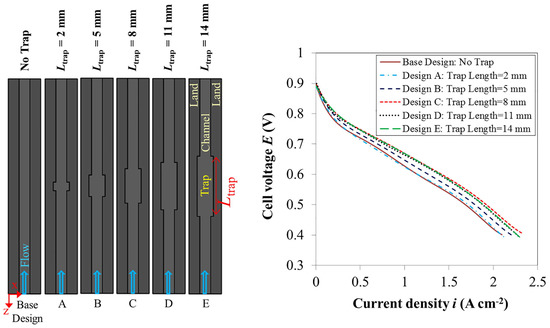
Figure 18.
Study of the effect of traps and their lengths on the cell performance: the left picture shows (mono-trap or single-trap) channels with the different trap lengths of 2, 5, 8, 11, and 14 mm, here named as Cases or Designs A, B, C, D, and E, respectively, and the simple straight (conventional) channel called the base design (the channel with no trap). The shown graph compares the polarization curves for these PEMFC Designs A to E and a PEMFC with no-trap straight (conventional) channel (base design) [75].
4.3. Placement of Baffles
Heidary et al. [76] looked at the effect of two types of baffle arrangement (linear and staggered) in the channel of a parallel flow field on cell performance and pressure drop of a proton exchange membrane fuel cell, as shown in Figure 19. The presence of baffles enabled the reactant gas to enter the gas diffusion layer via convection, increasing the molar concentration of oxygen within the catalytic layer and thus producing higher power and current density. The convective flow in an individual flow channel was intensified by the linear distribution; thus cell performance was also improved. The staggered distribution not only provided enhanced convection within the individual flow channel, but also allowed the reactant gas to be driven transversely due to the pressure difference between adjacent channels, creating convection of the reactant gas between different flow channels, which is superior to the linear baffle arrangement.
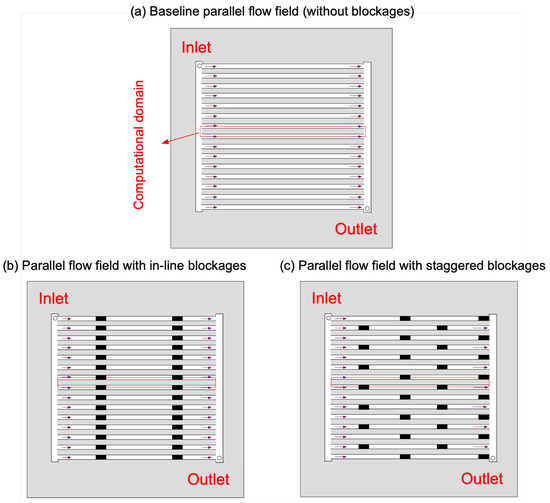
Figure 19.
The schematic diagrams for the two novel flow fields at cathode of PEMFC investigated. The anode flow fields are conventional (parallel without blockages as shown in (a)) [76].
Shen et al. [77] showed that baffles in the flow channel could effectively reduce the angle between the velocity vector and the concentration gradient, enhancing mass transfer of the reactants. Zhang et al. [78] studied wedge-shaped baffles and found that the drainage of the cell improved as the volume of the wedge-shaped baffle increased from 0.5 mm to 1.5 mm (Figure 20).
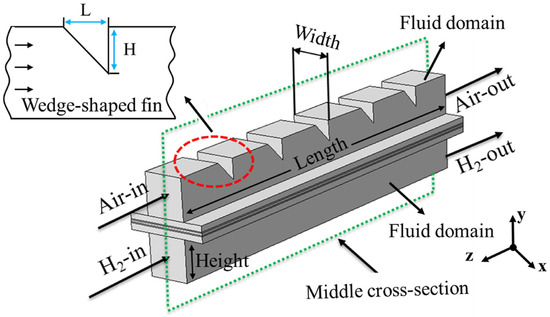
Figure 20.
The physical model of PEMFC with wedge-shaped fins [78].
Ghanbarian et al. [79] investigated the enhancement of the performance of PEMFCs with different shapes and distribution of baffles in the flow channel. It was found that the baffles resulted in a more uniform oxygen content in the catalyst layer due to a synergistic effect caused by diffusion and convection. The most significant improvement in net cell power density was obtained when the baffle shape was trapezoidal with a height of of the channel height. Yin et al. [80] observed that trapezoidal baffles significantly increased convective flux but also reduced the diffusive flux of oxygen in the gas diffusion layer near the baffle location. The optimum forward and backward inclination angles of the trapezoidal baffle were both , which balanced the strength of the convective effect and its effect area and eliminated the backflow phenomenon, thus maintaining efficient mass transfer (Figure 21). A more detailed study of baffle height by Yin et al. [81] concluded that the net power of the fuel cell is maximised when the baffle height is 0.8 times the channel height, and the optimum number of baffles along the channel is 5. Chen et al. [82] added porous media blocks in addition to the baffles to further increase the flow resistance from the inlet to the outlet in the flow field. The reactants were forced to transfer into the porous blocks and the gas diffusion layer, thus improving the cell performance. The low porosity of the porous blocks helped to remove the liquid water from the gas diffusion layer more effectively, contributing to a significant improvement in cell performance.
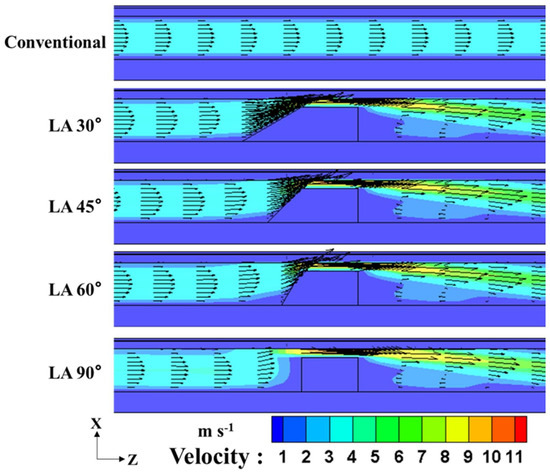
Figure 21.
The influence of the baffle block-leading sloping angle on the velocity distribution in the PEM fuel cell cathode flow channel [80].
Wave-shaped flow channels are formed by the periodic placement of baffles with rounded corners in the flow field. Numerical simulations of this new flow field by Li et al. [83] found that the periodic waveform structure of the wavy flow channel induced periodic changes in local flow direction, local flow rate, and local pressure, intensifying convection, thereby increasing the rate of oxygen transfer in the porous structure of the electrode and eliminating the accumulation of liquid water in the micropores, which improved cell performance. The optimisation of the wavy flow channel by Yan et al. [84] to reduce the depth of the flow channel gradually could result in a faster flow rate at the downstream of the flow channel, alleviating water accumulation and oxygen deficiency in the downstream region. Thus, a more uniform current density distribution could be achieved (Figure 22).
Figure 22.
The novel wavy flow channel design [84].
Chen et al. [85] showed that the optimal channel depth and wavelength for the wave flow channel were 0.45 mm and 2 mm, respectively, and that by the optimised parameters, the current density of the cell using a wave flow channel at 0.4 V was increased by compared to that of the conventional flow channel. The effect of the amplitude and frequency of pulsating pressure on the performance of a cell with a wave flow channel was further investigated by Ashorynejad et al. [86]. The results showed that the convective transport of substances to the reaction areas was enhanced by the pulsating pressure. In wavy flow channels, pulsating pressures with amplitudes up to 0.7 times the pressure drop across the cathode channel increased the performance of the fuel cell by approximately .
Wang et al. [87] devised a new parallel flow field by introducing the concept of sub-channels. As Figure 23 shows, sub-channels perpendicular to the flow direction were placed in the flow channel of the cathodic flow field, with the main channel being fed with moist air and the sub-channels being fed with dry air. A three-dimensional two-phase model was developed to investigate the effects of the flow rate and inlet location of the sub-channels. The results demonstrated that the percentage of air from the inlet of the sub-channel to the total cathode flow rate and the position of the inlet of the sub-channel placed along the cathode had a significant effect on the distribution of air into the cell and the removal of liquid water. The performance of the PEM fuel cell is significantly better than the conventional design when the inlet of the sub-channel is positioned at approximately of the inlet channel length of the main channel, and the air from the inlet of the sub-channel accounts for approximately of the total cathode flow rate.
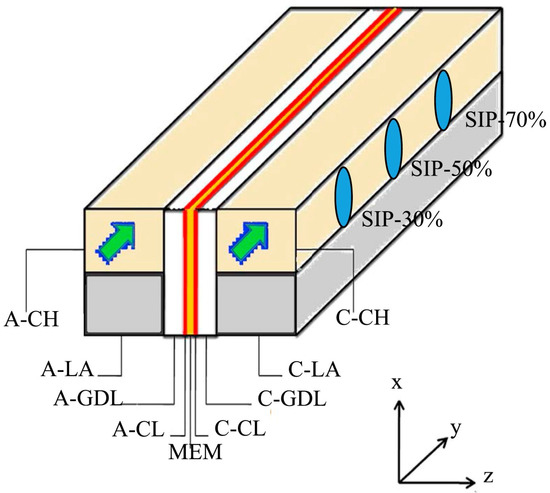
Figure 23.
The schematic diagram of a PEMFC channel having sub-channels [87].
5. Conclusions
This paper reviews the influence of the geometry of the gas flow channels on the performance of the PEMFC, summarises some specific parameters that must be considered when designing the flow channel geometry, such as the length of the channel, parameters of the cross section, and the use of baffles, and analyses the relationship between these parameters of the flow channel geometry and mass transfer, heat transfer, electrical conductivity, and output power density. Conventional flow fields and some morphing designs based on them are also discussed. Optimisation of the parameters of the structure of the flow field can improve the uniformity of the distribution of the reacting gas within the flow field while increasing its concentration. The cell performance is best when the channel to rib ratio is kept around three. Too large a ratio would have a high resistance to mass transfer and the removal of water, affecting the cell performance; too small a ratio would have an impact on the loss of performance due to the contact resistance between the bipolar plate and the gas diffusion layer. Due to the accumulation of liquid water in channels, the current density is noticeably lower in the central region of the flow field for high aspect ratios and more uniformly distributed for low aspect ratios. The effect of the width of the converging channel at the outlet on the oxygen concentration and the uniformity of distribution varies in different flow fields. The narrowing of the distribution channel at the inlet in parallel flow channels could improve the oxygen concentration and the uniformity of the oxygen distribution. Unconventional flow field designs, such as tortuous flow channels and unfixed cross sections, have their own advantages in terms of increasing the distribution uniformity of the reactant gases, optimising the capacity to remove water from the flow field and thus improving cell performance. The placement of baffles in the flow channel can facilitate the flow of the fuel and oxygen through the gas diffusion layer towards the catalyst layer, significantly enhancing the transport of the substances in the catalyst layer and improving cell performance.
One important issue the simulation of proton exchange membrane fuel cells faces is the lack of full-scale PEM fuel cell models. How to solve the problem of coupling between individual components while investigating each component in detail is the key to developing a full-scale fuel cell model. Another problem is the absence of single-cell models of PEM fuel cells with standardised designs of cell components and benchmark operating conditions, which has led to discrepancies and possibly even complete contradictions in the results of numerical simulation studies of PEM fuel cells under different operating conditions, using the same common flow path design (parallel, serpentine, and interdigitated flow channels). This considerably increases the difficulty of making use of the latest research results. Therefore, the establishment of clear industry standard design criteria for PEM fuel cells and the modularity of the cell components are important for subsequent studies of the effect of the design of gas flow channels on cell performance. In addition, water management in new flow fields is relatively poorly investigated, and future work on the novel flow field will continue to rely on CFD simulations, given the difficulty and cost of manufacturing. Further research work is required, including more accurate CFD models that consider liquid water formation and droplet transport, as well as more detailed model validation. Different flow field structures have different effects on the overall performance of the PEMFC. These effects are mutually constraining. Relatively minor factors have to be discarded in order to achieve different design objectives, depending on their needs. In most studies, the arrangement and morphology of the channels is the main factor in the design of the structure. Therefore, from the perspective of structural parameter design and optimisation, the design of the flow field should be a multi-objective collaborative optimisation process that takes into account performance characteristics, such as water and thermal management in the cell and the net power output of the cell, in order to achieve stable and efficient long-term operation of the PEMFC.
Author Contributions
Data curation, M.G. and M.C.; writing—original draft preparation, M.G.; writing—review and editing, X.Z. and Y.R.; funding acquisition, X.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Zhejiang Natural Science Foundation [project code LY18E060004].
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors acknowledge the financial support from the Zhejiang Natural Science Foundation [project code LY18E060004].
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| AR | aspect ratio |
| BEV | Battery electric vehicle |
| CFD | Computational Fluid Dynamics |
| CL | Catalyst layer |
| CO | carbon monoxide |
| CO | carbon dioxide |
| E | cell voltage, V |
| electron | |
| FECV | Fuel cell electric vehicle |
| GDL | Gas diffusion layer |
| GFCs | Gas flow channels |
| H | height, mm |
| hydrogen ion | |
| hydrogen | |
| water | |
| ICEV | Internal combustion engine vehicle |
| i | current density, A cm |
| L | length, mm |
| channel length, mm | |
| length of computational domain, mm | |
| length of trap, mm | |
| LA | leading angle, |
| LCA | Life-cycle assessment |
| MEA | Membrane electrode assemblies |
| NEDE | New European Driving Cycle |
| NO | nitrogen oxide |
| oxygen | |
| PEMFC | Proton Exchange Membrane Fuel Cell |
| RDE | real driving emission |
| SIP | Sub-channel Inlet Position, % |
| US | United States |
| VOF | Volume of Fluid |
| width of computational domain | |
| WTW | well to wheel |
| channel to rib width ratio |
References
- O’hayre, R.; Cha, S.W.; Colella, W.; Prinz, F.B. Fuel cell fundamentals; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Barbir, F. PEM Fuel Cells: Theory and Practice; Academic Press: Cambridge, MA, USA, 2012. [Google Scholar]
- Lamir, J.; Dicks, A. Fuel Cell System Principle Design Application; Science Press: Beijing, China, 2006. [Google Scholar]
- Wang, Y.; Pang, Y.; Xu, H.; Martinez, A.; Chen, K.S. PEM Fuel cell and electrolysis cell technologies and hydrogen infrastructure development—A review. Energy Environ. Sci. 2022, 15, 2288–2328. [Google Scholar] [CrossRef]
- Nonobe, Y. Development of the fuel cell vehicle mirai. IEEJ Trans. Electr. Electron. Eng. 2017, 12, 5–9. [Google Scholar] [CrossRef]
- Stroman, R.O.; Schuette, M.W.; Swider-Lyons, K.; Rodgers, J.A.; Edwards, D.J. Liquid hydrogen fuel system design and demonstration in a small long endurance air vehicle. Int. J. Hydrogen Energy 2014, 39, 11279–11290. [Google Scholar] [CrossRef]
- Lee, B.; Park, P.; Kim, C.; Yang, S.; Ahn, S. Power managements of a hybrid electric propulsion system for UAVs. J. Mech. Sci. Technol. 2012, 26, 2291–2299. [Google Scholar] [CrossRef]
- Lapeña-Rey, N.; Blanco, J.; Ferreyra, E.; Lemus, J.; Pereira, S.; Serrot, E. A fuel cell powered unmanned aerial vehicle for low altitude surveillance missions. Int. J. Hydrogen Energy 2017, 42, 6926–6940. [Google Scholar] [CrossRef]
- Alaswad, A.; Baroutaji, A.; Achour, H.; Carton, J.; Al Makky, A.; Olabi, A.G. Developments in fuel cell technologies in the transport sector. Int. J. Hydrogen Energy 2016, 41, 16499–16508. [Google Scholar] [CrossRef]
- Wilberforce, T.; Alaswad, A.; Palumbo, A.; Dassisti, M.; Olabi, A.G. Advances in stationary and portable fuel cell applications. Int. J. Hydrogen Energy 2016, 41, 16509–16522. [Google Scholar] [CrossRef]
- Ogungbemi, E.; Ijaodola, O.; Khatib, F.N.; Wilberforce, T.; El Hassan, Z.; Thompson, J.; Ramadan, M.; Olabi, A.G. Fuel cell membranes – Pros and cons. Energy 2019, 172, 155–172. [Google Scholar] [CrossRef]
- Ous, T.; Arcoumanis, C. Degradation aspects of water formation and transport in Proton Exchange Membrane Fuel Cell: A review. J. Power Sources 2013, 240, 558–582. [Google Scholar] [CrossRef]
- Kone, J.P.; Zhang, X.; Yan, Y.; Hu, G.; Ahmadi, G. Three-dimensional multiphase flow computational fluid dynamics models for proton exchange membrane fuel cell: A theoretical development. J. Comput. Multiph. Flows 2017, 9, 3–25. [Google Scholar] [CrossRef]
- Das, P.K.; Li, X.; Liu, Z.S. Analysis of liquid water transport in cathode catalyst layer of PEM fuel cells. Int. J. Hydrogen Energy 2010, 35, 2403–2416. [Google Scholar] [CrossRef]
- Esfandiari, A.; Kazemeini, M.; Bastani, D. Synthesis, characterization and performance determination of an Ag@Pt/C electrocatalyst for the ORR in a PEM fuel cell. Int. J. Hydrogen Energy 2016, 41, 20720–20730. [Google Scholar] [CrossRef]
- Liu, D.; Lin, R.; Feng, B.; Yang, Z. Investigation of the effect of cathode stoichiometry of proton exchange membrane fuel cell using localized electrochemical impedance spectroscopy based on print circuit board. Int. J. Hydrogen Energy 2019, 44, 7564–7573. [Google Scholar] [CrossRef]
- Schmittinger, W.; Vahidi, A. A review of the main parameters influencing long-term performance and durability of PEM fuel cells. J. Power Sources 2008, 180, 1–14. [Google Scholar] [CrossRef]
- Jiao, K.; Li, X. Water transport in polymer electrolyte membrane fuel cells. Prog. Energy Combust. Sci. 2011, 37, 221–291. [Google Scholar] [CrossRef]
- Li, H.; Tang, Y.; Wang, Z.; Shi, Z.; Wu, S.; Song, D.; Zhang, J.; Fatih, K.; Zhang, J.; Wang, H.; et al. A review of water flooding issues in the proton exchange membrane fuel cell. J. Power Sources 2008, 178, 103–117. [Google Scholar] [CrossRef]
- Mobility 2030: Meeting the Challenges to Sustainability. Available online: https://www.wbcsd.org/Programs/Cities-and-Mobility/Transforming-Mobility/TransformingUrban-Mobility/SiMPlify/Resources/Mobility-2030-Meeting-the-challengesto-sustainability-Executive-Summary-2004 (accessed on 12 February 2023).
- Ahmadi, P.; Torabi, S.H.; Afsaneh, H.; Sadegheih, Y.; Ganjehsarabi, H.; Ashjaee, M. The effects of driving patterns and PEM fuel cell degradation on the lifecycle assessment of hydrogen fuel cell vehicles. Int. J. Hydrogen Energy 2020, 45, 3595–3608. [Google Scholar] [CrossRef]
- Global Greenhouse Gas Emissions Data | Greenhouse Gas (GHG) Emissions | US EPA. Available online: https://www.epa.gov/ghgemissions/global-greenhouse-gas-emissions-data (accessed on 12 February 2023).
- Bakas, I.; Hauschild, M.Z.; Astrup, T.F.; Rosenbaum, R.K. Preparing the ground for an operational handling of long-term emissions in LCA. Int. J. Life Cycle Assess. 2015, 20, 1444–1455. [Google Scholar] [CrossRef]
- Cazzola, P.; Scheffer, S.; Paoli, L.; Craglia, M.; Tietge, U.; Yang, Z. Fuel Economy in Major Car Markets: Technology and Policy Drivers, 2005–2017; Technical Report; International Energy Agency: Paris, France, 2019. [Google Scholar]
- Williams, S.E.; Davis, S.C.; Boundy, R.G. Transportation Energy Data Book, 36th ed.; Technical report; Oak Ridge National Lab. (ORNL): Oak Ridge, TN, USA, 2017. [Google Scholar]
- Zhou, N.; Price, L.; Yande, D.; Creyts, J.; Khanna, N.; Fridley, D.; Lu, H.; Feng, W.; Liu, X.; Hasanbeigi, A.; et al. A roadmap for China to peak carbon dioxide emissions and achieve a 20% share of non-fossil fuels in primary energy by 2030. Appl. Energy 2019, 239, 793–819. [Google Scholar] [CrossRef]
- Wróbel, K.; Wróbel, J.; Tokarz, W.; Lach, J.; Podsadni, K.; Czerwiński, A. Hydrogen Internal Combustion Engine Vehicles: A Review. Energies 2022, 15, 8937. [Google Scholar] [CrossRef]
- Ahmed, A.A.; Nazzal, M.A.; Darras, B.M.; Deiab, I.M. A Comprehensive Sustainability Assessment of Battery Electric Vehicles, Fuel Cell Electric Vehicles, and Internal Combustion Engine Vehicles through a Comparative Circular Economy Assessment Approach. Sustainability 2023, 15, 171. [Google Scholar] [CrossRef]
- Dhanushkodi, S.; Mahinpey, N.; Srinivasan, A.; Wilson, M. Life Cycle Analysis of Fuel Cell Technology. J. Environ. Informatics 2008, 11, 36–44. [Google Scholar] [CrossRef]
- Buberger, J.; Kersten, A.; Kuder, M.; Eckerle, R.; Weyh, T.; Thiringer, T. Total CO2-equivalent life-cycle emissions from commercially available passenger cars. Renew. Sustain. Energy Rev. 2022, 159, 112158. [Google Scholar] [CrossRef]
- Hwang, J.J.; Kuo, J.K.; Wu, W.; Chang, W.R.; Lin, C.H.; Wang, S.E. Lifecycle performance assessment of fuel cell/battery electric vehicles. Int. J. Hydrogen Energy 2013, 38, 3433–3446. [Google Scholar] [CrossRef]
- Evangelisti, S.; Tagliaferri, C.; Brett, D.J.L.; Lettieri, P. Life cycle assessment of a polymer electrolyte membrane fuel cell system for passenger vehicles. J. Clean. Prod. 2017, 142, 4339–4355. [Google Scholar] [CrossRef]
- Ahmadi, P.; Kjeang, E. Realistic simulation of fuel economy and life cycle metrics for hydrogen fuel cell vehicles. Int. J. Energy Res. 2017, 41, 714–727. [Google Scholar] [CrossRef]
- Hussain, M.M.; Dincer, I.; Li, X. A preliminary life cycle assessment of PEM fuel cell powered automobiles. Appl. Therm. Eng. 2007, 27, 2294–2299. [Google Scholar] [CrossRef]
- Ahmadi, P.; Kjeang, E. Comparative life cycle assessment of hydrogen fuel cell passenger vehicles in different Canadian provinces. Int. J. Hydrogen Energy 2015, 40, 12905–12917. [Google Scholar] [CrossRef]
- Zamel, N.; Li, X. Life cycle analysis of vehicles powered by a fuel cell and by internal combustion engine for Canada. J. Power Sources 2006, 155, 297–310. [Google Scholar] [CrossRef]
- Yang, Z.; Wang, B.; Jiao, K. Life cycle assessment of fuel cell, electric and internal combustion engine vehicles under different fuel scenarios and driving mileages in China. Energy 2020, 198, 117365. [Google Scholar] [CrossRef]
- Iannuzzi, L.; Hilbert, J.A.; Silva Lora, E.E. Life Cycle Assessment (LCA) for use on renewable sourced hydrogen fuel cell buses vs diesel engines buses in the city of Rosario, Argentina. Int. J. Hydrogen Energy 2021, 46, 29694–29705. [Google Scholar] [CrossRef]
- Liu, X.; Reddi, K.; Elgowainy, A.; Lohse-Busch, H.; Wang, M.; Rustagi, N. Comparison of well-to-wheels energy use and emissions of a hydrogen fuel cell electric vehicle relative to a conventional gasoline-powered internal combustion engine vehicle. Int. J. Hydrogen Energy 2020, 45, 972–983. [Google Scholar] [CrossRef]
- Seol, E.; Yoo, E.; Lee, C.; Kim, M.; Cho, M.; Choi, W.; Song, H.H. Well-to-wheel nitrogen oxide emissions from internal combustion engine vehicles and alternative fuel vehicles reflect real driving emissions and various fuel production pathways in South Korea. J. Clean. Prod. 2022, 342, 130983. [Google Scholar] [CrossRef]
- Garche, J.; Dyer, C.; Moseley, P.T.; Ogumi, Z.; Rand, D.A.; Scrosati, B. Encyclopedia of Electrochemical Power Sources; Newnes: Oxford, UK, 2013. [Google Scholar]
- Manso, A.P.; Marzo, F.F.; Barranco, J.; Garikano, X.; Garmendia Mujika, M. Influence of geometric parameters of the flow fields on the performance of a PEM fuel cell. A review. Int. J. Hydrogen Energy 2012, 37, 15256–15287. [Google Scholar] [CrossRef]
- Yu, L.j.; Ren, G.p.; Qin, M.j.; Jiang, X.m. Transport mechanisms and performance simulations of a PEM fuel cell with interdigitated flow field. Renew. Energy 2009, 34, 530–543. [Google Scholar] [CrossRef]
- Ahmed, D.H.; Sung, H.J. Effects of channel geometrical configuration and shoulder width on PEMFC performance at high current density. J. Power Sources 2006, 162, 327–339. [Google Scholar] [CrossRef]
- Kumar, A.; Reddy, R.G. Effect of channel dimensions and shape in the flow-field distributor on the performance of polymer electrolyte membrane fuel cells. J. Power Sources 2003, 113, 11–18. [Google Scholar] [CrossRef]
- Zhu, X.; Liao, Q.; Sui, P.C.; Djilali, N. Numerical investigation of water droplet dynamics in a low-temperature fuel cell microchannel: Effect of channel geometry. J. Power Sources 2010, 195, 801–812. [Google Scholar] [CrossRef]
- Wang, X.D.; Lu, G.; Duan, Y.Y.; Lee, D.J. Numerical analysis on performances of polymer electrolyte membrane fuel cells with various cathode flow channel geometries. Int. J. Hydrogen Energy 2012, 37, 15778–15786. [Google Scholar] [CrossRef]
- Lorenzini-Gutierrez, D.; Kandlikar, S.G.; Hernandez-Guerrero, A.; Elizalde-Blancas, F. Residence time of water film and slug flow features in fuel cell gas channels and their effect on instantaneous area coverage ratio. J. Power Sources 2015, 279, 567–580. [Google Scholar] [CrossRef]
- Mohammedi, A.; Sahli, Y.; Ben Moussa, H. 3D investigation of the channel cross-section configuration effect on the power delivered by PEMFCs with straight channels. Fuel 2020, 263, 116713. [Google Scholar] [CrossRef]
- Kahraman, H.; Orhan, M.F. Flow field bipolar plates in a proton exchange membrane fuel cell: Analysis & modeling. Energy Convers. Manag. 2017, 133, 363–384. [Google Scholar] [CrossRef]
- Kerkoub, Y.; Benzaoui, A.; Haddad, F.; Ziari, Y.K. Channel to rib width ratio influence with various flow field designs on performance of PEM fuel cell. Energy Convers. Manag. 2018, 174, 260–275. [Google Scholar] [CrossRef]
- Qiu, D.; Peng, L.; Tang, J.; Lai, X. Numerical analysis of air-cooled proton exchange membrane fuel cells with various cathode flow channels. Energy 2020, 198, 117334. [Google Scholar] [CrossRef]
- Rahimi-Esbo, M.; Ranjbar, A.; Ramiar, A.; Alizadeh, E.; Aghaee, M. Improving PEM fuel cell performance and effective water removal by using a novel gas flow field. Int. J. Hydrogen Energy 2016, 41, 3023–3037. [Google Scholar] [CrossRef]
- Wang, X.D.; Duan, Y.Y.; Yan, W.M. Numerical study of cell performance and local transport phenomena in PEM fuel cells with various flow channel area ratios. J. Power Sources 2007, 172, 265–277. [Google Scholar] [CrossRef]
- Wang, X.D.; Yan, W.M.; Duan, Y.Y.; Weng, F.B.; Jung, G.B.; Lee, C.Y. Numerical study on channel size effect for proton exchange membrane fuel cell with serpentine flow field. Energy Convers. Manag. 2010, 51, 959–968. [Google Scholar] [CrossRef]
- Feser, J.P.; Prasad, A.K.; Advani, S.G. On the relative influence of convection in serpentine flow fields of PEM fuel cells. J. Power Sources 2006, 161, 404–412. [Google Scholar] [CrossRef]
- Shimpalee, S.; Greenway, S.; Van Zee, J.W. The impact of channel path length on PEMFC flow-field design. J. Power Sources 2006, 160, 398–406. [Google Scholar] [CrossRef]
- Santamaria, A.D.; Cooper, N.J.; Becton, M.K.; Park, J.W. Effect of channel length on interdigitated flow-field PEMFC performance: A computational and experimental study. Int. J. Hydrogen Energy 2013, 38, 16253–16263. [Google Scholar] [CrossRef]
- Cooper, N.J.; Santamaria, A.D.; Becton, M.K.; Park, J.W. Investigation of the performance improvement in decreasing aspect ratio interdigitated flow field PEMFCs. Energy Convers. Manag. 2017, 136, 307–317. [Google Scholar] [CrossRef]
- Limjeerajarus, N.; Charoen-amornkitt, P. Effect of different flow field designs and number of channels on performance of a small PEFC. Int. J. Hydrogen Energy 2015, 40, 7144–7158. [Google Scholar] [CrossRef]
- Boddu, R.; Marupakula, U.K.; Summers, B.; Majumdar, P. Development of bipolar plates with different flow channel configurations for fuel cells. J. Power Sources 2009, 189, 1083–1092. [Google Scholar] [CrossRef]
- Sajid Hossain, M.; Shabani, B.; Cheung, C.P. Enhanced gas flow uniformity across parallel channel cathode flow field of Proton Exchange Membrane fuel cells. Int. J. Hydrogen Energy 2017, 42, 5272–5283. [Google Scholar] [CrossRef]
- Chen, S.; Xia, Z.; Zhang, X.; Wu, Y. Numerical studies of effect of interdigitated flow field outlet channel width on PEM fuel cell performance. Energy Procedia 2019, 158, 1678–1684. [Google Scholar] [CrossRef]
- Xiong, C.; Luo, M.; Chen, B.; Tu, Z. Effect of channel structure on oxygen distribution in cathode of fuel cells. Chi. J. Power Sources 2018, 42, 230–232. [Google Scholar]
- Arun Saco, S.; Thundil Karuppa Raj, R.; Karthikeyan, P. A study on scaled up proton exchange membrane fuel cell with various flow channels for optimizing power output by effective water management using numerical technique. Energy 2016, 113, 558–573. [Google Scholar] [CrossRef]
- Atyabi, S.A.; Afshari, E. A numerical multiphase CFD simulation for PEMFC with parallel sinusoidal flow fields. J. Therm. Anal. Calorim. 2019, 135, 1823–1833. [Google Scholar] [CrossRef]
- Anyanwu, I.S.; Hou, Y.; Xi, F.; Wang, X.; Yin, Y.; Du, Q.; Jiao, K. Comparative analysis of two-phase flow in sinusoidal channel of different geometric configurations with application to PEMFC. Int. J. Hydrogen Energy 2019, 44, 13807–13819. [Google Scholar] [CrossRef]
- Monsaf, T.; Hocine, B.M.; Youcef, S.; Abdallah, M. Unsteady three-dimensional numerical study of mass transfer in PEM fuel cell with spiral flow field. Int. J. Hydrogen Energy 2017, 42, 1237–1251. [Google Scholar] [CrossRef]
- Zhang, S.; Liu, S.; Xu, H.; Liu, G.; Wang, K. Performance of proton exchange membrane fuel cells with honeycomb-like flow channel design. Energy 2022, 239, 122102. [Google Scholar] [CrossRef]
- Kloess, J.P.; Wang, X.; Liu, J.; Shi, Z.; Guessous, L. Investigation of bio-inspired flow channel designs for bipolar plates in proton exchange membrane fuel cells. J. Power Sources 2009, 188, 132–140. [Google Scholar] [CrossRef]
- Ouellette, D.; Ozden, A.; Ercelik, M.; Colpan, C.O.; Ganjehsarabi, H.; Li, X.; Hamdullahpur, F. Assessment of different bio-inspired flow fields for direct methanol fuel cells through 3D modeling and experimental studies. Int. J. Hydrogen Energy 2018, 43, 1152–1170. [Google Scholar] [CrossRef]
- Zehtabiyan-Rezaie, N.; Arefian, A.; Kermani, M.J.; Noughabi, A.K.; Abdollahzadeh, M. Effect of flow field with converging and diverging channels on proton exchange membrane fuel cell performance. Energy Convers. Manag. 2017, 152, 31–44. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, Q.; Lu, J.; Shen, S.; Yan, X.; Zhu, F.; Cheng, X.; Zhang, J. Effect of height/width-tapered flow fields on the cell performance of polymer electrolyte membrane fuel cells. Int. J. Hydrogen Energy 2017, 42, 23107–23117. [Google Scholar] [CrossRef]
- Jia, Y.; Sunden, B.; Xie, G. A parametric comparison of temperature uniformity and energy performance of a PEMFC having serpentine wavy channels. Int. J. Energy Res. 2019, 43, 2722–2736. [Google Scholar] [CrossRef]
- Ramin, F.; Sadeghifar, H.; Torkavannejad, A. Flow field plates with trap-shape channels to enhance power density of polymer electrolyte membrane fuel cells. Int. J. Heat Mass Transf. 2019, 129, 1151–1160. [Google Scholar] [CrossRef]
- Heidary, H.; Kermani, M.J.; Prasad, A.K.; Advani, S.G.; Dabir, B. Numerical modelling of in-line and staggered blockages in parallel flowfield channels of PEM fuel cells. Int. J. Hydrogen Energy 2017, 42, 2265–2277. [Google Scholar] [CrossRef]
- Shen, J.; Zeng, L.; Liu, Z.; Liu, W. Performance investigation of PEMFC with rectangle blockages in Gas Channel based on field synergy principle. Heat Mass Transf. 2019, 55, 811–822. [Google Scholar] [CrossRef]
- Zhang, S.; Qu, Z.; Xu, H.; Talkhoncheh, F.K.; Liu, S.; Gao, Q. A numerical study on the performance of PEMFC with wedge-shaped fins in the cathode channel. Int. J. Hydrogen Energy 2021, 46, 27700–27708. [Google Scholar] [CrossRef]
- Ghanbarian, A.; Kermani, M.J. Enhancement of PEM fuel cell performance by flow channel indentation. Energy Convers. Manag. 2016, 110, 356–366. [Google Scholar] [CrossRef]
- Yin, Y.; Wu, S.; Qin, Y.; Otoo, O.N.; Zhang, J. Quantitative analysis of trapezoid baffle block sloping angles on oxygen transport and performance of proton exchange membrane fuel cell. Appl. Energy 2020, 271, 115257. [Google Scholar] [CrossRef]
- Yin, Y.; Wang, X.; Shangguan, X.; Zhang, J.; Qin, Y. Numerical investigation on the characteristics of mass transport and performance of PEMFC with baffle plates installed in the flow channel. Int. J. Hydrogen Energy 2018, 43, 8048–8062. [Google Scholar] [CrossRef]
- Chen, H.; Guo, H.; Ye, F.; Ma, C.F.; Liao, Q.; Zhu, X. Mass transfer in proton exchange membrane fuel cells with baffled flow channels and a porous-blocked baffled flow channel design. Int. J. Energy Res. 2019, 43, 2910–2929. [Google Scholar] [CrossRef]
- Li, W.; Zhang, Q.; Wang, C.; Yan, X.; Shen, S.; Xia, G.; Zhu, F.; Zhang, J. Experimental and numerical analysis of a three-dimensional flow field for PEMFCs. Appl. Energy 2017, 195, 278–288. [Google Scholar] [CrossRef]
- Yan, X.; Guan, C.; Zhang, Y.; Jiang, K.; Wei, G.; Cheng, X.; Shen, S.; Zhang, J. Flow field design with 3D geometry for proton exchange membrane fuel cells. Appl. Therm. Eng. 2019, 147, 1107–1114. [Google Scholar] [CrossRef]
- Chen, X.; Yu, Z.; Yang, C.; Chen, Y.; Jin, C.; Ding, Y.; Li, W.; Wan, Z. Performance investigation on a novel 3D wave flow channel design for PEMFC. Int. J. Hydrogen Energy 2021, 46, 11127–11139. [Google Scholar] [CrossRef]
- Ashorynejad, H.R.; Javaherdeh, K.; Van den Akker, H.E.A. The effect of pulsating pressure on the performance of a PEM fuel cell with a wavy cathode surface. Int. J. Hydrogen Energy 2016, 41, 14239–14251. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, S.; Wang, G.; Yue, L. Numerical study of a new cathode flow-field design with a sub-channel for a parallel flow-field polymer electrolyte membrane fuel cell. Int. J. Hydrogen Energy 2018, 43, 2359–2368. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).