Atmospheric Instability and Its Associated Oscillations in the Tropics
Abstract
:1. Introduction
2. Are Convective Clouds Active or Passive?
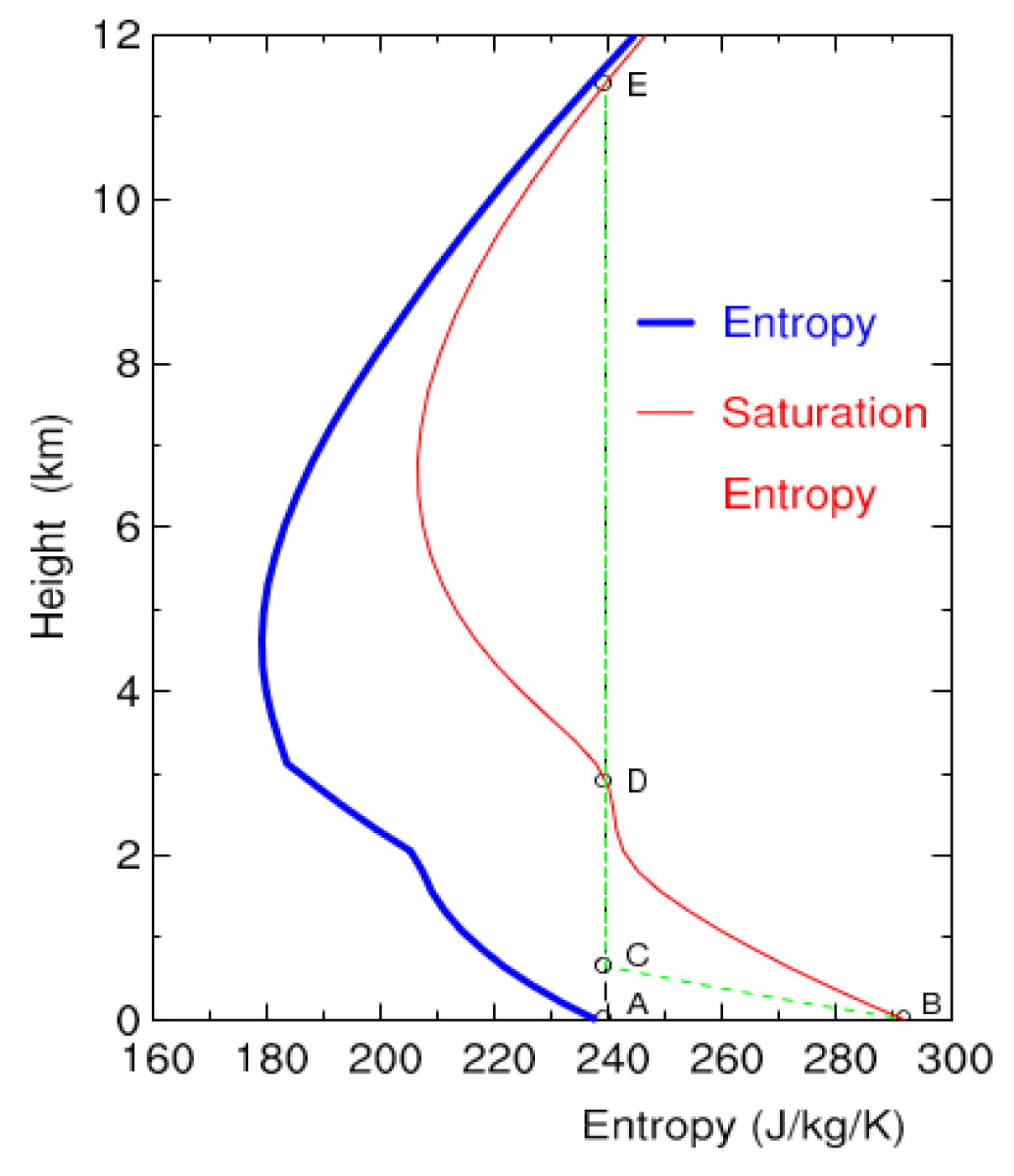
2.1. Expression of Moist Entropy
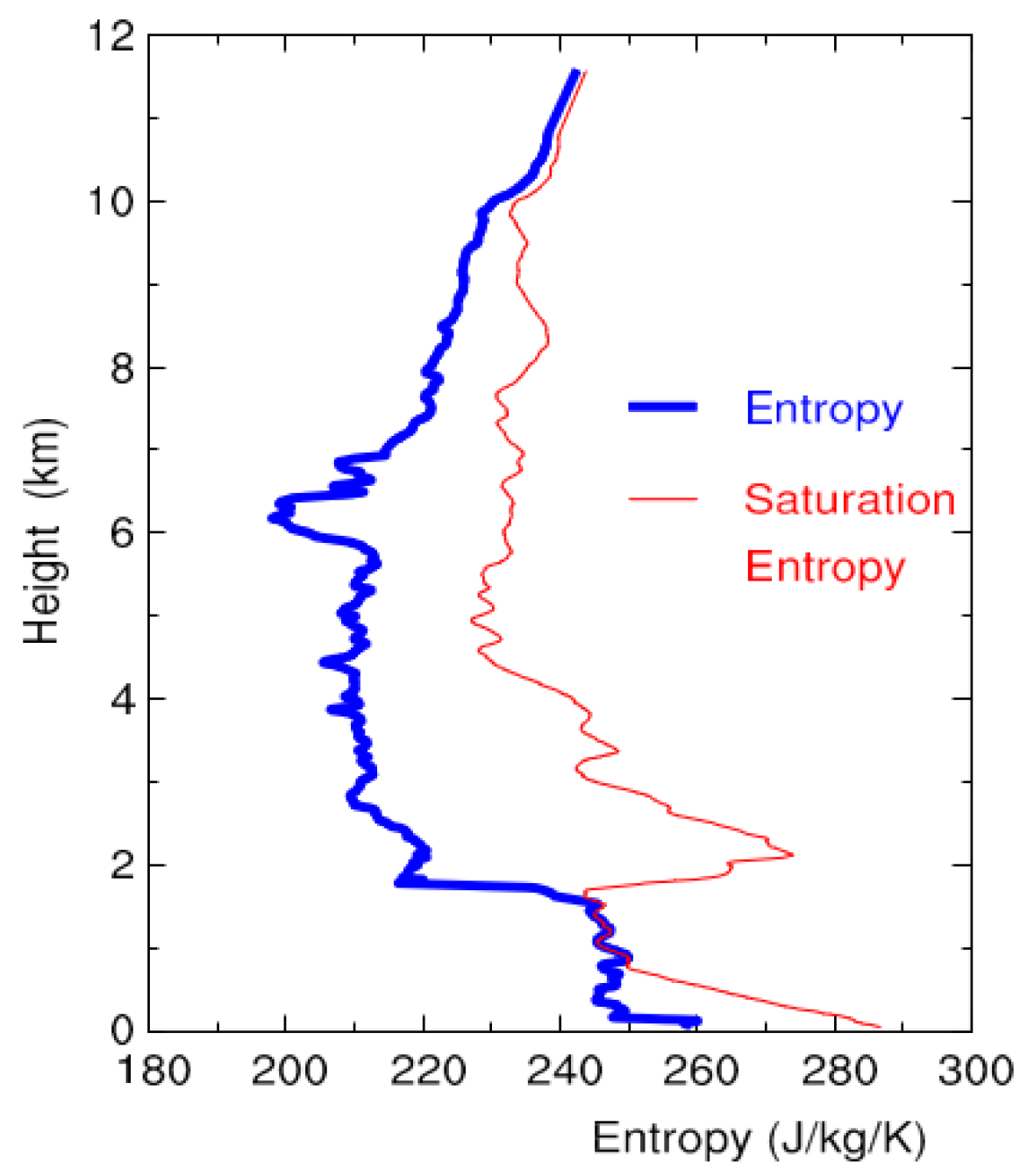
2.2. Approach of the RCE
2.3. Ideal Experiments of the RCE
3. Instability of the RCE
3.1. The WTG and Its Application
3.2. Origin of the Instability
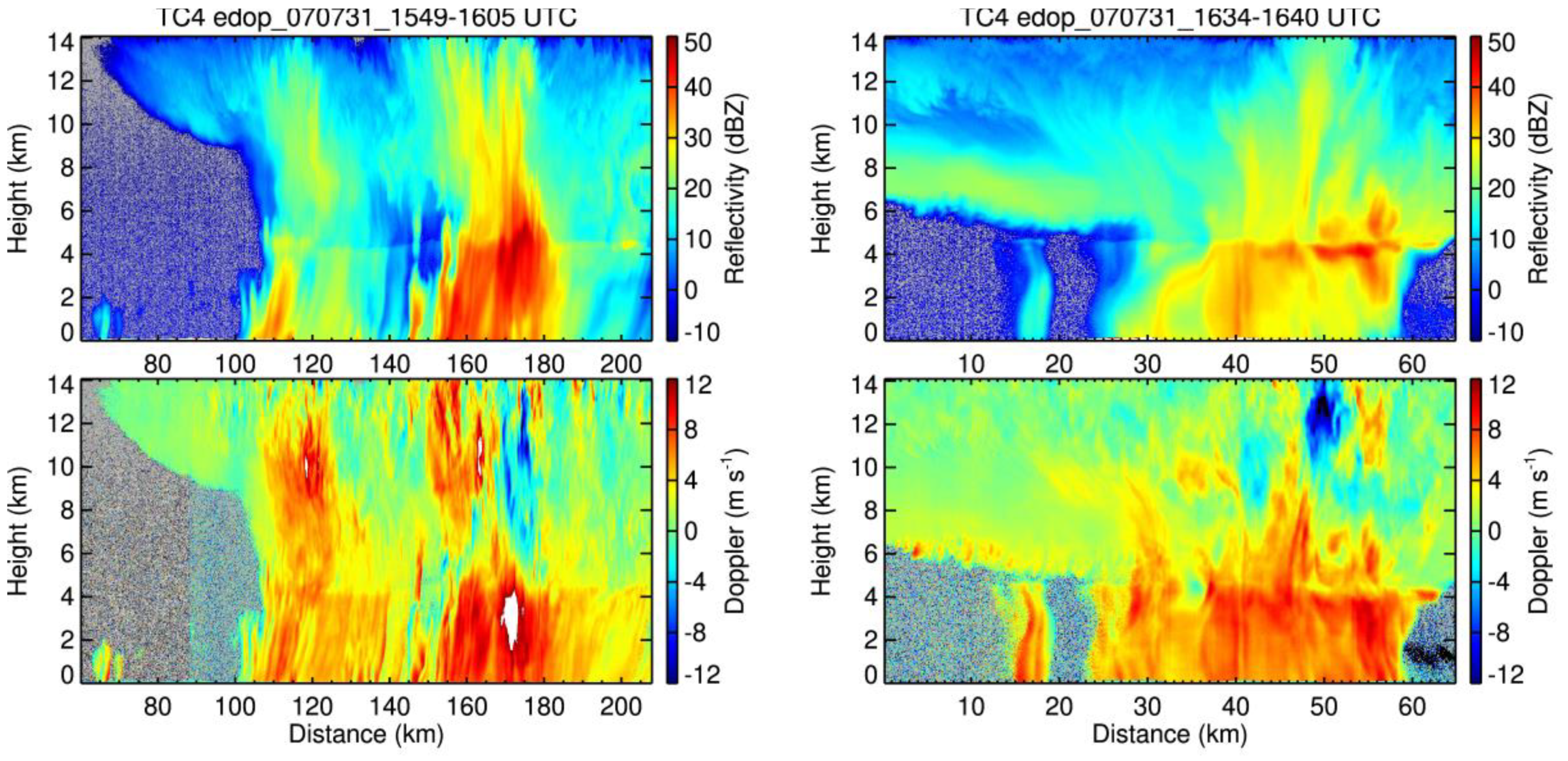
3.3. Convective Downdrafts
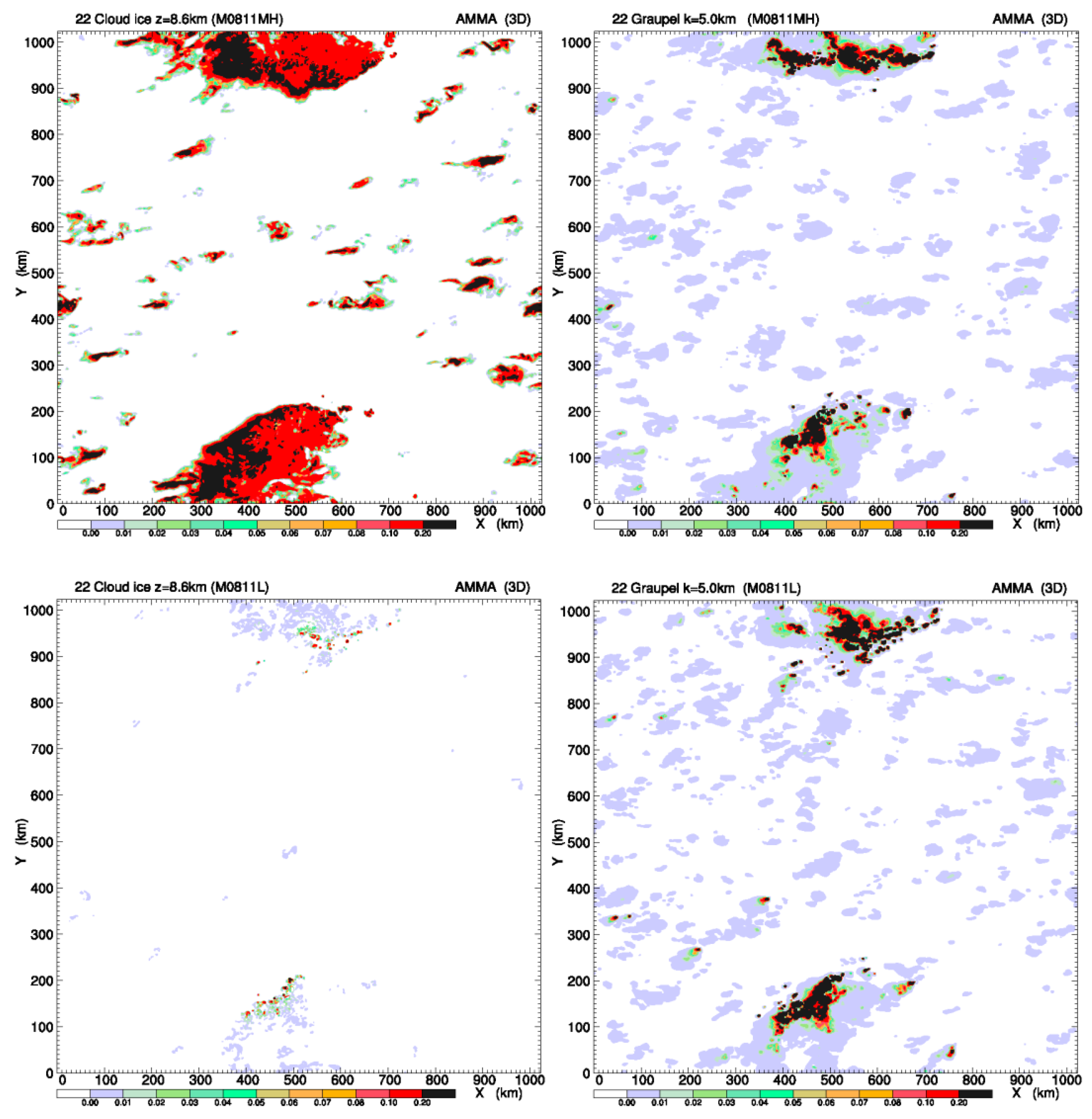
3.4. Cirrus Clouds and Their Radiation
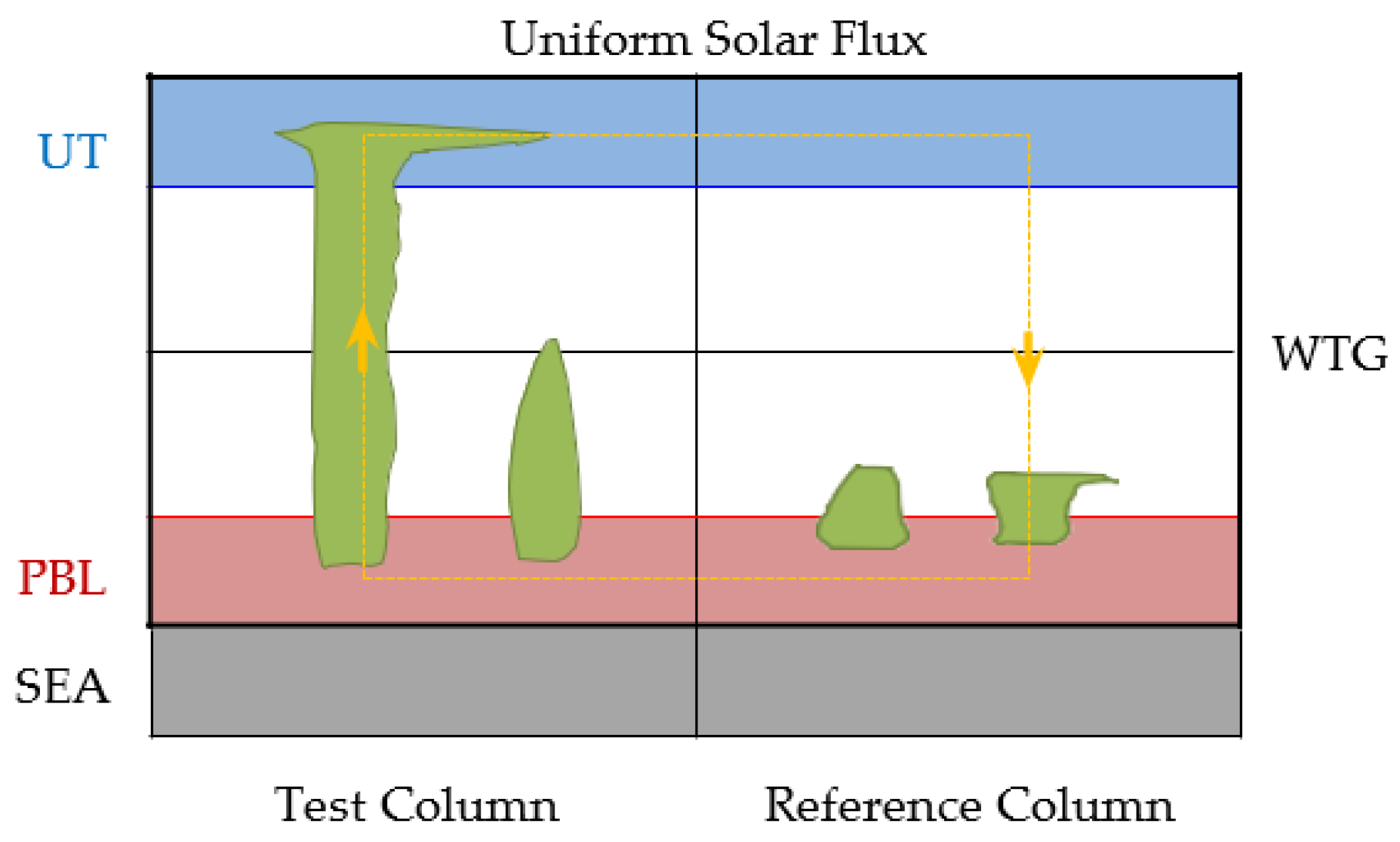
4. A Two-Column Two-Layer Model
4.1. Model Structure
4.2. Stability Criteria of the RCE
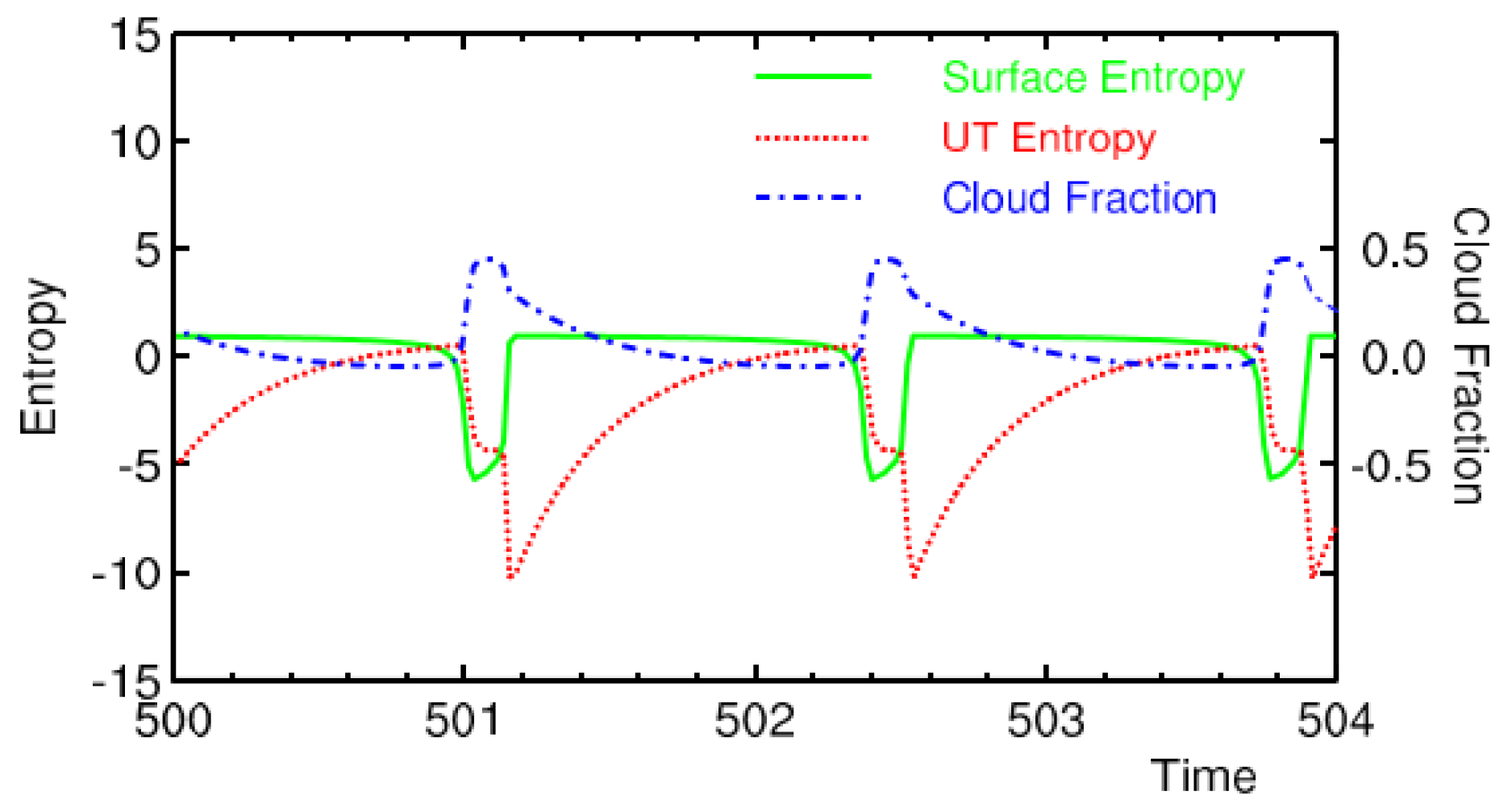
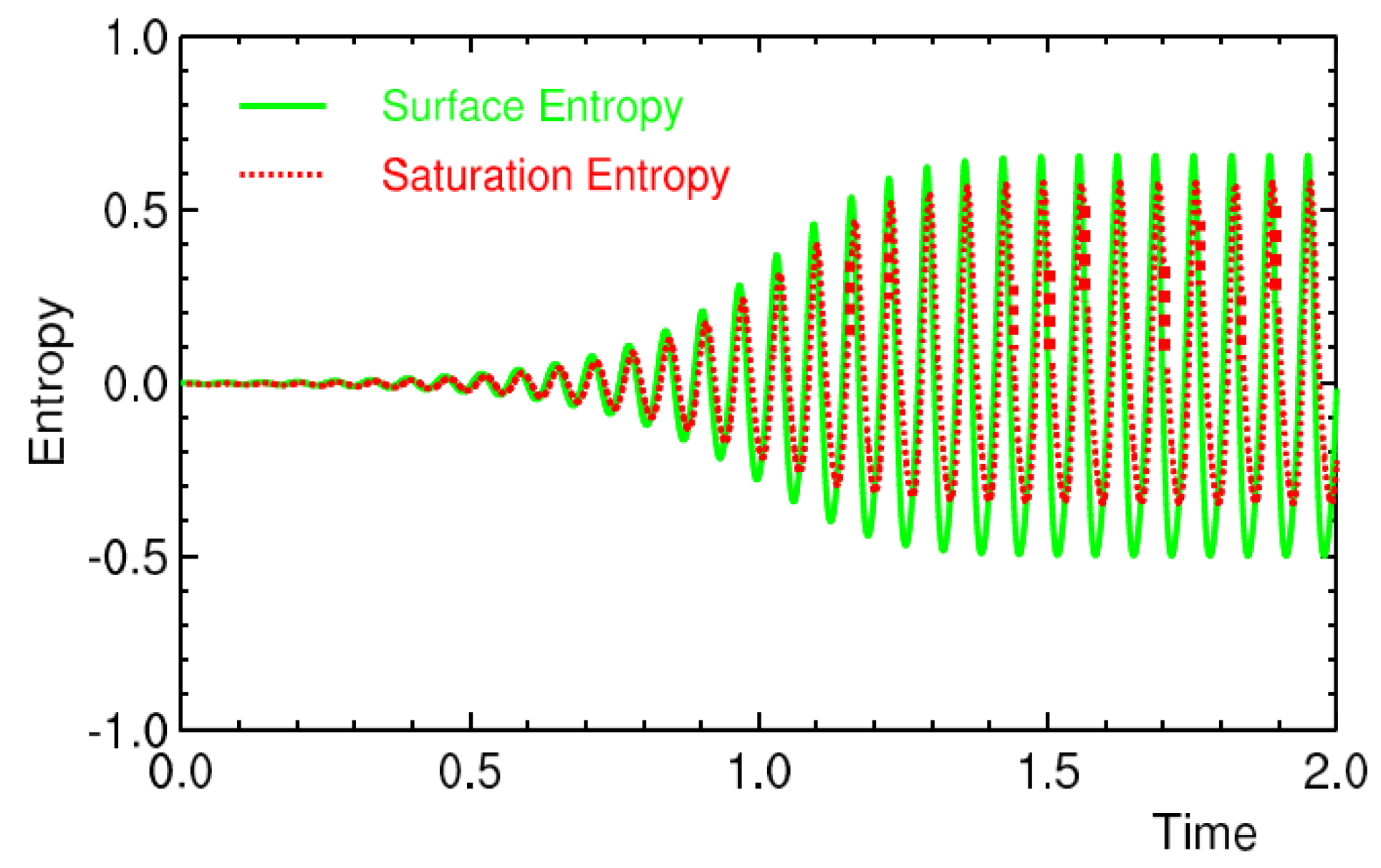
4.3. Oscillation and an Unstable RCE
5. Other Forms of Instability
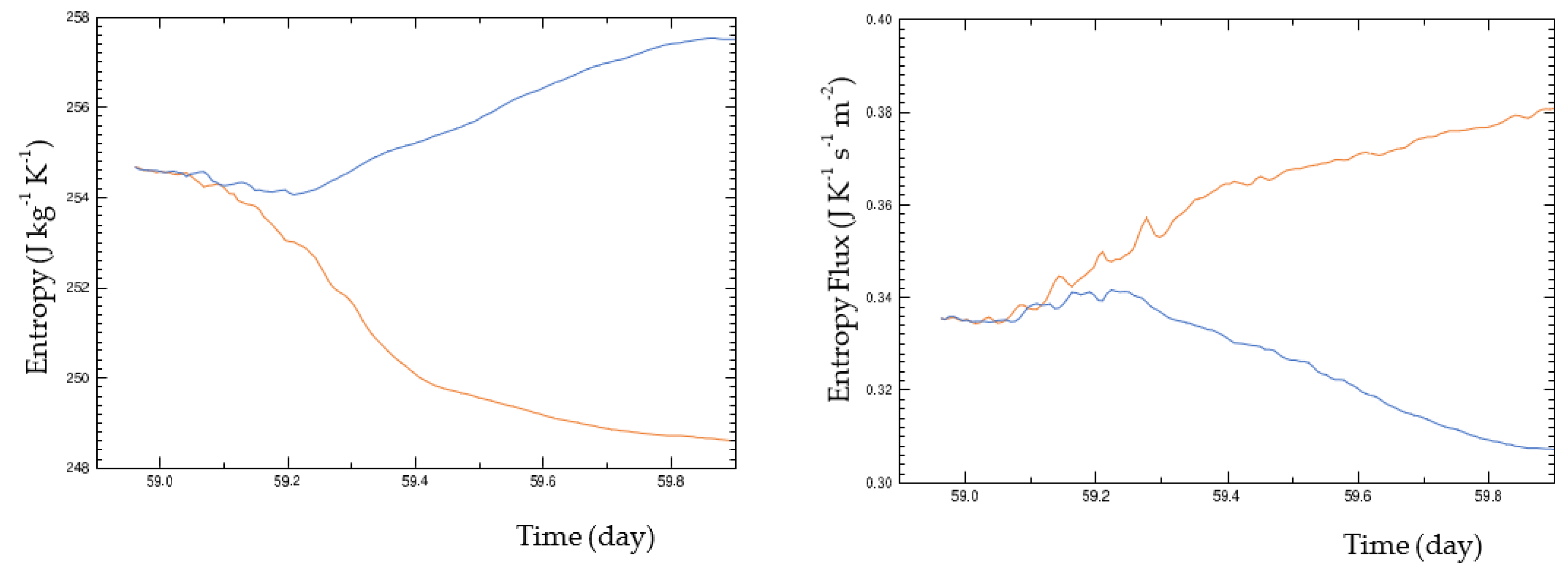
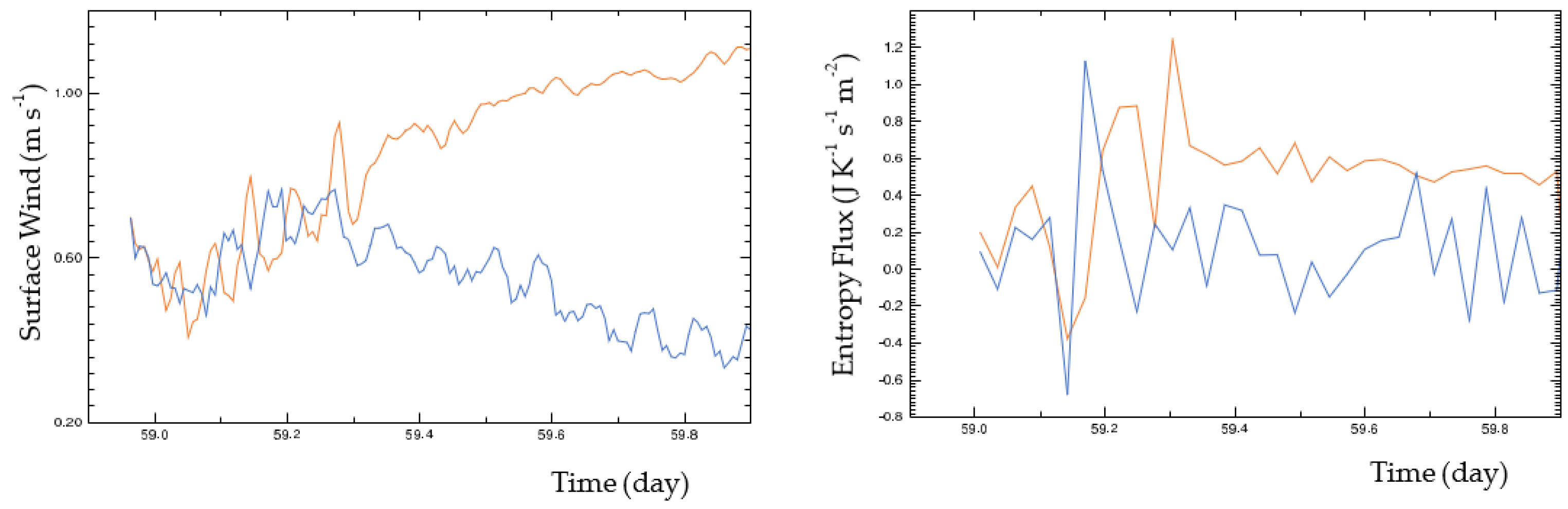
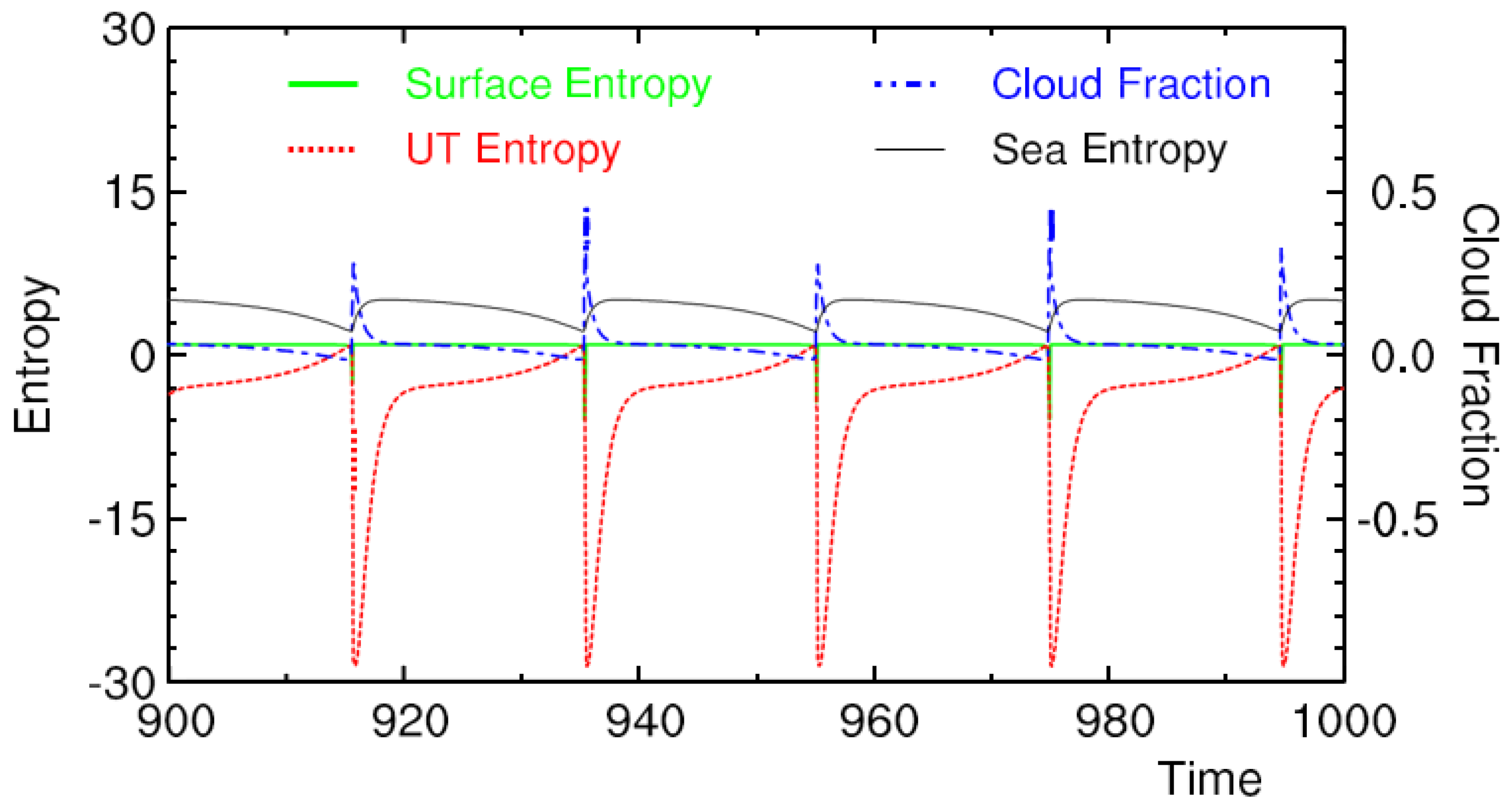
5.1. Boundary Layer Quasi-Equilibrium
5.2. Radiative Convective Flux Equilibrium
6. Conclusions and Discussion
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Stability Analysis of the RCE

Appendix B. Stability Analysis of the Radiative Convective Flux Equilibrium

Appendix C. Stability Analysis of the Boundary Layer Quasi-Equilibrium
Appendix D. Zonal Asymmetry of Atmospheric Response to Diabatic Heating
Appendix D.1. Forced Modes versus Free Modes
Appendix D.2. Analytic Solution
Appendix D.3. Resonance in the Westward Travelling Modes
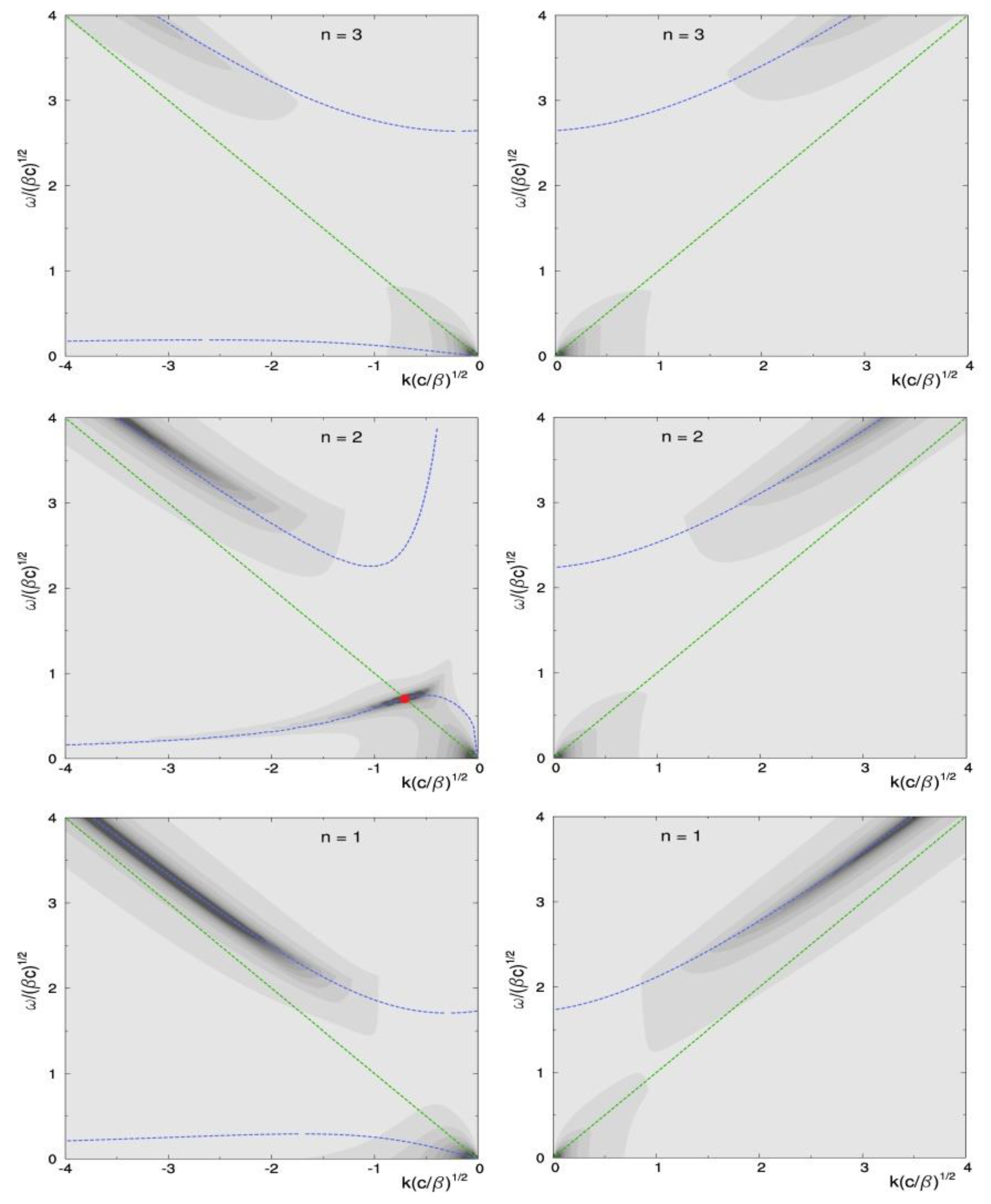
Appendix D.4. Resonance in the Eastward Travelling Modes

References
- Lorenz, E.N. Deterministic nonperiodic flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef]
- Shen, B.-W.; Pielke, R.A., Sr.; Zeng, X.; Baik, J.-J.; Faghih-Naini, S.; Cui, J.; Atlas, R. Is Weather Chaotic? Coexistence of Chaos and Order within a Generalized Lorenz Model. Bull. Am. Meteorol. Soc. 2021, 2, E148–E158. [Google Scholar]
- Shen, B.-W.; Pielke, R., Sr.; Zeng, X.; Cui, J.; Faghih-Naini, S.; Paxson, W.; Kesarkar, A.; Zeng, X.; Atlas, R. The Dual Nature of Chaos and Order in the Atmosphere. Atmosphere 2022, 13, 1892. [Google Scholar] [CrossRef]
- Lorenz, E.N. The predictability of a flow which possesses many scales of motion. Tellus 1969, 21, 289–307. [Google Scholar] [CrossRef]
- Lorenz, E.N. Can chaos and intransitivity lead to interannual variability? Tellus 1990, 42, 378–389. [Google Scholar] [CrossRef]
- Riehl, H.; Malkus, J.S. On the heat balance in the equatorial trough zone. Geophysica 1958, 6, 503–537. [Google Scholar]
- Raymond, D.J.; Zeng, X. Instability and large-scale circulations in a two-column model of the troposphere. Q. J. R. Meteorol. Soc. 2000, 126, 3117–3135. [Google Scholar] [CrossRef]
- Teschl, G. Ordinary Differential Equations and Dynamical Systems; American Mathematical Society: Providence, RL, USA, 2012; ISBN 978-0-8218-8328-0. [Google Scholar]
- Manabe, S.; Strickler, R.F. Thermal equilibrium of the atmosphere with a convective adjustment. J. Atmos. Sci. 1964, 21, 361–385. [Google Scholar] [CrossRef]
- Zeng, X.; Tao, W.-K.; Simpson, J. An equation for moist entropy in a precipitating and icy atmosphere. J. Atmos. Sci. 2005, 62, 4293–4309. [Google Scholar] [CrossRef]
- Hauf, T.; Höller, H. Entropy and potential temperature. J. Atmos. Sci. 1987, 44, 2887–2901. [Google Scholar] [CrossRef]
- Zeng, X.; Tao, W.-K.; Simpson, J. A choice of prognostic variables for long-term cloud-resolving model simulations. J. Meteorol. Soc. Jpn. 2008, 86, 839–856. [Google Scholar] [CrossRef]
- Charney, J.G.; Eliassen, A. On the growth of the hurricane depression. J. Atmos. Sci. 1964, 21, 68–75. [Google Scholar] [CrossRef]
- Emanuel, K.A.; Neelin, J.D.; Bretherton, C.S. On large-scale circulations in convecting atmospheres. Q. J. R. Meteorol. Soc. 1994, 120, 1111–1143. [Google Scholar] [CrossRef]
- Raymond, D.J.; Torres, D.J. Fundamental moist modes of the equatorial troposphere. J. Atmos. Sci. 1998, 55, 1771–1790. [Google Scholar] [CrossRef]
- Emanuel, K.A. Atmospheric Convection; Oxford University Press: New York, NY, USA, 1994; p. 580. [Google Scholar]
- Robe, F.R.; Emanuel, K.A. Moist convective scaling: Some inferences from three-dimensional cloud ensemble simulations. J. Atmos. 1996, 53, 3265–3275. [Google Scholar] [CrossRef]
- Tompkins, A.M.; Craig, G.C. Radiative-convective equilibrium in a three-dimensional cloud ensemble model. Q. J. R. Meteorol. Soc. 1998, 124, 2073–2098. [Google Scholar]
- Zeng, X. Ensemble Simulation of Tropical Convection. Ph.D. Dissertation, New Mexico Institute of Mining and Technology, Socorro, NM, USA, 2001; p. 124. [Google Scholar]
- Madden, R.; Julian, P.R. Detection of a 40–50 day oscillation in the zonal wind in the tropical Pacific. J. Atmos. Sci. 1971, 28, 702–708. [Google Scholar] [CrossRef]
- Madden, R.; Julian, P.R. Description of global-scale circulation cells in the Tropics with a 40–50 day period. J. Atmos. Sci. 1972, 29, 1109–1123. [Google Scholar] [CrossRef]
- Madden, R.; Julian, P.R. Observations of the 40–50 day tropical oscillation—A review. Mon. Wea. Rev. 1994, 122, 814–837. [Google Scholar] [CrossRef]
- Sessions, S.L.; Sugaya, S.; Raymond, D.J.; Sobel, A.H. Multiple equilibria in a cloud resolving model using the weak temperature gradient approximation. J. Geophys. Res. 2010, 115, D12110. [Google Scholar] [CrossRef]
- Raymond, D.J. Thermodynamic control of tropical rainfall. Q. J. R. Meteorol. Soc. 2000, 126, 889–898. [Google Scholar] [CrossRef]
- Bretherton, C.S.; Smolarkiewicz, P.K. Gravity waves, compensating subsidence and detrainment around cumulus clouds. J. Atmos. Sci. 1989, 46, 740–759. [Google Scholar] [CrossRef]
- Sobel, A.H.; Bretherton, C.S. Modeling tropical precipitation in a single column. J. Climate 2000, 13, 4378–4392. [Google Scholar] [CrossRef]
- Bretherton, C.S.; Sobel, A.H. A simple model of a convectively coupled Walker circulation using the weak temperature gradient approximation. J. Climate 2002, 15, 2907–2920. [Google Scholar] [CrossRef]
- Nilsson, J.; Emanuel, K.A. Equilibrium atmosphere of a two-column radiative convective model. Q. J. R. Meteorol. Soc. 1999, 125, 2239–2264. [Google Scholar] [CrossRef]
- Raymond, D.J.; Zeng, X. Modeling tropical atmospheric convection in the context of the weak temperature gradient approximation. Q. J. R. Meteorol. Soc. 2005, 131, 1301–1320. [Google Scholar] [CrossRef]
- Zeng, X.; Wang, Y.; MacCall, B.T. A k−ε turbulence model for the stable atmosphere. J. Atmos. Sci. 2020, 77, 167–184. [Google Scholar] [CrossRef]
- Zeng, X.; Tao, W.-K.; Lang, S.; Hou, A.Y.; Zhang, M.; Simpson, J. On the sensitivity of the atmospheric ensembles to cloud microphysics in long-term cloud-resolving model simulations. J. Meteorol. Soc. Jpn. 2008, 86, 45–65. [Google Scholar] [CrossRef]
- LeMone, M.A.; Zipser, E.J. Cumulonimbus vertical velocity events in GATE. Part I: Diameter, intensity and mass flux. J. Atmos. Sci. 1980, 37, 2444–2457. [Google Scholar] [CrossRef]
- Wei, D.; Blyth, A.M.; Raymond, D.J. Buoyancy of convective clouds in TOGA COARE. J. Atmos. Sci. 1998, 55, 3381–3391. [Google Scholar] [CrossRef]
- Igau, R.C.; LeMone, M.A.; Wei, D. Updraft and downdraft cores in TOGA COARE: Why so many buoyant downdraft cores? J. Atmos. Sci. 1999, 56, 2232–2245. [Google Scholar] [CrossRef]
- Zipser, E.J. Some view on “hot towers” after 50 years of tropical field programs and two years of TRMM data. In Cloud Systems, Hurricanes, and the Tropical Rainfall Measuring Mission (TRMM); Tao, W.-K., Adler, R., Eds.; Meteorological Monographs; American Meteorological Society: Boston, MA, USA, 2003; Volume 29, pp. 49–58. [Google Scholar]
- Toon, O.B.; Starr, D.O.; Jensen, E.J.; Newman, P.A.; Platnick, S.; Schoeberl, M.R.; Wennberg, P.O.; Wofsy, S.C.; Kurylo, M.J.; Maring, H.; et al. Planning, Implementation, and First Results of the Tropical Composition, Cloud and Climate Coupling Experiment (TC4). J. Geophys. Res. 2010, 115, D00J04. [Google Scholar] [CrossRef]
- Heymsfield, G.M.; Tian, L.; Heymsfield, A.J.; Li, L.; Guimond, S. Characteristics of Deep Tropical and Subtropical Convection from Nadir-Viewing High-Altitude Airborne Doppler Radar. J. Atmos. Sci. 2010, 67, 285–308. [Google Scholar] [CrossRef]
- Heymsfield, G.M.; Tian, L.; Li, L.; McLinden, M.; Cervantes, J.I. Airborne Radar Observations of Severe Hailstorms: Implications for Future Spaceborne Radar. J. Appl. Meteorol. Climatol. 2013, 52, 1851–1867. [Google Scholar] [CrossRef]
- Houze, R.A., Jr. Cloud clusters and large-scale vertical motion in the tropics. J. Meteorol. Soc. Japan 1982, 60, 396–410. [Google Scholar] [CrossRef]
- Zeng, X.; Tao, W.-K.; Zhang, M.; Hou, A.Y.; Xie, S.; Lang, S.; Li, X.; Starr, D.; Li, X. A contribution by ice nuclei to global warming. Q. J. R. Meteorol. Soc. 2009, 135, 1614–1629. [Google Scholar] [CrossRef]
- Zeng, X.; Tao, W.-K.; Zhang, M.; Hou, A.Y.; Xie, S.; Lang, S.; Li, X.; Starr, D.; Li, X.; Simpson, J. An indirect effect of ice nuclei on atmospheric radiation. J. Atmos. Sci. 2009, 66, 41–61. [Google Scholar] [CrossRef]
- Zeng, X.; Tao, W.-K.; Matsui, T.; Xie, S.; Lang, S.; Zhang, M.; Starr, D.; Li, X. Estimating the Ice Crystal Enhancement Factor in the Tropics. J. Atmos. Sci. 2011, 68, 1424–1434. [Google Scholar] [CrossRef]
- Zeng, X.; Tao, W.-K.; Powell, S.W.; Houze, R.A., Jr.; Ciesielski, P.; Guy, N.; Pierce, H.; Matsui, T. A comparison of the water budgets between clouds from AMMA and TWP-ICE. J. Atmos. Sci. 2013, 70, 487–503. [Google Scholar] [CrossRef]
- Fletcher, N.H. The Physics of Rain Clouds; Cambridge University Press: Cambridge, UK, 1962; p. 386. [Google Scholar]
- DeMott, P.J.; Hill, T.C.J.; McCluskey, C.S.; Prather, K.A.; Collins, D.B.; Sullivan, R.C.; Ruppel, M.J.; Mason, R.H.; Irish, V.E.; Lee, T.; et al. Sea spray aerosol as a unique source of ice nucleating particles. Proc. Natl. Acad. Sci. USA 2016, 113, 5797–5803. [Google Scholar] [CrossRef]
- Roberts, P.; Hallett, J. A laboratory study of the ice nucleating properties of some mineral particulates. Q. J. R. Meteorol. Soc. 1968, 94, 25–34. [Google Scholar] [CrossRef]
- Edwards, G.R.; Evans, L.F. The mechanism of activation of ice nuclei. J. Atmos. Sci. 1971, 28, 1443–1447. [Google Scholar] [CrossRef]
- Zeng, X.; Heymsfield, A.J.; Ulanowski, Z.; Neely III, R.R.; Li, X.; Gong, J.; Wu, D.L. The radiative effect on cloud microphysics from the Arctic to the Tropics. Bull. Am. Meteorol. Soc. 2022, 103, E2108–E2129. [Google Scholar] [CrossRef]
- Fuchs, Z.; Raymond, D.J. Large-scale modes in a rotating atmosphere with radiative–convective instability and WISHE. J. Atmos. Sci. 2005, 62, 4084–4094. [Google Scholar] [CrossRef]
- Fuchs, Ž.; Raymond, D.J. A simple model of intraseasonal oscillations. J. Adv. Model. Earth Syst. 2017, 9, 1195–1211. [Google Scholar] [CrossRef]
- Emanuel, K.A. Slow modes of the equatorial waveguide. J. Atmos. Sci. 2020, 77, 1575–1582. [Google Scholar] [CrossRef]
- Wang, S.; Sobel, A.H. A unified moisture mode theory for the Madden–Julian oscillation and the boreal summer intraseasonal oscillation. J. Clim. 2022, 35, 1267–1291. [Google Scholar] [CrossRef]
- Emanuel, K.A. An air-sea interaction theory for tropical cyclones. Part I: Steady state maintenance. J. Atmos. Sci. 1986, 43, 585–604. [Google Scholar] [CrossRef]
- Rotunno, R.; Emanuel, K.A. An air-sea interaction theory for tropical cyclones. Part II: Evolutionary study using a non-hydrostatic axisymmetric numerical model. J. Atmos. Sci. 1987, 44, 542–561. [Google Scholar] [CrossRef]
- Yano, J.-I.; Emanuel, K.A. An improved model of the equatorial troposphere and its coupling with the stratosphere. J. Atmos. Sci. 1991, 48, 377–389. [Google Scholar] [CrossRef]
- Emanuel, K.A. The behavior of a simple hurricane model using a convective scheme based on subcloud-layer entropy equilibrium. J. Atmos. Sci. 1995, 52, 3960–3968. [Google Scholar] [CrossRef]
- Raymond, D.J. Regulation of moist convection over the west Pacific warm pool. J. Atmos. Sci. 1995, 52, 3945–3959. [Google Scholar] [CrossRef]
- Takayabu, Y. Large-scale cloud disturbances associated with equatorial waves. Part II: Western-propagating inertio-gravity waves. J. Meteorol. Soc. Jpn. 1994, 72, 451–465. [Google Scholar] [CrossRef]
- Chen, S.S.; Houze, R.A., Jr.; Mapes, B.E. Mutiscale variability of deep convection in relation to large-scale circulation in TOGA COARE. J. Atmos. Sci. 1996, 53, 1380–1409. [Google Scholar] [CrossRef]
- Takayabu, Y.; Lau, K.M.; Sui, C.H. Observation of a quasi-two-day wave during TOGA COARE. Mon. Wea. Rev. 1996, 124, 1892–1913. [Google Scholar] [CrossRef]
- Haertel, P.T.; Johnson, R.H. Two-day disturbances in the equatorial western Pacific. Q. J. R. Meteorol. Soc. 1998, 124, 615–636. [Google Scholar] [CrossRef]
- Bretherton, C.S.; Blossey, P.N.; Khairoutdinov, M. An energy-balance analysis of deep convective self-aggregation above uniform SST. J. Atmos. Sci. 2005, 62, 4273–4292. [Google Scholar] [CrossRef]
- Zeng, X.; Tao, W.-K.; Houze, R.A., Jr. Modeling Mesoscale Convective Systems in a Highly Simplified Environment. The First Science Team Meeting of the Atmospheric System Research (ASR) Program. Bethesda, Maryland. 15–19 March 2010 . Available online: http://asr.science.energy.gov/meetings/stm/posters/poster_pdf/2010/P000163.pdf (accessed on 10 January 2023).
- Barnston, A.G.; Tippett, M.K.; L’Heureux, M.L.; Li, S.; DeWitt, D.G. Skill of real-time seasonal ENSO model predictions during 2002-2011: Is Our Capability Increasing? Bull. Am. Meteorol. Soc. 2012, 93, 631–651. [Google Scholar] [CrossRef]
- Rotunno, R.; Klemp, J.B. The influence of shear-induced pressure gradient on thunderstorm motion. Mon. Wea. Rev. 1982, 110, 136–151. [Google Scholar] [CrossRef]
- Houze, R.A., Jr. 2004: Mesoscale convective systems. Rev. Geophys. 2004, 42, RG4003. [Google Scholar] [CrossRef]
- Zhang, M.H.; Lin, W.Y.; Klein, S.; Bacmeister, J.T.; Bony, S.; Cederwall, R.T.; Del Genio, A.D.; Hack, J.J.; Loeb, N.G.; Lohmann, U.; et al. Comparing clouds and their seasonal variations in 10 atmospheric general circulation models with satellite measurements. J. Geophy. Res. 2001, 110, D15S02. [Google Scholar] [CrossRef]
- Nam, C.; Bony, S.; Dufresne, J.-L.; Chepfer, H. The ‘too few, too bright’ tropical low-cloud problem in CMIP5 models. Geophys. Res. Lett. 2012, 39, L21801. [Google Scholar] [CrossRef]
- Jiang, J.H.; Su, H.; Zhai, C.; Perun, V.S.; Del Genio, A.; Nazarenko, L.S.; Donner, L.J.; Horowitz, L.; Seman, C.; Cole, J.; et al. Evaluation of cloud and water vapor simulations in CMIP5 climate models using NASA “A-Train” satellite observations. J. Geophys. Res. 2012, 117, D14105. [Google Scholar] [CrossRef]
- Jiang, J.H.; Su, H.; Zhai, C.; Wu, L.; Minschwaner, K.; Molod, A.M.; Tompkins, A.M. An assessment of upper troposphere and lower stratosphere water vapor in MERRA, MERRA2, and ECMWF re-analyses using Aura MLS observations. J. Geophys. Res. 2015, 120, 11468–11485. [Google Scholar] [CrossRef]
- Zhang, C. Madden-Julian Oscillation. Rev. Geophys. 2005, 43, RG2003. [Google Scholar] [CrossRef]
- Zeng, X.; Gong, J.; Li, X.; Wu, D.L. Modeling the radiative effect on microphysics in cirrus clouds against satellite observations. J. Geophys. Res. 2021, 126, e2020JD033923. [Google Scholar] [CrossRef]
- Henrici, P. Applied and Computational Complex Analysis, Vol II; Wiley: New York, NY, USA, 1977. [Google Scholar]
- Shen, B.-W. Limit Cycles, Closed Orbits and Poincare-Bendixson Theorem in 2D Systems. Course Mater. M537 2017, 102. [Google Scholar] [CrossRef]
- Matsuno, T. 1966: Quasi-geostrophic motions in the equatorial area. J. Meteorol. Soc. Jpn. 1966, 44, 25–43. [Google Scholar] [CrossRef]
- Yanai, M.; Maruyama, T. Stratospheric wave disturbances propagating over the equatorial Pacific. J. Meteorol. Soc. Japan 1966, 44, 291–294. [Google Scholar] [CrossRef]
- Wheeler, M.; Kiladis, G.N. Convectively coupled equatorial waves: Analysis of clouds and temperature in the wavenumber–frequency domain. J. Atmos. Sci. 1999, 56, 374–399. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, X. Atmospheric Instability and Its Associated Oscillations in the Tropics. Atmosphere 2023, 14, 433. https://doi.org/10.3390/atmos14030433
Zeng X. Atmospheric Instability and Its Associated Oscillations in the Tropics. Atmosphere. 2023; 14(3):433. https://doi.org/10.3390/atmos14030433
Chicago/Turabian StyleZeng, Xiping. 2023. "Atmospheric Instability and Its Associated Oscillations in the Tropics" Atmosphere 14, no. 3: 433. https://doi.org/10.3390/atmos14030433
APA StyleZeng, X. (2023). Atmospheric Instability and Its Associated Oscillations in the Tropics. Atmosphere, 14(3), 433. https://doi.org/10.3390/atmos14030433





